Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.2.1. Integrated Scheduling in Container Terminal
- (1)
- Integrated scheduling of QC and horizontal transportation equipment
- (2)
- Other integrated scheduling problems
1.2.2. Energy Saving and Emission Reduction in Container Terminal
1.3. Research Gaps
- (1)
- To mitigate QC delay, some studies opt for an excessive number of horizontal transport vehicles. However, this configuration provides limited actual effectiveness in reducing QC delay, diminishes the utilization rate of transport vehicles, and elevates transportation energy consumption;
- (2)
- Previous studies have arbitrarily determined the loading order of containers, overlooking the influence of the ship’s actual stowage on this order. When formulating the ship’s stowage plan, constraints such as preventing heavy containers from exerting pressure on lighter ones, heeling moment limitations, and avoiding placing containers in midair significantly impact the loading sequence;
- (3)
- Most studies uniformly define the loading and transportation speed of containers. However, they overlook the impact of container weight on equipment loading rates. The operational speed of equipment varies based on the weight category of containers;
- (4)
- Some studies address the operational process of QC and horizontal transportation equipment in distinct stages. This approach undermines the linkage between the two operational phases, hinders the flexible operation of equipment, and adversely affects the quality of the final scheduling scheme.
2. Problem Description and Formulation
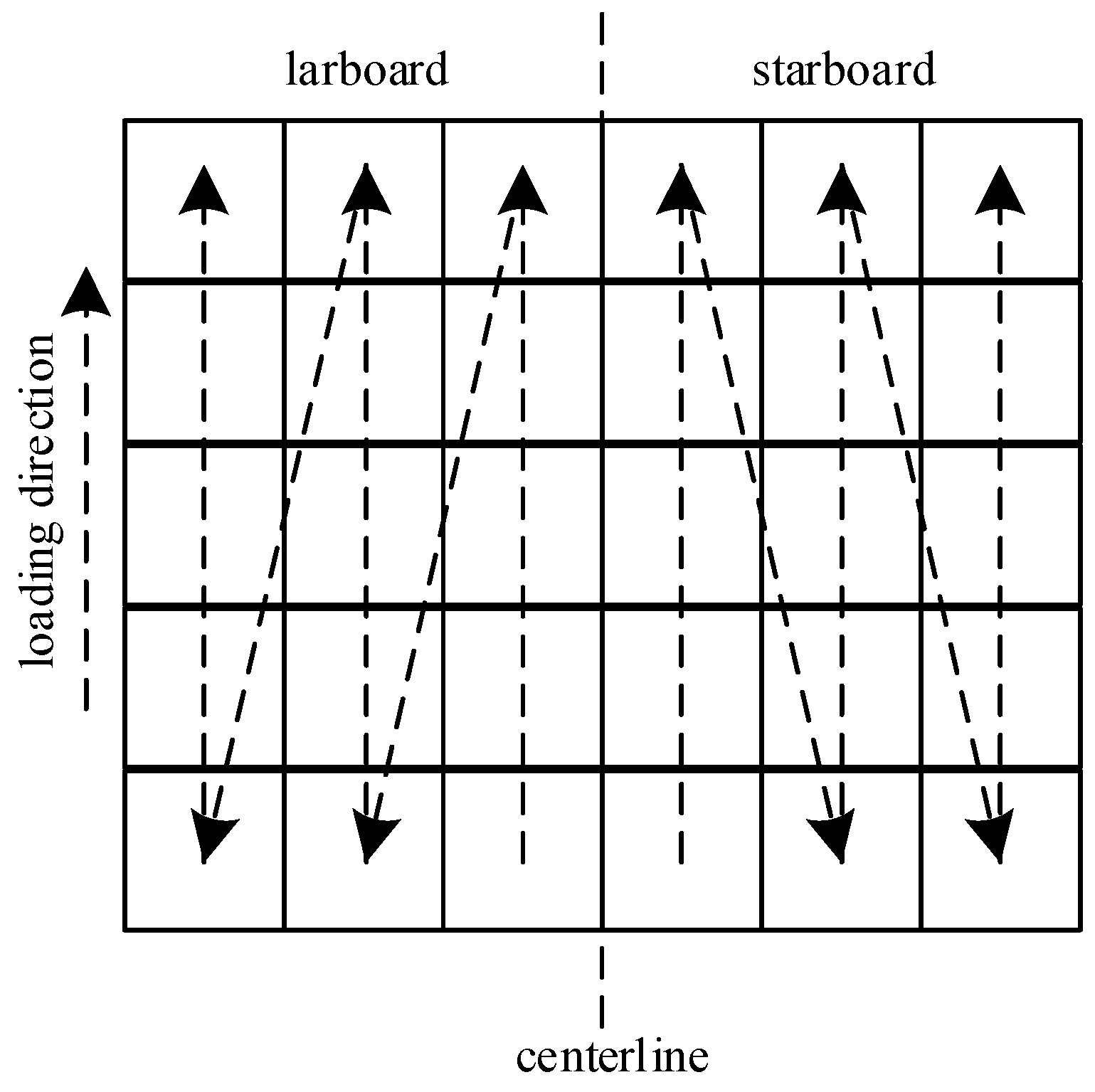
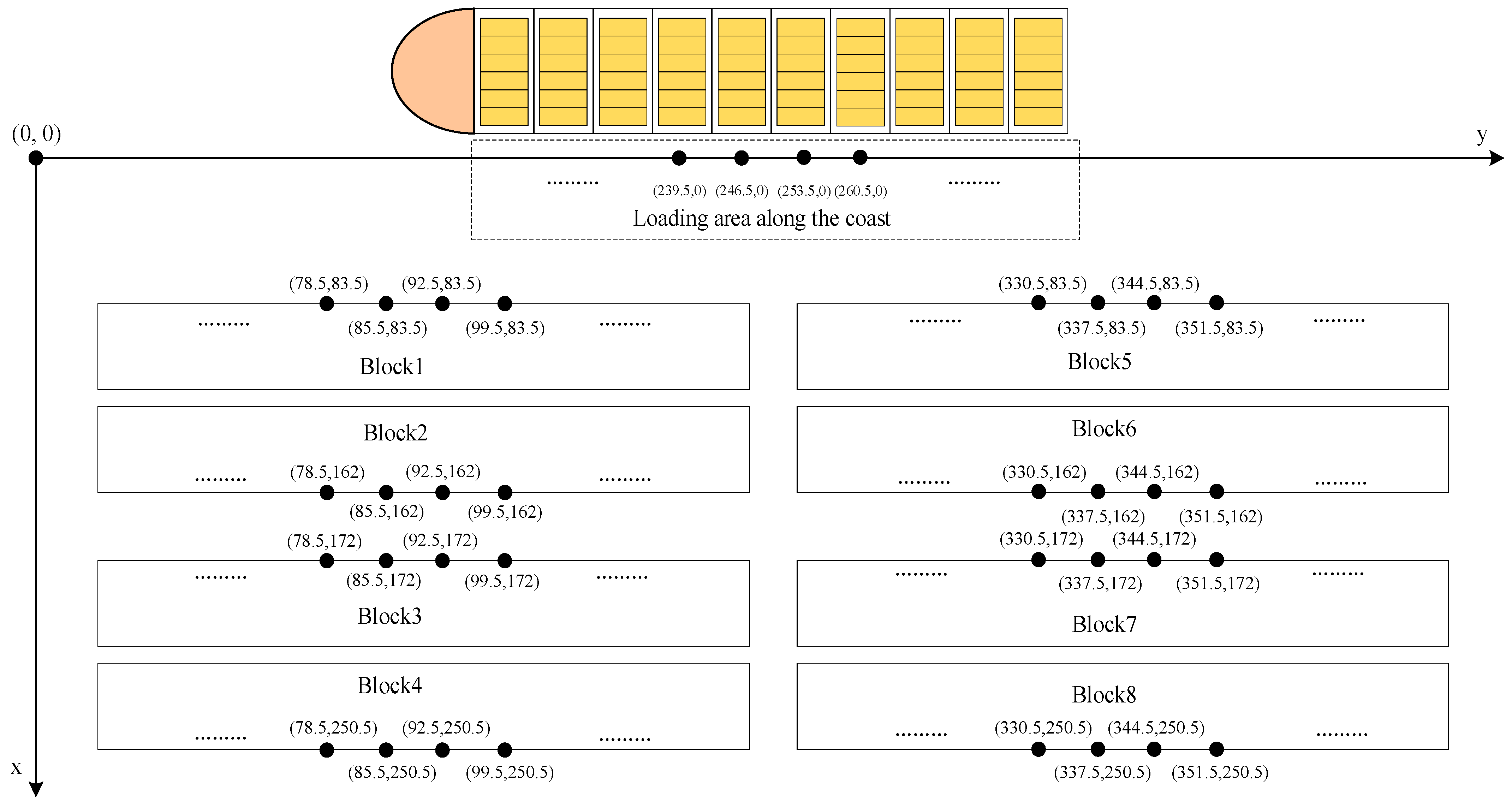
2.1. Problem Description
- (1)
- The stacking yard is equipped with an ample number of yard cranes, eliminating the need for IGVs to wait in the yard;
- (2)
- Details including the destination port, weight, and quantity of the containers to be loaded have been provided. All containers are of uniform size;
- (3)
- All IGVs transport containers with uniform power. The operation process maintains a consistent speed. Containers of varying weights are transported at distinct speeds. Path conflicts among IGVs are not taken into account;
- (4)
- All QCs load containers with uniform power and operate on a shared track. Loading containers of varying weights incurs distinct time durations. QCs maintain a minimum safe operating distance of one bay;
- (5)
- Unforeseen circumstances such as equipment failure, adverse weather effects, and temporary operational schedule adjustments are ignored.
2.2. Definition of Notations and Variables
2.3. Mathematical Model
2.3.1. Objective Function
2.3.2. Constraints
- (1)
- IGV operational constraints
- (2)
- QC operational constraints
- (3)
- Ship stowage constraints
3. Solution Design
3.1. Standard Sparrow Search Algorithm
3.2. Improved Sparrow Search Algorithm
3.2.1. Cat Chaotic Mapping
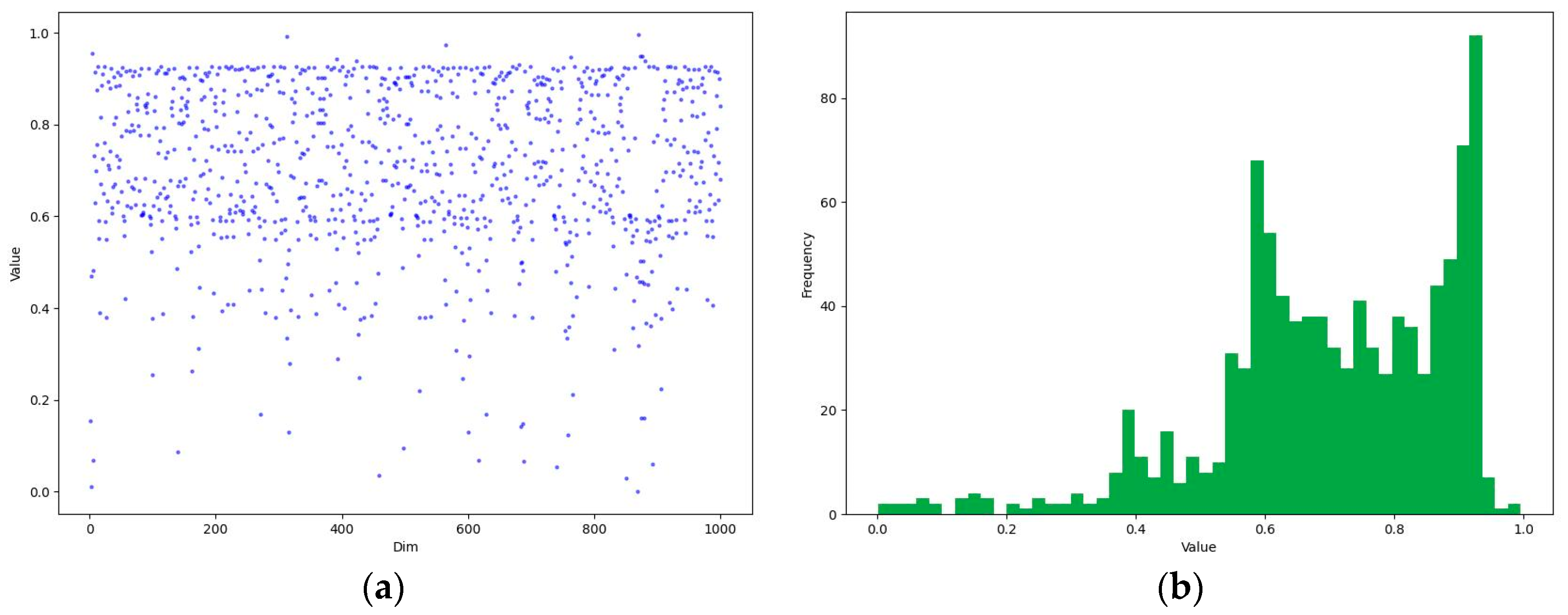
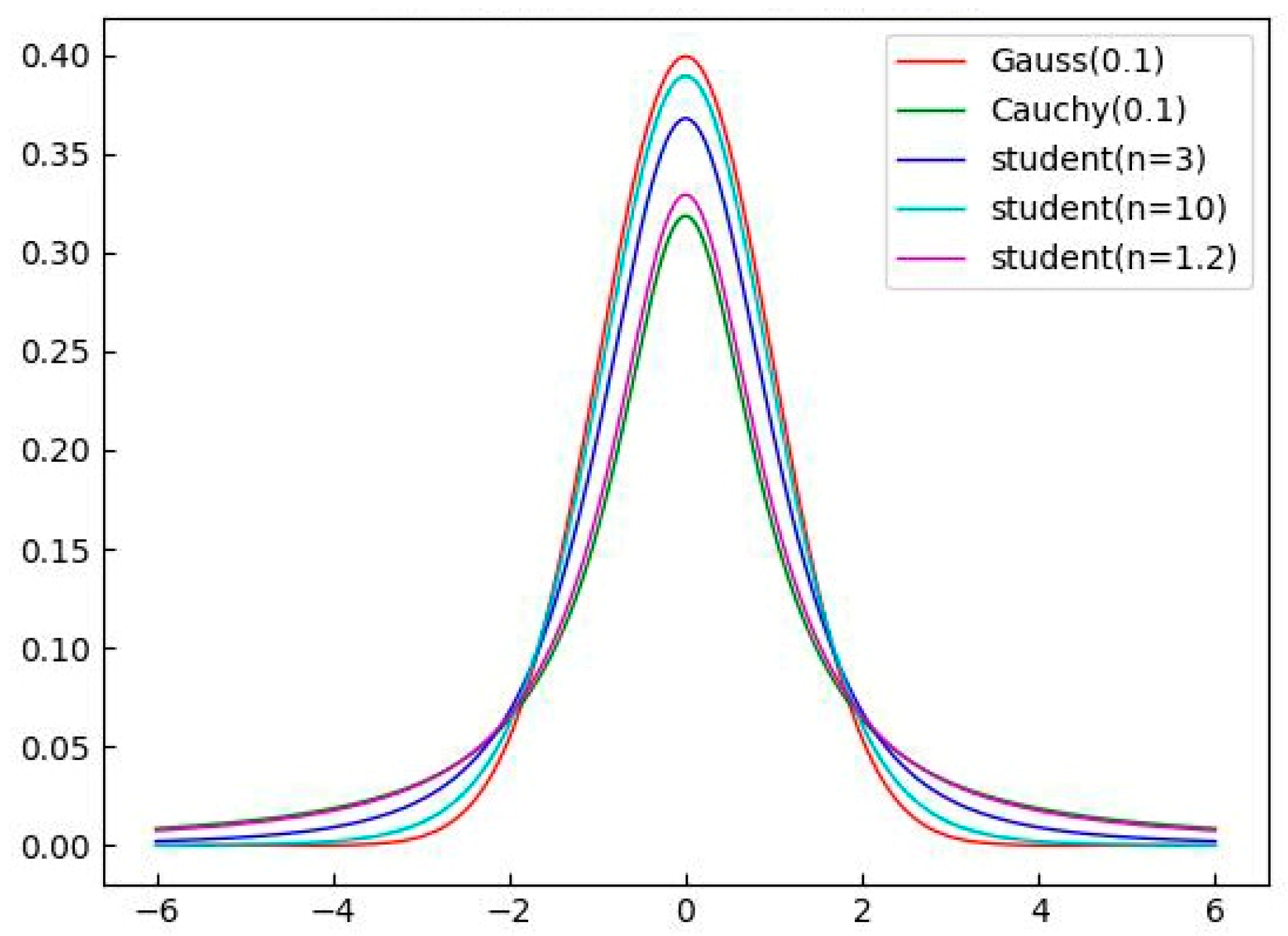
3.2.2. Adaptive t-Distribution Mutation
3.3. Encoding and Decoding
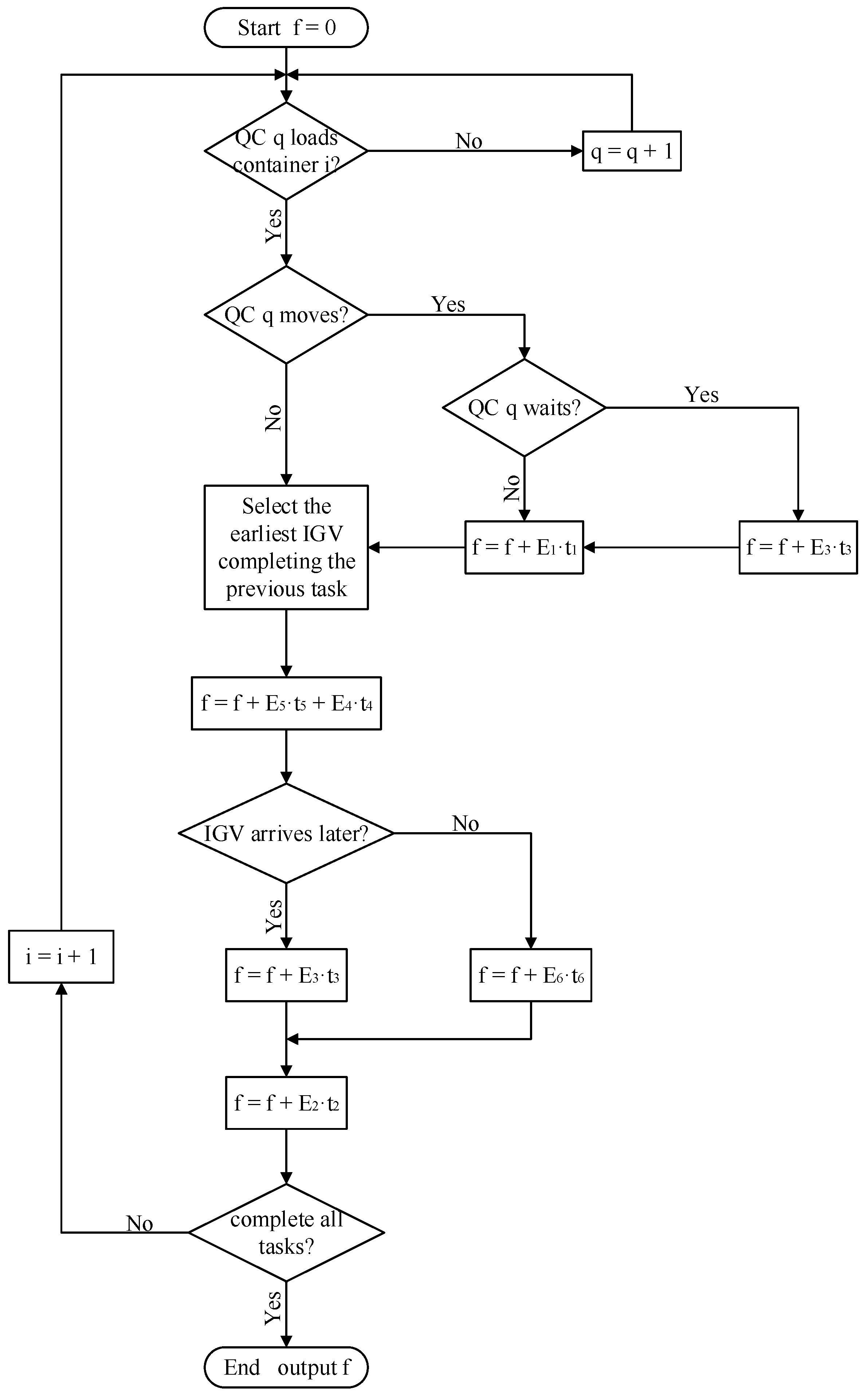
3.4. Overall Flow of DMSSA
4. Numerical Experiments
4.1. Instances Generation and Parameters Setting
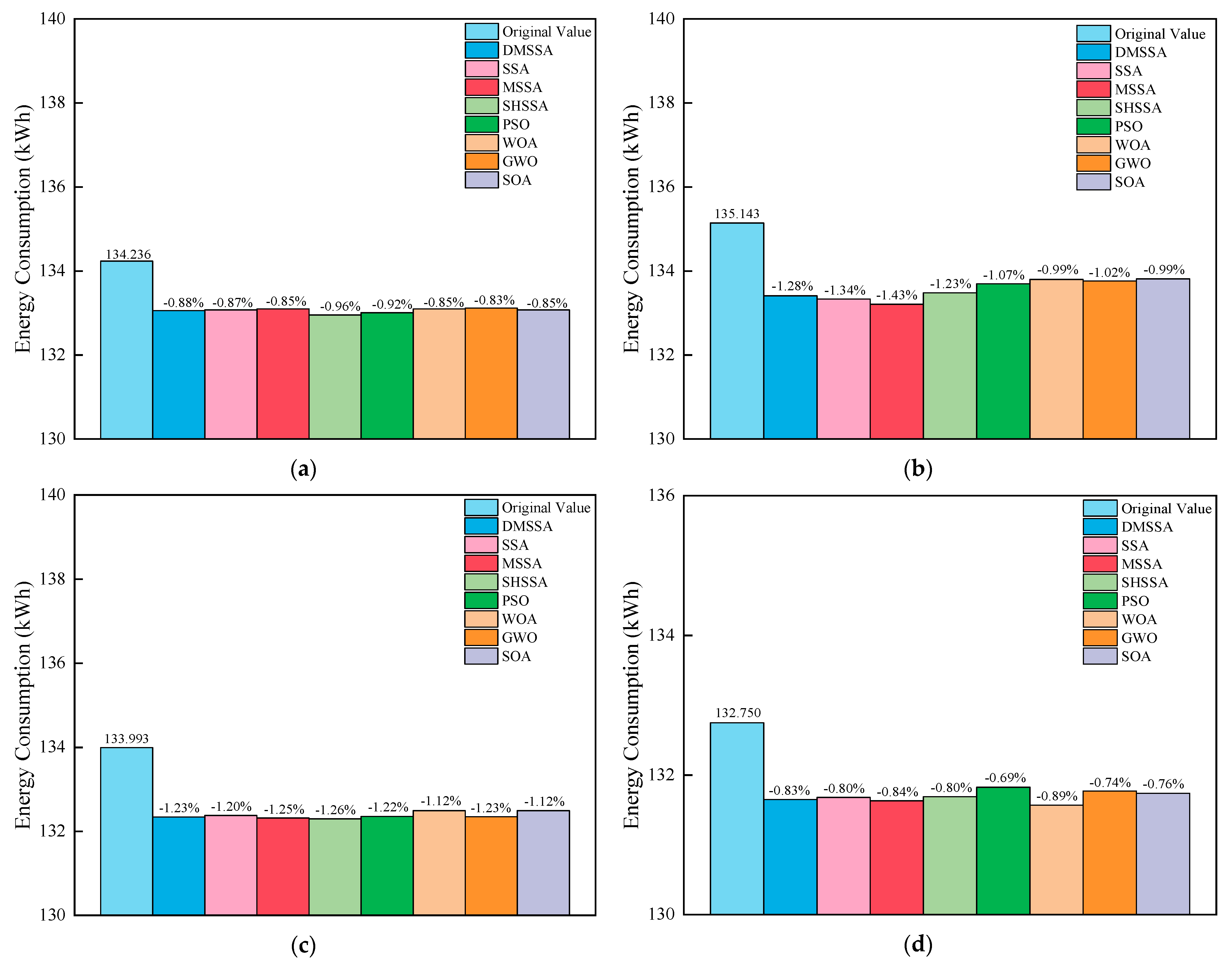
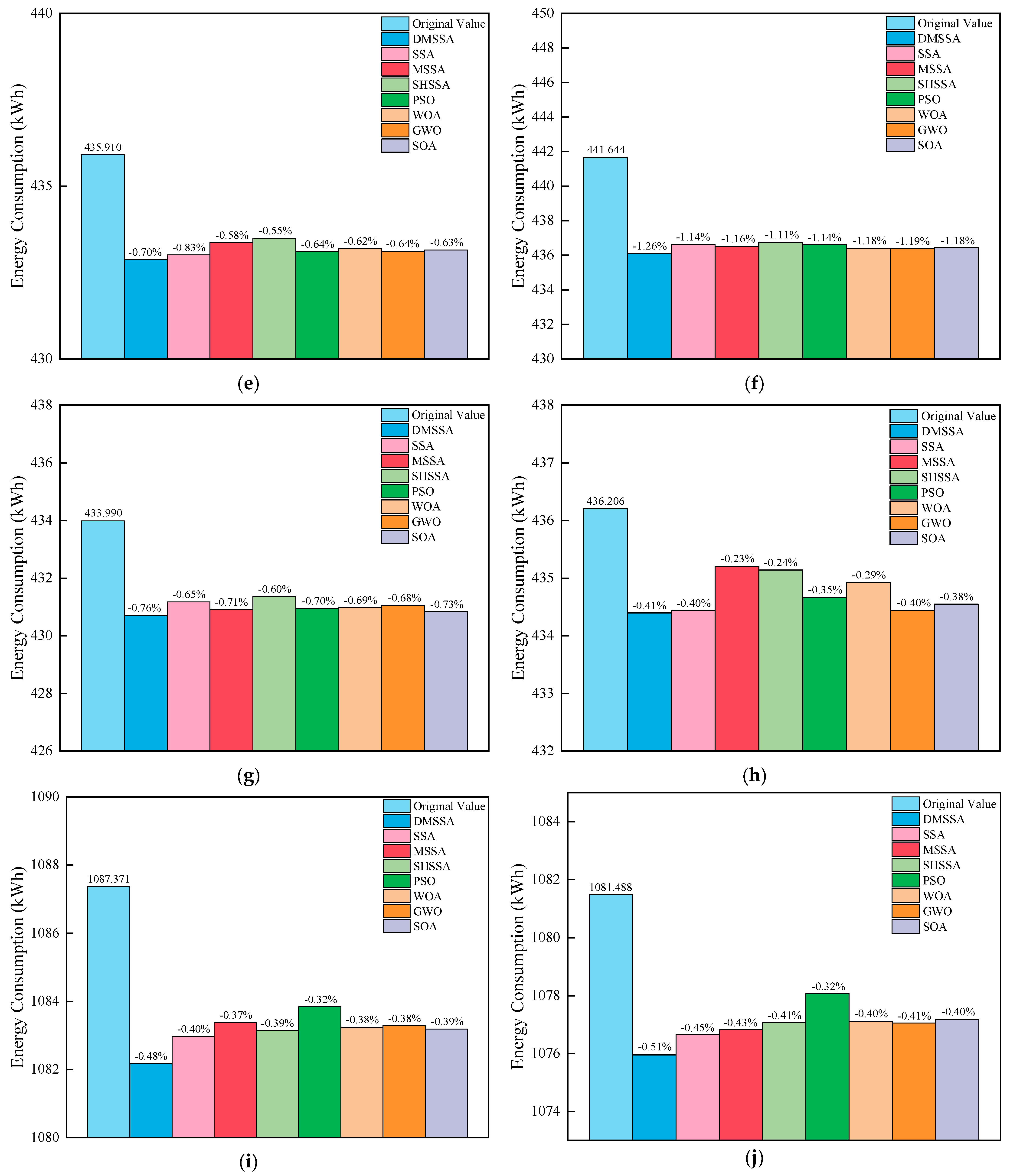
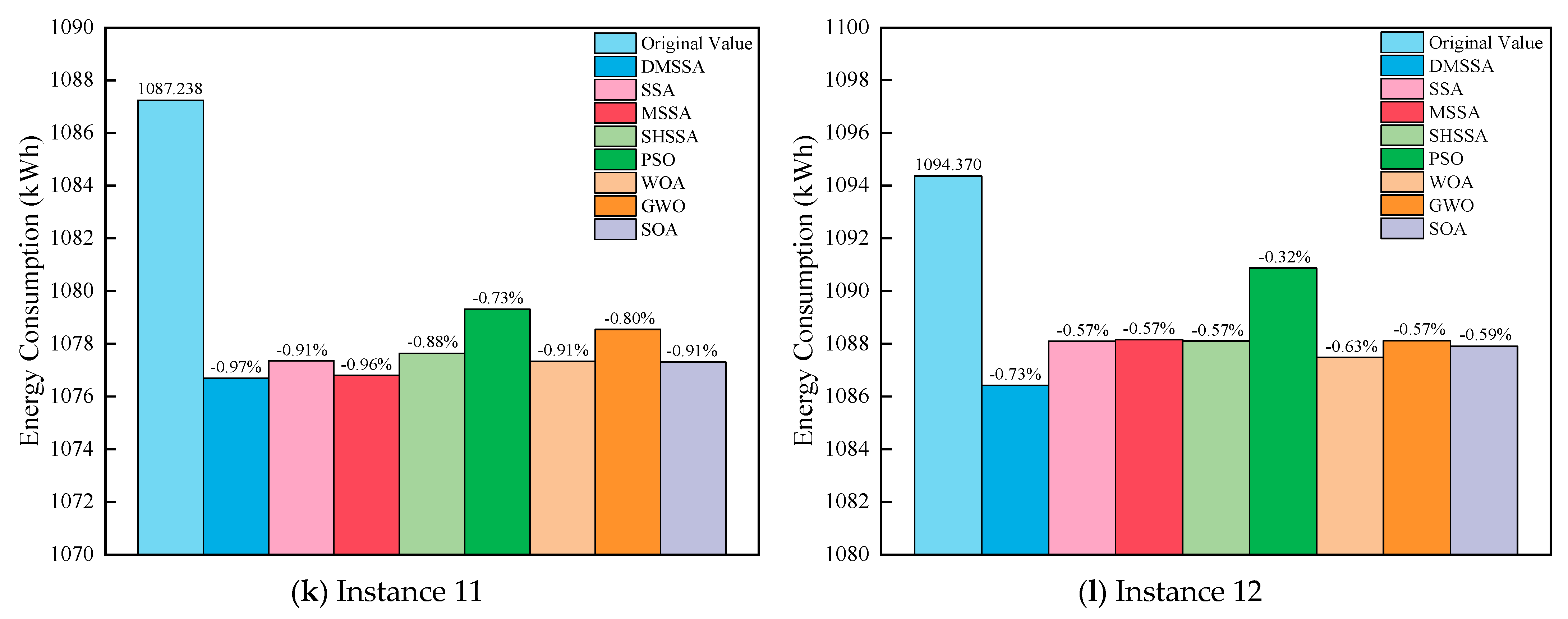
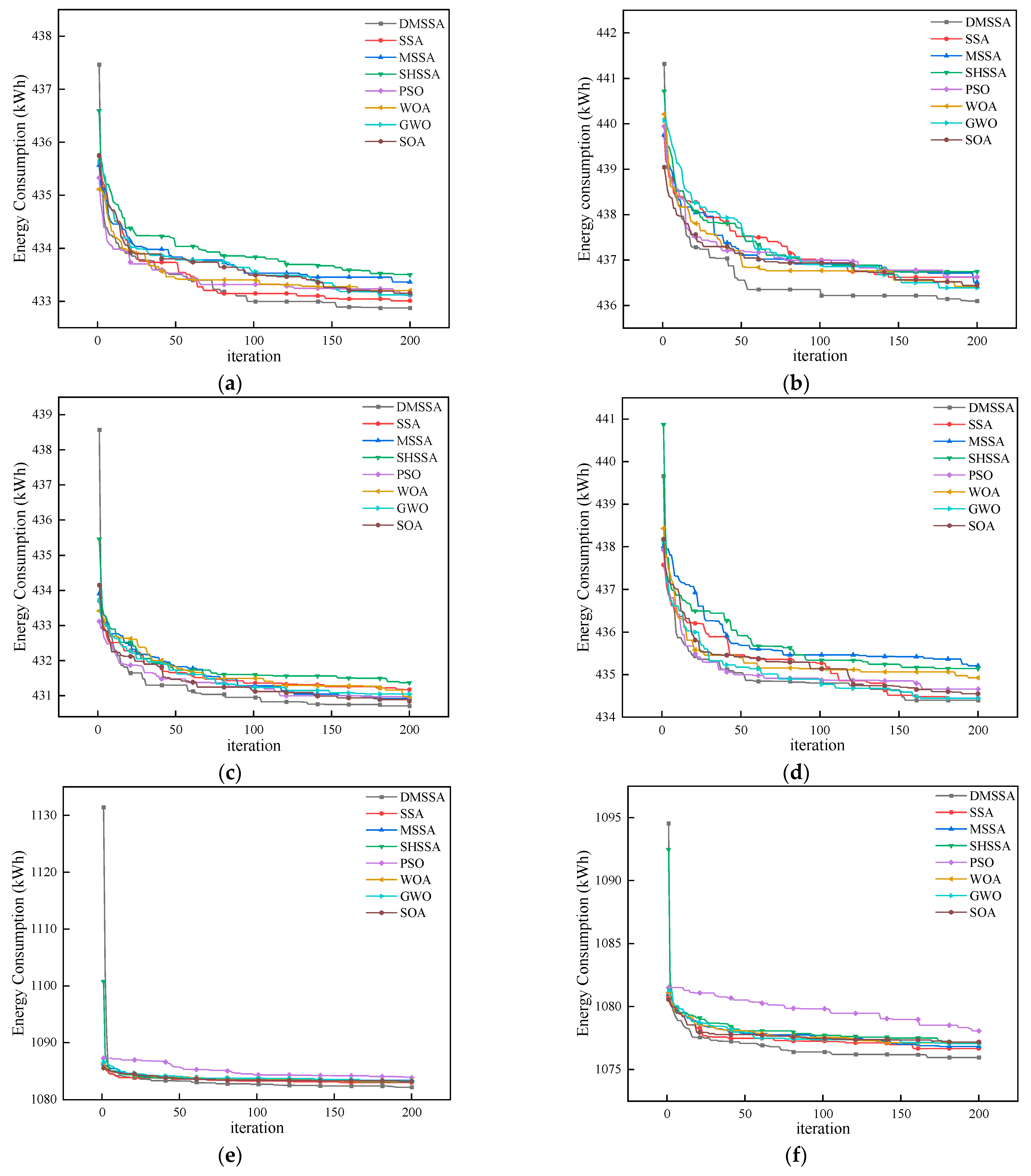
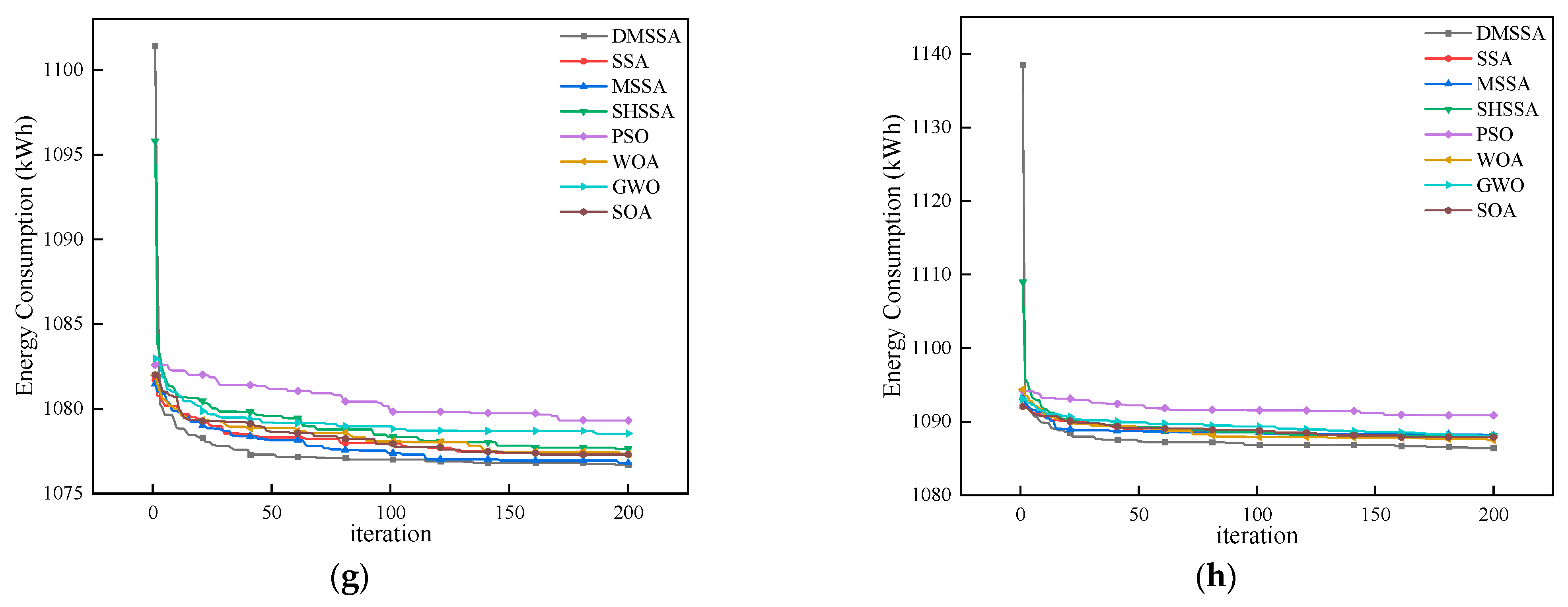
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, E.; El-Abbasy, M.S.; Zayed, T.; Alfalah, G.; Alkass, S. Synchronized scheduling model for container terminals using simulated double-cycling strategy. Comput. Ind. Eng. 2021, 154, 107118. [Google Scholar] [CrossRef]
- Alamoush, A.S.; Ballini, F.; Ölçer, A.I. Ports’ technical and operational measures to reduce greenhouse gas emission and improve energy efficiency: A review. Mar. Pollut. Bull. 2020, 160, 111508. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Lee, H.; Aluko, O. Multi-objective decision support to enhance environmental sustainability in maritime shipping: A review and future directions. Transp. Res. Part E Logist. Transp. Rev. 2015, 78, 3–18. [Google Scholar] [CrossRef]
- Homayouni, S.M.; Hong, T.S.; Ismail, N.; Ariffin, M. Optimization of Integrated Scheduling of Quay Cranes and Automated Guided Vehicles using Simulated Annealing Algorithm. In Proceedings of the 2011 International Conference on Industrial Engineering and Operations Management, Kuala Lumpur, Malaysia, 22–24 January 2011; pp. 22–24. [Google Scholar]
- Homayouni, S.; Tang, S.; Ismail, N.; Ariffin, M. Using simulated annealing algorithm for optimization of quay cranes and automated guided vehicles scheduling. Int. J. Phys. Sci. 2011, 6, 6286–6294. [Google Scholar] [CrossRef]
- Homayouni, S.M.; Tang, S.H.; Motlagh, O. A genetic algorithm for optimization of integrated scheduling of cranes, vehicles, and storage platforms at automated container terminals. J. Comput. Appl. Math. 2014, 270, 545–556. [Google Scholar] [CrossRef]
- Xiong, Z.; Han, X. Research on joint scheduling optimization with AGVs and quay cranes consider replacement processes. Highlights Sci. Eng. Technol. 2022, 9, 459–468. [Google Scholar] [CrossRef]
- Yin, Y.-Q.; Zhong, M.; Wen, X.; Ge, Y.-E. Scheduling quay cranes and shuttle vehicles simultaneously with limited apron buffer capacity. Comput. Oper. Res. 2023, 151, 106096. [Google Scholar] [CrossRef]
- Zhao, Q.; Ji, S.; Guo, D.; Du, X.; Wang, H. Research on cooperative scheduling of automated quayside cranes and automatic guided vehicles in automated container terminal. Math. Probl. Eng. 2019, 2019, 6574582. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Zhai, C. Joint configuration and scheduling optimization of the dual trolley quay crane and AGV for automated container terminal. J. Phys. Conf. Ser. 2020, 1486, 072080. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Ma, M. Optimizing configuration and scheduling of double 40 ft dual-trolley quay cranes and AGVs for improving container terminal services. J. Clean. Prod. 2021, 292, 126019. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Wang, H.; Guo, D. Research on integrated scheduling optimization of double-trolley quay crane and AGV in automated terminal. IOP Conf. Ser. Mater. Sci. Eng. 2020, 790, 012071. [Google Scholar] [CrossRef]
- Duan, Y.; Ren, H.; Xu, F.; Yang, X.; Meng, Y. Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles. J. Mar. Sci. Eng. 2023, 11, 1492. [Google Scholar] [CrossRef]
- Bouzekri, H.; Alpan, G.; Giard, V. Integrated Laycan and Berth Allocation and time-invariant Quay Crane Assignment Problem in tidal ports with multiple quays. Eur. J. Oper. Res. 2021, 293, 892–909. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An almost robust optimization model for integrated berth allocation and quay crane assignment problem. Omega 2021, 104, 102455. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. An exact robust approach for the integrated berth allocation and quay crane scheduling problem under uncertain arrival times. Eur. J. Oper. Res. 2021, 295, 499–516. [Google Scholar] [CrossRef]
- Wang, C.; Miao, L.; Zhang, C.; Wu, T.; Liang, Z. Robust optimization for the integrated berth allocation and quay crane assignment problem. Naval Res. Logist. (NRL) 2023. [Google Scholar] [CrossRef]
- Nourmohammadzadeh, A.; Voß, S. A robust multiobjective model for the integrated berth and quay crane scheduling problem at seaside container terminals. Ann. Math. Artif. Intell. 2022, 90, 831–853. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Yang, Y.; Wen, F.; Song, H. Integrated scheduling optimization of U-shaped automated container terminal under loading and unloading mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Cahyono, R.T.; Kenaka, S.P.; Jayawardhana, B. Simultaneous Allocation and Scheduling of Quay Cranes, Yard Cranes, and Trucks in Dynamical Integrated Container Terminal Operations. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8564–8578. [Google Scholar] [CrossRef]
- Cai, L.; Guo, W.; He, L.; Li, W. Port integrated scheduling under uncertain operation time and cascade effects: A complex network structure entropy solution. Comput. Ind. Eng. 2023, 182, 109435. [Google Scholar] [CrossRef]
- Naeem, D.; Eltawil, A.; Iijima, J.; Gheith, M. Integrated Scheduling of Automated Yard Cranes and Automated Guided Vehicles with Limited Buffer Capacity of Dual-Trolley Quay Cranes in Automated Container Terminals. Logistics 2022, 6, 82. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Zhang, Q.; Tan, K.C. Integrated Scheduling of Yard and Rail Container Handling Equipment and Internal Trucks in a Multimodal Port. IEEE Trans. Intell. Transp. Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Tan, C.; Yan, W.; Yue, J. Quay crane scheduling in automated container terminal for the trade-off between operation efficiency and energy consumption. Adv. Eng. Inform. 2021, 48, 101285. [Google Scholar] [CrossRef]
- Li, H.; Li, X. A Branch-and-Bound Algorithm for the Bi-Objective Quay Crane Scheduling Problem Based on Efficiency and Energy. Mathematics 2022, 10, 4705. [Google Scholar] [CrossRef]
- Zhong, L.; He, L.; Li, Y.; Zhang, Y.; Zhou, Y.; Li, W. Enhanced Multi-Objective Evolutionary Algorithm for Green Scheduling of Heterogeneous Quay Cranes Considering Cooperative Movement and Safety. J. Mar. Sci. Eng. 2023, 11, 1884. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Zhai, C. Joint configuration and scheduling optimization of a dual-trolley quay crane and automatic guided vehicles with consideration of vessel stability. Sustainability 2019, 12, 24. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.; Hegner Reinau, K. Energy-efficient and integrated allocation of berths, quay cranes, and internal trucks in container terminals. Sustainability 2020, 12, 3202. [Google Scholar] [CrossRef]
- Hong, C.; Guo, Y.; Wang, Y.; Li, T. The Integrated Scheduling Optimization for Container Handling by Using Driverless Electric Truck in Automated Container Terminal. Sustainability 2023, 15, 5536. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, M.; Wang, Z.; Xiao, Y. A Genetic Algorithm for Integrated Scheduling of Container Handing Systems at Container Terminals from a Low-Carbon Operations Perspective. Sustainability 2023, 15, 6035. [Google Scholar] [CrossRef]
- Zhong, Z.; Guo, Y.; Zhang, J.; Yang, S. Energy-aware Integrated Scheduling for Container Terminals with Conflict-free AGVs. J. Syst. Sci. Syst. Eng. 2023, 32, 411–443. [Google Scholar] [CrossRef]
- Sun, B.; Zhai, G.; Li, S.; Pei, B. Multi-resource collaborative scheduling problem of automated terminal considering the AGV charging effect under COVID-19. Ocean Coast. Manag. 2023, 232, 106422. [Google Scholar] [CrossRef]
- Jiang, M.; Feng, J.; Zhou, J.; Zhou, L.; Ma, F.; Wu, G.; Zhang, Y. Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost. Sustainability 2023, 15, 5018. [Google Scholar] [CrossRef]
- Zhen, L.; Yu, S.; Wang, S.; Sun, Z. Scheduling quay cranes and yard trucks for unloading operations in container ports. Ann. Oper. Res. 2019, 273, 455–478. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Gu, Q.; Jiang, B.; Chang, Z.; Li, X. An improved sparrow search algorithms for solving large-scale optimization problems. Control Dec. 2023, 38, 1960–1968. [Google Scholar] [CrossRef]
- Hu, S.; Wei, L. Improved Sparrow Search Algorithm Based on Hybrid Strategy. Comput. Technol. Dev. 2023, 33, 146–153, 160. [Google Scholar]
- Chai, Y.; Sun, X.; Ren, S. Chaotic Sparrow SearchAlgorithm Based on Multi-Directional Learning. Comput. Eng. Appl. 2023, 59, 81–91. [Google Scholar]
- Chen, G.; Zeng, G.; Huang, B.; Liu, J. Sparrow Search Algorithm Based on Spiral Exploration and Adaptive Hybrid Mutation. J. Chin. Comput. Syst. 2023, 44, 779–786. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]




| Literature | Problem | Objective | Method |
|---|---|---|---|
| Tan et al. [24] | QCSP | Time and Energy | CPLEX |
| Li et al. [25] | QCSP | Time and Energy | Branch-and-bound Algorithm |
| Zhong et al. [26] | QCSP | Time and Energy | EMOEA |
| Yue et al. [27] | QASP | Energy | Enumeration Algorithm |
| Karam et al. [28] | BACATAP | Energy | Lagrangian Solution |
| Hong et al. [29] | BACATAP | Time and Energy | Genetic Algorithm |
| Zheng et al. [30] | P_QAY | Emissions | Genetic Algorithm |
| Zhong et al. [31] | P_QAY | Energy | Bi-level Genetic Algorithm |
| Sun et al. [32] | P_QAY | Time and Energy | SA-GA |
| Jiang et al. [33] | BQCASP | Emissions | Adaptive Genetic Algorithm |
| Notation | Description |
|---|---|
| I | The set of containers. S and E denote the start and the end of the loading operation, respectively. IS = I ∪ [1]. IE = I ∪ [2,3]. |
| i, j | The index of each container. |
| Q | The set of QCs. |
| q | The index of each QC. |
| V | The set of IGVs. |
| v | The index of each IGV. |
| Ni | The moment when a QC completes loading container i. |
| Oi | The time required for a QC to load container i. |
| P | The time it takes for a quay crane to traverse one bay width. |
| M | A large enough positive number. |
| Ri | The moment when a IGV completes transporting container i. |
| Sil | The time required for an empty IGV to move from the QC operating area to the yard to receive container i. |
| Siu | The time required for a IGV to transport container i from the yard to the QC operating area. |
| t1 | The time required for a QC to load a light container. |
| t2 | The time required for a QC to load a heavy container. |
| v0 | The moving speed of IGV with no load. |
| v1 | The moving speed of IGV under light load. |
| v2 | The moving speed of IGV under heavy load. |
| a | The index of each bay. |
| UaS | The start time of the operation on bay a. |
| UaE | The end time of the operation on bay a. |
| A | The set of bays. S and E denote the start and end of the operation at the bays. AS = A ∪ [4]. AE = I ∪ [5]. |
| AF | The set of bays in the forward half of the ship. |
| AA | The set of bays in the back half of the ship. |
| lq | The first bay to be served by QC q. |
| B | The set of stacks in a bay. |
| b | The index of each stack. |
| BL | The set of stacks on the larboard side. |
| BR | The set of stacks on the starboard side. |
| C | The set of layers in a bay. |
| c | The index of each layer. |
| wi | The weight of container i. |
| wab | The weight of containers in stack b within bay a. |
| ei | Container i has a weight type, denoted by values 1 and 2, representing light and heavy containers. |
| f | The width of a container is 2.438 m. |
| g | The gap between containers is 0.3 m. |
| α | Moment sensitivity factor, taking the value of 10 t. |
| HM | Heeling moment. HM = (B − 1) (f + g) α/2. |
| LG | Maximum longitudinal weight difference. |
| E1 | Energy consumption per unit time for QC loading. |
| E2 | Energy consumption per unit time for QC waiting. |
| E3 | Energy consumption per unit time during QC waiting, attributed to IGV delays or disruptions by other QCs. |
| E4 | Energy consumption per unit time for IGV transporting a container. |
| E5 | Energy consumption per unit time for IGV movement without a load. |
| E6 | Energy consumption per unit time during IGV waiting caused by QC delay. |
| Variable | Description |
|---|---|
| Equal to 1 if QC q loads container j immediately after loading container i, and 0 otherwise. | |
| Equal to 1 if QC q loads container i, and 0 otherwise. | |
| Equal to 1 if IGV v transports container j immediately after transporting container i, and 0 otherwise. | |
| Equal to 1 if IGV v transports container i, and 0 otherwise. | |
| Equal to 1 if QC q operates on bay a, and 0 otherwise. | |
| Equal to 1 if QC q operates on bay a before bay a′, 0 otherwise. | |
| Equal to 1 if container i is loaded in position (a, b, c) and 0 otherwise. |
| Container | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xi | 0.12 | 0.34 | 0.32 | 0.67 | 1.44 | 1.56 | 2.87 | 2.64 | 3.54 | 3.78 | 4.22 | 5.33 |
| bay | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 6 |
| Container | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bay | 1 | 5 | 1 | 6 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 6 |
| Bay | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| QC | 1 | 2 | 3 | |||
| Loading sequence in bay | 1→3 | 6→5 | 8→7 | 9→10 | 2→11 | 4→12 |
| Loading sequence at QC | 1→3→6→5 | 8→7→9→10 | 2→11→4→12 | |||
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| v0 | 350 | m·min−1 | C | 5 | - |
| v1 | 280 | m·min−1 | E1 | 90.24 | kWh·(h·veh)−1 |
| v2 | 210 | m·min−1 | E2 | 70.18 | kWh·(h·veh)−1 |
| t1 | 111 | s | E3 | 49.6 | kWh·(h·veh)−1 |
| t2 | 92 | s | E4 | 21 | kWh·(h·veh)−1 |
| A | 10 | - | E5 | 14 | kWh·(h·veh)−1 |
| B | 6 | - | E6 | 9 | kWh·(h·veh)−1 |
| Instance | Size | I/Q/V | Energy Consumption (kWh) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DMSSA | SSA | MSSA | SHSSA | PSO | WOA | GWO | SOA | |||
| 1 | Small | 30/2/3 | 133.056 | 133.073 | 133.096 | 132.953 | 133.007 | 133.097 | 133.119 | 133.073 |
| 2 | 30/2/4 | 133.410 | 133.333 | 133.207 | 133.482 | 133.696 | 133.802 | 133.762 | 133.811 | |
| 3 | 30/3/4 | 132.342 | 132.379 | 132.320 | 132.299 | 132.357 | 132.495 | 132.350 | 132.495 | |
| 4 | 30/3/5 | 131.651 | 131.682 | 131.632 | 131.692 | 131.828 | 131.570 | 131.772 | 131.739 | |
| 5 | Medium | 100/3/4 | 432.873 | 433.008 | 433.362 | 433.498 | 433.107 | 433.202 | 433.121 | 433.153 |
| 6 | 100/3/6 | 436.097 | 436.618 | 436.510 | 436.745 | 436.627 | 436.412 | 436.389 | 436.438 | |
| 7 | 100/4/6 | 430.709 | 431.175 | 430.920 | 431.370 | 430.958 | 430.978 | 431.050 | 430.837 | |
| 8 | 100/4/8 | 434.398 | 434.442 | 435.208 | 435.142 | 434.661 | 434.924 | 434.444 | 434.550 | |
| 9 | Large | 250/5/6 | 1082.168 | 1082.977 | 1083.385 | 1083.148 | 1083.841 | 1083.242 | 1083.287 | 1083.191 |
| 10 | 250/5/7 | 1075.953 | 1076.656 | 1076.820 | 1077.068 | 1078.063 | 1077.120 | 1077.055 | 1077.175 | |
| 11 | 250/5/8 | 1076.705 | 1077.349 | 1076.810 | 1077.641 | 1079.315 | 1077.335 | 1078.541 | 1077.305 | |
| 12 | 250/5/10 | 1086.418 | 1088.097 | 1088.156 | 1088.103 | 1090.878 | 1087.487 | 1088.109 | 1087.907 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Liang, X.; Zhang, Y.; Tang, K.; Li, W. Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal. J. Mar. Sci. Eng. 2024, 12, 376. https://doi.org/10.3390/jmse12030376
Luo Y, Liang X, Zhang Y, Tang K, Li W. Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal. Journal of Marine Science and Engineering. 2024; 12(3):376. https://doi.org/10.3390/jmse12030376
Chicago/Turabian StyleLuo, Yuedi, Xiaolei Liang, Yu Zhang, Kexin Tang, and Wenting Li. 2024. "Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal" Journal of Marine Science and Engineering 12, no. 3: 376. https://doi.org/10.3390/jmse12030376
APA StyleLuo, Y., Liang, X., Zhang, Y., Tang, K., & Li, W. (2024). Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal. Journal of Marine Science and Engineering, 12(3), 376. https://doi.org/10.3390/jmse12030376






