Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies
Abstract
:1. Introduction
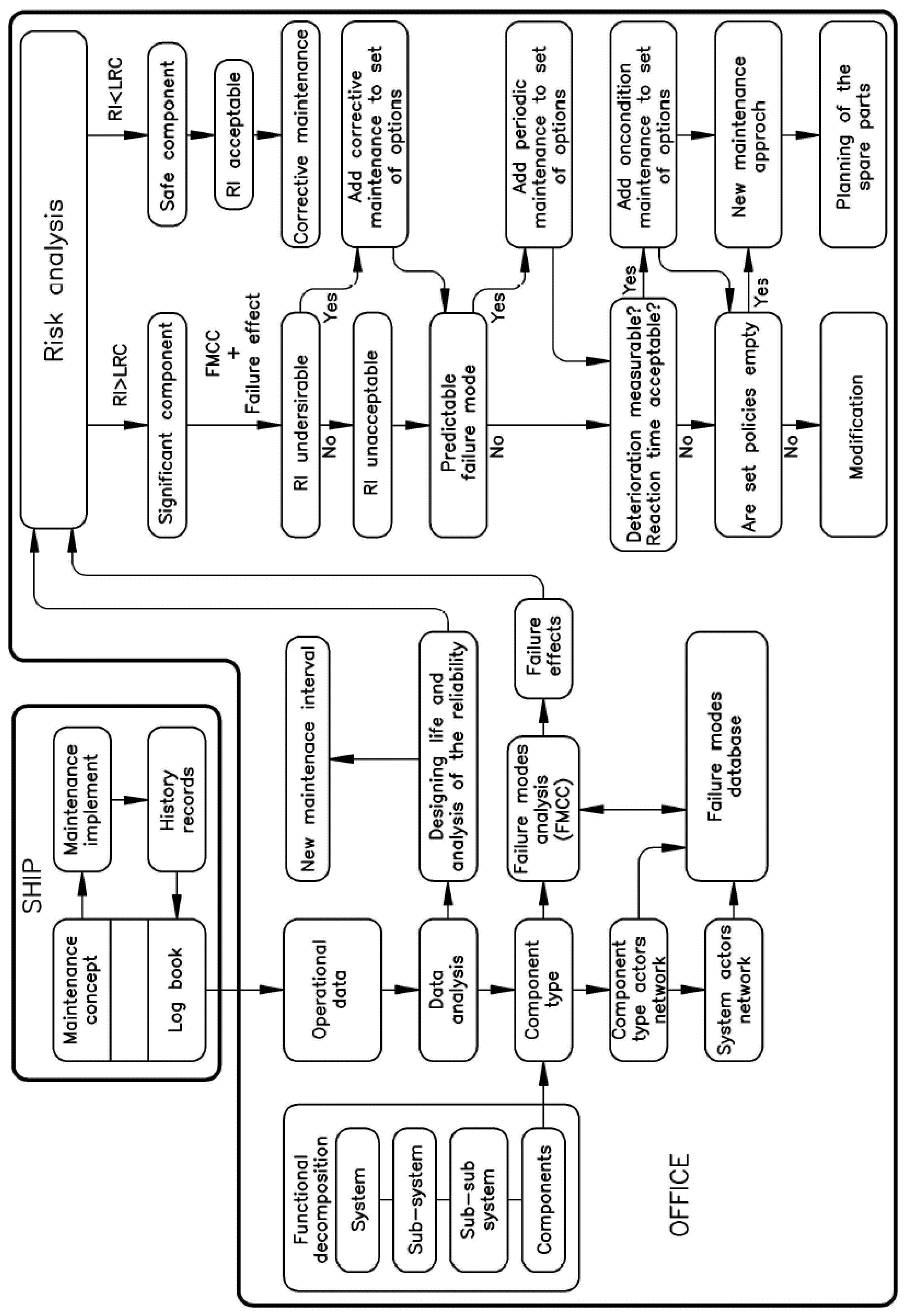
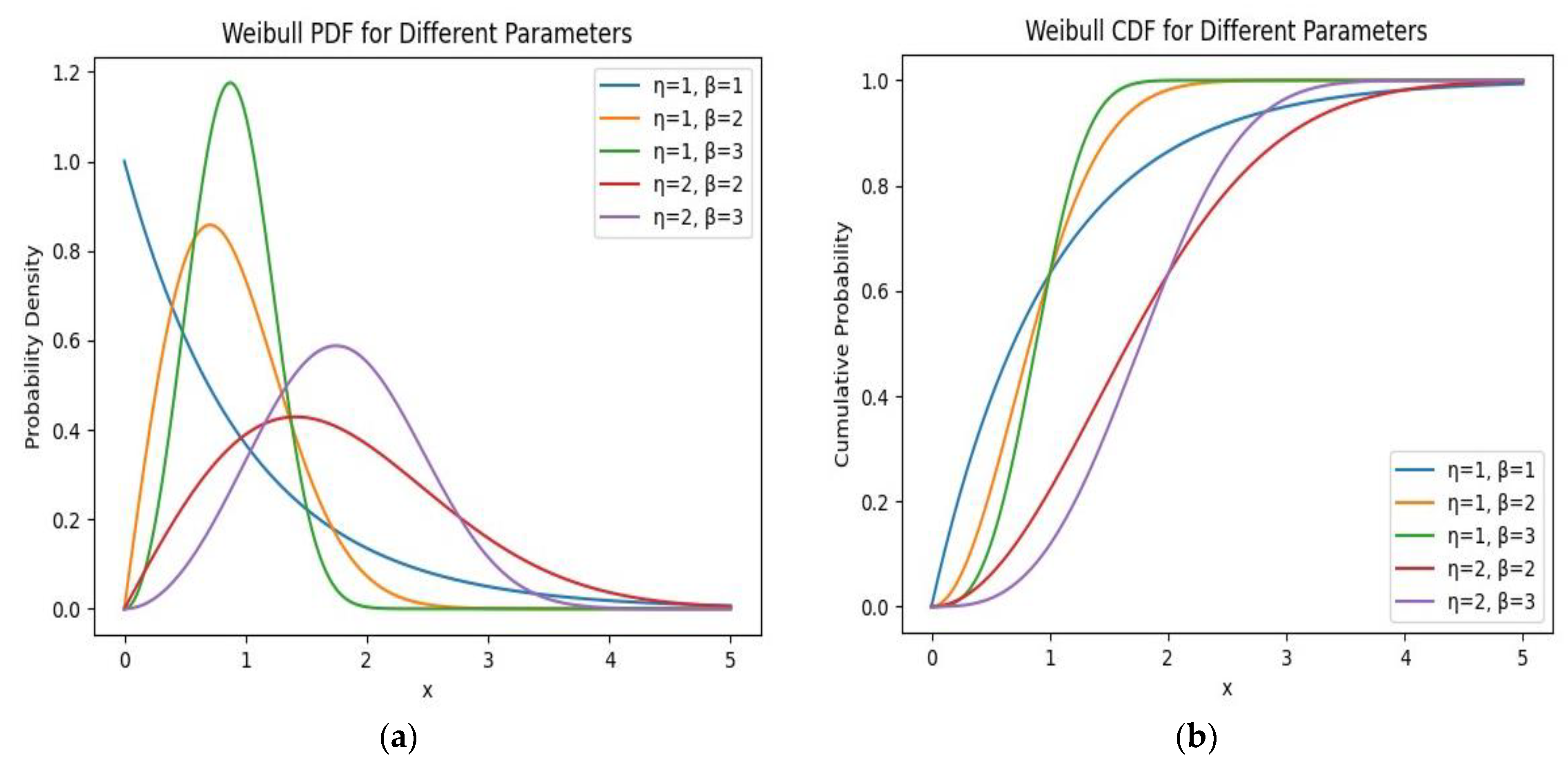
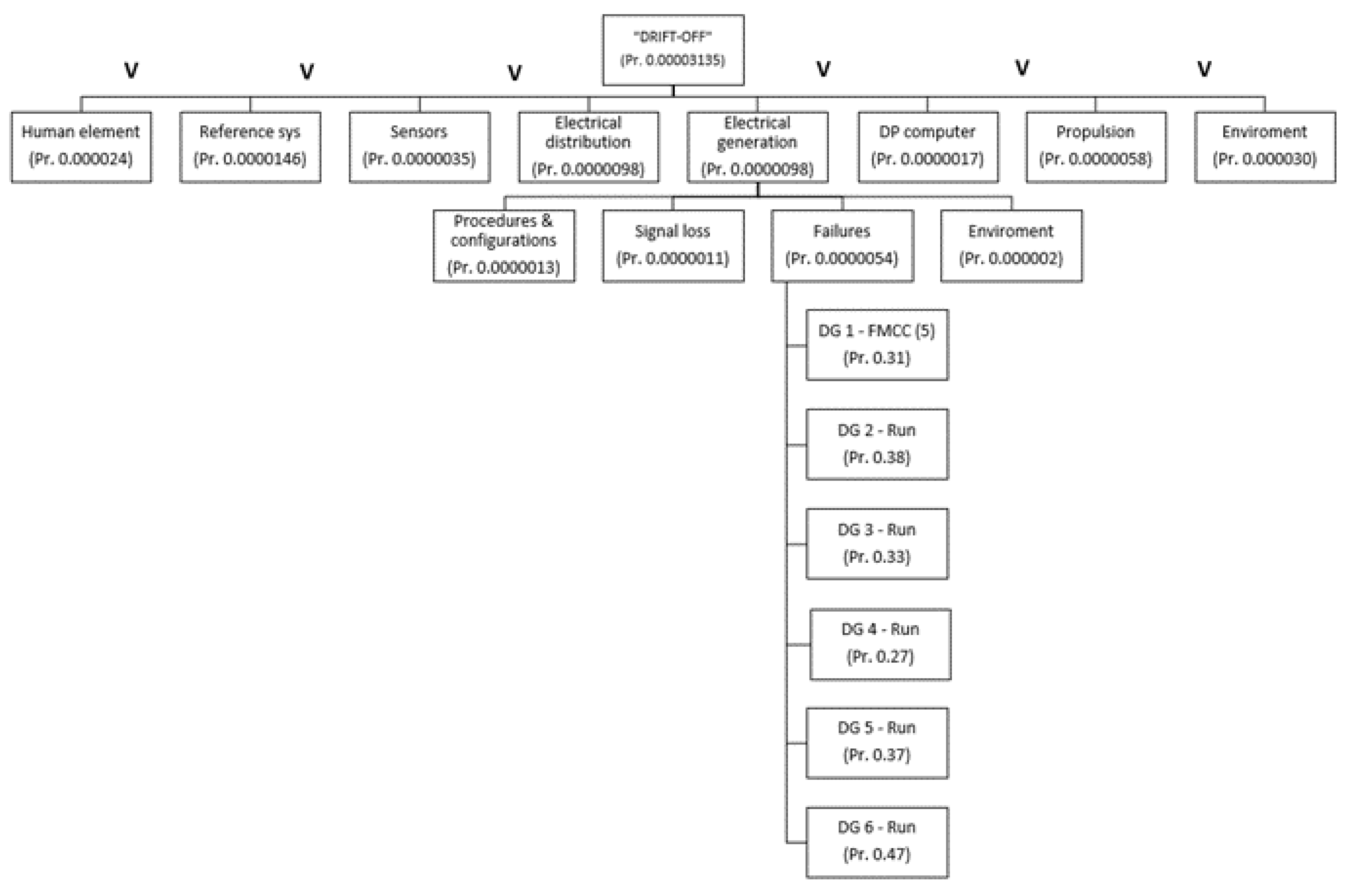
- Operational data analysis—consists of identifying components and analysing their failure causes, i.e., creating a network of actors and Failure Mode Cause Combination (FMCC). Based on the available historical data of failures, the predictability of failures (p) is calculated based on the Weibull distribution and its parameters ratio (η), shape (β), and position (t0). The position parameter (t0) represents the minimum lifetime of the component, i.e., the so-called initial time, which is assumed to be 0 in our case because the occurrence of defects is possible immediately after the installation of the component. Therefore, the two-parameter Weibull distribution (W(η, β)) is used for the calculation.
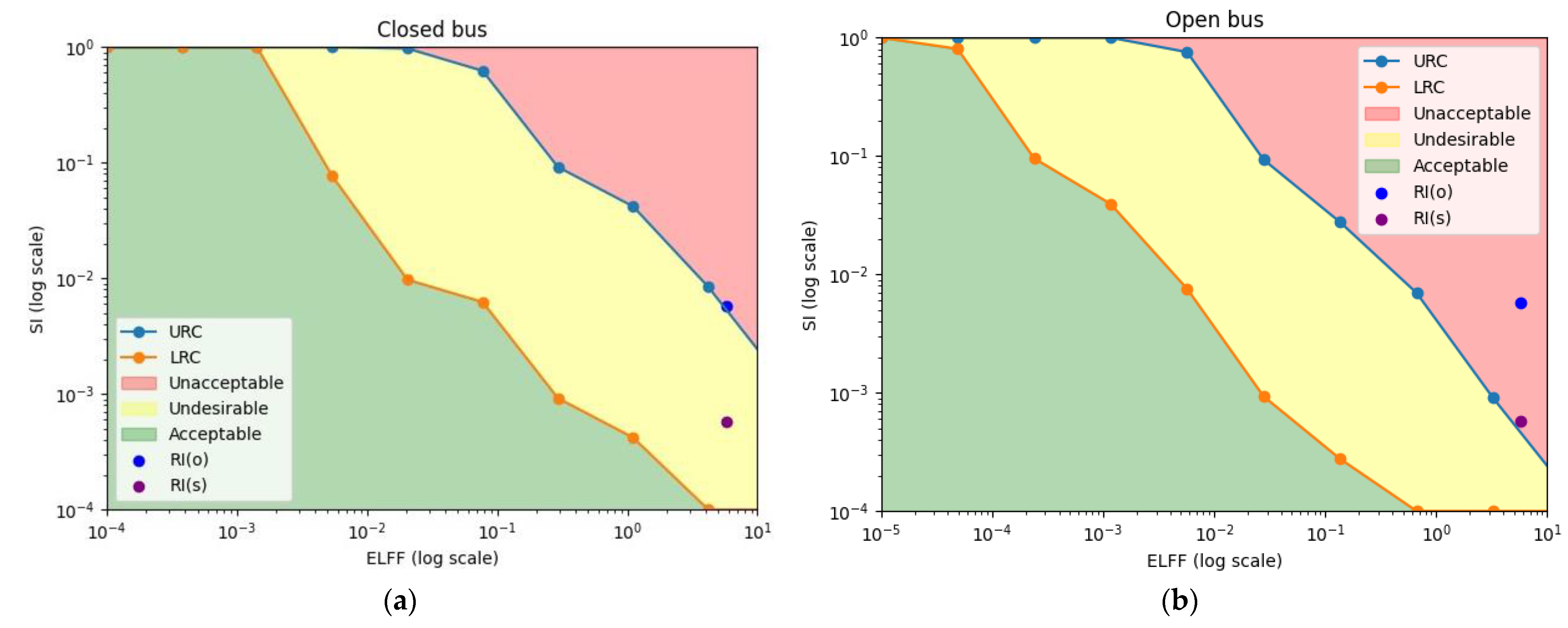
- Risk analysis—in which the limits of the lower risk criterion (LRC), upper risk Criterion (URC) and the risk index (RI) are defined as the mathematical probability of occurrence and consequences of the event. This consequence of the event is expressed as the significance index parameter (SI) and the probability of occurrence is expressed as the Expected Life Failure Frequency (ELFF).
- The selection of the maintenance concept is based on the value of the obtained RI and the predictability, i.e., on the parameters of the shape and ratio of the Weibull distribution.
2. Methodology and Data Source
2.1. Data Source and Characteristics of the Drillship
2.2. Calculation Methodology
2.2.1. Operational Data Analysis
2.2.2. Risk Analysis
3. Analysis Results
3.1. Adjustment of Maintenance Intervals Based on Operating Data Analysis
3.2. Risk Analysis
4. Results Review
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roberts, K.H. Managing High Reliability Organizations. Calif. Manag. Rev. 1990, 32, 101–113. [Google Scholar] [CrossRef]
- Sullivan, J.; Beach, R. Understanding system development and operation in high reliability organizations: A conceptual model. In Proceedings of the First Security Conference, Richmond, VA, USA, 23 April 2003. [Google Scholar]
- North Highland. Principle of High Reliability Organizations. Available online: https://www.northhighland.com/sites/default/files/2020-01/WP_Principles_Of_High_Reliability_Orgs.pdf (accessed on 28 February 2022).
- Lower & Associates. Building High Reliability Organization. Available online: https://www.lowersrisk.com/lp/building-a-high-reliability-organization (accessed on 1 March 2022).
- Vučinić, B. MA-CAD Maintenance Concept Adjustment & Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 20 September 1994. [Google Scholar]
- Bukša, A. Modeliranje Održavanja Brodskog Porivnog Sustava. Ph.D. Thesis, Faculty of Maritime Studies, University of Rijeka, Rijeka, Croatia, 2005. [Google Scholar]
- Šegulja, I.; Bukša, A.; Tomas, V. Maintenance Interval Adjustment of Significant Ship Propulsion Components. Promet–Traffic–Traffico 2009, 21, 175–182. [Google Scholar] [CrossRef]
- Bukša, A.; Šegulja, I.; Tomas, V. Adjustment of Maintenance Approach for Improved Operability and Safety of Ship Navigation. Promet–Traffic–Traffico 2010, 22, 95–103. [Google Scholar] [CrossRef]
- Stazić, L.; Knežević, V.; Orović, J.; Mihanović, L. Maintenance Interval Adjustment Based on the Experience, Case Study of Marine Air Compressor System. Nase More 2019, 67, 146–152. [Google Scholar] [CrossRef]
- Andriulo, S.; Arleo, M.A.; de Carlo, F.; Gnoni, M.G.; Tucci, M. Effectivness of maintenance approaches for High Reliability Organiozations. IFAC-PapersOnline 2015, 48, 466–471. [Google Scholar] [CrossRef]
- Okoh, P.; Haugen, S. Improving the robustness and resilience properties on maintenance. Process Saf. Environ. Prot. 2015, 94, 212–226. [Google Scholar] [CrossRef]
- Okoh, P.; Haugen, S. The Effect of Maintenance Seen From Different Perspectives on Major Accident Risk. In Proceedings of the 2012 IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong, China, 10–13 December 2012. [Google Scholar]
- Herrera, I.A.; Hovden, J. Leading indicators applied to maintenance in the framework of resilience engineering: A conceptual approach. In Proceedings of the 3rd Resiliance Engineering Symposium, Antibes-Juan Les Pins, France, 28–30 October 2008. [Google Scholar]
- Engine Logbook extracts for drillship. Technical documentation, May 2009–December 2016.
- ABB Automation Technology Marine. Power Distribution Single Line Diagram 5500 kW Thrusters. Technical drawings, 2006.
- ISO 14224:2006; Petroleum, Petrochemical and Natural Gas Industries—Collection and Exchange of Reliability and Maintenance Data for Equipment. 2nd ed. International Organization for Standardization: Geneva, Switzerland, 2006.
- Kızılersü, A.; Kreer, M.; Thomas, A.W. The Weibull Distribution. Significance 2018, 15, 10–11. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Modarres, M.; Kaminskiy, M.P.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- MAN Diesel SE. Engine Operating Instruction, Engine 14V32/40; Technical documentation; MAN Diesel SE: Augsburg, Germany, 2002. [Google Scholar]
- Varela, Z.S.; Falces, D.B.; Barrena, J.L.L.; Solaeche, M.A.G. Risk Analysis of DP Incidents during Drilling Operations. Trans. Marit. Sci. 2021, 10, 84–100. [Google Scholar] [CrossRef]
- Journal of Petroleum Technology. Lifetime Revenue vs. Construction Cost—A Metric for Assessing Drillship Retirements. Available online: https://jpt.spe.org/lifetime-revenue-vs-construction-cost-metric-assessing-drillship-retirements#:~:text=The%209.2%2Dyear%20average%20attrition,for%20the%2016%20semisubmersible%20retirements.&text=The%20five%20drillships%20retired%20so,by%20Valaris%20and%20Noble%20Drilling (accessed on 15 March 2023).
- Knežević, V.; Stazić, L.; Orović, J.; Pavić, Z. Optimisation of Reliability and Maintenance Plan of the High-Pressure Fuel Pump System on Marine Engine. Pol. Marit. Res. 2022, 29, 97–104. [Google Scholar] [CrossRef]
- Altosole, M.; Balsamo, F.; Acanfora, M.; Mocerino, L.; Campora, U.; Perra, F. A digital twin approach to the diagnostic analysis of a marine diesel engine. In Proceedings of the 20th International Conference on Ships and Maritime Research, Genoa, Italy, 15–17 June 2022. [Google Scholar]
- Cullum, J.; Binns, J.; Lansdale, M.; Abbassi, R.; Garaniya, V. Risk-Based Maintenance Scheduling with application to naval vessels and ships. Ocean Eng. 2018, 148, 476–485. [Google Scholar] [CrossRef]
- Mishra, C.; Fanar, A.; Samson, A. Study of the causes of engine failure in ship and maintenance required to prevent engine failure. Int. J. Contemp. Res. Rev. 2017, 8, 20218–20241. [Google Scholar] [CrossRef] [PubMed]
- Alamri, T.O.; Mo, J.P.T. Optimisation of preventive maintenance regime based on failure mode system modelling considering reliability. Arab. J. Sci. Eng. 2022, 49, 3455–3477. [Google Scholar] [CrossRef]
- Cicek, K.; Celik, M. Application of failure modes and effects analysis to main engine crankcase explosion failure on-board ship. Saf. Sci. 2013, 51, 6–10. [Google Scholar] [CrossRef]



| Class | Magnitude | SI | Possible Failure Effects |
|---|---|---|---|
| Safety | Catastrophic | 1 | Deaths, loss of ship, environmental catastrophe |
| Critical | 0.1 | Critical injury, major ship damage, damage to the environment | |
| Severe | 0.01 | Minor injury, damage to ship, secondary damage | |
| Marginal | 0.001 | Possible injury, possible damage to ship | |
| Negligible | <0.0001 | No injury, no damage to ship or environment | |
| Operation | Not Available | 0.01 | The ship is unavailable for operation during some days |
| Partially Available | 0.001 | The ship is unavailable for operation during some hours | |
| Reduced Performance | 0.0001 | The ship operates with reduced performance | |
| Available | <0.00001 | The ship is fully operational |
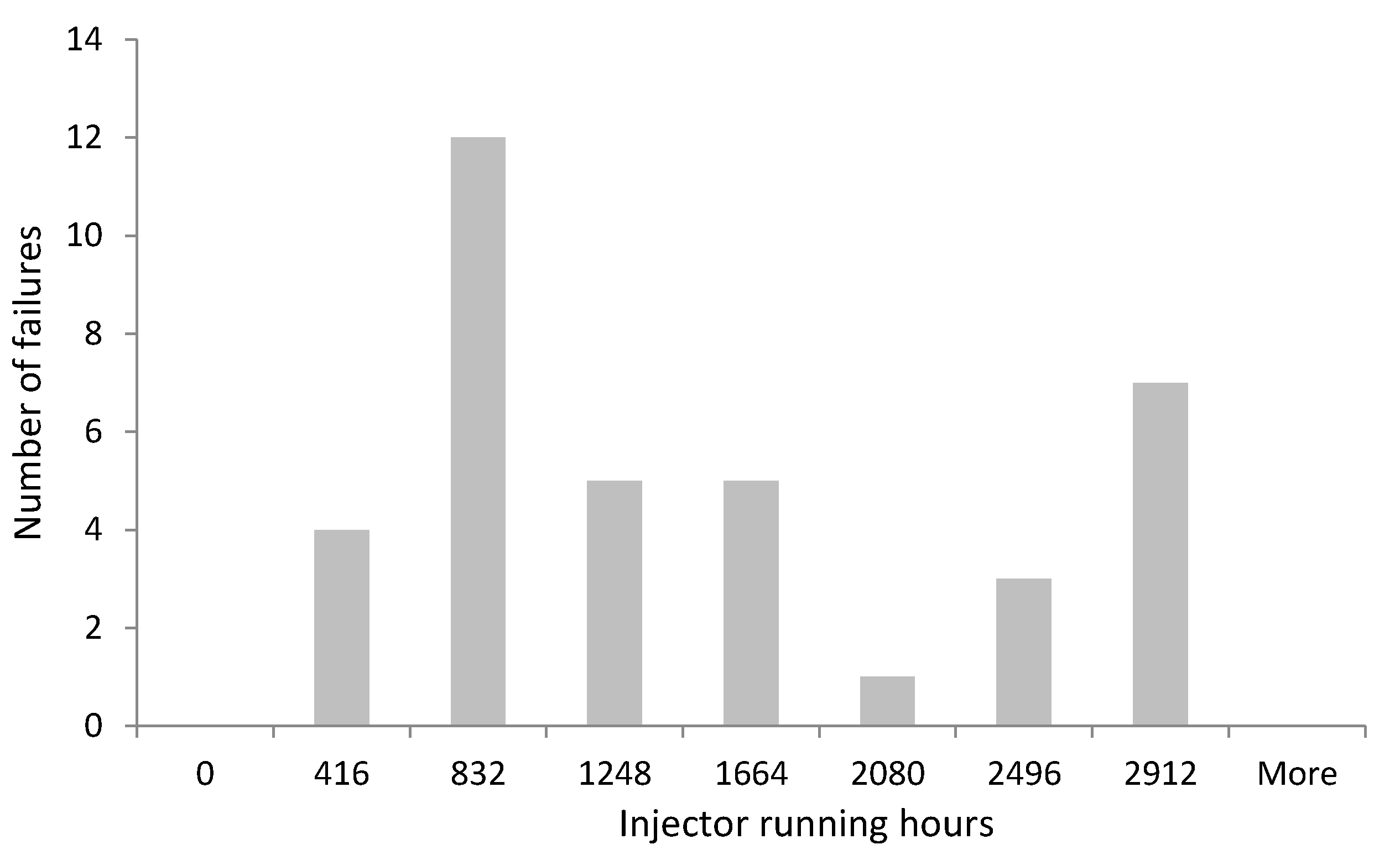
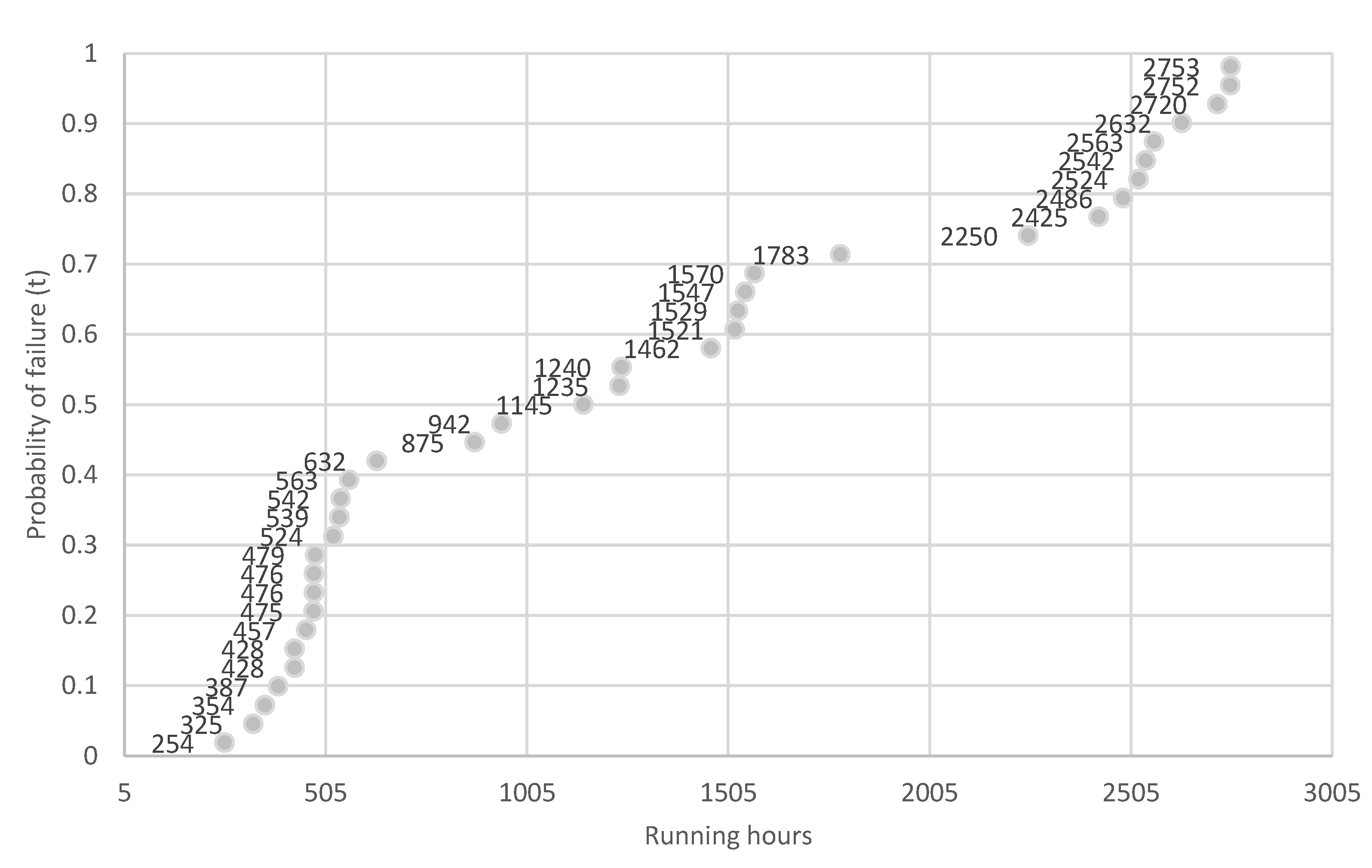
| Cylinder Injectors Fail | Engine RH | Total RH of Injector Since Last Service | Cylinder Injectors Fail | Engine RH | Total RH of Injector Since Last Service |
|---|---|---|---|---|---|
| Cyl A2 injector | 14,632 | 2632 | Cyl B4 injector | 12,387 | 387 |
| Cyl A6 injector | 11,524 | 2524 | Cyl B3 injector | 16,570 | 1570 |
| Cyl B4 injector | 8425 | 2425 | Cyl B2 injector | 14,752 | 2752 |
| Cyl B3 injector | 4521 | 1521 | Cyl A8 injector | 6479 | 479 |
| Cyl A5 injector | 1462 | 1462 | Cyl A4 injector | 1240 | 1240 |
| Cyl A1 injector | 325 | 325 | Cyl B8 injector | 563 | 563 |
| Cyl B3 injector | 18,542 | 542 | Cyl A1 injector | 428 | 428 |
| Cyl B8 injector | 12,354 | 354 | Cyl A3 injector | 428 | 428 |
| Cyl A7 injector | 6942 | 942 | Cyl B3 injector | 254 | 254 |
| Cyl A5 injector | 8250 | 2250 | Cyl B5 injector | 1783 | 1783 |
| Cyl A6 injector | 20,539 | 539 | Cyl A5 injector | 5486 | 2486 |
| Cyl B4 injector | 12,457 | 457 | Cyl A4 injector | 8720 | 2720 |
| Cyl B3 injector | 8563 | 2563 | Cyl A3 injector | 13,529 | 1529 |
| Cyl A2 injector | 1235 | 1235 | Cyl B2 injector | 18,475 | 475 |
| Cyl A4 injector | 15,476 | 476 | Cyl A1 injector | 20,145 | 1145 |
| Cyl A7 injector | 15,476 | 476 | Cyl B4 injector | 20,632 | 632 |
| Cyl B1 injector | 19,875 | 875 | Cyl A4 injector | 8542 | 2542 |
| Cyl A7 injector | 6524 | 524 | Cyl A6 injector | 13,547 | 1547 |
| Cyl A1 injector | 8753 | 2753 |
| Β | t0 | η |
|---|---|---|
| 1.46862 | 0 | 1446.01 |
| Σ | MTBF | p |
|---|---|---|
| 890.02 | 1308 | 0.68 |
| Component | SI(S) | SI(O) | ELFF | RI(S) | RI(O) |
|---|---|---|---|---|---|
| Fuel injector (open/closed bus) | 0.0001 | 0.001 | 5.73 | 0.000573 | 0.00573 |
| Operational Configuration | ELFF Values | SI | ||||
|---|---|---|---|---|---|---|
| 1 | 0.01 | 0.01 | 0.001 | 0.0001 | ||
| CLOSED BUS | URC = 0.01627 | 0.01627 | 0.1627 | 1.627 | 16.27 | 162.7 |
| LRC = 0.0001627 | 0.0001627 | 0.001627 | 0.01627 | 0.1627 | 1.627 | |
| OPEN BUS | URC = 0.00165 | 0.00165 | 0.0165 | 0.165 | 1.65 | 16.5 |
| LRC = 0.0000165 | 0.0000165 | 0.000165 | 0.00165 | 0.0165 | 0.165 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dujmović, J.; Glujić, D.; Kralj, P.; Pelić, V. Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies. J. Mar. Sci. Eng. 2024, 12, 388. https://doi.org/10.3390/jmse12030388
Dujmović J, Glujić D, Kralj P, Pelić V. Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies. Journal of Marine Science and Engineering. 2024; 12(3):388. https://doi.org/10.3390/jmse12030388
Chicago/Turabian StyleDujmović, Josip, Darko Glujić, Predrag Kralj, and Vladimir Pelić. 2024. "Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies" Journal of Marine Science and Engineering 12, no. 3: 388. https://doi.org/10.3390/jmse12030388
APA StyleDujmović, J., Glujić, D., Kralj, P., & Pelić, V. (2024). Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies. Journal of Marine Science and Engineering, 12(3), 388. https://doi.org/10.3390/jmse12030388






