Transient Tests for Checking the Trieste Subsea Pipeline: Diving into Fault Detection
Abstract
:1. Introduction
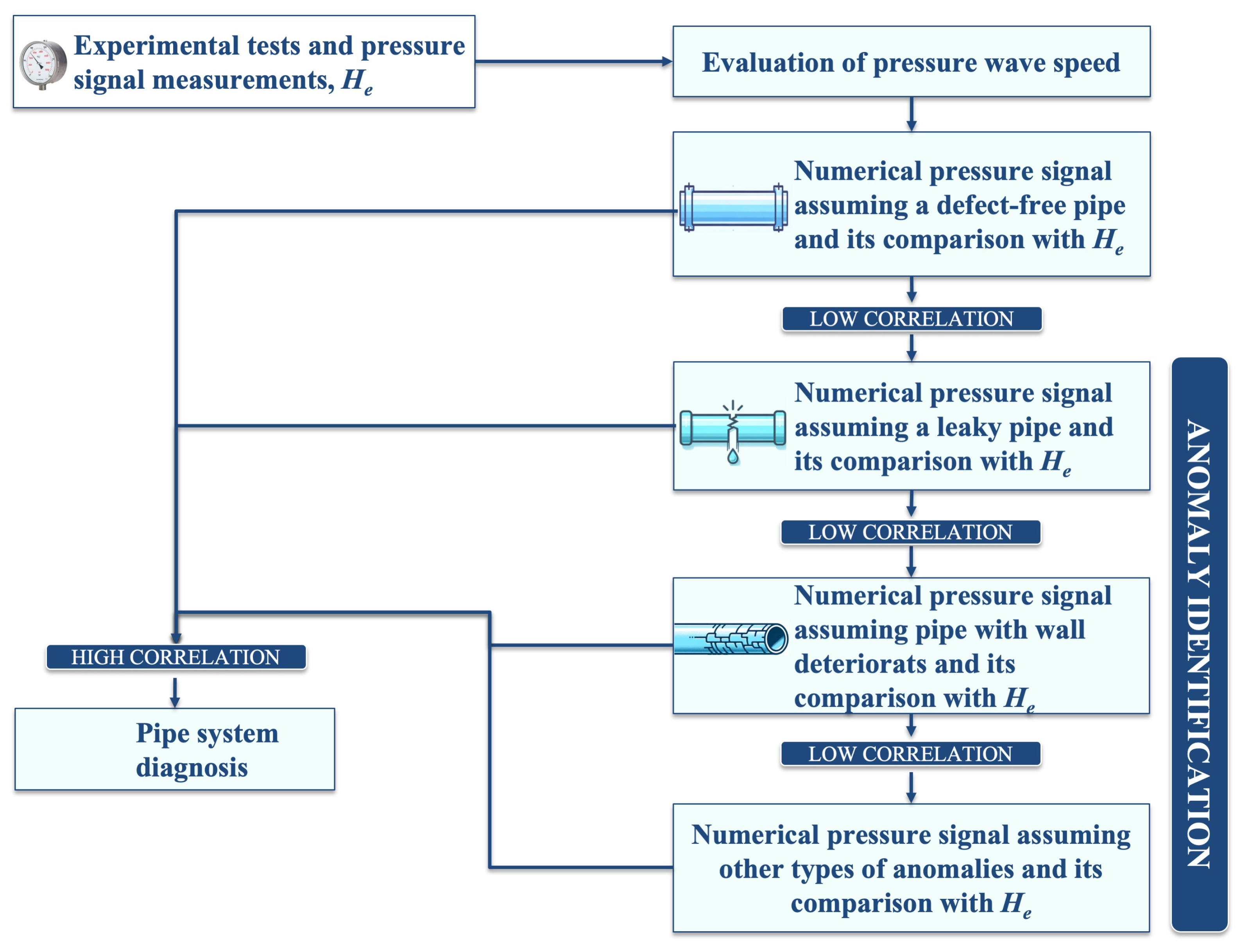
2. Materials and Methods
2.1. One-Dimensional Numerical Model
2.2. Boundary Conditions
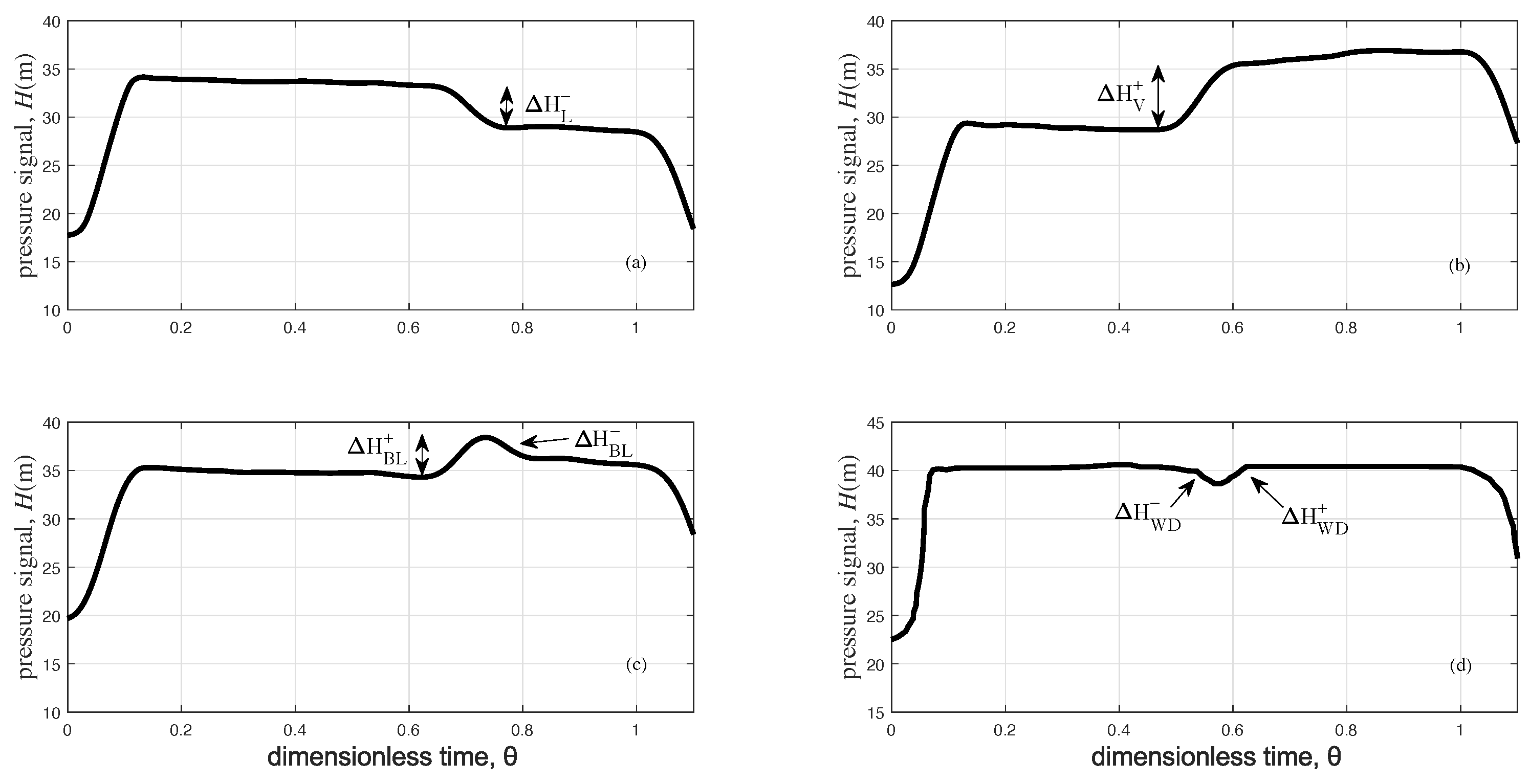
2.3. Analytical Model for Evaluating the Effect of the Anomalies
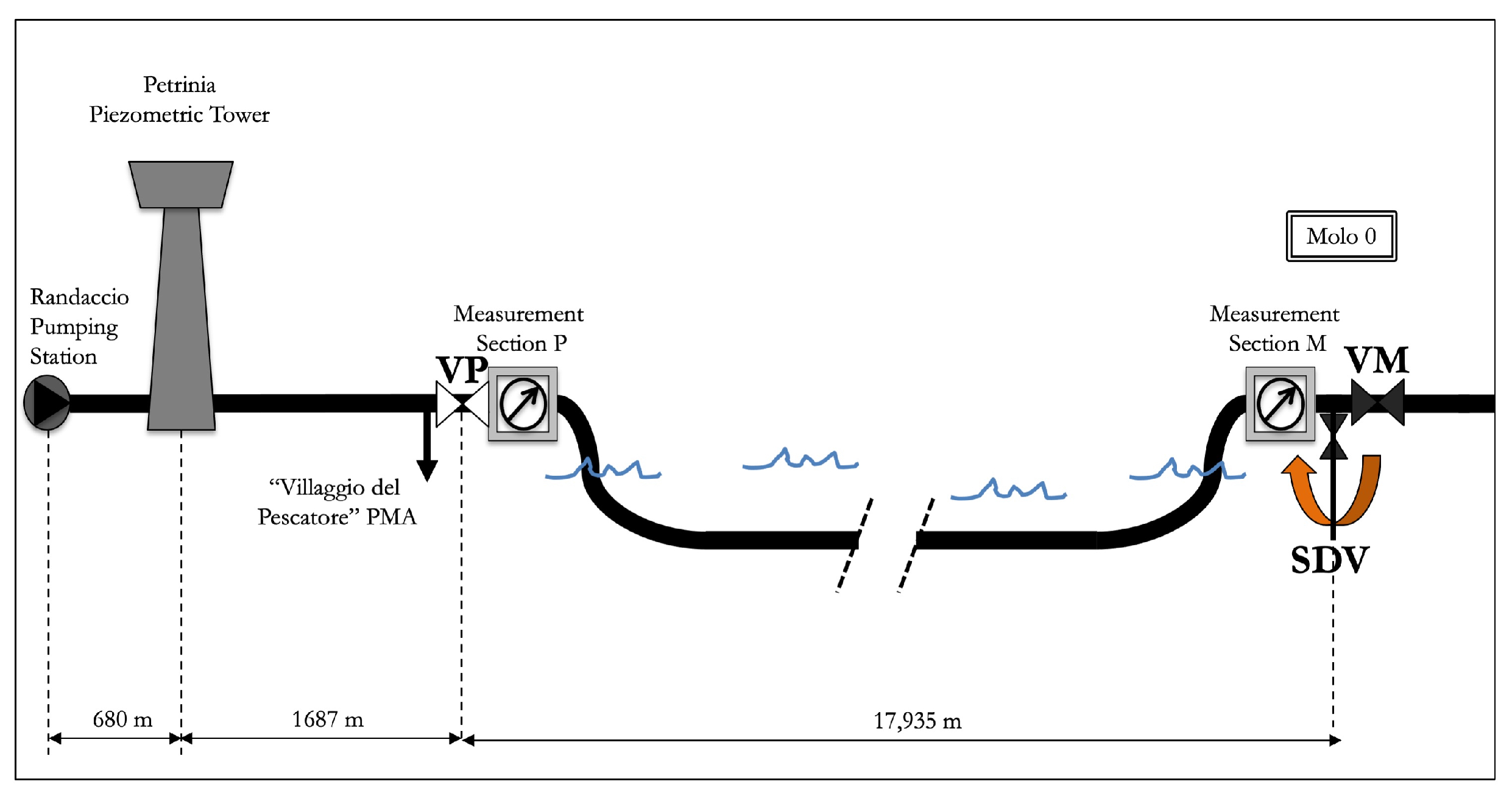
3. Field Tests
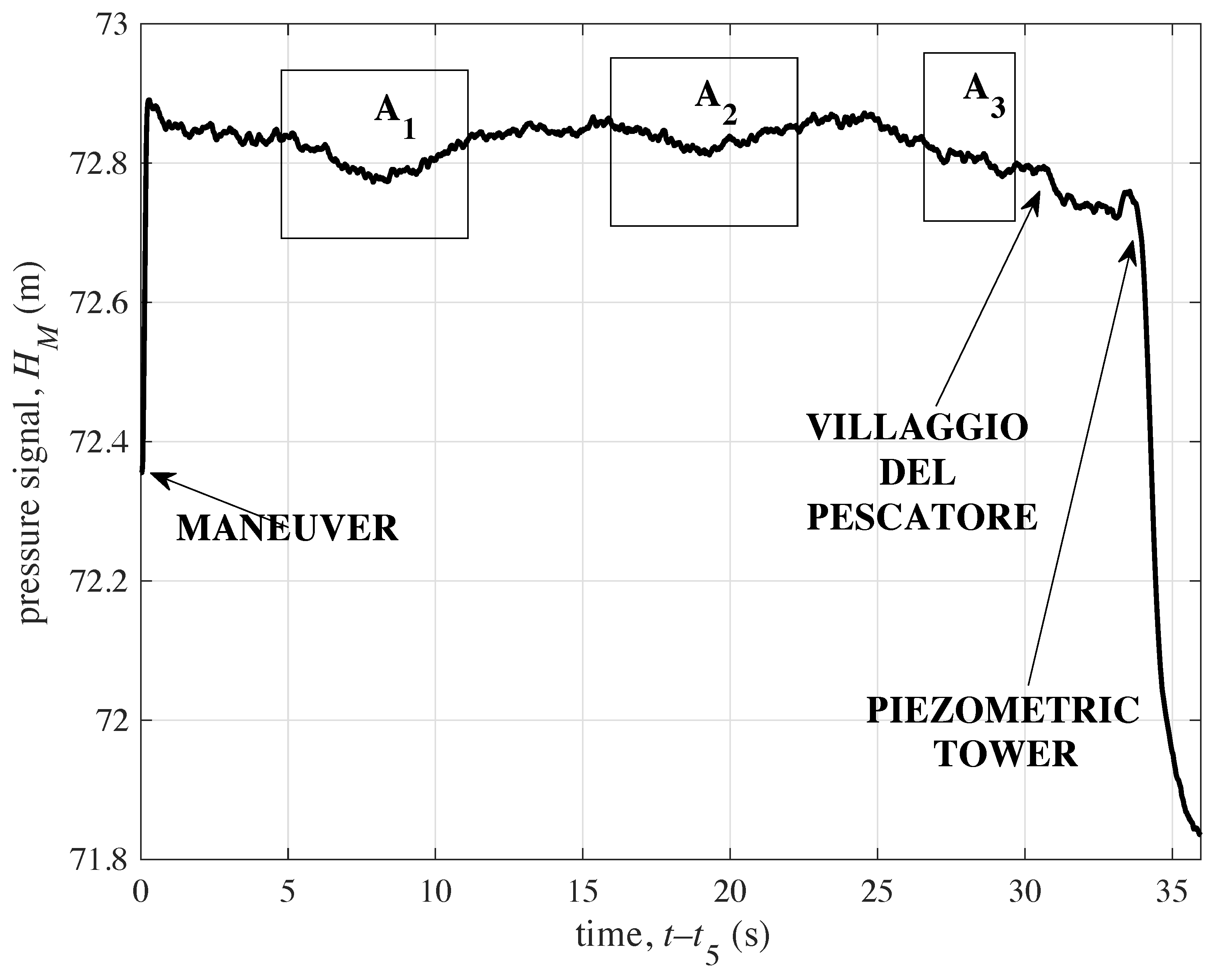
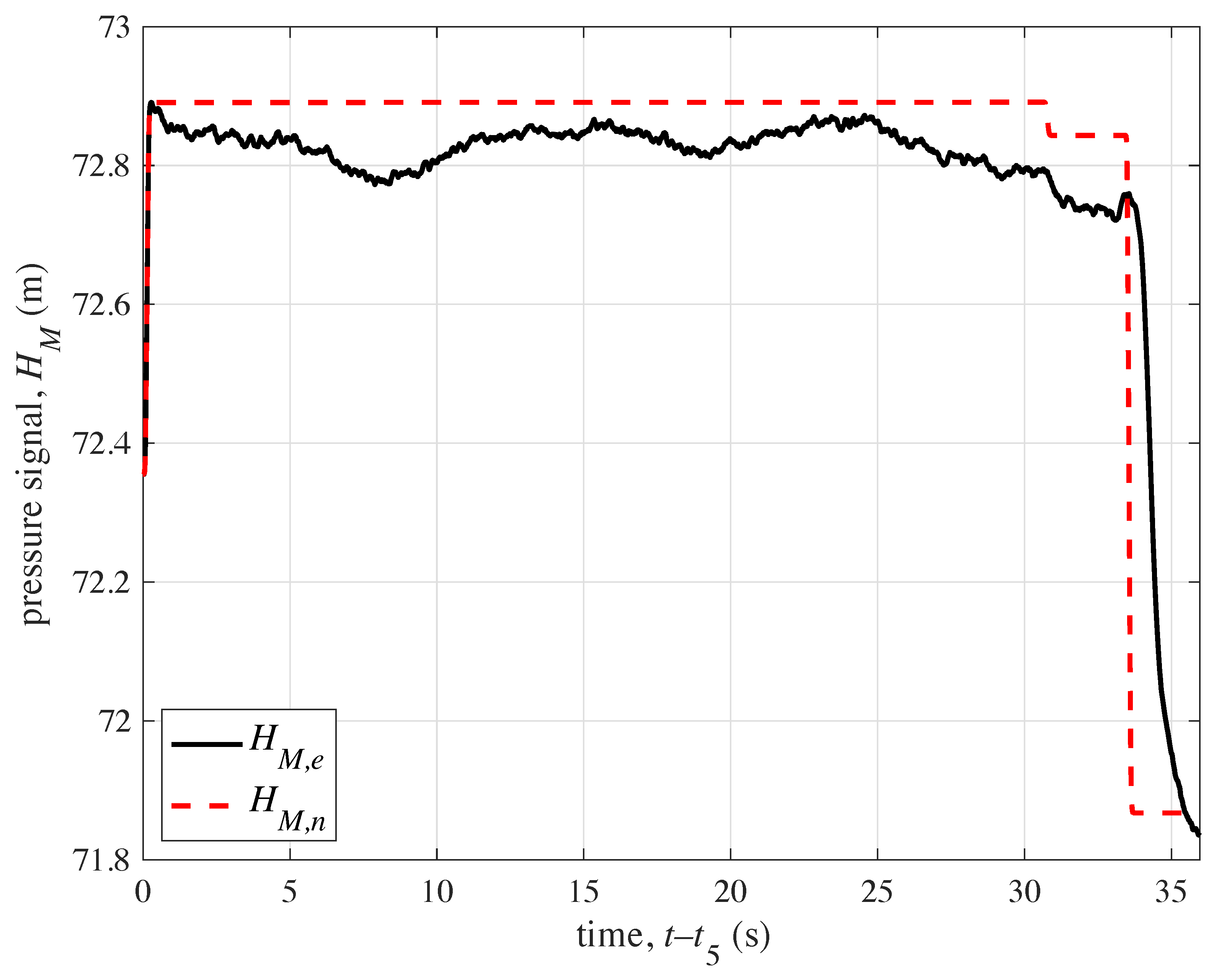
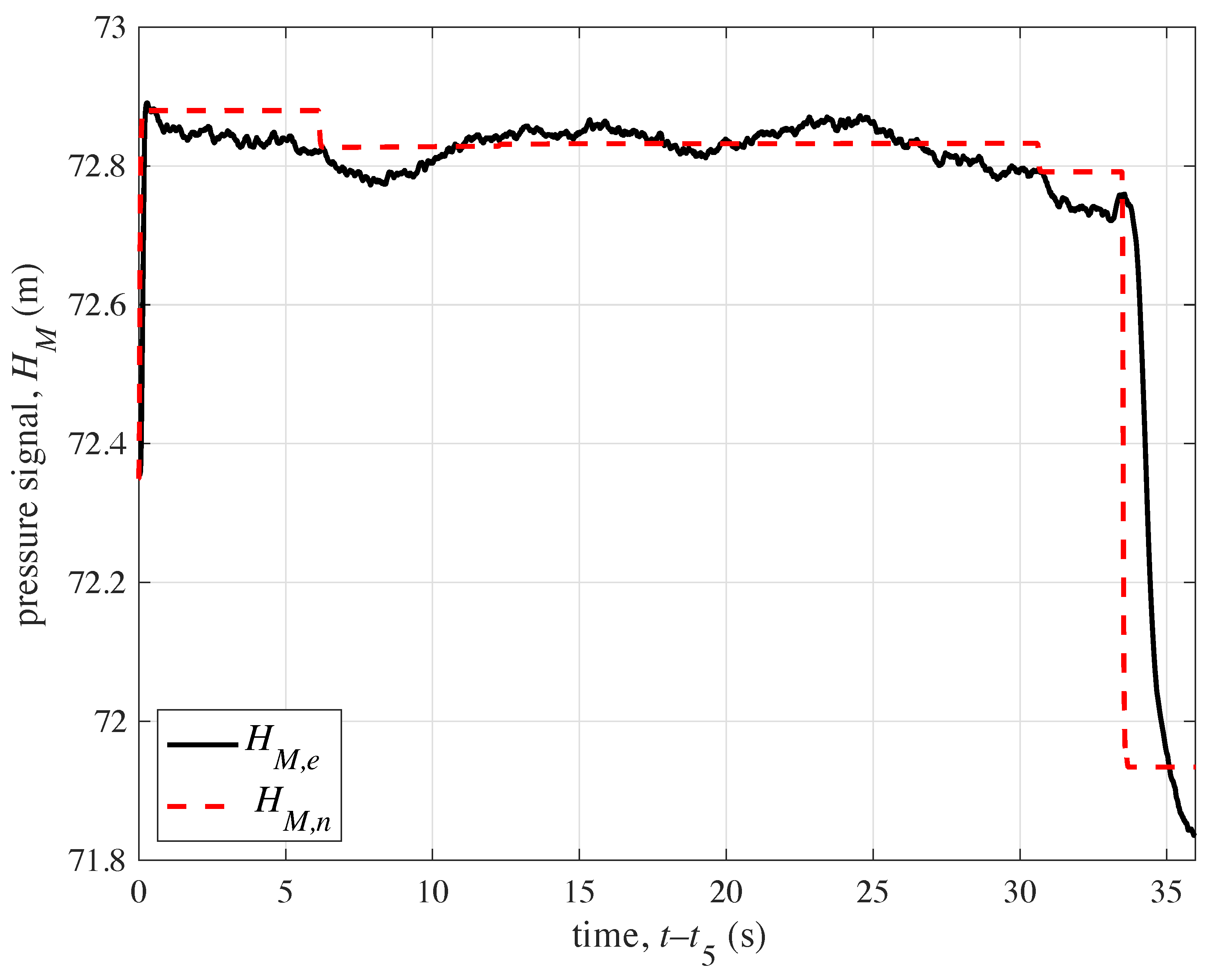
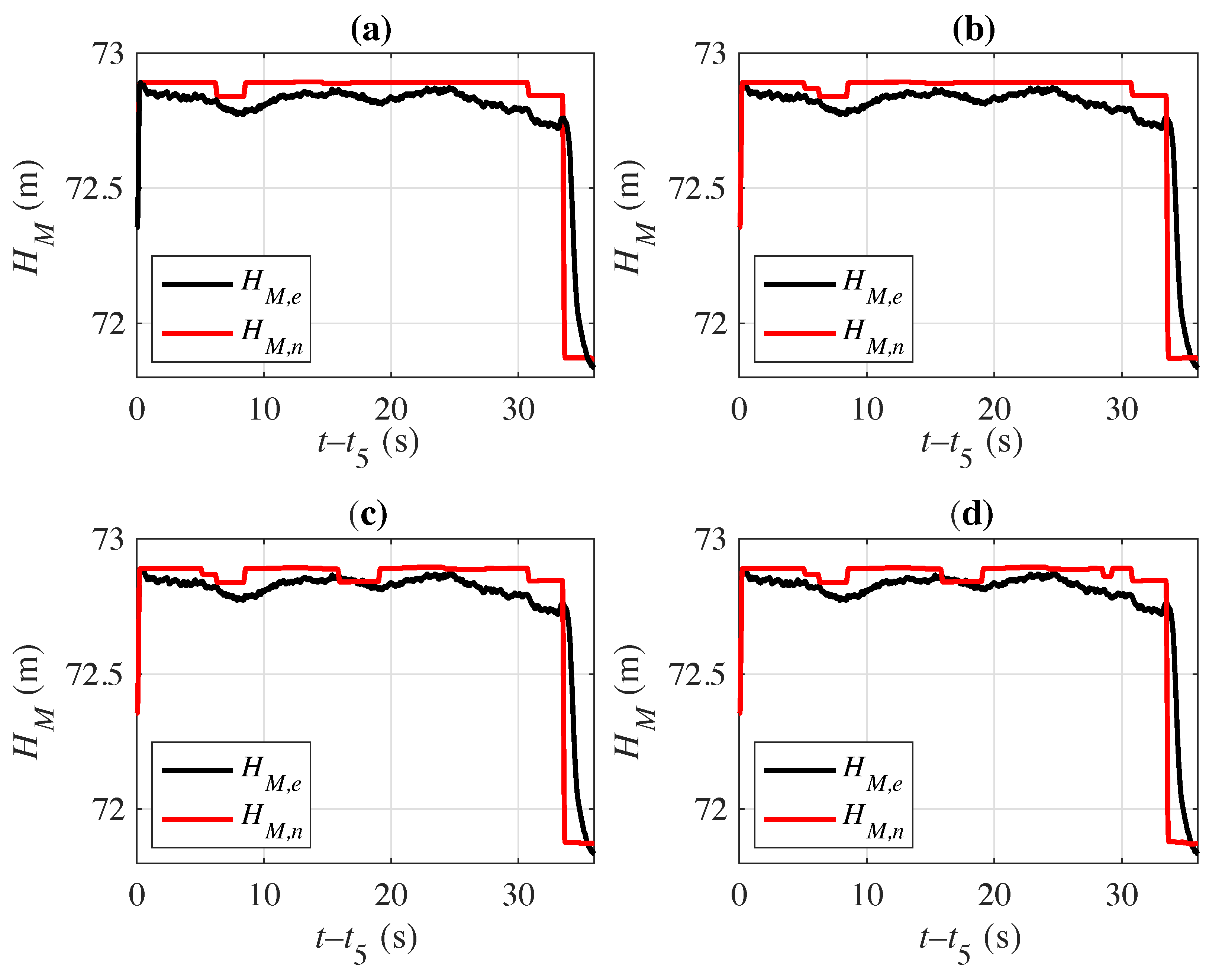
4. Field Tests Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laven, L.; Lambert, A.O. What do we know about real losses on transmission mains? In Proceedings of the IWA Specialised Conference “Water Loss 2012”, Manila, Philipines, 26–29 February 2012. [Google Scholar]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Towards the field tests. J. Mar. Sci. Eng. 2024, 12, 374. [Google Scholar] [CrossRef]
- Ho, M.; El-Borgh, S.; Patil, D.; Song, G. Inspection and monitoring systems subsea pipelines: A review paper. Struct. Health Monit. 2020, 19, 606–645. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Hosie, G.; Reda, A. Review on subsea pipeline integrity management: An operator’s perspective. Energies 2022, 16, 98. [Google Scholar] [CrossRef]
- Cawley, P.; Lowe, M.; Alleyne, D.; Pavlakovic, B.; Wilcox, P. Practical long range guided wave testing: Applications to pipes and rail. Mater. Eval. 2003, 61, 66–74. [Google Scholar]
- Gazis, D.C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. 1. Analytical foundation. J. Acoust. Soc. Am. 1959, 31, 568573. [Google Scholar] [CrossRef]
- Reda, A.; Shahin, M.A.; Sultan, I.A.; Amaechi, C.V.; McKee, K.K. Necessity and suitability of in-line inspection for corrosion resistant alloy (CRA) clad pipelines. Ships Offshore Struct. 2023, 18, 1360–1366. [Google Scholar] [CrossRef]
- Kazeminasab, S.; Sadeghi, N.; Janfaza, V.; Razavi, M.; Ziyadidegan, S.; Banks, M.K. Localization, mapping, navigation, and inspection methods in in-pipe robots: A review. IEEE Access 2021, 9, 162035–162058. [Google Scholar] [CrossRef]
- Taghvaei, M.; Beck, S.B.M.; Boxall, J.B. Leak detection in pipes using induced water hammer pulses and cepstrum analysis. Int. J. COMADEM 2010, 13, 19–25. [Google Scholar]
- Alawadhi, A.; Tartakovsky, D.M. Bayesian update and method of distributions: Application to leak detection in transmission mains. Water Resour. Res. 2020, 56, e2019WR025879. [Google Scholar] [CrossRef]
- Brunone, B.; Maietta, F.; Capponi, C.; Keramat, A.; Meniconi, S. A review of physical experiments for leak detection in water pipes through transient tests for addressing future research. J. Hydraul. Res. 2022, 60, 894–906. [Google Scholar] [CrossRef]
- Contractor, D. The reflection of waterhammer pressure waves from minor losses. J. Basic Eng. 1965, 87, 445–451. [Google Scholar] [CrossRef]
- Mohapatra, P.; Chaudhry, M.; Kassem, A.; Moloo, J. Detection of partial blockage in single pipelines. J. Hydraul. Eng. 2006, 132, 200–206. [Google Scholar] [CrossRef]
- Sattar, A.M.; Chaudhry, M.H.; Kassem, A.A. Partial blockage detection in pipelines by frequency response method. J. Hydraul. Eng. 2008, 134, 76–89. [Google Scholar] [CrossRef]
- Wang, X.; Lin, J.; Keramat, A.; Ghidaoui, M.S.; Meniconi, S.; Brunone, B. Matched-field processing for leak localization in a viscoelastic pipe: An experimental study. Mech. Syst. Signal Process. 2019, 124, 459–478. [Google Scholar] [CrossRef]
- Brunone, B.; Maietta, F.; Capponi, C.; Duan, H.F.; Meniconi, S. Detection of partial blockages in pressurized pipes by transient tests: A review of the physical experiments. Fluids 2023, 8, 19. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Kashima, A.; Lu, J.; Ghidaoui, M.S.; Tung, Y.K. Extended blockage detection in pipes using the system frequency response: Analytical analysis and experimental verification. J. Hydraul. Eng. 2013, 139, 763–771. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M.S.; Tuck, J. Transient wave-blockage interaction and extended blockage detection in elastic water pipelines. J. Fluids Struct. 2014, 46, 2–16. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Nguyen, S.T.N.; Zecchin, A.; Simpson, A.R. Detecting thinner-walled pipe sections using a spark transient pressure wave generator. J. Hydraul. Eng. 2018, 144, 06017027. [Google Scholar] [CrossRef]
- Liggett, J.A.; Chen, L.C. Inverse transient analysis in pipe networks. J. Hydraul. Eng. 1994, 120, 934–955. [Google Scholar] [CrossRef]
- Colombo, A.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro-Environ. Res. 2009, 2, 212–227. [Google Scholar] [CrossRef]
- Xu, X.; Karney, B. An overview of transient fault detection techniques. In Modeling and Monitoring of Pipelines and Networks; Springer: Cham, Switzerland, 2017; pp. 13–37. [Google Scholar]
- Ayati, A.H.; Haghighi, A.; Lee, P.J. Statistical review of major standpoints in hydraulic transient-based leak detection. J. Hydraul. Struct. 2019, 5, 1–26. [Google Scholar]
- Che, T.C.; Duan, H.F.; Lee, P.J. Transient wave-based methods for anomaly detection in fluid pipes: A review. Mech. Syst. Signal Process. 2021, 160, 107874. [Google Scholar] [CrossRef]
- Capponi, C.; Martins, N.M.; Covas, D.I.C.; Brunone, B.; Meniconi, S. Transient test-based techniques for checking the sealing of in-line shut-off valves and capturing the effect of series junctions—Field tests in a real pipe system. Water 2024, 16, 3. [Google Scholar] [CrossRef]
- Duan, H.; Pan, B.; Wang, M.; Chen, L.; Zheng, F.; Zhang, Y. State-of-the-art review on the transient flow modeling and utilization for urban water supply system (UWSS) management. J. Water Supply Res. Technol.-AQUA 2020, 69, 858–893. [Google Scholar] [CrossRef]
- Covas, D.; Ramos, H. Case studies of leak detection and location in water pipe systems by inverse transient analysis. J. Water Resour. Plan. Manag. 2010, 136, 248–257. [Google Scholar] [CrossRef]
- Pickering, D.; Park, J.M.; Bannister, D.H. Utility Mapping and Record Keeping for Infrastructure; The World Bank: Washington, DC, USA, 1993; p. 69. [Google Scholar]
- Costello, S.; Chapman, D.; Rogers, C.; Metje, N. Underground asset location and condition assessment technologies. Tunn. Undergr. Space Technol. 2007, 22, 524–542. [Google Scholar] [CrossRef]
- King, M.; Shemirami, S. Smart Infrastructure: Mapping Underground Utilities; KPMG International Cooperative: Amstelveen, The Netherlands, 2017; p. 12. [Google Scholar]
- Capponi, C.; Meniconi, S.; Lee, P.J.; Brunone, B.; Cifrodelli, M. Time-domain analysis of laboratory experiments on the transient pressure damping in a leaky polymeric pipe. Water Resour. Manag. 2020, 34, 501–514. [Google Scholar] [CrossRef]
- Bohorquez, J.; Simpson, A.R.; Lambert, M.F.; Alexander, B. Merging fluid transient waves and artificial neural networks for burst detection and identification in pipelines. J. Water Resour. Plan. Manag. 2021, 147, 4020097. [Google Scholar] [CrossRef]
- Ayati, A.H.; Haghighi, A.; Ghafouri, H.R. Machine learning-assisted model for leak detection in water distribution networks using hydraulic transient flows. J. Water Resour. Plan. Manag. 2022, 148, 4021104. [Google Scholar] [CrossRef]
- Bohorquez, J.; Lambert, M.F.; Alexander, B.; Simpson, A.R.; Abbott, D. Stochastic Resonance Enhancement for Leak Detection in Pipelines Using Fluid Transients and Convolutional Neural Networks. J. Water Resour. Plan. Manag. 2022, 148, 4022001. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Simpson, A.R.; Zecchin, A.C. Detection of localized deterioration distributed along single pipelines by reconstructive MOC analysis. J. Hydraul. Eng. 2014, 140, 190–198. [Google Scholar] [CrossRef]
- Wylie, E.; Streeter, V. Fluid Transients in Systems; Prentice-Hall Inc.: Hoboken, NJ, USA, 1993; p. 463. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014; p. 583. [Google Scholar]
- Swaffield, J.; Boldy, A. Pressure Surges in Pipe and Duct Systems; Ashgate Publishing Group: Farnham, UK, 1993; p. 380. [Google Scholar]
- Pan, B.; Duan, H.F.; Meniconi, S.; Urbanowicz, K.; Che, T.C.; Brunone, B. Multistage frequency-domain transient-based method for the analysis of viscoelastic parameters of plastic pipes. J. Hydraul. Eng. 2020, 146, 04019068. [Google Scholar] [CrossRef]
- Pezzinga, G. Evaluation of unsteady flow resistances by quasi-2D or 1D models. J. Hydraul. Eng. 2000, 126, 778–785. [Google Scholar] [CrossRef]
- Brunone, B.; Golia, U.M. Discussion of “Systematic evaluation of one-dimensional unsteady friction models in simple pipelines” by J.P. Vitkovsky, A. Bergant, A.R. Simpson, and M.F. Lambert. J. Hydraul. Eng. 2008, 134, 282–284. [Google Scholar] [CrossRef]
- Liou, C. Pipeline leak detection by impulse response extraction. J. Fluids Eng. 1998, 120, 833–838. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient Tests for Checking the Trieste Subsea Pipeline: Diving into Fault Detection. J. Mar. Sci. Eng. 2024, 12, 391. https://doi.org/10.3390/jmse12030391
Meniconi S, Brunone B, Tirello L, Rubin A, Cifrodelli M, Capponi C. Transient Tests for Checking the Trieste Subsea Pipeline: Diving into Fault Detection. Journal of Marine Science and Engineering. 2024; 12(3):391. https://doi.org/10.3390/jmse12030391
Chicago/Turabian StyleMeniconi, Silvia, Bruno Brunone, Lorenzo Tirello, Andrea Rubin, Marco Cifrodelli, and Caterina Capponi. 2024. "Transient Tests for Checking the Trieste Subsea Pipeline: Diving into Fault Detection" Journal of Marine Science and Engineering 12, no. 3: 391. https://doi.org/10.3390/jmse12030391
APA StyleMeniconi, S., Brunone, B., Tirello, L., Rubin, A., Cifrodelli, M., & Capponi, C. (2024). Transient Tests for Checking the Trieste Subsea Pipeline: Diving into Fault Detection. Journal of Marine Science and Engineering, 12(3), 391. https://doi.org/10.3390/jmse12030391







