An Improved VO Method for Collision Avoidance of Ships in Open Sea
Abstract
1. Introduction
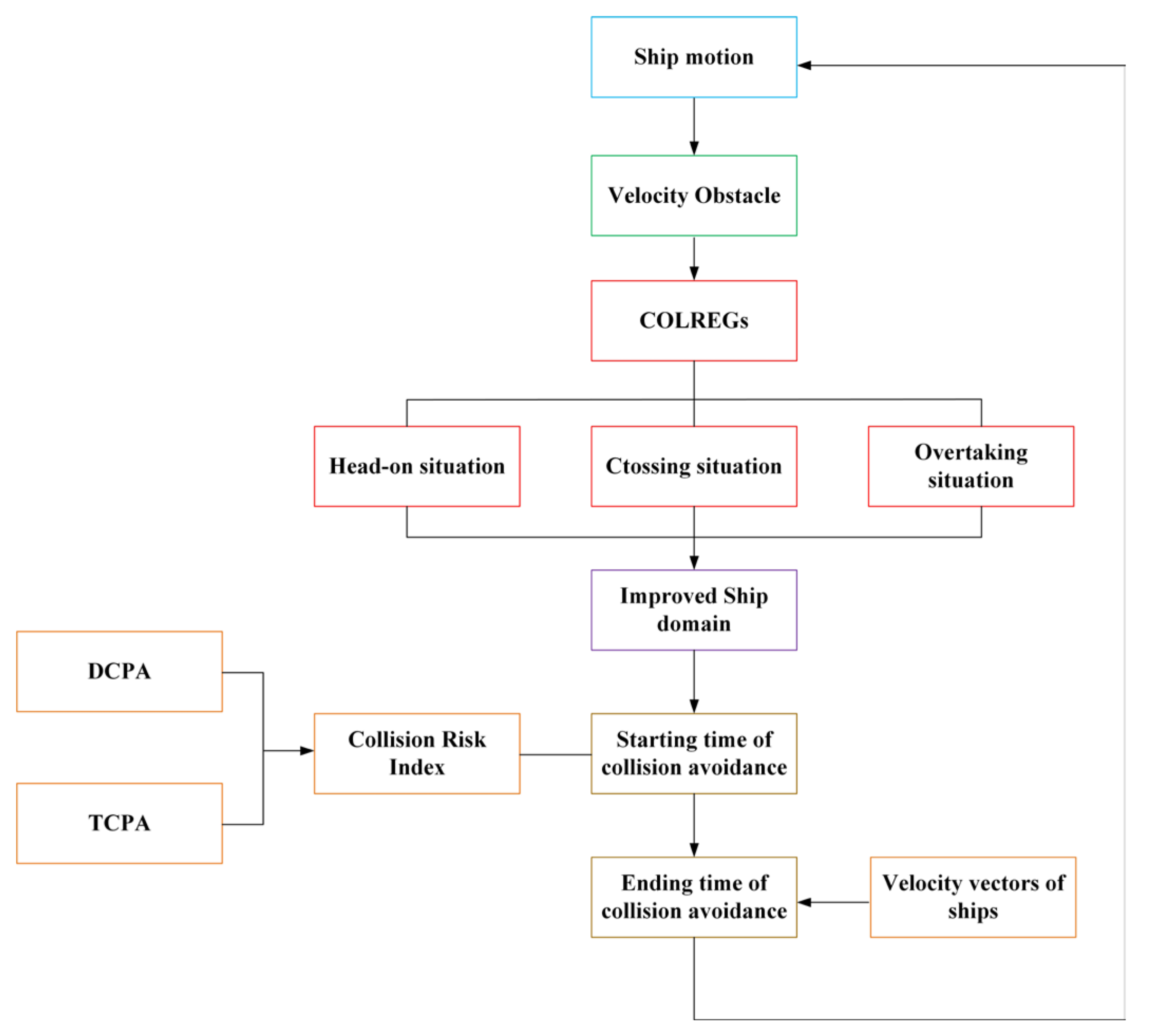
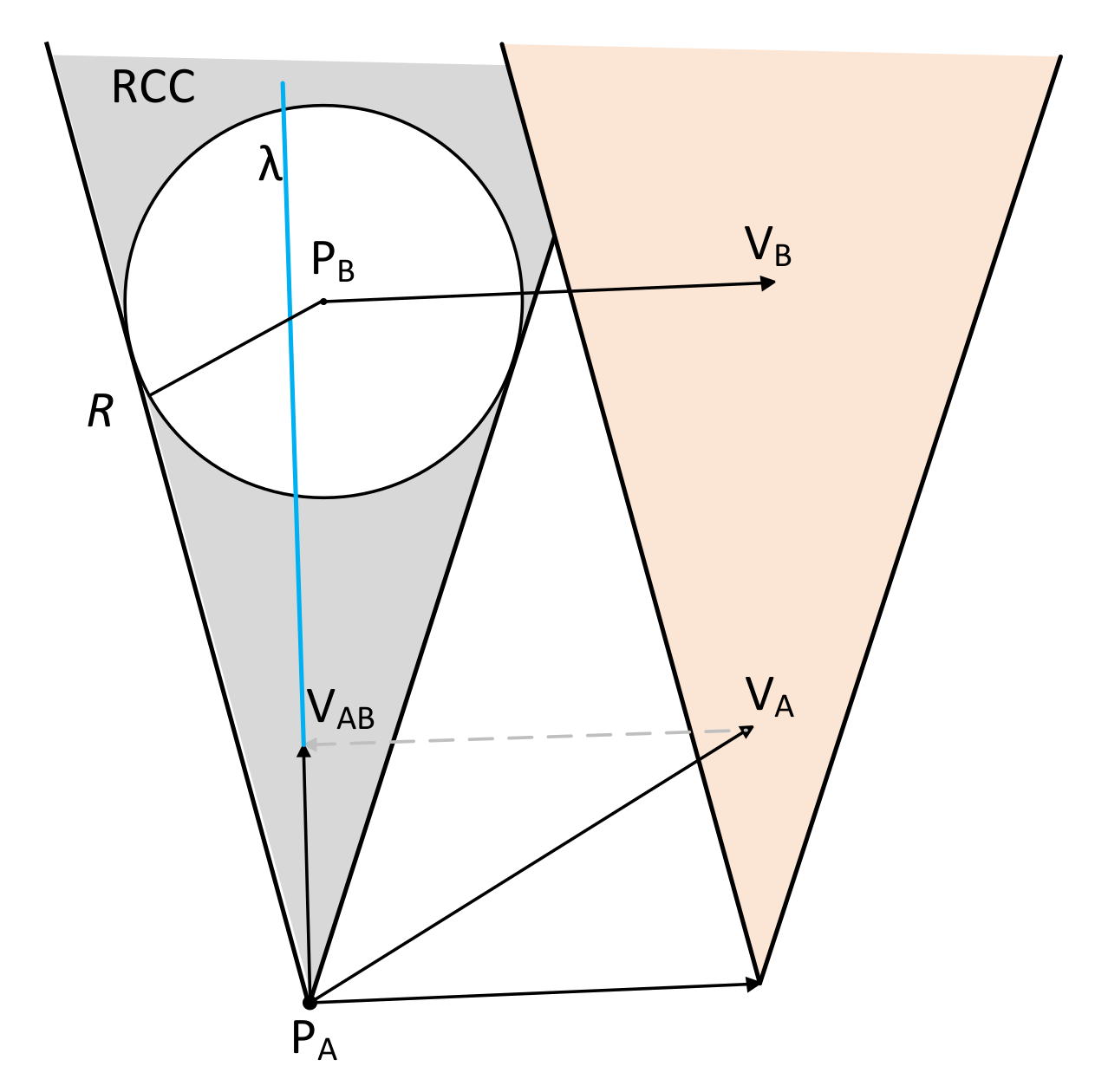
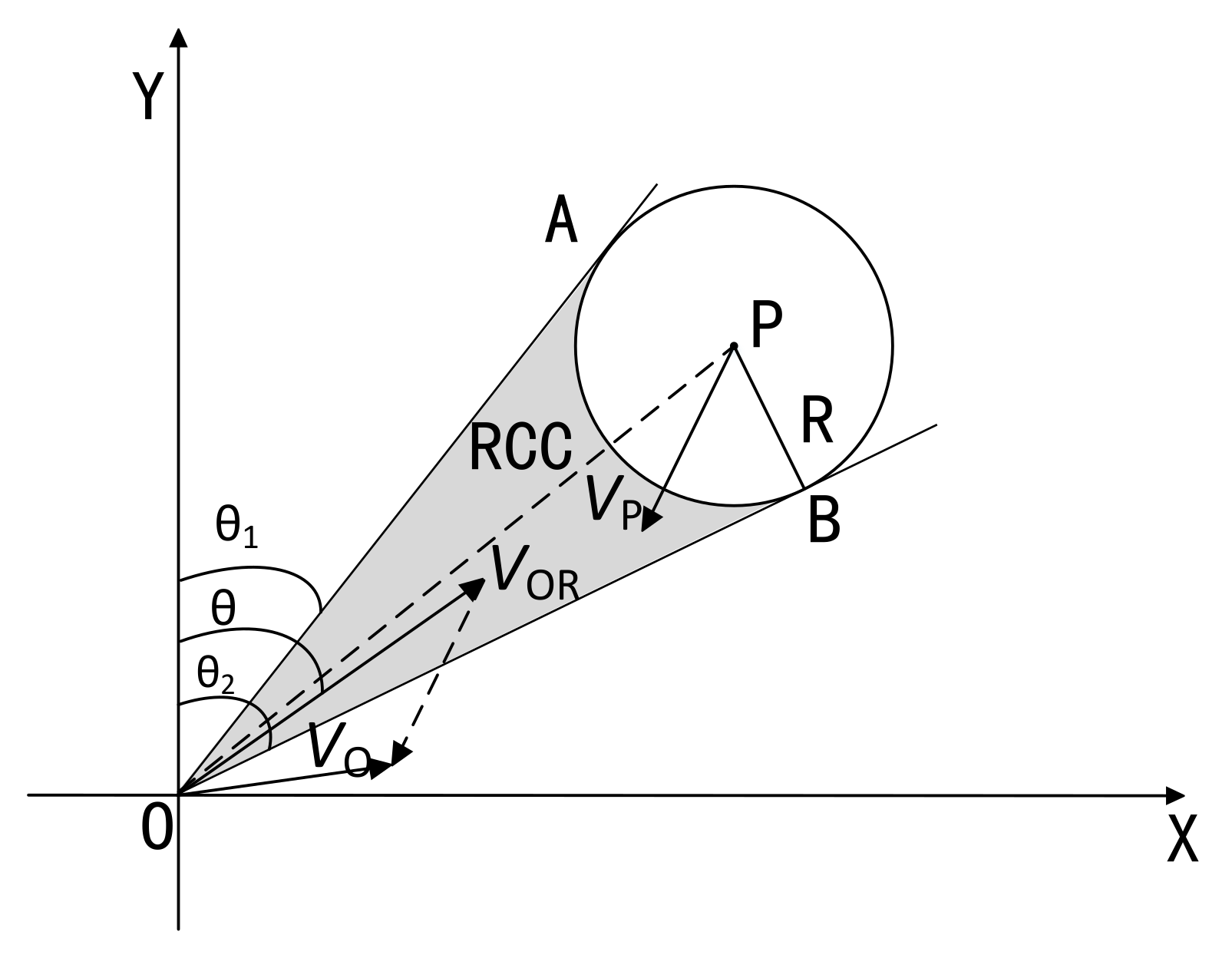
2. The Velocity Obstacle Algorithm
2.1. Methods and Principles
2.2. Application in Ship
3. Improved Velocity Obstacle
3.1. Velocity Obstacle Based on the Ship Domain
3.1.1. Determine the Ship Domain
- Head-on situation and crossing situation: ;
- Own ship being overtaken by the target ship: ;
- Own ship overtaking the target ship: ;
- Other situations: .
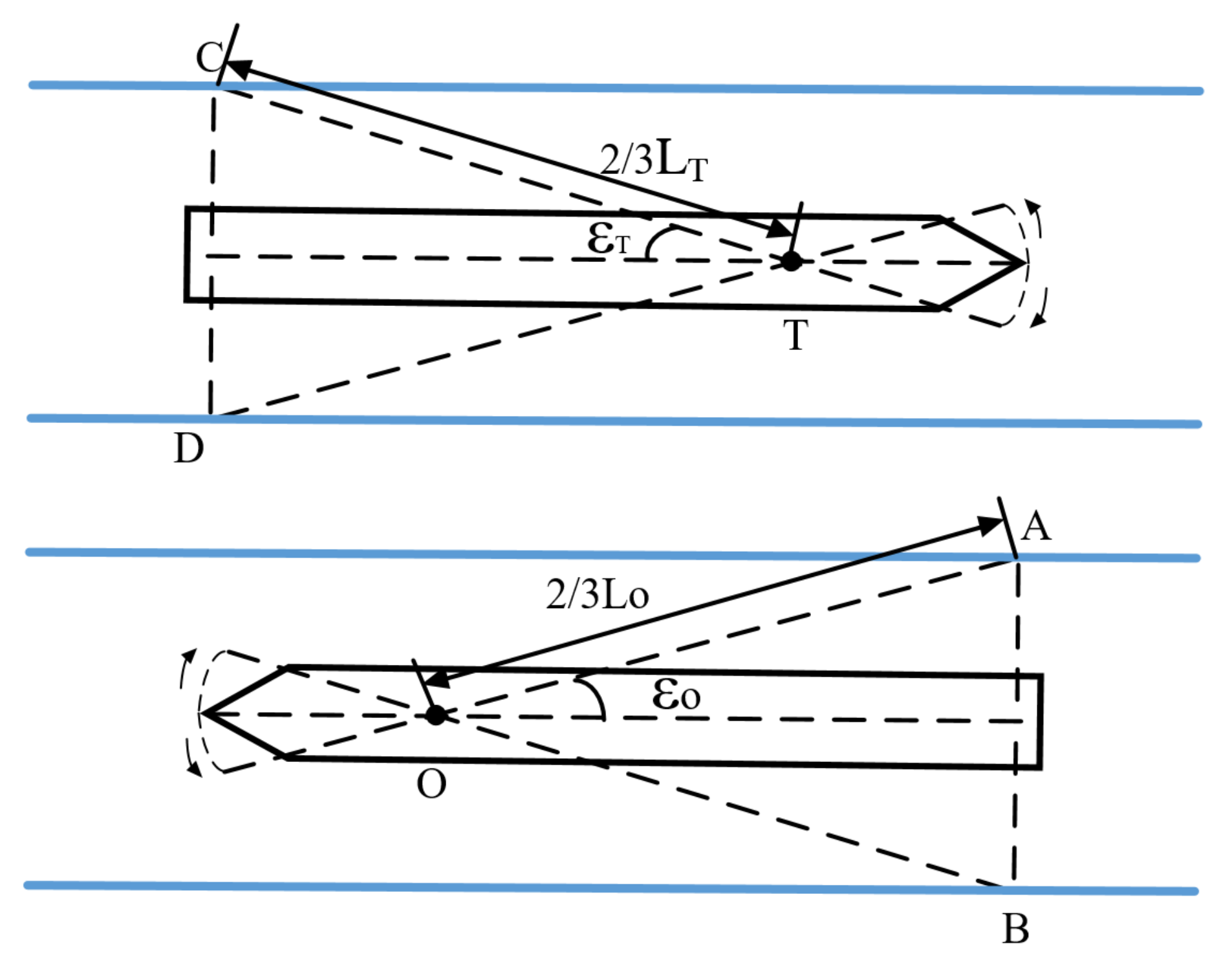
3.1.2. Collision Avoidance Analysis Based on Elliptical Ship Domain
3.2. Application to the Convention on the International Regulations for Preventing Collisions at Sea
- In head-on and starboard crossing, the ship is the give-way ship, and could alter its course according to the description in Table 1 to avoid collision. That is:
- For port side crossing encounter situation where the target ship overtakes the own ship, the own ship is the stand-on ship and should keep its course and speed, and there is no need to calculate ;
- When the own ship is overtaking the target ship and the own ship’s velocity module is greater than the target ship, the own ship is the give-way ship and should alter course to avoid collision. According to the 7–8th row of Table 1, the RV can be concluded as follows:
3.3. The Determination of the Start and End Time of Collision Avoidance
3.3.1. Collision Risk Determines the Start Time of Collision Avoidance
- Membership function of DCPA could be written as a piecewise function :where indicates the minimum distance between two ships, in this paper is the minimum distance at which the ship domains of the two ships are tangent; indicates the minimum distance at which the two ships can safely pass, .
- Membership function of TCPA could also be written as a piecewise function :where,where is the distance between these two ships at the last opportunity to use helm, which is generally 12 times the length of the own ship; is the dynamic boundary, that is, the distance at which the own ship starts turning, and is obtained as follows:where is the true direction of the target ship relative to own ship.
- The relative velocity vectors of the two ships are in the relative collision cone RCC;
- Based on the collision avoidance test results of multiple encounter situations and the collision avoidance suggestions of the experienced captain, the ship collision risk assessment is larger than 0.72.
3.3.2. Conditions for Ending Collision Avoidance
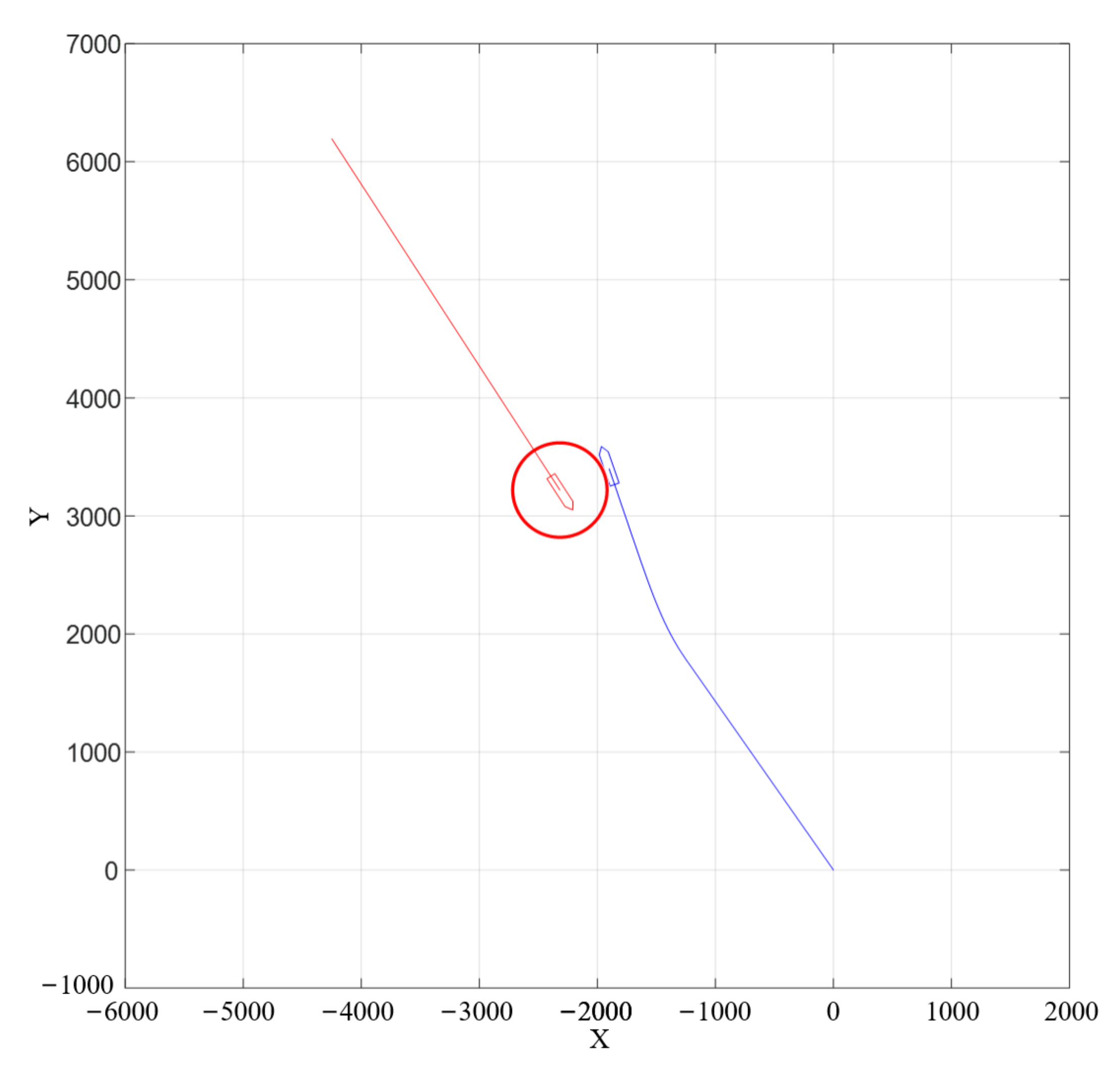
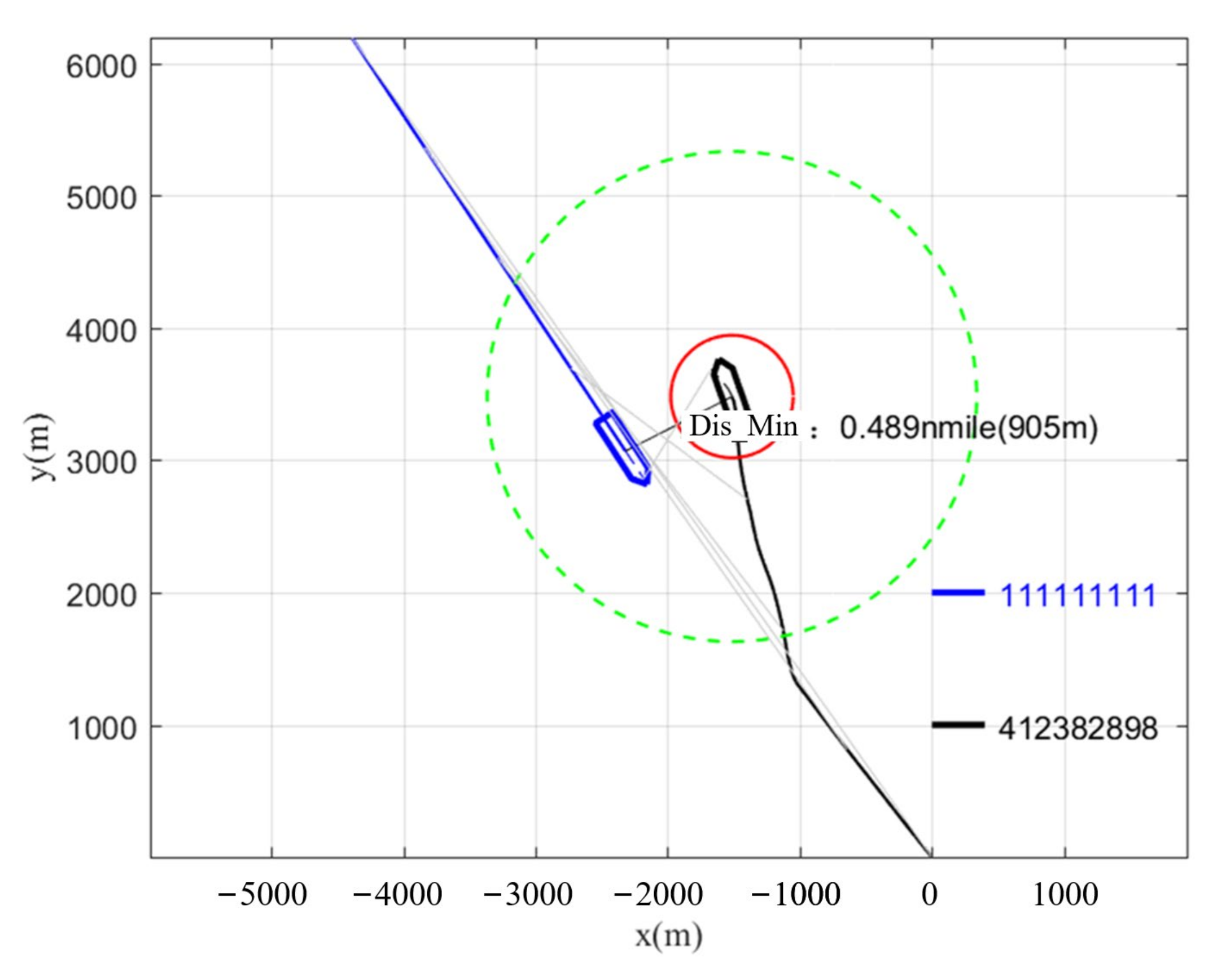
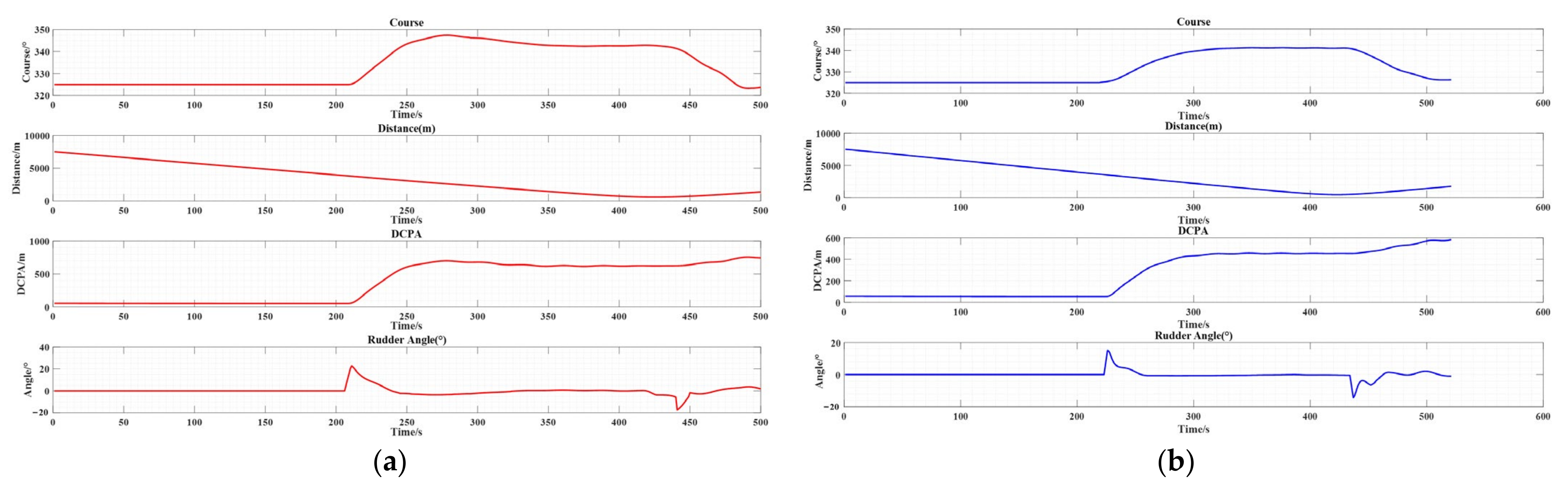
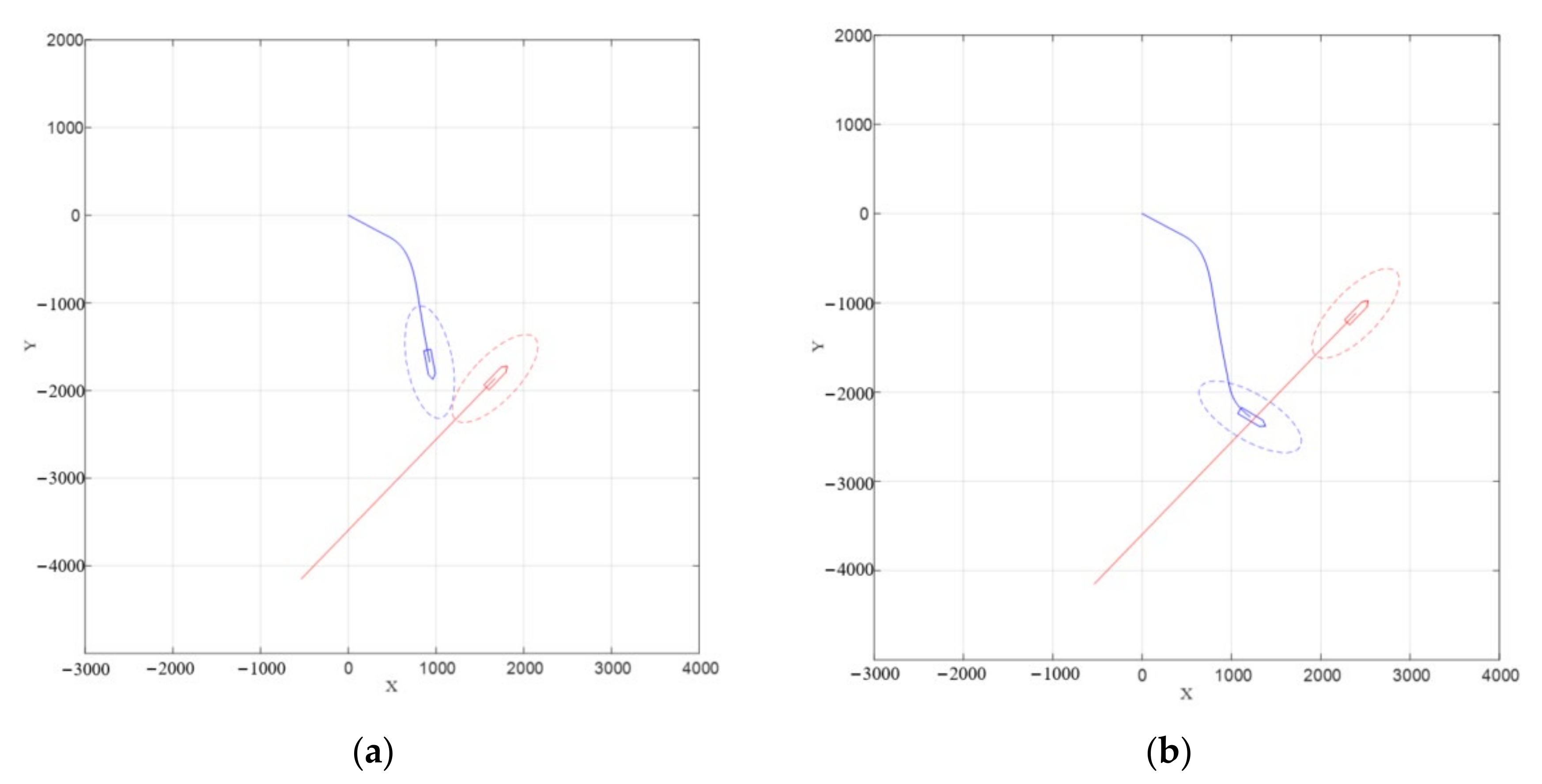
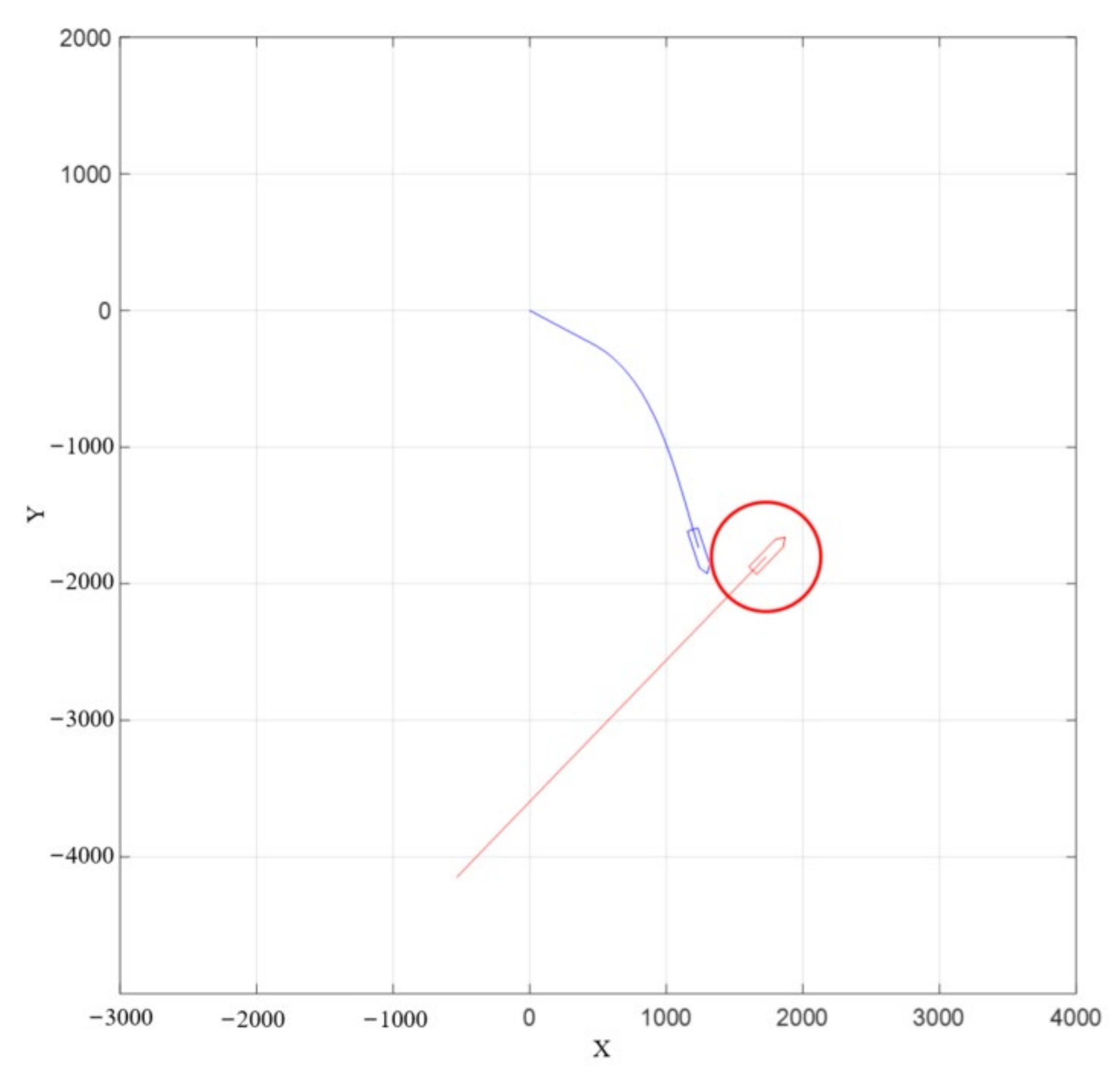
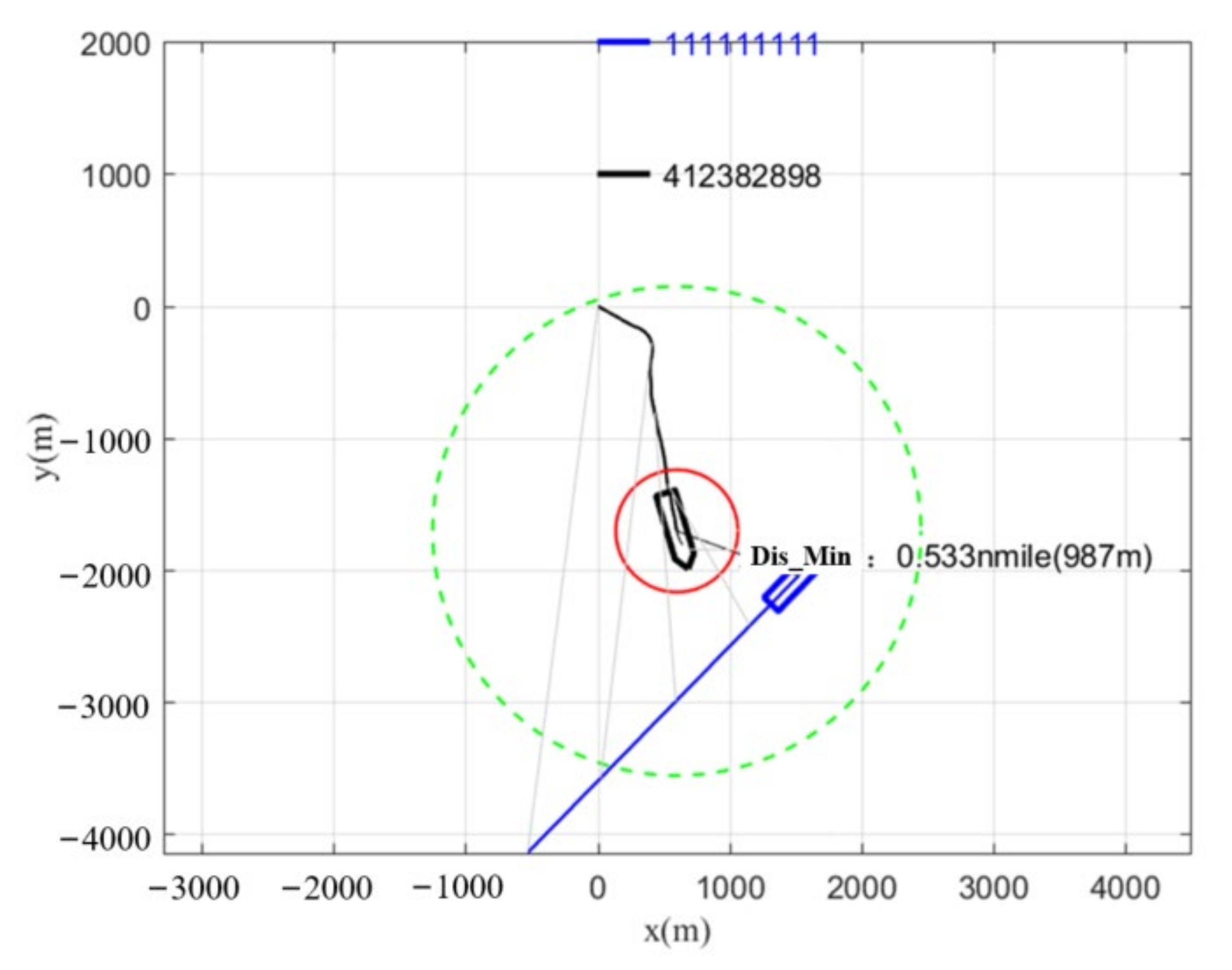
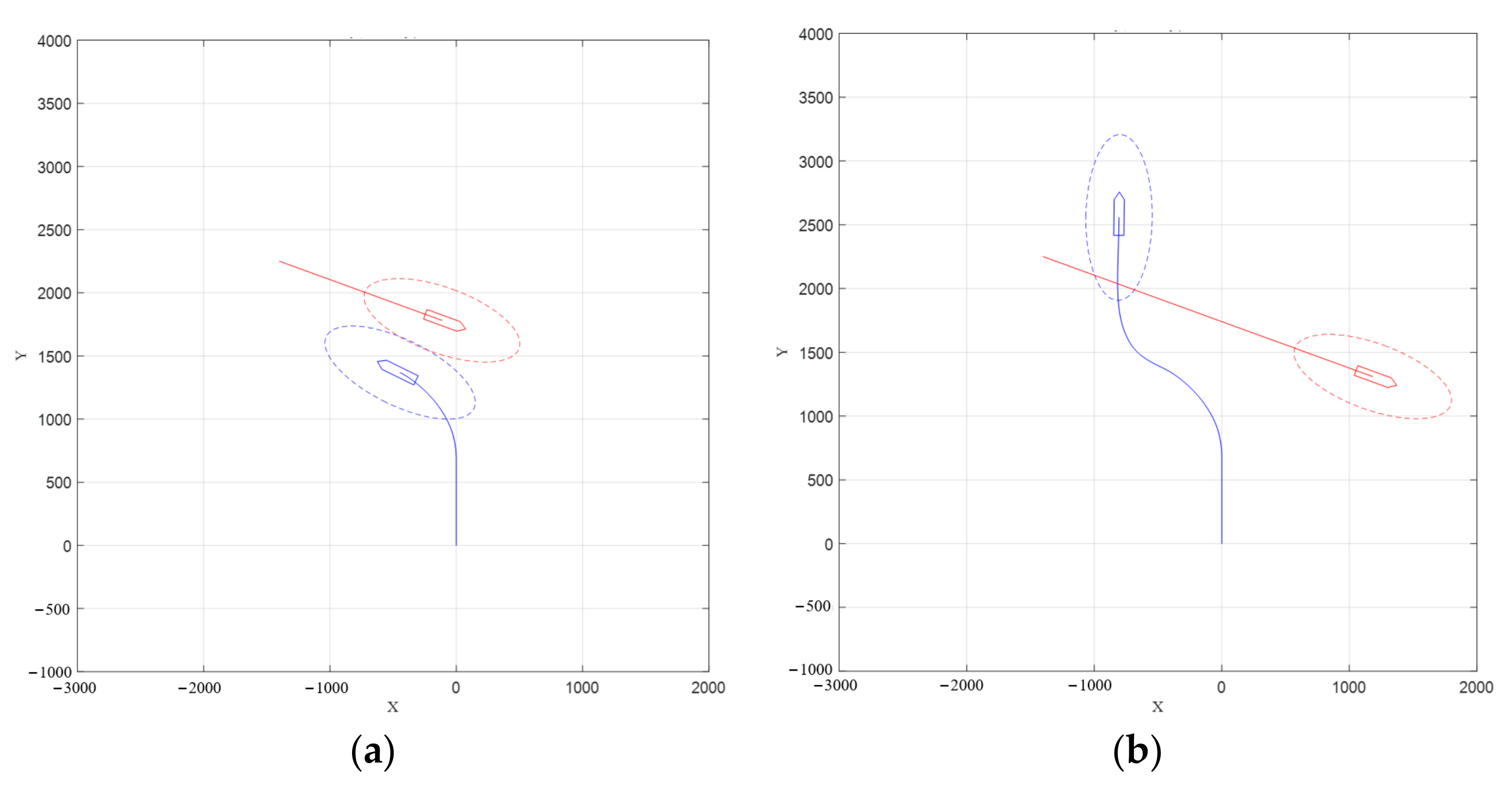
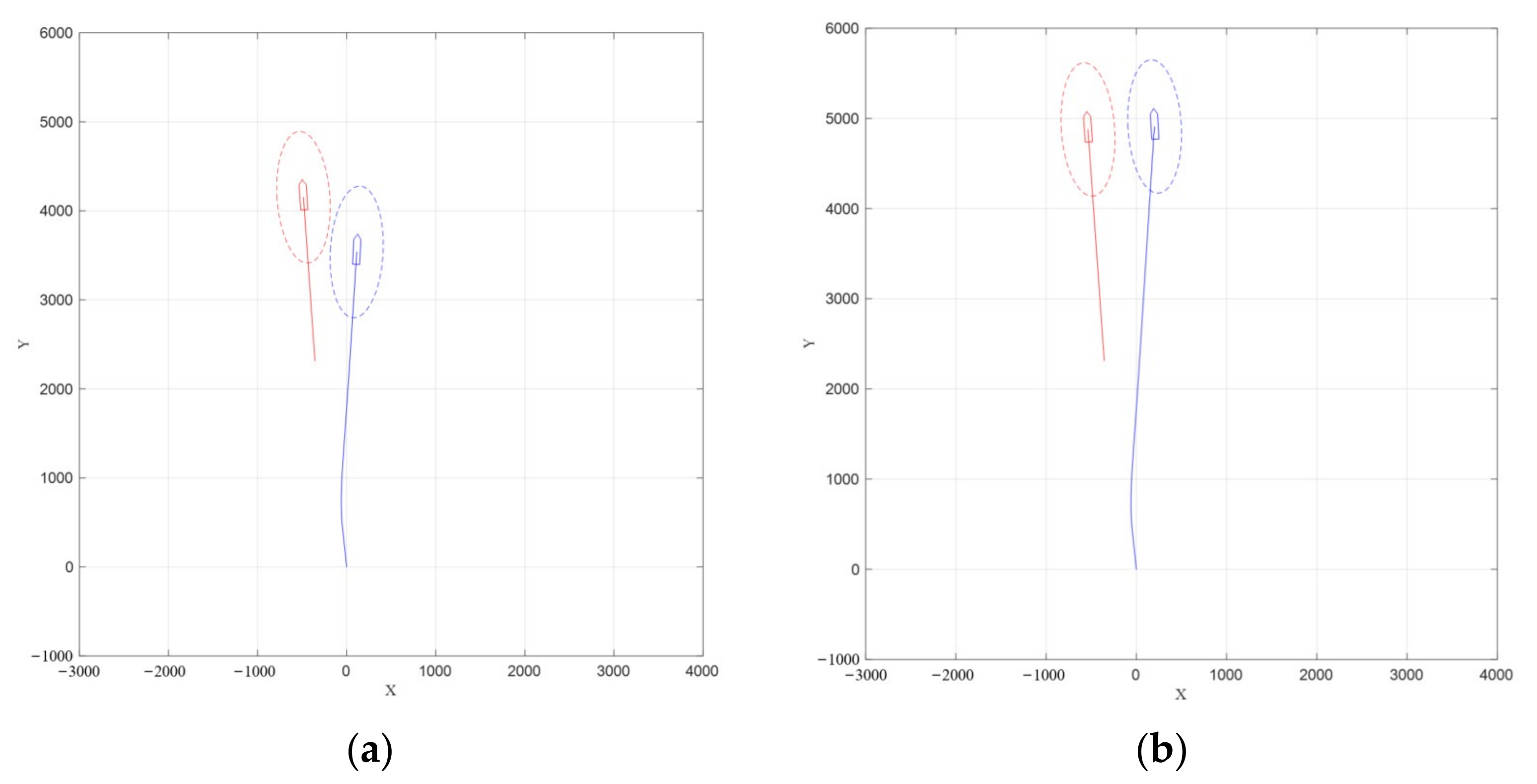
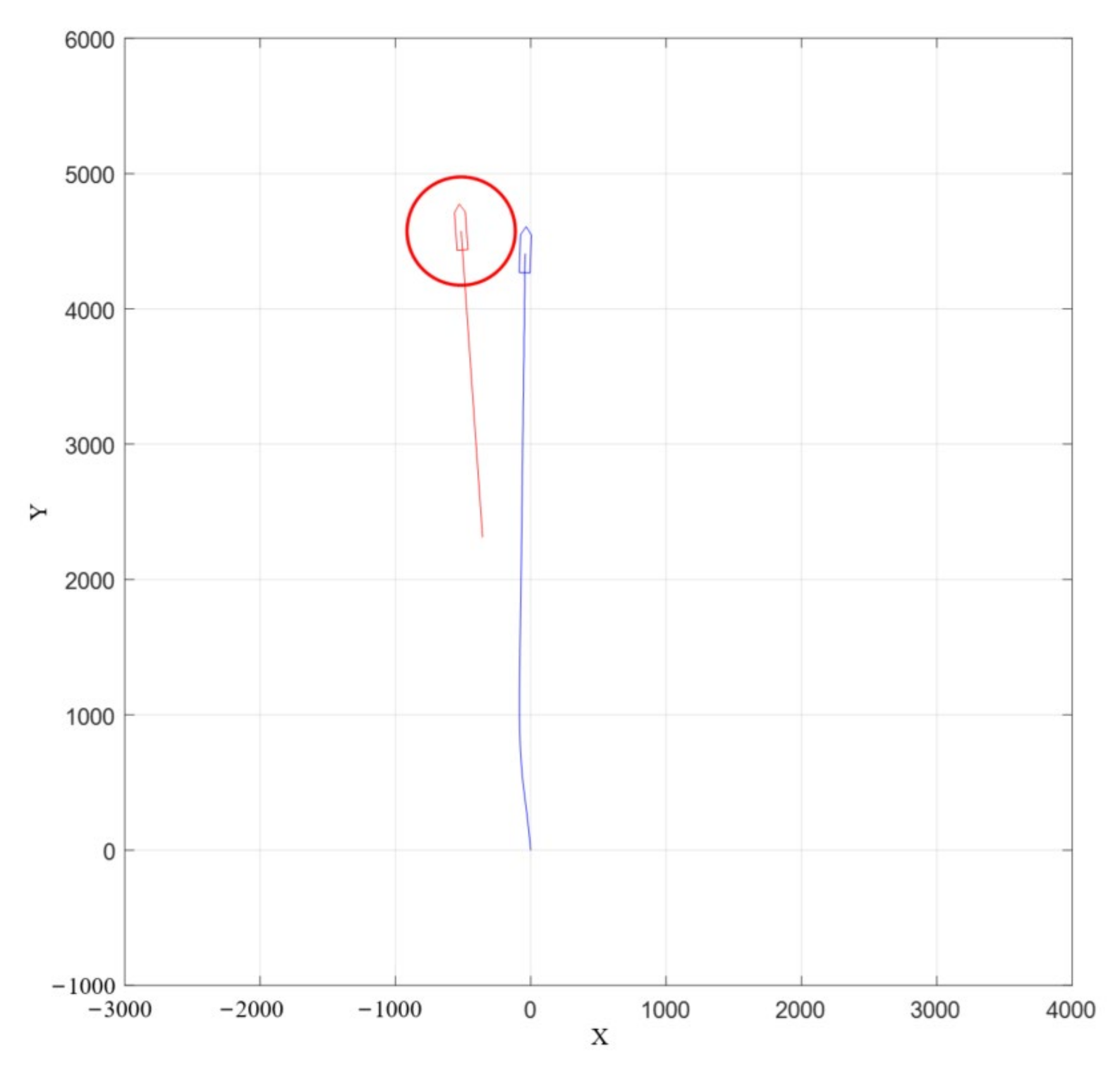
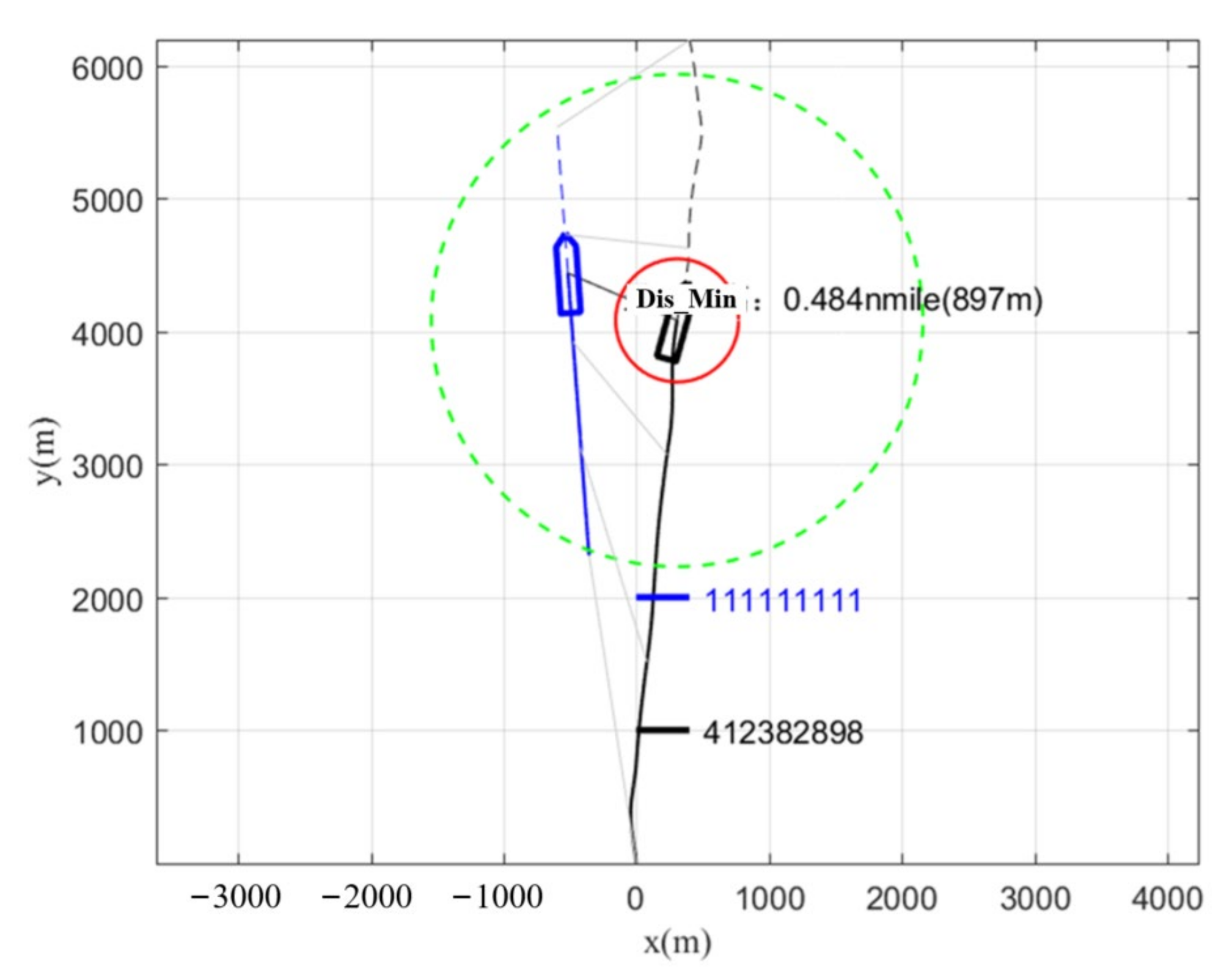
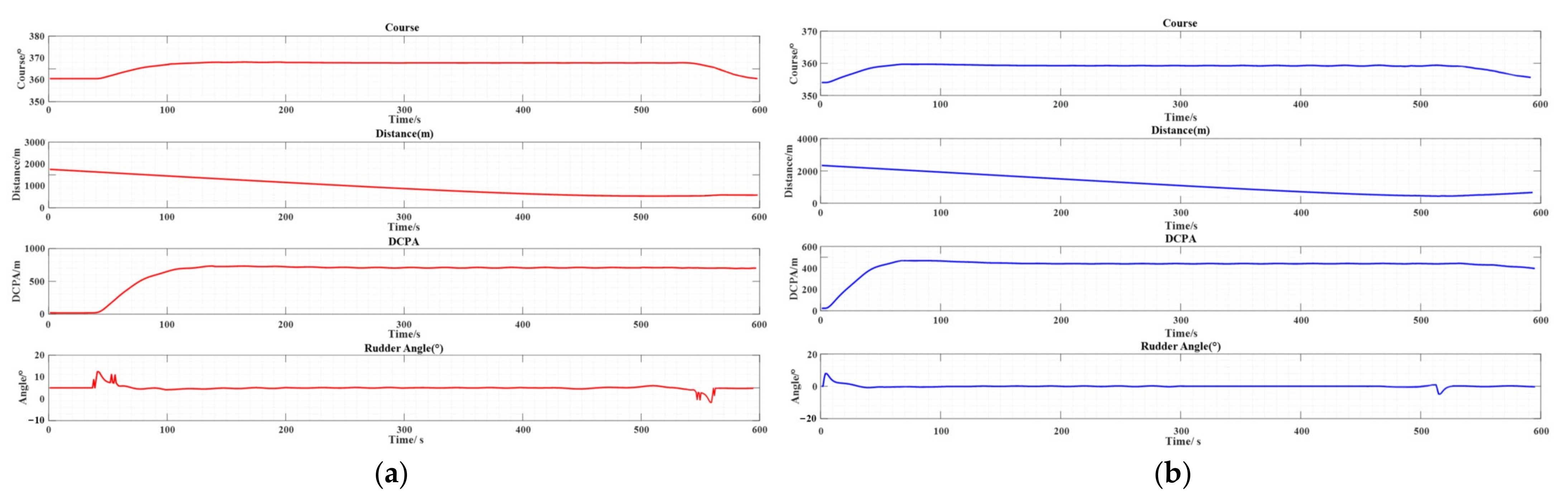
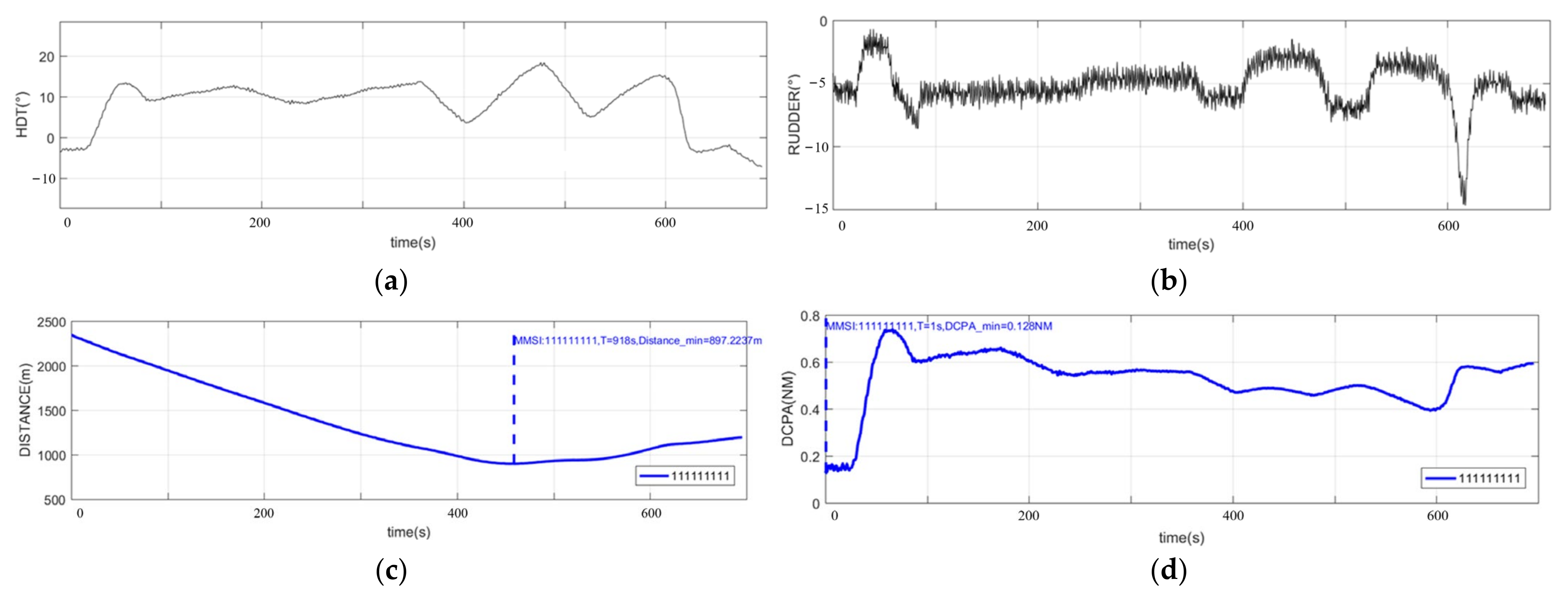
4. Experimental Results and Analysis
4.1. Actual Ship Experiment
4.2. The Evaluation of Experimental Data
- Head-on situation.
- Starboard side crossing situation.
- Port side crossing situation.
- Overtaking situation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, B.; Zheng, M.; Chu, X.; Mao, W.; Zhang, D.; Zhang, M. An overview of scholarly literature on navigation hazards in Arctic shipping routes. Environ. Sci. Pollut. Res. 2023, 1–17. [Google Scholar] [CrossRef]
- Shi, X.; Zhuang, H.; Xu, D. Structured survey of human factor-related maritime accident research. Ocean Eng. 2021, 237, 109561. [Google Scholar] [CrossRef]
- Weng, J.; Liao, S.; Wu, B.; Yang, D. Exploring effects of ship traffic characteristics and environmental conditions on ship collision frequency. Marit. Policy Manag. 2020, 47, 523–543. [Google Scholar] [CrossRef]
- Toyoda, S.; Fujii, Y. Marine traffic engineering. J. Navig. 1971, 24, 24–34. [Google Scholar] [CrossRef]
- Goodwin, E.M. A statistical study of ship domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Smierzchalski, R.; Michalewicz, Z. Modelling of a ship trajectory in collision situations at sea by evolutionary algorithm. IEEE Trans. Evol. Comput. 2000, 4, 227–241. [Google Scholar] [CrossRef]
- Wang, N. An intelligent spatial collision risk based on the quaternion ship domain. J. Navig. 2010, 63, 733–749. [Google Scholar] [CrossRef]
- Davis, P.V.; Dove, M.J.; Stockel, C.T. A computer simulation of marine traffic using domains and arenas. J. Navig. 1980, 33, 215–222. [Google Scholar] [CrossRef]
- Bukhari, A.C.; Tusseyeva, I.; Kim, Y.G. An intelligent real-time multi-vessel collision risk assessment system from VTS view point based on fuzzy inference system. Expert Syst. Appl. 2013, 40, 1220–1230. [Google Scholar] [CrossRef]
- Ma, D.; Chen, X.; Ma, W.; Zheng, H.; Qu, F. Neural Network Model-Based Reinforcement Learning Control for AUV 3-D Path Following. IEEE Trans. Intell. Veh. 2023, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Liu, K. A method of estimating ship collision risk based on fuzzy neural network. Ship Sci. Technol. 2008, 135–138. [Google Scholar]
- Zhao, G.; Wang, C.; Zhou, J.; Li, Y. Collision risk calculation of unmanned surface vehicle on improved fuzzy evaluation method. Syst. Eng. Electron. 2023, 1–9. [Google Scholar]
- Li, M.; Mou, J.; Chen, P.; Rong, H.; Chen, L.; van Gelder, P.H.A.J.M. Towards real-time ship collision risk analysis: An improved R-TCR model considering target ship motion uncertainty. Reliab. Eng. Syst. Saf. 2022, 226, 108650. [Google Scholar] [CrossRef]
- Abebe, M.; Noh, Y.; Seo, C.; Kim, D.; Lee, I. Developing a ship collision risk Index estimation model based on Dempster-Shafer theory. Appl. Ocean Res. 2021, 113, 102735. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- He, Z.; Liu, C.; Chu, X.; Negenborn, R.R.; Wu, Q. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl. Ocean Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Shang, Z.; Guo, S.; Du, Y. A decision-making method for ship collision avoidance based on improved cultural particle swarm. J. Adv. Transp. 2021, 2021, 8898507. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef]
- Hong, X.; Xu, Z.; Wei, X.; Zhu, K.; Chen, Y. Dynamic obstacle avoidance of unmanned surface vehicle based on improved speed obstacle method. Opt. Precis. Eng. 2021, 29, 2126–2139. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Qu, D.; Ke, J.; Li, X. Dynamic obstacle avoidance for USV based on velocity obstacle and dynamic window method. J. Shanghai Univ. Nat. Sci. Ed. 2017, 23, 1–16. [Google Scholar]
- Ma, J.; Su, Y.; Xiong, Y.; Zhang, Y.; Yang, X. Decision-making method for collision avoidance of ships in confined waters based on velocity obstacle and artificial potential field. Chin. J. Saf. Sci. 2020, 30, 60–66. [Google Scholar]
- Zhang, G.; Wang, Y.; Liu, J.; Cai, W.; Wang, H. Collision-avoidance decision system for inland ships based on velocity obstacle algorithms. J. Mar. Sci. Eng. 2022, 10, 814. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Li, L. A collision avoidance decision-making system for autonomous ship based on modified velocity obstacle method. Ocean Eng. 2020, 215, 107910. [Google Scholar]
- Kuwata, Y.; Wolf, M.T.; Zarzhitsky, D.; Huntsberger, T.L. Safe maritime autonomous navigation with COLREGS, using velocity obstacles. IEEE J. Ocean. Eng. 2013, 39, 110–119. [Google Scholar] [CrossRef]
- Zhao, L.; Fu, X. A novel index for real-time ship collision risk assessment based on velocity obstacle considering dimension data from AIS. Ocean Eng. 2021, 240, 109913. [Google Scholar] [CrossRef]
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Du, P.; Ouahsine, A.; Tran, K.T.; Sergent, P. Simulation of the overtaking maneuver between two ships using the non-linear maneuvering model. J. Hydrodyn. 2018, 30, 791–802. [Google Scholar] [CrossRef]
- Sun, F.; Cai, Y.; Ma, J. A Study of Test Methods and Indicators for Marine Intelligent Anti-collision strategy. Traffic Inf. Saf. 2019, 37, 84–93. [Google Scholar]
- Zhang, L.; Wang, H.; Meng, Q. Big data–based estimation for ship safety distance distribution in port waters. Transp. Res. Rec. 2015, 2479, 16–24. [Google Scholar] [CrossRef]
- Li, L. Determination of elements such as the safe distances of approach in automatic collision avoidance studies of ships. J. Dalian Marit. Univ. 2002, 23–26. [Google Scholar] [CrossRef]
- Chen, C.; Li, G.; Li, F.; Li, L.; Chen, G. The Risk Threshold of Ship Collision in Different Waters. China Navig. 2020, 43, 27–32. [Google Scholar]
- Perera, L.P.; Soares, C.G. Ocean vessel trajectory estimation and prediction based on extended Kalman filter. In Proceedings of the Second International Conference on Adaptive and Self-Adaptive Systems and Applications, Lisbon, Portugal, 21–26 November 2010; pp. 14–20. [Google Scholar]
- Zhao, J. Principles of Ship Collision Avoidance; Dalian Maritime University Press: Dalian, China, 1998. [Google Scholar]
- Naeem, W.; Irwin, G.W.; Yang, A. COLREGs-based collision avoidance strategies for unmanned surface vehicles. Mechatronics 2012, 22, 669–678. [Google Scholar] [CrossRef]
- Zhong, J. Analysis of the risk of collision, close quarters situation and immediate Danger. J. Shanghai Marit. Univ. 1999, 20, 77–79. [Google Scholar]
- Hu, Y.; Zhang, A.; Tian, W.; Zhang, J.; Hou, Z. Multi-ship collision avoidance decision-making based on collision risk index. J. Mar. Sci. Eng. 2020, 8, 640. [Google Scholar] [CrossRef]


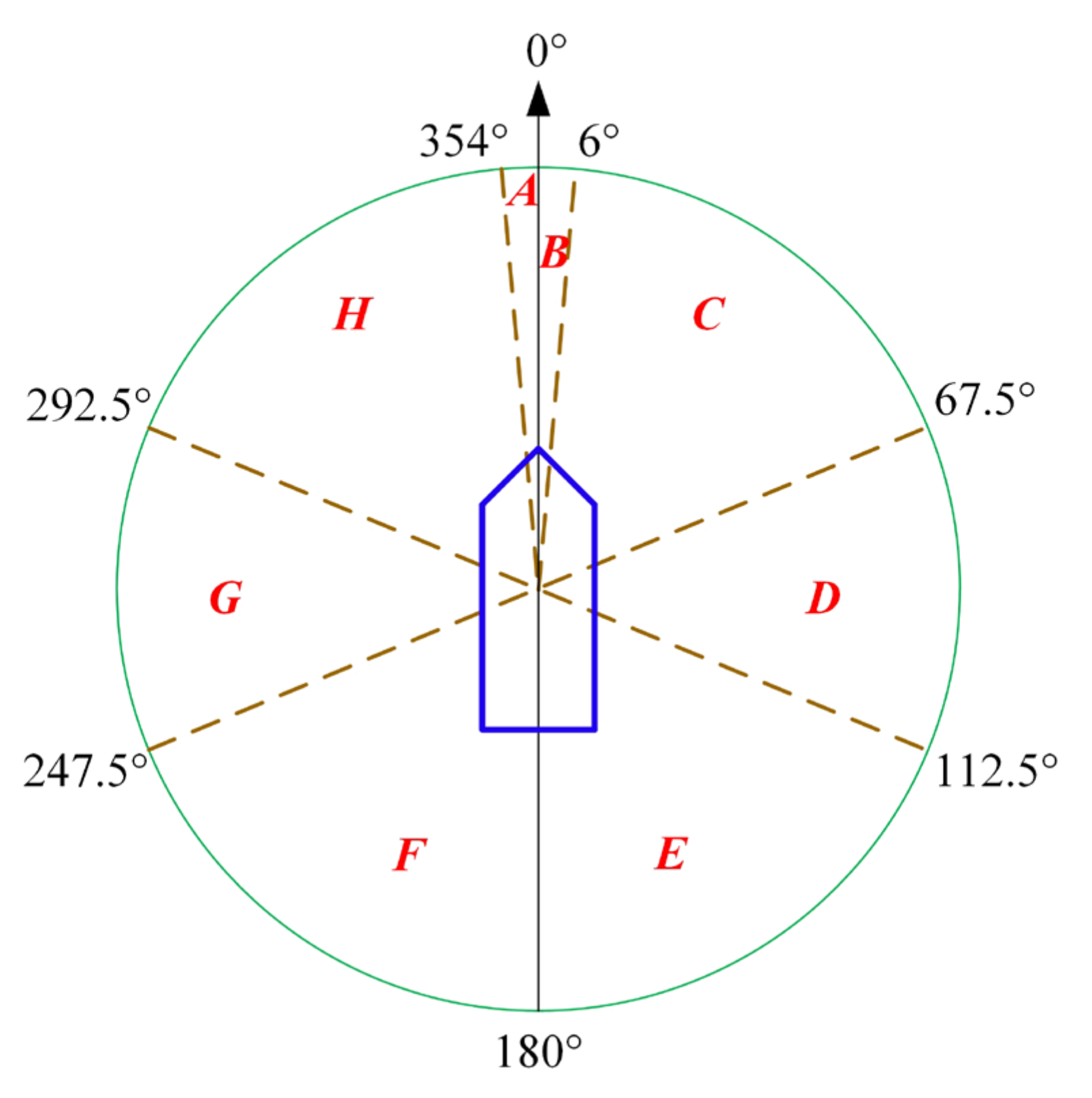






| Types of Encounter | The Area Where the Target Ship Is Located | Course Difference | Encounter Situation | Suitable Action for Own Ship |
|---|---|---|---|---|
| Head-on | A, B | 175–185° | Head-on | Turning right |
| Starboard side crossing | D | 270–360° | Large course difference crossing form starboard side | Turning right |
| C | 180–270° | Small course difference crossing form starboard side | Turning right | |
| Port side crossing | G | 0–90° | port large angle crossing | Keeping course and speed |
| H | 90–180° | port large angle crossing | Keeping course and speed | |
| Overtaking | A, H | 0–67.5° | Own ship pass on the starboard side of the target ship | Turning right |
| B, C | 292.5–360° | Own ship pass on the port side of the target ship | Turning left | |
| Being overtaken | E | 0–67.5° 292.5–360° | Target ship pass on the starboard side of own ship | Keeping course and speed |
| F | Target ship pass on the port side of own ship | Keeping course and speed |
| Type | Minimum Distance (n Mile) | Maximum Distance (n Mile) |
|---|---|---|
| Collision risk | 1 | 6 |
| Close-quarters situation | 0.25 | 1 |
| Imminent danger | 0 | 0.25 |
| Length (m) | Width (m) | Total Tonnage (t) | Speed (kn) |
|---|---|---|---|
| 43.9 | 7.3 | 353 | 3–12 |
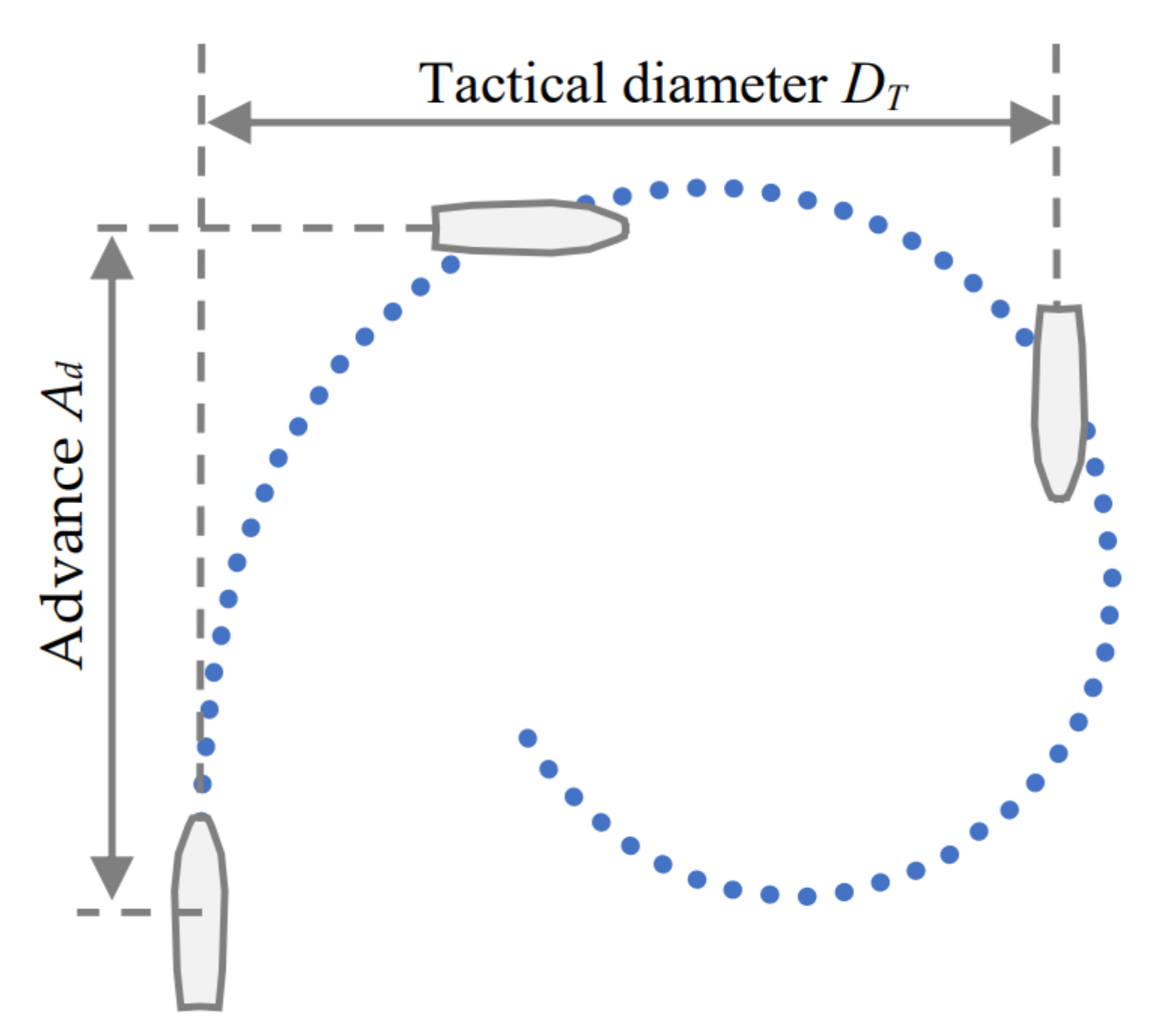
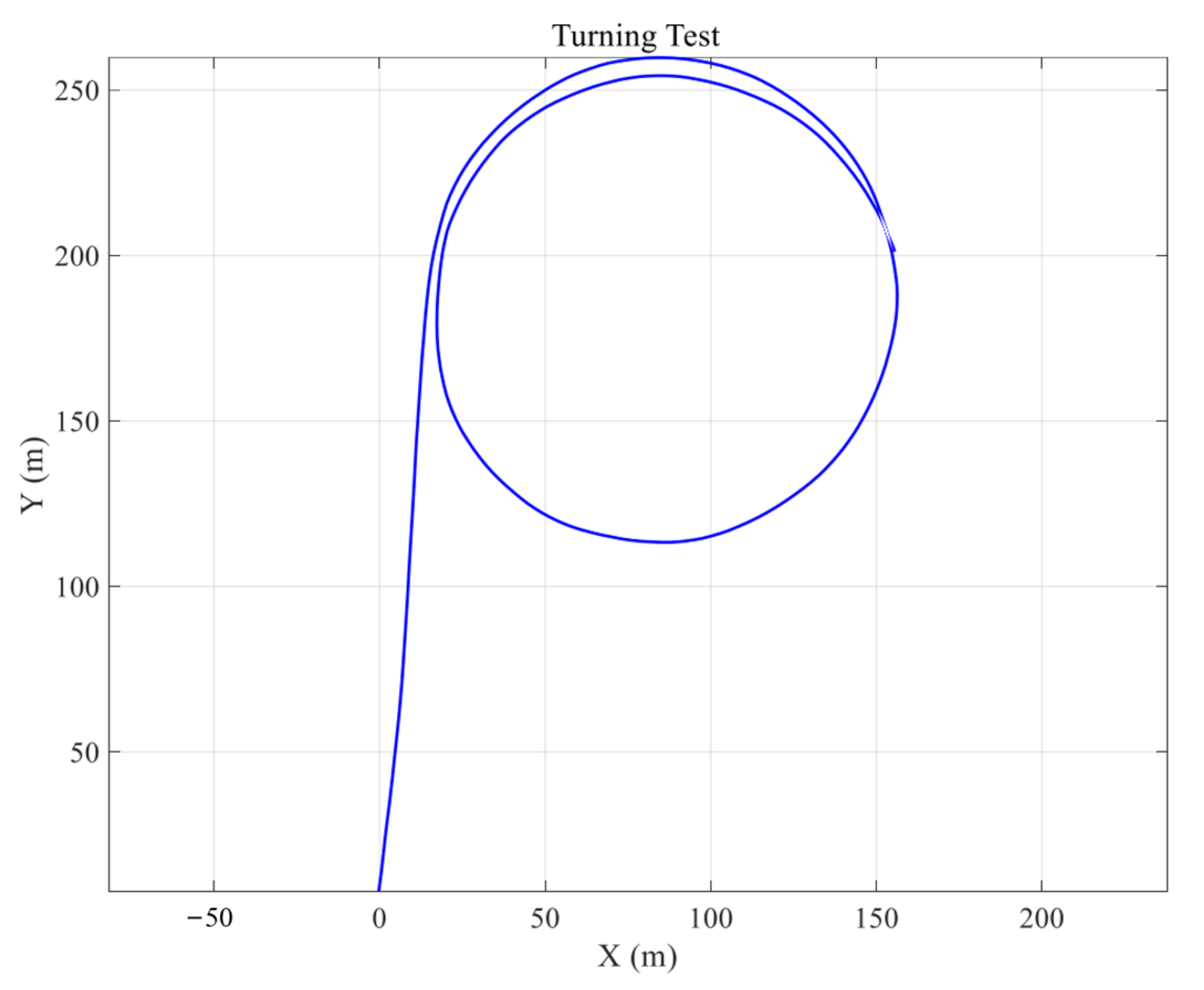
| /(m) | /(m) | (m) | (m) | /(s) | |
|---|---|---|---|---|---|
| Full rudder 30° | 148.1256 | 146.4241 | 109.3487 | 76.8136 | 44 |
| Situation | Own Ship | Target Ship | ||||
|---|---|---|---|---|---|---|
| Initial Coordinates (N, E) | Course (°) | Speed (kn) | Initial Coordinates (N, E) | Course (°) | Speed (kn) | |
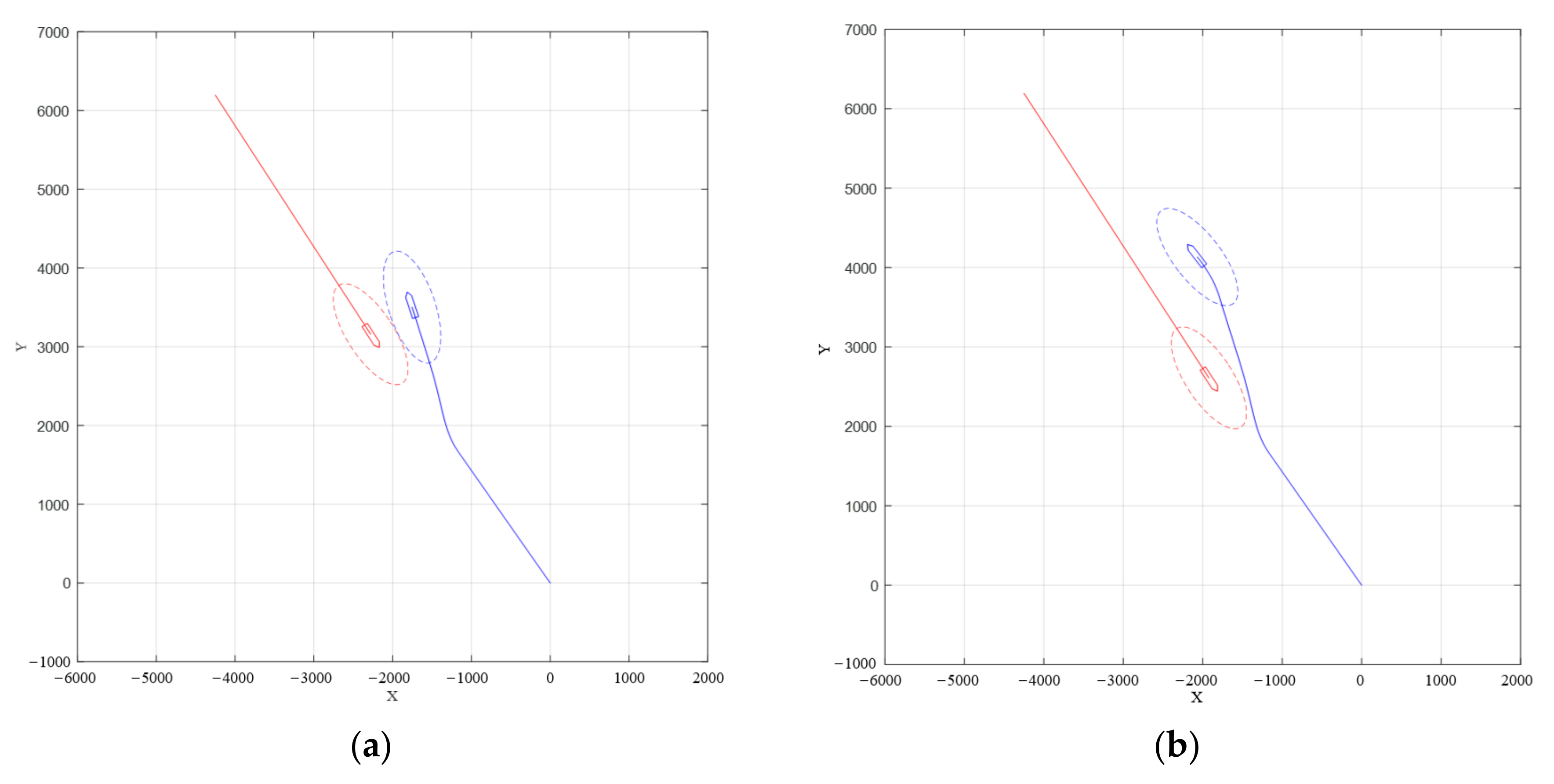
| Head-on | (20.756941°, 110.625902°) | 324.4 | 9.1 | (20.812550°, 110.583753°) | 147 | 8.6 |
| Starboard side crossing | (20.784380°, 110.616869°) | 117.2 | 7.9 | (20.747173°, 110.611780°) | 44 | 12.5 |
| Overtaking | (20.689691°, 110.630284°) | 356.7 | 8.6 | (20.710497°, 110.626862°) | 356 | 4.5 |
| Evaluation Index | Improved VO | Traditional VO | Manual Ship Handling |
|---|---|---|---|
| Own ship is in imminent danger | ① | ③ | ① |
| Minimum encounter distance | ② | ③ | ① |
| Deviation factor | ② | ① | ③ |
| Maximum alteration of course | ② | ③ | ① |
| Collision avoidance time | ② | ① | ② |
| Steering frequency | ① | ① | ③ |
| Total | ① | ③ | ② |
| Evaluation Index | Improved VO | Traditional VO | Manual Ship Handling |
|---|---|---|---|
| Own ship is in imminent danger | ① | ③ | ① |
| Minimum encounter distance | ② | ③ | ① |
| Deviation factor | ② | ① | ③ |
| Maximum alteration of course | ② | ③ | ① |
| Collision avoidance time | ① | ③ | ① |
| Steering frequency | ① | ① | ③ |
| Total | ① | ③ | ② |
| Evaluation Index | Improved VO | Traditional VO | Manual Ship Handling |
|---|---|---|---|
| Own ship is in imminent danger | ① | ③ | ① |
| Minimum encounter distance | ② | ③ | ① |
| Deviation factor | ② | ① | ③ |
| Maximum alteration of course | ② | ③ | ① |
| Collision avoidance time | ② | ① | ③ |
| Steering frequency | ① | ① | ③ |
| Total | ① | ③ | ② |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Zhang, K.; Han, B.; Lin, B.; Zhou, H.; Ding, S.; Zou, T.; Yang, Y. An Improved VO Method for Collision Avoidance of Ships in Open Sea. J. Mar. Sci. Eng. 2024, 12, 402. https://doi.org/10.3390/jmse12030402
Zheng M, Zhang K, Han B, Lin B, Zhou H, Ding S, Zou T, Yang Y. An Improved VO Method for Collision Avoidance of Ships in Open Sea. Journal of Marine Science and Engineering. 2024; 12(3):402. https://doi.org/10.3390/jmse12030402
Chicago/Turabian StyleZheng, Mao, Kehao Zhang, Bing Han, Bowen Lin, Haiming Zhou, Shigan Ding, Tianyue Zou, and Yougui Yang. 2024. "An Improved VO Method for Collision Avoidance of Ships in Open Sea" Journal of Marine Science and Engineering 12, no. 3: 402. https://doi.org/10.3390/jmse12030402
APA StyleZheng, M., Zhang, K., Han, B., Lin, B., Zhou, H., Ding, S., Zou, T., & Yang, Y. (2024). An Improved VO Method for Collision Avoidance of Ships in Open Sea. Journal of Marine Science and Engineering, 12(3), 402. https://doi.org/10.3390/jmse12030402





