Next Article in Journal
Mangroves as Coastal Protection for Restoring Low-Energy Waterfront Property
Next Article in Special Issue
Seafloor Sediment Acoustic Properties on the Continental Slope in the Northwestern South China Sea
Previous Article in Journal
Time Domain Vibration Analysis of an Ice Shelf
Previous Article in Special Issue
Propagation Velocity of Excitation Waves Caused by Turbidity Currents
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 12
Issue 3
10.3390/jmse12030469
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Centrifuge Modelling of Composite Bucket Foundation Breakwater in Clay under Monotonic and Cyclic Loads

by
Minmin Jiang
1,2,
Zhao Lu
3,*,
Zhengyin Cai
4 and
Guangming Xu
4
1
College of Civil Engineering, Henan University of Technology, Zhengzhou 450001, China
2
Henan Key Laboratory of Grain and Oil Storage Facility & Safety, Henan University of Technology (HAUT), Zhengzhou 450001, China
3
Marine Geotechnical Research Center, HKUST Shenzhen-Hong Kong Collaborative Innovation Research Institute, Shenzhen 518048, China
4
Department of Geotechnical Engineering, Nanjing Hydraulic Research Institute, Nanjing 210024, China
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2024, 12(3), 469; https://doi.org/10.3390/jmse12030469
Submission received: 17 January 2024 / Revised: 25 February 2024 / Accepted: 27 February 2024 / Published: 9 March 2024
(This article belongs to the Special Issue Advances in Marine Engineering: Geological Environment and Hazards II)
Browse Figures
Versions Notes

Abstract

:
This study investigates the monotonic and cyclic performance of composite bucket foundation breakwater in clay through centrifuge modeling. The application of monotonic loads simulates extreme wave conditions, and cyclic load corresponds to long-term serviceability conditions. In centrifuge tests, three typical soil strengths were tested, and two load eccentricities were simulated to check the influence of wave force height. Multiple measurements were conducted, including rotation angle, horizontal displacement, vertical settlement, and pore pressure variation. When soil strength increases in monotonic centrifuge tests, the ultimate bearing capacity of the bucket foundation experiences significant growth, and the foundation failure pattern varies. In responding to the monotonic test, the foundation’s rotation center constantly moved downward during the loading process, indicating that the deeper soil would be activated to resist the horizontal loading. In contrast, the rotation center movement in the symmetric centrifuge test was opposed to the non-symmetric test because the deeper soil was required to provide resistance to balance the more severe load under the non-symmetric loading condition. It should be noted that non-symmetric loading does not impact the bucket foundation as seriously as symmetric loading. The utilization of deep-soil resistance in non-symmetric tests is beneficial in controlling deformation.

1. Introduction

Breakwaters are important marine structures for protecting harbor facilities from severe storm wave loads. Caisson breakwater is one of the most widely used types of breakwater; however, it is often restricted in its application due to harsh conditions such as deep water and soft soil [1,2,3,4,5,6,7,8]. To address this issue, most recently, composite bucket foundation breakwater has become a competitive alternative [9,10,11,12]. A composite bucket foundation comprises four upside-down buckets combined by connecting walls, as illustrated in Figure 1. Compared with the traditional solid breakwater structure, the composite bucket foundation breakwater structure has a light weight, and the interaction between soil and the structure is strong due to the multiple compartments, making it suitable for application in coastal soft soil layers [12]. Meanwhile, it can be prefabricated on shore, and the installation is convenient, since the impact of filed construction can be controlled without cast-in-place work, etc. However, failure of the composite bucket foundation often occurs due to large displacements and excessive pore pressures when subjected to severe storm wave loads. Guo et al. [13,14,15,16] have conducted a comprehensive study about the structure and pipelines in the seabed. Therefore, understanding the performance of composite bucket foundation breakwater under storm wave loading conditions becomes considerably crucial for its design and construction in practice.
Over recent decades, various studies have been conducted to investigate the behavior of bucket foundations under storm wave loads. Bransby et al. [16], Achmus et al. [17], and Thieken et al. [18] have the impact of investigated bucket geometry, embedment ratio, loading conditions, and soil permeability on the bearing capacity of bucket foundations. Hong et al. [19,20], Park et al. [21,22], Wang et al. [23,24], Choo et al. [25], and Tasiopoulou et al. [26] have performed numerical and centrifuge studies to investigate the bearing capacity of bucket foundations, and equations for estimating the vertical, lateral, and tensile bearing capacities were proposed. Zhang et al. [27] have explored the cyclic failure modes of bucket foundations in silt. They indicated that the structure failed due to large displacements after long-term excitations, or foundation liquefaction in early excitations. Bransby et al. [16], Barari et al. [28], and Liu et al. [29] have studied the failure envelopes of bucket foundations, and the results indicate that failure envelopes under combined vertical, horizontal, and moment loading present an ellipsoid shape. Byrne et al. [30], Cox et al. [31], and Zhu et al. [32,33] have also studied the cyclic deformation behavior of bucket foundations. They found that a power relationship with a number of load cycles can describe vertical load-dependent displacement. Achmus et al. [17], Cox et al. [31], Wang et al. [10,24], and Grecu et al. [34] have studied the stiffness of the bucket soil system and revealed that initial stiffness is dependent on bucket geometry, the relative density of sand, and load eccentricity. Ding et al. [35] have performed a model test and numerical study to investigate the deformation mechanism and ultimate bearing capacity of composite bucket foundations for wind turbines. Kim et al. [36,37] and Hong et al. [19,20] have studied the bearing capacity of tripod bucket foundations, found that the bearing capacity of a tripod foundation was lower than that of a monopod foundation, and proposed the group efficiency factor to quantify the group effect of tripod bucket foundations.
The centrifugal model test has advantages over the 1 g model, field test, and numerical simulation method [13,16]. First, the stress state in the 1 g laboratory model test is significantly smaller than that of the engineering prototype. The engineering characteristic of soil is influenced by the stress state and has nonlinear and elastic-plastic characteristics [16]. Hence, the 1 g model test can not fully reflect the practice’s stress state and response characteristics. On the other hand, field tests are resource- and time-consuming methods, so the number of tests is limited. A field test is generally conducted to check the serviceability of infrastructures and cannot investigate the extreme state. With respect to numerical simulations, the assumptions of the numerical model are generally idealized, and the parameters are simplified. The centrifugal model test provides one effective solution to the above problems. Following the similarity law, the model is placed in a high gravitational field, which can reproduce the field stress state and reflect the characteristics of geotechnical engineering. Therefore, the centrifugal test is used to investigate the characteristics of the composite bucket foundation structure in clay.
However, the majority of the above studies are limited to single-bucket foundations, while very limited attention has been paid to composite bucket foundations. In addition, the existing studies have mainly focused on wind turbine and offshore platform structures; nevertheless, the load conditions applied on breakwater differ significantly from that for those structures [35,38,39,40]. Moreover, the existing studies were mainly conducted by employing numerical analysis, with a focus on the stability of bucket foundations and the distribution of earth pressure against bucket walls under monotonic loading conditions [23,24,40], while experimental studies on the behaviors of bucket foundation breakwater are rather limited, especially when it is subjected to long-term cyclic loading conditions.
In this study, a series of centrifuge tests were carried out to investigate the performance of composite foundation breakwater in clay under different loading conditions. Based on a monotonic loading apparatus, a non-contact cyclic loading system was developed to apply both symmetric and non-symmetric loading. Both monotonic and cyclic loading models were conducted, simulating the extreme wave and long-term serviceability states, respectively. Three typical clay soils with different undrained strengths were used to construct the foundation soil, and two loading eccentricities were tested to check the influence of wave force height. In all tests, multiple measurements were adopted, including rotation angle, horizontal displacement, vertical settlement, and pore pressure variation. Based on the centrifuge tests, the displacement pattern at both extreme and regular service states could be analyzed.

2. Laboratory Investigations

2.1. Geotechnical Centrifuge Test Setup

The centrifuge modeling method is a powerful means to study the soil structure interaction, in that stress in the model test equals the prototype conditions [41]. The scaling laws for the geotechnical centrifuge test in this study are listed in Table 1. The tests in this study were conducted at Nanjing Hydraulic Research Institute on a 400 g-t geotechnical centrifuge, which has a radius of 5 m and a maximum acceleration of 200 g under the weight of 2000 kg. The centrifuge test was conducted at 105 g. The model container on the swing platform had an inner dimension of 685 mm × 350 mm × 475 mm (length × width × height), which corresponded to a prototype scale dimension of 72 m × 36.8 m × 47.3 m. This paper’s parameters and test results are presented on a prototype scale.

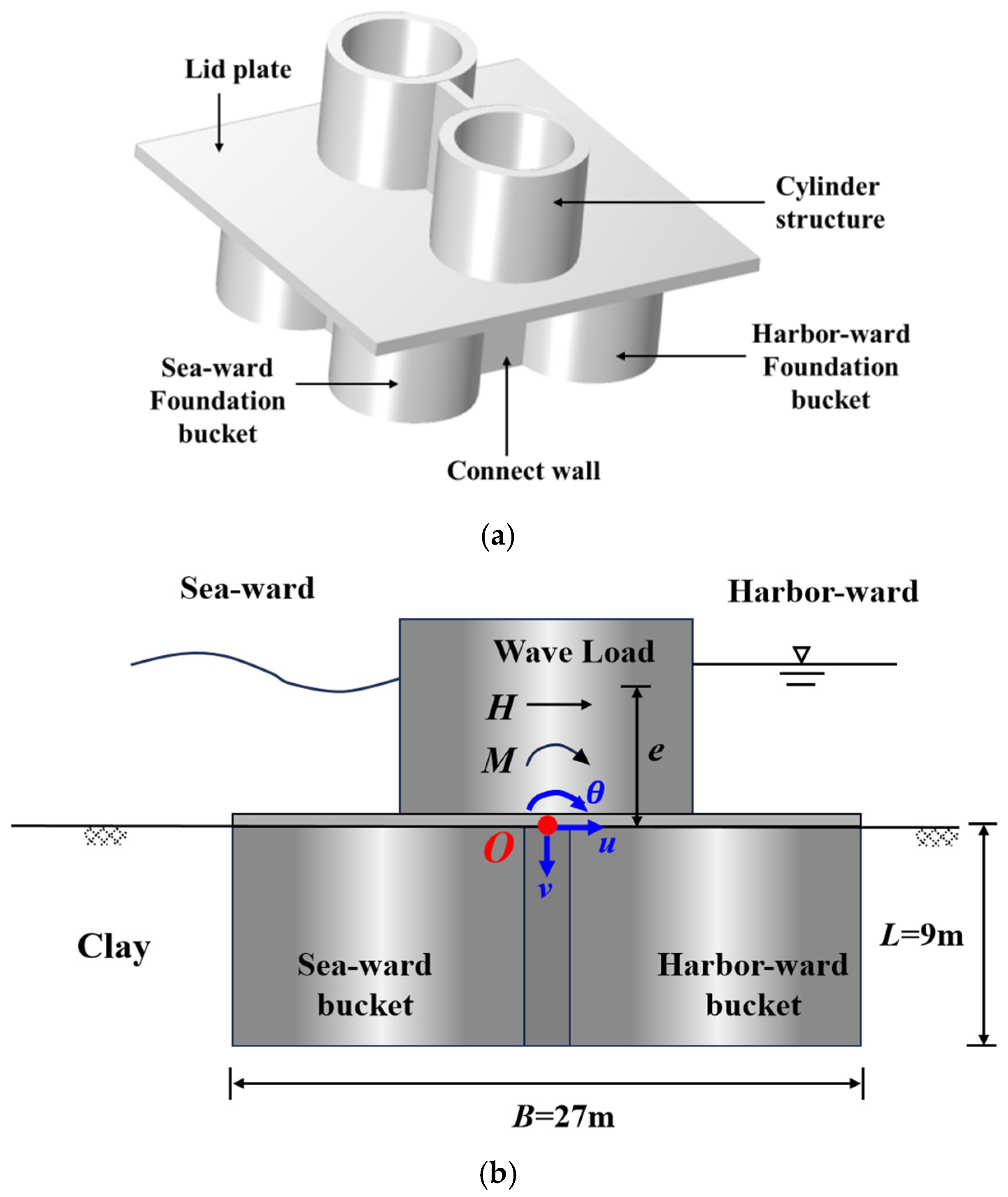
2.2. Modeling of Composite Bucket Foundation Breakwater

The composite bucket foundation comprised four upside-down buckets and vertical connection walls, forming five compartments. Above the foundation, a lid plate was fixed. Then, two vertical cylinder structures were erected on top of the lid plate to resist storm wave load. The structure of the composite bucket foundation breakwater is illustrated in Figure 1. Composite bucket foundation breakwater was sunk into the soil by weight and under pressure inside the compartments until the lid plate contacted the seabed.
The length of the structure, force on the structure, frequency of cyclic load, and bending moment on the structure were modeled according to the geotechnical centrifuge scaling law, as illustrated in Table 1. The model breakwater in this study was made of aluminum alloy with an elastic modulus of 70 GPa and a density of 2.7 g/cm3. The model was designed according to the centrifuge scaling law at a scale of 1:105. The wall thickness was modelled according to the flexural rigidity law [42,43] as follows:
t m = t p E p N E m 3
where Ep is the elastic modulus in the prototype, Em is the elastic modulus in the centrifuge model, tp is the thickness of the breakwater wall in the prototype, tm is the thickness of the breakwater wall in the centrifuge model, N is the scaling number of the centrifuge test, and subscripts p and m stand for the prototype and centrifuge model, respectively. The dimensions of the breakwater were as follows: the outer diameter of the foundation bucket and cylinder structure on top of the breakwater was 12 m, the thickness of the walls was 0.3 m, the length of the foundation bucket skirt and cylinder structure were 9 m and 8.3 m, respectively, the lid plate was square with a side length of 27 m and a thickness of 0.5 m. The model composite bucket foundation breakwater is shown in Figure 1a.

2.3. Preparation of Test Soil

The offshore area in Tianjin, China, was selected as the target site, and is primarily composed of a thick layer of clay. In the centrifuge study, a clay foundation was prepared using the consolidation method. The foundation soil was constructed with clay obtained from Tianjin engineering sites, as the clay parameters are introduced in Table 2. The clay was made into a uniform slurry with a water content two times that of the liquid limit. Then, the clay was poured into a model container and consolidated under constant vertical pressure. The undrained shear strength of the clay foundation was measured by a mini cone penetrometer after consolidation; the average undrained shear strength of the clay foundation is shown in Table 3. The soil with undrained shear strength of 23 kPa represents the deep soft soil condition on the Tianjin Port breakwater project site. And the clay foundations with higher soil strengths of 37 kPa and 45 kPa (all represent typical soil strengths tested from Tianjin Port soft soil) were also simulated in the centrifugal test, to check the soil strength effect.
According to the centrifuge scaling law illustrated in Table 1, the soils’ densities and undrained strengths in the centrifuge model test were equal to the prototype value and time for consolidation, and the dynamic stage is 1/N2 and 1/N of the prototype value. The same pore fluid and soil were utilized in the centrifuge model study as in the prototype condition. The time-scaling law for consolidation is inconsistent with dynamic events in cyclic tests, i.e., pore pressure dissipates faster than in prototype conditions, which is known as time-scaling law conflict. However, in this study, the permeability of clay was about 1.3 × 10−7 cm/s, and the dissipation of excess pore pressure was not apparent during cyclic loads; therefore, scaling law conflict can be neglected, and pore pressure was considered to be correctly replicated in cyclic centrifuge tests [44,45].

2.4. Simulation of Storm Wave Load on Composite Bucket Foundation

In the monotonic centrifuge test, the load was applied on breakwater through an actuator, which was driven by a low-speed permanent-magnet synchronous motor. Consequently, the monotonic load was applied under a constant displacement rate. A schematic of the device is shown in Figure 2a.
In the cyclic centrifuge test, a cyclic wave load was applied through a newly developed non-contact loading device. This novel device comprised an armature iron, a load transfer unit, and two electromagnetic actuators on the sea-ward and harbor-ward sides. Armature iron was fixed beneath the top cover of the model test chamber, and a load transfer unit was installed between the two electromagnetic actuators. The cyclic load exerted by electromagnetic actuators on both sides was imposed on the armature iron, and then acted on breakwater through the load transfer unit. There was no connection between the electromagnetic actuators and breakwater; hence, the structure could be displaced freely without contact constraint. A sketch of the non-contact cyclic loading device is shown in Figure 2b. In this study, the loading system was improved, as the non-contact cyclic loading system was both symmetrically and non-symmetrically developed. It should be noted that the effect of wave pressure on the surface of the subsea foundation was not considered in this study, and this might be improved in future experiments and numerical simulations.
Clay exhibits complicated mechanical properties under cyclic loads, such as plasticity, viscosity, and hysteresis. In particular, the interaction between the breakwater structure and clay foundation is complex, which causes difficulty in applying cyclic load on the breakwater precisely. Hence, a real-time control system was developed. The cyclic load was controlled by a fuzzy increment proportional–integral–differential (abbreviated as PID) algorithm programmed by using LabVIEW (version 2016). The control signal was composed of a primary component and a feedback component. The data acquisition frequency reached 1000 Hz, conforming to the cyclic test’s record requirements. A low-pass digital filter was used to eliminate the noise of test data. Schematics of the real-time control system are illustrated in Figure 2c.

2.5. Test Program

A series of monotonic and cyclic tests were designed to study the behavior of composite bucket foundation breakwater under the influence of soil undrained shear strength, load eccentricity, and the characteristics of cyclic load.
Wave parameters in the Tianjin Port site are as follows: the water depth in front of the breakwater is 8.6 m, the wave height is 5.2 m, and the wave period is 8.1 s. Wave load on the breakwater structure was estimated based on Goda formulas [46,47], the design horizontal load acted by the wave crest Hd was 8.45 MN, design moment Md is 38 MN·m, and the negative load acted by the wave trough was −3.38 MN (about −0.4 Hd). The horizontal load was 4.5 m above the seabed level, referred to as loading eccentricity e, as is illustrated in Figure 1b (equals 38 MN·m/8.45 MN).
The monotonic load was applied to the breakwater structure by a monotonic loading device at a rate of 0.02 mm/s, and the horizontal load was normalized by the design horizontal load on the Tianjin Port site. The time history of the monotonic load is illustrated in Figure 3a. Cyclic loads were applied by non-contact cyclic loading at a period of 8.1 s, which is the same as Tianjin Port’s conditions. Two parameters, ζb and ζc, were employed to describe the characteristics of cyclic load:
ζ b = H max H d
ζ c = H min H max
where Hd is the designed horizontal load calculated by Goda’s method, and Hmax and Hmin are the maximum and minimum load in a single period acted by wave crest and wave trough [48]. ζb denotes the size of the cyclic load, and ζc represents the type of cyclic loading. When ζc is −1, the cyclic load is symmetrical; when ζc is −0.4, the cyclic load is a non-symmetric load corresponding to the Tianjin Port conditions. The total cycle number reached 46,800 in the cyclic centrifuge test, corresponding to 105 h of storm wave load. Schematics of the load history for the cyclic test are presented in Figure 3b.
The undrained shear strength of soil was 23.9 kPa, and load eccentricity was 4.5 m in test S1. The parameters corresponding to the Tianjin Port site situation were applied in test S1, the reference test. In tests S2, S3, and S4, the undrained shear strength of soil increased from 23 kPa to 37.4 and 45 kPa, respectively. Meanwhile, load eccentricity increased from 4.5 m to 10.5 m, and tests S2, S3, and S4 were performed to investigate the effect of the undrained shear strength of soil and the height of wave load on composite bucket foundation breakwater performance. Details of the centrifuge test program are illustrated in Table 3.
After the clay foundation was prepared, the model composite bucket foundation breakwater was jacked into seabed soil. Then, the model test chamber was placed in a forced gravitational field to simulate the clay foundation’s consolidation under the breakwater’s weight. Finally, the monotonic and cyclic horizontal loads were applied to the breakwater structure, until the prescribed displacement or cycle number were attained.
Schematics of the side elevation of the model setups in the monotonic and cyclic loading tests are presented in Figure 4. The displacement of the breakwater structure was measured by a high-performance laser distance sensor (abbreviated as LDS). Positive rotation and horizontal displacement are toward the harbor, and positive vertical displacement corresponds to settlement. Two pore pressure transducers (PPTs) were embedded in clay foundations outside the sea-ward bucket and harbor-ward bucket at a depth of 6 m, monitoring excess pore pressure under monotonic and cyclic loading conditions.

3. Results

First, the repeatability of centrifuge tests was checked. Static model tests S1-1 and S1-2 were performed with identical experimental conditions, and the rotation angle responses for the two tests are presented in Figure 5. It is demonstrated that the parallel test shows good consistency in geotechnical performance. According to the locating inflection point method, the lateral capacity for the S1 model calculated by Xiao [40,49] is 2.66 Hd, which is in line with the centrifuge test result of 2.69 Hd. This demonstrates that the centrifuge experiment method is applicable in evaluating bucket foundation performance. In centrifuge models, the test condition on the bucket foundation can achieve an extreme failure state, and a more systematic study of the foundation can be conducted. For field practice models, the experiment condition is generally limited to a regular service state, which is restricted to describing the full performance of geotechnical structures.

3.1. Behavior Breakwater under Monotonic Load

3.1.1. Displacement Properties of Breakwater

Under monotonic load toward the harbor-ward direction, the influences of soil strength and load eccentricity on the displacement of composite bucket foundation breakwater are shown in Figure 6. The load–displacement curve can be divided into two stages: the initial elastic and the plastic stages [50,51]. A distinct transition is observed in the load–rotation angle curve as the load increases significantly beyond the inflection point. The initial elastic range and plastic range are fitted with straight lines, and the value at the inflection point is defined as the bearing capacity of the breakwater [32]. The ultimate bearing capacity load is depicted in Figure 6a, denoted by Hu. When the soil undrained shear strength increases from 23 kPa to 44.5 kPa, the bearing capacity load (Hu) increases significantly from 1.31 Hd to 4.29 Hd. When the soil undrained shear strength remains 23 kPa, the ultimate bearing capacity load Hu decreases from 2.69 Hd to 1.31 Hd with the rise in loading eccentricity.
The influence of soil strength and load eccentricity on the horizontal load–horizontal displacement relationship of the bucket foundation is presented in Figure 6b. When the horizontal load exceeds the critical value (ultimate bearing capacity load Hu), horizontal displacement increases significantly. For tests with a low undrained shear strength of soils (i.e., Su is about 23 kPa in tests S1 and S2), the transition points are found in the horizontal load–vertical displacement curve, beyond which vertical displacement increased significantly. In discussing medium soil strengths (37.4 kPa in test S3), vertical displacement increases roughly linearly with horizontal load. In contrast, for the test with a high undrained shear strength of soils (44.5 kPa in test S4), vertical displacement decreases with horizontal load after reaching the critical value.
The relationship between the rotation center depth and the horizontal load of the composite bucket foundation is illustrated in Figure 7, which considers different load eccentricities and soil strengths. The test result shows that the rotation center is located above the seabed level when the horizontal load is small. As the momentum increases, the rotation center moves downward below the seabed level, and the rotation center stays stable around the bucket tip when the bearing capacity load is approached. Consequently, the depth of the rotation center can be considered to be located at a depth of L (L is the length of the bucket skirt) below the seabed level at failure [33,35].

3.1.2. Excess Pore Pressure in the Foundation under Monotonic Load

The variation in excess pore pressure in the clay foundation at a depth of 6m outside of the sea-ward and harbor-ward buckets are illustrated in Figure 8, and the pore pressure transducers’ position is demonstrated in Figure 4a. It is observed that positive excess pore pressure is generated outside of the harbor-ward bucket. Negative excess pore pressure was generated outside the sea-ward bucket, although minor positive excess pressure arose under low-load levels in stiff clay. This is attributed to the stress variation in clay foundations outside the foundation bucket under monotonic load. Vertical stress was kept constant, and radial stress increased outside the harbor-ward bucket, causing soil contraction behavior, which induced positive excess pore pressure. In contrast, radial stress decreased outside of the sea-ward bucket, caused dilatant behavior in the soil, and generated negative excess pore pressure. Additionally, the contraction of stiff clay under low stress levels could induce minor positive excess pore pressure [41,52].
The variation in excess pore pressure with the loading increase is also plotted in Figure 8. The results show that excess pore pressure increases when soil strength increases. When soil strength rises from 23.9 kPa (test S2) to 44.5 kPa (test S4), positive excess pore pressure outside the harbor-ward bucket increases from 4.1 kPa to 38.6 kPa, and negative excess pore pressure outside the sea-ward bucket increases from 7.3 kPa to 30.0 kPa. Regarding the load eccentricity effect, the magnitude of excess pore pressure decreases when loading eccentricity rises from 4.5 m (test S1) to 10.5 m (test S2). In detail, positive excess pore pressure outside the harbor-ward bucket decreases from 29.6 kPa to 4.1 kPa, and negative excess pore pressure outside the sea-ward bucket decreases from 16.1 kPa to 7.3 kPa.

3.2. Behavior of Breakwater under Cyclic Load

3.2.1. Cyclic Displacement of Breakwater

Since the total number of cyclic loads applied on the breakwater reaches 46,800, the analysis of bucket foundation movement by processing the raw data of several cycles as proposed by Zhang would be more efficient and concise [7,27]. All the displacement and pore pressure values in the cyclic centrifuge test are the average result of every 13 cycles.
The relationship between three critical displacements (rotation, horizontal, and vertical displacement) and the cyclic loading process are depicted in Figure 9, and all displacement signs are illustrated in Figure 1b. Notably, rotation and vertical displacement roughly increased linearly with cycle number; the symmetric load test (test C1) has a larger rotation angle and vertical displacement than the non-symmetric load test (test C2). The development of rotation and vertical displacement are significantly affected by the loading magnitude. Horizontal displacement has different trends for two types of cyclic loading: the bucket foundations moves towards the sea-ward horizontally and increases with cycle number under symmetric loading condition. Regarding the non-symmetric loading tests, the horizontal displacement of the foundation increases towards the harbor-ward direction, containing two stages. In detail, the displacement increases when the cycle number is below 22,000 and decreases afterwards. It is evident that the displacement in the cyclic test is significantly smaller than in the monotonic test, indicating that the displacement of the breakwater might be overestimated when designed based on the monotonic test result.
The variations in rotation center depth under cyclic loads are shown in Figure 10. It is demonstrated that the rotation center mobilized above the seabed level constantly in the symmetric load test (C1); however, in the non-symmetric load test (C2), the rotation center moved downward below the seabed level after about 7000 cycles. After about 30,000 cycles, the rotation center depth came to a stable stage, approximately 0.5 L above seabed level in the symmetric test and 0.3 L below the seabed level in the non-symmetric test. The movement of the rotation center in cyclic tests is complicated, and has upward and downward tendencies. Specifically, the rotation center would rise above the seabed level in symmetric centrifuge tests, while it would move downward from the original seabed level in non-symmetric tests.

3.2.2. Excess Pore Pressure under Cyclic Load

The excess pore pressure developments in clay foundations around buckets at a depth of 6m are presented for the symmetric load tests (test C1) and non-symmetric load tests (test C2), as shown in Figure 11. It was observed that positive excess pore pressure was generated outside both sea-ward and harbor-ward buckets under cyclic loading conditions, except that a small negative value was monitored outside the sea-ward bucket of the C1 test at the initial loading stage. The excess pore pressures for both tests increased significantly with the increasing load cycles, and the increase in excess pore pressure under non-symmetric loading was higher than under symmetric loading. In the non-symmetric test, the excess pore pressures outside sea-ward and harbor-ward sides attained 9.1 kPa and 8.5 kPa, respectively. When the bucket foundation was subjected to a symmetric load, the pressures were registered with minimum values of 0.7 kPa and 1.5 kPa, respectively. The variations in excess pore pressure demonstrate that non-symmetric loading would lead to considerable pore pressure, indicating that a more robust interaction was developed between the bucket foundation and surrounding soils. This is also consistent with previous observations of rotation centers in non-symmetric conditions. When the rotation center moves downward, the deep soils provide more resistance in sustaining the cyclic loading, and the horizontal displacement can be restricted considerably. In addition, it was found that the magnitude of excess pore pressure at the sea-ward (PPT1) side is close to that at the harbor-ward (PPT2) side for both symmetric and non-symmetric load tests.

4. Discussions

The failure mode of bucket foundations under monotonic load is further discussed to interpret the response of the bucket foundation. A sketch of foundation displacement for test S1 is illustrated in Figure 12. Under horizontal load, the breakwater rotates and moves horizontally toward the harbor side, and the harbor-ward bucket settles vertically. While the sea-ward bucket heaves, it tends to uplift with soil, and the harbor-ward bucket compresses with surrounding soil. The displacement pattern for a bucket foundation is composed of three components: rotational movement, horizontal movement, and vertical movement. As listed in Table 4, the displacements, considering different soil strength and load eccentricity, are generalized. In test S1 (soil strength 23.9 kPa and load eccentricity 4.5 m), the rotational angle, normalized horizontal displacement, and normalized vertical displacement were 0.035 rad, 0, and 0.023, respectively, which indicates the failure mode of test S1 is a combination of rotational and vertical movement. When the load eccentricity increased from 4.5 m (test S1) to 10.5 m (test S2), the horizontal displacement increased significantly, expressing that the failure mode converted to a combination of rotational, horizontal, and vertical movement. When soil undrained shear strength increased from about 23.9 kPa (test S2) to 44.5 kPa (test S4), the rotation angle and horizontal displacement continuously increased, and vertical displacement decreased considerably. This indicates that the failure mode was converted to rotational and horizontal movement, as soil undrained shear strength increased two times from test S2 to test S4.

5. Conclusions

This study investigated the monotonic and cyclic performance of composite foundation breakwater in clay through a series of centrifuge tests. Based on a monotonic loading device, a novel non-contact loading device and a real-time control system were developed to apply cyclic load. The effects of soil undrained shear strength and load eccentricity on monotonic failure mode were investigated. Two types of cyclic load (symmetric and non-symmetric) were applied to the bucket foundation to investigate cyclic deformation and excess pore pressure, and the results were compared with the monotonic test results.
When the soil strength increased in monotonic centrifuge tests, the foundation failure pattern varied from a complicated mode (including rotation, horizontal displacement, and vertical displacement) to a simplified mode (only including rotation, and horizontal displacement). As expected, the ultimate bearing capacity Hu of the bucket foundation experienced a significant growth (from 1.31 Hd to 4.29 Hd) as the soil strength increased. The foundation’s rotation center was constantly moving downward during the loading process, indicating that the deeper soil would be activated to resist the horizontal loading. In discussing the influence of wave force height, centrifuge models with two loading eccentricities were tested. It is shown that the ultimate capacity (2.69 Hd) of the lower eccentricity case is about two times that of the higher case (1.31 Hd) because the higher wave load would induce a larger bending moment on the structure, as tested by S2. Under the horizontal loading in all tests, the bucket foundation moved towards the harbor-ward direction, and the surrounding soil was compressed, resulting in positive excess pore pressure. The negative pore pressure was generated on the outside of the sea-ward bucket foundation due to the unloading effect.
In the cyclic loading tests, the variation in rotation center depth for the symmetric loading test (test C1) and non-symmetric loading test (test C2) shows a noticeable difference. In detail, the rotation center rose above the seabed level in the symmetric centrifuge test, while the center moved downward in the non-symmetric test. The low-position rotation center observed in the non-symmetric test resulted from the deeper soil required to provide resistance to balance more severe load by non-symmetric loading. Consequently, all parameters involving rotation angle, horizontal displacement, and vertical displacement in the non-symmetric centrifuge test (C2) were smaller than in the symmetric test (C1), as the utilization of deep-soil resistance in the non-symmetric test was beneficial in controlling deformation. The non-symmetric loading test also produced considerable pore pressure, indicating that a stronger interaction between the bucket foundation and surrounding soils was developed.
From the results of centrifuge tests, the stability of coastal structures can be significantly improved by the replacement of foundation soils because the ultimate bearing capacity in this study shows a significant growth with soil strength. Wave force height is one crucial factor in influencing the failure pattern of composite bucket foundations, which needs to be considered in designing coastal structures. It should be noted that non-symmetric loading does not impact the bucket foundation as seriously as symmetric loading. Utilizing deep-soil resistance in non-symmetric tests is beneficial in controlling deformation; however, future work in comparing the symmetric and non-symmetric conditions is suggested to be undertaken by using numerical simulation and experiment studies.

Author Contributions

Conceptualization, M.J. and Z.C.; methodology, M.J., Z.L. and G.X.; validation, Z.C. and G.X.; formal analysis, M.J. and G.X.; investigation, M.J., Z.L., G.X. and Z.C.; resources, Z.C. and G.X.; data curation, M.J. and Z.L.; writing—original draft preparation, M.J. and Z.L.; writing—review and editing, Z.C. and G.X.; visualization, M.J. and Z.C.; supervision, Z.C. and G.X.; project administration, Z.C. and G.X.; funding acquisition, M.J., Z.C. and Z.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by the National Natural Science Foundation of China (Grant No. 51179105, 51408197), Henan Key Laboratory of Grain and Oil Storage Facility & Safety, HAUT, Zhengzhou, 450001, China (grant number: 2021KF-B03), Key Project of Science and Technology Research of Henan Education Department (grant number: 23B560002), Project of Hetao Shenzhen-Hong Kong Science and Technology Innovation Cooperation Zone (HZQB-KCZYB-2020083), Shenzhen Science and Technology Program (No. KCXFZ20211020163816023). The authors also acknowledge the help of the geotechnical centrifuge laboratory in Nanjing Hydraulic Research Institute.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Andersen, K.H.; Dyvik, R.; Schrøder, K.; Hansteen, O.E.; Bysveen, S. Field tests of anchors in clay II: Predictions and interpretation. J. Geotech. Eng. 1993, 119, 1532–1549. [Google Scholar] [CrossRef]
  2. Kim, S.-R.; Hung, L.C.; Oh, M. Group effect on bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 79, 1–9. [Google Scholar] [CrossRef]
  3. Liu, X.; Wang, Y.; Zhang, H.; Guo, X. Susceptibility of typical marine geological disasters: An overview. Geoenvironmental Disasters 2023, 10, 10. [Google Scholar] [CrossRef]
  4. Liu, X.-L.; Jia, Y.-G.; Zheng, J.-W.; Hou, W.; Zhang, L.; Zhang, L.-P.; Shan, H.-X. Experimental evidence of wave-induced inhomogeneity in the strength of silty seabed sediments: Yellow River Delta, China. Ocean Eng. 2013, 59, 120–128. [Google Scholar] [CrossRef]
  5. Wang, Y.Z.; Yan, Z.; Wang, Y.C. Numerical analyses of caisson breakwaters on soft foundations under wave cyclic loading. China Ocean. Eng. 2016, 30, 1–18. [Google Scholar] [CrossRef]
  6. Xiao, Z.; Tian, Y.; Gourvenec, S. A practical method to evaluate failure envelopes of shallow foundations considering soil strain softening and rate effects. Appl. Ocean Res. 2016, 59, 395–407. [Google Scholar] [CrossRef]
  7. Zhang, X.; Leung, C.; Lee, F. Centrifuge modelling of caisson breakwater subject to wave-breaking impacts. Ocean Eng. 2009, 36, 914–929. [Google Scholar] [CrossRef]
  8. Zhang, X.; Lee, F.; Leung, C. Response of caisson breakwater subjected to repeated impulsive loading. Géotechnique 2009, 59, 3–16. [Google Scholar] [CrossRef]
  9. Pan, Z.; Guan, Y.; Han, X. Reliability analysis of bucket foundation breakwater considering water-level variations under complex natural conditions. Eng. Fail. Anal. 2023, 149, 107250. [Google Scholar] [CrossRef]
  10. Wang, Y.Z.; Xiao, Z.; Chi, L.H.; Xie, S.W.; Li, Y.Y. A simplified calculation method for stability of bucket foundation breakwater. Rock Soil Mech. 2009, 30, 1367–1372. [Google Scholar] [CrossRef]
  11. Xiao, Z.; Wang, Y.Z.; Ji, C.N. Stability analysis of bucket foundation breakwaters based on limit equilibrium method. Chin. J. Geotech. Eng. 2013, 35, 828–833. [Google Scholar]
  12. Zhu, X.; Chen, Z.; Guan, Y.-F.; Ni, P.; Fan, K.-F.; Jing, Y.-X.; Yang, C.-J. Field test on the mechanism of composite bucket foundation penetrating sandy silt overlying clay. Ocean Eng. 2023, 288, 116102. [Google Scholar] [CrossRef]
  13. Guo, X.; Fan, N.; Zheng, D.; Fu, C.; Wu, H.; Zhang, Y.; Song, X.; Nian, T. Predicting impact forces on pipelines from deep-sea fluidized slides: A comprehensive review of key factors. Int. J. Min. Sci. Technol. 2024, 34, 187–201. [Google Scholar] [CrossRef]
  14. Guo, X.; Liu, X.; Li, M.; Lu, Y. Lateral force on buried pipelines caused by seabed slides using a CFD method with a shear interface weakening model. Ocean Eng. 2023, 280, 114663. [Google Scholar] [CrossRef]
  15. Guo, X.; Fan, N.; Liu, Y.; Liu, X.; Wang, Z.; Xie, X.; Jia, Y. Deep seabed mining: Frontiers in engineering geology and environment. Int. J. Coal Sci. Technol. 2023, 10, 23. [Google Scholar] [CrossRef]
  16. Bransby, M.F.; Yun, G.-J. The undrained capacity of skirted strip foundations under combined loading. Géotechnique 2009, 59, 115–125. [Google Scholar] [CrossRef]
  17. Achmus, M.; Akdag, C.; Thieken, K. Load-bearing behavior of suction bucket foundations in sand. Appl. Ocean Res. 2013, 43, 157–165. [Google Scholar] [CrossRef]
  18. Thieken, K.; Achmus, M.; Schröder, C. On the behavior of suction buckets in sand under tensile loads. Comput. Geotech. 2014, 60, 88–100. [Google Scholar] [CrossRef]
  19. Hong, Y.; Chen, X.Y.; Wang, L.Z.; Wang, L.L.; He, B. A bounding-surface based cyclic ‘p-y+M-θ’ model for unified description of laterally loaded piles with different failure modes in clay. Can. Geotech. J. 2024. [Google Scholar] [CrossRef]
  20. Hong, Y.; Yao, M.H.; Wang, L.Z. A multi-axial bounding surface p-y model with application in analyzing pile responses under multi-directional lateral cycling. Comput. Geotech. 2023, 157, 105301. [Google Scholar] [CrossRef]
  21. Park, J.-S.; Park, D.; Yoo, J.-K. Vertical bearing capacity of bucket foundations in sand. Ocean Eng. 2016, 121, 453–461. [Google Scholar] [CrossRef]
  22. Park, J.-S.; Park, D. Vertical bearing capacity of bucket foundation in sand overlying clay. Ocean Eng. 2017, 134, 62–76. [Google Scholar] [CrossRef]
  23. Wang, X.; Yang, X.; Zeng, X. Centrifuge modeling of lateral bearing behavior of offshore wind turbine with suction bucket foundation in sand. Ocean Eng. 2017, 139, 140–151. [Google Scholar] [CrossRef]
  24. Wang, X.; Yang, X.; Zeng, X. Lateral response of improved suction bucket foundation for offshore wind turbine in centrifuge modelling. Ocean Eng. 2017, 141, 295–307. [Google Scholar] [CrossRef]
  25. Choo, Y.W.; Kim, D.-J.; Youn, J.-U.; Hossain, M.S.; Seo, J.; Kim, J.-H. Behavior of a Monopod Bucket Foundation Subjected to Combined Moment and Horizontal Loads in Silty Sand. J. Geotech. Geoenvironmental Eng. 2021, 147, 107250. [Google Scholar] [CrossRef]
  26. Tasiopoulou, P.; Chaloulos, Y.; Gerolymos, N.; Giannakou, A.; Chacko, J. Cyclic lateral response of OWT bucket foundations in sand: 3D coupled effective stress analysis with Ta-Ger model. Soils Found. 2021, 61, 371–385. [Google Scholar] [CrossRef]
  27. Zhang, J.; Zhang, L.; Lu, X. Centrifuge modeling of suction bucket foundations for platforms under ice-sheet-induced cyclic lateral loadings. Ocean Eng. 2007, 34, 1069–1079. [Google Scholar] [CrossRef]
  28. Barari, A.; Ibsen, L. Undrained response of bucket foundations to moment loading. Appl. Ocean Res. 2012, 36, 12–21. [Google Scholar] [CrossRef]
  29. Liu, M.; Yang, M.; Wang, H. Bearing behavior of wide-shallow bucket foundation for offshore wind turbines in drained silty sand. Ocean Eng. 2014, 82, 169–179. [Google Scholar] [CrossRef]
  30. Byrne, B.W.; Houlsby, G.T. Experimental investigations of the response of suction caissons to transient combined loading. J. Geotech. Geoenvironmental Eng. 2004, 130, 240–253. [Google Scholar] [CrossRef]
  31. Cox, J.A.; O’Loughlin, C.D.; Cassidy, M.; Bhattacharya, S.; Gaudin, C.; Bienen, B. Centrifuge study on the cyclic performance of caissons in sand. Int. J. Phys. Model. Geotech. 2014, 14, 99–115. [Google Scholar] [CrossRef]
  32. Zhu, B.; Byrne, B.W.; Houlsby, G.T. Long-term lateral cyclic response of suction caisson foundations in sand. J. Geotech. Geoenvironmental Eng. 2013, 139, 73–83. [Google Scholar] [CrossRef]
  33. Zhu, B.; Kong, D.-Q.; Chen, R.-P.; Kong, L.-G.; Chen, Y.-M. Installation and lateral loading tests of suction caissons in silt. Can. Geotech. J. 2011, 48, 1070–1084. [Google Scholar] [CrossRef]
  34. Grecu, S.; Ibsen, L.B.; Barari, A. Winkler springs for axial response of suction bucket foundations in cohesionless soil. Soils Found. 2021, 61, 64–79. [Google Scholar] [CrossRef]
  35. Ding, H.; Liu, Y.; Zhang, P.; Le, C. Model tests on the bearing capacity of wide-shallow composite bucket foundations for offshore wind turbines in clay. Ocean Eng. 2015, 103, 114–122. [Google Scholar] [CrossRef]
  36. Kim, D.-J.; Choo, Y.W.; Kim, J.-H.; Kim, S. Investigation of monotonic and cyclic behavior of tripod suction bucket foundations for offshore wind towers using centrifuge modeling. J. Geotech. Geoenvironmental Eng. 2014, 140, 04014008. [Google Scholar] [CrossRef]
  37. Kim, S.-W.; Suh, K.-D. Determining the stability of vertical breakwaters against sliding based on individual sliding distances during a storm. Coast. Eng. 2014, 94, 90–101. [Google Scholar] [CrossRef]
  38. DNV-OS-J101; Design of Offshore Wind Turbine Structures. Det Norske Veritas (DNV): Oslo, Norway, 2007.
  39. Wang, Y.Z.; Xiao, Z.; Li, Y.Y.; Xie, S.W. Finite element analysis for earth pressure on bucket foundation of breakwater. Chin. J. Geotech. Eng. 2009, 31, 622–627. [Google Scholar]
  40. Xiao, Z.; Wang, Y.Z.; Ji, C.N.; Li, Y.Y.; Xie, S.W. Finite element analysis of the stability of bucket foundation breakwater. China Civ. Eng. J. 2009, 42, 119–125. [Google Scholar]
  41. Cai, Y.; Hao, B.; Gu, C.; Wang, J.; Pan, L. Effect of anisotropic consolidation stress paths on the undrained shear behavior of reconstituted Wenzhou clay. Eng. Geol. 2018, 242, 23–33. [Google Scholar] [CrossRef]
  42. Ha, J.G.; Lee, S.-H.; Kim, D.-S.; Choo, Y.W. Simulation of soil–foundation–structure interaction of Hualien large-scale seismic test using dynamic centrifuge test. Soil Dyn. Earthq. Eng. 2014, 61–62, 176–187. [Google Scholar] [CrossRef]
  43. Loh, C.K.; Tan, T.S.; Lee, F.H. Three-dimensional excavation test. Centrifuge 1998, 98, 85–90. [Google Scholar]
  44. Garnier, J.; Gaudin, C.; Springman, S.M.; Culligan, P.J.; Goodings, D.; Konig, D.; Kutter, B.; Phillips, R.; Randolph, M.R.; Thorel, L. Catalogue of scaling laws and similitude questions in geotechnical centrifuge modelling. Int. J. Phys. Model. Geotech. 2007, 8, 1–23. [Google Scholar] [CrossRef]
  45. Kutter, B.L. Recent Advances in Centrifuge Modeling of Seismic Shaking. In Proceedings of the 3rd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, St. Louis, MO, USA, 5 April 1995; Volume 2, pp. 927–942. [Google Scholar]
  46. Ling, H.I.; Cheng, A.H.-D.; Mohri, Y.; Kawabata, T. Permanent displacement of composite breakwaters subject to wave impact. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 1–8. [Google Scholar] [CrossRef]
  47. Mustapa, M.; Yaakob, O.; Ahmed, Y.M.; Rheem, C.-K.; Koh, K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
  48. Leblanc, C.; Houlsby, G.T.; Byrne, B.W. Response of stiff piles in sand to long-term cyclic lateral loading. Géotechnique 2010, 60, 79–90. [Google Scholar] [CrossRef]
  49. Xiao, Z.; Ge, B.; Wang, Y. Capacities and failure modes of suction bucket foundation with internal bulkheads. J. Ocean Univ. China 2017, 16, 627–634. [Google Scholar] [CrossRef]
  50. Hung, L.C.; Kim, S.-R. Evaluation of undrained bearing capacities of bucket foundations under combined loads. Mar. Georesources Geotechnol. 2014, 32, 76–92. [Google Scholar] [CrossRef]
  51. Villalobos, F.A.; Byrne, B.W.; Houlsby, G.T. An experimental study of the drained capacity of suction caisson foundations under monotonic loading for offshore applications. Soils Found. 2009, 49, 477–488. [Google Scholar] [CrossRef]
  52. Tanaka, H.; Tsutsumi, A.; Ohashi, T. Unloading behavior of clays measured by CRS test. Soils Found. 2014, 54, 81–93. [Google Scholar] [CrossRef]
Jmse 12 00469 g001
Figure 1. Composite bucket foundation breakwater. (a) Composite bucket foundation breakwater model. (b) Sketch of composite bucket foundation breakwater under storm wave load.
Figure 1. Composite bucket foundation breakwater. (a) Composite bucket foundation breakwater model. (b) Sketch of composite bucket foundation breakwater under storm wave load.
Jmse 12 00469 g001
Jmse 12 00469 g002
Figure 2. Load device and real-time control system in centrifuge test; (a) Schematic of monotonic loading device; (b) Schematic of non-contact cyclic loading device; (c) Schematic of real-time control system in cyclic test.
Figure 2. Load device and real-time control system in centrifuge test; (a) Schematic of monotonic loading device; (b) Schematic of non-contact cyclic loading device; (c) Schematic of real-time control system in cyclic test.
Jmse 12 00469 g002
Jmse 12 00469 g003
Figure 3. Time history of load in the monotonic and cyclic tests; (a) Monotonic load; (b) Cyclic load.
Figure 3. Time history of load in the monotonic and cyclic tests; (a) Monotonic load; (b) Cyclic load.
Jmse 12 00469 g003
Jmse 12 00469 g004aJmse 12 00469 g004b
Figure 4. Sketch of experimental setup and instrumentation in centrifuge test; (a) Monotonic test; (b) Cyclic test.
Figure 4. Sketch of experimental setup and instrumentation in centrifuge test; (a) Monotonic test; (b) Cyclic test.
Jmse 12 00469 g004aJmse 12 00469 g004b
Jmse 12 00469 g005
Figure 5. The repeatability check of centrifuge tests.
Figure 5. The repeatability check of centrifuge tests.
Jmse 12 00469 g005
Jmse 12 00469 g006aJmse 12 00469 g006b
Figure 6. Load–displacement relations for breakwater under monotonic load; (a) Rotational angle; (b) Horizontal displacement; (c) Vertical displacement.
Figure 6. Load–displacement relations for breakwater under monotonic load; (a) Rotational angle; (b) Horizontal displacement; (c) Vertical displacement.
Jmse 12 00469 g006aJmse 12 00469 g006b
Jmse 12 00469 g007
Figure 7. Rotation center depth with horizontal load for breakwater under monotonic load.
Figure 7. Rotation center depth with horizontal load for breakwater under monotonic load.
Jmse 12 00469 g007
Jmse 12 00469 g008
Figure 8. Excess pore pressure in foundation under monotonic load.
Figure 8. Excess pore pressure in foundation under monotonic load.
Jmse 12 00469 g008
Jmse 12 00469 g009
Figure 9. Average displacement of breakwater under cyclic load; (a) Rotational angle; (b) Horizontal displacement; (c) Vertical displacement.
Figure 9. Average displacement of breakwater under cyclic load; (a) Rotational angle; (b) Horizontal displacement; (c) Vertical displacement.
Jmse 12 00469 g009
Jmse 12 00469 g010
Figure 10. Rotation center depth under cyclic load.
Figure 10. Rotation center depth under cyclic load.
Jmse 12 00469 g010
Jmse 12 00469 g011
Figure 11. Excess pore pressure under cyclic load.
Figure 11. Excess pore pressure under cyclic load.
Jmse 12 00469 g011
Jmse 12 00469 g012
Figure 12. Schematic of movement of breakwater under bearing capacity load for test S1.
Figure 12. Schematic of movement of breakwater under bearing capacity load for test S1.
Jmse 12 00469 g012
Table 1. Scaling law for geotechnical centrifuge test.
Table 1. Scaling law for geotechnical centrifuge test.
ParametersScaling Law (Model/Prototype)
Length1/N
Density1
Force1/N2
Bending moment1/N3
Undrained shear strength1
Moment of inertia1/N4
Flexural stiffness1/N4
FrequencyN
Time (consolidation)1/N2
Time (dynamic)1/N
AccelerationN
Table 2. Clay parameters.
Table 2. Clay parameters.
The Specific Gravity of Soil
Gs		Density
ρ		Water Content
w		Liquid Limit
wL		Plastic Limit
wP		Plasticity Index
Ip
/g·cm−3/%/%/%
2.751.6561.54223.518.5
Table 3. Centrifuge test program.
Table 3. Centrifuge test program.
Test No.Loading Eccentricity
e (m)		Soil Undrained Shear Strength
Su (kPa)		ζbζcCycle Number
N
S14.523.9---
S210.522.9---
S310.537.4---
S410.544.5---
C14.522.51−146,800
C24.522.31−0.446,800
Note: ζb and ζc were calculated based on Equations (2) and (3).
Table 4. Failure modes of monotonic tests.
Table 4. Failure modes of monotonic tests.
Test No.Huθf (rad)uf (mm)vf (mm)
S12.69 Hd0.0352207
S21.31 Hd0.028110162
S33.05 Hd0.044189144
S44.29 Hd0.04915318
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Jiang, M.; Lu, Z.; Cai, Z.; Xu, G. Centrifuge Modelling of Composite Bucket Foundation Breakwater in Clay under Monotonic and Cyclic Loads. J. Mar. Sci. Eng. 2024, 12, 469. https://doi.org/10.3390/jmse12030469

AMA Style

Jiang M, Lu Z, Cai Z, Xu G. Centrifuge Modelling of Composite Bucket Foundation Breakwater in Clay under Monotonic and Cyclic Loads. Journal of Marine Science and Engineering. 2024; 12(3):469. https://doi.org/10.3390/jmse12030469

Chicago/Turabian Style

Jiang, Minmin, Zhao Lu, Zhengyin Cai, and Guangming Xu. 2024. "Centrifuge Modelling of Composite Bucket Foundation Breakwater in Clay under Monotonic and Cyclic Loads" Journal of Marine Science and Engineering 12, no. 3: 469. https://doi.org/10.3390/jmse12030469

APA Style

Jiang, M., Lu, Z., Cai, Z., & Xu, G. (2024). Centrifuge Modelling of Composite Bucket Foundation Breakwater in Clay under Monotonic and Cyclic Loads. Journal of Marine Science and Engineering, 12(3), 469. https://doi.org/10.3390/jmse12030469

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop