Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm
Abstract
:1. Introduction
- (1)
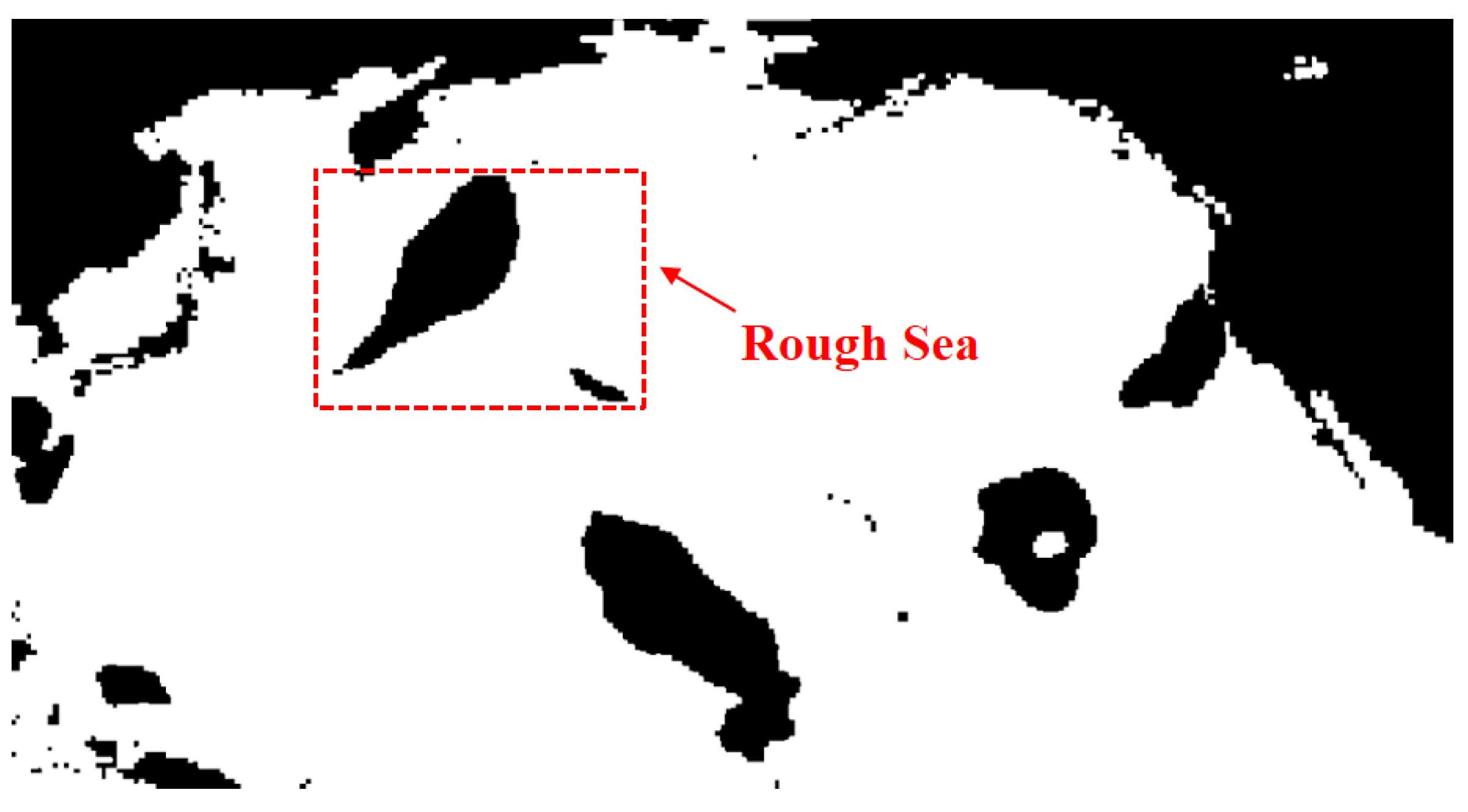
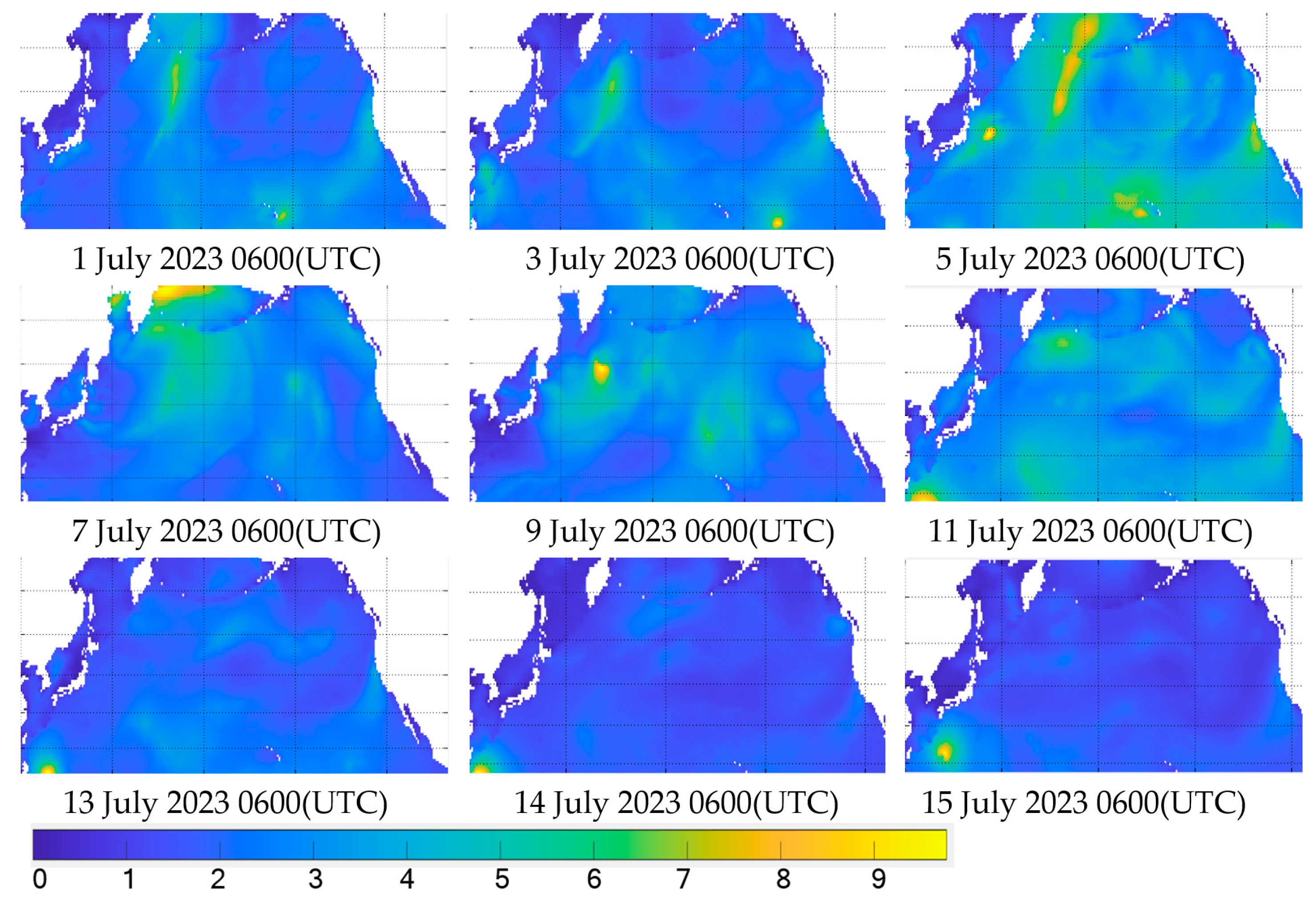
- A model for sea conditions using weather data is established. The complex sea area exceeding the threshold is marked as a dangerous area as a danger zone according to the set safety threshold, and the calibrated dangerous area is updated by updating the environmental data.
- (2)
- Considering the speed loss of ships in different marine environments, a speed-loss model of ships is established.
- (3)
- On the basis of the above model, a route-optimization model considering both ship navigation time and fuel consumption is established by using a non-dominated sorting genetic algorithm (NSGA-II), and ship stability is added to the constraint factor to make the optimal path safer and more energy-saving.
2. Materials and Methods
2.1. Complex Sea Environment Model
2.2. Speed Loss Model of Ship
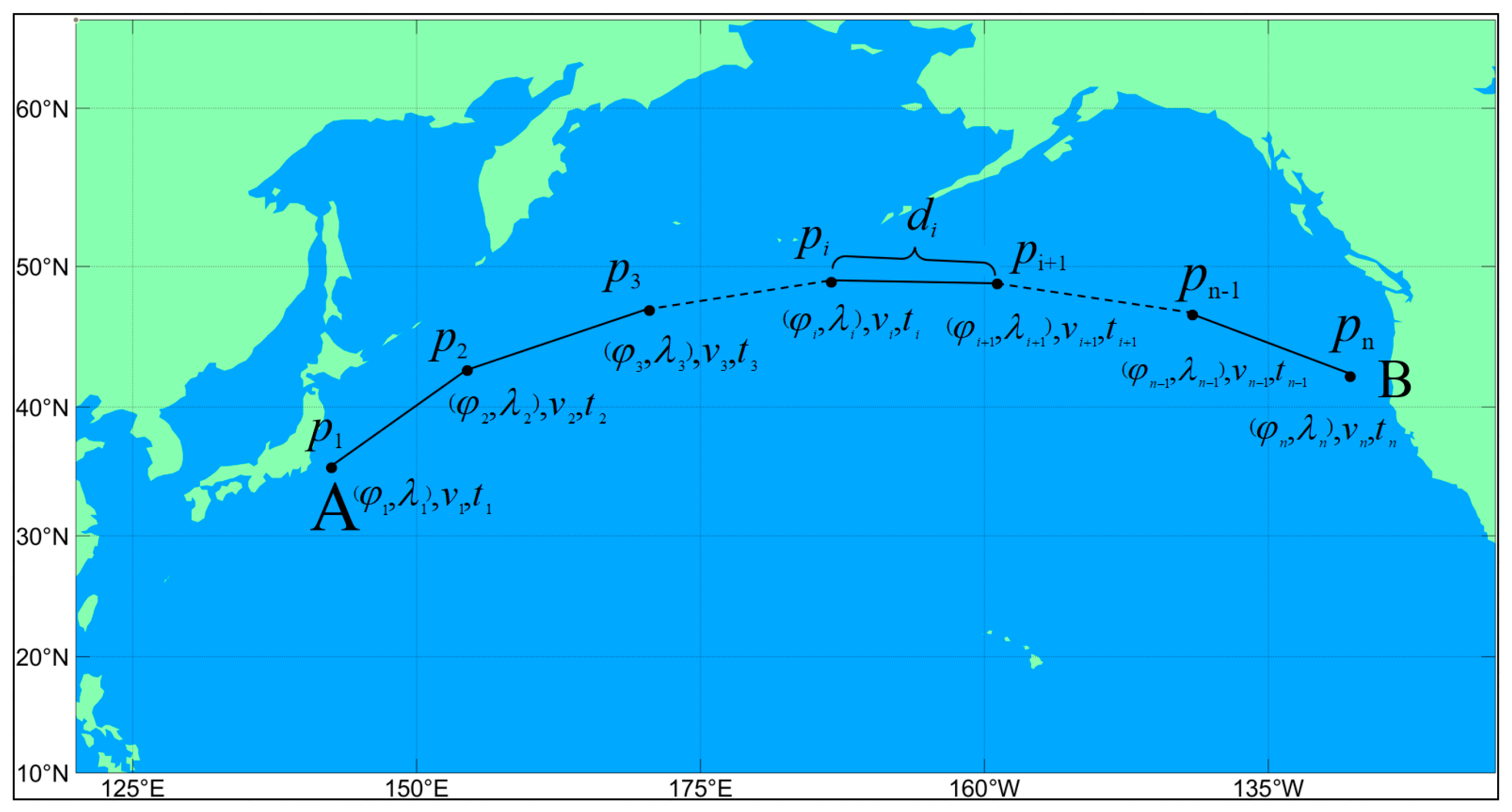
2.2.1. Definition of Route Model
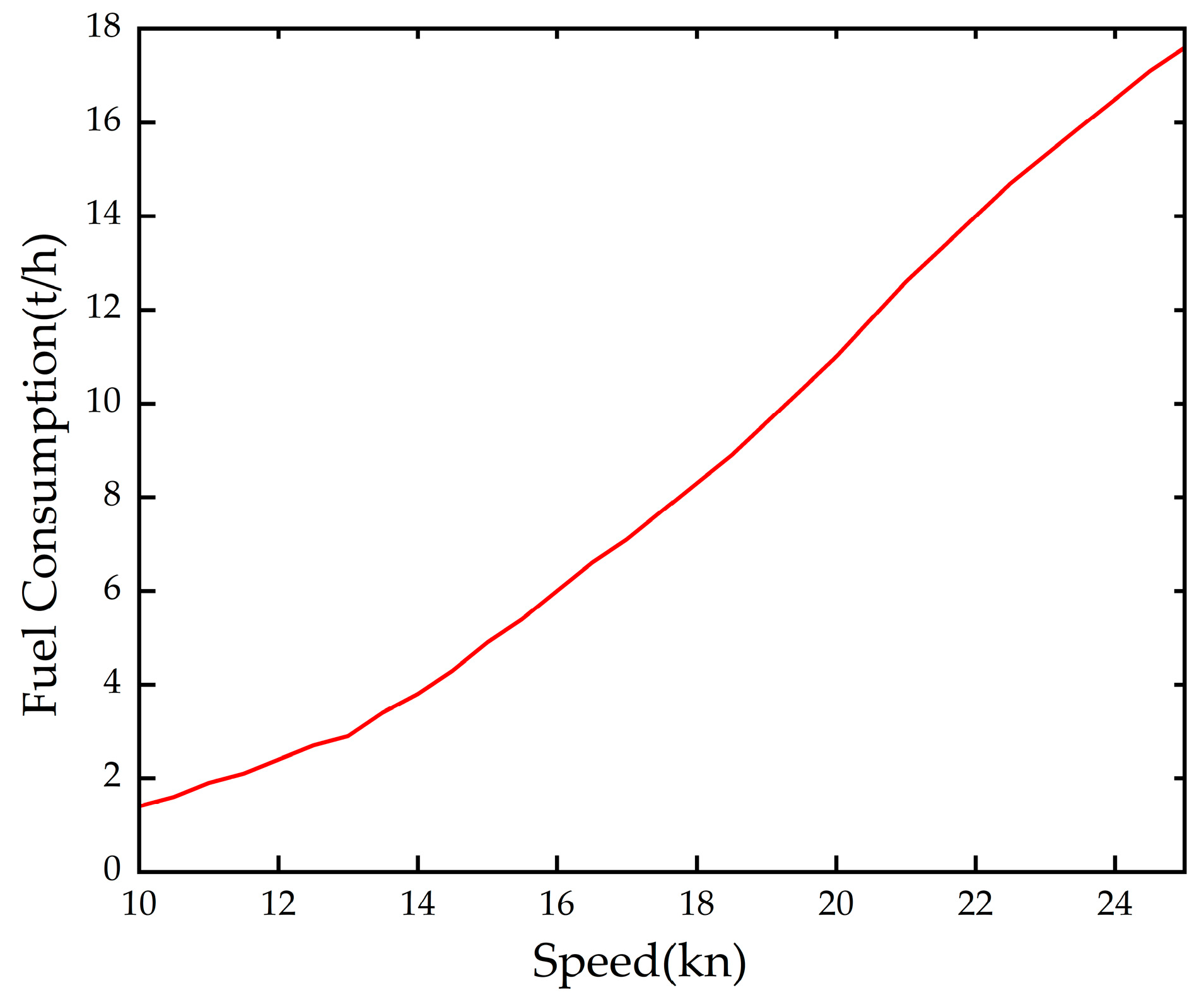
2.2.2. Configuring Ship Speed
3. Multi-Objective Route Optimization Model of the Ship
3.1. Objective Functions
3.2. Designing the Algorithm
4. Experiment Analysis
4.1. Data Acquisition
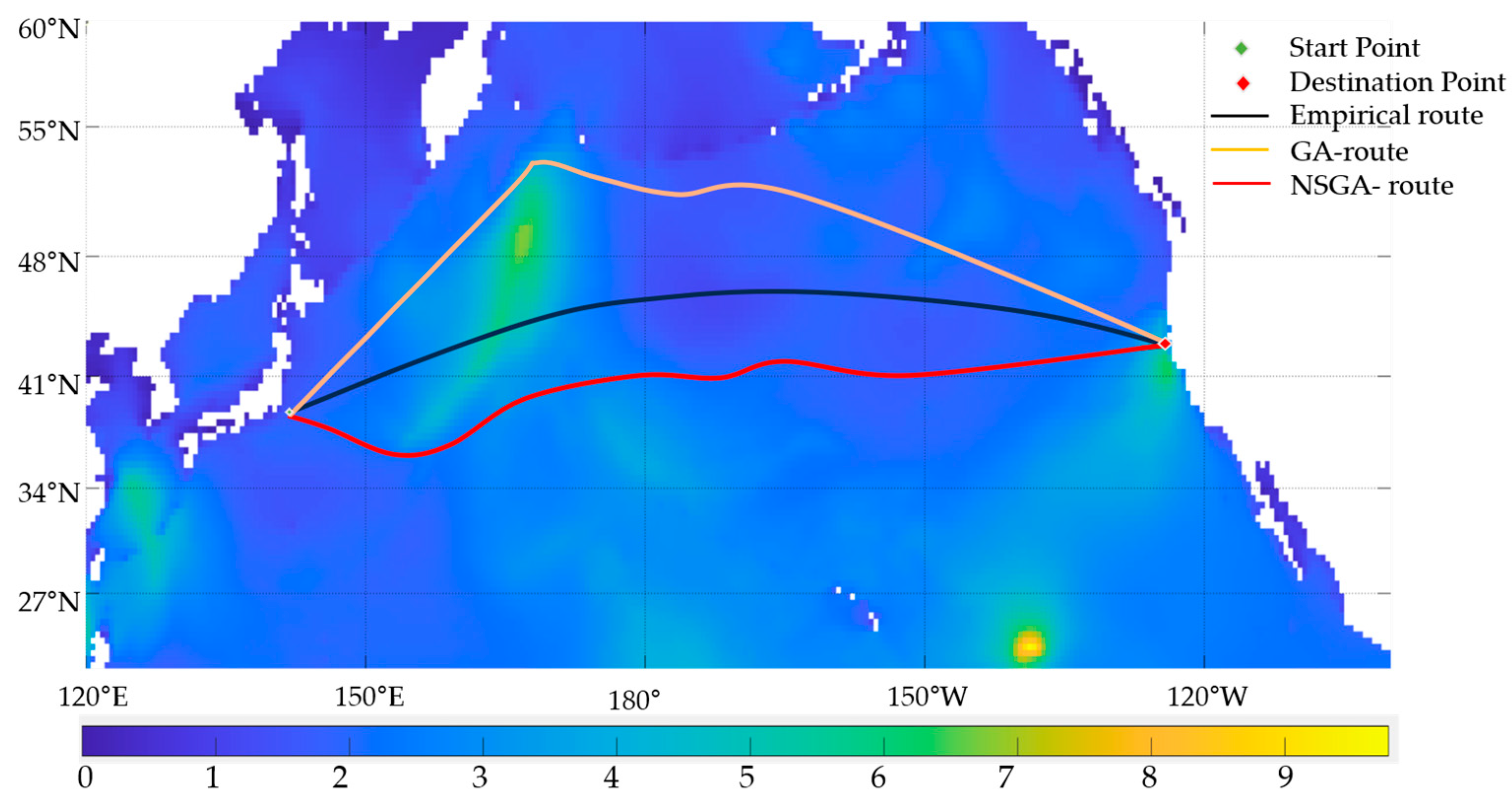
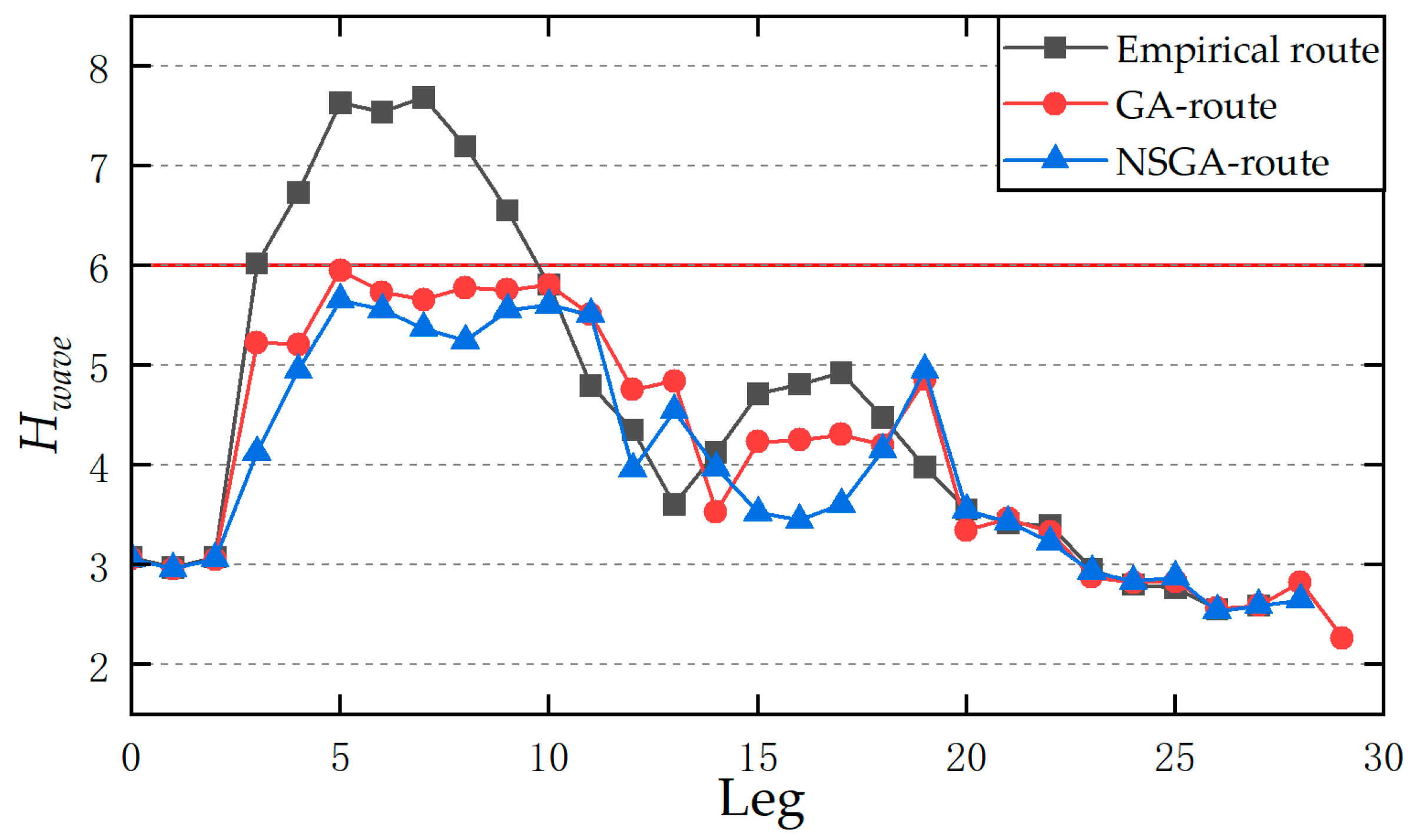
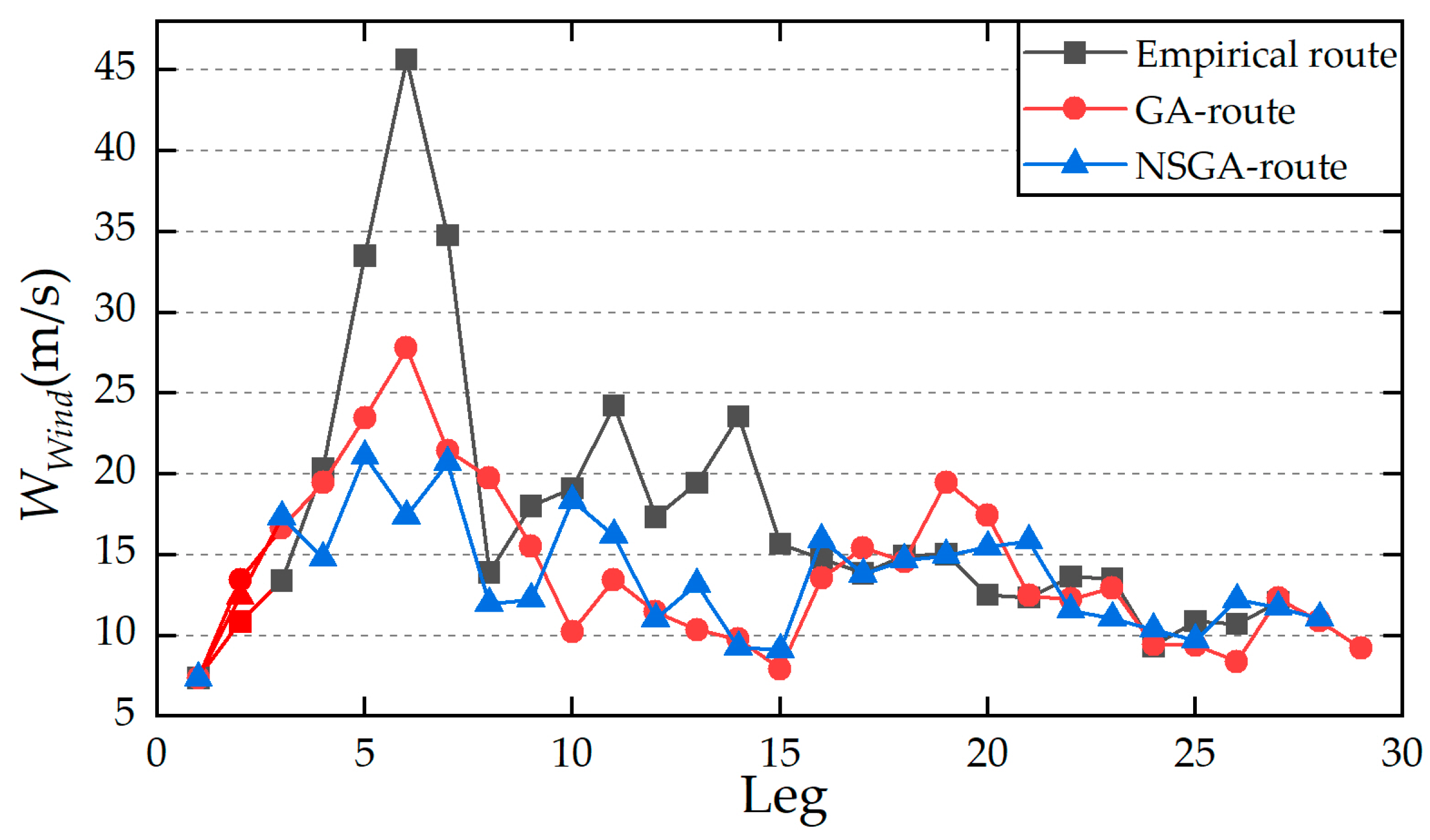
4.2. Route Optimization Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bullock, S.; Mason, J.; Broderick, J.; Larkin, A. Shipping and the Paris climate agreement: A focus on committed emissions. BMC Energy 2020, 2, 5. [Google Scholar] [CrossRef]
- Müller-Casseres, E.; Edelenbosch, O.Y.; Szklo, A.; Schaeffer, R.; van Vuuren, D.P. Global futures of trade impacting the challenge to decarbonize the international shipping sector. Energy 2021, 237, 121547. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Liu, R.W.; Wu, H.; Han, B.; Zhao, J. Quantifying Arctic oil spilling event risk by integrating an analytic network process and a fuzzy comprehensive evaluation model. Ocean. Coast. Manag. 2022, 228, 106326. [Google Scholar] [CrossRef]
- Wu, G.; Atilla, I.; Tahsin, T.; Terziev, M.; Wang, L. Long-voyage route planning method based on multi-scale visibility graph for autonomous ships. Ocean Eng. 2021, 219, 108242. [Google Scholar] [CrossRef]
- Seo, C.; Noh, Y.; Abebe, M. Ship collision avoidance route planning using CRI-based A∗ algorithm. Int. J. Nav. Archit. Ocean. Eng. 2023, 15, 100551. [Google Scholar] [CrossRef]
- Silveira, P.; Teixeira, A.P.; Guedes-Soares, C. AIS based shipping routes using the Dijkstra algorithm. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 565–571. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. A Three-Dimensional Dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Xu, H. PE-A* Algorithm for Ship Route Planning Based on Field Theory. IEEE Access 2022, 10, 36490–36504. [Google Scholar] [CrossRef]
- Shin, Y.W.; Abebe, M.; Noh, Y.; Lee, S.; Lee, I.; Kim, D.; Bae, J.; Kim, K.C. Near-Optimal Weather Routing by Using Improved A* Algorithm. Appl. Sci. 2020, 10, 6010. [Google Scholar] [CrossRef]
- Mannarini, G.; Subramani, D.N.; Lermusiaux, P.F.; Pinardi, N. Graph-search and differential equations for time-optimal vessel route planning in dynamic ocean waves. IEEE Trans. Int. Trans. Syst. 2019, 21, 3581–3593. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Zhu, Q.; Ma, S. Ship route planning based on double-cycling genetic algorithm considering ship maneuverability constraint. IEEE Access 2020, 8, 190746–190759. [Google Scholar] [CrossRef]
- Goez, G.D.; Velasquez, R.A.; Botero, J.S. UAV route planning optimization using PSO implemented on microcontrollers. IEEE Lat. Am. Trans. 2016, 14, 1705–1710. [Google Scholar] [CrossRef]
- Zhou, P.; Zhou, Z.; Wang, Y.; Wang, H. Ship weather routing based on hybrid genetic algorithm under complicated sea conditions. J. Ocean Uni. China 2023, 22, 28–42. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Zhao, W.; Guan, Z.; Li, P. Application of improved multi-objective ant colony optimization algorithm in ship weather routing. J. Ocean Uni. China 2021, 20, 45–55. [Google Scholar] [CrossRef]
- Svanberg, M.; Santén, V.; Hörteborn, A.; Holm, H.; Finnsgård, C. AIS in maritime research. Mar. Policy 2019, 106, 103520. [Google Scholar] [CrossRef]
- Liu, D.; Rong, H.; Soares, C.G. Shipping route modelling of AIS maritime traffic data at the approach to ports. Ocean Eng. 2023, 289, 115868. [Google Scholar] [CrossRef]
- Xiao, G.; Chen, L.; Chen, X.; Jiang, C.; Ni, A.; Zhang, C.; Zong, F. A hybrid visualization model for knowledge mapping: Scientometrics, SAOM, and SAO. IEEE Trans. Int. Trans. Syst. 2023. [Google Scholar] [CrossRef]
- Cai, J.; Chen, G.; Lützen, M.; Rytter, N.G.M. A practical AIS-based route library for voyage planning at the pre-fixture stage. Ocean Eng. 2021, 236, 109478. [Google Scholar] [CrossRef]
- Gao, X.; Dong, Y.; Han, Y. An Optimized Path Planning Method for Container Ships in Bohai Bay Based on Improved Deep Q-learning. IEEE Access 2023, 11, 91275–91292. [Google Scholar] [CrossRef]
- Comert, S.E.; Yazgan, H.R. A new approach based on hybrid ant colony optimization-artificial bee colony algorithm for multi-objective electric vehicle routing problems. Eng. Appl. Artificial. Int. 2023, 123, 106375. [Google Scholar] [CrossRef]
- Chen, X.; Wang, M.; Ling, J.; Wu, H.; Wu, B.; Li, C. Ship imaging trajectory extraction via an aggregated you only look once (YOLO) model. Eng. Appl. Art. Int. 2024, 130, 107742. [Google Scholar] [CrossRef]
- Srivastava, G.; Singh, A.; Mallipeddi, R. NSGA-II with objective-specific variation operators for multiobjective vehicle routing problem with time windows. Expert Syst. Appl. 2021, 176, 114779. [Google Scholar] [CrossRef]
- Pingale, R.P.; Shinde, S.N. Multi-objective sunflower based grey wolf optimization algorithm for multipath routing in IoT network. Wirel. Pers. Commun. 2021, 117, 1909–1930. [Google Scholar] [CrossRef]
- Zhang, L.; Bienkowski, A.; Macesker, M.; Pattipati, K.R.; Sidoti, D.; Hansen, J.A. Many-Objective Maritime Path Planning for Dynamic and Uncertain Environments. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–10. [Google Scholar]
- Du, W.; Li, Y.; Zhang, G.; Wang, C.; Zhu, B.; Qiao, J. Ship weather routing optimization based on improved fractional order particle swarm optimization. Ocean Eng. 2022, 248, 110680. [Google Scholar] [CrossRef]
- Ma, W.; Lu, T.; Ma, D.; Wang, D.; Qu, F. Ship route and speed multi-objective optimization considering weather conditions and emission control area regulations. Mari Policy Manag. 2021, 48, 1053–1068. [Google Scholar] [CrossRef]
- Yuan, Q.; Wang, S.; Zhao, J. Uncertainty-informed ship voyage optimization approach for exploiting safety, energy saving and low carbon routes. Ocean Eng. 2022, 266, 112887. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J.; Vettor, R. Ship weather routing featuring w-MOEA/D and uncertainty handling. Appl. Soft Computing. 2023, 138, 110142. [Google Scholar] [CrossRef]
- Kwon, Y.J. Speed loss due to added resistance in wind and waves. Nav. Archit. 2008, 3, 14–16. [Google Scholar]
- Lu, R.; Turan, O.; Boulougouris, E.; Banks, C.; Incecik, A. A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping. Ocean Eng. 2015, 110, 18–28. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Trans. Res. Part D Transport. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Sang, Y.; Ding, Y.; Xu, J.; Sui, C. Ship voyage optimization based on fuel consumption under various operational conditions. Fuel 2023, 352, 129086. [Google Scholar] [CrossRef]
- Cepowski, T.; Drozd, A. Measurement-based relationships between container ship operating parameters and fuel consumption. Appl. Energy 2023, 347, 121315. [Google Scholar] [CrossRef]


| Wave (Wind) Direction | Direction Angle β | |
|---|---|---|
| Top wave, headwind | 0° | |
| Oblique wave, facing wave | 30–60° | |
| Transverse wave, crosswinds | 60–150° | |
| Following seas, tailwind | 150–180° |
| Ship Blocking Coefficient CB | Ship Load Situation | |
|---|---|---|
| 0.55 | Normal | |
| 0.60 | Normal | |
| 0.65 | Normal | |
| 0.70 | Normal | |
| 0.75 | Full load or normal | |
| 0.80 | Full load or normal | |
| 0.85 | Full load or normal |
| Ship Form | |
|---|---|
| Full load conditions of all ship types (except cargo ships) | |
| Preloading conditions of all ship types (except cargo ships) | |
| Normal loading of cargo ships |
| Parameter | Numerical Value |
|---|---|
| Length/m | 348 |
| Ship width/m | 51.2 |
| Average draft/m | 13.5 |
| Displacement/m3 | 169,700 |
| Ship blocking coefficient | 0.693 |
| Initial metacentric height/m | 4 |
| Algorithm | Parameter | Value |
|---|---|---|
| Genetic algorithm | Population size | 50 |
| Maximum number of iterations | 200 | |
| Penalty factor | 1 × 1010 | |
| Cross probability | 0.6 | |
| Mutation probability | 0.1 | |
| Step factor | 0.3 | |
| NSGA-II | Population size | 50 |
| Iterations | 200 | |
| Penalty factor | 1 × 1010 |
| Route | Distance/nm | Voyage Time/h | Fuel Consumption/t |
|---|---|---|---|
| Empirical route | 4864.50 | 324.3 | 1329.78 |
| GA route | 5182.66 | 341.7 | 1296.36 |
| NSGA route | 4965.73 | 334.2 | 1237.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zhao, S. Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm. J. Mar. Sci. Eng. 2024, 12, 485. https://doi.org/10.3390/jmse12030485
Zhao S, Zhao S. Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm. Journal of Marine Science and Engineering. 2024; 12(3):485. https://doi.org/10.3390/jmse12030485
Chicago/Turabian StyleZhao, Shuling, and Sishuo Zhao. 2024. "Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm" Journal of Marine Science and Engineering 12, no. 3: 485. https://doi.org/10.3390/jmse12030485
APA StyleZhao, S., & Zhao, S. (2024). Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm. Journal of Marine Science and Engineering, 12(3), 485. https://doi.org/10.3390/jmse12030485






