A Weakly Nonlinear System for Waves and Sheared Currents over Variable Bathymetry

Abstract

The wave–current–seabed interaction problem is studied by using a coupled-mode system developed for modeling wave scattering by non-homogeneous, sheared currents in variable bathymetry regions. The model is based on a modal series expansion of wave velocity based on vertical eigenfunctions, dependent on local depth and flow parameters, including propagating and evanescent modes. The latter representation is able to accurately satisfy the wave flow continuity condition and the no-entrance boundary condition on the sloping parts of the seabed. A new derivation of a simplified nonlinear system is introduced using decomposition to a mean flow and a perturbative wave field. To force the system to consider incoming waves at the inlet, boundary knowledge of periodic, travelling nonlinear water waves over a flat bottom is required. For this purpose, specific solutions are derived using the semi-analytical method based on the stream function formulation, for cases of water waves propagating above linearly and exponentially sheared currents. Results obtained by the application of the CMS concerning the propagation of waves and currents—in particular, examples characterized by depth inhomogeneities—are presented and discussed, illustrating the applicability and performance of the method.

1. Introduction

The problem of water propagating on top of vortical flows has attracted the attention of many scientists within the water wave community. Indeed, it has recently been shown that waves interacting with an opposing shear current over variable bathymetry can have a significant effect on the focusing of the wave field; see Rey et al. [1]. Such situations can be observed in natural conditions, when strong currents interact with the bathymetry [2,3], or in cases of strong wind forcing on the ocean–atmosphere interface; see, e.g., [4], and the recent review by Zhan et al. [5]. The propagation of periodic waves in the presence of a uniform shear background current has been studied by using complete description of the flow in the framework of Euler equations by Nwogu [6] and by Zhang et al. [7] using RANS equations.

For both coastal safety and engineering purposes, including the estimation of loads on structures in nearshore and coastal regions, the development and application of efficient models for predicting the nonlinear, phase-resolved behavior of water waves and currents in such areas are important. Results in this direction, for several case studies, have been presented by various authors; see, e.g., Refs. [8,9,10,11]. In particular, wave- and current-dominated orthogonal flows over fixed rough beds have recently been considered by Faraci et al. [12], where a review of coastal research also focused on wave–current flows, either collinear or at an angle can be found.

It is remarked that in many cases of wave–current–seabed interaction, computational difficulties are encountered in the analysis, since large areas often need to be considered, and the evolution of water waves propagating in such inhomogeneous media involves multiple-scale phenomena. In such cases, simplified models can be derived, allowing to separate the scales, solving the background flow on the one hand and the perturbative flow corresponding to water waves on the other hand. The latter can be solved by expanding its vertical structure on a selected basis consisting of modes and applying a Galerkin projection method to derive coupled equations with respect to the horizontal mode amplitudes. Indeed, by applying such a technique, a significant reduction in unknowns can be obtained, depending on the truncation made for the expansion. This approach has been widely studied in the absence of currents [13,14,15,16,17] or in the presence of vertically uniform currents, as in, e.g., [17,18,19]. When it comes to flows interacting with vorticity, Yang and Liu [20] recently introduced a Boussinesq-type formulation, projecting the velocity field on a polynomial basis. Also, an analysis of solitary wave and linear shear current interaction by using Green–Naghdi (GN) equations was described by Duan et al. [21].

Moreover, coupled-mode systems have been derived, involving propagating and evanescent modes, which are suitable to describe wave dispersion in intermediate water depth. Such models are applied to the scattering of water waves by horizontally shearing currents in variable bathymetry. In the case of wave propagation in the presence of vertically sheared currents, a generalized mild-slope equation was derived by Touboul et al. [22] by retaining only the propagation mode in the expansion, with a restriction to vertically linear currents. Extensions of the above approach to multi-mode systems for waves propagating over arbitrarily sheared currents were presented in [23], but they were essentially restricted to the framework of linear theory. The incorporation of non-linear effects in the above systems to describe the evolution of the flow in the framework of Euler equations was introduced in [24].

The present work is in continuation with the above developments. It aims to provide a weakly nonlinear, simplified system, in the framework of water waves propagating in the presence of currents, the latter being supposed to be known a priori. There are various motivations for proceeding so. The first to be cited is numerical efficiency. Indeed, describing a complex flow, constituted by both the current and the wave-induced flow, might require more modes to reach enough accuracy. Additionally, in order to tackle the multiscale aspects involved in coastal regions, there is a growing interest in coupling numerical models, relying on separate tools to resolve the dynamics of the slow scales (the currents) and the faster ones (the water waves), which the present work focuses on. A physical argument should also be cited. Disentangling the influence of water waves on the mean flow and the modifications enforced to the perturbative field by the mean flow is a necessary step to better understand wave–current interactions.

The structure of the paper is as follows: The derivation of the nonlinear CMS, separating the mean flow from the perturbative field, is presented in Section 2. The reduction of this model to a single mode allows us to obtain a simplified, two-equation system, aiming to model the dynamics of weakly nonlinear water waves propagating over varying bathymetry, on top of arbitrarily sheared currents.

The forcing of this model, at the wavemaking boundary, requires the knowledge of periodic, traveling nonlinear water waves in the presence of vertically sheared currents over a flat bottom. For this specific purpose, appropriate solutions are derived here by means of the stream function formulation, following the semi-analytical method initially introduced by Rienecker and Fenton [25] and extended to the specific case of water waves propagating above linearly sheared currents by Francius and Kharif [26]. A further extension of this approach, to more general cases of currents, is described in Section 3.

Finally, the numerical results illustrating the performance of the nonlinear CMS integrated in the time domain are presented in Section 4, and finally, conclusions and directions for future research are discussed in Section 5.

2. The Weakly Nonlinear Coupled-Mode System

The present work is based on the derivation initially presented in Ref. [24]. In the following subsections, a description of the problem under consideration is presented, briefly reminding readers of the basic theory and explaining its extension.

2.1. Decomposition of the Perturbative Field in a Local-Mode Series

As illustrated in Figure 1, we consider for simplicity the two-dimensional problem of weakly nonlinear water waves propagating over currents which vary with depth according to a general vertical profile. Both the bathymetry characterized by the depth function $h\left(x\right)$ and the vertical structure of the steady current ${\mathit{U}}_0\left(x,z\right)$ are considered to be known, where bold notation is used to indicate vector quantites. The flow domain $D\left(t\right)$ is bounded below by an impermeable boundary defined the depth function $z=-h\left(x\right),$ and it is bounded above by the free surface, which is modeled by the function $z=\eta \left(x,t\right)$, denoting the free surface elevation. It is assumed that $\eta \left(x,t\right)+h\left(x\right)>0$. The velocity field is considered to result from the contribution of steady rotational currents and a perturbative flow describing water waves:

$$\mathit{U}\left(x,z,t\right)={\mathit{U}}_0\left(x,z\right)+\mathit{u}\left(x,z,t\right).$$

(1)

The problem to be solved only considers the perturbative field, $\mathit{u}\left(x,z,t\right)$. Following this purpose, this field can be described by a spectral-type representation defined as a series expansion, with the general expression given by the summation of local modes (indexed by an integer n) as follows:

$$\mathit{u}\left(x,z,t\right)=\sum _{n=0}^{+\infty }{\mathit{u}}_{\mathit{n}}\left(x,t\right)Z_n\left(z;h\left(x\right),\eta \left(x,t\right)\right),$$

where $Z_n\left(z;h\left(x\right),\eta \left(x,t\right)\right)$ denote vertical functions which will be separately defined below for the horizontal and the vertical flow components. The latter vertical modes are different for each component of the wave velocity and are parametrically dependent on the local depth function and the free surface elevation, having the property of accurately treating the continuity equation and the no-entrance bottom boundary condition. In addition, the system of local vertical modes is complete in the interval $z\in \left[-h\left(x\right),\eta \left(x,t\right)\right]$ for each horizontal x position.

More specifically, if the perturbative velocity field is noted $\mathit{u}\left(x,z,t\right)=\left(u\left(x,z,t\right),w\left(x,z,t\right)\right)$, the horizontal wave component is given by

$$u\left(x,z,t\right)=\sum _{n=0}^{+\infty }{u}_n\left(x,t\right)Z_n^{\left(1\right)}\left(z;h\left(x\right),\eta \left(x,t\right)\right)$$

(2)

where $Z_n^{\left(1\right)}\left(z;h\left(x\right),\eta \left(x,t\right)\right)$ are defined by

$$Z_n^{\left(1\right)}\left(z;h,\eta \right)=\frac{\cos \left[k_n\left(z+h\right)\right]}{\cos \left[k_n\left(\eta +h\right)\right]}, n=0, 1, 2, 3, \dots$$

(3)

and the quantities $k_n=k_n\left(h\left(x\right),\eta (x,t)\right),n=\mathrm{0,1},2\dots ,$ are obtained as the roots of the following (dispersion-like) equation:

$${\mu }_0+k_n\mathit{tan}\left[k_n\left(h+\eta \right)\right]=0$$

(4)

The first root is imaginary ($k_0=i\left|k_0\right|$), while the positive index roots $k_n,n=\mathrm{1,2}\dots ,$ are real, with $k_n\approx \frac{n\pi }{\left(h + \eta \right)},n\to \infty$. Function (3), together with the dispersion Equation (4), are obtained from regular eigenvalue problems in the local vertical interval $z\in \left[-h\left(x\right),\eta \left(x,t\right)\right]$, controlled by the frequency-type parameter ${\mu }_0$; see [16]. This directly ensures the completeness property of the vertical basis; see, e.g., [27,28].

The vertical component $w\left(x,z,t\right)$ of the wave field is modeled by a corresponding modal expansion based on another set of z-functions $Z_n^{\left(2\right)}\left(z;h\left(x\right),\eta \left(x,t\right)\right)$, as follows:

$$w\left(x,z,t\right)=-\sum _{n=0}^{+\infty }\left(\frac{\partial u_n}{\partial x}\left(x;t\right)Z_n^{\left(2\right)}\left(z;h;\eta \right)+u_n\left(x;t\right)\frac{\partial Z_n^{\left(2\right)}}{\partial x}\left(z;h;\eta \right)\right)$$

(5)

The functions $Z_n^{\left(2\right)}(z;h,\eta )$ are defined as follows:

$$Z_n^{\left(2\right)}\left(z;h,\eta \right)=\frac{1}{k_n}\frac{\mathit{sin}\left[k_n\left(z+h\right)\right]}{\mathit{cos}\left[k_n\left(\eta +h\right)\right]},n=\mathrm{0,1},\mathrm{2,3}, \dots$$

(6)

At the seabed, they fulfill $Z_n^{\left(2\right)}\left(z=-h;h,\eta \right)=0$, as well as the condition that $\partial Z_n^{\left(2\right)}/\partial z \left(z\right)=Z_n^{\left(1\right)} \left(z\right)$ over the whole water column (see also Appendix A of Ref. [24]). Using the latter relations, in conjunction with the definition of $u\left(x,z,t\right)$, given by Equations (2) and (3), and $w\left(x, z, t\right)$, given by Equations (5) and (6), in the continuity equation $u_x+w_z=0$ and in the bottom boundary condition $w\left(x, z=-h, t\right)+\partial h/\partial x u\left(x,z=-h,t\right)=0,$ it is easily seen that both these equations are automatically satisfied by the present modal-type expansion of the wave velocity components. This property greatly facilitates the treatment of the considered problem, since only the momentum and the free surface boundary conditions are left to be satisfied. Furthermore, the substitution of the above local-mode expansions in the momentum equations will lead to a nonlinear coupled-mode system of equations on the horizontal plane with respect to the unknown velocity amplitudes $u_n\left(x,t\right)$ and the wave elevation $\eta \left(x,t\right).$ Based on the fast convergence properties of the local mode series, the above coupled-mode system facilitates the numerical solution of the problem and will be discussed in the sequel.

2.2. Momentum Equations

As discussed in the previous subsection, the kinematics of the problem are analytically satisfied by means of the specific modal expansions of the wave velocity. We might now address the dynamics of the problem, by introducing this representation in the momentum equations. We shall start with the Euler equations describing the total flow $\mathit{U}=\left(U,W\right)$, so that (see, e.g., [29])

$$\begin{gathered} \frac{\partial U}{\partial t}+\frac{1}{2}\frac{\partial {\left|\mathit{U}\right|}^2}{\partial x}-E=-\frac{1}{\rho }\frac{\partial p}{\partial x}, \\ \frac{\partial W}{\partial t}+\frac{1}{2}\frac{\partial {\left|\mathit{U}\right|}^2}{\partial z}-e=-\frac{1}{\rho }\frac{\partial \left(p+\rho gz\right)}{\partial z}, \end{gathered}$$

(7)

where ${\left|\mathit{U}\right|}^2=U^2+W^2$ and $\mathit{e}=U\times \mathsf{\Omega }=\left(E,e\right)$ is a helicity-type field, with $\mathsf{\Omega }$ denoting the vorticity $\mathsf{\Omega }=\mathsf{\nabla }\times \mathit{U}=\Omega \widehat{j}$, which, in accordance with Equation (1), is split into two terms: $\mathsf{\Omega }={\Omega }_0+\omega$. In the present two-dimensional case, the vorticity is fixed in the transverse direction (with $\widehat{j}$ denoting the corresponding unit vector), and thus,

$$E=-W\Omega ,\hspace{1em}e=U\Omega$$

(8)

Subsequently, at each horizontal x position, we may consider the vertical momentum Equation (7) and perform its integration in the vertical direction from a depth level z up to the free surface elevation $\eta \left(x,t\right)$. In conjunction with the dynamic free surface boundary condition, $p\left(x,z=\eta \left(x,t\right),t\right)=0$, an expression of the local pressure in the column is obtained and reads as follows:

$$\frac{p\left(x,z,t\right)}{\rho }=g\left(\eta \left(x,t\right)-z\right)-{\int }_z^{\eta \left(x,t\right)}e\left(z\right)dz+{\int }_z^{\eta \left(x,t\right)}\left(\frac{\partial W}{\partial t}+\frac{1}{2}\frac{\partial {\left[U^2+W^2\right]}^{z=\eta \left(x,t\right)}}{\partial z}\right)dz.$$

(9)

This expression of the local pressure might now be differentiated with respect to the horizontal coordinate, and it comes out to

$$-\frac{1}{\rho }\frac{\partial p}{\partial x}\left(\mathrm{x},\mathrm{z},\mathrm{t}\right)=-g\frac{\partial \eta }{\partial x}\left(x,t\right)+\frac{\partial }{\partial x}\left({\int }_z^{\eta \left(x,t\right)}e\left(z\right)dz\right)-\frac{\partial }{\partial x}\left({\int }_z^{\eta \left(x,t\right)}\frac{\partial W}{\partial t}dz\right)-\frac{1}{2}\frac{\partial }{\partial x}\left(\frac{\partial {\left[{\left|\mathit{U}\right|}^2\right]}^{z=\eta \left(x,t\right)}}{\partial z}\right)$$

which, substituted back into Equation (7), finally results in

$$\frac{\partial U}{\partial t}-E=-g\frac{\partial \eta }{\partial x}\left(x,t\right)+\frac{\partial F}{\partial x}-\frac{\partial }{\partial x}\left({\int }_z^{\eta \left(x,t\right)}\frac{\partial W}{\partial t}dz\right)-{\left[U\frac{\partial U}{\partial x}+W\frac{\partial W}{\partial x}\right]}^{z=\eta (x,t)},$$

(10)

for all $x$ and $h\left(x\right)<z<\eta \left(x,t\right)$, and where $F\left(x,z,t\right)={\int }_z^{\eta \left(x,t\right)}e\left(z\right)dz$. At this point, we might introduce the flow decomposition (1) in Equation (10), to obtain the horizontal momentum equation satisfied by the only perturbative field. It follows that

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial t}-E_1-E_2-E_3& \\ & =-g\frac{\partial \eta }{\partial x}+\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial x}+\frac{\partial F_3}{\partial x}-\frac{\partial }{\partial x}\left({\int }_z^{\eta \left(x,t\right)}\frac{\partial w}{\partial t}dz\right)\hfill \\ & -{\left[U_0\frac{\partial u}{\partial x}+W_0\frac{\partial w}{\partial x}\right]}^{\eta \left(x,t\right)}-{\left[u\frac{\partial U_0}{\partial x}+w\frac{\partial W_0}{\partial x}\right]}^{\eta \left(x,t\right)}\hfill \\ & -{\left[u\frac{\partial u}{\partial x}+w\frac{\partial w}{\partial x}\right]}^{\eta \left(x,t\right)}\hfill \end{array}$$

(11)

where the quantities $E_1,E_2,E_3,F_1,F_2$, $F_3$ are associated with the expansion of the helicity field, and are defined as follows:

$$\begin{gathered} E_1=-W_0\omega , \\ {E}_2=-w{\mathsf{\Omega }}_0, \\ {E}_3=-w\omega , \\ {F}_1={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}{\mathrm{e}}_1\left(\mathrm{z}\right)\mathrm{d}\mathrm{z}={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}{U}_0\mathsf{\omega }dz, \\ {F}_2={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}{e}_2\left(\mathrm{z}\right)dz={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}u{\mathsf{\Omega }}_{0}dz, \\ {F}_3={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}{e}_3\left(z\right)dz={\int }_{\mathrm{z}}^{\mathsf{\eta }\left(\mathrm{x},\mathrm{t}\right)}u\omega dz \end{gathered}$$

(12)

In Equation (11), the terms involving only the current have been dropped, since it is understood that the current flow is a solution of this equation by itself.

Finally, Equation (11), in conjunction with the kinematic free surface boundary condition,

$$\frac{\partial \eta }{\partial t}+U_0\frac{\partial \eta }{\partial x}+u\frac{\partial \eta }{\partial x}-w=0, on\hspace{1em}\hspace{1em}z=\eta \left(x,t\right),$$

(13)

constitutes the remaining system to be solved.

2.3. A Weakly Nonlinear Coupled-Mode System

In this section, the remaining horizontal momentum Equation (11) of an inviscid liquid with a free surface and the kinematic free surface boundary condition, Equation (13), are reformulated as a non-linear coupled-mode system with respect to the unknown amplitudes of the velocity field ${\left(u_n\left(x,t\right)\right)}_{n=\mathrm{0,1},2,\dots }$ and the free surface elevation $\eta \left(x,t\right).$ Using the completeness properties of the local vertical functions $\left\{Z_m^{\left(1\right)}\left(z;h\left(x\right),\eta \left(x,t\right)\right),m=\mathrm{0,1},2,\dots \right\}$, both sides of Equation (11) are projected into this basis, for each horizontal x position, and we obtain

$$\begin{array}{cc}\hfill ⟨\frac{\partial u}{\partial t},Z_m^{\left(1\right)}⟩+⟨\frac{\partial }{\partial x}\left({\int }_z^{\eta } \frac{\partial w}{\partial t}d\xi \right),Z_m^{\left(1\right)}⟩& \hfill \\ & +⟨1,Z_m^{\left(1\right)}⟩[\frac{\partial }{\partial x}\left[U_0\left(\eta \right)\cdot u\left(\eta \right)+W_0\left(\eta \right)w\left(\eta \right)\right]+\frac{1}{2}\frac{\partial }{\partial x}\left[u{\left(\eta \right)}^2+w{\left(\eta \right)}^2\right]\hfill \\ & +g\frac{\partial \eta }{\partial x}]-⟨E_1,Z_m^{\left(1\right)}⟩-⟨E_2,Z_m^{\left(1\right)}⟩-⟨E_3,Z_m^{\left(1\right)}⟩-⟨\frac{\partial F_1}{\partial x},Z_m^{\left(1\right)}⟩-⟨\frac{\partial F_2}{\partial x},Z_m^{\left(1\right)}⟩\hfill \\ & -⟨\frac{\partial F_3}{\partial x},Z_m^{\left(1\right)}⟩=0, \mathrm{for} \mathrm{m}=\mathrm{0,1},2,\cdots ,\mathrm{M},\hfill \end{array}$$

(14)

where $⟨f_1\left(z\right),f_2\left(z\right)⟩={\int }_{z=-h}^{z=\eta }{f}_1\left(z\right)f_2\left(z\right)dz$. As already mentioned, this equation is to be supplemented with the kinematic free surface boundary condition, which, in terms of the wave velocity modal amplitudes, reads as follows:

$$\begin{gathered} \frac{\partial \mathsf{\eta }}{\partial t}+U_0\frac{\partial \mathsf{\eta }}{\partial x}+\sum _{n=0}^M\left\{\left(Z_n^{\left(1\right)}\left(z=\mathsf{\eta };h,\mathsf{\eta }\right)\frac{\partial \eta }{\partial x}+\frac{\partial Z_n^{\left(2\right)}}{\partial x}\left(z=\mathsf{\eta };h,\mathsf{\eta }\right)\right)u_n \\ +Z_n^{\left(2\right)}\left(z=\mathsf{\eta };h,\mathsf{\eta }\right)\frac{\partial u_n}{\partial x}\right\}=0,\hspace{1em}\mathrm{on} z=\eta . \end{gathered}$$

(15)

The final form of the above coupled-mode system, Equations (14) and (15), is derived by using the particular forms of the vertical functions defined by Equations (3) and (6), as provided with more details in Appendix A, and the involved coefficients are given in Appendix B. Moreover, a weakly nonlinear system is obtained, as presented with more details in Appendix B, by treating the nonlinear terms as second-order terms of the unknows $\eta$ and ${\left(u_n\left(x,t\right)\right)}_{n=\mathrm{0,1},2,\dots }$, which is studied in present work for the propagation of waves interacting with sheared currents over general bathymetry.

Furthermore, the convergence of the vertical expansion discussed in [24] reveals that, in most cases, the contribution of the first mode $n=0$ is dominant. Thus, it is tempting to produce a two-equation system obtained by considering only this term. By approximating the vertical structure of the wave field, keeping only the mode $n=0$ in the wave velocity expansion Equation (2), and assuming relatively slow currents and dropping approximately higher-order terms, a simplified version of the above system of Equations (13) and (14) reduces to the following:

$$\begin{gathered} A{1}_{00}\frac{\partial u_0}{\partial t}+B{1}_{00}\frac{{\partial }^2{u}_0}{\partial t\partial x}+C{1}_{00}\frac{{\partial }^3{u}_0}{\partial t\partial x^2}+D{1}_{00}{u}_0+E{1}_{00}\frac{\partial u_0}{\partial x}+F{1}_{00}\frac{{\partial }^2{u}_0}{\partial x^2} \\ +G{1}_{00}\frac{{\partial }^3{u}_0}{\partial x^3}+H{1}_0\frac{\partial \eta }{\partial x}=N{L}_0^{\left(1\right)},\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d} \\ \frac{\partial \eta }{\partial t} + A{2}_0\frac{\partial \eta }{\partial x}+ \sum _{n=0}^M\left\{B{2}_0 u_0 + C{2}_0 \frac{\partial u_0}{\partial x}\right\} =N{L}^{\left(2\right)} \end{gathered}$$

(16)

where $N{L}_0^{\left(1\right)}=⟨E_3,Z_0^{\left(1\right)}⟩+⟨\frac{\partial F_3}{\partial x},Z_0^{\left(1\right)}⟩-⟨1,Z_0^{\left(1\right)}⟩\frac{1}{2}\frac{\partial }{\partial x}\left[u_0 {\left(0\right)}^2\right]$,$N{L}^{\left(2\right)}=-u_0 \left(0\right)\frac{\partial \eta }{\partial x},$ and the coefficients are defined in Appendix B. Here, the brackets denote $⟨f_1,f_2⟩={\int }_{z=-h}^{z=0}{f}_1{f}_{2}dz$. The above simplified version of the weakly nonlinear CMS could be useful to obtain approximate numerical results at relatively low-cost supporting engineering applications concerning waves propagating in the presence of shear currents over inhomogeneous domains.

3. Nonlinear Solutions of Steady Traveling Waves and Sheared Currents in Constant Depth

Following the purpose of initializing our numerical solver of the coupled-mode system (either by means of the boundary condition or the initial condition in the restrictive case of an undisturbed boundary), we need to have access to the modal amplitude corresponding to a traveling wave over unperturbed bathymetry. This purpose can be achieved by solving the fully nonlinear problem and then computing its projection on the CMS modal base. The purpose of this section is to present the method used here.

Restricting ourselves to the case of periodic, two-dimensional, steady-traveling waves at a constant depth h, in the presence of a shear current $U_0\left(z\right)$, we consider a coordinate system $\left(\xi , z\right)$ moving with the wave speed $c$ so that $\xi =x-ct$, with the origin at some point on the undisturbed free surface. Following [26,30], a specific solution is constructed in this section, obtained as solution of the modified Helmholtz equation for the stream function $\Psi \left(\xi ,z\right)$:

$${\nabla }^2\Psi -a\Psi =b$$

(17)

with $a, b$ constants subjected to Dirichlet boundary conditions at the bottom and at the free surface:

$$\Psi \left(\xi ,z=-h\right)=0,\hspace{1em} \Psi \left(\xi ,z=\eta \left(\xi \right)\right)=-Q$$

(18)

where $\eta \left(\xi \right)$ denotes the free surface elevation and $Q$ is a constant controlling the flowrate. The solution is constructed to also satisfy the dynamic free surface boundary condition as it will be described below, in conjunction with horizontal periodicity for a cell of length $\lambda$. Also, the above solution corresponds to a field where the vorticity is proportional to the stream function:

$$\mathsf{\Omega }=a\Psi +b$$

(19)

In the sequel, we will consider examples in the case where $a>0;$ however, extension to $a<0$ is also possible. We consider the following partial solution of Equation (18):

$${\mathsf{\Psi }}_0\left(z\right)=\frac{B_0}{a^{1/2}}\sinh \left(a^{1/2}\left(z+h\right)\right)+\frac{b}{a}\left(\cosh \left(a^{1/2}\left(z+h\right)\right)-1\right),$$

(20)

where $B_0$ is an unknown coefficient that will be connected with the phase speed of the waves $c=-B_0$. It is easily verified that the function provided by Equation (21) satisfies the partial differential Equation (18) and the bottom boundary condition. By differentiating with respect to z we obtain that it corresponds to a horizontal flow with exponential structure in the vertical direction:

$$U_0\left(z\right)=\frac{\partial {\mathsf{\Psi }}_0}{\partial z}=B_0\cosh \left(a^{1/2}\left(z+h\right)\right)+\frac{b}{a^{1/2}}\sinh \left(a^{1/2}\left(z+h\right)\right),$$

(21)

with vorticity described as follows:

$${\mathsf{\Omega }}_0\left(z\right)=\frac{\partial U_0}{\partial z}=B_0{a}^{\frac{1}{2}}\sinh \left(a^{\frac{1}{2}}\left(z+h\right)\right)+b\cosh \left(a^{\frac{1}{2}}\left(z+h\right)\right).$$

(22)

It can be further seen that in the case of small $a,$ Equations (21)–(23) above reduce to the following approximate vertical profile:

$${\Psi }_0\left(z\right)\approx B_0\left(z+h\right)+\frac{b{\left(z+h\right)}^2}{2}+O(a)$$

(23)

$$U_0\left(z\right)=\frac{\partial {\Psi }_0}{\partial z}\approx B_0+b\left(\mathrm{z}+\mathrm{h}\right)+\mathrm{O}(a)$$

(24)

$${\mathsf{\Omega }}_0\left(z\right)=\frac{\partial U_0}{\partial z}\approx b+O(a).$$

(25)

Comparing the above with the result of Ref. [26] we obtain a result that is similar to the corresponding case of waves propagating in the presence of a linearly sheared current with constant vorticity ${\mathsf{\Omega }}_0\approx b.$ On the other hand, for $b=0$, the vertical current profile is described by the hyperbolic cosine function, and in cases of relatively large $a$ values, it takes the form of an exponential distribution.

3.1. Solution Based on Fourier Modal Expansion Method

We proceed now to the formulation of the Fourier series method for the solution of the above problem, based on the following representation:

$$\mathsf{\Psi }\left(\xi ,z\right)=\frac{B_0}{a^{1/2}}\mathit{sinh}\left(a^{1/2}\left(z+h\right)\right)+\frac{b}{a}\left(\mathit{cosh}\left(a^{1/2}\left(z+h\right)\right)-1\right)+\sum _{n=1}^{\infty }{B}_n{\Psi }_n\left(\xi ,z\right),$$

(26)

where ${\Psi }_n\left(\xi ,z\right)$ are eigen solutions of the homogeneous modified Helmholtz equation, Equation (18) with $b=0$, in the domain fulfilling the bottom boundary condition):

$${\Psi }_n\left(\xi ,z\right)=\frac{\mathit{sinh}\left(k_n\left(z+h\right)\right)}{\mathit{cosh}\left(k_{n}h\right)}\mathit{cos}\left(nk\xi \right),\hspace{1em}\mathrm{with} { k}_n^2=a+{\left(nk\right)}^2,$$

(27)

where $k=2\pi /\lambda$ is the horizontal periodicity parameter. In the present case, where the vorticity is assumed to be proportional to the stream function (20), the Euler equations are integrated after being expressed in the moving frame of reference using $\tilde{u}=u-c \mathrm{a}\mathrm{n}\mathrm{d} \mathsf{\xi }=x-ct$, providing Bernoulli’s equation as follows:

$$\frac{p}{\rho }-R-\frac{a}{2}{\Psi }^2-b\mathsf{\Psi }+gz+\frac{1}{2}\left(u^2+w^2\right)=0,$$

(28)

where $R$ denotes the Bernoulli constant; see, e.g., [25,29]. In Equation (29), the horizontal and vertical flow velocity components are obtained from the corresponding derivatives of the stream function representation as follows:

$$\tilde{u}\left(\xi ,z\right)=\frac{\partial \Psi \left(\xi ,z\right)}{\partial z}, w\left(\xi ,z\right)=-\frac{\partial \Psi \left(\xi ,z\right)}{\partial \xi }.$$

(29)

Obviously, the case $a=b=0$ results to the method of Rienecker and Fenton [25] corresponding to periodic waves without current. Using the above equations, the following system of nonlinear equations is defined:

$$\begin{gathered} \frac{B_0}{a^{-1/2 }}\sinh \left(a^{1/2}\left(\eta \left(\xi \right)+h\right)\right)+\frac{b}{a}\left(\cosh \left(a^{1/2}\left(\eta \left(\xi \right)+h\right)\right)-1\right) \\ +\sum _{n=1}{B}_n{\Psi }_n\left(\xi ,z=\eta \left(\xi \right)\right)+Q=0, \end{gathered}$$

(30)

$$g\eta \left(\xi \right)+\frac{1}{2}\left(u^2\left(\mathsf{\xi },z=\mathsf{\eta }\left(\mathsf{\xi }\right)\right)+w^2\left(\mathsf{\xi },z=\mathsf{\eta }\left(\mathsf{\xi }\right)\right)\right)-R – \frac{a}{2}{Q}^2=0,$$

(31)

From which the unknown coefficients $\left\{B_n,n=0, 1, 2,\dots ..\right\}$, the free surface elevation $\eta \left(\xi \right)$, and the unknown constants $Q$ and $R$ are calculated for given values of the parameters a and b. For the numerical solution of the above system, the representation of the stream function is truncated, keeping the first $N$ terms $\left\{B_n,n=\mathrm{1,2},\dots .N\right\}$. The free surface elevation is discretized to $N$ equidistant points ${\eta }_i=\eta \left({\xi }_i\right)$ with constant step $\Delta \xi ={\xi }_{i+1}-{\xi }_i$, and the discrete version of the system (31) and (32) with $2N+2$ unknowns (including $R$ and $Q$) is numerically solved by the Newton–Raphson method, similarly as presented by [25]. The additional two equations are provided by using the data for the wave height H:

$$\mathrm{m}\mathrm{a}\mathrm{x}\left({\eta }_i\right)-\mathit{min}\left({\eta }_i\right)=H,$$

(32)

and the requirement that the mean water level is at $z=0$:

$$\mathrm{Mean}\left({\eta }_i\right)=0.$$

(33)

3.2. Examples of Fields and Dispersion Relation Characteristics

In this subsection, indicative numerical solutions are presented as obtained by using the stream function method described above, for periodic waves characterized by the nonlinear parameter $\epsilon =0.5Hk=0.15$, where $H$ denotes the waveheight, and the dispersive parameter is chosen to be $kh=2\pi /10.$ The cases of linearly and exponentialy sheared currents are considered here. The selection of the linear case is motivated by the literature review, and the willingness to provide a comparison with already existing results. Water waves propagating in the presence of a vertically linear distribution of the current has been widely studied in previous years for mathematical reasons (see, e.g., Touboul et al. [22]). However, this configuration finds applications in geophysical flows, for instance, when considering rip currents, as demonstrated by Haas and Svendsen [2]. The selection of the exponential case is now allowed by the abilities newly obtained with this approach. It corresponds to the current distribution obtained under the action of wind. By comparing these two solutions, the strong influence of the current distribution is clearly illustrated. Here, the analysis is restricted to opposing currents; however, it could be extended to following currents and will be examined in future work. For normalizing the results, a water depth measured from the mean level of the free surface elevation equal to $h=1 \mathrm{m}$ is used in the computations.

(i) Linearly sheared current: In this example, the current vorticity coefficients in Equation (21) are chosen, such as $a\simeq 0 {\mathrm{m}}^{-2}$ and $b=-1 {\mathrm{s}}^{-1}$. The current profile and the resulting free surface elevation are presented in Figure 2. It is observed that the wavelength-to-depth ratio is $\lambda /h=10$ and the wave nonlinearity parameter is $H/h=0.46$, and thus, the Ursell number takes moderate values $Ur=(H/h){(\lambda /h)}^2=46$, corresponding to nonlinear Stokes (short) waves.

The free surface presents a strong vertical asymmetry, as it is classically observed in nonlinear periodic wave solutions. The results are obtained by using a number of grid points ($N=40$) corresponding to a total of $80$ grid points per wavelength, which are found to be enough for numerical convergence. In Figure 3, color plots of the calculated stream function and the vorticity corresponding to the total field are presented. In addition, the streamlines are indicated in the subplots using thin black lines. It is observed that the total flow vorticity, in the major part of the domain, presents a value close to $\mathsf{\Omega }=-1 {\mathrm{s}}^{-1}$, which is due to the constant value of the background current characterized by the linear vertical profile of Figure 2a. Deviations from the latter value are observed close to the free surface and especially near the wave crests as a result of the interaction of the current with the wave flow, which becomes rotational. Along with the solution concerning the free surface elevation and the stream function, the wave celerity is also calculated ($c=-B_0$). Systematic results concerning the dispersion characteristics of the above non-linear solutions will be presented in Section 3.3.

(ii) Exponentially sheared current: In this case, we consider an exponentially sheared current field. A particular example is calculated by using the parameters $a=0.7 {\mathrm{m}}^{-2}$ and $b=0 {\mathrm{s}}^{-1}.$ The corresponding profile is presented in Figure 4. The free surface obtained numerically by applying the present stream function method is also plotted in this figure. The wave parameters are as before, with $\epsilon =0.5Hk=0.15$ concerning the nonlinear parameter and $kh=2\pi /10$ for the dispersive parameter, while the numerical configuration is kept identical to the previous case. The free surface elevation obtained with these parameters is found to be close to the one obtained in the presence of a linearly sheared current; this is as expected since the two vertical profiles of Figure 2a and Figure 4a differ mostly at a submergence close to half of the depth, where the wave is relatively attenuated.

In this case, also, the vertical asymmetry of the wave profile is important, presenting very close values of the wave crests and through as before in Figure 2. This is further verified by the values of the constant controlling the flowrate, which is calculated to be $Q=2.991 {\mathrm{m}}^2/\mathrm{s}$, which is very close to the value in the linearly sheared current case ($Q=2.998 {\mathrm{m}}^2/\mathrm{s})$.

In Figure 5, color plots of the computed stream function and derived vorticity are presented. As before, the streamlines are indicated in both subplots using thin black lines. As far as it concerns the calculated stream function $\Psi$ (Figure 5a), a strong similarity with the linear sheared current is observed, although some fine differences might be noticed. Yet, when comparing the total vorticity field $\mathsf{\Omega }$ between the linear sheared current (Figure 3b) and the exponential sheared current (Figure 5b), specific differences are observed. Indeed, it appears clearly in the example of the exponentially sheared current that the vorticity is much smaller (almost zero) in the vicinity of the bottom, which is a direct consequence of the vertical distribution of the shear current $U_0\left(z\right)$ and its derivatives in the neighborhood of $z=-h$, which, for the relatively large $a$ value of this example, is approximated by an exponential distribution, resulting in ${\omega }_0\left(z\right)=\partial U_0/\partial z\simeq$ 0 in the vicinity of the bottom. Here, again, the total vorticity including the waves is observed to present a deviation from the corresponding field associated with the current ${\mathsf{\Omega }}_0\left(z\right)$ in the vicinity of the free surface and finds its maximum (in magnitude) at the surface.

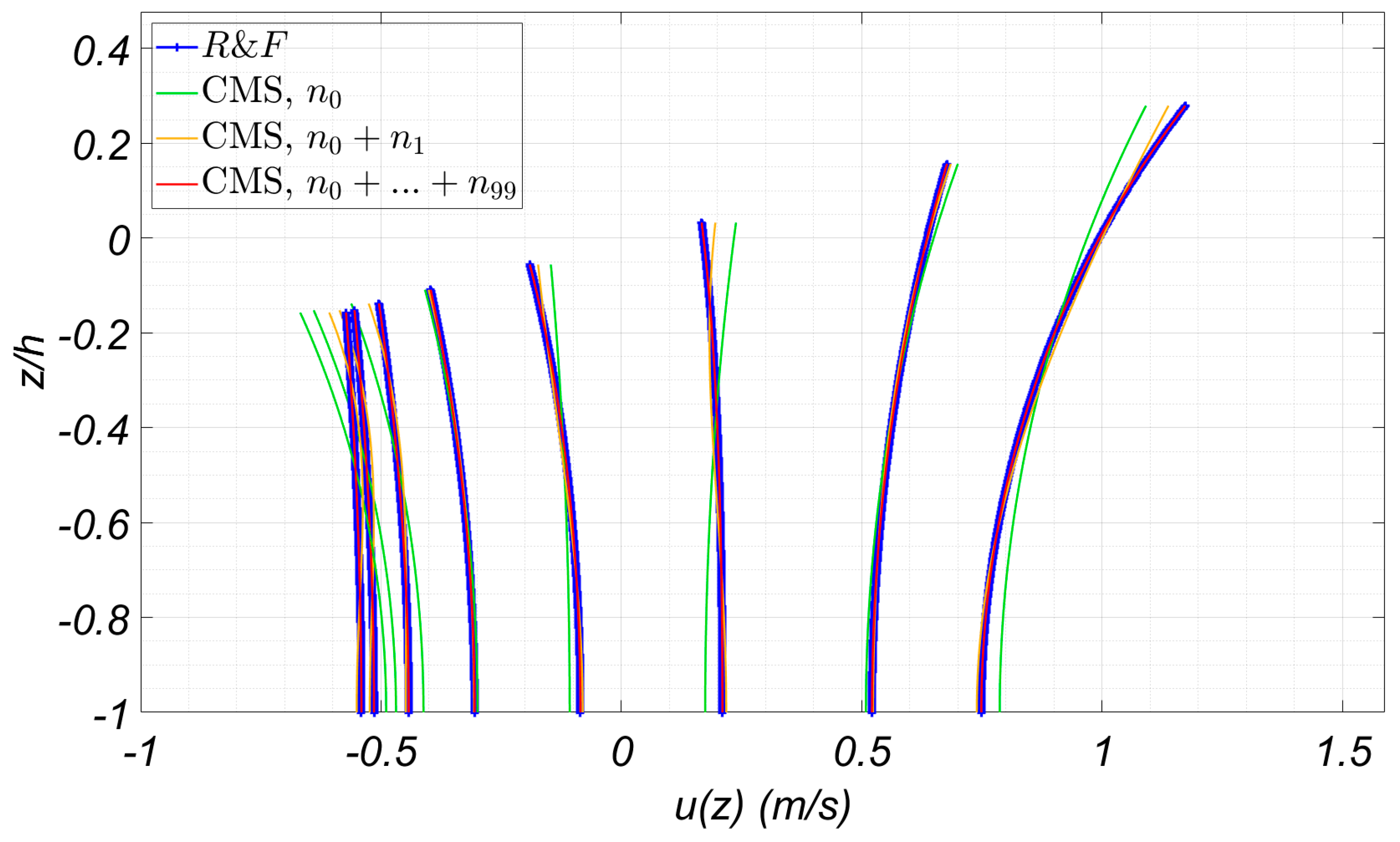
3.3. Projection of the Fully Nonlinear Solution on a CMS Basis

Having obtained the numerical solution for the fully nonlinear stream function, the components of the wave field are obtained by spatial differentiation of the field using Equation (30). The latter components, in conjunction with the transformation from moving to the laboratory-fixed coordinate system, can be projected accordingly on the vertical basis of Equation (3). Indeed, considering the nonlinear solution of the horizontal component of the velocity, $u$, obtained by the method described in Section 3.1, and selecting a number of modes $M$ for truncation of Equation (2), a classical Galerkin approach can be used. This is easily obtained by considering that

$$\sum _{n=1}^M{u}_n\left(x,t\right){\int }_{-h}^{\eta \left(x,t\right)}{Z_m^{\left(1\right)}Z}_n^{\left(1\right)}dz={\int }_{-h}^{\eta \left(x,t\right)}u\left(x,z,t\right)Z_m^{\left(1\right)}\left(x,z;h,\eta \right)dz,\hspace{1em}1\le m\le M,$$

(34)

which, in matrix form, reads as $\mathit{u}={\mathit{M}}^{-1}\mathit{U}$, with the following elements:

$$M_{mn}={\int }_{-h}^{\eta \left(x,t\right)}{Z_m^{\left(1\right)}Z}_n^{\left(1\right)}dz,{ U}_m={\int }_{\left\{-h\right\}}^{\eta \left(x,t\right)}u\left(x,z,t\right)Z_m^{\left(1\right)}\left(x,z;h,\eta \left(x,t\right)\right)dz.$$

(35)

Here, the functions $Z_n^{\left(1\right)}\left(z;h,\eta \right)$ and $Z_m^{\left(1\right)}\left(z;h,\eta \right)$ are provided by Equation (3). The modal amplitudes ${\left(u_n\right)}_{1\le n\le M}$ are immediately obtained by inverting the linear system of Equation (34). These modal amplitudes $u_n\left(x,t\right)$ together with the free surface elevation $\mathsf{\eta }\left(x,t\right)$ constitute incident wave data for the CMS Equations (14) and (15) or the simplified system Equation (16). Yet, it is emphasized that these integrals differ from the scalar product defined earlier, since the limit of integration is now between $z=-h$ and $z=\eta \left(x,t\right)$. The system in (34) is inverted to obtain the expected distribution of $u_n\left(x,t=0\right)$. Whenever needed, boundary data $u_n\left(x=0,t\right)$ at the entrance $(x=0)$ of the CMS domain are obtained by multiplying the above modal amplitude functions by the nonlinear phase velocity. Examples of applications of the latter for various cases will be presented in Section 4.

Yet, it is interesting to consider the converging behavior of the solution represented by the modal expansion of the CMS with the fully nonlinear solution of Section 3.2. In Figure 6, the vertical distribution of the horizontal component of the velocity, obtained in our first example of linearly sheared current ($a\simeq 0$, $b=-1s^{-1}, \epsilon =0.15$, and $kh=2\pi /10$), is presented. The blue crosses correspond to the fully nonlinear solution, obtained at various phase values. The green curves correspond to the solution obtained for the only mode $n=0$, at the same phase values. The orange curves present the solution involving the two first modes, $n=0$ and $n=1$, while the red curves are the solution obtained with $100$ modes. These results are presented in order to provide an idea of the rate of convergence of the solution presented on the basis of the CMS. If only the mode $n_0$ shows some limitations (yet, the reader is reminded that the vorticity and the nonlinearity considered here are really significant), taking into account two modes already provides a very satisfying solution. A few differences can still be observed, located near the free surface. The example involving $M=100$ modes shows absolutely no difference with the fully nonlinear solution. Another possibility is to consider the modal amplitude and its evolution with the number of modes considered. This is presented in Figure 7. From this figure, it is clear that the modal amplitude provides a rate of convergence which is larger than an order of two.

3.4. Phase Velocity of the Nonlinear Waves

The method presented in this section also allows us to compute the nonlinear phase velocity, since it is related to the constant $B_0=-c$. Furthermore, the linear phase velocity can be obtained in the case of arbitrary current flow by solving the Rayleigh equation (see [31] for more details).

Thus, it is interesting to compute the phase velocity obtained here for the specific current profiles, Equation (21), with the phase velocity of linearized waves computed by solving the Rayleigh equation. Results are presented in Figure 7, from systematic solutions as the ones examined before in the water strip with depth h = 1 m.

In particular, three current configurations are examined and results are presented: (i) water waves propagating in the absence of current $\left(a,b\right)=\left(\mathrm{0,0}\right)$, (ii) the current configuration presenting a linear variation in depth $\left(a,b\right)\simeq \left(0,-1 {\mathrm{s}}^{-1}\right)$, and (iii) the current varying exponentially with depth $\left(a,b\right)=\left(0.7 {\mathrm{m}}^{-2},0\right)$. For each of these current configurations, three values of the dispersive parameter are considered: $kh=\pi$, $kh=2\pi /5$, and $kh=\pi /5$, corresponding to water waves propagating in relatively deep water, intermediate water depth, and water waves propagating in relatively shallow water. These configurations constitute the nine curves presented in Figure 8, where the calculated normalized phase speed $c/{\left(gh\right)}^{1/2}$ is plotted. Each curve is obtained by varying the nonlinear parameter ε in the vertical axis in the range $0.001\le \epsilon \le 0.2$.

The above results illustrate the effect of the nonlinear parameter on the phase celerity of traveling waves in the presence of sheared currents. The vertical black lines represent the values obtained for each of the cases considered by solving the Rayleigh equation, which match the calculated results for limiting small nonlinearity $\epsilon \simeq 0$.

Several classical results are confirmed through this figure. First, when considering a given current configuration, the effect of the dispersive parameter $kh$ is observed. The longer the waves, the faster they propagate. Also, for a given current configuration, it is seen that the effect of the nonlinear parameter $\epsilon$ is more important for more shallow waves. The deviation from the linear theory (the vertical black lines) is faster when $kh$ is small. Finally, when intercomparing the effect of the current on the phase celerity, for a given $kh$, the opposing current is found to slow down propagation. The linearly sheared current presents a stronger effect than the exponentially sheared one, as expected.

4. Weakly Nonlinear Propagation over Varying Depth and Currents

In this section, numerical results are presented in the case of waves propagating in constant depth in the presence of shear currents, as obtained by the time integration of the weakly nonlinear coupled-mode system (Equations (14) and (15)). Taking into account the observed fast convergence characteristics of the modal expansion, the simplified model based on Equation (16) is finally used to illustrate results of simulations of waves and shear currents in variable-bathymetry regions.

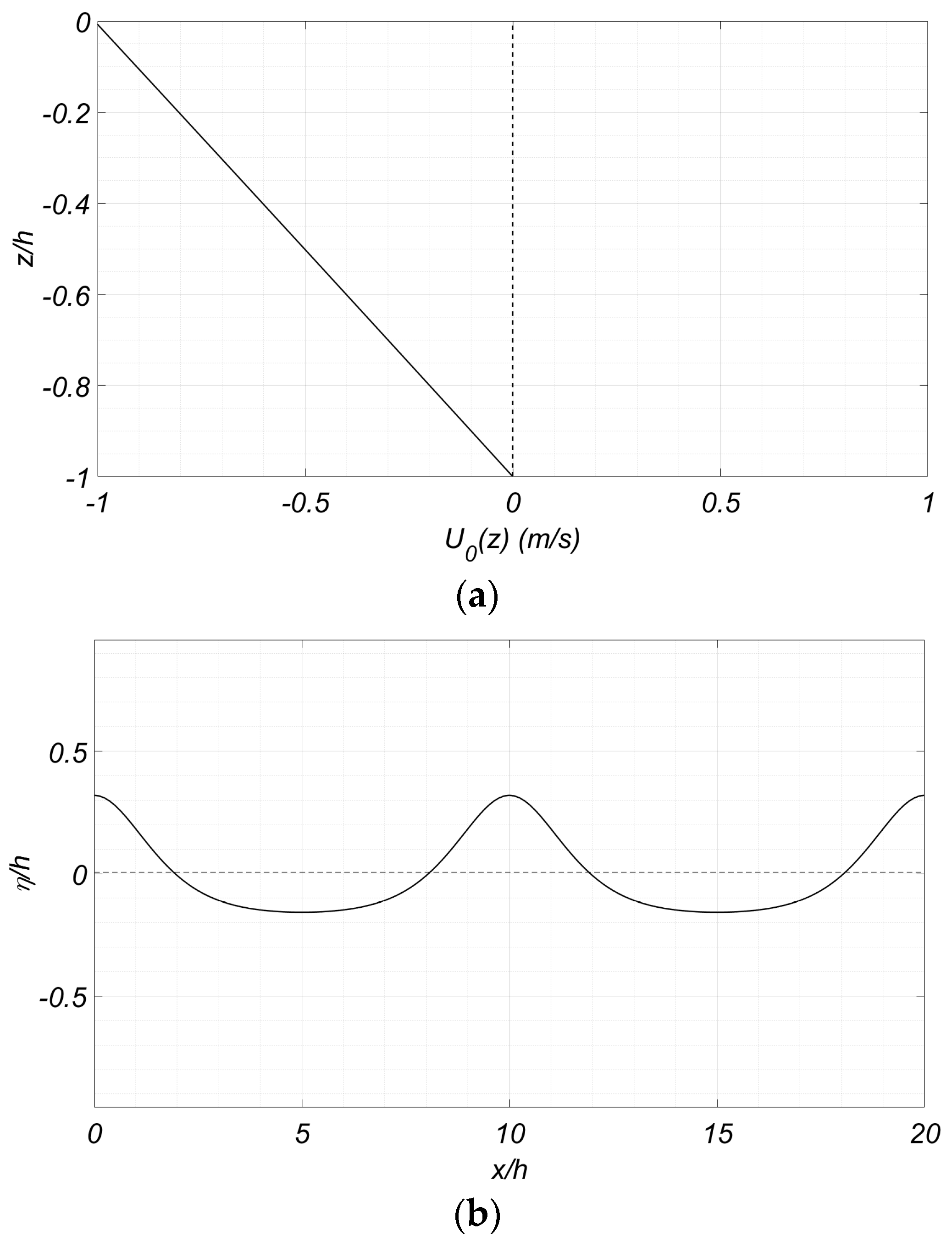
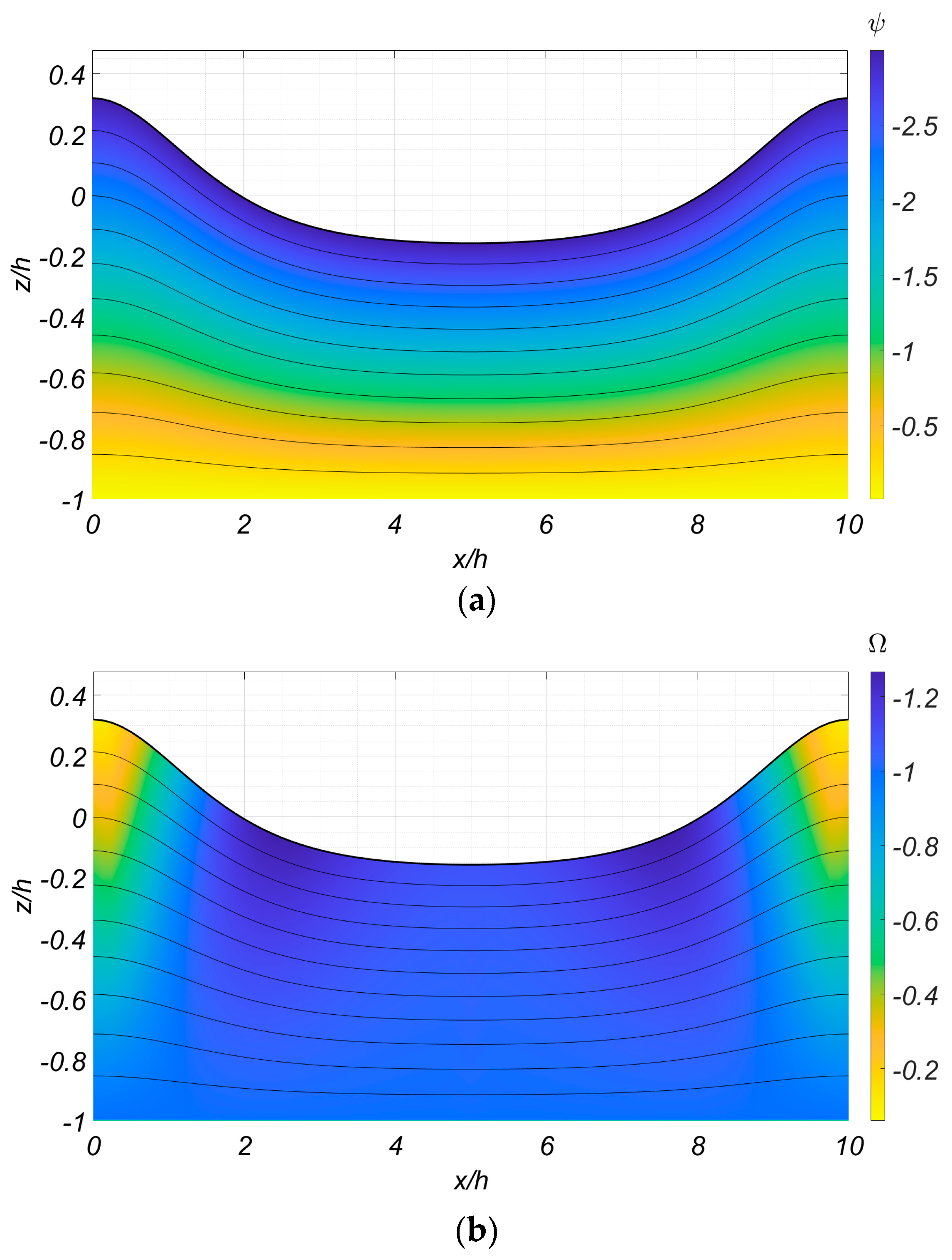
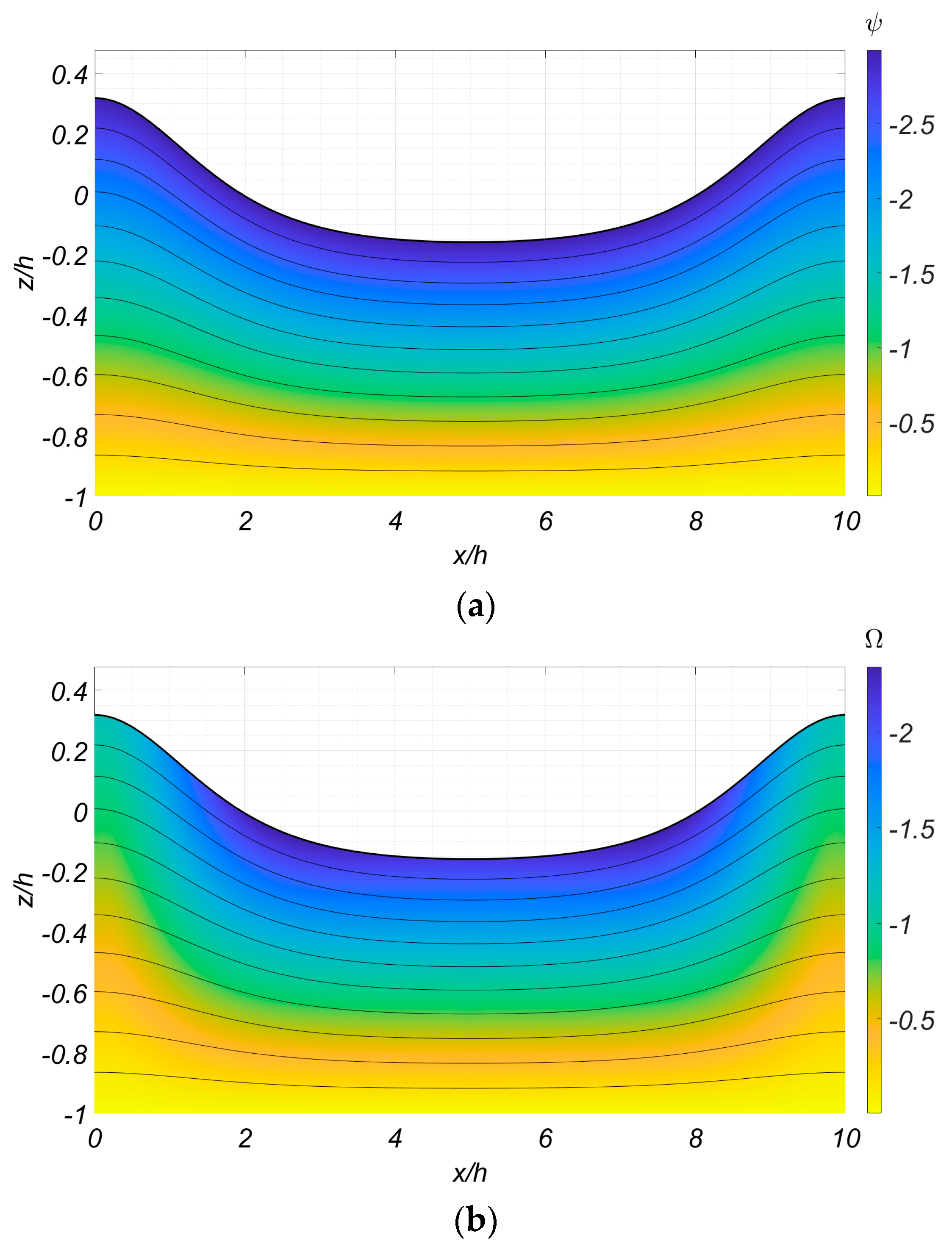
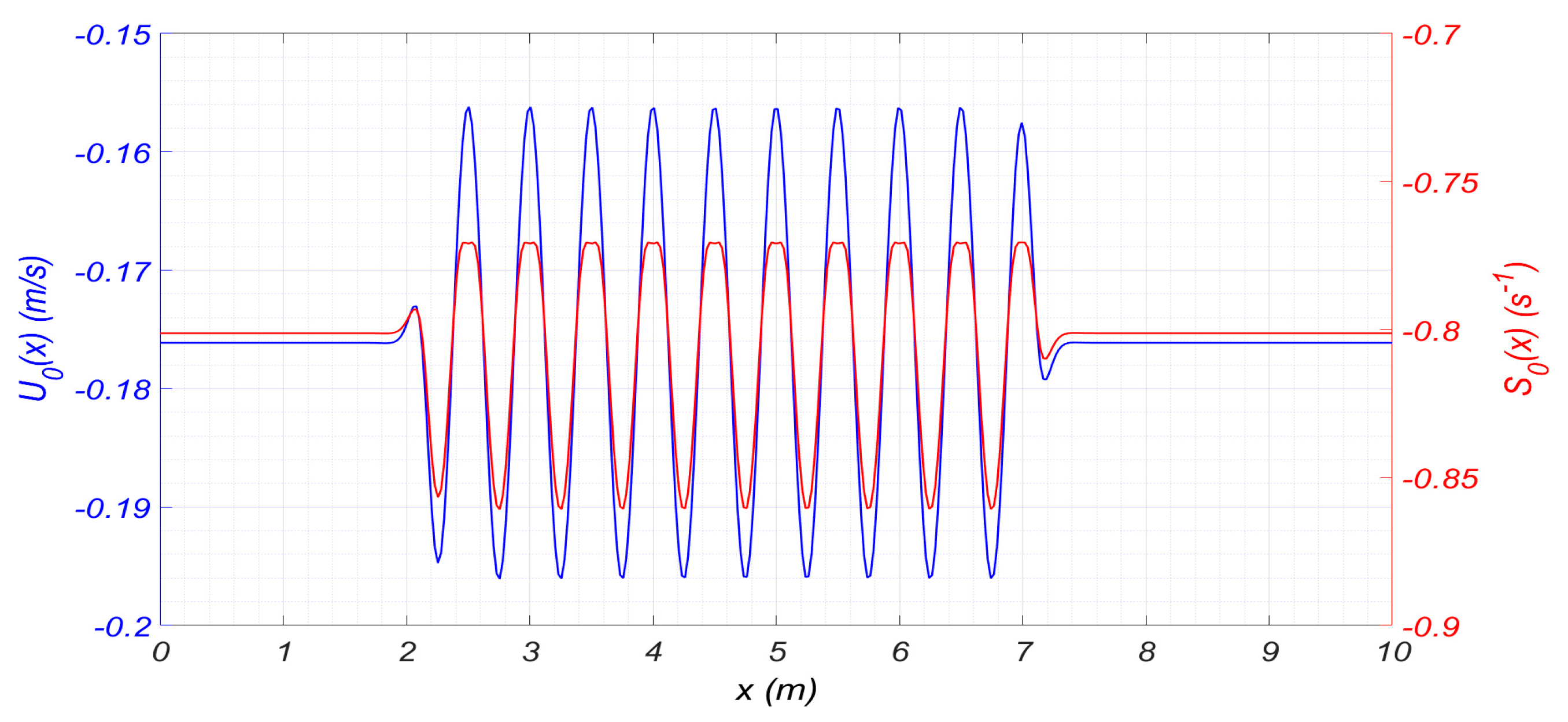
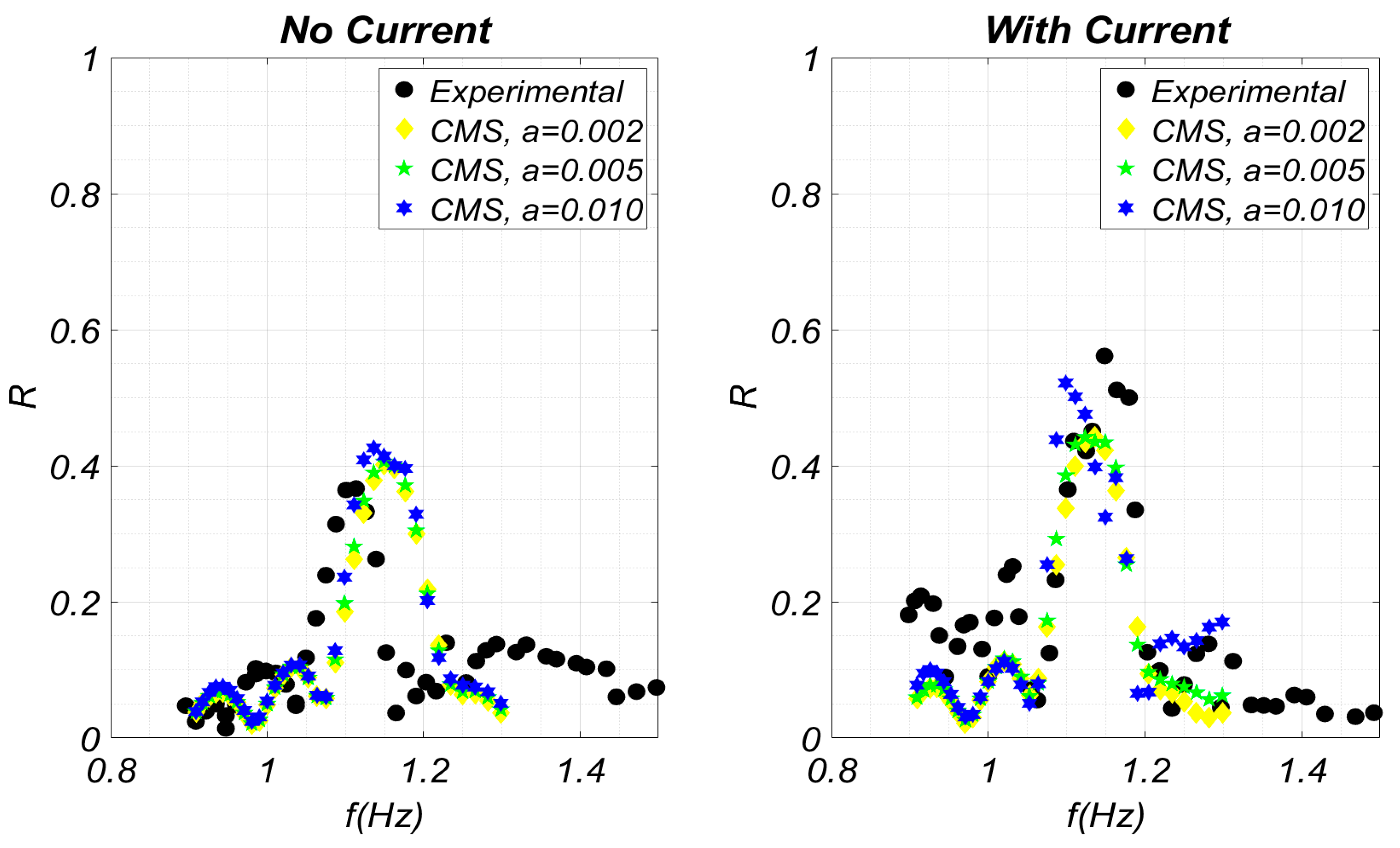
4.1. Initialization of the CMS and Comparison with the Fully Nonlinear Method

The purpose of this section is to investigate the ability of the CMS to reproduce the behavior of water waves in the presence of vortical flow in weakly nonlinear conditions. To stay consistent with this aim, three cases are considered, involving weakly nonlinear water waves and various current configurations. First, a no-current case in which $\left(a,b\right)\simeq \left(\mathrm{0,0}\right)$ is presented. The case of linear shear current in which $\left(a,b\right)\simeq \left(0,-0.5{\mathrm{s}}^{-1}\right)$ is then analyzed. Finally, an exponential case is presented, in which $\left(a,b\right)=\left(0.15 {\mathrm{m}}^{-2}, 0\right)$. For these three cases, the water waves parameters are $kh=2\pi /10$ and $\epsilon =0.05$, characterizing weakly non-linear conditions in intermediate water depth. Results will be compared to those provided by the fully nonlinear method presented in Section 3.

The configuration of the coupled-mode system considered here involves periodical boundary conditions, while time integration of an initial condition is performed. To produce the initial condition, two methods were investigated. The first approach was to use a linear solution and to apply a relaxation term for the nonlinear terms in the first period of propagation (see, e.g., [22,23]). Another possibility is to start from the fully nonlinear solution obtained from the model presented in Section 3, providing the full solution in terms of $\eta$ and $u$ [32]. In this case, it is necessary to obtain its projection on the solution on the basis of the CMS, as described in Section 3.3. For the sake of clarity, it is reminded that the system provided by Equation (34) is solved for each location $x$ of the initial domain for the CMS, providing the data for $u_n\left(x,t=0\right)$.

The discrete version of the present CMS is obtained by using high-order finite differences to approximate horizontal and time derivatives of the wave mode amplitudes $u_n\left(x,t\right)$ and the free surface elevation $\eta \left(x,t\right)$, on a regular grid $\left(x_i=x_a+\left(i-1\right)\Delta x, t_n=\left(n-1\right)\mathsf{\Delta }t\right)$. The mesh is obtained by using M_x steps of equal length $\mathsf{\Delta }x=\left(x_b-x_a\right)/M_x$ to subdivide the horizontal interval $x_a\le x\le x_b$. Based on the above analysis concerning the dispersion characteristics of the present model, in most cases, the number of the retained modes required for convergence is very small, and the horizontal subdivision of the domain is based on using 30–40 points per wavelength. In all examples presented and discussed below, the dimension of the discrete coupled-mode system is of the order of several thousands, and for the time integration of the dynamic system, a fourth-order BDF scheme is used, with Courant number ${\left(C\mathsf{\Delta }t/\mathsf{\Delta }x\right)}_{max}$.

Both initializing procedures are compared in the case involving no current, and results are presented in Figure 9, concerning η$\left(x,t\right) \mathrm{a}\mathrm{n}\mathrm{d} u_n\left(x,t\right), n=\mathrm{0,1},2$. In this figure, results indicated by using red lines corresponding to the calculations based on the fully nonlinear method presented in Section 3, obtained by means of the stream function formulation. Green lines present the time evolution computed by means of the CMS using a linear initial condition, together with a relaxion scheme for the nonlinear terms. Finally, blue lines correspond to results obtained with by the CMS, initialized with the projection described by Equation (34). It appears that the results of computation are compatible with the steady traveling solutions, by using both initialization approaches, and in the next examples, only the projection method (Section 3.3) is used.

Next, in Figure 10, the time evolution of the free surface elevation and the first, second, and third mode of the horizontal velocity are shown, as obtained by the present CMS, in the case of an opposing linear shear current characterized by the parameters $\left(\mathrm{a},\mathrm{b}\right)=\left(0,-0.5 {\mathrm{s}}^{-1}\right)$, $\mathsf{\epsilon }=0.05$, and $kh=\mathsf{\pi }/5$.

Here again, the results presented are in good agreement with the fully nonlinear simulations. It is observed that no differences can be seen as far as the free surface elevation and the propagating mode $u_0$ are concerned. When it comes to modal amplitudes $u_1$ and $u_2$, and noting that the vertical scales of the last two subplots of Figure 10 have been increased by 25 and 50 times for comparison purposes, the results obtained by the present method are considered to be very satisfying, both in terms of phase and amplitude. Yet, some small oscillations in the modal amplitude are observed, related to the numerical integration. However, the latter differences are minor concerning the solution for the total velocity field u(x,z,t), which, in the examined nonlinear case, is approximated by truncating the present expansions defined by Equations (2) and (5) and keeping only the first three terms.

Finally, in Figure 11, similar results are presented in the case of an opposing current showing an exponential vertical profile, characterized by the parameters $\left(\mathrm{a},\mathrm{b}\right)=\left(0.15 {\mathrm{m}}^{-2},0\right)$, in the case of nonlinear waves in intermediate water depth $\mathsf{\epsilon }=0.05$ and $kh=\mathsf{\pi }/5$. The time evolution of the free surface elevation and the first, second, and third mode of the horizontal velocity are shown, as obtained by the present CMS, and compared to the fully nonlinear solution of Section 3.

In this example, the results presented in Figure 11 indicate a small discrepancy between the stream function solution and the CMS calculation, which is due to a very small difference (of the order of $1.25\%$) in wave celerity as calculated by the present CMS. Yet, when it comes to the behavior of the amplitudes, for the free surface elevation, but also for the modes $u_0$, $u_1$, and $u_2$, the agreement is still very satisfaying.

In both the above examples, we also observe the fast decay of the modal amplitudes (accordingly to Figure 7), indicating that in such cases, $u_n\left(x,t\right)$, for $n>0$, is more than an order of magnitude less than $u_0\left(x,t\right)$, confirming the applicability and usefulness of the simplified model provided by Equation (16). Still, some limitations of the numerical integrator of the system are observed, and future work will be devoted to further improving its performance.

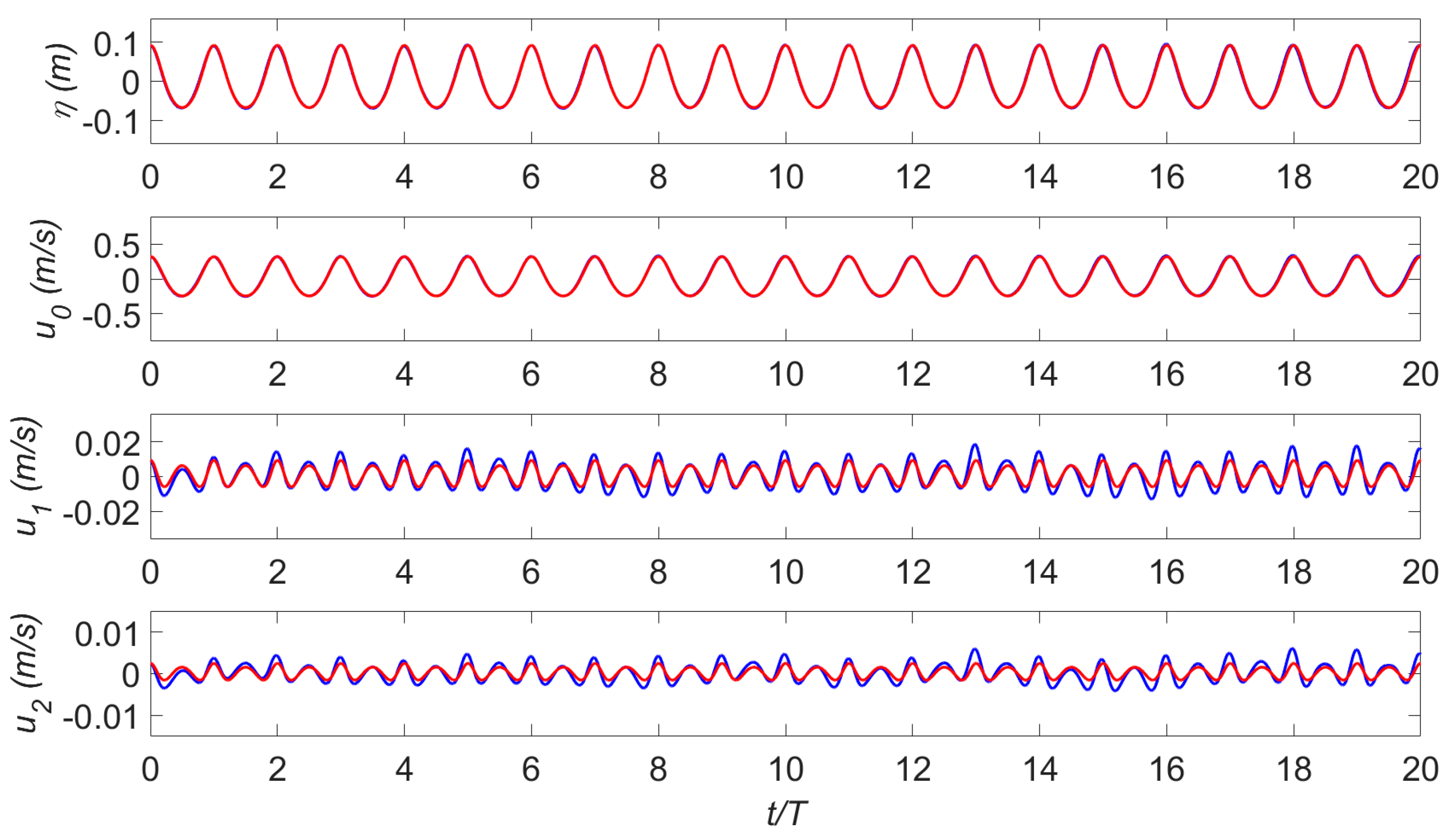
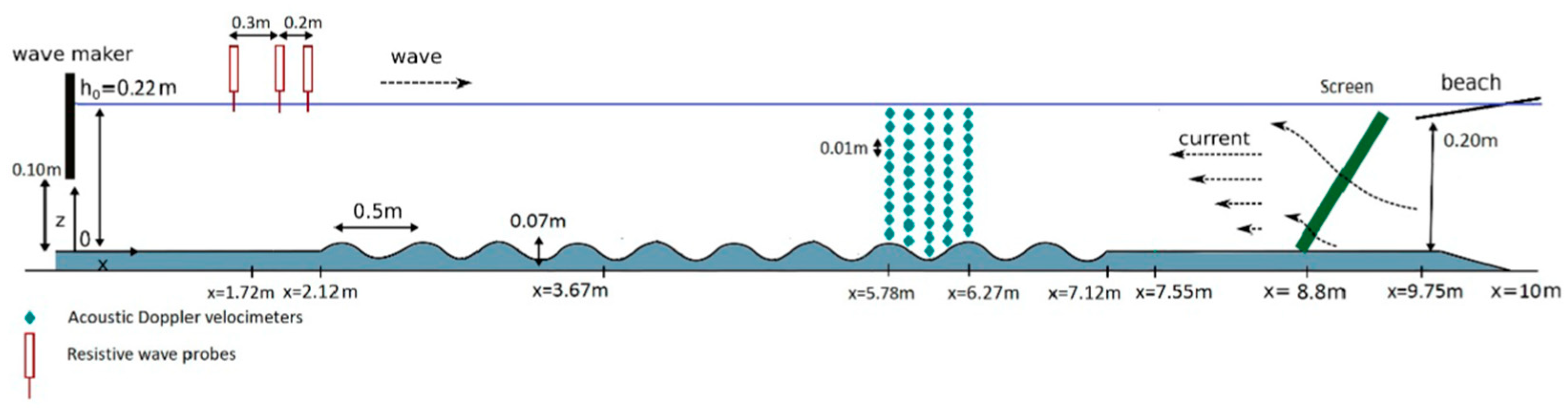
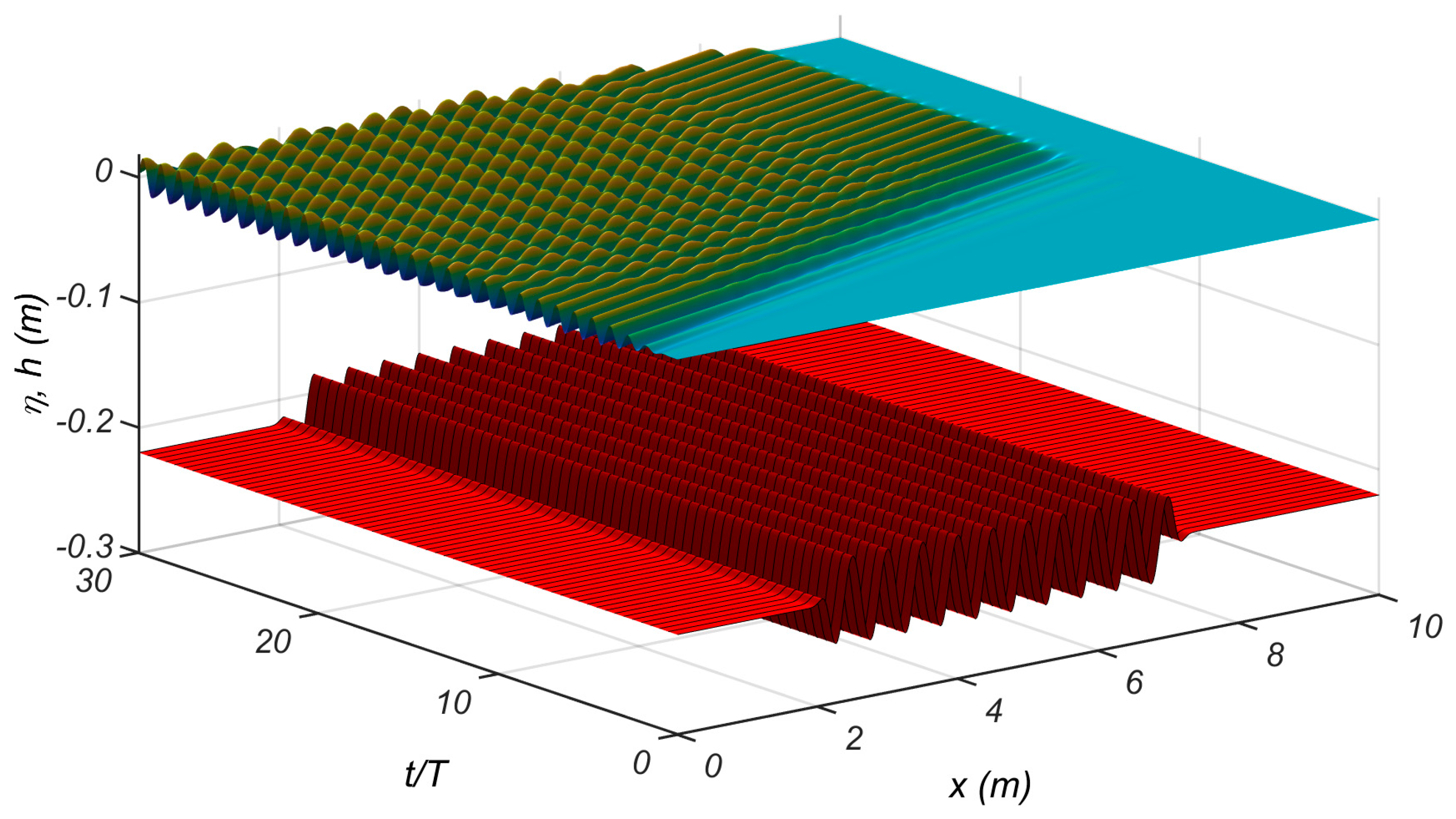
4.2. Wave Propagation over Rippled Bed in the Presence of Shear Current

Finally, we consider here the application of the present CMS for an example concerning wave propagation over variable bathymetry in the presence of an opposing sheared current. The problem of water waves reflected by periodic undulating topography, known as Bragg resonant reflection, has been studied extensively in the last few decades. When the surface wavelength is about twice the topographic wavelength, the incoming waves are significantly reflected by the periodic bottom, and only a small part of the wave energy is transmitted. Since the problem has strong implications in coastal engineering, it has been widely studied; see, e.g., the study by Mei [33] and the references therein. More recently, the nonlinearity involved in the process has attracted some of the attention of the scientific community [34,35]. In particular, an investigation of the effects of Bragg reflection on harbor oscillations has been presented by Gao et al. [36,37]. The nonlinear problem of wave–bottom interactions involving a piecewise linear depth varying current was investigated recently by Raj and Guha [38]. For this reason, the Bragg reflection problem constitutes an interesting configuration to explore through the CMS.

Here, we consider a sinusoidal bottom topography in the middle of the domain of an otherwise flat horizontal bottom of depth $h=0.22 \mathrm{m}$, i.e., the bottom slope and curvature are zero for a significant length at the ends of the domain. Such a configuration has been tested experimentally in the flume of SeaTech, University of Toulon, France, depicted in Figure 12, and measurements of the reflection coefficient were collected in order to study the Bragg resonance of wave and current systems and its effects on the reflection coefficient. An inclined perforated screen was used to generate the shear of the opposing current at the downwave end of the flume. The position of the wave probes for estimating the reflection and transmission of waves from measured wave data are shown in Figure 13. At the upwave end of the channel, an electromagnetic piston was used to generate regular waves. At the downwave end of the flume, a sloping beach was used to absorb waves. The opposing current was injected into the channel by a hydraulic pump, and a perforated screen was used to control the shear; see Figure 13. The sinusoidal bottom profile consists of 10 ripples of amplitude $0.035 \mathrm{m}$ and length $0.5 \mathrm{m}$. The opposing shear current vertical profile is approximately linear:

$$U\left(x,z\right)=U_0\left(x\right)+S\left(x\right)z$$

(36)

where $U_0\left(x\right)$ is the surface current and $S\left(x\right)$ denotes the shear. In this case, the current vorticity field is ${\Omega }_0\left(x\right)=S\left(x\right)$.

We consider as an example the reflection of waves over a rippled bed with the presence of an opposing current with a mean speed of $0.17 \mathrm{m}/\mathrm{s}$. More details are provided in Laffite et al. [39], where estimations concerning the spatial variation of shear $S\left(x\right)$ are available. In this case, the shear is estimated to be negative near the entrance of the wave and becomes oscillatory above the sinusoidal bottom. Based on the above, the horizontal distribution of the shear in the domain is calculated by assuming the conservation of the mass of the current flow as follows:

$$S\left(x\right)=\frac{2}{h\left(x\right)}\left(U_0\left(x\right)-\frac{h\left(0\right)}{h\left(x\right)}{U}_0(0)\right)+\frac{2h\left(0\right)}{h{\left(x\right)}^2}S(0)$$

(37)

where $x=a$ and $x=b$ denote the coordinates of the wave entrance and exit in the domain.

Indicative distributions of current parameters used in the sequel for calculations of waves by the present CMS are presented in Figure 14.

As concerns the conditions for Bragg resonance, it is known that the resonant reflection of surface water waves by sinusoidal bars in the presence of a current is manifested when

$$k_p+k_m=K_b,$$

(38)

where $K_b$ is the wavenumber of the bottom profile, and $k_p$ and $k_m$ are obtained as the roots of the dispersion relation for opposing and following current, respectively.

$${\sigma }^2\left(x\right)={\sigma }_0\left(x\right){\sigma }_2\left(x\right)=k_p\left(x\right)g\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(k_p\left(x\right)h\left(x\right)\right),$$

(39)

where g is the gravity acceleration. Equation (39) is formulated with respect to an average relative frequency estimated by

$$\sigma =\sqrt{{\sigma }_0{\sigma }_2}=\sqrt{(\omega \pm U_0\cdot k_{p,m})(\omega \pm U_2\cdot k_{p,m})},$$

(40)

where $U_0$ is the surface current and $U_2=U_0-S\left(2d\right)$ s the value of the current at a penetration depth defined as 2d; see also Touboul et al. [22]. An extended version of the above relation has been derived and discussed in Belibassakis et al. ([23], Section 2.4).

In the experimental tests, the incident wave frequencies ranged from $0.7 \mathrm{H}\mathrm{z}$ to $1.5 \mathrm{H}\mathrm{z}$ with amplitudes between $0.5-2 \mathrm{c}\mathrm{m}$, ensuring relatively small steepness, both without a current and with the vertically sheared current. Predictions obtained from the present model are presented in Figure 15 and Figure 16 in the case of sinusoidal incident waves with a frequency of $1.1 \mathrm{H}\mathrm{z}$, close to wave resonance conditions, and a wave amplitude of $1 \mathrm{c}\mathrm{m}$, without current and with the consideration of the sheared current. In these figures, a space–time plot of the free surface elevation $\eta (x,t)$ is shown, as calculated by the present method. The result corresponds to periodic waves propagating over a sinusoidal bed (also depicted in the figure at an average depth of 22 cm), without any current (Figure 15) and with the effects of a sheared current with a linear vertical profile (Figure 16), as modeled, respectively, by using the data in Figure 14. The bottom profile varies only along the x-axis, and the opposing current is also directed along the x-axis, as indicated in the figures. Since the wave generated at the upwave end of the flume is harmonic, the plot of the free surface history at $t=0$ (shown along the t-axis) is sinusoidal.

In both cases, a rapid decay of the mode amplitudes is observed. Moreover, we observe in Figure 15 and Figure 16, illustrating the history of the free surface elevation over the sinusoidal bed, that the results indicate strong reflection. In the case of waves opposing the shear current, we clearly observe the shortening of the wavelengths and the steepening of waves in Figure 16, especially over the sinusoidal bottom. Moreover, in this case, the disturbance of the flow due to the combined effect of the rippled bed and the vorticity contained in the vertically sheared current is seen to generate a more complicated pattern, related to the wavenumber asymmetry due to the presence of the current.

In Figure 17, the reflection coefficient, plotted as a function of the wave frequency (in the laboratory frame of reference), is presented for both cases, considering the current or not. Together with the experimental results, we present results obtained numerically by means of the present CMS model. These results were obtained by considering various incident wave conditions, namely $a=0.002 \mathrm{m}$, $a=0.005 \mathrm{m}$, and $a=0.01 \mathrm{m}$. Thus, the effect of nonlinearity in the reflection process is observed. It appears that both the peak frequency and its amplitude are better described when the considered wave amplitude approaches the one considered in the experiments. This result confirms that although Bragg reflection is a linear process, nonlinear hydrodynamical interactions play a role in the interaction process. Further investigation of the present CMS, including results concerning the calculation of reflection and transmission coefficients for various wave frequencies and comparisons with results from other works and experimental data, will be considered in future work, as well as an extension to three-dimensional problems; see, e.g., [31,40].

5. Conclusions

A coupled-mode system based on the velocity formulation of the wave field was developed and used for modeling wave scattering by inhomogeneous, sheared currents in variable bathymetry regions. The model is based on a modal series expansion of the wave velocity based on vertical eigenfunctions, which are dependent on local depth and flow parameters, including the propagating and evanescent modes. A new derivation of a simplified weakly nonlinear system was introduced using decomposition to a mean flow and a perturbative wave field, and it was subsequently used to study wave–current–seabed interaction problems in inhomogeneous domains. For defining data describing the incoming waves at the inlet boundary, knowledge of periodic traveling nonlinear water waves over a flat bottom is required. Specific solutions were derived using the semi-analytical method based on the stream function formulation for cases of water waves propagating above sheared currents with linear and exponential profiles. The obtained results clearly illustrate the effect of the current vortical distribution on the nonlinear behavior and phase speed of water waves, in the same order of magnitude as the dispersion parameter, suggesting that sheared currents are expected to have a strong influence on refraction and diffraction phenomena in variable-bathymetry regions. Examples concerning the propagation of waves and currents in cases with depth inhomogeneities were subsequently presented and discussed, illustrating the applicability and performance of the present model. In particular, Bragg reflection by sinusoidal bottom profiles was analyzed, and 5% to 10% differences in the reflection peak were observed in the presence of a current, due to the combined effects of nonlinearity and vorticity on the behavior of water waves. Future work is planned towards the extension of the model to three-dimensional problems, including the case of waves interacting with currents at an angle.