Abstract
This paper addresses the issues of maximum power point tracking (MPPT) and fault-tolerant control in tidal steam turbines under complex marine environments. In order to solve the conflicting problems in the existing sliding mode control between dynamic performance and chatter reduction as well as the use of fault estimation link in the fault-tolerant control, which increases the system complexity, an adaptive non-singular fast terminal sliding mode and adaptive robust fault tolerance method (ANFTSMC-ARC) is proposed. First, a speed controller equipped with adaptive non-singular fast terminal sliding mode control (ANFTSMC) is designed to improve the power capture efficiency under swell disturbances. This design achieves fast convergence and circumvents the singularity problem. Then, a new reach law is proposed based on the adaptive hybrid exponential reaching law (AHERL), which ensures high tracking performance while reducing chattering. In addition, considering that the hydraulic pitch system is prone to failure, a fault-tolerant controller with automatically adjustable gain is designed under the adaptive robust scheme. With the help of Lyapunov theory, the closed-loop system is proved to be uniform and ultimately bounded. Finally, comparative simulation results verify the efficiency of the proposed control strategy.
1. Introduction
With the rapid development of the global economy, the energy structure, which is dominated by fossil energy sources such as coal and oil, has put pressure on the ecological environment. In recent years, many renewable energy sources have been studied, among which tidal current energy has received widespread attention for its predictability and high energy density. As shown in Figure 1, the tidal stream turbine (TST) consists of a turbine that produces mechanical energy, a generator that produces electrical energy, and a power converter for power control and connection to the grid. The control objective of a tidal stream turbine is to maximize energy capture, and the power it produces is proportional to the cube of the current flow velocity () and the power coefficient (Cp). Due to the variation of tidal current flow rate, the power variation of TST is divided into different regions, in which the maximum power point tracking (MPPT) and variable pitch control are the two common control methods to obtain the maximum power. The pitch angle () is usually kept zero below the rated current flow rate, and Cp depends on the tip speed ratio (TSR,λ), which allows the MPPT control speed to track the optimal speed and thus maximize the output power. However, the MPPT faces the challenge of internal disturbances such as system nonlinearities and model uncertainties as well as external disturbances due to swell effects and turbulence. In order to maximize the power in the presence of varying tidal velocity, it is necessary to design control strategies to improve the real-time performance, interference immunity, and stability of the TST [1]. And, variable pitch control is usually used to maintain a constant power output above the rated current speed [2]. It is necessary to consider that under high speed currents or strong sea conditions [3], the pitch system may suffer from mechanical fatigue, which causes the pitch angle not to reach the desired value, and in extreme cases, it may even lead to faults such as the failure of the pitch system. Therefore, it is necessary to design control strategies with fault tolerance to stabilize the output power of the TST system when it operates above the rated power.
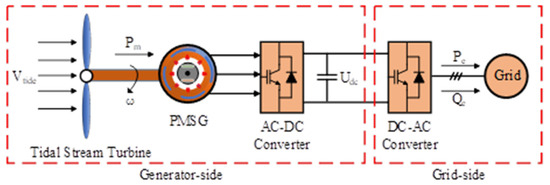
Figure 1.
The structure of the PMSG tidal stream turbine.
For MPPT, researchers have conducted many studies. The classical PI controller is widely used because of its simple structure and easy parameter adjustment [1], but it is not sufficient to cope with the nonlinearity of the system as well as parameter variations. In [4,5], fuzzy adaptive PI control is used to adjust the controller parameters. In [6], a fuzzy fractional order PID controller based on passivity is proposed which is robust to swell effects and parameter variations. But the control accuracy and dynamic characteristics of the fuzzy control under transient disturbances are not satisfactory. In [7,8], a backstepping control method is proposed for MPPT. In [9], an MPC control strategy based on economic metrics is proposed for a TST system, which improves the speed of solving the traditional quadratic function. However, these methods require precise system parameters, and the control accuracy decreases when the nonlinearity and uncertainty of the system are large. Sliding mode control methods have received wide attention in tidal power generation control for their robustness, low sensitivity to parameter changes, and fast response speed. In [10], the second-order sliding mode control method is used to solve the demagnetization problem of the PMSG, and the simulation results show that the method is robust to demagnetization. In [11], continuous approximation and saturation function are used to reduce the chattering of the sliding mode control for wind turbine systems, but there is a finite steady state error. A higher order sliding mode control based on a super-twisting algorithm was investigated in [12,13] to reduce torque pulsation in the DSPMG, but the strongly coupled system makes the parameter tuning complex. In [14,15], a fractional order sliding mode control (FOSMC) was proposed to improve the output power quality of the PMSG; however, this method requires accurate tuning of the fractional operators. In [16], an integral sliding mode surface was proposed to improve the power extraction efficiency of wind turbines. In [17], an adaptive super-twisting sliding mode control was proposed to reduce chattering through adaptive gain and second-order sliding mode. In [18,19], the application of fast terminal sliding mode in a wind power generation system was investigated. But the fractional order term in the sliding mode control may lead to a singularity problem, which makes the control signal tend to become infinite in some regions. In [20,21], for the trajectory tracking problem with system uncertainty and external interference, the NFTSM theory is used to ensure a fast convergence speed, avoid singular points, and be robust to uncertainty and external interference. In [22], a non-singular fast terminal sliding mode was used for the first time for MPPT in wind power systems and avoided unnecessary singularities. However, the parameter tuning of the above method under external disturbances and parameter uncertainties is complicated, the convergence speed and chattering of the system depend on the control parameters, and there is a contradiction between the reduction of chattering and fast convergence. Therefore, a trade-off is required.
In the full load region, variable pitch control is required to keep the output power at the rated value for system reliability. In [23,24,25], the design and life prediction of variable pitch blades of a TST were studied to protect the turbine under strong tidal conditions. In [26,27], variable pitch controllers with variable gain scaling and composite stratification strategies were designed to stabilize the output power of the TST at high tidal current speeds. In [28,29], a pitch control strategy with tidal current speed preview was proposed to reduce the frequent actions of the pitch mechanism. In [30], an independent pitch control method was investigated to reduce the asymmetric loading on the blades. The aforementioned studies on TST pitch systems have focused on blade design, load reduction, and power quality optimization. However, TST blades are subjected to harsh environmental conditions and the pitch system inevitably fails. The most common failures include pump wear, hydraulic leaks, and high air content in the oil, which cause the dynamic response of the pitch angle to slow down and fail to track the desired value, leading to fluctuations in generator speed and power output [31,32]. Current research on fault-tolerant control of pitch systems has focused on wind power generation systems. In [33,34], a disturbance observer is used for fault diagnosis and combined adaptive neural networks with sliding mode control to achieve fault-tolerant control. In [35,36], a fault detection and isolation scheme based on a sliding mode observer is proposed for the case where actuator faults exist in both the pitch and drive train systems of a wind turbine. In [37,38], faults and uncertainties are estimated using a time delay estimator and then active fault-tolerant control is used to remove the effects of the faults. In [39,40,41,42], an unknown input observer is used to estimate and compensate for pitch actuator faults. In [43], an adaptive sliding mode observer is investigated, which estimates actuator and sensor faults and compensates for them. However, all these methods rely on fault estimation links, and fault observers are susceptible to parameter uncertainties and nonlinearities, in addition to the fact that adding fault estimation links affects the real-time nature of the control. Additional sensors are also required to measure the system state, increasing the complexity of the system. In addition, much research has been conducted on fault-tolerant control in wave energy converters. In [44], the current research progress in fault-tolerant control of wave energy converters is described in detail. In [45], a nonlinear servo compensator based on a generalized internal model is proposed for the faults that tend to occur in the WEC braking subsystem. However, the passive FTC requires high accuracy of the system model. In [46], a multi-controller FTC based on an adaptive fault observer and a suitable H-performance metric is proposed for improving the fault tolerance of WEC. In [47], a WEC control method based on Bayesian policy gradient is proposed, which is useful for being able to adapt to sensor failures and return to almost full power operation. However, a large amount of data training is required.
Therefore, this paper investigates the MPPT problem and pitch fault-tolerant control of a TST when there are swell disturbances, parameter uncertainties, and sudden changes in flow velocity. In this paper, adaptive non-singular fast terminal sliding mode control (ANFTSMC) and adaptive robust controller (ARC) are proposed for power stabilization control of a TST at full tidal velocity. The non-singular fast terminal sliding mode surface is designed in order to achieve fast convergence and avoid singularities. An adaptive hybrid exponential reaching law (AHERL) is proposed to balance the conflict between chatter reduction and dynamic performance. The proposed ARC method correlates pitch angle with torque, establishes the error dynamic relationship between rotational speed and pitch angle, and enables the pitch system to adaptively adjust parameters to actuator faults through the constructed adaptive hybrid exponential convergence rate; the fault observation link is avoided, the calculation is simplified, and the real-time performance of the system is improved.
This paper is organized as follows: Section 2 describes the model of the TST and the control objective. Section 3 designs the AHERL-based ANFTSMC controller. Section 4 designs the ARC pitch fault-tolerant controller. In Section 5, the simulation results are analyzed and compared to verify the superiority of the proposed method. Finally, the results are summarized in Section 6.
2. Problem Description
In this section, the TST model and operating regions are described. The control framework of the method proposed in this paper is introduced, including the MPPT control of the ANFTSMC and the pitch angle fault-tolerant control of the ARC.
2.1. Tidal Stream Turbine Modeling
In this paper, a PMSG-based direct-drive, horizontal-axis TST system is investigated, and the mechanical power and torque captured by the TST are as follows:
where is the density of water, is the radius of the turbine blade, is the tidal current speed, is the pitch angle of the TST system, is the rotor speed, is the power coefficient, and is the tip speed ratio. The tip speed ratio, which is the ratio of the tip speed to the tidal current speed, can be expressed as follows:
The is a function of the blade tip speed ratio and pitch angle [48], which is generally obtained by the look-up table method and can be approximated using curve fitting as follows:
where = 0.5176, = 116, = 0.4, = 5, = 21, and = 0.0068.
Typically, the TST operates in three operating regions due to the variation in tidal current speed. Figure 2 shows the control block diagram of the TST system studied in this paper, and Figure 3 shows the operating regions of the TST. The operating process of the TST can be divided into three stages: startup, MPPT, and constant power operation. The tidal current speed between the cut-in speed and the rated speed corresponds to region II, and MPPT control is required at this stage to ensure maximized power capture; when the rated speed is reached (region III), the rated power needs to be maintained in order to ensure the structural safety of the TST. The cut-off speed is the maximum tidal current speed that the turbine can withstand, and when the tidal current speed exceeds this value, the blades should be smoothly paddled for protection.
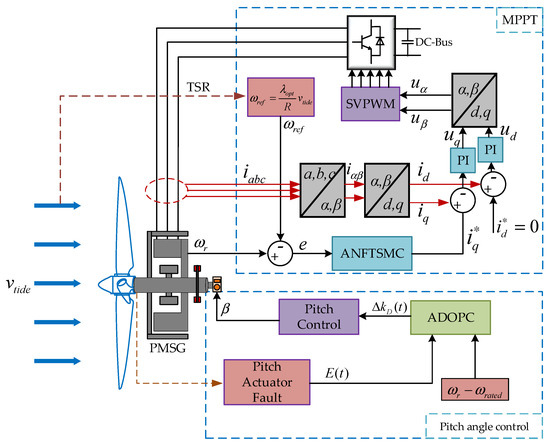
Figure 2.
The control scheme of direct-driven TST system.
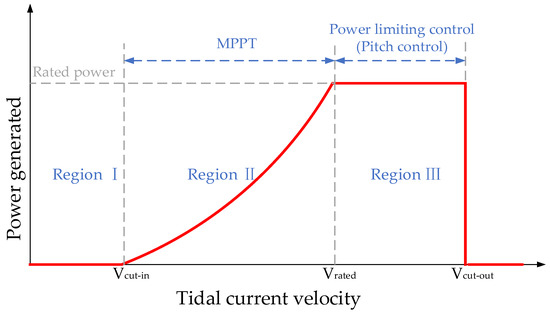
Figure 3.
Operational region of the TST in the full tidal flow range.
In order to achieve MPPT, it is necessary to obtain the maximum Cp. The Cp curve is shown in Figure 4. When the TST is operated in region II and the pitch angle is kept at 0°, the maximum power coefficient Cp is obtained as long as is kept at its maximum value at any tidal current speed. In this paper, the optimum blade tip speed ratio method is used to obtain the optimum reference speed of the TST:
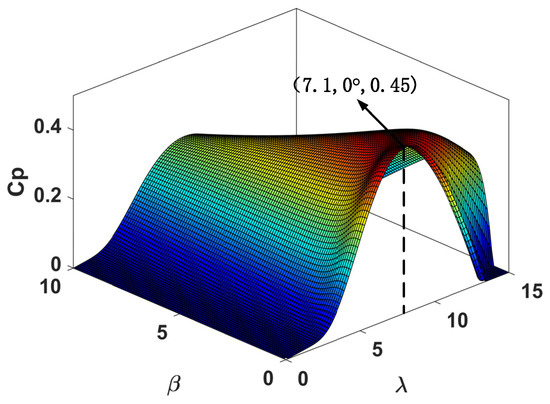
Figure 4.
Power coefficient plotted against and .
The dynamical model of the TST system is expressed as follows:
where is the electromagnetic torque of the PMSG, is the friction coefficient, and is the generator inertia. From Equation (6), the rotor speed of the TST is made optimal by controlling of the PMSG.
2.2. Pitch System Modeling
The pitch system can be represented by the following second-order dynamics model:
where is the desired value of the pitch angle and and are the natural frequency and damping ratio of the pitch system, respectively. The pitch actuator needs to satisfy certain constraints in practical operation, and its operating range is considered to be ; the pitch rate is between and .
The effect of the failure of the pitch actuator on the system dynamics is reflected in the and of the pitch system, which can be expressed as follows, respectively:
where indicate the degree of failure of the three faults of pump wear, hydraulic leakage, and high air content in the oil, respectively. and are the values under the three faults, respectively. Pump wear is an early failure that occurs slowly and results in low pump pressure. Hydraulic leaks occur more quickly than pump wear and result in a pressure drop so low that the vanes cannot move. indicates normal condition and corresponds to 75% pump pressure, 50% hydraulic pressure loss, and 15% air content in the oil [49].
Figure 5 shows the operation of the pitch system under different fault conditions. The fault parameters are shown in Table 1. It can be seen that the pitch angle cannot reach the desired value due to the fault. The corresponding output power is shown in Figure 6, where the fault caused the output power to exceed the rated power, causing the generator to be overloaded, thus affecting the lifetime of the generator in long-term operation. In addition, the pitch actuator may fail in extreme cases, resulting in degradation or deviation of the pitch action performance from the desired value, which can be represented as follows:
where is the control input for the pitch actuator, represents the effectiveness of the pitch actuator, indicates that the actuator is normal, and indicates that the actuator is completely disabled. represents the unknown pitch actuator bias. Combining Equations (7)–(9), the dynamic changes and failures of the pitch actuator are expressed as follows:
where , , and .
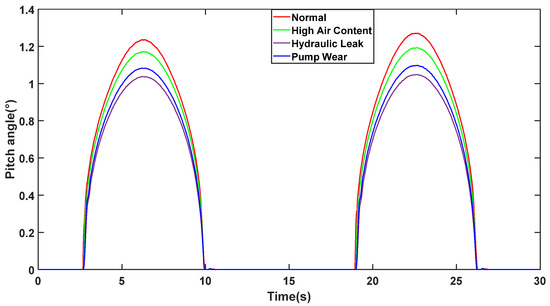
Figure 5.
Operation of pitch angle with different faults.

Table 1.
Effects of different faults on the dynamics of the pitch system.
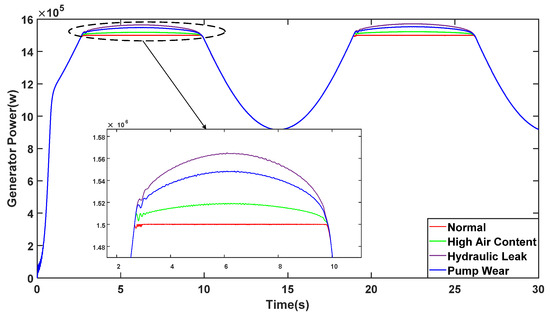
Figure 6.
Output power under different faults.
In summary, the main problems of the TST system are poor tracking accuracy of the MPPT in region II due to disturbances such as swells and turbulence, and in region III, the output power fluctuates due to the failure of the pitch actuator resulting in the pitch angle not tracking the desired value. The traditional sliding mode control is robust to disturbances, but there is a contradiction between the convergence speed and the suppression of chattering, and the fast terminal sliding mode also suffers from the singularity problem. Moreover, traditional fault-tolerant control relies on fault estimators, and the fault-tolerance performance suffers due to the uncertainty and nonlinearity of the TST system. Therefore, the next sections present the ANFTSMC-ARC method proposed in this paper to solve these problems.
3. Adaptive Non-Singular Fast Terminal Sliding Mode Controller
To solve the problem of poor MPPT accuracy due to swell and turbulence disturbances as well as system nonlinearities and parameter uncertainties, the ANFTSMC method is proposed in this section. It consists of three main parts: (1) The design of a non-singular fast terminal slip mode surface is used to avoid the singularity problem. (2) Adaptive hybrid exponential reaching law balances the conflict between dynamic performance and chatter reduction. (3) Construction of the Lyapunov function to prove system stability.
3.1. Adaptive Hybrid Exponential Reaching Law
The conventional exponential reaching law consists of an exponential term and a constant velocity term with the following expression:
where is the constant velocity term coefficient, is the exponential term coefficient, , and is the sliding mode surface function.
The sliding mode controller moves away from the sliding mode surface when is large, at which point the exponential term stabilizes the system to the sliding mode surface quickly, with the convergence velocity depending on . When the controller reaches the sliding mode surface, it slides down to the origin with the constant velocity term, with the convergence velocity depending on . The sign function maintains the system’s sliding modes, but it also introduces chattering.
Increasing the exponential term coefficient can speed up the convergence rate, but it will cause chattering when approaching the sliding mode surface. Decreasing can reduce chattering, but at the same time, it slows down the convergence rate. Therefore, the traditional exponential reaching law makes it difficult to balance the contradiction between convergence speed and chattering reduction.
To address the shortcomings of the exponential reaching law, this paper proposes an adaptive hybrid exponential reaching law:
where is the state variable; are the power term coefficients, is odd and ; is the variable speed term coefficients, ; and , .
When the system is far away from the sliding mode surface, and are large, is negligible, the variable speed term is approximately equal to , and the system converges to the sliding mode surface at a faster speed under the action of the exponential and variable speed terms. As the system approaches the sliding mode surface, approaches 0, the exponential term is negligible, the variable speed term is approximately equal to , and the system tends to the origin under the action of the variable speed term. During this process becomes gradually smaller, so the switching band near the sliding mode surface decreases and chattering is suppressed.
3.2. Proposed Adaptive Non-Singular Fast Terminal Sliding Mode Controller
An ANFTSMC controller is designed to track the rotor speed of the PMSG. The reference optimal speed is obtained from Equation (5) and combined with Equation (6), and the dynamic expression for the speed tracking error can be obtained as follows:
The non-singular fast terminal sliding mode surface is designed to
where , are all odd and satisfy .
The derivation for the sliding mode surface (16) is obtained as follows:
This can be obtained by combining AHERL (12):
Then, continued simplification yields the following:
Bringing Equation (15) into Equation (19) yields the following:
Integrating both its sides, the control output of ANFTSMC is obtained as follows:
Finally, the input of the current loop is obtained as follows:
where is the pole pair number of the PMSG and is the permanent magnet magnetic flux.
3.3. Stability Analysis
TST is able to make the system error converge quickly in finite time under the action of the ANFTSMC. The stability of the system is proved by constructing Lyapunov functions and using Lyapunov stability theorem.
Combining Equations (15), (17) and (19), the derivative of Equation (23) is as follows:
Since and is odd, . The designed controller satisfies Lyapunov stability, and the system state asymptotically converges to the sliding mode surface.
4. Adaptive Robust Fault-Tolerant Controller
The ARC fault-tolerant control method is proposed in this section for the pitch actuator failure of the TST. First, the system error dynamics are described in order to relate the pitch angle to the rotational speed. Second, the controller is designed based on the error dynamics. Then, the adaptive rate is designed for adaptively adjusting the controller gain in the presence of uncertain faults.
4.1. Error Dynamics Analysis
From Equations (1) and (2), the hydrodynamic torque can be expressed as a non-affine function of the variable pitch angle, which can be handled by using the median theorem in [50]. For any given , there exists such that
where is the pitch angle corresponding to the given , .
Remark 1.
Obviously, the torque
is bounded and there exists Z and D as positive con stants such that and . This indicates that the hydrodynamic torque decreases as the paddle pitch angle increases for increasing tidal flow velocity . The derivative of (25) yields , which can be obtained by taking it into Equation (6):
This can be obtained by bringing Equation (10) into (27):
When the TST operates in region III, the control objective is to stabilize the rotor speed at the rated speed by adjusting the pitch angle, and the rotor tracking error is expressed as follows:
where is the rated speed, which in this paper is set to 2.84 rad/s.
Assumption 1: the range of variation of the paddle pitch angle is bounded, and therefore, the uncertainty terms and are also bounded, and there exist unknown positive constants and such that and ; in addition, the variation of the torque is bounded due to the fact that .
4.2. Proposed Adaptive Robust Fault-Tolerant Controller
Inspired by [51,52], a tracking control scheme in the form of PID can be designed for the error dynamics (29) as follows:
where parameters are constants and are time-varying parameters. To simplify the design, a designable value is introduced to associate these parameters:
According to Equations (30) and (31), the controller can be further represented as follows:
The simplified controller only requires the design of two gains, and , where is a constant and can be automatically adjusted by the designed adaptive robust method.
The generalized error is defined as follows:
The derivation of this is obtained by relating it to the system dynamics model:
where the coefficients and uncertainty terms of the above Equation are denoted as and , respectively, with and .
According to Assumption 1 and the system properties, and the uncertainty term are bounded and can be expressed as follows:
where are unknown positive constants and is a core function [53]:
Definition 1.
For a system within an open set D, there exists a positive constant , and a positive definite continuously differentiable scalar function with as the variable converges to the boundary of the set D. Then, is known as the barrier Lyapunov function as in Equation (38) [54,55].
The adaptive robust gain of the controller can be designed as follows:
where and are positive constants, is the estimated value of , and according to Definition 1, is the error boundary of the design, satisfying .
4.3. Stability Analysis
The Lyapunov function is constructed to prove the stability of the proposed controller:
where is the parameter estimation error. The derivative of Equation (40) is obtained as follows:
From the square inequality, and , which can be obtained by bringing (39) into Equation (41):
According to Equation (39), there is for all . Hence
So can be further derived as follows:
where . From the above derivation, it is clear that is bounded, and according to Equation (39), and are bounded; the boundedness of ensures the boundedness of , as seen in Equation (32). According to Definition 1, it is known that the value of is restricted to a certain range , i.e., the error is also restricted to a certain range. Therefore, from Equations (31), (32), (35), and (39), it can be concluded that are bounded, the signals within the system are bounded, and the system errors are uniformly and ultimately bounded.
5. Simulation Results and Analysis
In order to validate the effectiveness of the proposed method, in this section, numerical simulation of 1.5 MW TST has been carried out using Matlab/Simulink, and the system parameters are shown in Table 2. Table 3 and Table 4 show the parameters of the proposed ANFTSMC and ARC, respectively. The proposed ANFTSMC method is evaluated below the rated tidal current speed and the results are compared with fuzzy adaptative backstepping control (FABC) , active disturbance rejection control (ADRC) [1], integral sliding mode control (ISMC) [56], and non-singular fast terminal sliding mode control (NFTSMC) [22]. Then, a comparison of variable pitch control methods, including gain scheduling proportional integral derivative (GSPID) [57], ISMC, and pseudo-tip-speed ratio and adaptive genetic algorithm (PTSRAGA) [58], are considered. The effectiveness of the proposed ANFTSMC-ARC method above the rated tidal velocity was evaluated by comparing the ANFTSMC-ARC method with the FABC-GSPID, ISMC-ISMC, and ADRC-PTSRAGA methods by combining MPPT with pitch control.

Table 2.
Parameters of the TST system.

Table 3.
The parameters of the ANFTSMC controller.

Table 4.
The parameters of the ARC.
5.1. Simulation Results Below Rated Tidal Current Speeds
For the TST, swell and turbulence are unavoidable. Figure 7 shows the actual tidal current velocity data for the Xihoumen area in Zhoushan for 90 h. In this section, a flow velocity lower than the rated velocity of 3.2 m/s is selected to verify the performance of the proposed method. Figure 8 and Figure 9 show the generator rotor speed versus rotor speed error for different control methods, respectively. It can be seen that the FABC controller has a large amount of overshooting, especially during the change in flow velocity when there is a tracking error of 0.025 rad/s, which is about 1% of the reference value. The ISMC method has a smaller amount of overshooting, but there is a significant chattering phenomenon, with an error of about 0.02 rad/s. The ADRC method has a much better tracking accuracy, but there is a chattering of 0.01 rad/s near the reference rotor speed. The NFTSMC method significantly reduces chattering; however, there is a tracking error of 0.015 rad/s. The proposed ANFTSMC method has minimized chattering and accurately tracks the optimal rotational speed with a tracking error around 0.08%, as the flow rate varies.
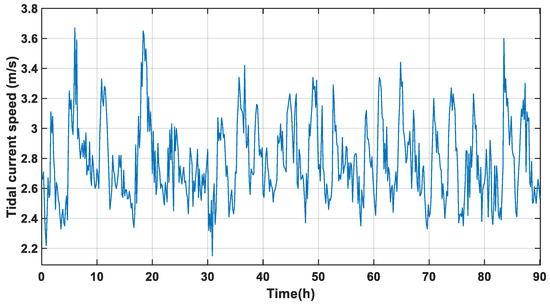
Figure 7.
Actual 90 h tidal current velocity at Xihoumen.
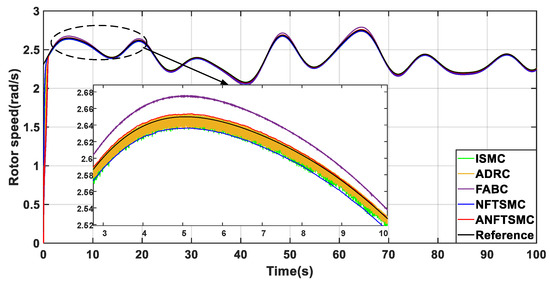
Figure 8.
Comparison of rotor speed.
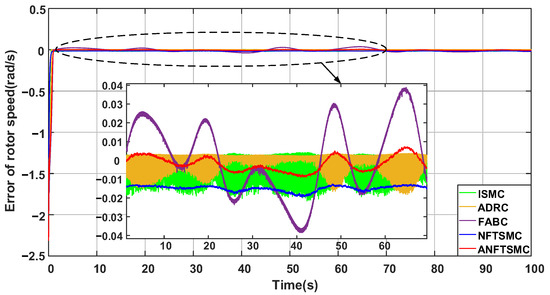
Figure 9.
Rotor speed error.
To evaluate the performance of the proposed method even further, the ISE (Integral of the Square Error) and ITAE (Integral of the Time-weighted Absolute Error) are used:
where denotes the error, ISE reflects the overall performance of the controller tracking, and ITAE reflects the persistence of the error; the smaller the value of ISE and ITAE, the better its error suppression ability.
The rotor speed error and power error are evaluated separately as shown in Table 5, and the above metrics are denoted as . It can be seen that, although the chattering of FABC and NFTSMC is not serious, the presence of large tracking errors leads to larger values of both ISE and ITAE; the chattering of ADRC is smaller than that of ISMC, and thus its metrics are smaller than ISMC; and the proposed ANFTSMC method has the smallest evaluation metrics compared with the other methods, which shows the excellent error suppression capability of the proposed method.

Table 5.
Performance metrics for comparative methods.
Figure 10 and Figure 11 show the comparison of power coefficient Cp and output power, respectively. From this, the same conclusion can be drawn that the proposed ANFTSMC method has minimum chattering and optimal power tracking accuracy when compared to other methods.
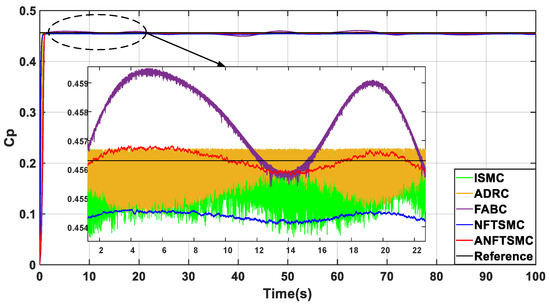
Figure 10.
Comparison of power coefficients.
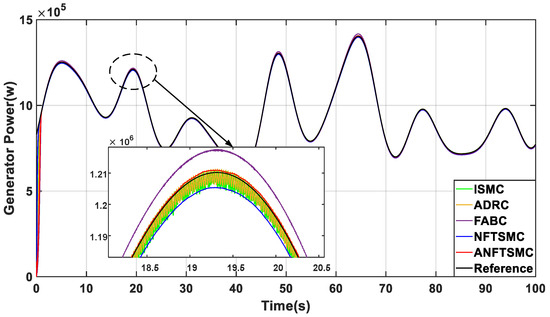
Figure 11.
Comparison of output power.
5.2. Simulation Results for Higher-Than-Rated Tidal Current Speeds
5.2.1. Fault-Free Scenarios
In this section, ARC is compared with GSPID, ISMC, and PTSRAGA in a fault-free system, and the speed controllers are ANFTSMC, FABC, ISMC, and ADRC, respectively, to evaluate the performance of the maximum power tracking and pitch controllers of the proposed method.
When the tidal current speed exceeds the rated speed of 3.2 m/s, the change in the pitch angle is shown in Figure 12. The PTSRAGA method has the effect of reducing the frequent pitch change, so it has the smallest pitch angle, which results in the output power not being stabilized at the rated power, and the rotor speed exhibits a tracking error of 0.005 rad/s, as shown in Figure 13 and Figure 14. The pitch angle of the ISMC and GSPID methods exhibit some chattering, the rotor speed oscillates around the rated value, and there is some chattering in the output power. The proposed ARC method has the best pitch angle dynamic performance and can ensure the stability of the rated power, and the ANFTSMC method has the best speed tracking performance. Table 6 also shows that the proposed method has the smallest rotor speed error and power tracking error, which verifies the superiority of the proposed method.
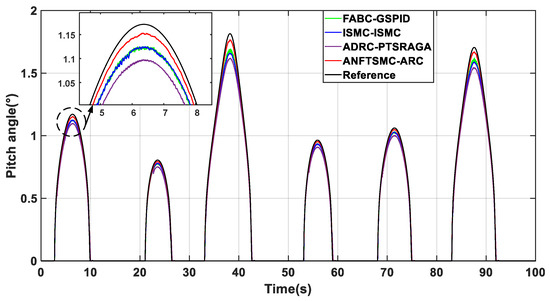
Figure 12.
Comparison of pitch angle.
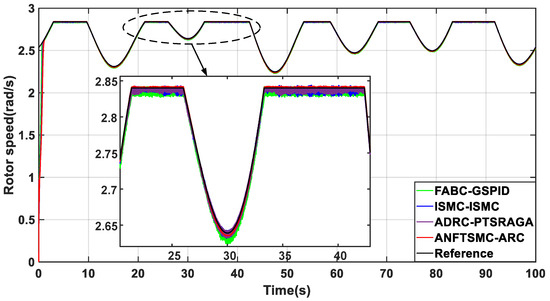
Figure 13.
Comparison of rotor speed.
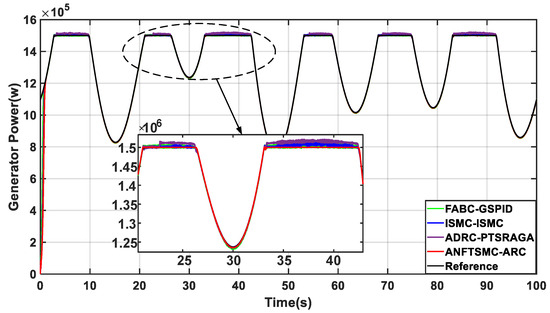
Figure 14.
Comparison of output power.

Table 6.
Performance metrics for comparative methods.
5.2.2. Fault Scenarios
This section considers a situation where there are multiple failures of the pitch actuator occurring simultaneously, including pump wear, hydraulic leaks, high air content in the oil, actuator bias, and loss of efficiency, with the following fault settings:
As shown in Figure 15, in the presence of actuator failure, bias, and efficiency loss, the proposed ARC method is still able to maintain accurate tracking of the pitch angle compared to other methods. Figure 16 shows that the rotor speed is maintained at the rated speed with a significantly smaller error than the other methods. Figure 17 shows that the output power is also stably controlled at a rated power above the rated flow rate with minimal fluctuation error. Comparing the performance metrics in Table 7, it is obvious that the proposed ARC method has the best performance in both speed tracking error and output power error. Therefore, the simulation results verify the stable speed tracking performance of the proposed method under swell fluctuations, and it is still able to generate an accurate pitch angle when the pitch actuator fails, which ensures the maximum power capture and fault tolerance of the tidal stream turbine.
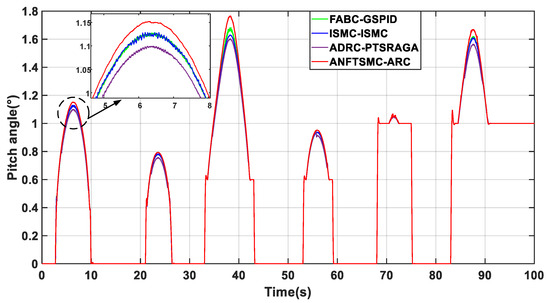
Figure 15.
Comparison of pitch angle.
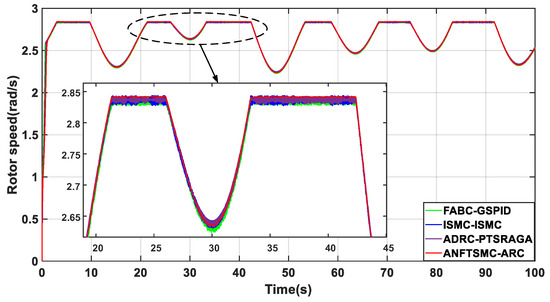
Figure 16.
Comparison of rotor speed.
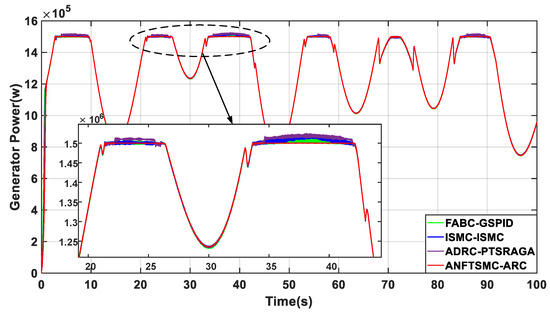
Figure 17.
Comparison of output power.

Table 7.
Performance metrics for comparative methods.
6. Conclusions
In order to improve the power capture efficiency of the TST in the case of swell and to consider the susceptibility of the pitch actuator to failure, an ANFTSMC-ARC is proposed in this study. Extensive comparisons are made with existing methods through simulation experiments. The advantages of the proposed method are as follows:
(1) Different from the traditional exponential reaching law, AHERL balances the conflicting issues of convergence and chattering suppression in sliding mode control.
(2) ANFTSMC is robust to uncertain disturbances and nonlinearities in the TST system and reduces chattering, improving the efficiency of MPPT.
(3) The ARC automatically adjusts the controller gain according to the fault state, which mitigates the fault-induced deviation of the pitch angle action and improves the fault tolerance of the pitch system.
The analyzed ISE and ITAE performance metrics reflect the best performance of the ANFTSMC-ARC in terms of speed tracking and output power. The experimental results show that the proposed control method can achieve accurate rotor speed tracking at full tidal current speed, and the variable pitch angle can respond quickly and control the rated power stably even in the case of actuator failure. Future research can consider tidal current speed prediction for better maximum power tracking and can combine modeling and data approaches to improve fault tolerance performance.
Author Contributions
Conceptualization, M.W., T.W. and X.W.; methodology, M.W. and T.W.; software, M.W. and T.W.; validation, M.W., T.W. and X.W.; formal analysis, M.W., T.W. and X.W.; investigation, M.W. and T.W.; resources, M.W., T.W. and X.W.; data curation, M.W. and T.W.; writing—original draft preparation, M.W., T.W. and X.W.; writing—review and editing, M.W., T.W. and X.W.; visualization, M.W. and T.W.; supervision, T.W. and X.W.; project administration, T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MPPT | Maximum power point tracking |
| ANFTSMC | Adaptive non-singular fast terminal sliding mode control |
| AHERL | Adaptive hybrid exponential reaching law |
| TST | Tidal stream turbine |
| TSR | Tip speed ratio |
| MPC | Model predictive control |
| PMSG | Permanent magnet synchronous generator |
| FOSMC | Fractional order sliding mode control |
| ARC | Adaptive robust controller |
| ANFTSMC-ARC | Adaptive non-singular fast terminal sliding mode control and adaptive robust controller |
| FABC | Fuzzy adaptative backstepping control |
| ADRC | Active disturbance rejection control |
| ISMC | Integral sliding mode control |
| FABC-GSPID | Fuzzy adaptative backstepping control and gain scheduling proportional integral derivative |
| PTSRAGA | Pseudo-tip-speed ratio and adaptive genetic algorithm |
| ADRC-PTSRAGA | Active disturbance rejection control and pseudo-tip-speed ratio and adaptive genetic algorithm |
| ISE | Integral of the Square Error |
| ITAE | Integral of the Time-weighted Absolute Error |
Nomenclature
| Cp | Power coefficient |
| Tidal flow velocity | |
| The pitch angle | |
| Tip speed ratio | |
| Mechanical power | |
| Mechanical torque | |
| Density of water | |
| Radius of the turbine blade | |
| Rotor speed | |
| Blade tip speed ratio related quantity | |
| Reference speed | |
| Generator inertia | |
| Electromagnetic torque | |
| Friction coefficient | |
| Desired value of the pitch angle | |
| Natural frequency | |
| Damping ratio | |
| Natural frequency at fault | |
| Damping ratio at fault | |
| Failure degree coefficient | |
| Failure degree coefficient | |
| Natural frequencies at different faults | |
| Damping ratio at different faults | |
| Control input for the pitch actuator | |
| Effectiveness of the pitch actuator | |
| Constant velocity term coefficient | |
| Exponential term coefficient | |
| Sliding mode surface function | |
| State variable | |
| Power term coefficients | |
| Power term coefficients | |
| Variable speed term coefficients | |
| Constant term | |
| Power term coefficients | |
| Sliding mode surface coefficient | |
| Sliding mode surface coefficient | |
| Positive odd number | |
| Positive odd number | |
| Positive odd number | |
| Positive odd number | |
| Number of pole pairs of the generator | |
| Permanent magnet flux | |
| Lyapunov functions | |
| Define scalar | |
| Pitch angle corresponding to different flow rates and rotational speeds | |
| Pitch angle intermediate variable | |
| Constant | |
| Constant | |
| Uncertainty terms | |
| Unknown positive constants | |
| Unknown positive constants | |
| Controller constant parameters | |
| Controller variable parameters | |
| Controller intermediate variables | |
| Unknown positive constants | |
| Unknown positive constants | |
| Unknown positive constants | |
| Core function | |
| Positive constant | |
| Barrier Lyapunov function | |
| Positive constants | |
| Positive constants |
References
- Zhou, Z.B.; Ben Elghali, S.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E.; Feld, G. Tidal stream turbine control: An active disturbance rejection control approach. Ocean Eng. 2020, 202, 107190. [Google Scholar] [CrossRef]
- Whitby, B.; Ugalde-Loo, C.E. Performance of Pitch and Stall Regulated Tidal Stream Turbines. IEEE Trans. Sustain. Energy 2014, 5, 64–72. [Google Scholar] [CrossRef]
- Zhou, Z.B.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.E.; Tang, T.H. Power Control of a Nonpitchable PMSG-Based Marine Current Turbine at Overrated Current Speed with Flux-Weakening Strategy. IEEE J. Ocean. Eng. 2015, 40, 536–545. [Google Scholar] [CrossRef]
- Falahati, S.; Taher, S.A.; Shahidehpour, M. Grid Secondary Frequency Control by Optimized Fuzzy Control of Electric Vehicles. IEEE Trans. Smart Grid 2018, 9, 5613–5621. [Google Scholar] [CrossRef]
- Ghefiri, K.; Garrido, I.; Bouallègue, S.; Haggège, J.; Garrido, A.J. Hybrid Neural Fuzzy Design-Based Rotational Speed Control of a Tidal Stream Generator Plant. Sustainability 2018, 10, 3746. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A.; Ullah, N.; Shaw, R.N.; Chowdhury, S.; Techato, K. Energy-based fuzzy supervisory non integer control for performance improvement of PMSG-Based marine energy system under swell effect and parameter uncertainties. Renew. Energy 2022, 186, 457–468. [Google Scholar] [CrossRef]
- Yin, X.X.; Zhao, X.W. Optimal power extraction of a two-stage tidal turbine system based on backstepping disturbance rejection control. Int. J. Electr. Power Energy Syst. 2021, 132, 107158. [Google Scholar] [CrossRef]
- Shen, X.S.; Xie, T.; Wang, T.Z. A Fuzzy Adaptative Backstepping Control Strategy for Marine Current Turbine under Disturbances and Uncertainties. Energies 2020, 13, 6550. [Google Scholar] [CrossRef]
- Teng, Y.M.; Hu, D.W.; Wu, F.; Zhang, R.D.; Gao, F.R. Fast economic model predictive control for marine current turbine generator system. Renew. Energy 2020, 166, 108–116. [Google Scholar] [CrossRef]
- Toumi, S.; Elbouchikhi, E.; Amirat, Y.; Benbouzid, M.; Feld, G. Magnet failure-resilient control of a direct-drive tidal turbine. Ocean Eng. 2019, 187, 106207. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A. A Novel PI-Type Sliding Surface for PMSG-Based Wind Turbine with Improved Transient Performance. IEEE Trans. Energy Convers. 2018, 33, 834–844. [Google Scholar] [CrossRef]
- Chen, H.; Tang, S.F.; Han, J.G.; Tang, T.H.; Aït-Ahmed, N.; Zhou, Z.B.; Benbouzid, M. High-order sliding mode control of a doubly salient permanent magnet machine driving marine current turbine. J. Ocean Eng. Sci. 2021, 6, 12–20. [Google Scholar] [CrossRef]
- Chen, H.; Li, Q.; Tang, S.F.; Ait-Ahmed, N.; Han, J.G.; Wang, T.Z.; Zhou, Z.B.; Tang, T.H.; Benbouzid, M. Adaptive super-twisting control of doubly salient permanent magnet generator for tidal stream turbine. Int. J. Electr. Power Energy Syst. 2021, 128, 106772. [Google Scholar] [CrossRef]
- Huang, S.H.; Wang, J.; Huang, C.; Zhou, L.D.; Xiong, L.Y.; Liu, J.Y.; Li, P.H. A fixed-time fractional-order sliding mode control strategy for power quality enhancement of PMSG wind turbine. Int. J. Electr. Power Energy Syst. 2022, 134, 107354. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Li, P.H.; Ma, M.L.; Wang, Z.Q.; Wang, J. Output power quality enhancement of PMSG with fractional order sliding mode control. Int. J. Electr. Power Energy Syst. 2020, 115, 105402. [Google Scholar] [CrossRef]
- Periyanayagam, A.R.; Joo, Y.H. Integral sliding mode control for increasing maximum power extraction efficiency of variable-speed wind energy system. Int. J. Electr. Power Energy Syst. 2022, 139, 107958. [Google Scholar] [CrossRef]
- Zholtayev, D.; Rubagotti, M.; Do, T.D. Adaptive super-twisting sliding mode control for maximum power point tracking of PMSG-based wind energy conversion systems. Renew. Energy 2022, 183, 877–889. [Google Scholar] [CrossRef]
- Zafran, M.; Khan, L.; Khan, Q.; Ullah, S.; Sami, I.; Ro, J.S. Finite-Time Fast Dynamic Terminal Sliding Mode Maximum Power Point Tracking Control Paradigm for Permanent Magnet Synchronous Generator-Based Wind Energy Conversion System. Appl. Sci. 2020, 10, 6361. [Google Scholar] [CrossRef]
- Dursun, E.H.; Kulaksiz, A.A. Second-Order Fast Terminal Sliding Mode Control for MPPT of PMSG-based Wind Energy Conversion System. Elektron. Ir Elektrotechnika 2020, 26, 39–45. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef]
- Liu, W.; Chen, S.; Huang, H. Adaptive Nonsingular Fast Terminal Sliding Mode Control for Permanent Magnet Synchronous Motor Based on Disturbance Observer. IEEE Access 2019, 7, 153791–153798. [Google Scholar] [CrossRef]
- Maaruf, M.; Shafiullah, M.; Al-Awami, A.T.; Al-Ismail, F.S. Adaptive Nonsingular Fast Terminal Sliding Mode Control for Maximum Power Point Tracking of a WECS-PMSG. Sustainability 2021, 13, 3427. [Google Scholar] [CrossRef]
- Kennedy, C.R.; Jaksic, V.; Leen, S.B.; Brádaigh, C.M.O. Fatigue life of pitch- and stall-regulated composite tidal turbine blades. Renew. Energy 2018, 121, 688–699. [Google Scholar] [CrossRef]
- Wang, B.Z.; Ke, W.; Zhang, Y.F.; Duan, Y.Q. Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine. J. Mar. Sci. Eng. 2022, 10, 1578. [Google Scholar] [CrossRef]
- Dong, Y.J.; Guo, J.F.; Chen, J.M.; Sun, C.; Zhu, W.Q.; Chen, L.W.; Zhang, X.M. Development of a 300 kW horizontal-axis tidal stream energy conversion system with adaptive variable-pitch turbine and direct-drive PMSG. Energy 2021, 226, 120361. [Google Scholar] [CrossRef]
- Yin, X.X.; Zhao, X.W. Composite Hierarchical Pitch Angle Control for a Tidal Turbine Based on the Uncertainty and Disturbance Estimator. IEEE Trans. Ind. Electron. 2020, 67, 329–339. [Google Scholar] [CrossRef]
- Wang, B.Z.; Hu, T.Y.; Guo, Y.; Zhang, Y.F. Research on Pitch Control Strategies of Horizontal Axis Tidal Current Turbine. China Ocean Eng. 2020, 34, 223–231. [Google Scholar] [CrossRef]
- Gu, Y.J.; Lin, Y.G.; Xu, Q.K.; Liu, H.W.; Li, W. Blade-pitch system for tidal current turbines with reduced variation pitch control strategy based on tidal current velocity preview. Renew. Energy 2018, 115, 149–158. [Google Scholar] [CrossRef]
- Liu, H.W.; Li, H.T.; Gu, Y.J.; Lin, Y.G.; Xie, B.L. Collective pitch for horizontal axis marine current turbine. Ocean Eng. 2023, 271, 113732. [Google Scholar] [CrossRef]
- Liu, H.W.; Li, Y.J.; Lin, Y.G.; Li, W.; Gu, Y.J. Load reduction for two-bladed horizontal-axis tidal current turbines based on individual pitch control. Ocean Eng. 2020, 207, 107183. [Google Scholar] [CrossRef]
- Li, D.Y.; Li, P.; Cai, W.C.; Song, Y.D.; Chen, H.J. Adaptive Fault-Tolerant Control of Wind Turbines with Guaranteed Transient Performance Considering Active Power Control of Wind Farms. IEEE Trans. Ind. Electron. 2018, 65, 3275–3285. [Google Scholar] [CrossRef]
- Habibi, N.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Shi, Y.R.; Li, S.T.; Wang, S.X.; Zhai, Y.J.; Tian, Y.T.; Yu, D.L. Pitch angle control with fault diagnosis and tolerance for wind turbine generation systems. Proc. Inst. Mech. Eng. Part I-J. Syst. Control Eng. 2021, 235, 1355–1366. [Google Scholar] [CrossRef]
- Wang, L.; Jin, F.J.; Chen, J.W.; Gao, Y.; Du, X.; Zhang, Z.H.; Xu, Z.L.; Yang, J.M. Performance improvement for large floating wind turbine by using a non-linear pitch system based on neuro-adaptive fault-tolerant control. IET Renew. Power Gener. 2022, 16, 1636–1648. [Google Scholar] [CrossRef]
- Azizi, A.; Youssef, T.; Kouadri, A.; Mansouri, M.; Mimouni, M.F. Robust fault estimation for wind turbine pitch and drive train systems. Int. J. Electr. Power Energy Syst. 2024, 155, 109673. [Google Scholar] [CrossRef]
- Borja-Jaimes, V.; Adam-Medina, M.; García-Morales, J.; Guerrero-Ramírez, G.V.; López-Zapata, B.Y.; Sánchez-Coronado, E.M. Actuator FDI Scheme for a Wind Turbine Benchmark Using Sliding Mode Observers. Processes 2023, 11, 1690. [Google Scholar] [CrossRef]
- Mazare, M.; Taghizadeh, M.; Ghaf-Ghanbari, P. Pitch actuator fault-tolerant control of wind turbines based on time delay control and disturbance observer. Ocean Eng. 2021, 238, 109724. [Google Scholar] [CrossRef]
- Mazare, M.; Taghizadeh, M. Uncertainty estimator-based dual layer adaptive fault-tolerant control for wind turbines. Renew. Energy 2022, 188, 545–560. [Google Scholar] [CrossRef]
- Liu, Y.H.; Patton, R.J.; Shi, S. Actuator fault tolerant offshore wind turbine load mitigation control. Renew. Energy 2023, 205, 432–446. [Google Scholar] [CrossRef]
- Mousavi, Y.; Bevan, G.; Kucukdemiral, I.B. Fault-tolerant optimal pitch control of wind turbines using dynamic weighted parallel firefly algorithm. ISA Trans. 2022, 128, 301–317. [Google Scholar] [CrossRef]
- Fekih, A.; Mobayen, S.; Chen, C.C. Adaptive Robust Fault-Tolerant Control Design for Wind Turbines Subject to Pitch Actuator Faults. Energies 2021, 14, 1791. [Google Scholar] [CrossRef]
- Palanimuthu, K.; Joo, Y.H. Reliability improvement of the large-scale wind turbines with actuator faults using a robust fault-tolerant synergetic pitch control. Renew. Energy 2023, 217, 119164. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S.; Fekih, A. Decoupling Adaptive Sliding Mode Observer Design for Wind Turbines Subject to Simultaneous Faults in Sensors and Actuators. IEEE-CAA J. Autom. Sin. 2021, 8, 837–847. [Google Scholar] [CrossRef]
- Mortazavizadeh, S.A.; Yazdanpanah, R.; Gaona, D.C.; Anaya-Lara, O. Fault Diagnosis and Condition Monitoring in Wave Energy Converters: A Review. Energies 2023, 16, 6777. [Google Scholar] [CrossRef]
- González-Esculpi, A.; Verde, C.; Maya-Ortiz, P. Nonlinear servocompensator for fault-tolerant control of a wave energy converter. J. Frankl. Inst. 2023, 360, 8339–8362. [Google Scholar] [CrossRef]
- Xu, N.; Chen, L.; Yang, R.; Zhu, Y. Multi-controller-based fault tolerant control for systems with actuator and sensor failures: Application to 2-body point absorber wave energy converter. J. Frankl. Inst. 2022, 359, 5919–5934. [Google Scholar] [CrossRef]
- Zadeh, L.G.; Brekken, T.K.A.; Fern, A.; Shahbaz, A.H. Hardware in the Loop Wave Energy Converter Control Under Control Faults and Model Mismatch. IEEE Trans. Sustain. Energy 2024, 15, 13–22. [Google Scholar] [CrossRef]
- Gaamouche, R.; Redouane, A.; El harraki, I.; Belhorma, B.; El Hasnaoui, A. Optimal Feedback Control of Nonlinear Variable-Speed Marine Current Turbine Using a Two-Mass Model. J. Mar. Sci. Appl. 2020, 19, 83–95. [Google Scholar] [CrossRef]
- Habibi, H.; Nohooji, H.R.; Howard, I. Optimum efficiency control of a wind turbine with unknown desired trajectory and actuator faults. J. Renew. Sustain. Energy 2017, 9, 063305. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S. Wind Turbine Pitch Actuator Regulation for Efficient and Reliable Energy Conversion: A Fault-Tolerant Constrained Control Solution. Actuators 2022, 11, 102. [Google Scholar] [CrossRef]
- Habibi, H.; Nohooji, H.R.; Howard, I. Adaptive PID Control of Wind Turbines for Power Regulation with Unknown Control Direction and Actuator Faults. IEEE Access 2018, 6, 37464–37479. [Google Scholar] [CrossRef]
- Song, Y.D.; Huang, X.C.; Wen, C.Y. Robust Adaptive Fault-Tolerant PID Control of MIMO Nonlinear Systems with Unknown Control Direction. IEEE Trans. Ind. Electron. 2017, 64, 4876–4884. [Google Scholar] [CrossRef]
- Song, Y.; Huang, X.; Wen, C. Tracking Control for a Class of Unknown Nonsquare MIMO Nonaffine Systems: A Deep-Rooted Information Based Robust Adaptive Approach. IEEE Trans. Autom. Control 2016, 61, 3227–3233. [Google Scholar] [CrossRef]
- Liu, Y.J.; Lu, S.M.; Tong, S.C.; Chen, X.K.; Chen, C.L.P.; Li, D.J. Adaptive control-based Barrier Lyapunov Functions for a class of stochastic nonlinear systems with full state constraints. Automatica 2018, 87, 83–93. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.H.; Yin, Z. Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans. Cybern. 2016, 46, 620–629. [Google Scholar] [CrossRef]
- Ameli, S.; Morshed, M.J.; Fekih, A. Adaptive Integral Sliding Mode Design for the Pitch Control of a Variable Speed Wind Turbine. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019; pp. 290–295. [Google Scholar]
- Gu, Y.-J.; Liu, H.-W.; Li, W.; Lin, Y.-G.; Li, Y.-J. Integrated design and implementation of 120-kW horizontal-axis tidal current energy conversion system. Ocean Eng. 2018, 158, 338–349. [Google Scholar] [CrossRef]
- Cai, Y.; Li, M.; Wang, T.; Wang, X.; Razik, H. An Output Power Interval Control Strategy Based on Pseudo-Tip-Speed Ratio and Adaptive Genetic Algorithm for Variable-Pitch Tidal Stream Turbine. J. Mar. Sci. Eng. 2022, 10, 1197. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).