Dynamic Projection Method of Electronic Navigational Charts for Polar Navigation
Abstract
:1. Introduction
- Conformal projection, in order to facilitate angle measurements and pilotage.
- Length and area distortions are kept as small as possible, in order to facilitate accurate measurement of distance and area measurements.
- The grid lines of latitude and longitude should be simple, in order to facilitate the construction of grids and the measurement of headings.
- Great circle routes should be as straight as possible, in order to facilitate navigation along them.
2. Complex Function Expression of Conformal Projection of Polar Charts Based on the Ellipsoid
2.1. Mercator Projection Coordinates in Complex Form
2.2. Polar Gauss-Krüger Projection Coordinates in Complex Form
2.3. Polar Stereographic Projection Coordinates in Complex Form
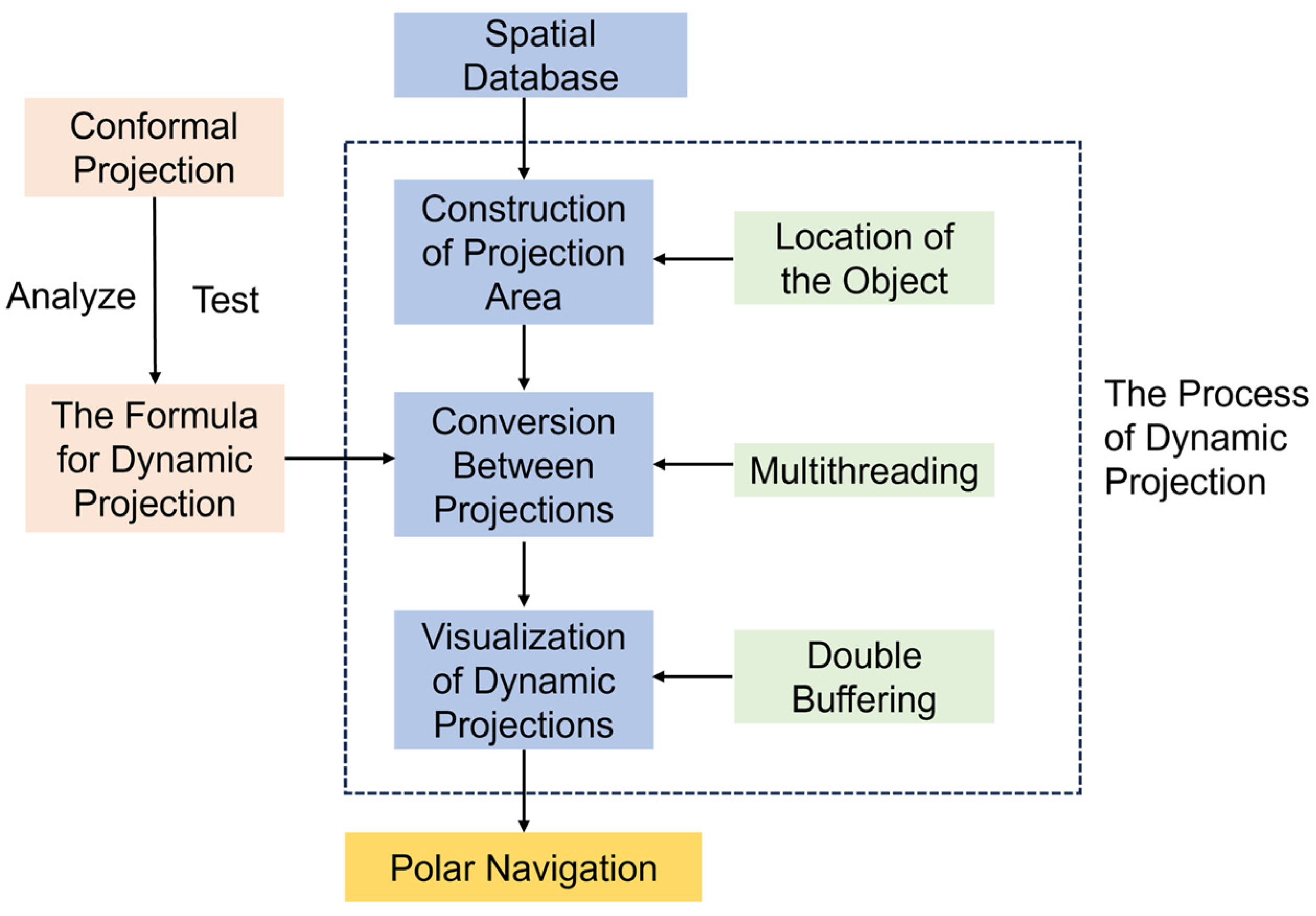
3. Method Design for Dynamic Chart Projection
3.1. Transformation between Mercator Projection and Polar Gauss-Krüger Projection
3.2. Transformation between Polar Gauss-Krüger Projection and Polar Stereographic Projection
3.3. Transformation between Polar Gauss-Krüger Projection and Polar Stereographic Projection
4. Evaluation of Dynamic Projection
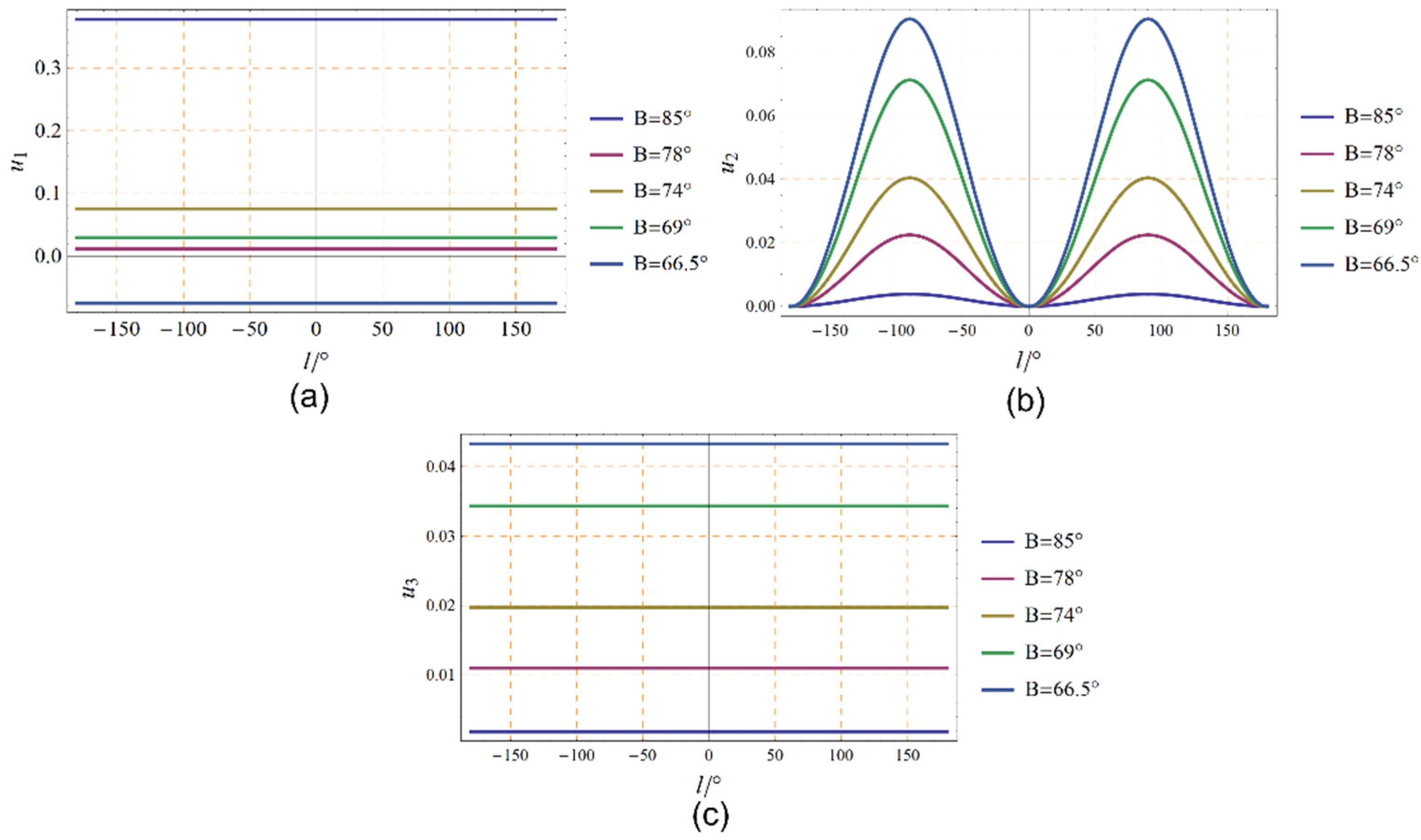
4.1. Length Distortion
- (1)
- In the Mercator projection, there is no length distortion at the reference latitude, while the length distortion is greater than 0 beyond the reference latitude and less than 0 within it. The length distortions are all less than 10% in the region up to , whereas in polar regions with very high latitudes, the maximum distortion can exceed 80%. This suggests that it is possible to control the degree of distortion of the Mercator projection by adjusting the reference latitude, but the Mercator projection is still significantly distorted at high latitudes.
- (2)
- The length distortions for are listed in Table 1. In the polar Gauss-Krüger projection, the farther away from the standard meridian, the larger the length distortion is for a fixed longitude difference. At the same latitude, the length distortion increases and then decreases with the longitude difference, reaching a maximum at . The maximum distortion is calculated to be no more than 10%. This shows that the bandwidth can be broadened by using a complex function to represent the Gauss-Krüger projection, which facilitates uniform representation of the land and nautical charts and provides an important reference for scientific research and nautical charting in the polar region.
- (3)
- The overall distortion of the double polar stereographic projection in the polar region is relatively small, especially above , where the distortion is less than 1%. It has been able to satisfy the compilation of large and medium scale marine charts, which is very important for the application of high-precision polar navigation.
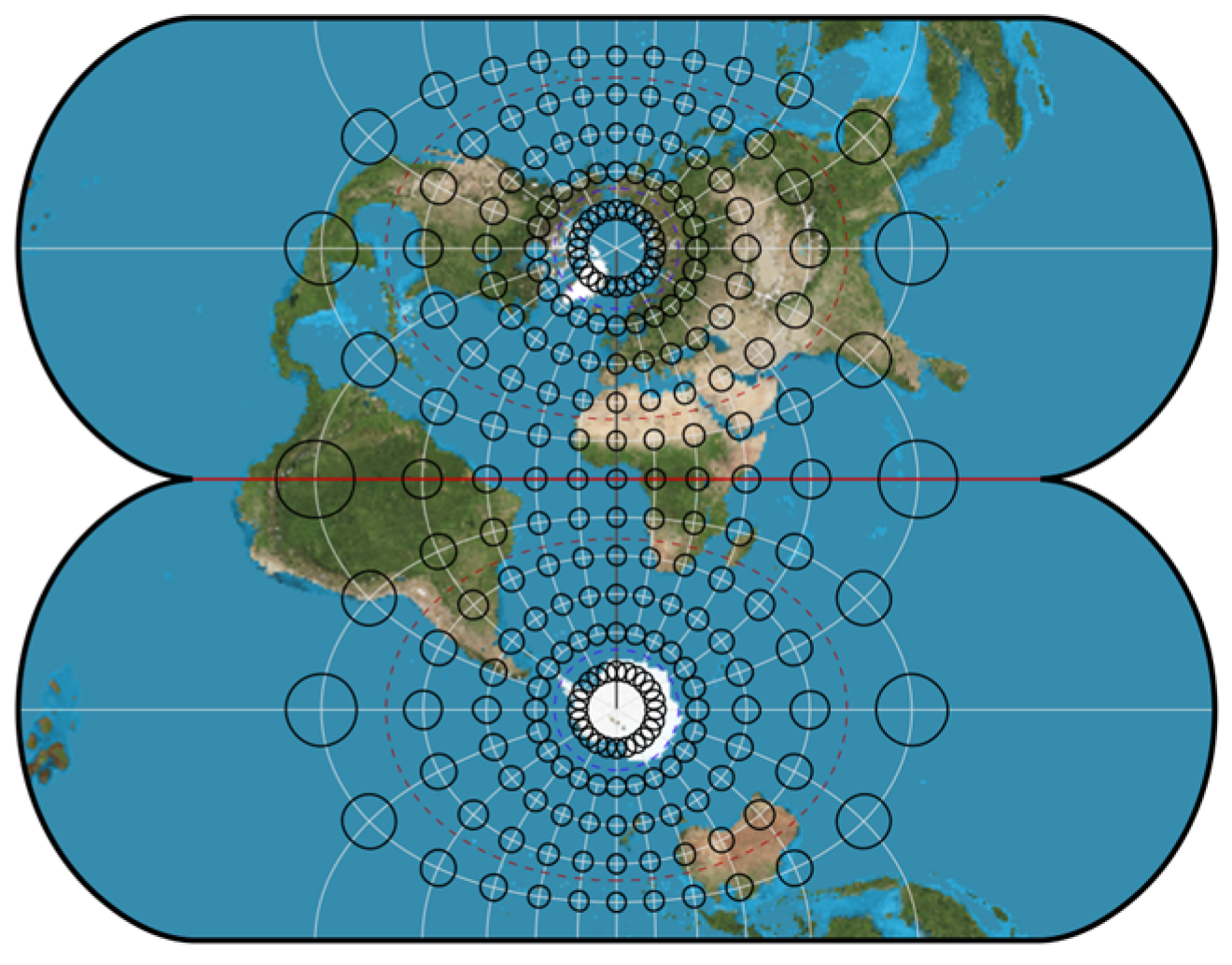
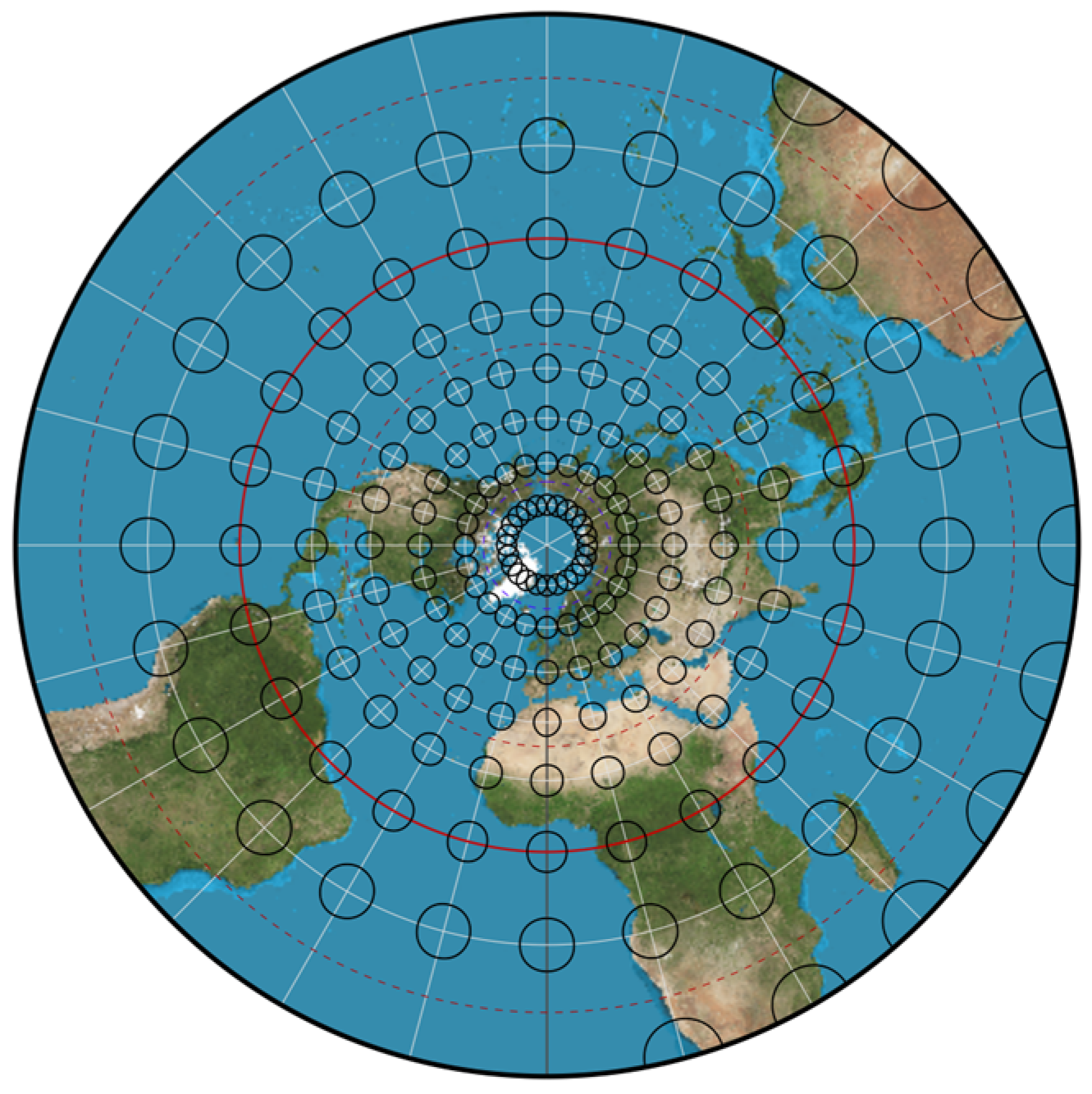
4.2. Distortions of Longitude and Latitude Grid Lines
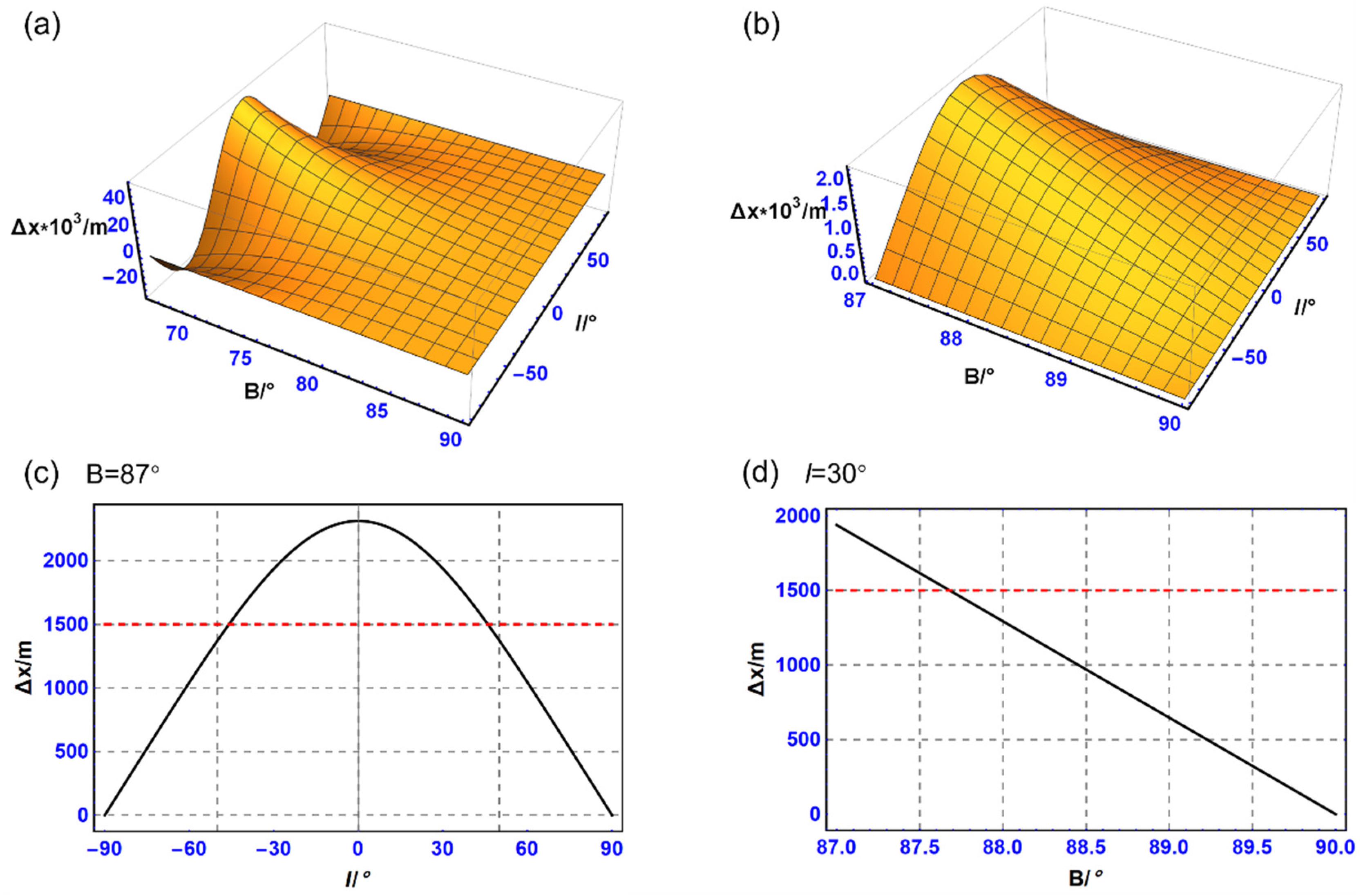
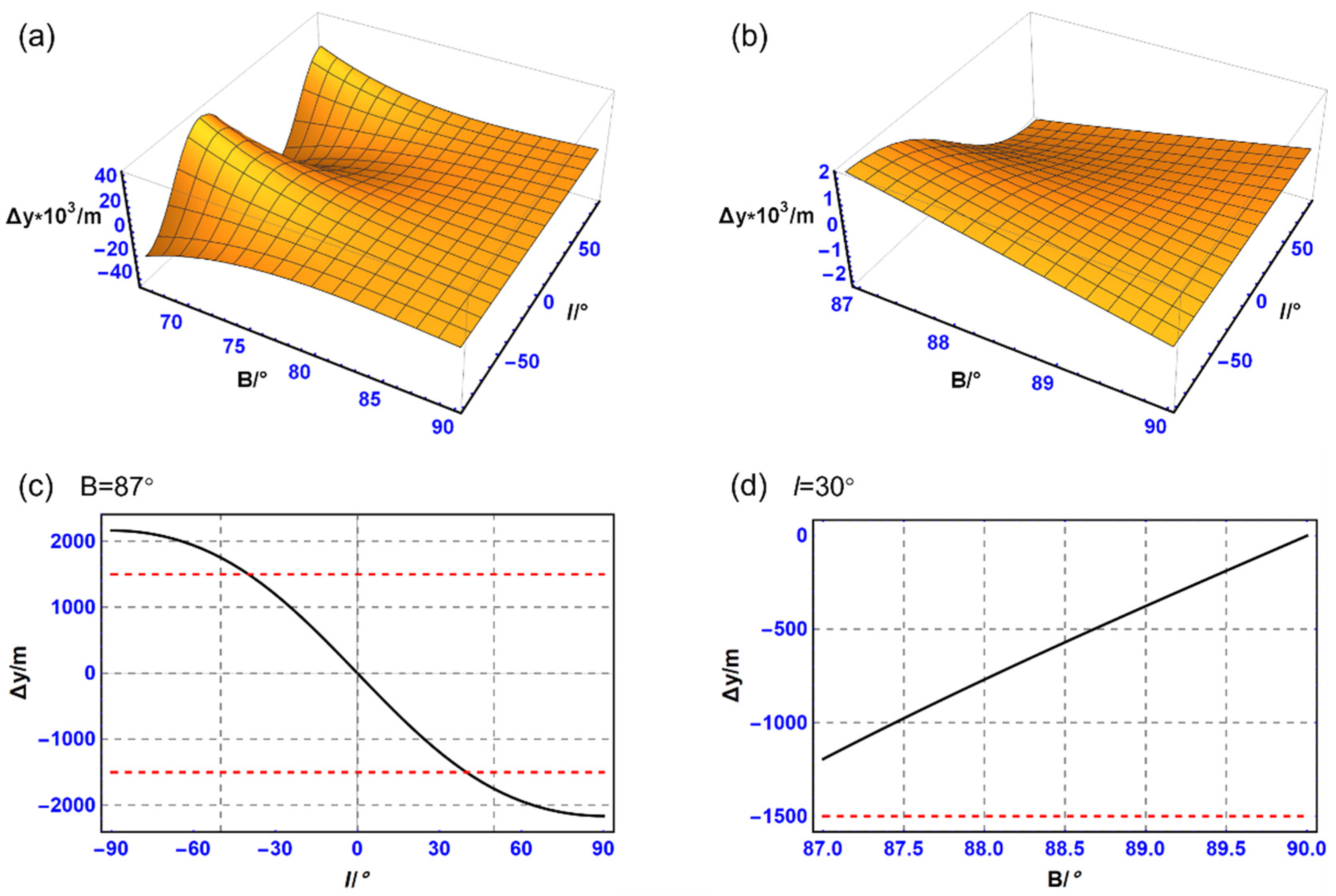
4.3. Accuracy of Direct Transformation between Projections
4.4. Calculation Efficiency Analysis
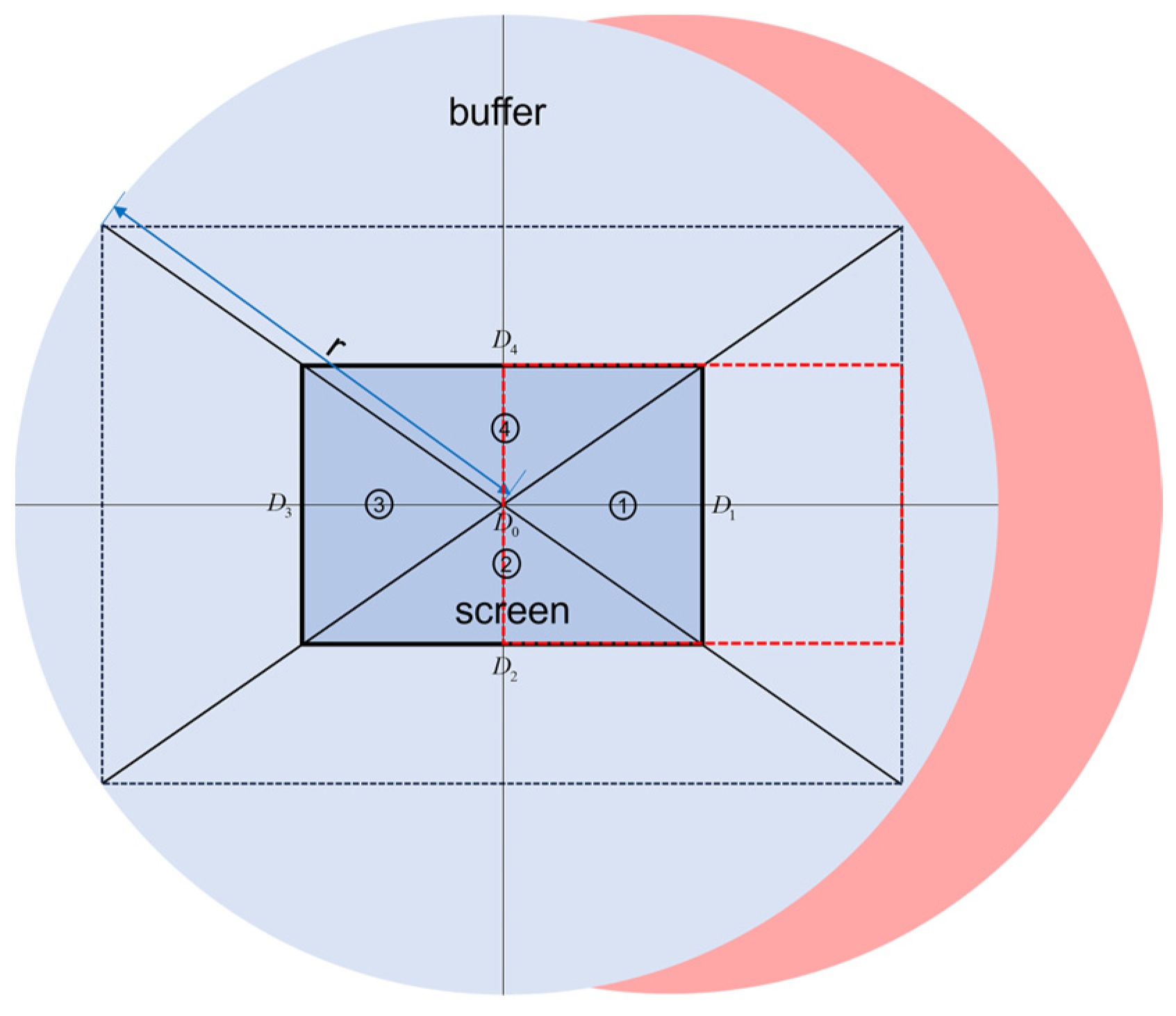
5. Visualization of Dynamic Chart Projection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yastrebova, A.; Höyhtyä, M.; Boumard, S. Positioning in the Arctic Region: State-of-the-Art and Future Perspectives. IEEE Access 2021, 9, 53964–53978. [Google Scholar] [CrossRef]
- Li, X.; Otsuka, N.; Brigham, L. Spatial and temporal variations of recent shipping along the Northern Sea Route. Polar Sci. 2021, 27, 100569. [Google Scholar] [CrossRef]
- Screen, J.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Beveridge, L.; Fournier, M.; Lasserre, F.; Huang, L. Interest of Asian Shipping Companies in Navigating the Arctic. Polar Sci. 2016, 10, 404–414. [Google Scholar] [CrossRef]
- Liang, S.; Zeng, J.; Li, Z. Spatio-temporal analysis of the melt onset dates over Arctic sea ice from 1979 to 2017. Acta Oceanol. Sin. 2022, 41, 146–156. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, J.; Zhao, L. Survey on polar marine navigation and positioning system. Chin. J. Ship Res. 2021, 16, 16–29. [Google Scholar]
- Plass, S.; Clazzer, F.; Bekkadal, F. Current situation and future innovations in Arctic communications. In Proceedings of the Vehicular Technology Conference, Boston, MA, USA, 6–9 September 2015; pp. 1–7. [Google Scholar]
- Liu, Z.; Zhang, B.; Zhang, M. A quantitative method for the analysis of ship collision risk using AIS data. Ocean Eng. 2023, 272, 113906. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Liu, R.W. Quantifying Arctic oil spilling event risk by integrating an analytic network process and a fuzzy comprehensive evaluation model. Ocean Coast. Manag. 2022, 228, 106326. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Li, Y. Transverse Navigation under the Ellipsoidal Earth Model and its Performance in both Polar and Non-polar areas. J. Nav. 2016, 1, 1–18. [Google Scholar] [CrossRef]
- Naumann, J. Grid navigation with polar stereographic charts. Eur. J. Navig. 2011, 9, 4–8. [Google Scholar]
- Lapon, L.; Ooms, K.; Maeyer, P. The Influence of Map Projections on People’s Global-Scale Cognitive Map: A Worldwide Study. Int. J. Geo Inf. 2020, 9, 196. [Google Scholar] [CrossRef]
- Baselga, S. Two Conformal Projections for Constant-Height Surface to Plane Mapping. J. Surv. Eng. 2021, 147, 06020004. [Google Scholar] [CrossRef]
- Beresford, P. Map Projection Used in Polar Regions. J. Nav. 1953, 6, 29–37. [Google Scholar] [CrossRef]
- Snyder, J. Map Projections-A Working Manual; United States Government Printing Office: Washington, DC, USA, 1987.
- Grafarend, E.; You, R.; Syffus, R. Map Projections; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Pearson, F. Map Projections: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Smith, L.; Stephenson, S. New Trans-Arctic shipping routes navigable by midcentury. Proc. Natl. Acad. Sci. USA 2013, 110, E1191–E1195. [Google Scholar] [CrossRef] [PubMed]
- Pallikaris, A.; Tsoulos, L. Map projections and visualization of navigational paths in electronic chart systems. In Proceedings of the 3rd International Conference on Cartography and GIS, Nessebar, Bulgaria, 15–20 June 2010; pp. 15–20. [Google Scholar]
- Skopeliti, A.; Tsoulos, L. Choosing a Suitable Projection for Navigation in the Arctic. Mar. Geod. 2013, 36, 234–259. [Google Scholar] [CrossRef]
- Peter, O. The Mercator Projections; Edinburgh University Press: Edinburgh, UK, 2008; pp. 23–29. [Google Scholar]
- Pallikaris, A. Choosing Suitable Map Projections for World-wide Depiction of Electronic Charts in ECDIS. Coordinates 2014, 10, 21–28. [Google Scholar]
- Xiong, J. Ellipsoid Geodesy; Chinese People’s Liberation Army Publishing House: Beijing, China, 1988. [Google Scholar]
- Wang, H.; Zhang, W.; Zhang, P. Polar Navigation Method Based on Polar Stereographic Projection. Command Control Simul. 2016, 38, 106–109. [Google Scholar]
- Wen, C.; Bian, H.; Gao, X. Availability Analysis of Mercator Projection in Nautical Charts’ Compilation in Polar Regions. Appl. Mech. Mater. 2014, 535, 556–561. [Google Scholar] [CrossRef]
- Bowring, B. The Transverse Mercator Projection—A Solution by Complex Numbers. Surv. Rev. 1978, 30, 325–342. [Google Scholar] [CrossRef]
- Bian, S.; Li, Z.; Li, H. The Non-singular Formula of Gauss Projection in Polar Regions by Complex Numbers. Acta Geod. Cartogr. Sin. 2014, 43, 348–352+359. [Google Scholar]
- Li, Z.; Bian, S.; Jin, L. Forward and Inverse Expressions of Polar Gauss Projection without Zoning Limitations. Acta Geod. Cartogr. Sin. 2017, 46, 780–788. [Google Scholar]
- Guo, J.; Shen, W.; Ning, J. Development of Lee’s exact method for Gauss-Krüger projection. J. Geod. 2020, 94, 58. [Google Scholar] [CrossRef]
- Wen, C.; Bian, H. Polar grid rumble route based on polar stereographic projection. Acta Geod. Cartogr. Sin. 2019, 48, 18–23. [Google Scholar]
- Jenny, B. Adaptive composite map projections. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2575–2582. [Google Scholar] [CrossRef]
- Jenny, B.; Šavrič, B.; Patterson, T. A compromise aspect-adaptive cylindrical projection for world maps. Int. J. Geogr. Inf. Sci. 2015, 29, 935–952. [Google Scholar] [CrossRef]
- Palikaris, A.; Mavraeidopoulos, A. Electronic navigational charts: International standards and map projections. J. Mar. Sci. Eng. 2020, 8, 248. [Google Scholar] [CrossRef]
- Gosling, P.; Symeonakis, E. Automated map projection selection for GIS. Cartogr. Geogr. Inf. Sci. 2020, 47, 261–276. [Google Scholar] [CrossRef]
- Jiao, C. Computer Algebraic Analysis and Optimization of Common Map Projection Deformation. Master’s Thesis, China University of Geosciences (Wuhan), Wuhan, China, 2022. [Google Scholar]
- Li, X.; Li, H.; Liu, G.; Bian, S. Optimization of Complex Function Expansions for Gauss-Krüger Projections. ISPRS Int. J. Geo Inf. 2022, 11, 566. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Liu, G.; Bian, S.; Jiao, C. Simplified Expansions of Common Latitudes with Geodetic Latitude and Geocentric Latitude as Variables. Appl. Sci. 2022, 12, 7818. [Google Scholar] [CrossRef]
- Karney, C.F.F. On auxiliary latitudes. Surv. Rev. 2023, 56, 165–180. [Google Scholar] [CrossRef]
- Bermejo, M.; Otero, J. Simple and highly accurate formulas for the computation of Transverse Mercator coordinates from longitude and isometric latitude. J. Geod. 2009, 83, 1–12. [Google Scholar] [CrossRef]
- Wang, K.; Ye, S.; Gao, P.; Yao, X.; Zhao, Z. Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates. Remote Sens. 2022, 14, 2056. [Google Scholar] [CrossRef]
- GB 12320-2022; Compilation Specifications for Chinese Nautical Charts. Standards Press of China: Beijing, China, 2022.
- International Hydrographic Organization. Electronic Navigational Charts (ENC)–Production, Maintenance and Distribution Guidance; Edition 2.1.0; Publication S-65; IHO: Monaco, France, 2017.


| B/° | Type of Projection | ||
|---|---|---|---|
| Mercator Projection | Polar Gauss-Krüger Projection (l = 60°) | Polar Stereographic Projection | |
| 66.5 | −0.074787 | 0.065517 | 0.043240 |
| 69 | 0.029360 | 0.051923 | 0.034335 |
| 70 | 0.078520 | 0.046964 | 0.031079 |
| 71 | −0.089466 | 0.042272 | 0.027993 |
| 74 | 0.075366 | 0.029762 | 0.019747 |
| 75 | 0.145209 | 0.026102 | 0.017328 |
| 76 | −0.130658 | 0.022693 | 0.015073 |
| 78 | 0.011497 | 0.016613 | 0.011045 |
| 79 | 0.102135 | 0.013938 | 0.009270 |
| 80 | 0.211028 | 0.011502 | 0.007653 |
| 81 | −0.232651 | 0.009304 | 0.006193 |
| 83 | −0.015044 | 0.005616 | 0.003741 |
| 85 | 0.377225 | 0.002861 | 0.001906 |
| 86 | −0.838213 | 0.001830 | 0.001219 |
| 88 | −0.676627 | 0.000457 | 0.000305 |
| 90 | ∞ | 0 | 0 |
| Name | Scale Range | Selectable Range (m) | Deformation | Range of Latitudes | Projection |
|---|---|---|---|---|---|
| Berthing | >1:4000 | 463 | <5% | Mercator Projection | |
| Polar Gauss-Krüger Projection | |||||
| Polar Stereographic Projection | |||||
| Harbor | 1:4000~1:22,000 | 2778 | <5% | Mercator Projection | |
| Polar Gauss-Krüger Projection | |||||
| Polar Stereographic Projection | |||||
| Approach | 1:1:22,000~1:90,000 | 11,112 | <10% | Mercator Projection | |
| Polar Gauss-Krüger Projection | |||||
| Polar Stereographic Projection | |||||
| Coastal | 1:90,000~1:350,000 | 44,448 | <30% | Mercator Projection | |
| Polar Stereographic Projection | |||||
| General | 1:350,000~1:1,500,000 | 177,792 | <40% | Mercator Projection | |
| Polar Stereographic Projection | |||||
| Overview | <1:1,500,000 | 407,440 | <50% | Mercator Projection | |
| Polar Stereographic Projection |
| Form | Time (s) | Resolution | ||
|---|---|---|---|---|
| 0.0018389 | 0.081655 | 197.8277 | ||
| 0.0019954 | 0.067192 | 203.3265 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, C.; Wan, X.; Li, H.; Bian, S. Dynamic Projection Method of Electronic Navigational Charts for Polar Navigation. J. Mar. Sci. Eng. 2024, 12, 577. https://doi.org/10.3390/jmse12040577
Jiao C, Wan X, Li H, Bian S. Dynamic Projection Method of Electronic Navigational Charts for Polar Navigation. Journal of Marine Science and Engineering. 2024; 12(4):577. https://doi.org/10.3390/jmse12040577
Chicago/Turabian StyleJiao, Chenchen, Xiaoxia Wan, Houpu Li, and Shaofeng Bian. 2024. "Dynamic Projection Method of Electronic Navigational Charts for Polar Navigation" Journal of Marine Science and Engineering 12, no. 4: 577. https://doi.org/10.3390/jmse12040577
APA StyleJiao, C., Wan, X., Li, H., & Bian, S. (2024). Dynamic Projection Method of Electronic Navigational Charts for Polar Navigation. Journal of Marine Science and Engineering, 12(4), 577. https://doi.org/10.3390/jmse12040577






