An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications
Abstract
1. Introduction
- Accelerated saturation in gear actuators is proposed for the first time. The model of this phenomenon is developed, and its influence on MISPs is analyzed. To address this problem, an anti-windup method based on an LADRC is proposed. This method can be conveniently implemented in a low-cost system;
- As part of the multiple activated anti-windup method, the limitations of immediate activations in dealing with accelerated saturation are analyzed. By combining the LESO with saturation feedback, the modified anticipatory activation anti-windup compensator is proposed and verified;
- The proposed method enhances the robustness of visual tracking by the MISP control system, effectively mitigating the high-frequency vibrations on the LOS induced by accelerated saturation, thereby improving the effectiveness of target identification.
2. Model of Accelerated Saturation
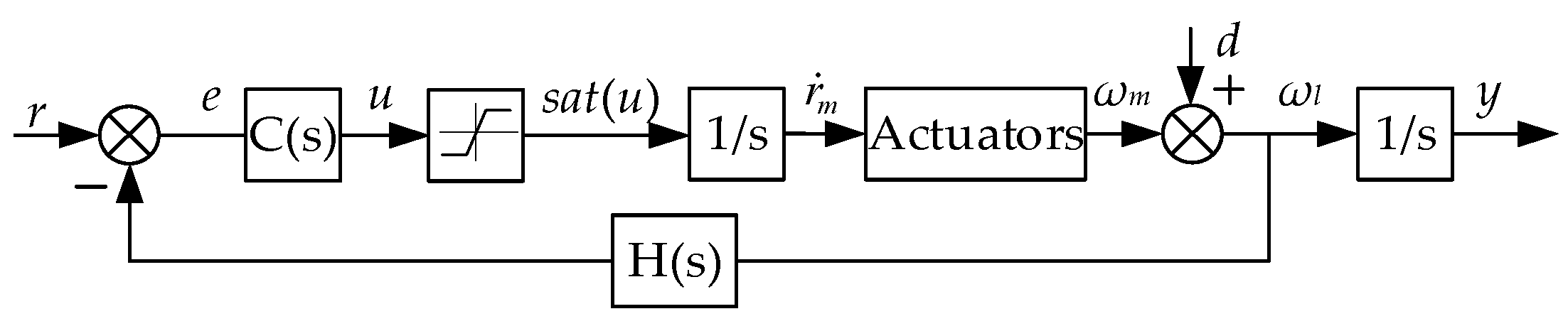
3. Tracking System with the Anti-Windup LADRC
3.1. Optimal Desgin for the Anti-Windup LADRC
3.2. Tracking Controller with a Modified LESO
3.3. Gains of the System for Robustness in Stability
4. Simulations and Analysis
4.1. Parameter Setting of the System
4.2. Simulations in the Normal Condition
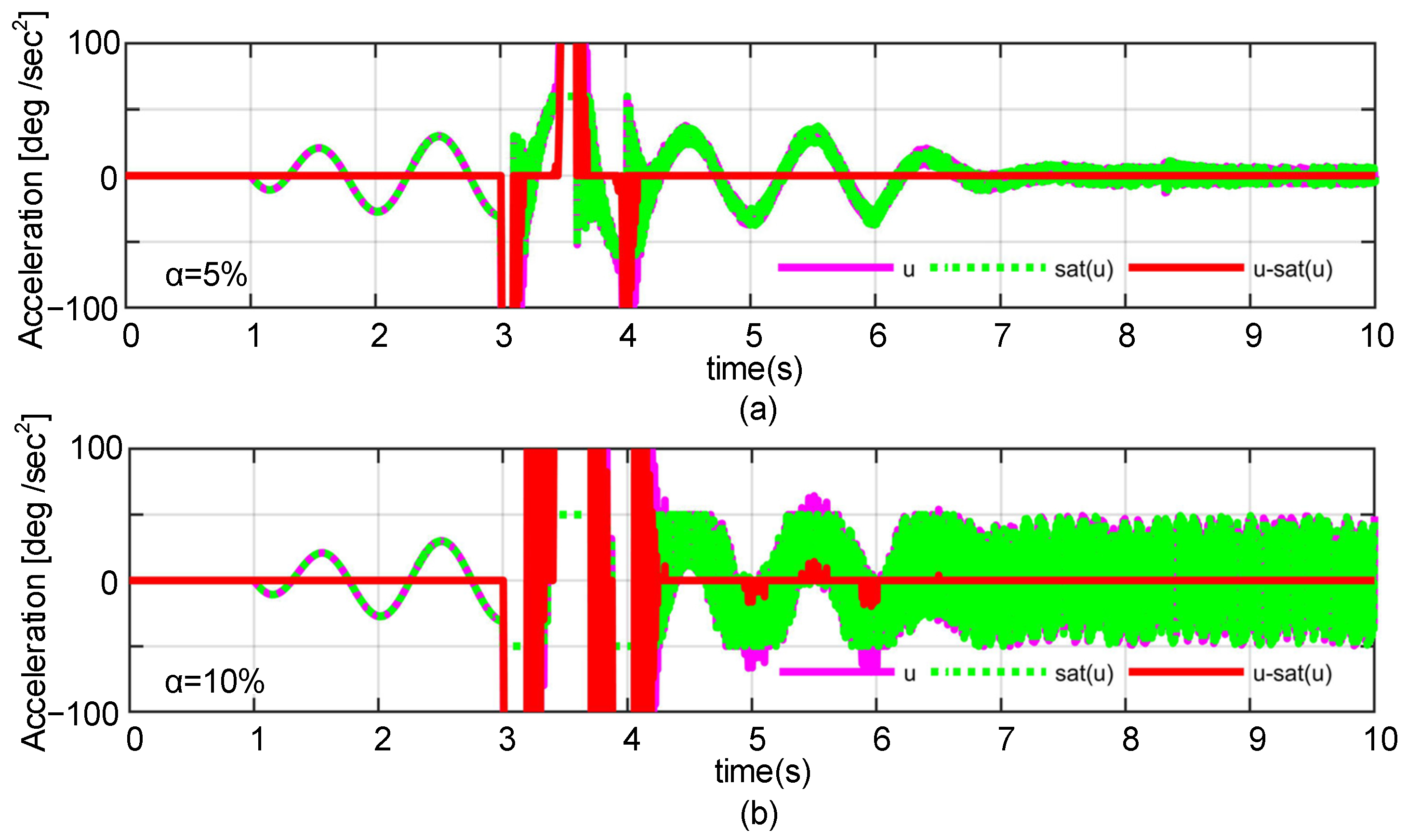
4.3. Simulations under Acceleration-Limitated Conditions
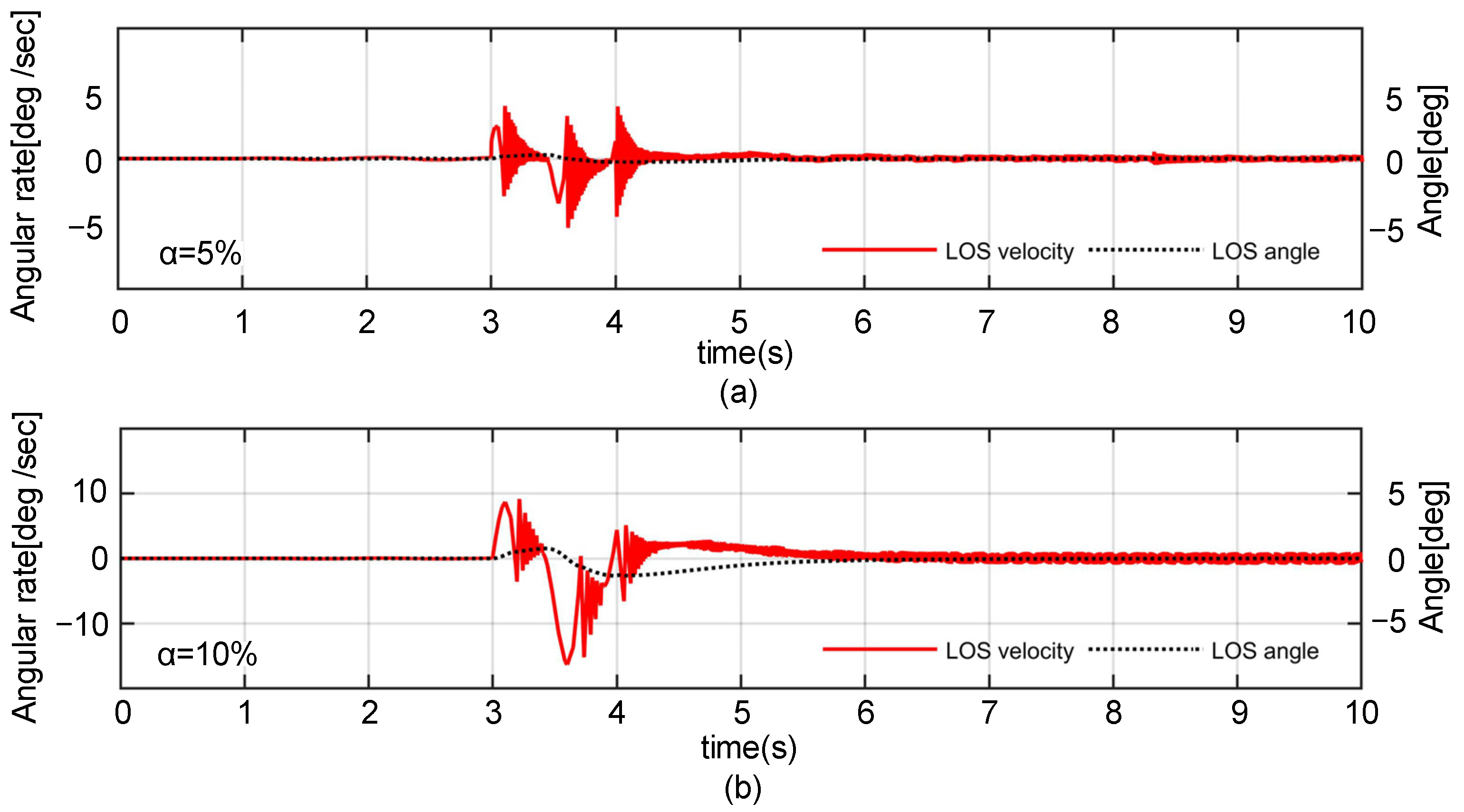
4.3.1. Immediate Activation Method
4.3.2. Anticipatory Activation Method
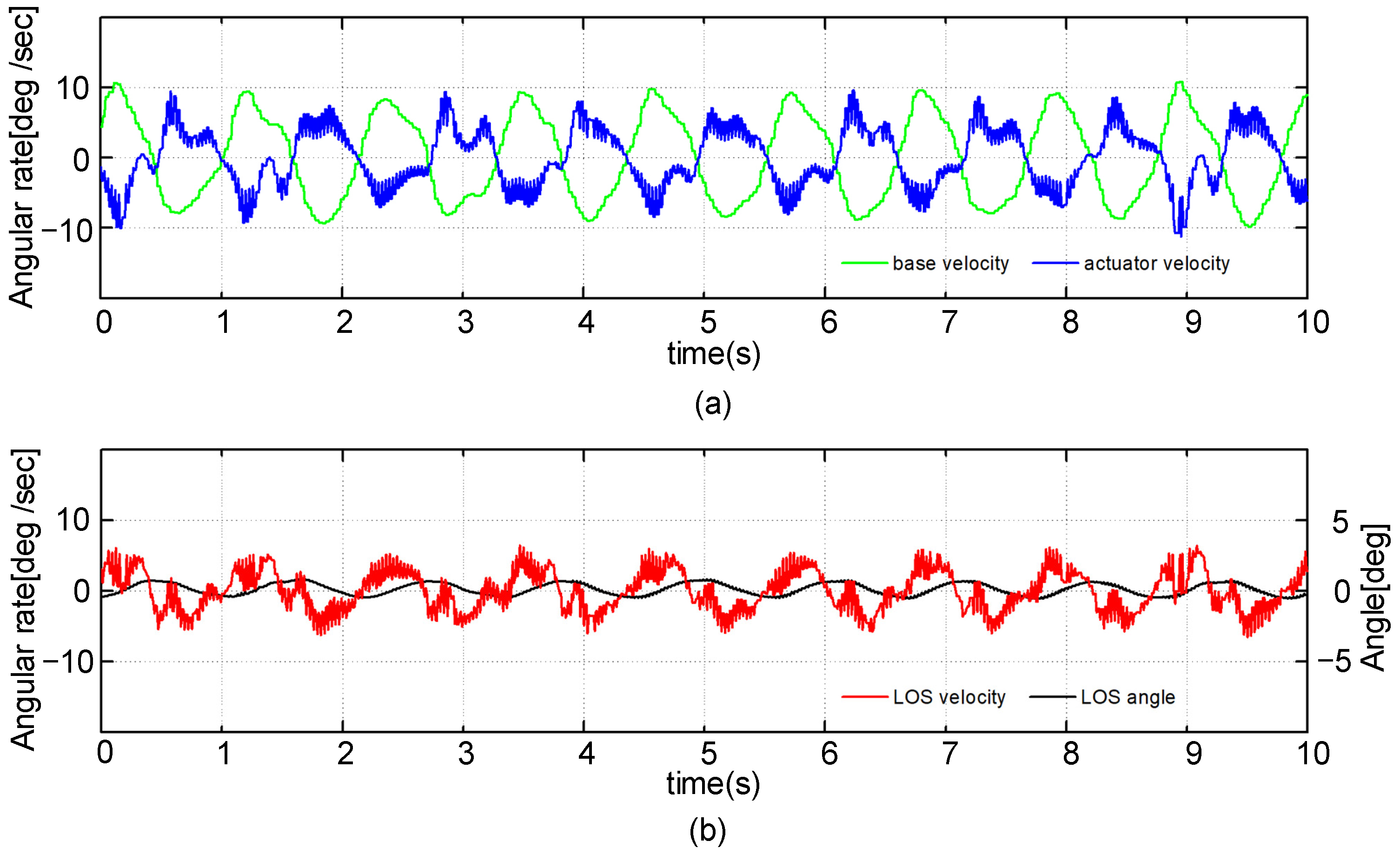
4.3.3. Simulations with Recorded Attitude Data
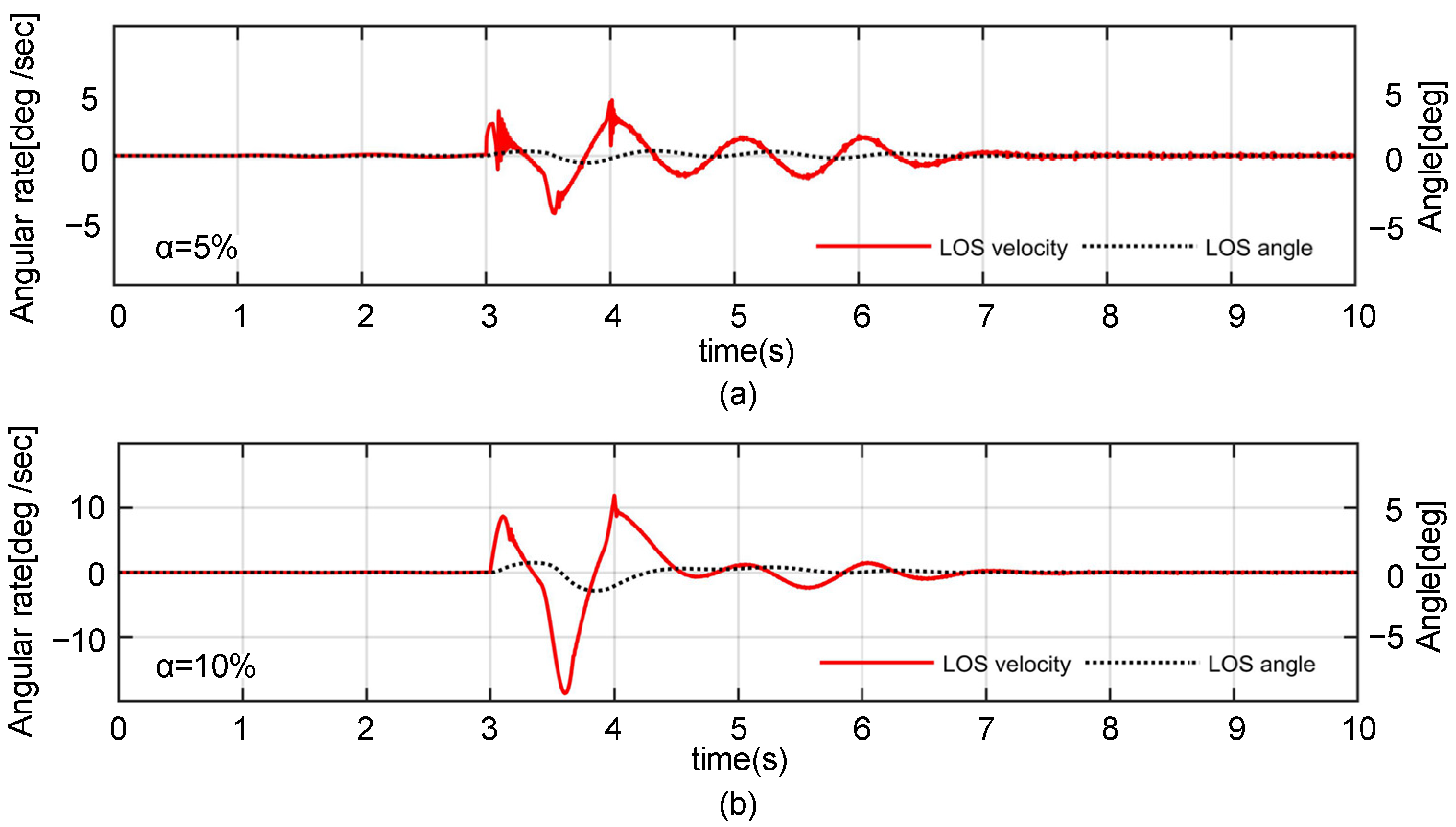
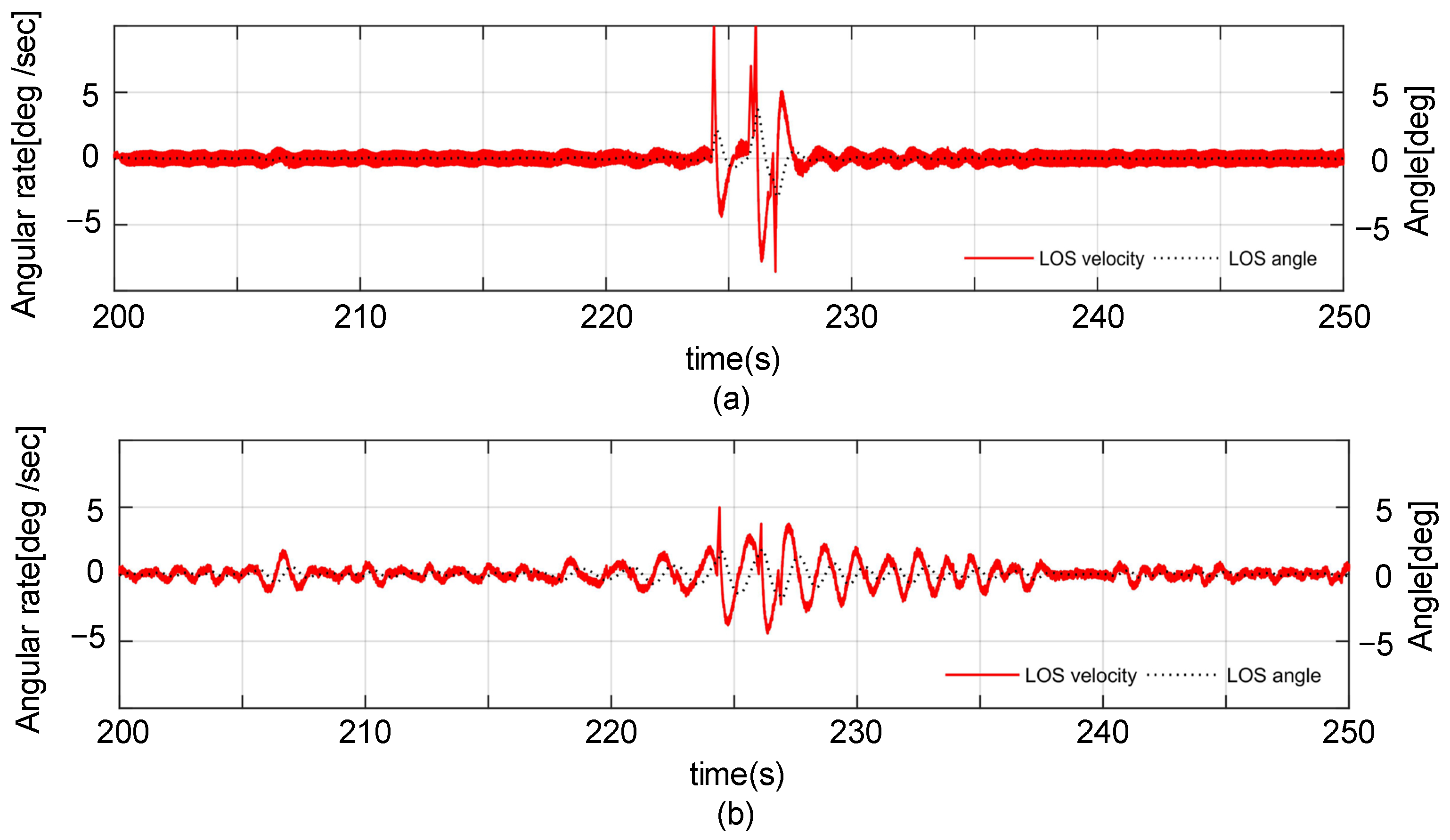
5. Experimental Verifications
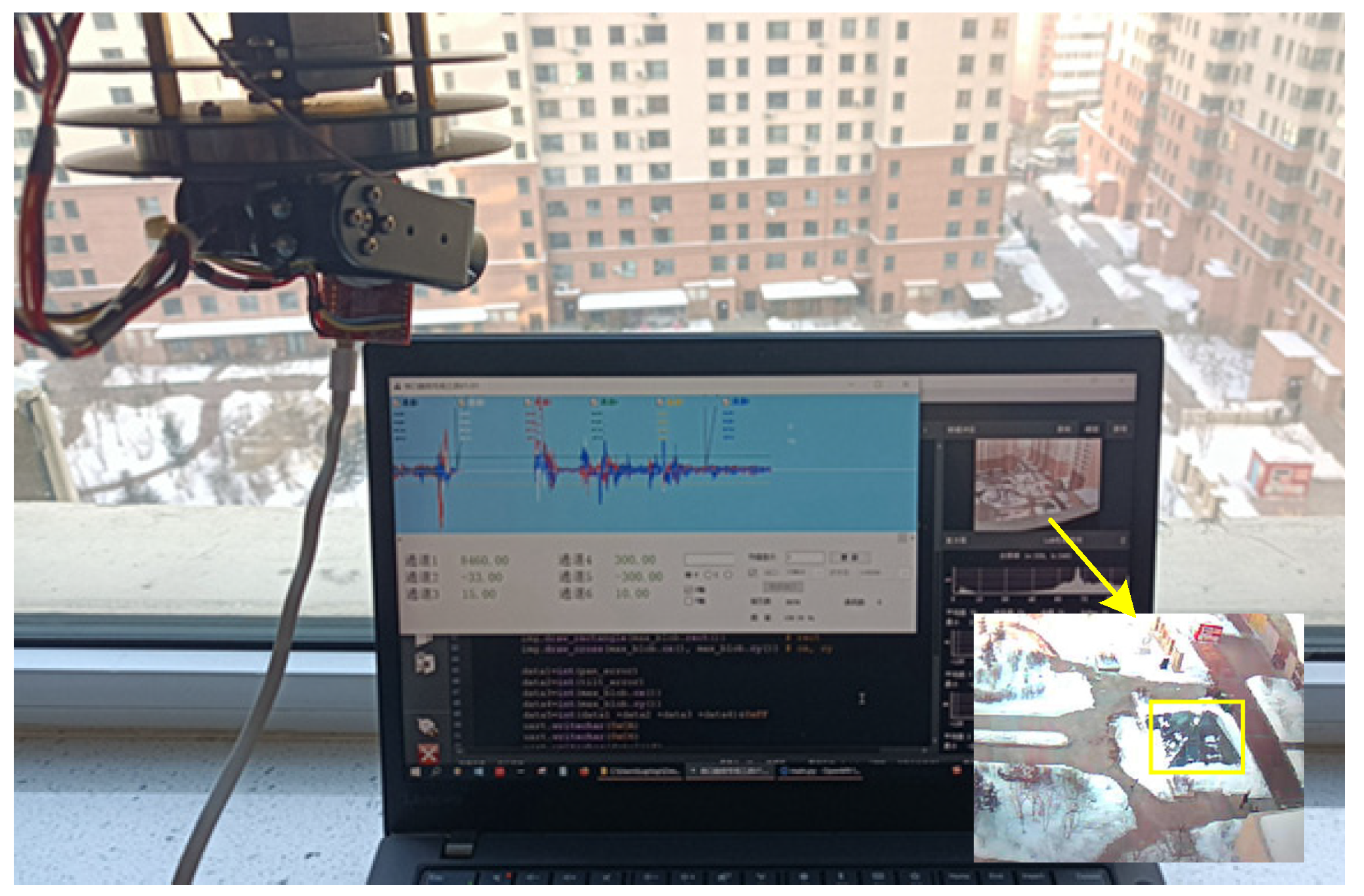
5.1. Hardware of the Dynamic Camera Platform
5.2. Comparison and Analyses
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.; Chen, J.; Wu, X.; Liang, H.; Zheng, Z.; Zhu, C.; Liu, Y.; Sun, C.; Wang, C.; He, D. Analysis and compensation of installation perpendicularity error in unmanned surface vehicle electro-optical devices by using sea-sky line images. J. Mar. Sci. Eng. 2023, 11, 863. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, W.; Shi, J. Tracking strategy of unmanned aerial vehicle for tracking moving target. Int. J. Control Autom. Syst. 2021, 19, 2183–2194. [Google Scholar] [CrossRef]
- Helgesen, H.; Leira, F.; Fossen, T.; Johansen, T. Tracking of ocean surface objects from unmanned aerial vehicles with a pan/tilt unit using a thermal camera. J. Intell. Robot. Syst. 2018, 91, 775–793. [Google Scholar] [CrossRef]
- Lee, D.; Tran, D.; Kim, Y.; Chakir, S. A robust double active control system design for disturbance suppression of a two-axis gimbal system. Electronics 2020, 9, 1638. [Google Scholar] [CrossRef]
- Lu, W.; Niu, C.; Lan, C.; Liu, W.; Wang, S.; Yu, J.; Hu, T. High-Quality Object Detection Method for UAV Images Based on Improved DINO and Masked Image Modeling. Remote Sens. 2023, 15, 4740. [Google Scholar] [CrossRef]
- Liu, Y.; Bai, J.; Wang, G.; Wu, X.; Sun, F.; Guo, Z.; Geng, H. UAV Localization in Low-Altitude GNSS-Denied Environments Based on POI and Store Signage Text Matching in UAV Images. Drones 2023, 7, 451. [Google Scholar] [CrossRef]
- Wang, P.; Liu, R.; Tian, X.; Zhang, X.; Qiao, L.; Wang, Y. Obstacle avoidance for environmentally-driven USVs based on deep reinforcement learning in large-scale uncertain environments. Ocean Eng. 2023, 270, 113670. [Google Scholar] [CrossRef]
- Huang, F.; Chen, X.; Xu, Y.; Yang, X.; Chen, Z. Immersive virtual simulation system design for the guidance, navigation and control of unmanned surface vehicles. Ocean Eng. 2023, 281, 114884. [Google Scholar] [CrossRef]
- Zhou, Z.; Jing, Z.; Wang, Q.; Qu, C. Object detection and tracking of unmanned surface vehicles based on spatial-temporal information fusion. J. Electron. Inf. Technol. 2021, 43, 1698–1705. [Google Scholar]
- Cortes-Vega, D.; Alazki, H.; Rullan-Lara, J. Visual odometry-based robust control for an unmanned surface vehicle under waves and currents in a urban waterway. J. Mar. Sci. Eng. 2023, 11, 515. [Google Scholar] [CrossRef]
- Lee, J.; Yoon, S.; Kim, B.; Gwon, G.; Kim, I.; Jung, H. A new image-quality evaluating and enhancing methodology for bridge inspection using an unmanned aerial vehicle. Smart Struct. Syst. 2021, 27, 209–226. [Google Scholar]
- Kwak, J.; Lee, S.; Baek, J.; Chu, B. Autonomous UAV Target Tracking and Safe Landing on a Leveling Mobile Platform. Int. J. Precis. Eng. Manuf. 2022, 23, 305–317. [Google Scholar] [CrossRef]
- Park, H.; Chakir, S.; Kim, Y.; Huynh, T. A nonlinear backstepping controller design for high-precision tracking applications with input-delay gimbal systems. J. Mar. Sci. Eng. 2021, 9, 530. [Google Scholar] [CrossRef]
- Chen, C.; Liu, D.; Du, J.; Li, Y. Research on Visual Perception for Coordinated Air-Sea through a Cooperative USV-UAV System. J. Mar. Sci. Eng. 2023, 11, 1978. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Liu, J.; Sun, C. Cooperative USV-UAV marine search and rescue with visual navigation and reinforcement learning-based control. ISA Trans. 2023, 137, 222–235. [Google Scholar] [CrossRef]
- Cho, G.; Choi, J.; Bae, G.; Oh, H. Autonomous ship deck landing of a quadrotor UAV using feed-forward image-based visual servoing. Aerosp. Sci. Technol. 2022, 130, 107869. [Google Scholar] [CrossRef]
- Mu, S.; Qiao, C. Ground-Target Geo-Location Method Based on Extended Kalman Filtering for Small-Scale Airborne Electro-Optical Platform. Acta Opt. Sin. 2019, 39, 0528001. [Google Scholar]
- Tullu, A.; Hassanalian, M.; Hwang, H. Design and Implementation of Sensor Platform for UAV-Based Target Tracking and Obstacle Avoidance. Drones 2022, 6, 89. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G. Visual-based obstacle detection and tracking, and conflict detection for small UAS sense and avoid. Aerosp. Sci. Technol. 2021, 119, 107167. [Google Scholar] [CrossRef]
- Kim, J. Autonomous rover guidance and localization by measuring the peak of a tall landmark. Asian J. Control 2022, 24, 2140–2152. [Google Scholar] [CrossRef]
- Warren, M.; Greeff, M.; Patel, B.; Collier, J.; Schoellig, A.P.; Barfoot, T.D. There’s No Place Like Home: Visual Teach and Repeat for Emergency Return of Multirotor UAVs During GPS Failure. IEEE Robot. Autom. Lett. 2019, 4, 161–168. [Google Scholar] [CrossRef]
- Rebello, J.; Li, C.; Waslander, S.L. DC-VINS: Dynamic Camera Visual Inertial Navigation System with Online Calibration. In Proceedings of the 2021 IEEE International Conference on Computer Vision Workshops, Electr Networks, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Shao, X.; Wang, H. Active disturbance rejection based trajectory linearization control for hypersonic reentry vehicle with bounded uncertainties. ISA Trans. 2015, 54, 27–38. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Anti-windup design for uncertain nonlinear systems subject to actuator saturation and external disturbance. Int. J. Robust Nonlinear Control 2016, 26, 3421–3438. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Stabilization of a class of nonlinear systems with actuator saturation via active disturbance rejection control. Automatica 2016, 63, 302–310. [Google Scholar] [CrossRef]
- Geng, X.; Hao, S.; Liu, T.; Wang, Q. Anti-windup design for discrete-time systems with time delay via predictor-based extended state observer. In Proceedings of the 2019 IEEE International Conference on Control and Automation, Edinburgh, UK, 16–19 July 2019; pp. 1161–1166. [Google Scholar]
- Geng, X.; Liu, T.; Hao, S.; Zhong, C.; Wang, Q. Anti-windup design of active disturbance rejection control for sampled systems with input delay. Int. J. Robust Nonlinear Control 2019, 30, 1311–1327. [Google Scholar] [CrossRef]
- Geng, X.; Wang, Z.; Hao, S.; Liu, T.; Nagy, Z. Anti-windup Disturbance Rejection Control Design for Sampled Systems with Output Delay and Asymmetric Actuator Saturation Constraint. In Proceedings of the 21st IFAC World Congress on Automatic Control, Electr Networks, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- Hao, S.; Liu, T.; Geng, X.; Wang, Y. Anti-windup ADRC design for temperature control systems with output delay against asymmetric input constraint. ISA Trans. 2023, 137, 519–530. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Sun, X.; Gao, Y. Active Disturbance Rejection Control for Uncertain Nonlinear Systems Subject to Magnitude and Rate Saturation: Application to Aeroengine. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 2201–2212. [Google Scholar] [CrossRef]
- Wang, H.; Zuo, Z.; Wang, Y.; Yang, H. Composite Nonlinear Path-Following Control for Unmanned Ground Vehicles with Anti-Windup ESO. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 5865–5876. [Google Scholar] [CrossRef]
- Wen, S.; Pan, Z.; Liu, K.; Sun, X. Practical Anti-windup for Open-Loop Stable Systems Under Magnitude and Rate Constraints: Application to Turbofan Engines. IEEE Trans. Ind. Electron. 2023, 70, 4128–4137. [Google Scholar] [CrossRef]
- Wu, X.; Lin, Z. On Immediate, Delayed and Anticipatory Activation of Anti-Windup Mechanism: Static Anti-Windup Case. IEEE Trans. Autom. Control 2012, 57, 711–777. [Google Scholar]
- Wu, X.; Lin, Z. Dynamic anti-windup design in anticipation of actuator saturation. Int. J. Robust Nonlinear Control 2014, 24, 295–312. [Google Scholar] [CrossRef]
- Wu, X.; Pang, J.; Yang, T. Anti-windup Design for Active Disturbance Rejection Control. In Proceedings of the 2014 33rd Chinese Control Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 2389–2395. [Google Scholar]
- Wu, X.; Meng, Z.; Cao, P.; Cai, K. A Multiple Activation Anti-windup Design for Systems with Input Saturation and Dead-zone: Experiments on A Satellite Receiver. In Proceedings of the 2016 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 1152–1157. [Google Scholar]
- Liang, K.; Lin, X.; Chen, Y.; Zhang, W.; Li, J. Robust adaptive multistage anti-windup dynamic surface control for dynamic positioning ships with mismatched disturbance. J. Frankl. Inst.-Eng. Appl. Math. 2021, 358, 2253–2278. [Google Scholar] [CrossRef]
- Le, D.; Ngo, M.; Dang, V.; Nguyen, T. A sensorless anti-windup speed control approach to axial gap bearingless motors with nonlinear lumped mismatched disturbance observers. ISA Trans. 2023, 138, 408–431. [Google Scholar] [CrossRef]


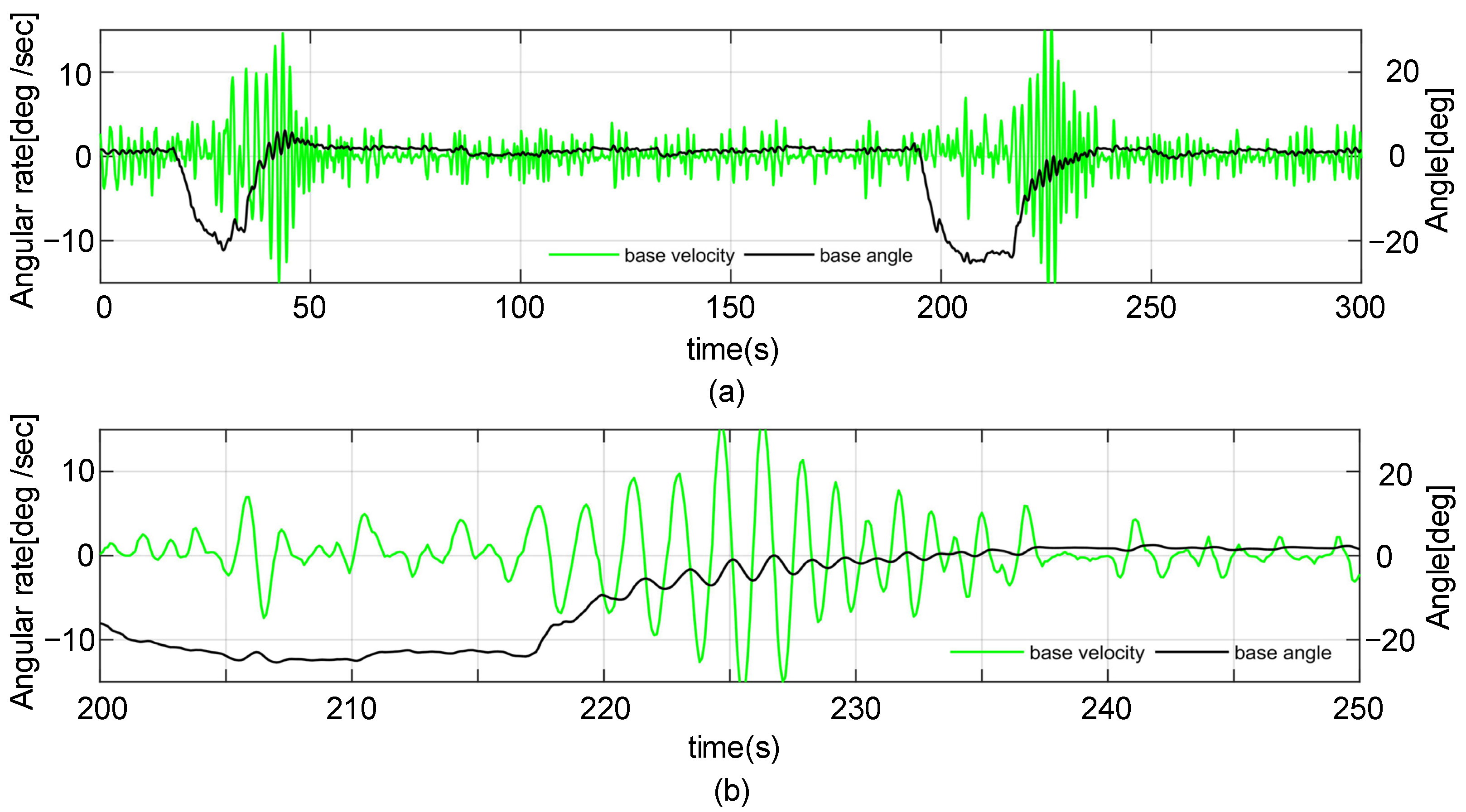
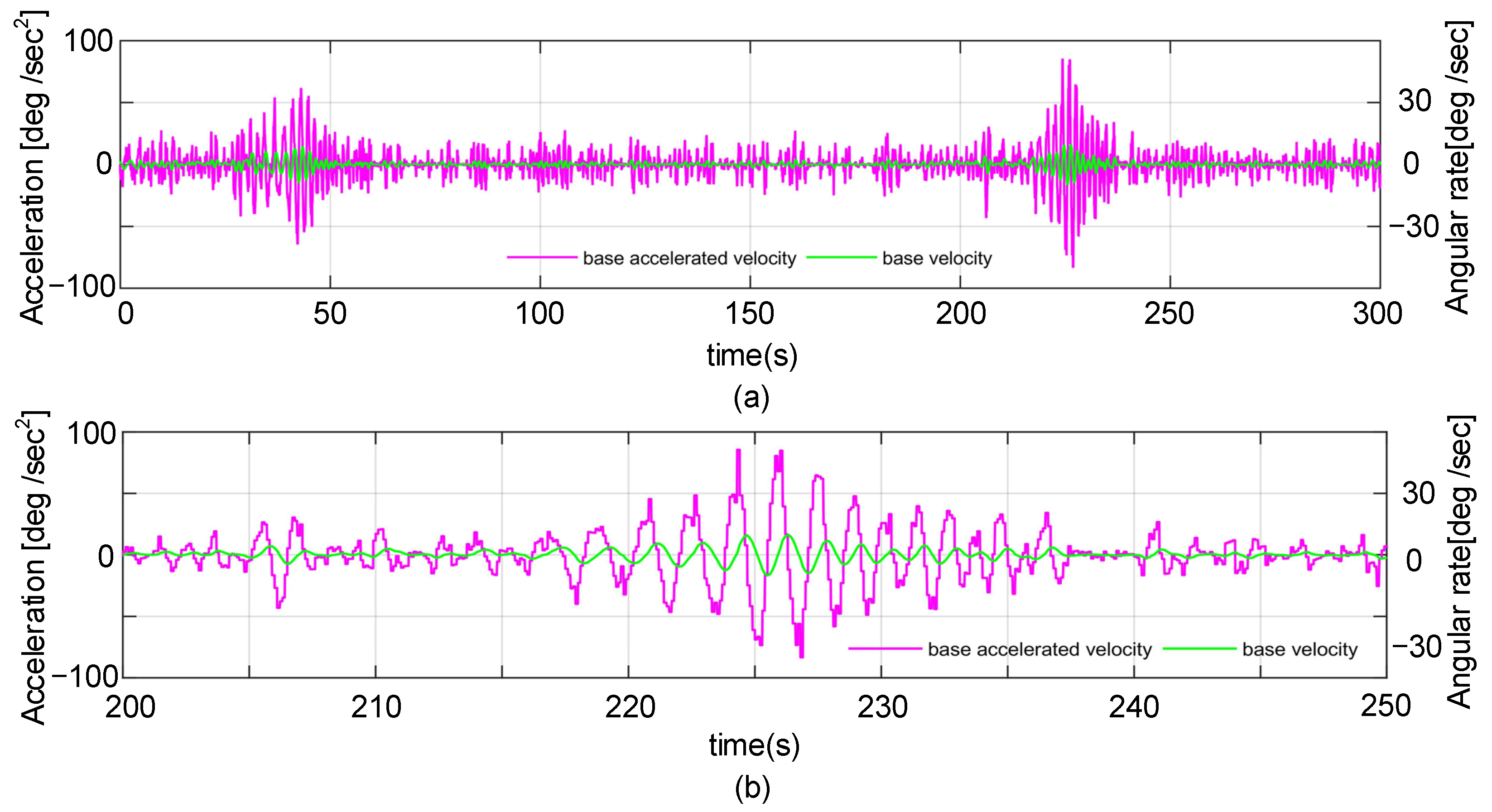
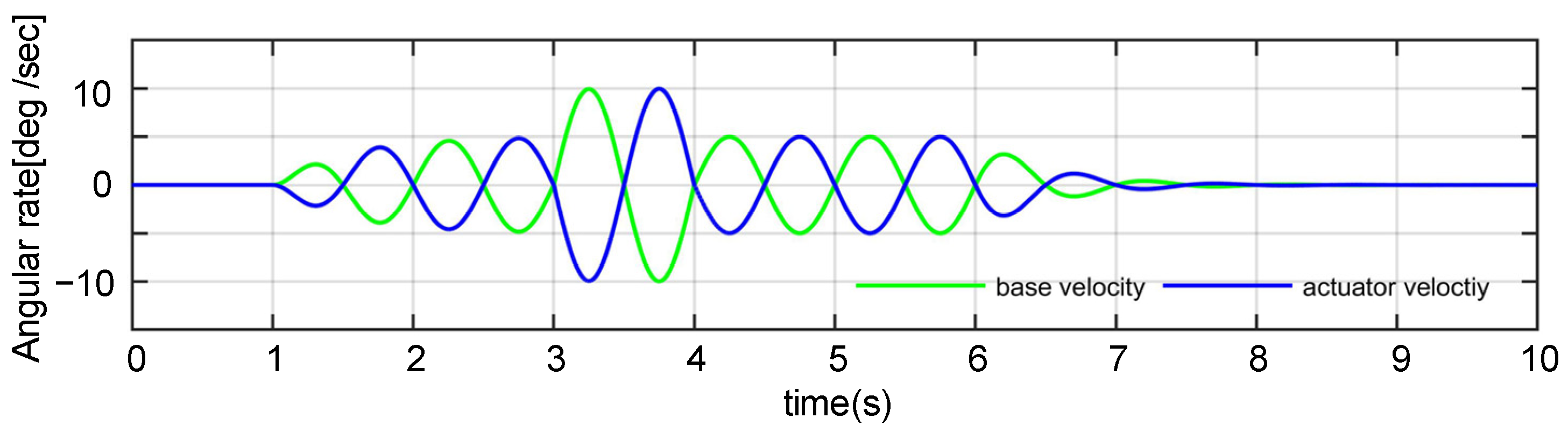







| External Disturbance | Maximal Velocity | Maximal Acceleration | Duration |
|---|---|---|---|
| base velocity | 5°/s | 35°/s2 | 8 s |
| Overshoot | 10°/s | 70°/s2 | 1 s |
| LESO Bandwidth | Gains for LESO |
|---|---|
| ωe = 0.5 | l1 = 1.5, l2 = 0.75, l3 = 0.125 |
| Gains for K | Conditions |
|---|---|
| k1 = 2.1786, k2 = 4.5847, −1/b0 = −2.3115 | γ = 1.0 |
| k1 = 2.1788, k2 = 4.5852, −1/b0 = −2.3062 | γ = 0.9 |
| k1 = 2.1790, k2 = 4.5855, −1/b0 = −2.3038 | γ = 0.8 |
| k1 = 2.1859, k2 = 4.6226, −1/b0 = −1.3038 | γ = 0.7 |
| k1 = 2.1864, k2 = 4.6237, −1/b0 = −1.3631 | γ = 0.6 |
| k1 = 2.1870, k2 = 4.6249, −1/b0 = −1.2995 | γ = 0.5 |
| Terms | Scope Range | Accuracy | |
|---|---|---|---|
| Pitch | Angular rate | ±190°/s | Gyro:0~±250°/s, 131 LSB/(°/s) |
| Angular acceleration | ±70°/s2 | ||
| Yaw | Pitch angle speed | ±170°/s | Gyro:0~±250°/s, 131 LSB/(°/s) |
| Yaw angle speed | ±70°/s2 | ||
| Visual resolution | 320 × 240 | 1 pixel | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, T.; Guan, L.; Gao, Y.; Qin, C. An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications. J. Mar. Sci. Eng. 2024, 12, 616. https://doi.org/10.3390/jmse12040616
Fu T, Guan L, Gao Y, Qin C. An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications. Journal of Marine Science and Engineering. 2024; 12(4):616. https://doi.org/10.3390/jmse12040616
Chicago/Turabian StyleFu, Tianlei, Lianwu Guan, Yanbin Gao, and Chao Qin. 2024. "An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications" Journal of Marine Science and Engineering 12, no. 4: 616. https://doi.org/10.3390/jmse12040616
APA StyleFu, T., Guan, L., Gao, Y., & Qin, C. (2024). An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications. Journal of Marine Science and Engineering, 12(4), 616. https://doi.org/10.3390/jmse12040616






