Container Yard Layout Design Problem with an Underground Logistics System
Abstract
1. Introduction
2. Literature Review
3. Problem Description
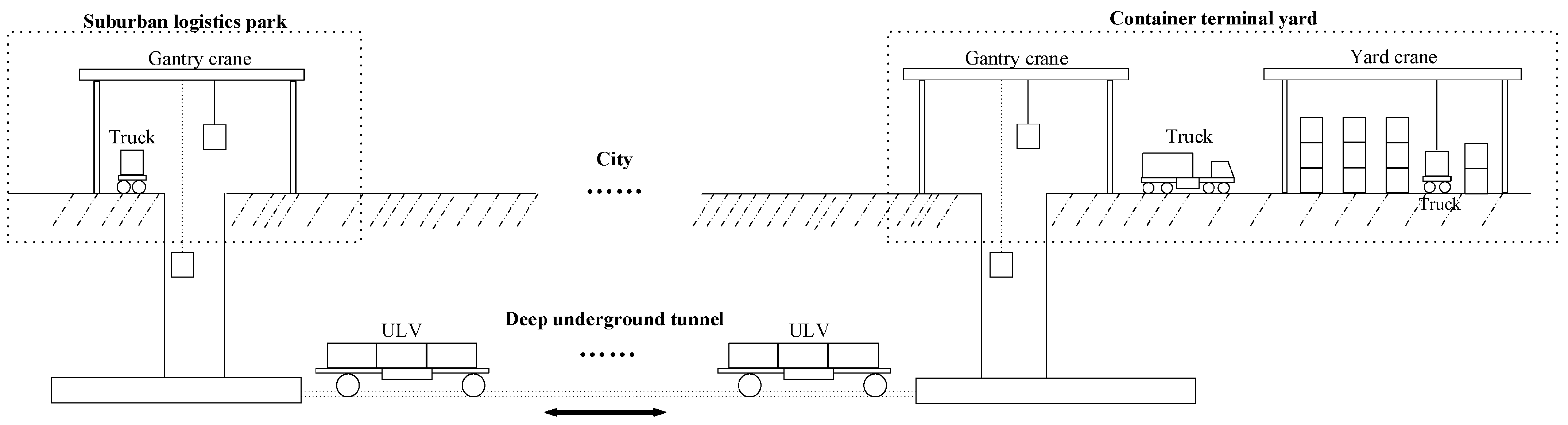
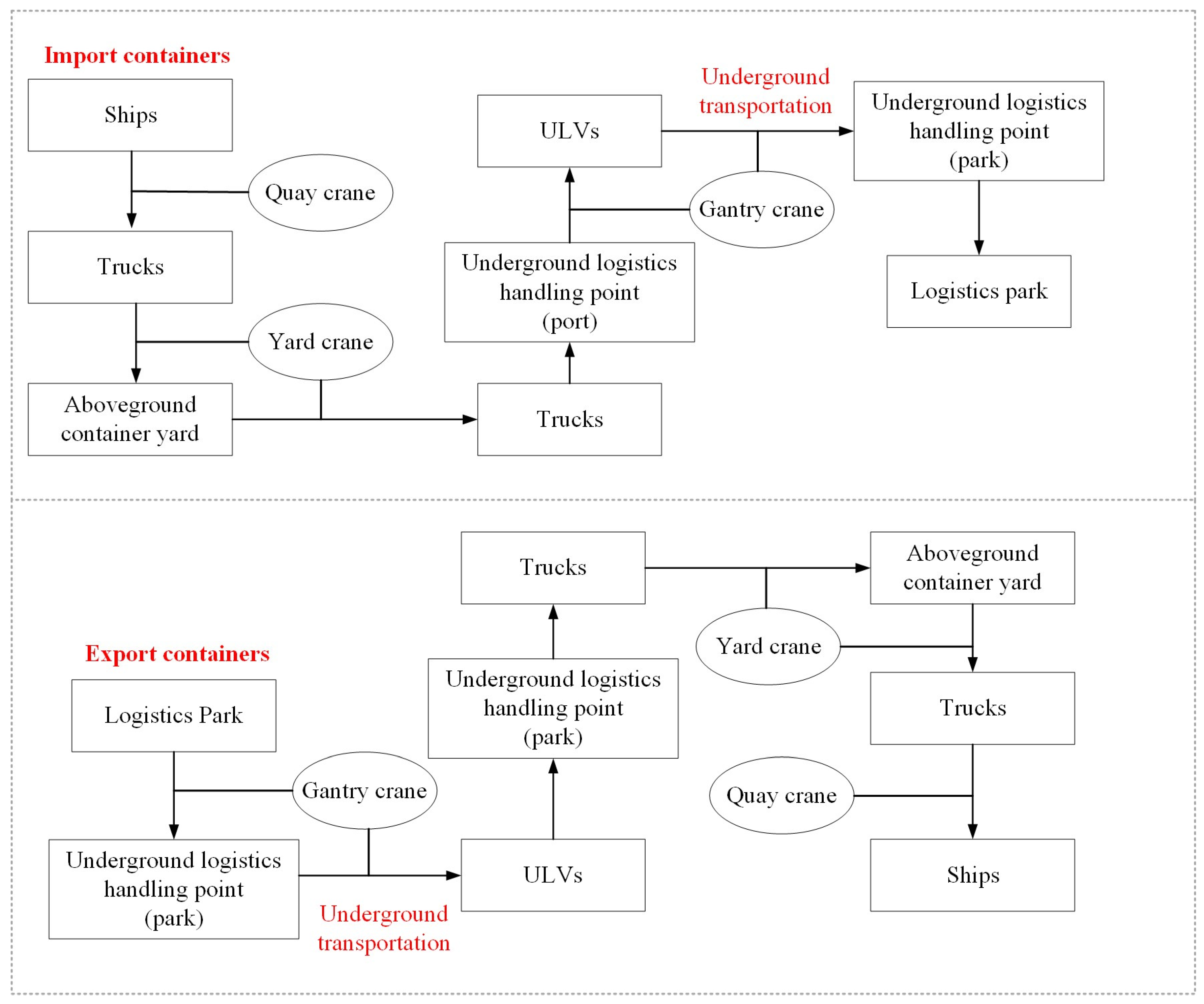
3.1. Container Yard Workflow with an Underground Logistics System
3.2. Container Yard Layout Design Problem with Underground Logistics System
4. Theoretical Model Formulation
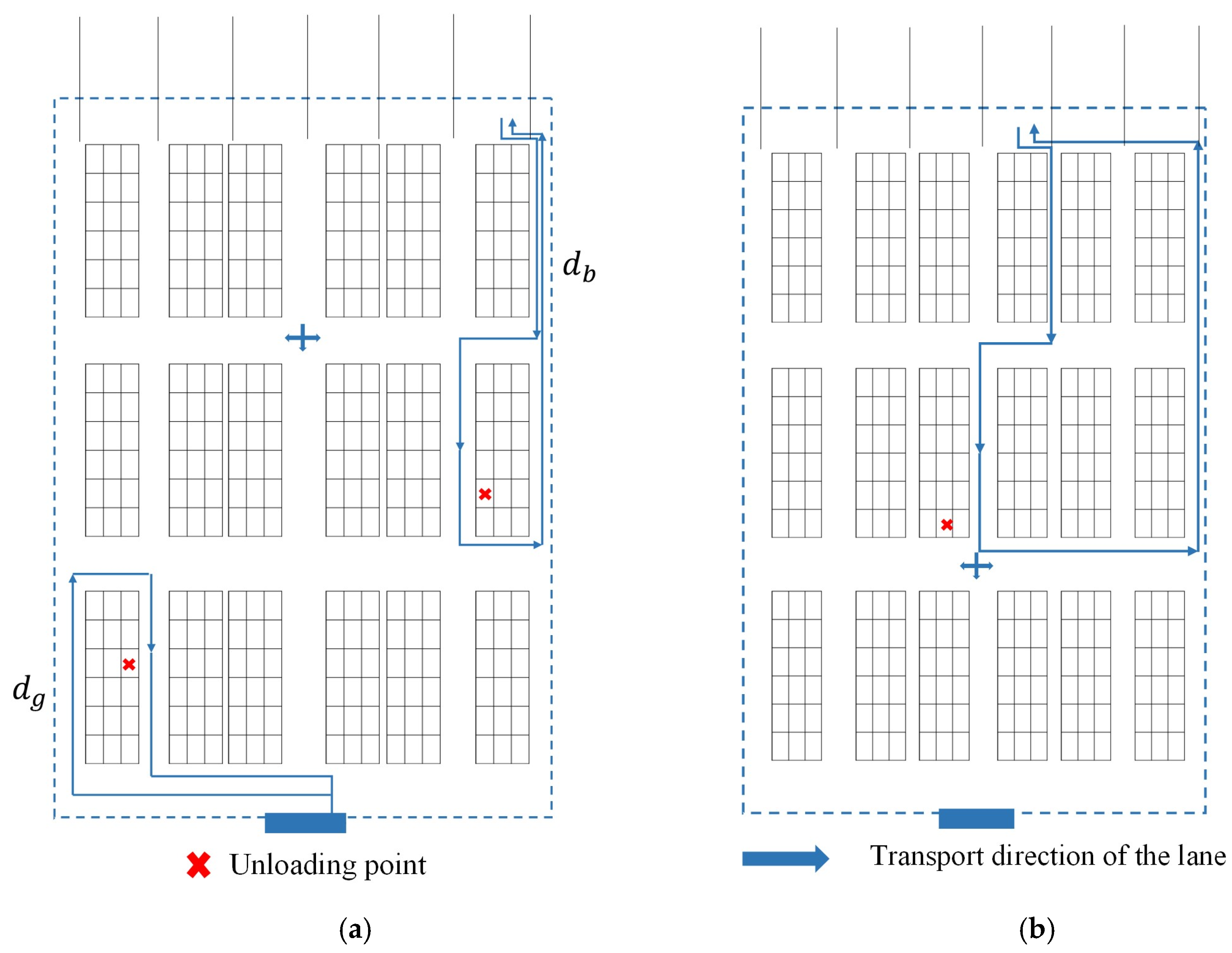
4.1. Estimated Transportation Distances of Trucks
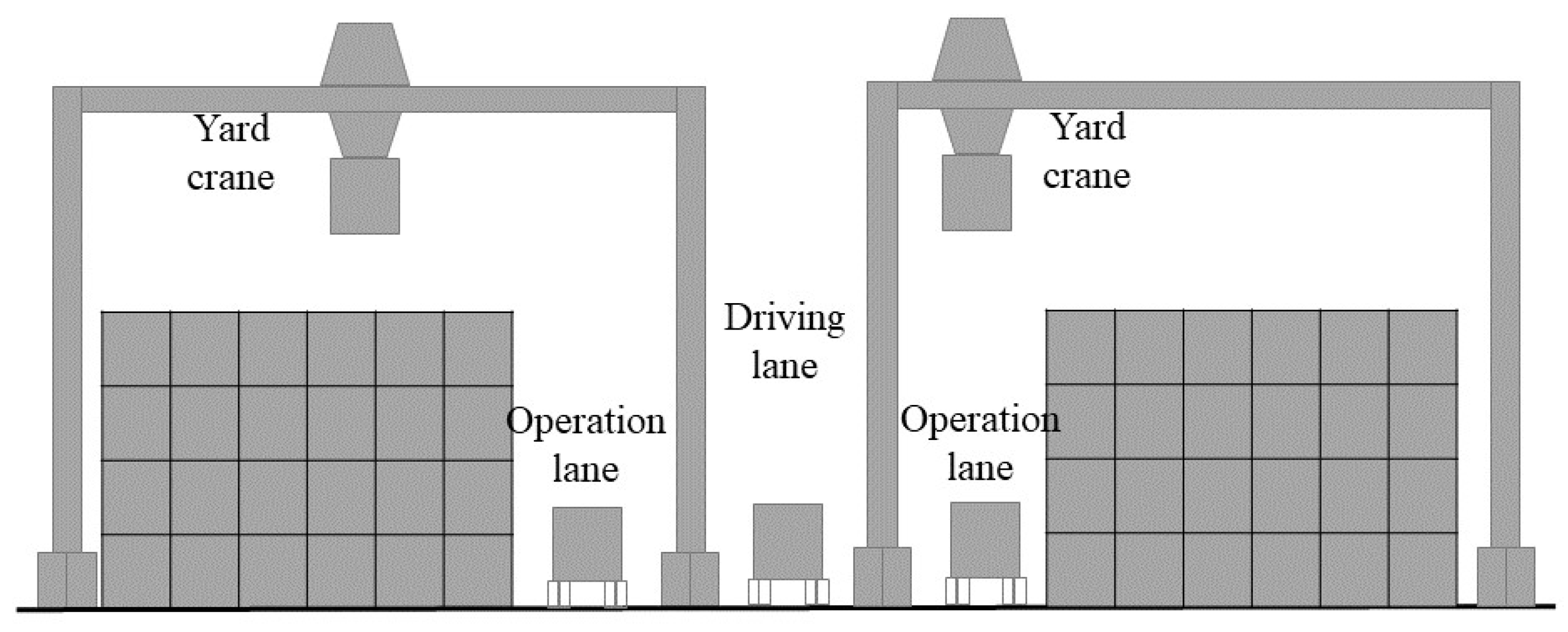
4.2. Estimated Size of Operational Area
4.3. Estimated Number of Container Turnovers
4.4. Estimated Container Throughputs
4.5. Total System Cost
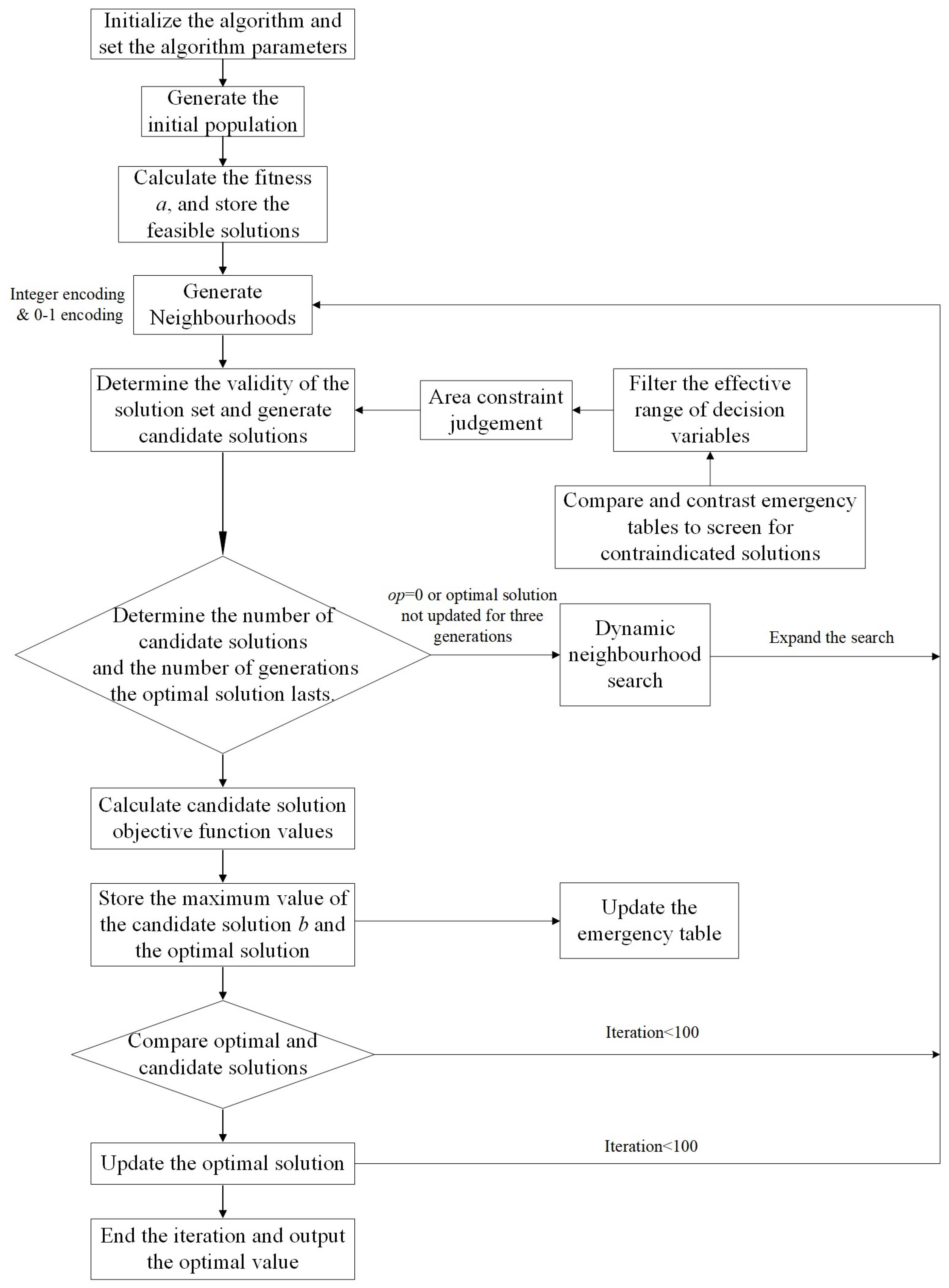
5. Algorithm and Experiments
5.1. Improved Tabu Search Algorithm
- (1)
- Tabu table: The tabu table records the local optimal point that has been reached. The tabu point will no longer be selected in the next search to prevent the search from looping. The main factors of the tabu table include tabu object, tabu length, and amnesty criterion. The tabu length is the number of times the object in the table stops participating in the search. The amnesty criterion is the appropriate relaxation of the tabu object. When the object in the tabu table meets certain conditions, it can jump out of the tabu table in advance. Too small a step length will reduce the algorithm’s ability to jump out of the local optimal point. We set the tabu length to 200. It increases once for each feasible solution. The tabu is lifted after the tabu step length reaches 200 times. The amnesty criterion sets that when the solution obtained by the object in the tabu table is better than the current neighborhood solution and the tabu step length exceeds 100 times, the tabu can be ended.
- (2)
- Coding: A candidate solution is defined as an array . The variables are integers as those defined in the theoretical model, which defines the size of each container block. , , , are 0–1 codes regarding the use of single-lane layout, double-lane layout, container block vertical to the underground logistics handling point, and that parallel to the handling point.
- (3)
- Improved dynamic neighborhood search: The neighborhood size in this algorithm represents the searchability of the tabu algorithm. The larger the neighborhood range, the longer the search time and the greater the probability of reaching the optimal solution. Randomly generate an initial solution , and define its neighborhood as , where is the random step size, and is the search direction. The initial search radius , that is, the neighborhood size is a 5 × 5 × 5 matrix. When the best solution remains unchanged for three generations or the candidate solutions are all in the tabu table, the search radius is expanded to equal to + current generation ⁄ 2 to improve the algorithm’s performance.
- (4)
- Evaluation function: Select the objective function as the evaluation function, namely , which indicates to maximize the estimated system throughput and minimize the total system cost.
- (5)
- Candidate solution selection: According to the generated neighborhood, the feasible solution is checked. If the candidate solution is not in the tabu table, the evaluation value of the candidate solution is calculated, and the candidate solution set is recorded. Otherwise, it is determined whether the amnesty criterion is triggered.
5.2. Instance Description and Parameters
5.3. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Description |
|---|---|
| The vertical and horizontal lengths of the container yard, respectively (meter). | |
| The average number of containers stacked (TEU). | |
| The average daily container capacity of the container operation area (TEU/day). | |
| The estimated transportation distance of the container truck in the vertical and horizontal directions, respectively (meter). | |
| The effective length of underground logistics loading and unloading lines (meter). | |
| The number of rows and columns of the container area, respectively. | |
| The number of containers issued, arriving, and empty containers, respectively. | |
| The number of on-dock container trucks. | |
| The number of gantry cranes at the handling points of the underground logistics. | |
| The annual cargo arrival and departure volume of underground logistics (ton). | |
| The annual shipment and arrival of cargoes in the container operation area, respectively (ton). | |
| The number of container area berths. | |
| The container operation area (square meter). | |
| The number of stacking layers in the container area. | |
| The container stacking height (meter). | |
| The total system cost (RMB). | |
| The container transportation costs, handling costs and yard space occupation costs, respectively (RMB). | |
| The estimated system throughput (TEU/year). | |
| The lane pattern of the yard. | |
| The loading and unloading crossings for lanes. | |
| The freight arrival and departure fluctuation factor. | |
| The container auxiliary area coefficient. | |
| The average system delay time (second) . | |
| The container yard capacity parameters. | |
| The system network homeostasis. | |
| The weight s of the container transportation costs, handling costs and yard space occupation costs, respectively. | |
| The daily pickup and delivery times of underground logistics. | |
| The spreader cost per second (RMB). | |
| The cost per second (RMB). | |
| The expression for the predicted transportation distance of the container truck in the yard (meter). | |
| The estimated transportation distance for underground logistics side container truck (meter). | |
| The estimated transportation distance of the underground logistics side container truck (meter). | |
| The horizontal estimated driving distance of the container truck (meter). | |
| The estimated transportation distance of the gate side container truck (meter). | |
| The predicted transportation distance of the container truck on the gate side (meter). | |
| The estimated transportation distance of the gate side container truck (meter). | |
| The predicted travel distance of the container truck from the gate to the yard (meter). | |
| The off-site handling distance (meter). | |
| The width of container area (meter). | |
| The bottom area of a single container (square meter). | |
| The horizontal aisle width (meter). | |
| The average Length of Underground Logistics Fleet (meter). | |
| The actual usable stacking area for containers. | |
| The average net container weight (ton). | |
| The average net weight of transportation trucks (ton). | |
| The time required for the transportation of a container truck to complete a cycle (second). | |
| The spreader handling time per trip (second). | |
| The truck travel time per meter (second). | |
| The detention time of the export container, imported container and empty container, respectively (second). | |
| The vertical aisle width (meter). | |
| The length of container area (meter). |
References
- Liu, W.; Yang, Y.; Luo, Q.; Zeng, X.; Chen, C.; Zhu, J.; Lin, W.; Chen, H.; Huo, W.; He, M.; et al. Study on the Contribution of Seaport to Urban Economy: An Empirical and Quantitative Analysis of Xiamen Port. J. Mar. Sci. Eng. 2022, 10, 1753. [Google Scholar] [CrossRef]
- Li, H.; Jiang, L.; Liu, J.; Su, D. Research on the Evaluation of Logistics Efficiency in Chinese Coastal Ports Based on the Four-Stage DEA Model. J. Mar. Sci. Eng. 2022, 10, 1147. [Google Scholar] [CrossRef]
- Liu, A.; Wei, Y.; Yu, B.; Song, W. Estimation of Cargo Handling Capacity of Coastal Ports in China Based on Panel Model and DMSP-OLS Nighttime Light Data. Remote Sens. 2019, 11, 582. [Google Scholar] [CrossRef]
- Ducruet, C.; Cuyala, S.; El Hosni, A. Maritime networks as systems of cities: The long-term interdependencies between global shipping flows and urban development (1890–2010). J. Transp. Geogr. 2018, 66, 340–355. [Google Scholar] [CrossRef]
- Rodrigue, J.P. The Geography of Transport Systems; Routledge: London, UK, 2020. [Google Scholar]
- Chen, J.; Fei, Y.; Zhu, Y.; Zhang, F. Allometric relationship between port throughput growth and urban population: A case study of Shanghai port and Shanghai city. Adv. Mech. Eng. 2018, 10, 1687814018760933. [Google Scholar] [CrossRef]
- Ren, M.; Fan, Z.; Wu, J.; Zhou, L.; Du, Z. Design and optimization of underground logistics transportation networks. IEEE Access 2019, 7, 83384–83395. [Google Scholar] [CrossRef]
- Guo, D.; Chen, Y.; Yang, J.; Tan, Y.; Zhang, C.; Chen, Z. Planning and application of underground logistics systems in new cities and districts in China. Tunn. Undergr. Space Technol. 2021, 113, 103947. [Google Scholar] [CrossRef]
- Hai, D.; Xu, J.; Duan, Z.; Chen, C. Effects of underground logistics system on urban freight traffic: A case study in Shanghai, China. J. Clean. Prod. 2020, 260, 121019. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, D.; Chen, Z.; Fan, Y.; Li, X. Using a multi-objective programming model to validate feasibility of an underground freight transportation system for the Yangshan port in Shanghai. Tunn. Undergr. Space Technol. 2018, 81, 463–471. [Google Scholar] [CrossRef]
- Liang, C.; Hu, X.; Shi, L.; Fu, H.; Xu, D. Joint dispatch of shipment equipment considering underground container logistics. Comput. Ind. Eng. 2022, 165, 107874. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Xu, N. Multi-period planning of integrated underground logistics system network for automated construction-demolition-municipal waste collection and parcel delivery: A case study. J. Clean. Prod. 2022, 330, 129760. [Google Scholar] [CrossRef]
- Abbas, F. Intelligent Container Stacking System at Seaport Container Terminal. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2016. [Google Scholar]
- Aulin, V.; Hrynkiv, A.; Lyashuk, O.; Vovk, Y.; Lysenko, S.; Holub, D.; Zamota, T.; Pankov, A.; Sokol, M.; Ratynskyi, V.; et al. Increasing the Functioning Efficiency of the Working Warehouse of the “UVK Ukraine” Company Transport and Logistics Center. Commun.-Sci. Lett. Univ. Zilina 2020, 22, 3–14. [Google Scholar] [CrossRef]
- Pielage, B.; Rijsenbrij, J. Developments in underground freight transportation. In The Future of Automated Freight Transport: Concepts, Design and Implementation; Edward Elgar Publishing: Cheltenham, UK, 2005; pp. 65–84. [Google Scholar]
- Böhm, M.; Del Rey, A.F.; Pagenkopf, J.; Varela, M.; Ploster, S.; Calderón, B. Review and comparison of worldwide hydrogen activities in the rail sector with special focus on on-board storage and refueling technologies. Int. J. Hydrogen Energy 2022, 47, 38003–38017. [Google Scholar] [CrossRef]
- Visser JG, S.N. The development of underground freight transport: An overview. Tunn. Undergr. Space Technol. 2018, 80, 123–127. [Google Scholar] [CrossRef]
- Gong, D.; Tian, J.; Hu, W.; Dong, J.; Chen, Y.; Ren, R.; Chen, Z. Sustainable Design and Operations Management of Metro-Based Underground Logistics Systems: A Thematic Literature Review. Buildings 2023, 13, 1888. [Google Scholar] [CrossRef]
- Vernimmen, B.; Dullaert, W.; Geens, E.; Notteboom T’Jollyn, B.; Gilsen, W.; Winkelmans, W. Underground logistics systems: A way to cope with growing internal container traffic in the port of Antwerp? Transp. Plan. Technol. 2007, 30, 391–416. [Google Scholar] [CrossRef]
- Fan, Y.; Liang, C.; Hu, X.; Li, Y. Planning connections between underground logistics system and container ports. Comput. Ind. Eng. 2020, 139, 106199. [Google Scholar] [CrossRef]
- Rezaeifar, F.; Najafi, M.; Kaushal, V.; Huff, B. Development of a Model to Optimize the Operations of an Intermodal Underground Logistics Transportation. J. Pipeline Syst. Eng. Pract. 2022, 13, 04022039. [Google Scholar] [CrossRef]
- Pan, Y.; Liang, C.; Dong, L. A two-stage model for an urban underground container transportation plan prob-lem. Comput. Ind. Eng. 2019, 138, 106113. [Google Scholar] [CrossRef]
- Gao, Y.; Chang, D.; Yuan, J.; Liang, C. Scheduling of yard truck considering loading and unloading simultaneously in an under-ground container logistics system. Transp. Res. Rec. 2023, 2677, 246–263. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, Y.M.; Jin, M.J. An optimal layout of container yards. Or Spectr. 2008, 30, 675–695. [Google Scholar] [CrossRef]
- Abu Aisha, T.; Ouhimmou, M.; Paquet, M. Optimization of container terminal layouts in the seaport—Case of port of Montre-al. Sustainability 2020, 12, 1165. [Google Scholar] [CrossRef]
- Taner, M.E.; Kulak, O.; Koyuncuoğlu, M.U. Layout analysis affecting strategic decisions in artificial container terminals. Comput. Ind. Eng. 2014, 75, 1–12. [Google Scholar] [CrossRef]
- Wiese, J.; Suhl, L.; Kliewer, N. Mathematical models and solution methods for optimal container terminal yard layouts. Or Spectr. 2010, 32, 427–452. [Google Scholar] [CrossRef]
- Petering, M.E.H. Effect of block width and storage yard layout on marine container terminal performance. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 591–610. [Google Scholar] [CrossRef]
- Woo, Y.J.; Kim, K.H. Estimating the space requirement for outbound container inventories in port container terminals. Int. J. Prod. Econ. 2011, 133, 293–301. [Google Scholar] [CrossRef]
- Lee, B.K.; Lee, L.H.; Chew, E.P. Analysis on container port capacity: A Markovian modeling approach. OR Spectr. 2014, 36, 425–454. [Google Scholar] [CrossRef]
- Stojaković, M.; Twrdy, E. Efficiency Evaluation of a Small Container Terminal with Perpendicular Yard Layout Using Shuttle Carriers. J. Mar. Sci. Eng. 2023, 11, 449. [Google Scholar] [CrossRef]
- Lee, B.K.; Kim, K.H. Optimizing the yard layout in container terminals. OR Spectr. 2013, 35, 363–398. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]


| Title 1 Research Content | Reference |
|---|---|
| System design of underground container logistics systems | [19] Vernimmen et al. (2007), [20] Fan et al. (2020) |
| System operations of underground container logistics systems | [10] Chen et al.(2018), [22] Pan et al. (2019) [21] Rezaeifar et al.(2022), [11] Liang et al. (2019) [23] Gao et al. (2023) |
| Container block planning | [24] Kim et al. (2008), [28] Petering et al. (2009) [27] Wiese et al. (2010), [26] Taner et al. (2014) [25] Abu Aisha et al. (2020) |
| Resource allocation of container yard | [29] Woo et al. (2011), [32] Lee et al. (2013) [30] Lee et al. (2014), [31] Stojaković et al. (2023) |
| Yard Design | Consider Throughput and Operating Costs | Consider Only Total Costs | Consider Only Throughput |
|---|---|---|---|
| Number of columns | 6 | 8 | 3 |
| Number of rows | 6 | 4 | 9 |
| Layout direction | Vertical to the loading port | Vertical to the loading port | Parallel to the loading port |
| Lane configuration | Single-lane layout | Single-lane layout | Dual-lane layout |
| Effective length of loading/unloading line (meter) | 205 | 205 | 205 |
| Vertical length of yard (meter) | 197 | 249 | 128 |
| Horizontal length of yard (meter) | 487 | 333 | 641 |
| Single operation cost (RMB/task) | 1242.55 | 1228.80 | 1878.50 |
| Estimated system throughput (10,000 TEU/year) | 1073.95 | 1072.08 | 1086.05 |
| Overall road network density (km/sq.km) | 19.8 | 18.8 | 30.5 |
| Cost Coefficients | 0.2 | 0.4 | 0.6 | 0.8 |
|---|---|---|---|---|
| Number of columns | 10 | 6 | 10 | 6 |
| Number of rows | 3 | 6 | 3 | 4 |
| Maximum Stacking Height | 4 | 3 | 4 | 5 |
| Layout direction | Vertical to the loading port | Vertical to the loading port | Vertical to the loading port | Vertical to the loading port |
| Lane configuration | Dual-lane layout | Single-lane layout | Single-lane layout | Single-lane layout |
| Footprint of the yard (Square meter) | 97,792 | 95,939 | 77,312 | 65,601 |
| Operating cost (RMB/task) | 122.96 | 124.26 | 123.67 | 122.89 |
| Estimated system throughput (10,000 TEU/year) | 1073.9 | 1073.75 | 1072.8 | 1071.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, B.; Zhang, M.; Xu, X.; Liang, C.; Wang, Y.; Liu, H. Container Yard Layout Design Problem with an Underground Logistics System. J. Mar. Sci. Eng. 2024, 12, 1103. https://doi.org/10.3390/jmse12071103
Lu B, Zhang M, Xu X, Liang C, Wang Y, Liu H. Container Yard Layout Design Problem with an Underground Logistics System. Journal of Marine Science and Engineering. 2024; 12(7):1103. https://doi.org/10.3390/jmse12071103
Chicago/Turabian StyleLu, Bin, Mengxia Zhang, Xiaojie Xu, Chengji Liang, Yu Wang, and Hongchen Liu. 2024. "Container Yard Layout Design Problem with an Underground Logistics System" Journal of Marine Science and Engineering 12, no. 7: 1103. https://doi.org/10.3390/jmse12071103
APA StyleLu, B., Zhang, M., Xu, X., Liang, C., Wang, Y., & Liu, H. (2024). Container Yard Layout Design Problem with an Underground Logistics System. Journal of Marine Science and Engineering, 12(7), 1103. https://doi.org/10.3390/jmse12071103






