Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units
Abstract
:1. Introduction
2. Research Methods
2.1. Numerical Simulation
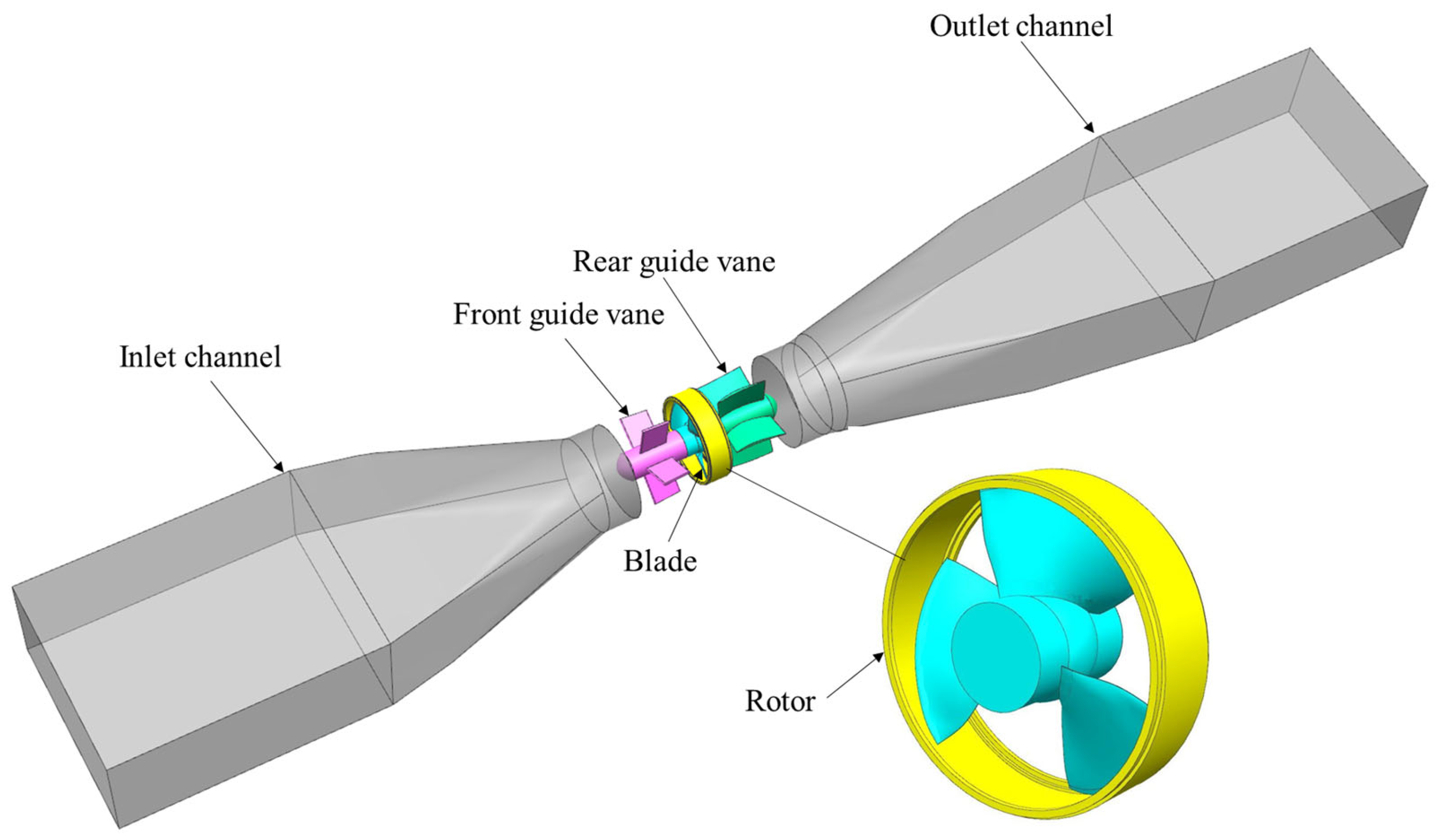
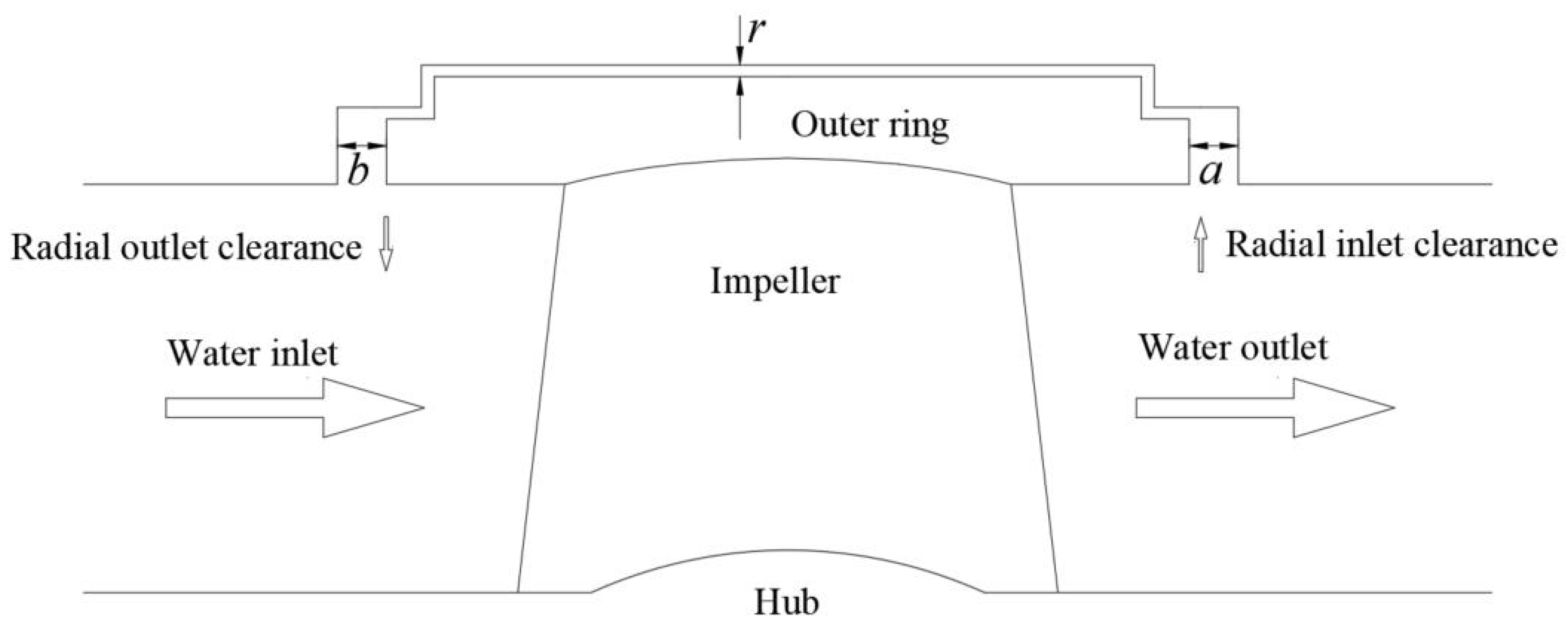
2.1.1. Calculation Area
2.1.2. Turbulence Model
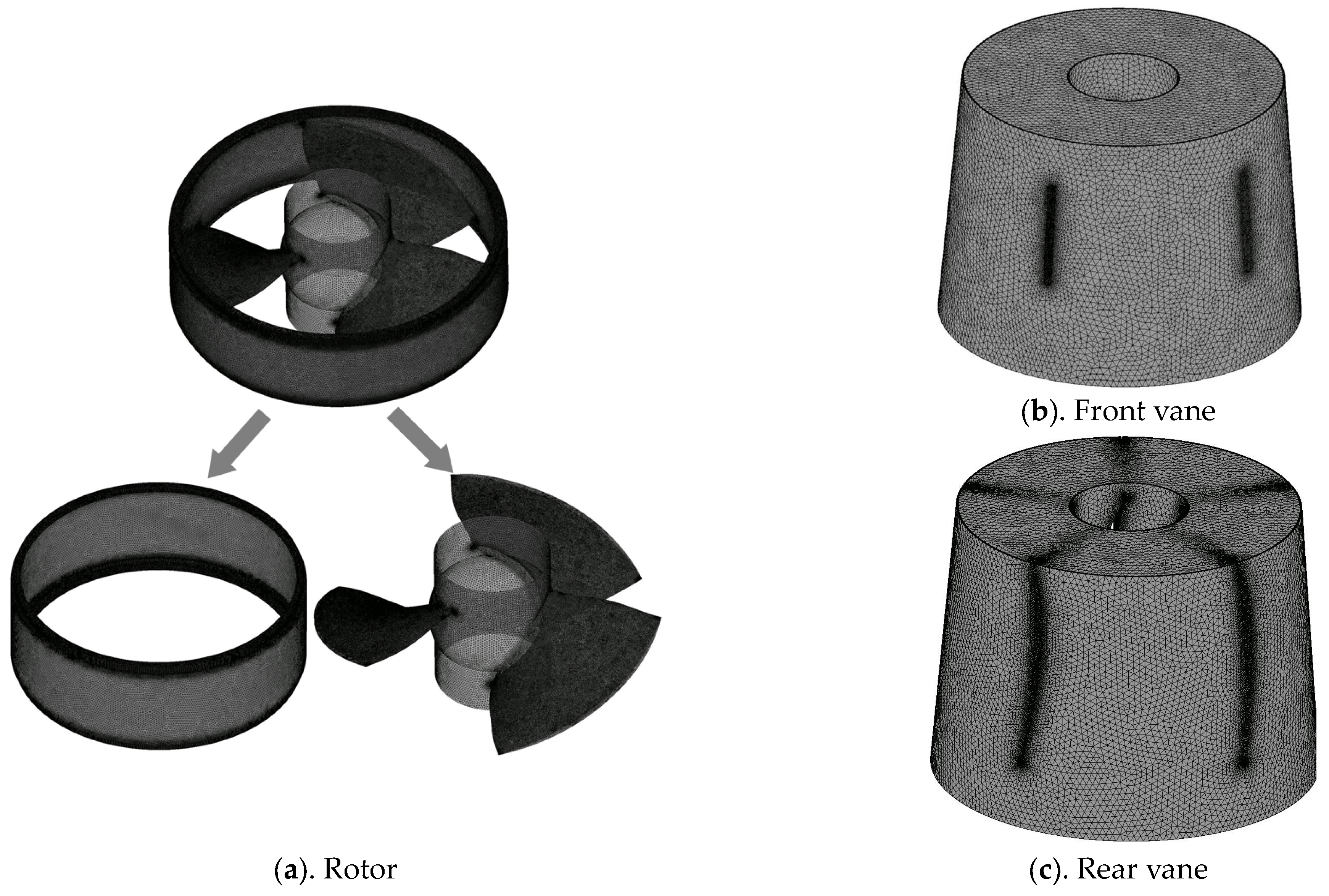
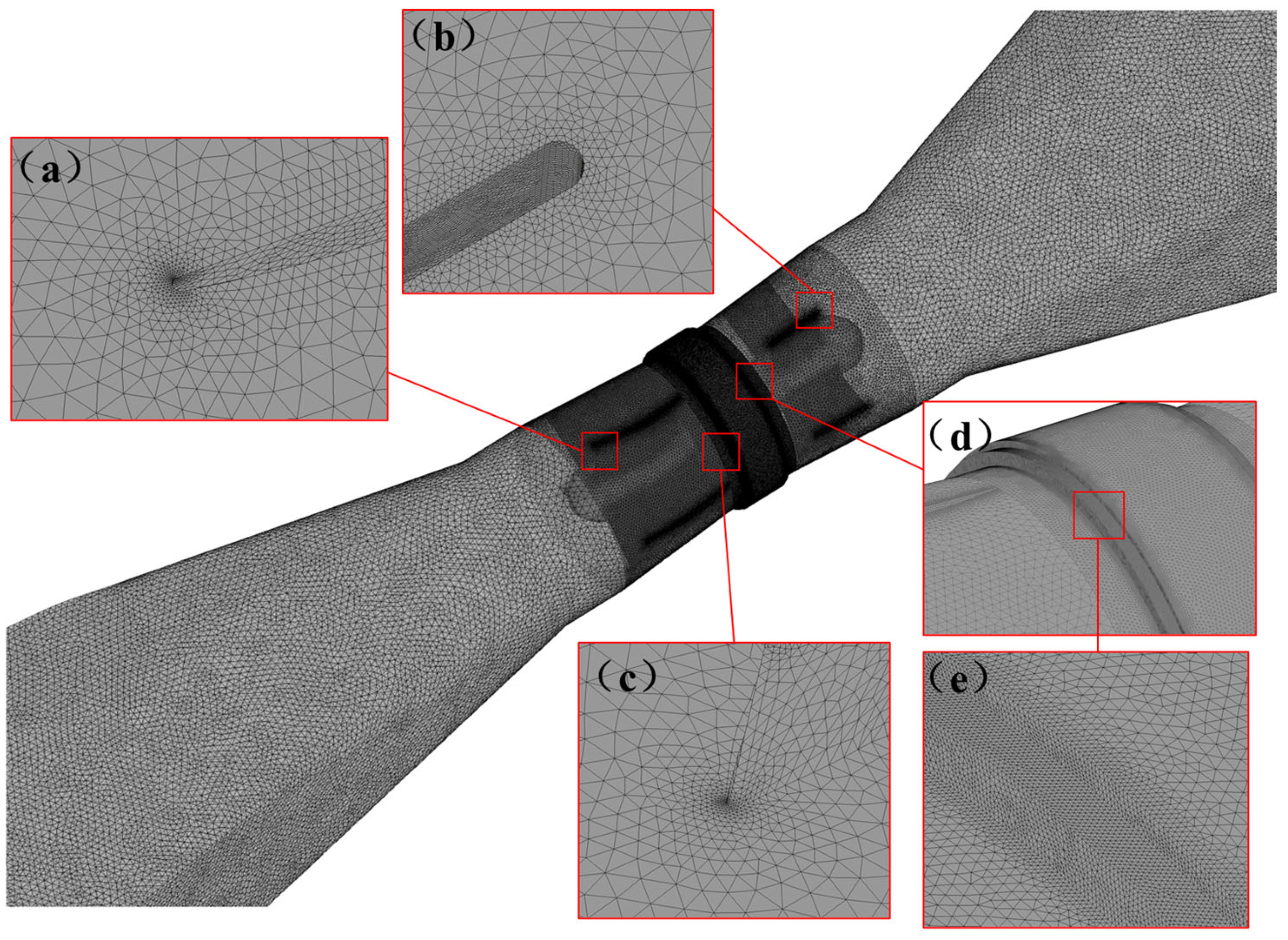
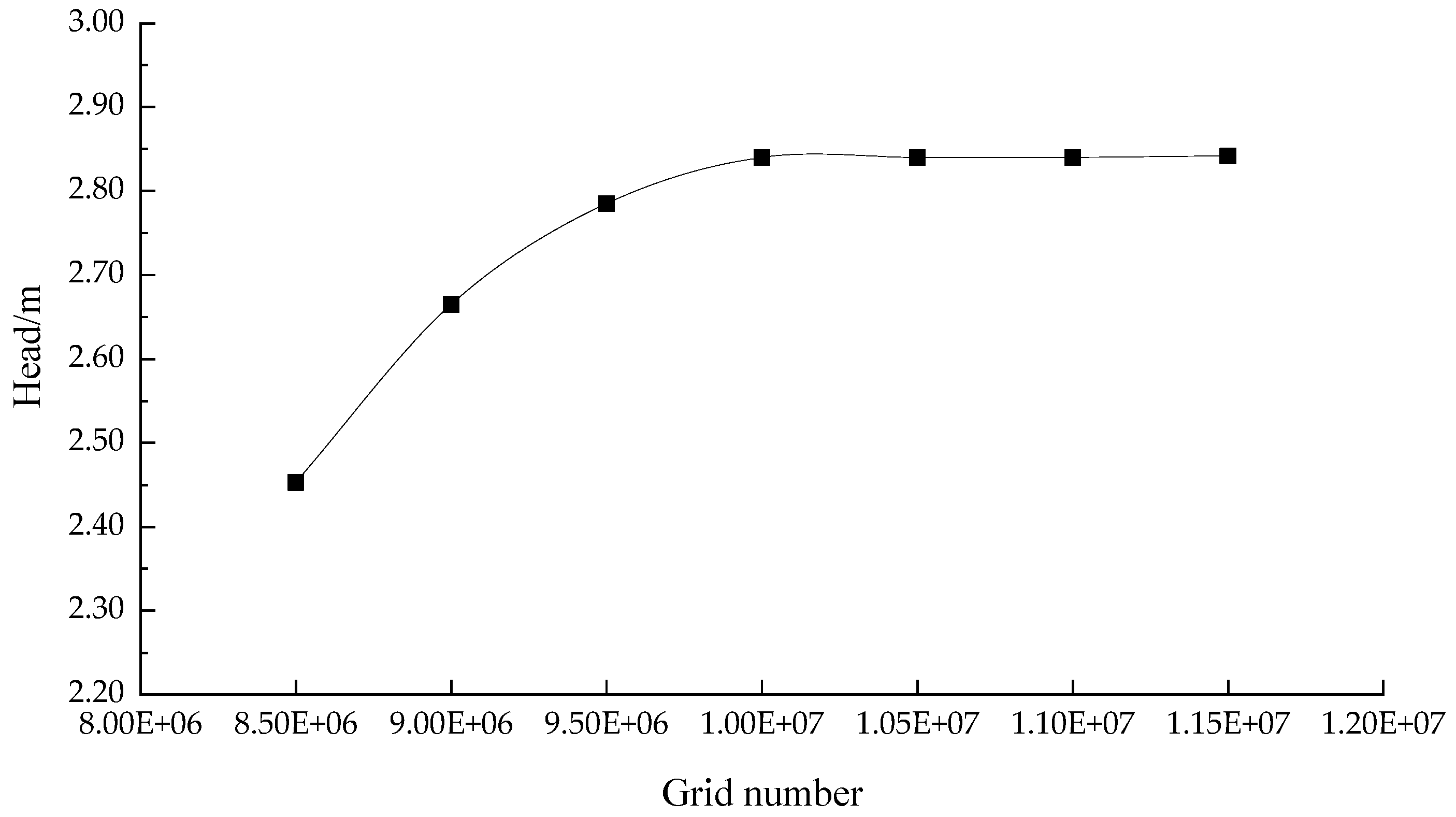
2.1.3. Grid Division
2.1.4. Boundary Condition
2.2. Physical Model Test
2.3. Multi-Objective Optimization Based on Information Weight Method
2.3.1. Selection of Research Parameters
2.3.2. Calculation Method of Evaluation Index
2.3.3. Multi-Objective Optimization Based on Information Weight Method
2.3.4. Sensitivity Analysis
3. Results and Analysis
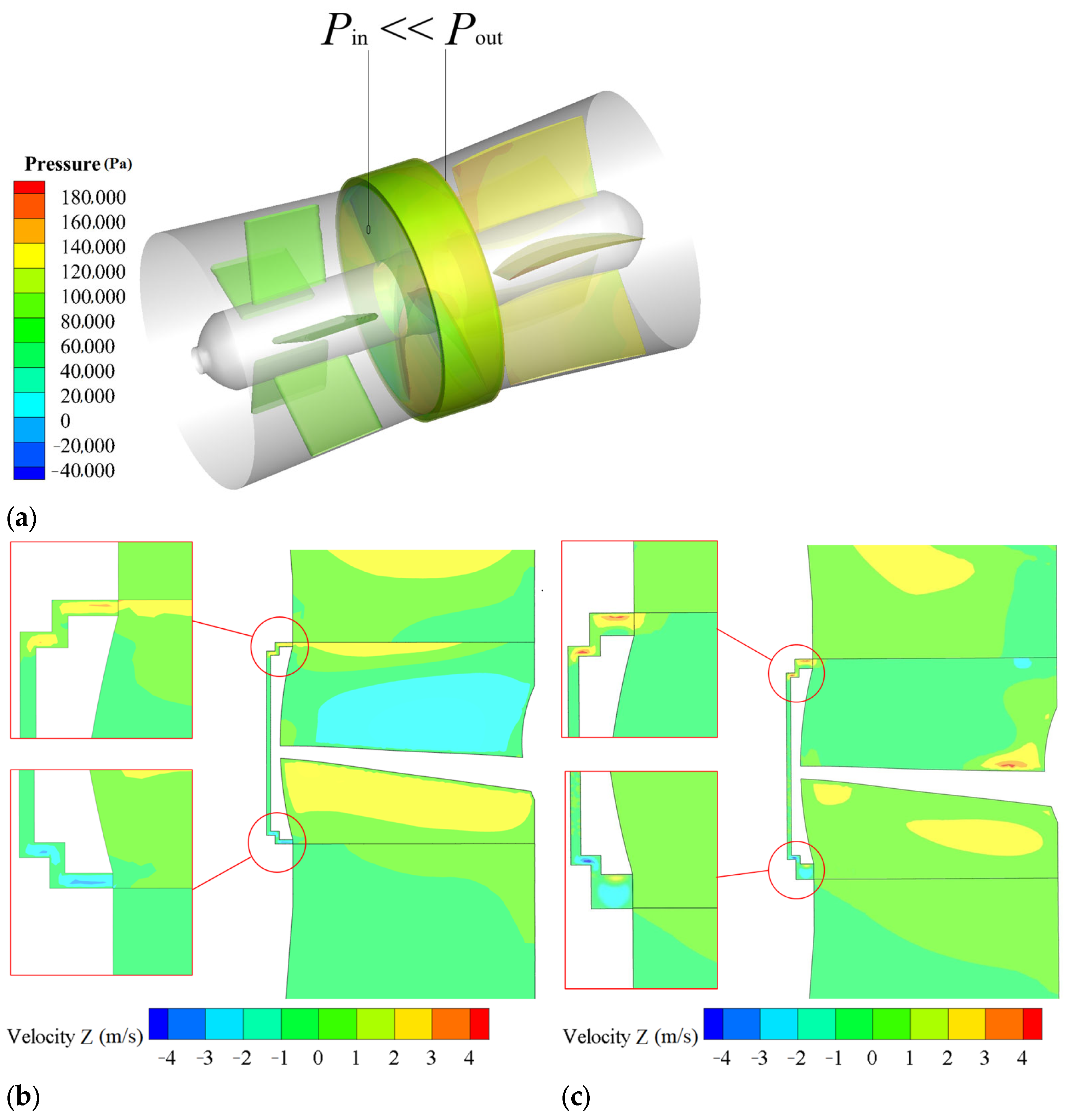
3.1. Numerical Simulation Results
3.2. Construction of Comprehensive Objective Function
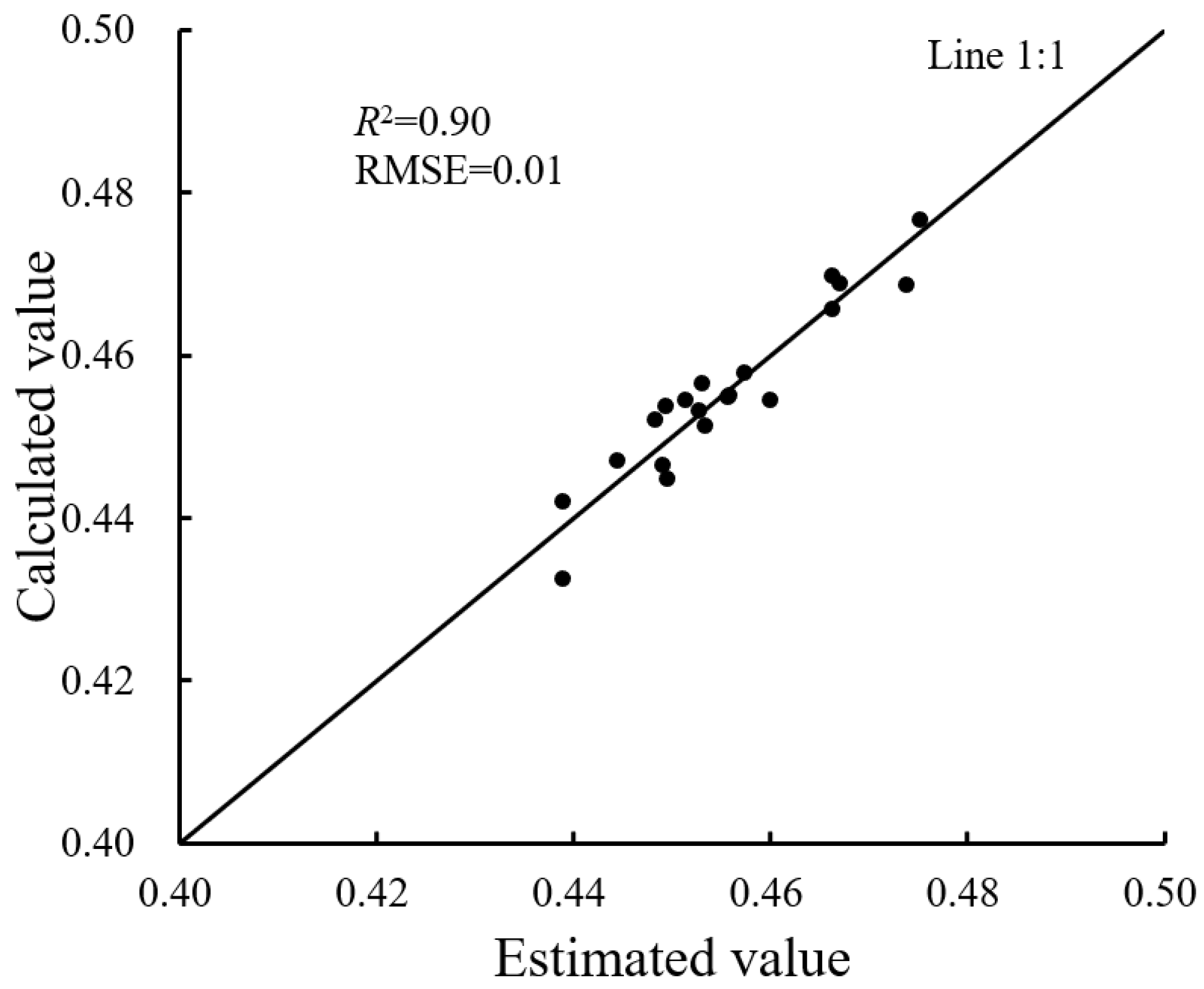
3.3. Construction of Response Surface Model Based on Comprehensive Objective Function
3.4. Sensitivity Analysis of Radial Clearance Parameters between Stator and Rotor
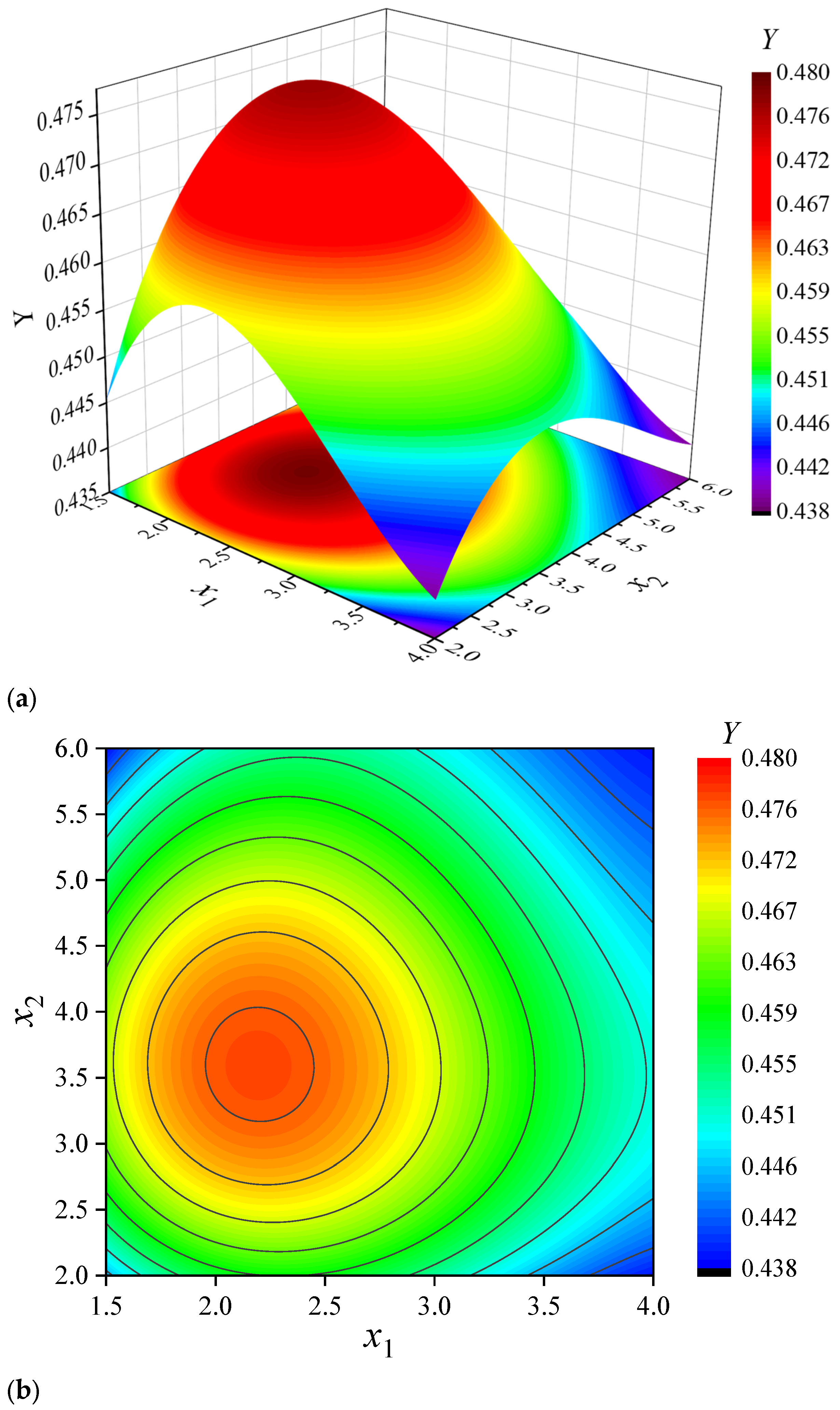
3.5. Analysis of the Influence of Radial Clearance Parameters between Stator and Rotor on Comprehensive Objective Function Based on Response Surface Model
3.6. Optimization of Radial Clearance Parameters between Stator and Rotor
4. Scheme Verification
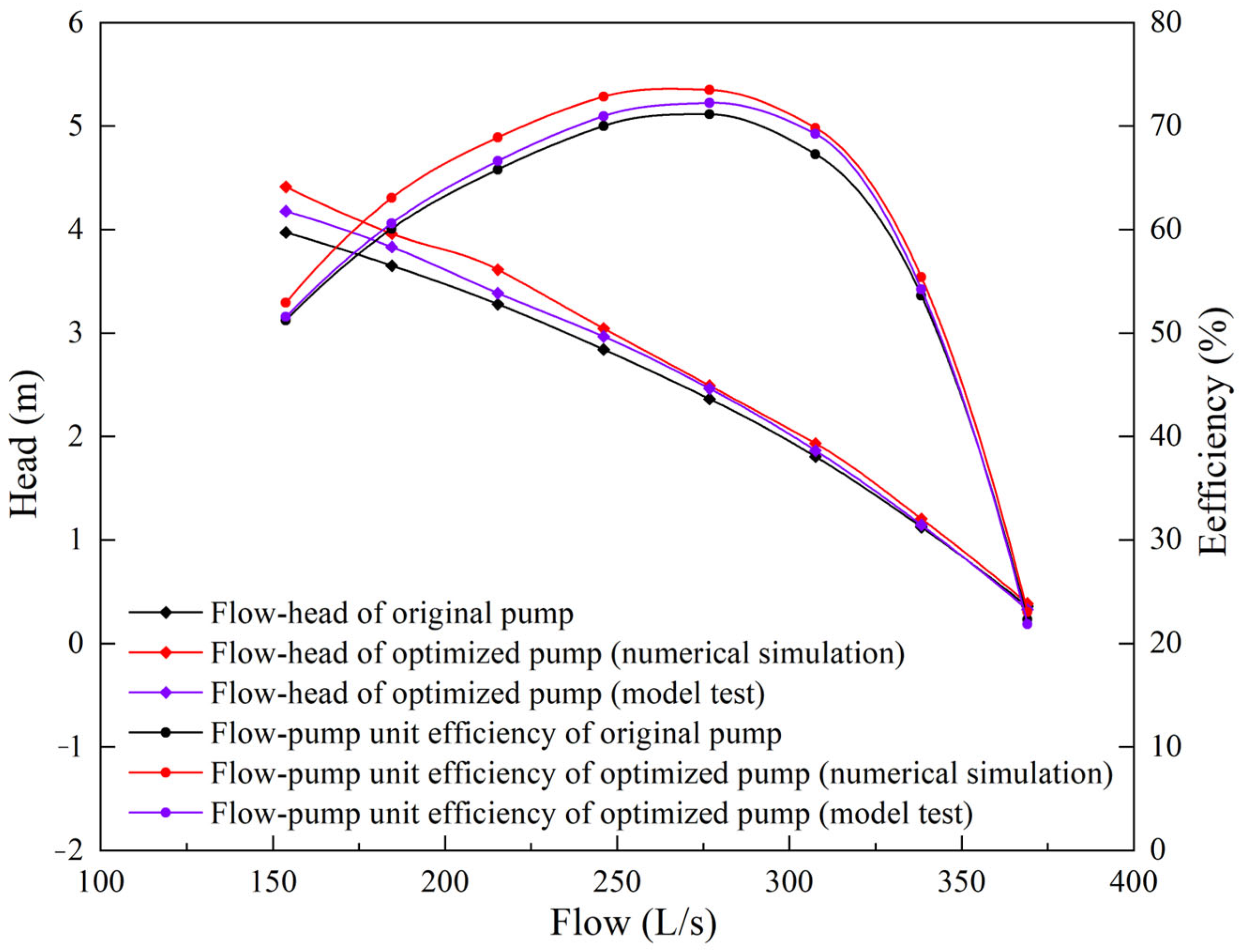
4.1. Operation Performance of Pump Device
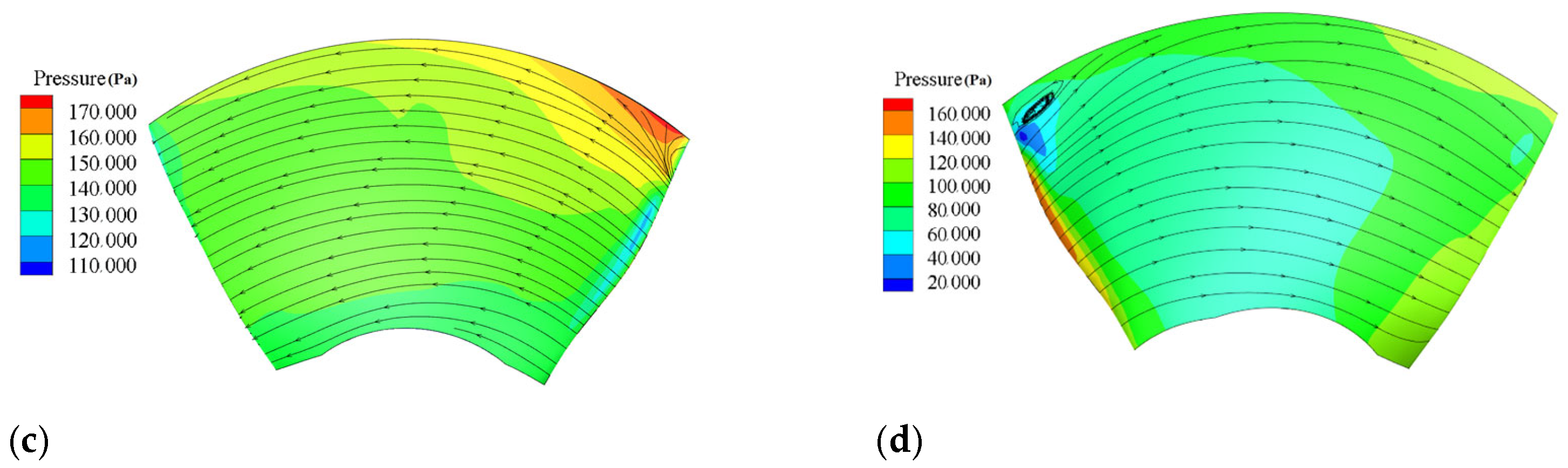
4.2. Internal Flow Characteristics of Pump Unit
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buono, D.; Frosina, E.; Mazzone, A.; Cesaro, U.; Senatore, A. Study of a pump as turbine for a hydraulic urban network using a tridimensional CFD modeling methodology. Energy Procedia 2015, 82, 201–208. [Google Scholar] [CrossRef]
- Rossi, M.; Comodi, G.; Piacente, N.; Renzi, M. Effects of viscosity on the performance of Hydraulic Power Recovery Turbines (HPRTs) by the means of Computational Fluid Dynamics (CFD) simulations. Energy Procedia 2018, 148, 170–177. [Google Scholar] [CrossRef]
- Shirazi, A.; Nazari, M.; Manshadi, M. Numerical and experimental investigation of the fluid flow on a full-scale pump jet thruster. Ocean Eng. 2019, 182, 527–539. [Google Scholar] [CrossRef]
- Jiao, H.; Shan, J.; Yang, G.; Wang, M.; Chen, S. Comparison of the Shutdown Transitions of the Full-Flow Pump and Axial-Flow Pump. J. Mar. Sci. Eng. 2023, 11, 2129. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, W.; Jiao, H.; Tang, F.; Wang, L.; Sun, D.; Shi, W. Numerical simulation and experimental study on the comparison of the hydraulic characteristics of an axial-flow pump and a full tubular pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Shi, L.; Jiang, Y.; Cai, Y.; Chen, B.; Tang, F.; Xu, T.; Zhu, J.; Chai, Y. Influence of inlet groove on flow characteristics in stall condition of full-tubular pump. Front. Energy Res. 2022, 10, 949639. [Google Scholar] [CrossRef]
- Sekar, K.; Kumar, N.; Vasanthakumar, P. Centrifugal pump as turbine for micro-hydro power scheme in rural areas of India: A review. Int. J. Chem. Tech. Res. 2017, 10, 106–109. [Google Scholar]
- Wang, C.; Zhao, C.; Zhang, T.; Liu, D. The numerical simulation of full flow field of Roto-Jet pump and analysis of energy losses. Adv. Mater. Res. 2012, 562, 1369–1372. [Google Scholar]
- Shi, L.; Zhu, J.; Wang, L.; Chu, S.; Tang, F. Comparative analysis of strength and modal characteristics of a full tubular pump and an axial flow pump impellers based on fluid-structure interaction. Energies 2021, 14, 6395. [Google Scholar] [CrossRef]
- Meng, F.; Li, Y.; Pei, J. Energy characteristics of full tubular pump unit with different backflow clearances based on entropy production. Appl. Sci. 2021, 11, 3376. [Google Scholar] [CrossRef]
- Shi, L.; Yuan, Y.; Jiao, H.; Tang, F.; Cheng, L.; Yang, F.; Zhu, J. Numerical investigation and experiment on pressure pulsation characteristics in a full tubular pump. Renew. Energy 2021, 163, 987–1000. [Google Scholar] [CrossRef]
- Xu, X. Research and Optimization Design of Maxwell Based Full Throughflow Pump Motor Characteristics. Master’s Thesis, Yangzhou University, Yangzhou, China, 2022. (In Chinese). [Google Scholar]
- Shi, L.; Zhu, J.; Li, J.; Tang, F.; Chen, B.; Jiang, Y.; Xu, T.; Chai, Y. Flow characteristics and optimization design of the stator–rotor cavity of the full tubular pump. Processes 2022, 10, 1688. [Google Scholar] [CrossRef]
- Xu, B.; Liu, J.; Lu, W.; Xu, L.; Xu, R. Design and Optimization of γ-Shaped Settlement Training Wall Based on Numerical Simulation and CCD-Response Surface Method. Processes 2022, 10, 1201. [Google Scholar] [CrossRef]
- Brunelli, C.; Castellani, F.; Garinei, A.; Biondi, L.; Marconi, M. A procedure to perform multi-objective optimization for sustainable design of buildings. Energies 2016, 9, 915. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Z.; Lei, X.; Li, X.; Liu, S.; Liu, Y. Correlation development and parametric investigation for thermal–hydraulic characteristics of flying-wing fin. Appl. Therm. Eng. 2023, 219, 119445. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; MacVicar, B.; Ghodsian, M. Evaluation of flow characteristics in labyrinth weirs using response surface methodology. Flow Meas. Instrum. 2019, 69, 101617. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, X.; Gao, Z.; Ju, W.; Yan, G. Research on cooperative optimization of multiphase pump impeller and diffuser based on adaptive refined response surface method. Adv. Mech. Eng. 2022, 14, 16878140211072944. [Google Scholar]
- El-Hadj, A.; Abd-Rahim, S. Optimization of an external gear pump using response surface method. J. Mech. 2020, 36, 567–575. [Google Scholar] [CrossRef]
- Velásquez, L.; Posada, A.; Chica, E. Optimization of the basin and inlet channel of a gravitational water vortex hydraulic turbine using the response surface methodology. Renew. Energy 2022, 187, 508–521. [Google Scholar] [CrossRef]
- Capurso, T.; Bergamini, L.; Camporeale, S.; Fortunato, B.; Torresi, M. CFD analysis of the performance of a novel impeller for a double suction centrifugal pump working as a turbine. In Proceedings of the 13th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar]
- Zong, Z.; Rui, W.; Lu, L.; Huang, X. Experimental investigation of broadband thrust and loading noise from pump jet due to turbulence ingestion. Ocean Eng. 2022, 255, 111408. [Google Scholar]
- Shahabi, M.; Ahadiyan, J.; Ghomeshi, M.; Narimousa, M.; Katopodis, C.; Nadian, H. Numerical study of the effect of a V-shaped weir on turbulence characteristics and velocity in V-weir fishways. River Res. Appl. 2023, 39, 21–34. [Google Scholar] [CrossRef]
- Mavrakos, A.; Konispoliatis, D.; Ntouras, D.; Papadakis, G.; Mavrakos, S. Hydrodynamic coefficients in heave of a moonpool-type floater using theoretical, numerical and CFD methodologies. Ocean Eng. 2023, 279, 114519. [Google Scholar] [CrossRef]
- Khanarmuei, M.; Rahimzadeh, H.; Sarkardeh, H. Effect of dual intake direction on critical submergence and vortex strength. J. Hydraul. Res. 2019, 57, 272–279. [Google Scholar] [CrossRef]
- Lv, Y.; Li, S.; Wang, Z.; Zhou, L. Study on pump mode cavitation characteristic of variable speed pump turbine. Phys. Fluids 2023, 35, 065111. [Google Scholar]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; Ramos, H. Velocities in a centrifugal PAT operation: Experiments and CFD analyses. Fluids 2017, 3, 3. [Google Scholar] [CrossRef]
- Jiao, H. Research on Hydraulic Performance and Throttling Radial Gap Size of Full Throughflow Pump. Master’s Thesis, Yangzhou University, Yangzhou, China, 2020. (In Chinese). [Google Scholar]
- Shibata, M.; Kawashima, T.; Yamashita, M.; Kawato, S. Theoretical analysis of a high efficiency blue-laser-diode-pumped Ti: Sapphire laser by high intensity pumping. Laser Phys. Lett. 2021, 18, 105001. [Google Scholar] [CrossRef]
- Hu, C.; Lang, J.; Xie, Y. Pumping performance analysis of negative ion based neutral beam injector cryosorption pump prototype. Fusion Eng. Des. 2023, 189, 113469. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, P.; Pu, Y.; Lei, H.; Zheng, X. Unit Operation Combination and Flow Distribution Scheme of Water Pump Station System Based on Genetic Algorithm. Appl. Sci. 2023, 13, 11869. [Google Scholar] [CrossRef]
- Chang, L.; Xu, Q.; Yang, C.; Su, X.; Dai, X.; Guo, L. Experimental Study on Gas–Liquid Performance and Prediction of Shaft Power and Efficiency by Dimensionless Coefficients in a Multistage Electrical Submersible Pump. J. Fluids Eng. 2023, 145, 071204. [Google Scholar] [CrossRef]
- Li, Z.; Yang, J. Filtering Feature Selection Algorithm Based on Entropy Weight Method. J. Northeast. Univ. (Nat. Sci.) 2022, 43, 921–929. [Google Scholar]
- Husnain, T.; Duan, H.; Mark, O. Global sensitivity analysis of bioretention cell design for stormwater system: A comparison of VARS framework and Sobol method. J. Hydrol. 2023, 617, 128895. [Google Scholar]
- Cao, X.; Feng, D. A direct analytical derivation of the multi-dimensional fragility spaces of structures under nonstationary mainshock-multi-aftershock sequences. Probabilistic Eng. Mech. 2024, 76, 103630. [Google Scholar] [CrossRef]
- Yang, D.; Lian, J.; Zhao, X.; Hou, Q.; Chen, Y.; Zhang, Y. A mathematical model for supercooling process and its application to frazil ice evolution. Sci. Rep. 2023, 13, 5801. [Google Scholar] [CrossRef] [PubMed]
- Liu, J. Optimization Study on the Hydrodynamic Characteristics of the Clearance between the Stator and Rotor of a Full through Flow Pump Device. Master’s Thesis, Yangzhou University, Yangzhou, China, 2023. (In Chinese). [Google Scholar]
- Zoratipour, E.; Mohammadi, A.; Zoratipour, A. Evaluation of SEBS and SEBAL algorithms for estimating wheat evapotranspiration (case study: Central areas of Khuzestan province). Appl. Water Sci. 2023, 13, 137. [Google Scholar] [CrossRef]
- He, S.; Zhang, W.; Yin, T. Inexact projection contraction method and hybrid steepest descent method for inverse variational inequalities. J. Nonlinear Convex Anal. 2022, 23, 2763–2774. [Google Scholar]




| Scheme Serial Number | Design Parameters | ψ | φ | μ | λ | Y | |
|---|---|---|---|---|---|---|---|
| a | b | ||||||
| 1 | 2r | 6r | 0.15 | 0.60 | 0.93 | 0.70 | 0.454 |
| 2 | 2r | 5r | 0.15 | 0.62 | 0.95 | 0.73 | 0.466 |
| 3 | 2r | 4r | 0.16 | 0.64 | 0.96 | 0.73 | 0.477 |
| 4 | 2r | 3r | 0.15 | 0.62 | 0.96 | 0.72 | 0.469 |
| 5 | 2r | 2r | 0.15 | 0.59 | 0.94 | 0.72 | 0.458 |
| 6 | 3r | 6r | 0.14 | 0.59 | 0.92 | 0.69 | 0.445 |
| 7 | 3r | 5r | 0.15 | 0.60 | 0.93 | 0.71 | 0.455 |
| 8 | 3r | 4r | 0.16 | 0.62 | 0.95 | 0.73 | 0.469 |
| 9 | 3r | 3r | 0.16 | 0.60 | 0.95 | 0.73 | 0.470 |
| 10 | 3r | 2r | 0.15 | 0.59 | 0.94 | 0.71 | 0.457 |
| 11 | 4r | 6r | 0.14 | 0.59 | 0.92 | 0.69 | 0.442 |
| 12 | 4r | 5r | 0.14 | 0.60 | 0.92 | 0.70 | 0.447 |
| 13 | 4r | 4r | 0.14 | 0.62 | 0.92 | 0.70 | 0.454 |
| 14 | 4r | 3r | 0.14 | 0.60 | 0.92 | 0.69 | 0.446 |
| 15 | 4r | 2r | 0.13 | 0.59 | 0.91 | 0.66 | 0.432 |
| 16 | 5r | 6r | 0.14 | 0.60 | 0.93 | 0.70 | 0.453 |
| 17 | 5r | 5r | 0.14 | 0.60 | 0.93 | 0.70 | 0.451 |
| 18 | 5r | 4r | 0.15 | 0.60 | 0.93 | 0.71 | 0.455 |
| 19 | 5r | 3r | 0.15 | 0.60 | 0.92 | 0.71 | 0.455 |
| 20 | 5r | 2r | 0.15 | 0.59 | 0.93 | 0.70 | 0.452 |
| 21 | 6r | 6r | 0.08 | 0.55 | 0.91 | 0.63 | |
| 22 | 6r | 5r | 0.09 | 0.56 | 0.91 | 0.62 | |
| 23 | 6r | 4r | 0.09 | 0.56 | 0.91 | 0.60 | |
| 24 | 6r | 3r | 0.08 | 0.57 | 0.90 | 0.59 | |
| 25 | 6r | 2r | 0.08 | 0.56 | 0.91 | 0.60 | |
| Standard deviation | 0.01 | 0.01 | 0.01 | 0.02 | |||
| Coefficient of variation | 0.05 | 0.02 | 0.01 | 0.02 | |||
| Information weight | 0.47 | 0.19 | 0.13 | 0.21 | |||
| Design Parameter | First-Order Global Sensitivity Coefficient | Overall Global Sensitivity Coefficient | Coefficient Difference |
|---|---|---|---|
| Width coefficient of radial inlet clearance between stator and rotor x1 | 0.50 | 0.59 | 0.09 |
| Width coefficient of radial outlet clearance between stator and rotor x2 | 0.41 | 0.50 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xi, W.; Lu, W. Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units. J. Mar. Sci. Eng. 2024, 12, 1124. https://doi.org/10.3390/jmse12071124
Liu J, Xi W, Lu W. Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units. Journal of Marine Science and Engineering. 2024; 12(7):1124. https://doi.org/10.3390/jmse12071124
Chicago/Turabian StyleLiu, Jianfeng, Wang Xi, and Weigang Lu. 2024. "Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units" Journal of Marine Science and Engineering 12, no. 7: 1124. https://doi.org/10.3390/jmse12071124
APA StyleLiu, J., Xi, W., & Lu, W. (2024). Optimization Design of Radial Clearance between Stator and Rotor of Full Cross-Flow Pump Units. Journal of Marine Science and Engineering, 12(7), 1124. https://doi.org/10.3390/jmse12071124





