An Invariant Filtering Method Based on Frame Transformed for Underwater INS/DVL/PS Navigation
Abstract
1. Introduction
- Utilizing a novel two-frame group filtering approach, along with a comprehensive formulation and validation, encompassing both fixed and body observations.
- Leveraging DVL and depth sensor data as primary observations, the methodology facilitates underwater navigation filtering, obviating the necessity for intricate transformations to satisfy group affine requirements.
- Algorithmic validation is conducted using simulated datasets and proprietary real-world underwater data, ensuring robustness and efficacy.
2. Related Works
2.1. Underwater Navigation Methods
2.2. Li Group Optimization and Application to Underwater Navigation
3. Methodology
3.1. Lie Group Theory
3.2. Two Frame Groups
3.3. Two Frame Groups IEKF
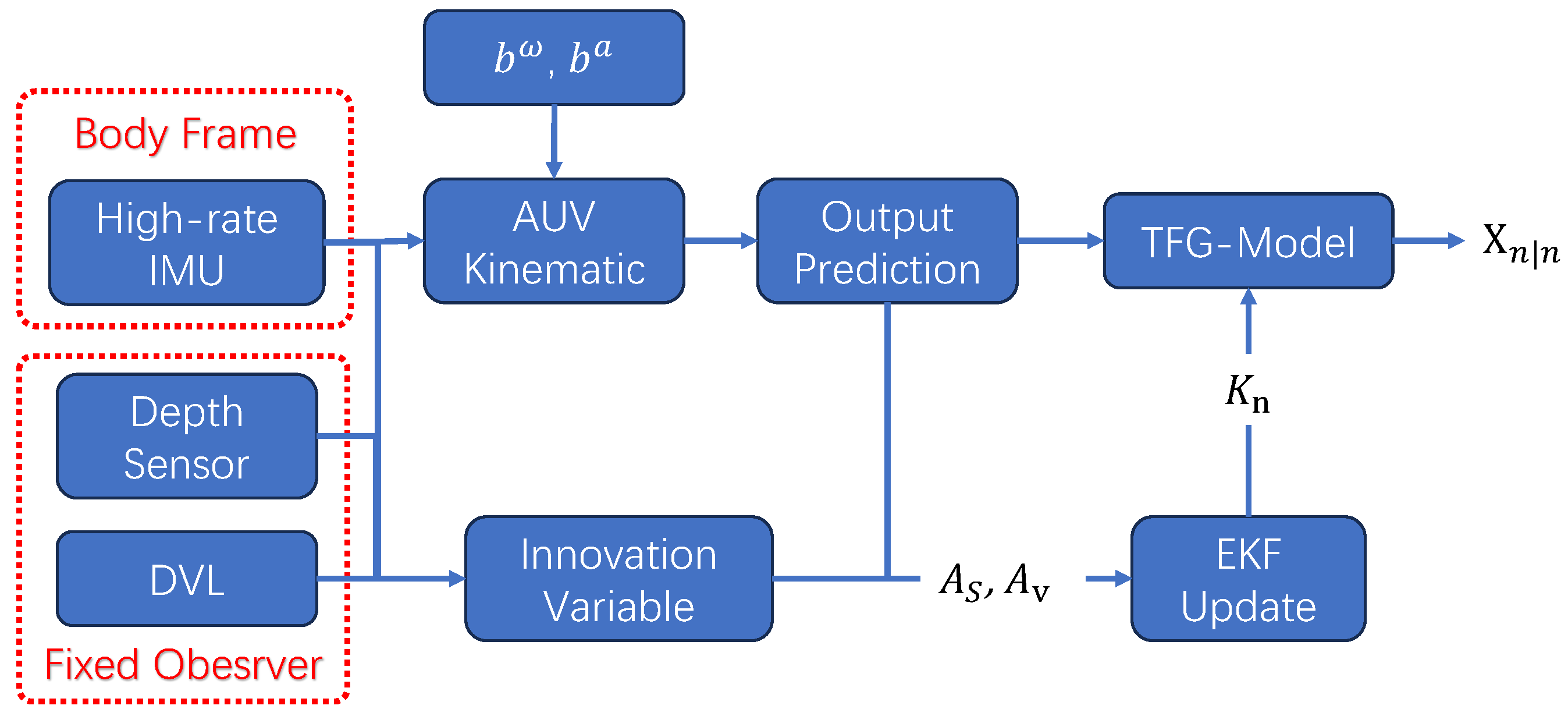
3.4. Algorithmic Implementation
3.5. Underwater Multi-Sensor TFG Model
4. Experimental Setup
4.1. Comparison Term
- IEKF [39]: By exploiting the “log-linear” property of error evolution, this method exhibits enhanced filtering capabilities and accelerated convergence, particularly addressing the challenges posed by initial large errors while maintaining group affine satisfaction.
- U/W-IEKF [48]: Tailored for IMU and DVL-equipped underwater vehicles, this approach integrates non-standard single-case measurements, such as depth readings from pressure transducers, into the Iterated Extended Kalman Filter framework via “pseudo” measurements. These pseudo measurements encapsulate current state estimates modeled with infinite covariance.
- Underwater-TFG-IEKF: This method, proposed in our study, introduces novel techniques for underwater localization.
4.2. Simulation
4.3. Natural Scenario Data
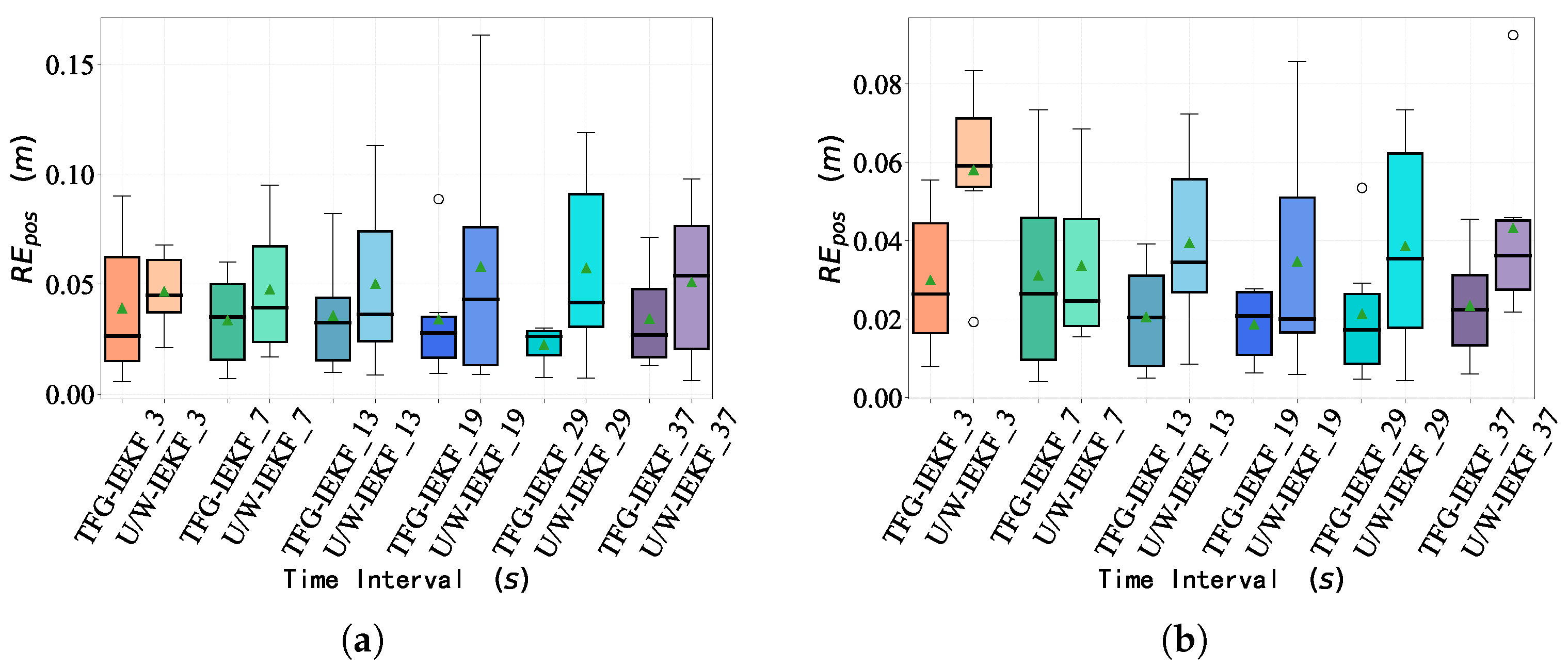
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IEKF | Invariant Extended Kalman filter |
| AUV | Autonomous Underwater Vehicle |
| DVL | Doppler Velocity Log |
| IMU | Inertial Measurement Unit |
| SO | special Orthogonal group |
| SE | special Euclidean groups |
| BCH | Baker–Campbell–Hausdorff |
References
- Yan, J.; Ban, H.; Luo, X.; Zhao, H.; Guan, X. Joint Localization and Tracking Design for AUV with Asynchronous Clocks and State Disturbances. IEEE Trans. Veh. Technol. 2019, 68, 4707–4720. [Google Scholar] [CrossRef]
- Naus, K.; Piskur, P. Applying the Geodetic Adjustment Method for Positioning in Relation to the Swarm Leader of Underwater Vehicles Based on Course, Speed, and Distance Measurements. Energies 2022, 15, 8472. [Google Scholar] [CrossRef]
- Huang, H.; Chen, X.; Zhang, B.; Wang, J. High accuracy navigation information estimation for inertial system using the multi-model EKF fusing adams explicit formula applied to underwater gliders. ISA Trans. 2017, 66, 414–424. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Kim, J.; Byun, S.W. A Comparison of Nonlinear Filter Algorithms for Terrain-referenced Underwater Navigation. Int. J. Control Autom. Syst. 2018, 16, 2977–2989. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, C.; Yang, D.; Liu, W.; Zhang, F. Underwater SLAM Based on Forward-Looking Sonar. In Proceedings of the Cognitive Systems and Signal Processing, Zhuhai, China, 25–27 December 2020; Sun, F., Liu, H., Fang, B., Eds.; Springer: Singapore, 2021; pp. 584–593. [Google Scholar]
- Bonin-Font, F.; Burguera Burguera, A. NetHALOC: A learned global image descriptor for loop closing in underwater visual SLAM. Expert Syst. 2021, 38, e12635. [Google Scholar] [CrossRef]
- Liu, R.; Liu, F.; Liu, C.; Zhang, P. Modified Sage-Husa Adaptive Kalman Filter-Based SINS/DVL Integrated Navigation System for AUV. J. Sens. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Pardos, J.; Balaguer, C. RHO humanoid robot bipedal locomotion and navigation using Lie groups and geometric algorithms. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3081–3086. [Google Scholar] [CrossRef]
- Barfoot, T. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017; pp. 1–368. [Google Scholar] [CrossRef]
- Barrau, A. Non-Linear State Error Based Extended Kalman Filters with Applications to Navigation. (Filtres de Kalman étendus Reposant sur une Variable d’erreur non linéaire Avec Applications à la Navigation). Ph.D. Thesis, Mines Paristech, Paris, France, 2015. [Google Scholar]
- Barrau, A.; Bonnabel, S. The Invariant Extended Kalman Filter as a Stable Observer. IEEE Trans. Autom. Control 2017, 62, 1797–1812. [Google Scholar] [CrossRef]
- Hartley, R.; Ghaffari, M.; Eustice, R.M.; Grizzle, J.W. Contact-aided invariant extended Kalman filtering for robot state estimation. Int. J. Robot. Res. 2020, 39, 402–430. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Xu, J. Strapdown Inertial Navigation System Initial Alignment Based on Group of Double Direct Spatial Isometries. IEEE Sens. J. 2022, 22, 803–818. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. A Mathematical Framework for IMU Error Propagation with Applications to Preintegration. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5732–5738. [Google Scholar] [CrossRef]
- Brossard, M.; Barrau, A.; Chauchat, P.; Bonnabel, S. Associating Uncertainty to Extended Poses for on Lie Group IMU Preintegration with Rotating Earth. IEEE Trans. Robot. 2022, 38, 998–1015. [Google Scholar] [CrossRef]
- Tang, H.; Xu, J.; Chang, L.; Shi, W.; He, H. Invariant Error-Based Integrated Solution for SINS/DVL in Earth Frame: Extension and Comparison. IEEE Trans. Instrum. Meas. 2023, 72, 9500617. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. The Geometry of Navigation Problems. IEEE Trans. Autom. Control 2023, 68, 689–704. [Google Scholar] [CrossRef]
- Shi, W.; Xu, J.; Li, D.; He, H. Attitude Estimation of SINS on Underwater Dynamic Base with Variational Bayesian Robust Adaptive Kalman Filter. IEEE Sens. J. 2022, 22, 10954–10964. [Google Scholar] [CrossRef]
- Jørgensen, E.K.; Fossen, T.I.; Bryne, T.H.; Schjølberg, I. Underwater Position and Attitude Estimation Using Acoustic, Inertial, and Depth Measurements. IEEE J. Ocean. Eng. 2020, 45, 1450–1465. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Yan, T.; Yang, S.; Li, R. A Robust INS/USBL/DVL Integrated Navigation Algorithm Using Graph Optimization. Sensors 2023, 23, 916. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Tang, J.; Zhang, B. Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle. Appl. Sci. 2021, 11, 7777. [Google Scholar] [CrossRef]
- OuYang, M.; Fan, H.; Du, P. Particle Swarm Optimization for Underwater Gravity-Matching: Applications in Navigation and Simulation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLVI-3/W1-2022, 149–154. [Google Scholar] [CrossRef]
- Jin, K.; Chai, H.; Su, C.; Xiang, M.; Hui, J. An optimization-based in-motion fine alignment and positioning algorithm for underwater vehicles. Measurement 2022, 202, 111746. [Google Scholar] [CrossRef]
- Russo, P.; Di Ciaccio, F.; Troisi, S. DANAE++: A Smart Approach for Denoising Underwater Attitude Estimation. Sensors 2021, 21, 1526. [Google Scholar] [CrossRef]
- Zhang, D.; Chang, S.; Zou, G.; Wan, C.; Li, H. A Robust Graph-Based Bathymetric Simultaneous Localization and Mapping Approach for AUVs. IEEE J. Ocean. Eng. 2024, 49, 1–21. [Google Scholar] [CrossRef]
- Rahman, S.; Li, A.Q.; Rekleitis, I. SVIn2: An Underwater SLAM System using Sonar, Visual, Inertial, and Depth Sensor. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1861–1868. [Google Scholar] [CrossRef]
- Ma, H.; Mu, X.; He, B. Adaptive Navigation Algorithm with Deep Learning for Autonomous Underwater Vehicle. Sensors 2021, 21, 6406. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Yu, H.; Fang, Y. NINT: Neural Inertial Navigation Based on Time Interval Information in Underwater Environments. IEEE Sens. J. 2024, 24, 21719. [Google Scholar] [CrossRef]
- Li, D.; Xu, J.; He, H.; Wu, M. An Underwater Integrated Navigation Algorithm to Deal With DVL Malfunctions Based on Deep Learning. IEEE Access 2021, 9, 82010–82020. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, S.; Zhang, G.; Liu, G.; Meng, W. FL-EKF Based Cooperative Localization Method for Multi-AUVs. IEEE Internet Things J. 2024, 11, 1–12. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Li, D.; Zhong, J.; Yang, K. A Survey on Visual Navigation and Positioning for Autonomous UUVs. Remote Sens. 2022, 14, 3794. [Google Scholar] [CrossRef]
- Kim, B.; Joe, H.; Yu, S.C. High-precision Underwater 3D Mapping Using Imaging Sonar for Navigation of Autonomous Underwater Vehicle. Int. J. Control Autom. Syst. 2021, 19, 3794. [Google Scholar] [CrossRef]
- Costanzi, R.; Fanelli, F.; Monni, N.; Ridolfi, A.; Allotta, B. An Attitude Estimation Algorithm for Mobile Robots under Unknown Magnetic Disturbances. IEEE/ASME Trans. Mechatron. 2016, 21, 1900–1911. [Google Scholar] [CrossRef]
- Ngatini; Apriliani, E.; Nurhadi, H. Ensemble and Fuzzy Kalman Filter for position estimation of an autonomous underwater vehicle based on dynamical system of AUV motion. Expert Syst. Appl. 2017, 68, 29–35. [Google Scholar] [CrossRef]
- Shariati, H.; Moosavi, H.; Danesh, M. Application of particle filter combined with extended Kalman filter in model identification of an autonomous underwater vehicle based on experimental data. Appl. Ocean. Res. 2019, 82, 32–40. [Google Scholar] [CrossRef]
- Pei, F.; Xu, H.; Jiang, N.; Zhu, D. A novel in-motion alignment method for underwater SINS using a state-dependent Lie group filter. Navigation 2020, 67, 451–470. [Google Scholar] [CrossRef]
- Xu, C.; Xu, C.; Wu, C.; Qu, D.; Liu, J.; Wang, Y.; Shao, G. A novel self-adapting filter based navigation algorithm for autonomous underwater vehicles. Ocean. Eng. 2019, 187, 106146. [Google Scholar] [CrossRef]
- Fossen, T.I. Feedback error-state Kalman filter with time-delay compensation for hydroacoustic-aided inertial navigation of underwater vehicles. Control. Eng. Pract. 2023, 138, 105603. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Invariant Kalman Filtering. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 237–257. [Google Scholar] [CrossRef]
- Chang, L.; Luo, Y. Log-Linear Error State Model Derivation without Approximation for INS. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2029–2035. [Google Scholar] [CrossRef]
- Li, J.; Zhang, S.; Yang, H.; Jiang, Z.; Bai, X. A Fast Continuous Self-Calibration Method for FOG Rotational Inertial Navigation System Based on Invariant Extended Kalman Filter. IEEE Sens. J. 2023, 23, 2456–2469. [Google Scholar] [CrossRef]
- Barfoot, T.D.; Furgale, P.T. Associating Uncertainty with Three-Dimensional Poses for Use in Estimation Problems. IEEE Trans. Robot. 2014, 30, 679–693. [Google Scholar] [CrossRef]
- Roux, A.; Changey, S.; Weber, J.; Lauffenburger, J.P. CNN-based Invariant Extended Kalman Filter for projectile trajectory estimation using IMU only. In Proceedings of the 2021 International Conference on Control, Automation and Diagnosis (ICCAD), Grenoble, France, 3–5 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chang, L.; Di, J.; Qin, F. Inertial-Based Integration With Transformed INS Mechanization in Earth Frame. IEEE/ASME Trans. Mechatron. 2022, 27, 1738–1749. [Google Scholar] [CrossRef]
- Xu, B.; Guo, Y. A Novel DVL Calibration Method Based on Robust Invariant Extended Kalman Filter. IEEE Trans. Veh. Technol. 2022, 71, 9422–9434. [Google Scholar] [CrossRef]
- Luo, L.; Huang, Y.; Zhang, Z.; Zhang, Y. A New Kalman Filter-Based In-Motion Initial Alignment Method for DVL-Aided Low-Cost SINS. IEEE Trans. Veh. Technol. 2021, 70, 331–343. [Google Scholar] [CrossRef]
- Qian, L.; Qin, F.; Li, K.; Zhu, T. Research on the Necessity of Lie Group Strapdown Inertial Integrated Navigation Error Model Based on Euler Angle. Sensors 2022, 22, 7742. [Google Scholar] [CrossRef]
- Potokar, E.R.; Norman, K.; Mangelson, J.G. Invariant Extended Kalman Filtering for Underwater Navigation. IEEE Robot. Autom. Lett. 2021, 6, 5792–5799. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, F.; Guo, C.; Liu, J. Matrix Lie Group-Based Extended Kalman Filtering for Inertial-Integrated Navigation in the Navigation Frame. IEEE Trans. Instrum. Meas. 2024, 73, 9503916. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, M.; Guo, C. The Geometry and Kinematics of the Matrix Lie Group SE_K(3). arXiv 2020, arXiv:2012.00950. [Google Scholar]
- Ashkenazi, V. Coordinate Systems: How to Get Your Position Very Precise and Completely Wrong. J. Navig. 1986, 39, 269–278. [Google Scholar] [CrossRef]
- Potokar, E.; Lay, K.; Norman, K.; Benham, D.; Neilsen, T.B.; Kaess, M.; Mangelson, J.G. HoloOcean: Realistic Sonar Simulation. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 8450–8456. [Google Scholar] [CrossRef]
- Potokar, E.; Ashford, S.; Kaess, M.; Mangelson, J.G. HoloOcean: An Underwater Robotics Simulator. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2022; pp. 3040–3046. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, C.; Yang, D.; Pan, G.; Zhang, F. Underwater AUV Navigation Dataset in Natural Scenarios. Electronics 2023, 12, 3788. [Google Scholar] [CrossRef]
- Nicolai, R.; Simensen, G. The New EPSG Geodetic Parameter Registry. In Proceedings of the 70th EAGE Conference and Exhibition incorporating SPE EUROPEC 2008, Rome, Italy, 9–12 June 2008. [Google Scholar] [CrossRef]
- Zhang, Z.; Scaramuzza, D. A Tutorial on Quantitative Trajectory Evaluation for Visual(-Inertial) Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar] [CrossRef]
- Tang, J.; Bian, H.; Ma, H.; Wang, R. Initialization of SINS/GNSS Error Covariance Matrix Based on Error States Correlation. IEEE Access 2023, 11, 94911–94917. [Google Scholar] [CrossRef]




| Author | Methodology | Conclusion |
|---|---|---|
| Shi et al. [18] | Variational Bayesian Robust Adaptive Kalman Filter (VBRAKF) | Error of 95.61% of KF |
| Huang et al. [21] | Statistical Regression Adaptive Kalman Filter (SRAKF) | 93.83% improvement over UKF |
| Ngatini et al. [34] | Integrated Kalman Filter and Fuzzy Kalman Filter | Position error is 92% of FKF; angle error is 93% of FKF |
| Pei et al. [36] | State-Dependent Lie Group-based Filter | Accuracy is 70% improved over Quaternion KF |
| Xu et al. [37] | Conditional Adaptive gain Expansion Kalman Filter (CAEKF) | 83% improvement over EKF |
| Proposed | Underwater Two-Frame Group IEKF | 77% improvement over IEKF |
| Sensor | Noise Type | Noise Standard Bias |
|---|---|---|
| IMU | Angular velocity | 0.00277 rad/s/Hz |
| Linear acceleration | 0.00123 m/s2/Hz | |
| Angular velocity bias | 0.00141 rad/s2/Hz | |
| Linear acceleration bias | 0.00388 m/s3/Hz | |
| DVL | Velocity per beam | 0.02626 m/s |
| Range per beam | 0.1 m | |
| PS | Depth sensor | 0.255 m |
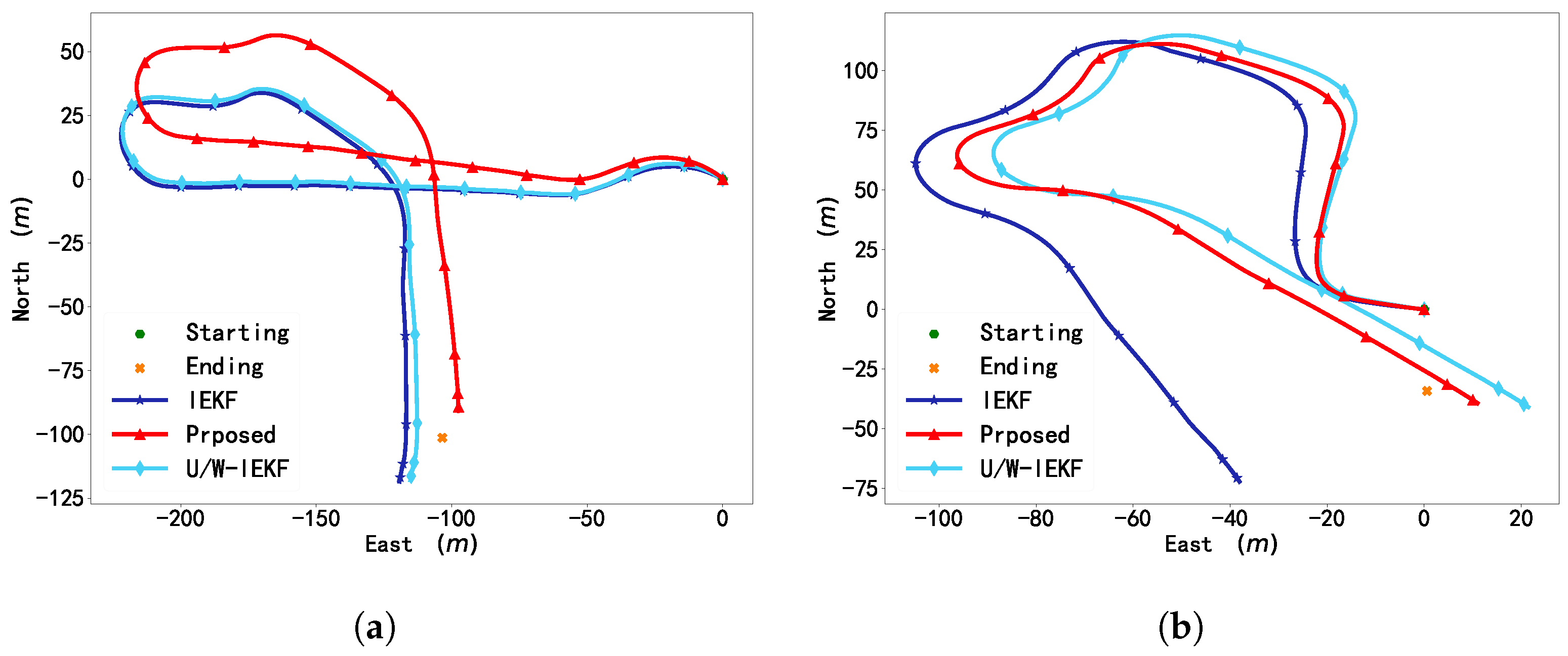
| Trajectory No. | Traj.1 | Traj.2 | Traj.3 | Traj.4 | |
|---|---|---|---|---|---|
| Position (m) | IEKF | 56.5914 | 69.6770 | 73.3606 | 48.9478 |
| U/W-IEKF | 50.8412 | 93.0147 | 72.7105 | 45.4038 | |
| Proposed | 11.6488 | 16.8054 | 20.5661 | 9.4366 | |
| Attitude (rad) | IEKF | −0.0249 | 0.0238 | −0.0208 | 0.0082 |
| U/W-IEKF | 0.0136 | 0.0205 | 0.0023 | −0.0142 | |
| Proposed | −0.0057 | 0.0074 | −0.0066 | −0.0013 | |
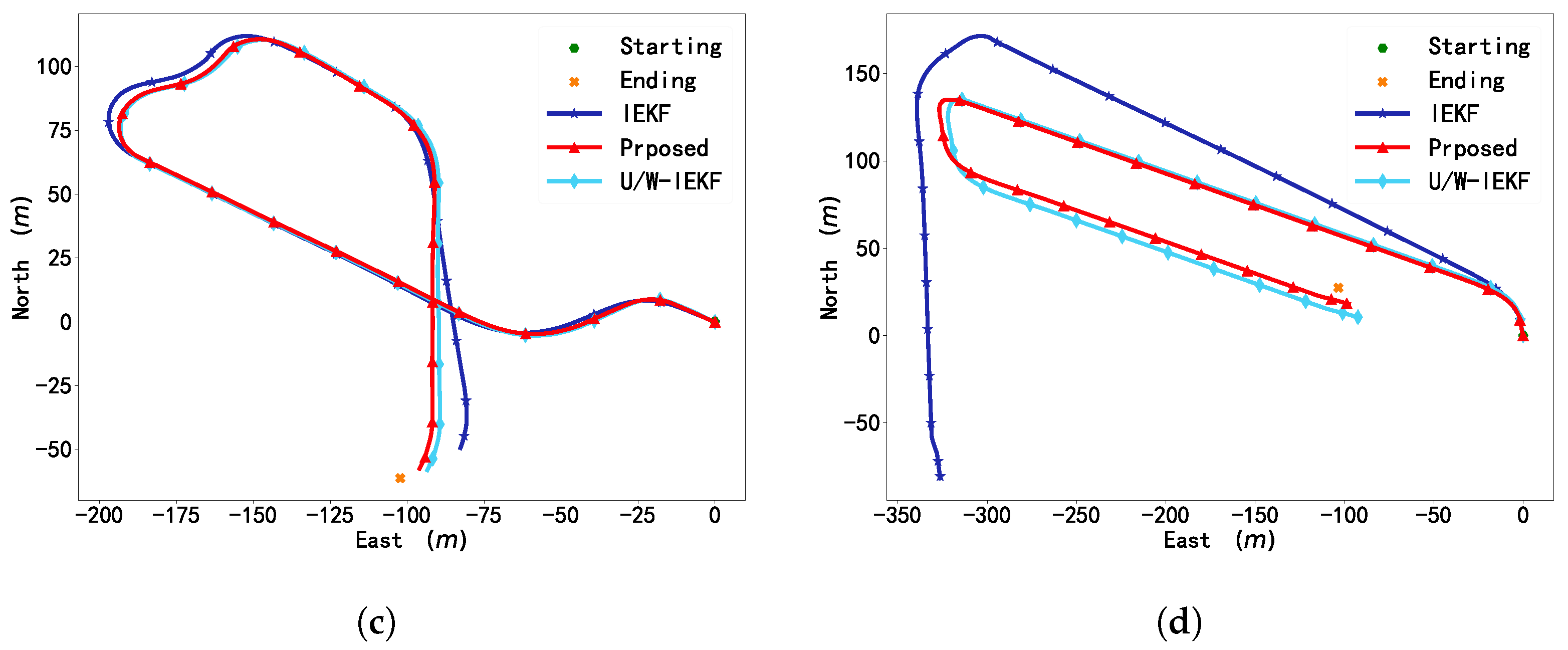
| Traj. Seq. | Total Mileage (m) | PEP | ||
|---|---|---|---|---|
| IEKF | U/W-IEKF | Proposed | ||
| 20210428_1_1 | 791.4829 | 0.0247 | 0.0052 | 0.0052 |
| 20210605_0_0 | 753.1149 | 0.0653 | 0.0208 | 0.0192 |
| 20220718_1_1 | 409.2852 | 0.1083 | 0.1010 | 0.0148 |
| 20220718_2_1 | 451.1789 | 0.0307 | 0.0141 | 0.0122 |
| 20220719_1_2 | 235.1641 | 0.0414 | 0.0249 | 0.0197 |
| 20220816_0_4 | 1138.8411 | 0.1127 | 0.0143 | 0.0142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Cheng, C.; Cao, C.; Guo, X.; Pan, G.; Zhang, F. An Invariant Filtering Method Based on Frame Transformed for Underwater INS/DVL/PS Navigation. J. Mar. Sci. Eng. 2024, 12, 1178. https://doi.org/10.3390/jmse12071178
Wang C, Cheng C, Cao C, Guo X, Pan G, Zhang F. An Invariant Filtering Method Based on Frame Transformed for Underwater INS/DVL/PS Navigation. Journal of Marine Science and Engineering. 2024; 12(7):1178. https://doi.org/10.3390/jmse12071178
Chicago/Turabian StyleWang, Can, Chensheng Cheng, Chun Cao, Xinyu Guo, Guang Pan, and Feihu Zhang. 2024. "An Invariant Filtering Method Based on Frame Transformed for Underwater INS/DVL/PS Navigation" Journal of Marine Science and Engineering 12, no. 7: 1178. https://doi.org/10.3390/jmse12071178
APA StyleWang, C., Cheng, C., Cao, C., Guo, X., Pan, G., & Zhang, F. (2024). An Invariant Filtering Method Based on Frame Transformed for Underwater INS/DVL/PS Navigation. Journal of Marine Science and Engineering, 12(7), 1178. https://doi.org/10.3390/jmse12071178







