Laboratory Study on Wave Attenuation by Elastic Mangrove Model with Canopy
Abstract
:1. Introduction
2. Theoretical Background
- Field Survey and Model Creation. Detailed measurements of the plant’s spatial features were obtained through field surveys and utilized for creating corresponding Kandelia obovata models. Detailed parameters of the plant space can be referred to in the subsequent Section 3.2.
- Control Experimental Conditions. The slope was kept constant in the present experiments, allowing to isolate and focus on other variables without the confounding effects of terrain slope variability. This constancy ensures uniformity in the influences of sidewall effects, bottom friction, and slope on the hydrodynamic behavior of waves.
3. Experimental Setup and Procedures
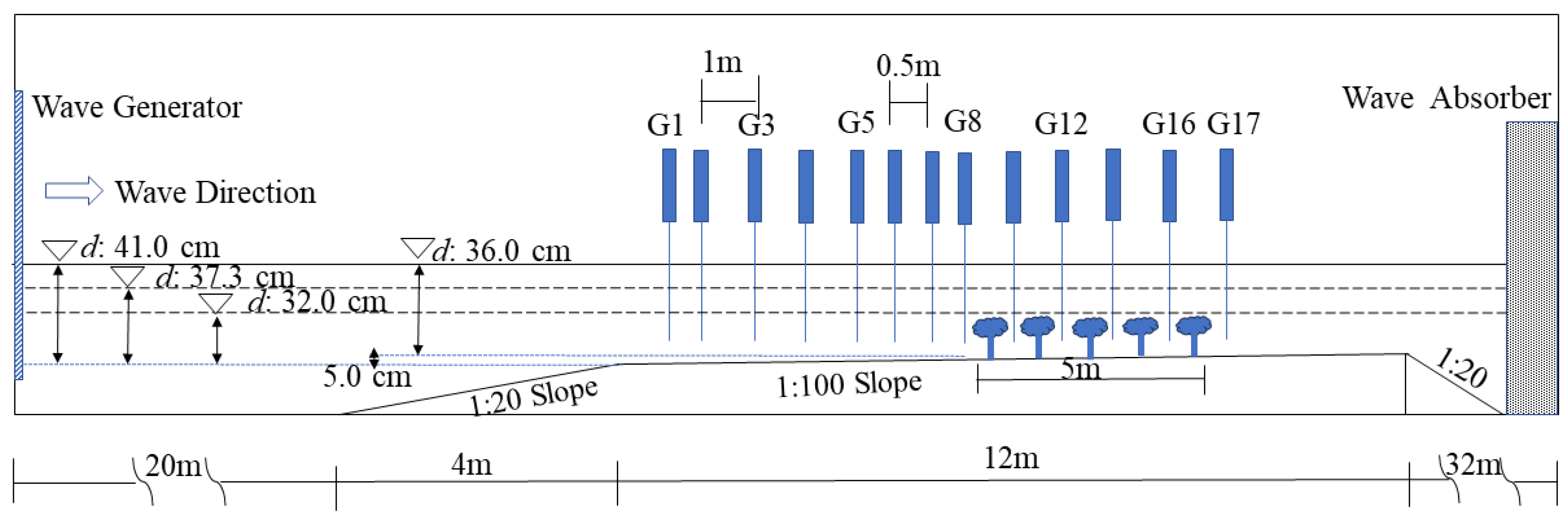
3.1. Experimental Facilities and Instrumentation
3.2. Experimental Conditions and Experimental Similarity
3.3. Mangrove Model Design
4. Result and Discussion
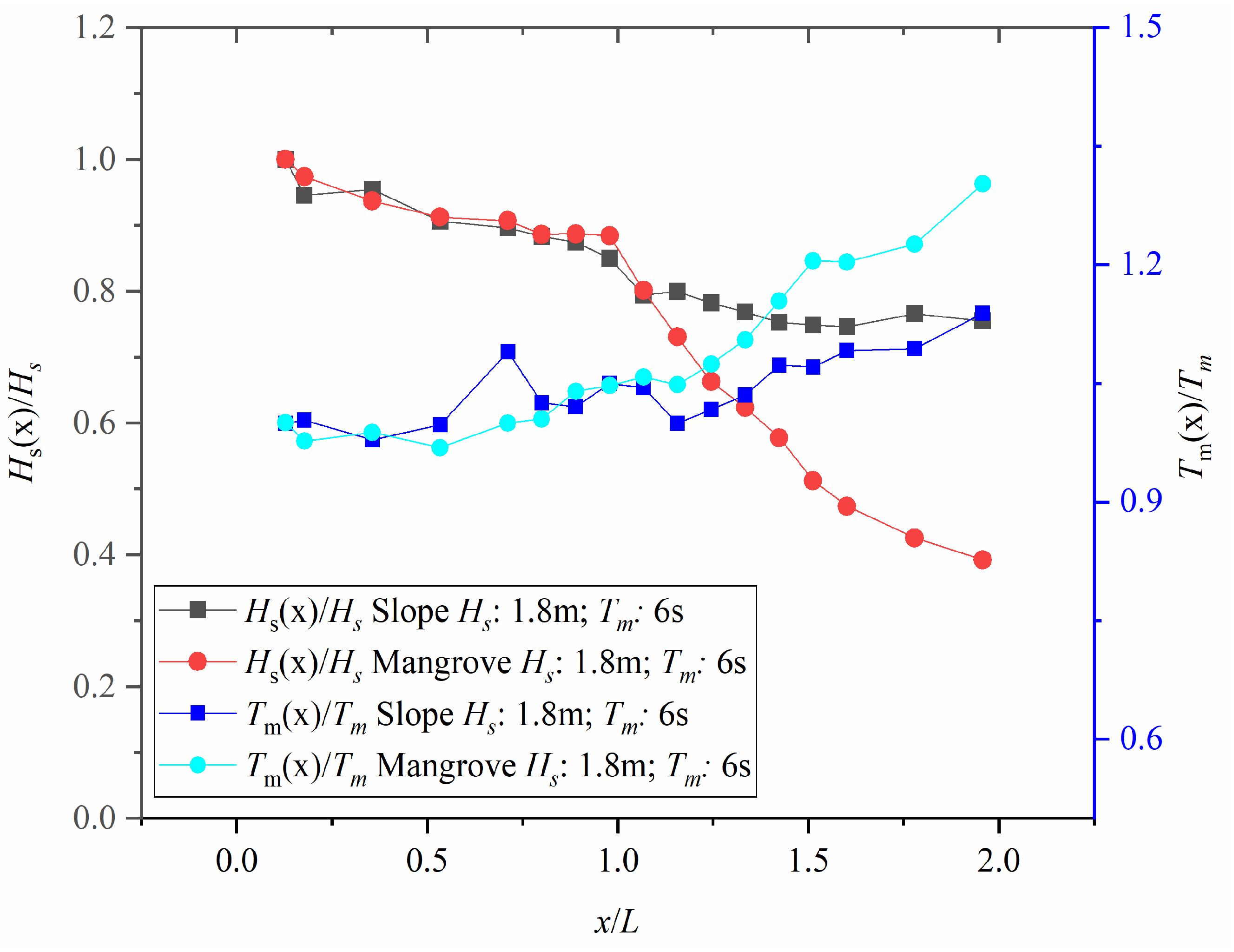
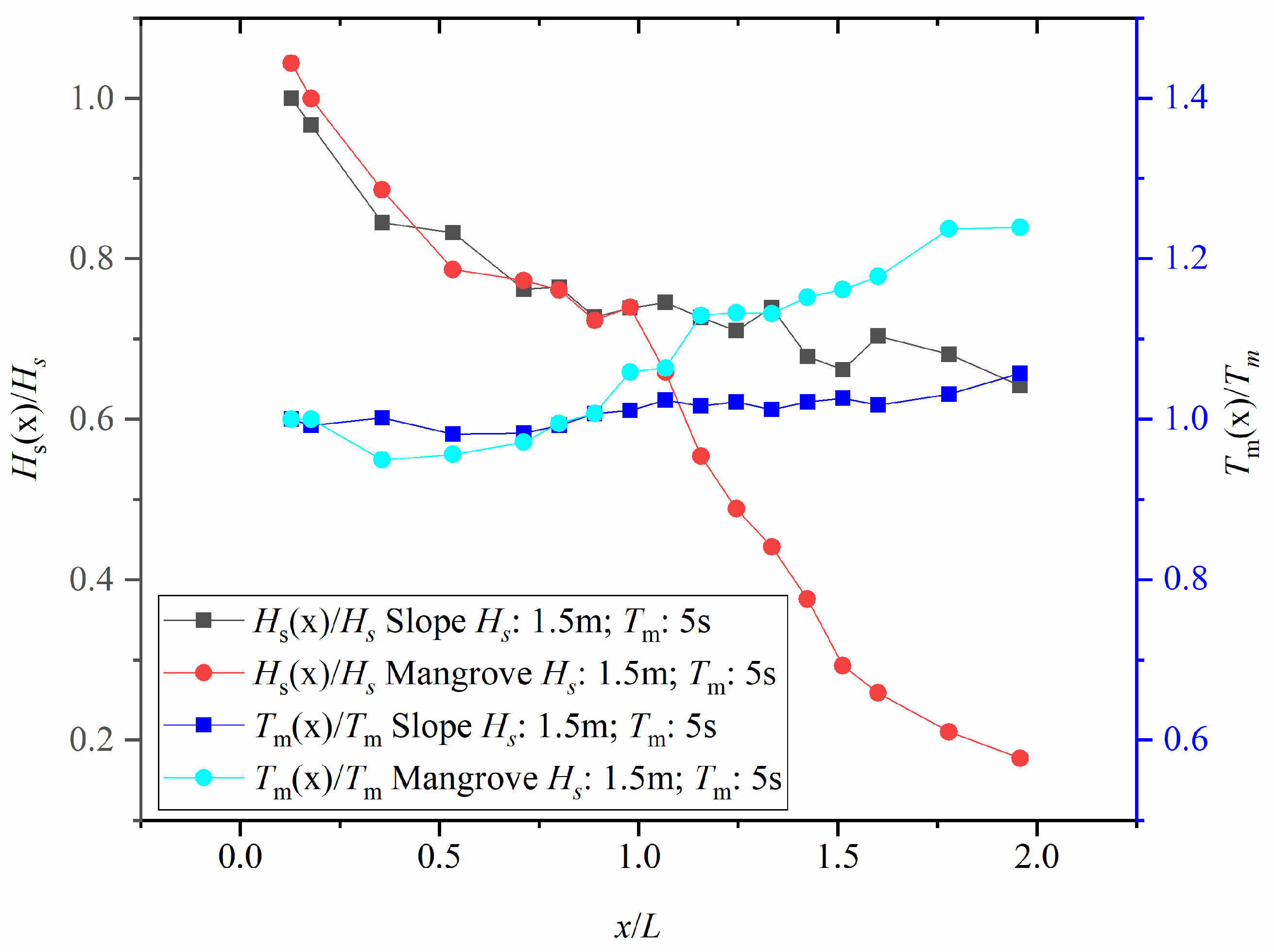
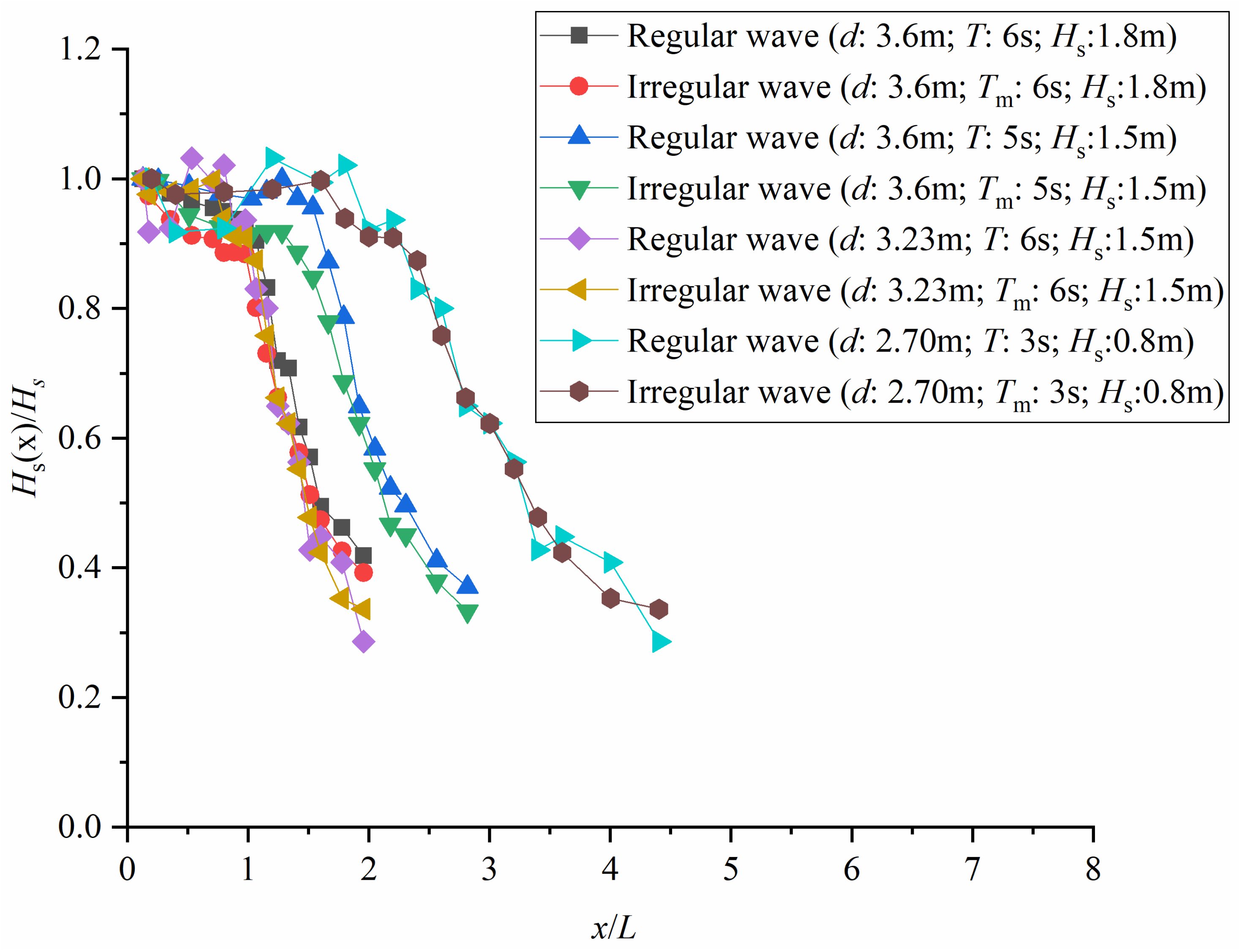
4.1. The Longitudinal Variation in Wave Parameters
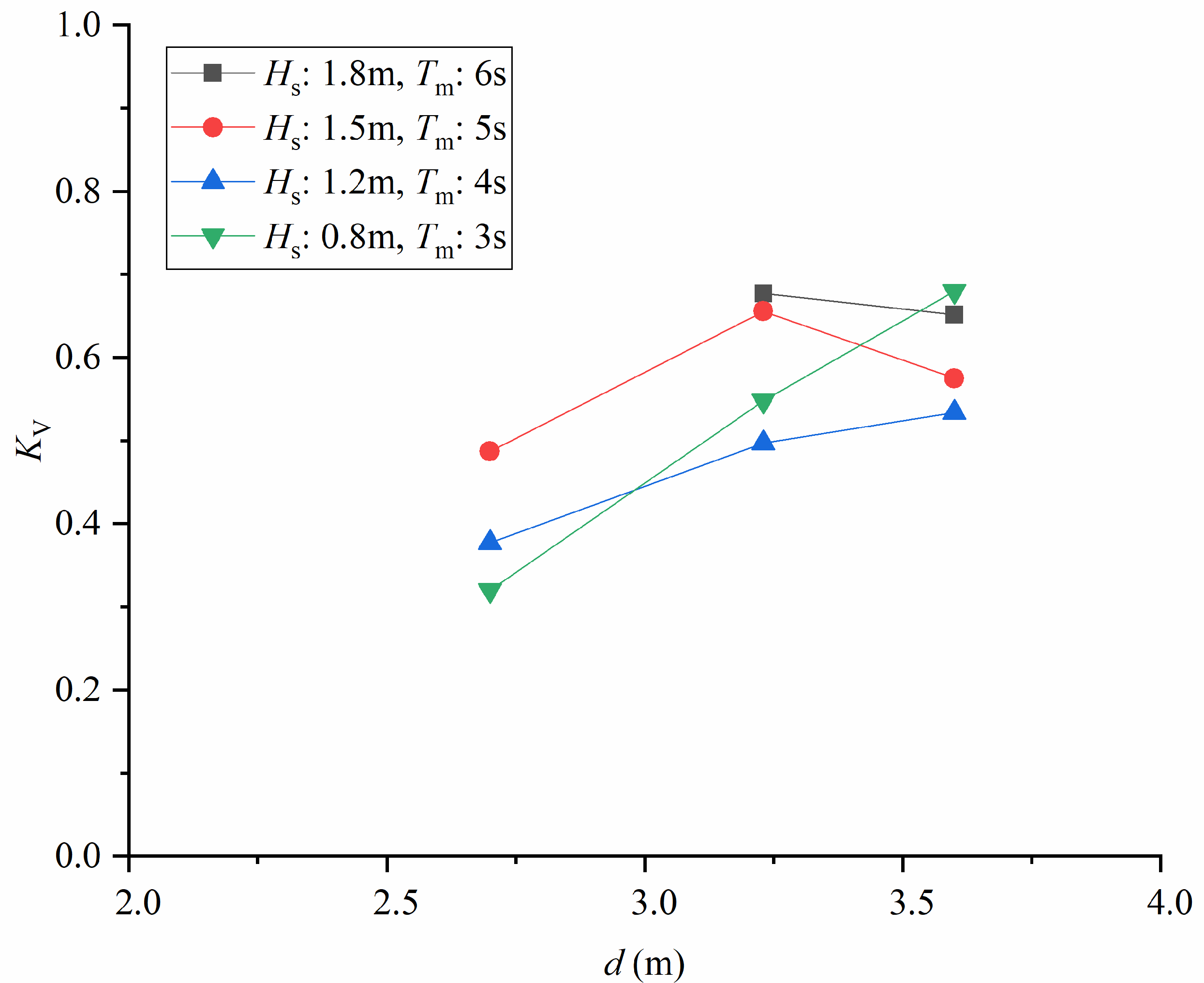
4.2. The Effect of Water Depth on Wave Attenuation
4.3. The Effect of Elastic Model with Canopy on Wave Attenuation
5. Prediction of Wave Transmission and Bulk Drag Coefficient
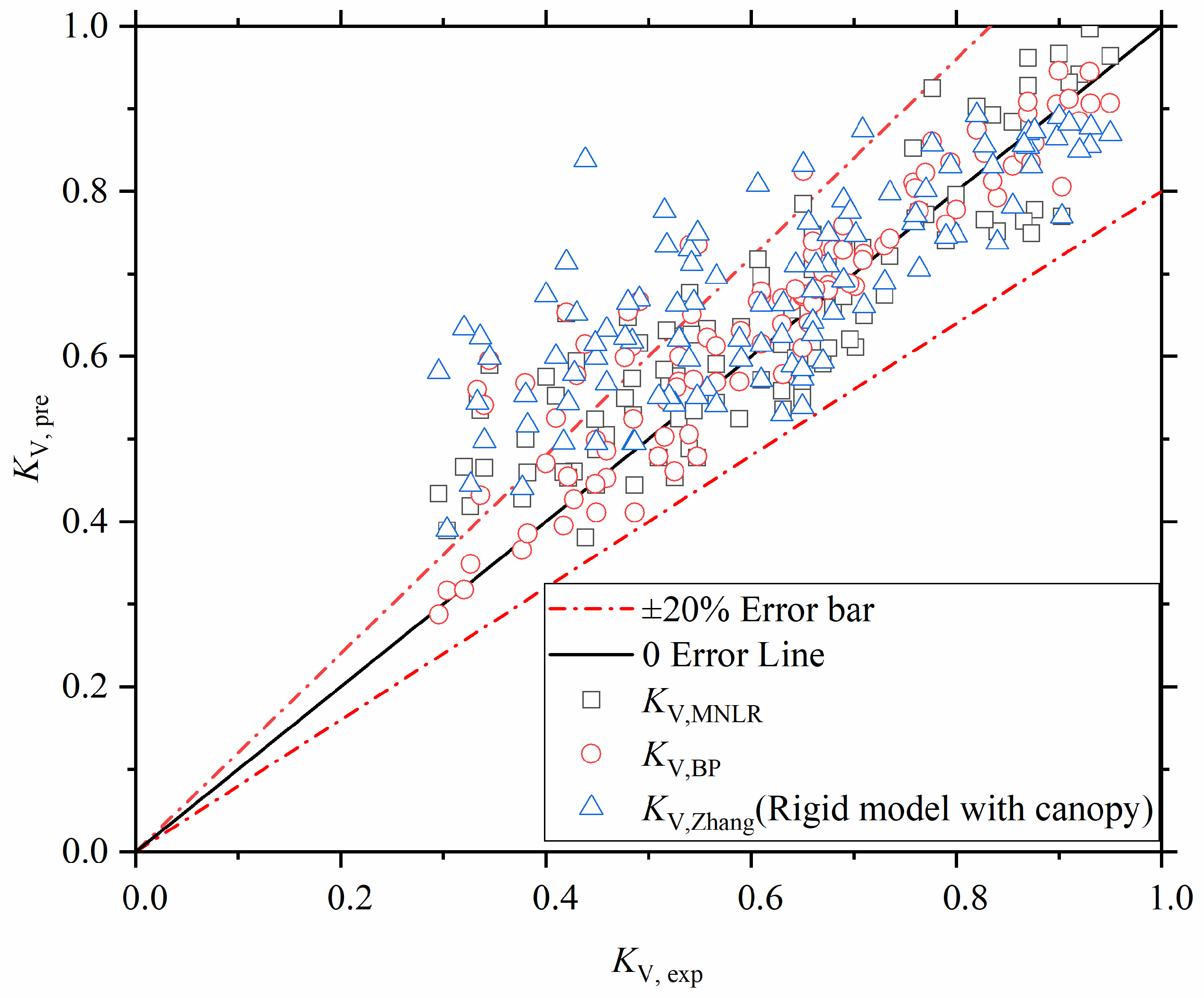
5.1. Multivariate Nonlinear Regression Method (MNLR)
5.2. Back Propagation (BP) Neural Network Method
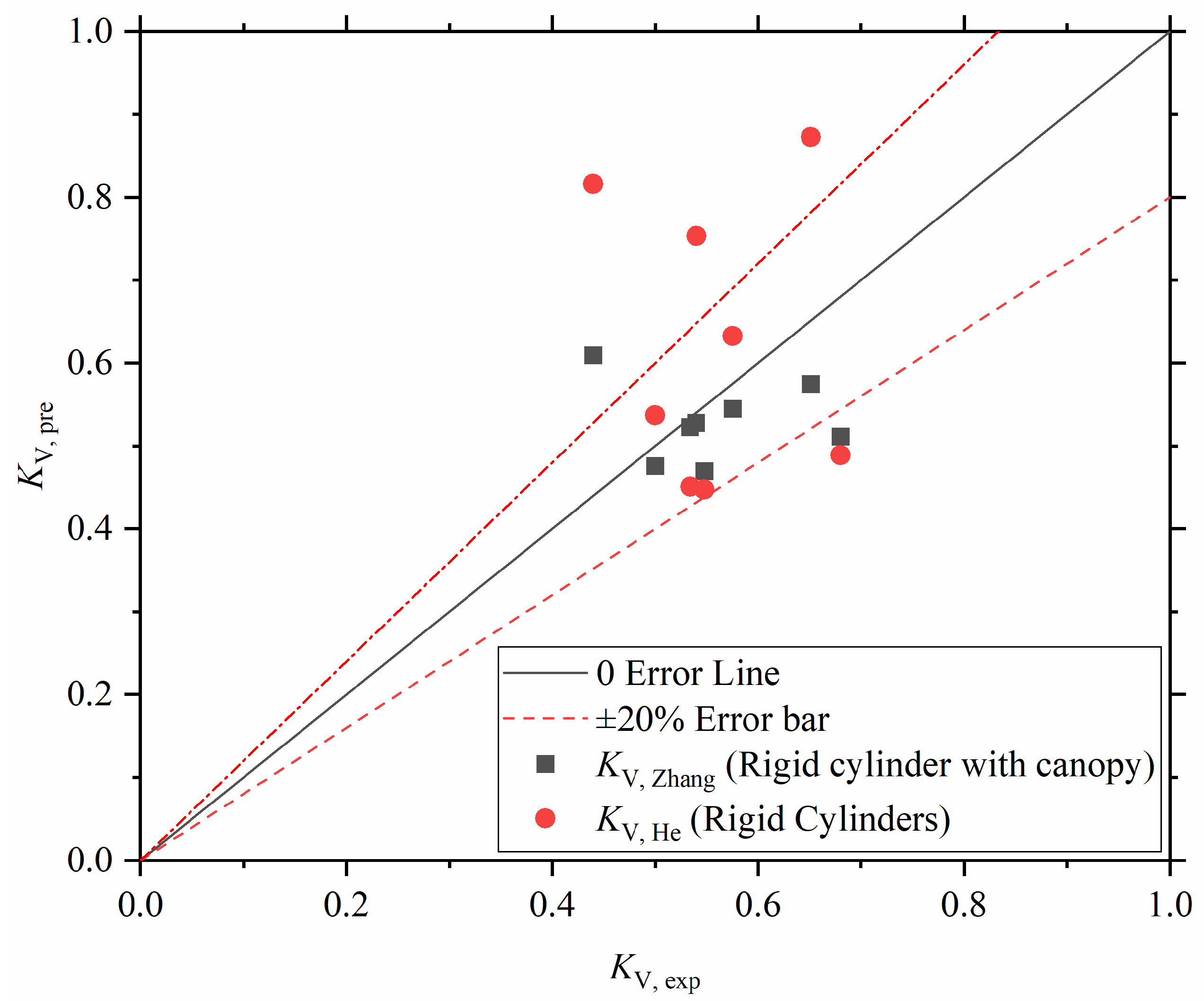
5.3. Bulk Drag Coefficient
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weaver, R.J.; Stehno, A.L. Mangroves as Coastal Protection for Restoring Low-Energy Waterfront Property. J. Mar. Sci. Eng. 2024, 12, 470. [Google Scholar] [CrossRef]
- Zeng, J.; Ai, B.; Jian, Z.; Ye, M.; Zhao, J.; Sun, S. Analysis of mangrove dynamics and its protection effect in the Guangdong-Hong Kong-Macao Coastal Area based on the Google Earth Engine platform. Front. Mar. Sci. 2023, 10, 1170587. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, P.; Chen, X. Coastal protection by planted mangrove forest during typhoon Mangkhut. J. Mar. Sci. Eng. 2022, 10, 1288. [Google Scholar] [CrossRef]
- Gijsman, R.; Horstman, E.M.; van der Wal, D.; Friess, D.A.; Swales, A.; Wijnberg, K.M. Nature-Based Engineering: A Review on Reducing Coastal Flood Risk with Mangroves. Front. Mar. Sci. 2021, 8, 702412. [Google Scholar] [CrossRef]
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Quartel, S.; Kroon, A.; Augustinus, P.G.E.F.; Van Santen, P.; Tri, N.H. Wave attenuation in coastal mangroves in the Red River Delta, Vietnam. J. Asian Earth Sci. 2007, 29, 576–584. [Google Scholar] [CrossRef]
- Mazda, Y.; Magi, M.; Kogo, M.; Hong, P.N. Mangroves as a coastal protection from waves in the Tong King delta, Vietnam. Mangroves Salt Marshes 1997, 1, 127–135. [Google Scholar] [CrossRef]
- Zhao, C.; Tang, J.; Shen, Y. Numerical investigation of the effects of rigid emergent vegetation on wave runup and overtopping. Ocean Eng. 2022, 264, 112502. [Google Scholar] [CrossRef]
- Borsje, B.W.; van Wesenbeeck, B.K.; Dekker, F.; Paalvast, P.; Bouma, T.J.; van Katwijk, M.M.; de Vries, M.B. How ecological engineering can serve in coastal protection. Ecol. Eng. 2011, 37, 113–122. [Google Scholar] [CrossRef]
- Ren, H.; Lu, H.; Shen, W.; Huang, C.; Guo, Q.; Li, Z.a.; Jian, S. Sonneratia apetala Buch.Ham in the mangrove ecosystems of China: An invasive species or restoration species? Ecol. Eng. 2009, 35, 1243–1248. [Google Scholar] [CrossRef]
- Mullarney, J.C.; Henderson, S.M.; Reyns, J.A.H.; Norris, B.K.; Bryan, K.R. Spatially varying drag within a wave-exposed mangrove forest and on the adjacent tidal flat. Cont. Shelf Res. 2017, 147, 102–113. [Google Scholar] [CrossRef]
- Mazda, Y.; Magi, M.; Ikeda, Y.; Kurokawa, T.; Asano, T. Wave reduction in a mangrove forest dominated by Sonneratia sp. Wetl. Ecol. Manag. 2006, 14, 365–378. [Google Scholar] [CrossRef]
- Horstman, E.M.; Dohmen-Janssen, C.M.; Narra, P.M.F.; van den Berg, N.J.F.; Siemerink, M.; Hulscher, S.J.M.H. Wave attenuation in mangroves: A quantitative approach to field observations. Coast. Eng. 2014, 94, 47–62. [Google Scholar] [CrossRef]
- Vo-Luong, P.; Massel, S. Energy dissipation in non-uniform mangrove forests of arbitrary depth. J. Mar. Syst. 2008, 74, 603–622. [Google Scholar] [CrossRef]
- Brinkman, R.M.; Massel, S.R.; Ridd, P.V.; Furukawa, K. Surface Wave Attenuation in Mangrove Forests. In Proceedings of the Pacific Coasts and Ports ’97: Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Christchurch, New Zealand, 7–11 September 1997; Volume 2. [Google Scholar]
- Wu, W.-C.; Cox, D.T. Effects of wave steepness and relative water depth on wave attenuation by emergent vegetation. Estuar. Coast. Shelf Sci. 2015, 164, 443–450. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Bouma, T.J.; De Vries, M.B.; Low, E.; Peralta, G.; Tánczos, I.C.; van de Koppel, J.; Herman, P.M.J. Trade-Offs Related to Ecosystem Engineering: A Case Study on Stiffness of Emerging Macrophytes. Ecology 2005, 86, 2187–2199. [Google Scholar] [CrossRef]
- van Veelen, T.J.; Fairchild, T.P.; Reeve, D.E.; Karunarathna, H. Experimental study on vegetation flexibility as control parameter for wave damping and velocity structure. Coast. Eng. 2020, 157, 103648. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Lei, J.; Zhou, X.; Yao, P.; Stive, M.J.F. Experimental investigation of wave attenuation by mangrove forests with submerged canopies. Coast. Eng. 2023, 186, 104403. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, Z.; Liu, Y. Experimental investigation of wave attenuation and bulk drag coefficient in mangrove forest with complex root morphology. Appl. Ocean Res. 2022, 118, 102974. [Google Scholar] [CrossRef]
- Piedrahita, M.; Osorio, A.; Urrego, L.; Gallego, J.D. Study of the Velocity and Wave Damping in a Physical Model of a Mangrove Forest Including Secondary Roots. In Proceedings of the Coastal Structures, Hannover, Germany, 29 September–2 October 2019; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2019. [Google Scholar]
- He, F.; Chen, J.; Jiang, C. Surface wave attenuation by vegetation with the stem, root and canopy. Coast. Eng. 2019, 152, 103509. [Google Scholar] [CrossRef]
- Sha, L.; Ming, C.; Gangfeng, M.; Shuguang, L.; Guihui, Z. Laboratory study of the effect of vertically varying vegetation density on waves, currents and wave-current interactions. Appl. Ocean Res. 2018, 79, 74–87. [Google Scholar] [CrossRef]
- Hashim, A.M.; Catherine, S.M.P. A Laboratory Study on Wave Reduction by Mangrove Forests. APCBEE Procedia 2013, 5, 27–32. [Google Scholar] [CrossRef]
- Kelty, K.; Tomiczek, T.; Cox, D.T.; Lomonaco, P.; Mitchell, W. Prototype-Scale Physical Model of Wave Attenuation through a Mangrove Forest of Moderate Cross-Shore Thickness: LiDAR-Based Characterization and Reynolds Scaling for Engineering with Nature. Front. Mar. Sci. 2022, 8, 780946. [Google Scholar] [CrossRef]
- Chang, C.W.; Mori, N.; Tsuruta, N.; Suzuki, K.; Yanagisawa, H. An Experimental Study of Mangrove-Induced Resistance on Water Waves Considering the Impacts of Typical Rhizophora Roots. J. Geophys. Res. Ocean. 2022, 127, e2022JC018653. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. Experimental analysis of wave attenuation and drag forces in a realistic fringe Rhizophora mangrove forest. Adv. Water Resour. 2019, 131, 103376. [Google Scholar] [CrossRef]
- Strusińska-Correia, A.; Husrin, S.; Oumeraci, H. Tsunami damping by mangrove forest: A laboratory study using parameterized trees. Nat. Hazards Earth Syst. Sci. 2013, 13, 483–503. [Google Scholar] [CrossRef]
- Malvin, N.; Pudjaprasetya, S.R.; Adytia, D. Neural Network Modelling on Wave Dissipation Due to Mangrove Forest. In Proceedings of the 2020 International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 5–6 August 2020; pp. 1–7. [Google Scholar]
- Yin, Z.; Li, J.; Wang, Y.; Wang, H.; Yin, T. Solitary wave attenuation characteristics of mangroves and multi-parameter prediction model. Ocean Eng. 2023, 285, 115372. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Kirby, J.T.; Hwang, P.A. Wave Diffraction Due to Areas of Energy Dissipation. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Maza, M.; Adler, K.; Ramos, D.; Garcia, A.M.; Nepf, H. Velocity and Drag Evolution from the Leading Edge of a Model Mangrove Forest. J. Geophys. Res. Ocean. 2017, 122, 9144–9159. [Google Scholar] [CrossRef]
- Bryant, M.; Bryant, D.; Provost, L.; Hurst, N.; McHugh, M.; Wargula, A.; Tomiczek, T. Wave Attenuation of Coastal Mangroves at a Near-Prototype Scale; US Army Engineer Research and Development Center (ERDC): Vicksburg, MS, USA, 2022. [Google Scholar]
- Cheng, N.S.; Nguyen, H.T. Hydraulic Radius for Evaluating Resistance Induced by Simulated Emergent Vegetation in Open-Channel Flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Goldstein, E.B.; Coco, G. A data-driven approach to develop physically sound predictors: Application to depth-averaged velocities on flows through submerged arrays of rigid cylinders. Water Resour. Res. 2015, 51, 1247–1263. [Google Scholar] [CrossRef]
- Hu, Z.; Suzuki, T.; Zitman, T.; Uittewaal, W.; Stive, M. Laboratory study on wave dissipation by vegetation in combined current–wave flow. Coast. Eng. 2014, 88, 131–142. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.; Ris, R. The” SWAN” wave model for shallow water. In Proceedings of the Coastal Engineering 1996, Orlando, FL, USA, 2–6 September 1996; pp. 668–676. [Google Scholar]
- Kalloe, S.A.; Hofland, B.; Van Wesenbeeck, B.K. Scaled versus real-scale tests: Identifying scale and model errors in wave damping through woody vegetation. Ecol. Eng. 2024, 202, 107241. [Google Scholar] [CrossRef]
- Reimann, S.; Husrin, S.; Strusińska, A.; Oumeraci, H. Damping Tsunami And Storm Waves By Coastal Forests—Parameterisation And Hydraulic Model Tests. In Proceedings of the FZK-Kolloquium “Potenziale für die Maritime Wirtschaft”, Hannover, Germany, 26 March 2009. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Company: Singapore, 2010; Volume 33. [Google Scholar]
- Foster-Martinez, M.R.; Lacy, J.R.; Ferner, M.C.; Variano, E.A. Wave attenuation across a tidal marsh in San Francisco Bay. Coast. Eng. 2018, 136, 26–40. [Google Scholar] [CrossRef]
- Phan, K.L.; Stive, M.J.F.; Zijlema, M.; Truong, H.S.; Aarninkhof, S.G.J. The effects of wave non-linearity on wave attenuation by vegetation. Coast. Eng. 2019, 147, 63–74. [Google Scholar] [CrossRef]




| No. | Source | Scale Ratio | Vegetation | Formula | Scope |
|---|---|---|---|---|---|
| 1 | Maza, Adler, Ramos, Garcia, and Nepf [34] | 1:12 | Model with stem and root | 500 < < 1700 | |
| 2 | He, Chen, and Jiang [23] | 1:10 | Model with stem, root, and canopy | 10 < < 37 | |
| 3 | Wang, Yin, and Liu [21] | 1:10 | Model with stem and root | 0.01 < < 0.28 | |
| 4 | Chang, Mori, Tsuruta, Suzuki, and Yanagisawa [27] | 1:7 | Model with stem and root | 2.5 < < 20 180 < < 1300 | |
| 5 | Bryant, et al. [35] | 1:2.1 | Model with stem and root | 0 < < 12 | |
| 6 | Kelty, Tomiczek, Cox, Lomonaco, and Mitchell [26] | 1:1 | Model with stem and root | 0 < < 12 | |
| 7 | Zhang, Chen, Lei, Zhou, Yao, and Stive [20] | 1:10 | Model with stem, root, and canopy | 500 < < 1700 34,900 < < 40,700 0.73 < < 21.33 |
| Case | Prototype | Model (G1) | Model (G8) | Wave Type | With Mangrove Model or Not | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (s) | (m) | (m) | (s) | (m) | (m) | (s) | (m) | |||
| A1 | 4.1 | 6.0 | 1.8 | 0.41 | 1.90 | 0.18 | 0.36 | 1.90 | 0.16 | Irregular | No Model |
| A2 | 4.1 | 5.0 | 1.5 | 0.41 | 1.58 | 0.15 | 0.36 | 1.58 | 0.14 | Irregular | No Model |
| A3 | 4.1 | 4.0 | 1.2 | 0.41 | 1.26 | 0.12 | 0.36 | 1.26 | 0.10 | Irregular | No Model |
| A4 | 4.1 | 3.0 | 0.8 | 0.41 | 0.95 | 0.08 | 0.36 | 0.95 | 0.08 | Irregular | No Model |
| A5 | 3.73 | 6.0 | 1.8 | 0.373 | 1.90 | 0.18 | 0.323 | 1.90 | 0.14 | Irregular | No Model |
| A6 | 3.73 | 5.0 | 1.5 | 0.373 | 1.58 | 0.15 | 0.323 | 1.58 | 0.14 | Irregular | No Model |
| A7 | 3.73 | 6.0 | 1.5 | 0.373 | 1.90 | 0.15 | 0.323 | 1.90 | 0.14 | Irregular | No Model |
| A8 | 3.73 | 7.0 | 1.2 | 0.373 | 2.21 | 0.12 | 0.323 | 2.21 | 0.13 | Irregular | No Model |
| A9 | 3.73 | 6.0 | 1.2 | 0.373 | 1.90 | 0.12 | 0.323 | 1.90 | 0.11 | Irregular | No Model |
| A10 | 3.73 | 5.0 | 1.2 | 0.373 | 1.58 | 0.12 | 0.323 | 1.58 | 0.12 | Irregular | No Model |
| A11 | 3.73 | 4.0 | 1.2 | 0.373 | 1.26 | 0.12 | 0.323 | 1.26 | 0.11 | Irregular | No Model |
| A12 | 3.73 | 6.0 | 0.8 | 0.373 | 1.90 | 0.08 | 0.323 | 1.90 | 0.09 | Irregular | No Model |
| A13 | 3.73 | 3.0 | 0.8 | 0.373 | 0.95 | 0.08 | 0.323 | 0.95 | 0.05 | Irregular | No Model |
| A14 | 3.2 | 5.0 | 1.5 | 0.32 | 1.58 | 0.15 | 0.27 | 1.58 | 0.12 | Irregular | No Model |
| A15 | 3.2 | 6.0 | 1.5 | 0.32 | 1.90 | 0.15 | 0.27 | 1.90 | 0.12 | Irregular | No Model |
| A16 | 3.2 | 7.0 | 1.2 | 0.32 | 2.21 | 0.12 | 0.27 | 2.21 | 0.12 | Irregular | No Model |
| A17 | 3.2 | 6.0 | 1.2 | 0.32 | 1.90 | 0.12 | 0.27 | 1.90 | 0.12 | Irregular | No Model |
| A18 | 3.2 | 5.0 | 1.2 | 0.32 | 1.58 | 0.12 | 0.27 | 1.58 | 0.12 | Irregular | No Model |
| A19 | 3.2 | 4.0 | 1.2 | 0.32 | 1.26 | 0.12 | 0.27 | 1.26 | 0.10 | Irregular | No Model |
| A20 | 3.2 | 6.0 | 0.8 | 0.32 | 1.90 | 0.08 | 0.27 | 1.90 | 0.08 | Irregular | No Model |
| A21 | 3.2 | 3.0 | 0.8 | 0.32 | 0.95 | 0.08 | 0.27 | 0.95 | 0.07 | Irregular | No Model |
| B1 | 4.1 | 6.0 | 1.8 | 0.41 | 1.90 | 0.18 | 0.36 | 1.90 | 0.16 | Irregular | With Model |
| B2 | 4.1 | 5.0 | 1.5 | 0.41 | 1.58 | 0.15 | 0.36 | 1.58 | 0.14 | Irregular | With Model |
| B3 | 4.1 | 4.0 | 1.2 | 0.41 | 1.26 | 0.12 | 0.36 | 1.26 | 0.10 | Irregular | With Model |
| B4 | 4.1 | 3.0 | 0.8 | 0.41 | 0.95 | 0.08 | 0.36 | 0.95 | 0.08 | Irregular | With Model |
| B5 | 4.1 | 6.0 | 1.8 | 0.41 | 1.90 | 0.18 | 0.36 | 1.90 | 0.16 | Regular | With Model |
| B6 | 4.1 | 5.0 | 1.5 | 0.41 | 1.58 | 0.15 | 0.36 | 1.58 | 0.14 | Regular | With Model |
| B7 | 3.73 | 6.0 | 1.8 | 0.373 | 1.90 | 0.18 | 0.323 | 1.90 | 0.14 | Irregular | With Model |
| B8 | 3.73 | 5.0 | 1.5 | 0.373 | 1.58 | 0.15 | 0.323 | 1.58 | 0.14 | Irregular | With Model |
| B9 | 3.73 | 6.0 | 1.5 | 0.373 | 1.90 | 0.15 | 0.323 | 1.90 | 0.14 | Irregular | With Model |
| B10 | 3.73 | 7.0 | 1.2 | 0.373 | 2.21 | 0.12 | 0.323 | 2.21 | 0.13 | Irregular | With Model |
| B11 | 3.73 | 6.0 | 1.2 | 0.373 | 1.90 | 0.12 | 0.323 | 1.90 | 0.11 | Irregular | With Model |
| B12 | 3.73 | 5.0 | 1.2 | 0.373 | 1.58 | 0.12 | 0.323 | 1.58 | 0.12 | Irregular | With Model |
| B13 | 3.73 | 4.0 | 1.2 | 0.373 | 1.26 | 0.12 | 0.323 | 1.26 | 0.11 | Irregular | With Model |
| B14 | 3.73 | 6.0 | 0.8 | 0.373 | 1.90 | 0.08 | 0.323 | 1.90 | 0.09 | Irregular | With Model |
| B15 | 3.73 | 3.0 | 0.8 | 0.373 | 0.95 | 0.08 | 0.323 | 0.95 | 0.05 | Irregular | With Model |
| B16 | 3.73 | 6.0 | 1.5 | 0.373 | 1.90 | 0.15 | 0.323 | 1.90 | 0.14 | Regular | With Model |
| B17 | 3.73 | 5.0 | 1.5 | 0.373 | 1.90 | 0.15 | 0.323 | 1.90 | 0.14 | Regular | With Model |
| B18 | 3.2 | 5.0 | 1.5 | 0.32 | 1.58 | 0.15 | 0.27 | 1.58 | 0.12 | Irregular | With Model |
| B19 | 3.2 | 6.0 | 1.5 | 0.32 | 1.90 | 0.15 | 0.27 | 1.90 | 0.12 | Irregular | With Model |
| B20 | 3.2 | 7.0 | 1.2 | 0.32 | 2.21 | 0.12 | 0.27 | 2.21 | 0.12 | Irregular | With Model |
| B21 | 3.2 | 6.0 | 1.2 | 0.32 | 1.90 | 0.12 | 0.27 | 1.90 | 0.12 | Irregular | With Model |
| B22 | 3.2 | 5.0 | 1.2 | 0.32 | 1.58 | 0.12 | 0.27 | 1.58 | 0.12 | Irregular | With Model |
| B23 | 3.2 | 4.0 | 1.2 | 0.32 | 1.26 | 0.12 | 0.27 | 1.26 | 0.10 | Irregular | With Model |
| B24 | 3.2 | 6.0 | 0.8 | 0.32 | 1.90 | 0.08 | 0.27 | 1.90 | 0.08 | Irregular | With Model |
| B25 | 3.2 | 3.0 | 0.8 | 0.32 | 0.95 | 0.08 | 0.27 | 0.95 | 0.07 | Irregular | With Model |
| B26 | 3.2 | 7.0 | 1.2 | 0.32 | 2.21 | 0.12 | 0.27 | 2.21 | 0.12 | Regular | With Model |
| B27 | 3.2 | 6.0 | 1.5 | 0.32 | 1.90 | 0.15 | 0.27 | 1.90 | 0.12 | Regular | With Model |
| B28 | 3.2 | 6.0 | 1.2 | 0.32 | 1.90 | 0.12 | 0.27 | 1.90 | 0.12 | Regular | With Model |
| B29 | 3.2 | 6.0 | 0.8 | 0.32 | 1.90 | 0.08 | 0.27 | 1.90 | 0.12 | Regular | With Model |
| B30 | 3.2 | 5.0 | 1.5 | 0.32 | 1.58 | 0.15 | 0.27 | 1.58 | 0.12 | Regular | With Model |
| B31 | 3.2 | 5.0 | 1.2 | 0.32 | 1.58 | 0.12 | 0.27 | 1.58 | 0.10 | Regular | With Model |
| B32 | 3.2 | 4.0 | 1.2 | 0.32 | 1.26 | 0.12 | 0.27 | 1.26 | 0.08 | Regular | With Model |
| B33 | 3.2 | 3.0 | 0.8 | 0.32 | 0.95 | 0.08 | 0.27 | 0.95 | 0.07 | Regular | With Model |
| Kandelia obovata | Tree Height (m) | Tree Diameter (m) | Canopy Width (m) | Canopy Height (m) | Leaf Length (cm) | Leaf Width (cm) | Plant Spacing (m) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|---|---|
| Prototype | 1.90 | 0.10 | 1.20 | 0.70 | 2.5~4.5 | 1.5~2 | 1.0 | 0.1~0.11 × 105 |
| Model | 0.19 | 0.01 | 0.12 | 0.07 | 0.4 | 0.2 | 0.1 | 0.01 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Luo, Y.; Zeng, J.; Zhang, Z.; Hu, J.; Xu, Y.; Cheng, W. Laboratory Study on Wave Attenuation by Elastic Mangrove Model with Canopy. J. Mar. Sci. Eng. 2024, 12, 1198. https://doi.org/10.3390/jmse12071198
Lu Y, Luo Y, Zeng J, Zhang Z, Hu J, Xu Y, Cheng W. Laboratory Study on Wave Attenuation by Elastic Mangrove Model with Canopy. Journal of Marine Science and Engineering. 2024; 12(7):1198. https://doi.org/10.3390/jmse12071198
Chicago/Turabian StyleLu, Youxiang, Yongjun Luo, Jian Zeng, Zhiyong Zhang, Jielong Hu, Yanan Xu, and Wenlong Cheng. 2024. "Laboratory Study on Wave Attenuation by Elastic Mangrove Model with Canopy" Journal of Marine Science and Engineering 12, no. 7: 1198. https://doi.org/10.3390/jmse12071198





