Investigation on Calm Water Resistance of Wind Turbine Installation Vessels with a Type of T-BOW
Abstract
:1. Introduction
- (1)
- Ship general layout optimization: Given that the majority of the operational time for WTIVs is spent in elevated conditions, it is crucial to maximize the platform’s anti-overturning stability and the working area on the main deck during this state. Consequently, the legs of the WTIV are typically positioned as far towards the bow and stern as possible. Additionally, within the limited available space, the leg and spudcans must be accommodated at the bottom and along the sides of the vessel.
- (2)
- Ship main dimension optimization: Given the importance of the vessel’s DP capabilities, precise control over the main dimensions is critical. The common formula used in ocean engineering to estimate bow tunnel thruster force (Huang et al. [1]), , where denotes the required thrust, and represent the lateral areas above and below the waterline affected by wind and flow loads, respectively, with as the thrust ratios. The T-BOW design minimizes vessel length to reduce lateral exposure to wind and flow, thus enhancing dynamic positioning capabilities.
- (3)
- Thruster efficiency optimization: The new generation WTIVs are typically equipped with two or three sets of bow tunnel thrusters to maximize thruster efficiency while balancing the constraints of initial investment costs and requirements for DP-2 level dynamic positioning capabilities. Engineering principles dictate that the length of bow thruster tunnel structures should not exceed approximately six times the diameter of the propeller. However, design requirements for anti-overturning stability and a broad operational deck area often lead to vessel widths of 40–60 m. Traditional bows would result in excessively long rear bow thruster tunnels, which could compromise thruster efficiency. The T-BOW design effectively reduces the length of lateral thruster tunnels to enhance propeller efficiency.
- (1)
- Impact of Hull Form on Resistance: WTIVs generally feature a wide beam and a high block coefficient (CB), leading to a bow design that exhibits a full and blunt form. This characteristic tends to induce blockage effects in the surrounding fluid flow, and the prominent shoulder region at the bow is prone to generating shoulder waves, which adversely affects wave-making resistance.
- (2)
- Bow and Stern Design Constraints: The necessity to accommodate spudcan structures results in rapid transitions in the hull lines at the bow and stern shoulder areas, characteristic of a full and blunt hull form. The limited space at the bow and stern necessitates sharp transitions towards the parallel midbody, which can lead to boundary layer separation and vortex formation. These phenomena adversely impact the viscous pressure resistance of the vessel.
- (3)
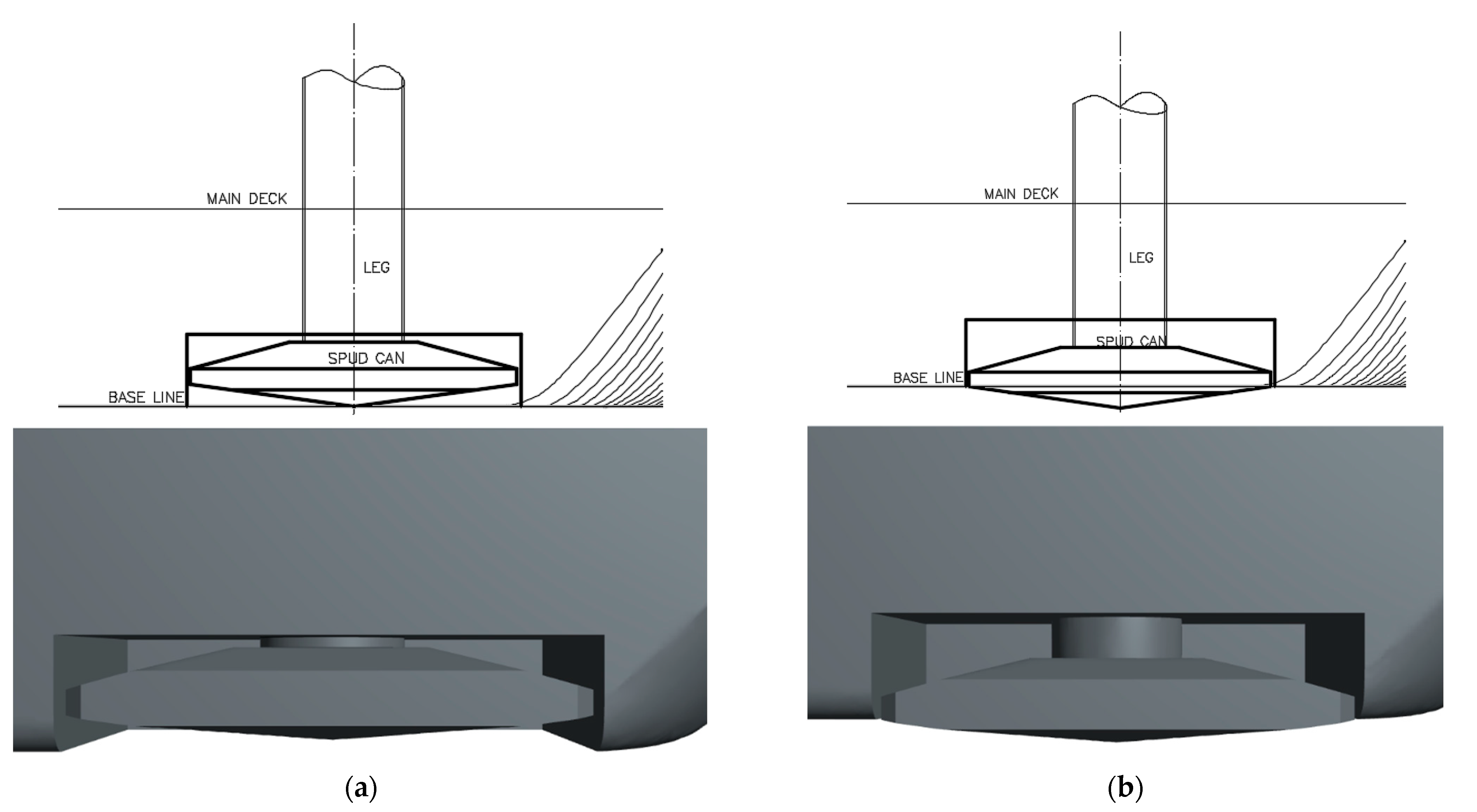
- Additional Resistance Due to Appendages: WTIVs are equipped with various appendages, including skegs, sea chests, and bow tunnel thruster openings, as well as spudcan retraction well areas, which are vertical cavities that connect the deck to the hull bottom. For large WTIVs, the spudcan retraction well area can exceed 200 m2, leading to significant “moonpool additional resistance” during navigation. Therefore, optimizing the spudcan structure design to align with the hull shell plate is crucial. Minimizing gaps and maintaining good flow continuity between the hull and spudcan structures is key to improving the vessel’s resistance performance.
2. Methods for Resistance Prediction of WTIVs
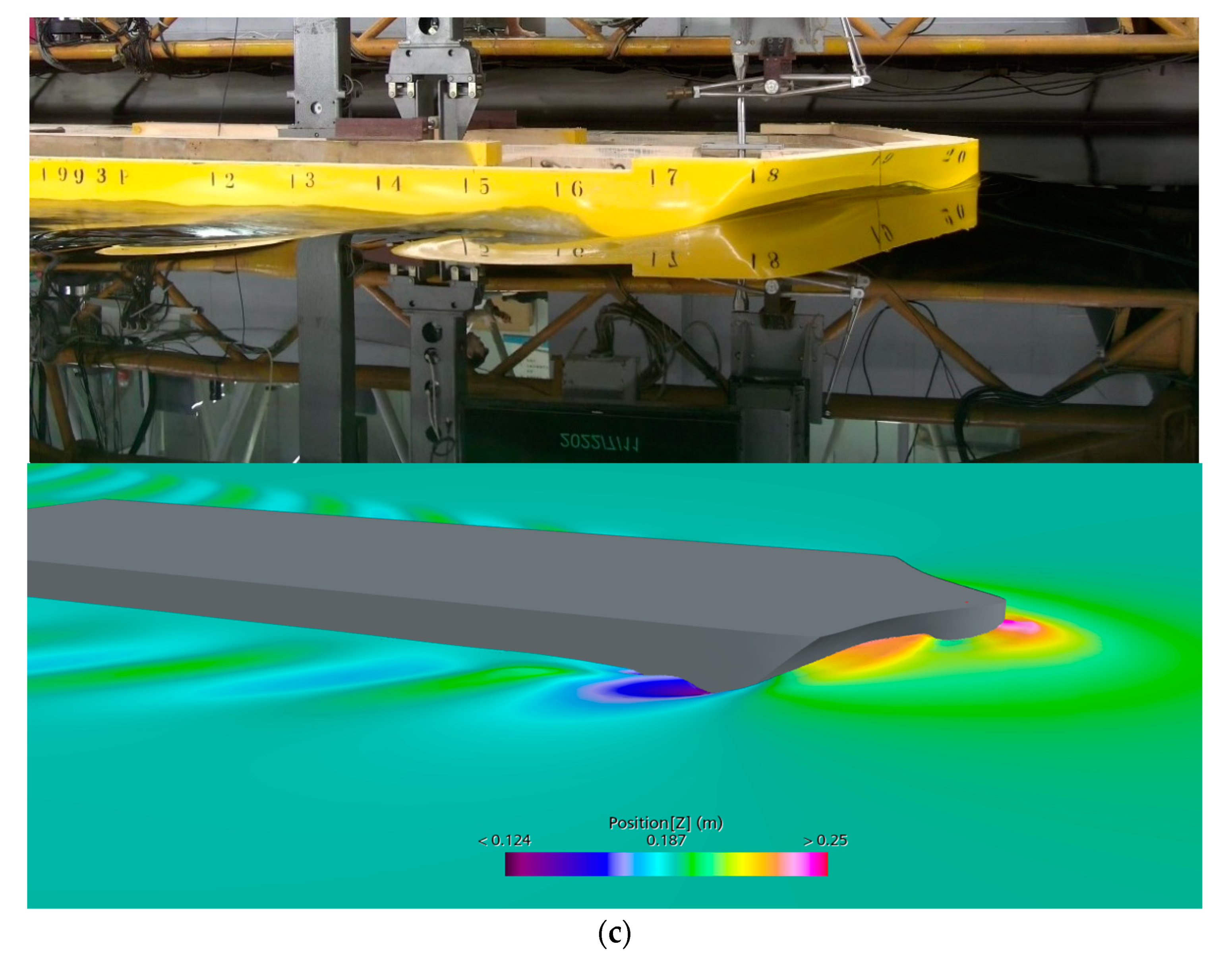
2.1. Model Test Method
2.2. Numerical Simulation Method
2.2.1. Governing Equations and Turbulence Model
2.2.2. CFD Modelling
2.3. Empirical Formula Estimation Method
3. Analysis of Calm Water Resistance of WTIV_O
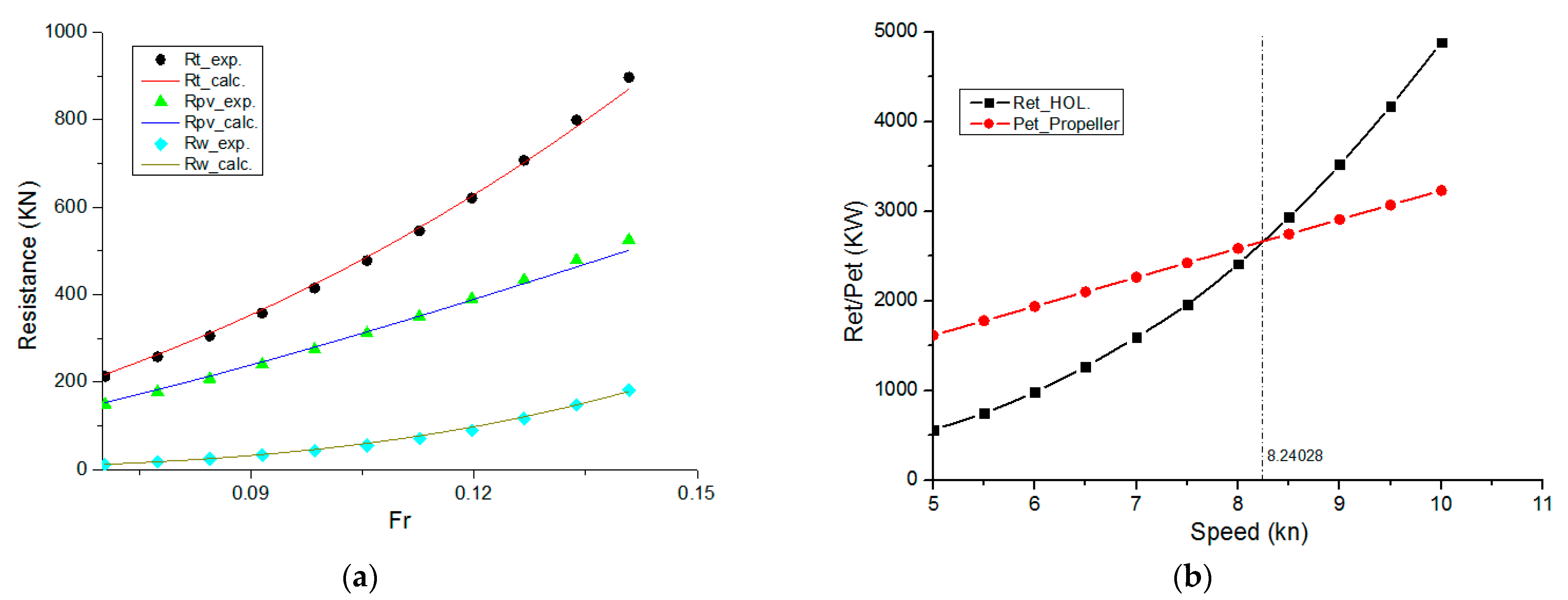
3.1. Test Results of Calm Water Resistance
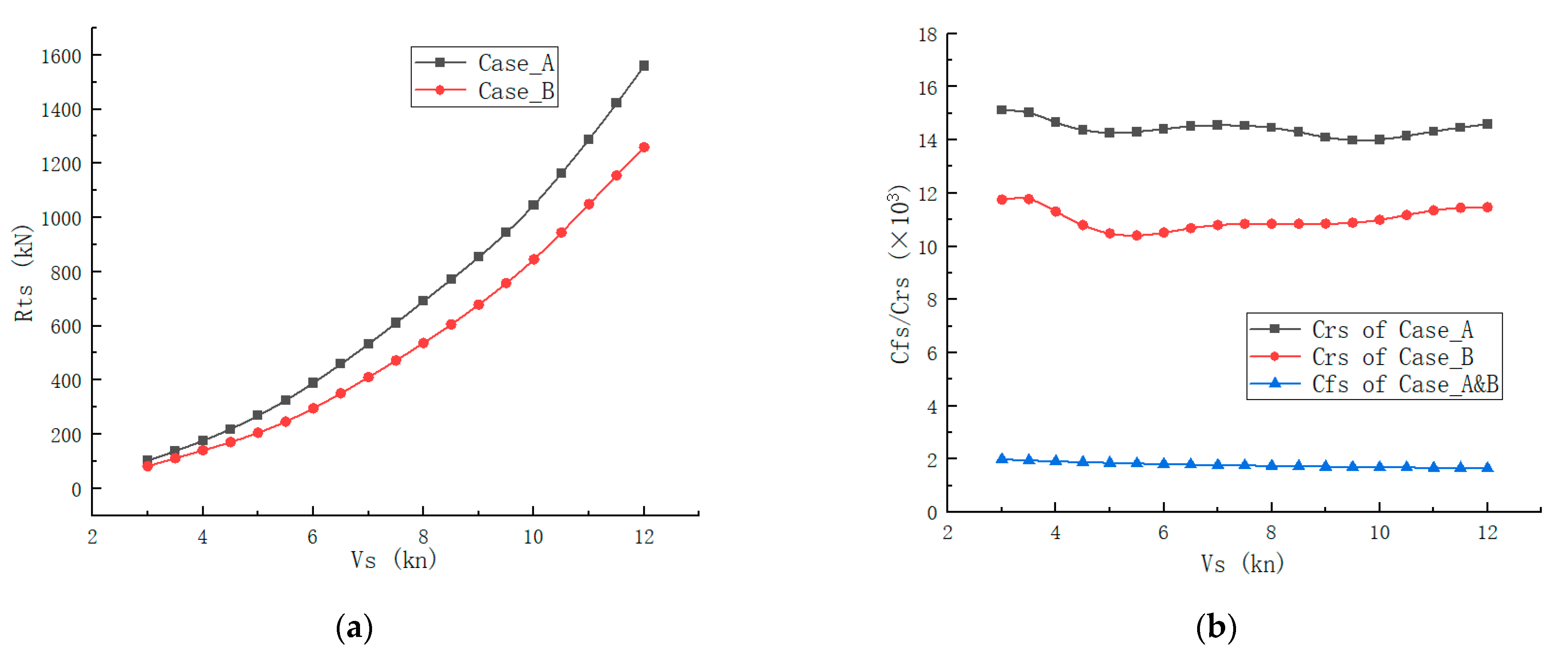
3.2. Analysis of Components of Calm Water Resistance
3.3. Numerical Results of Calm Water Resistance
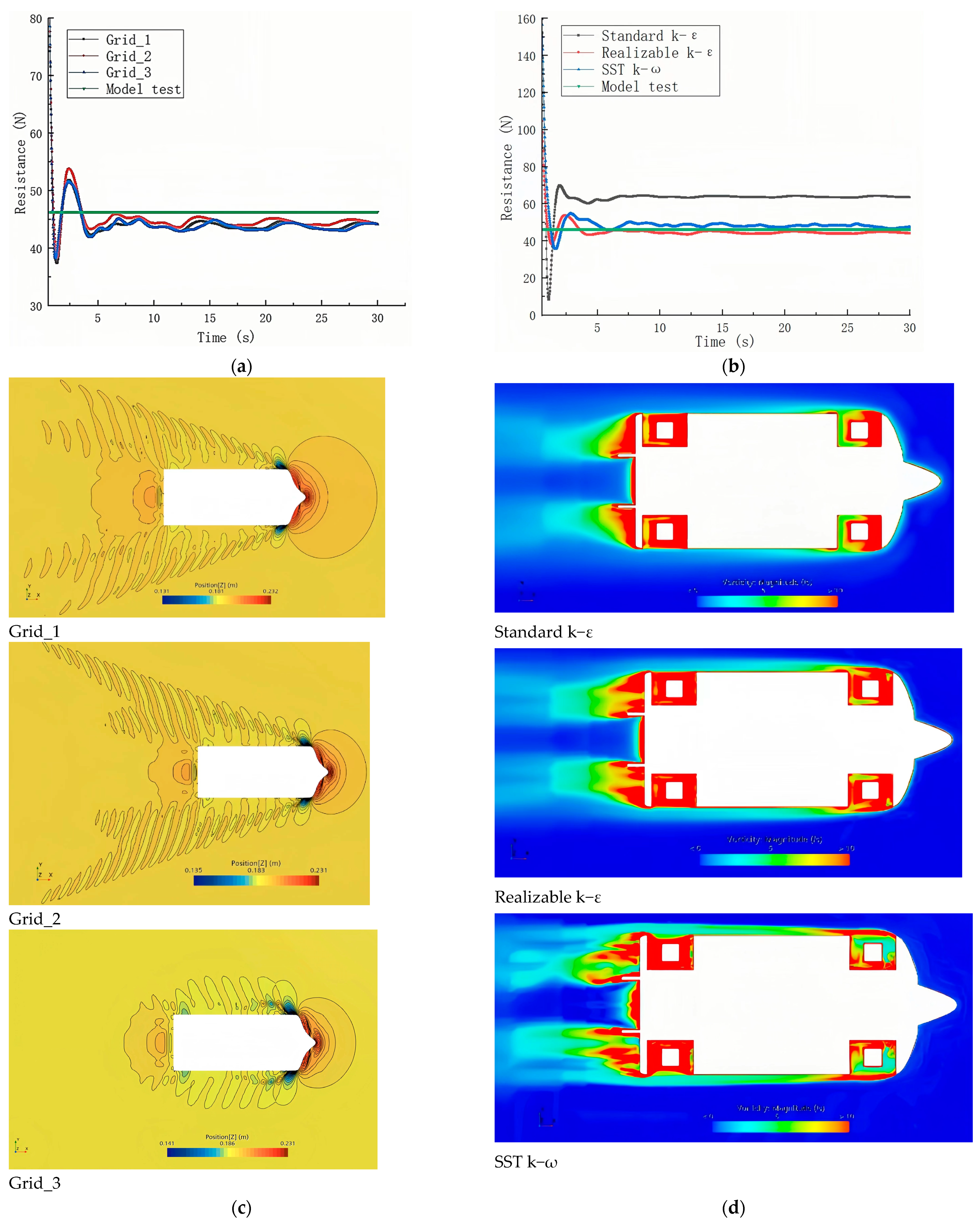
3.3.1. Precision and Convergence Analysis of the Numerical Method
- (1)
- Mesh generation
- (2)
- Turbulence Models
- (3)
- Selection of Time Step
3.3.2. Numerical Results of WTIV_O
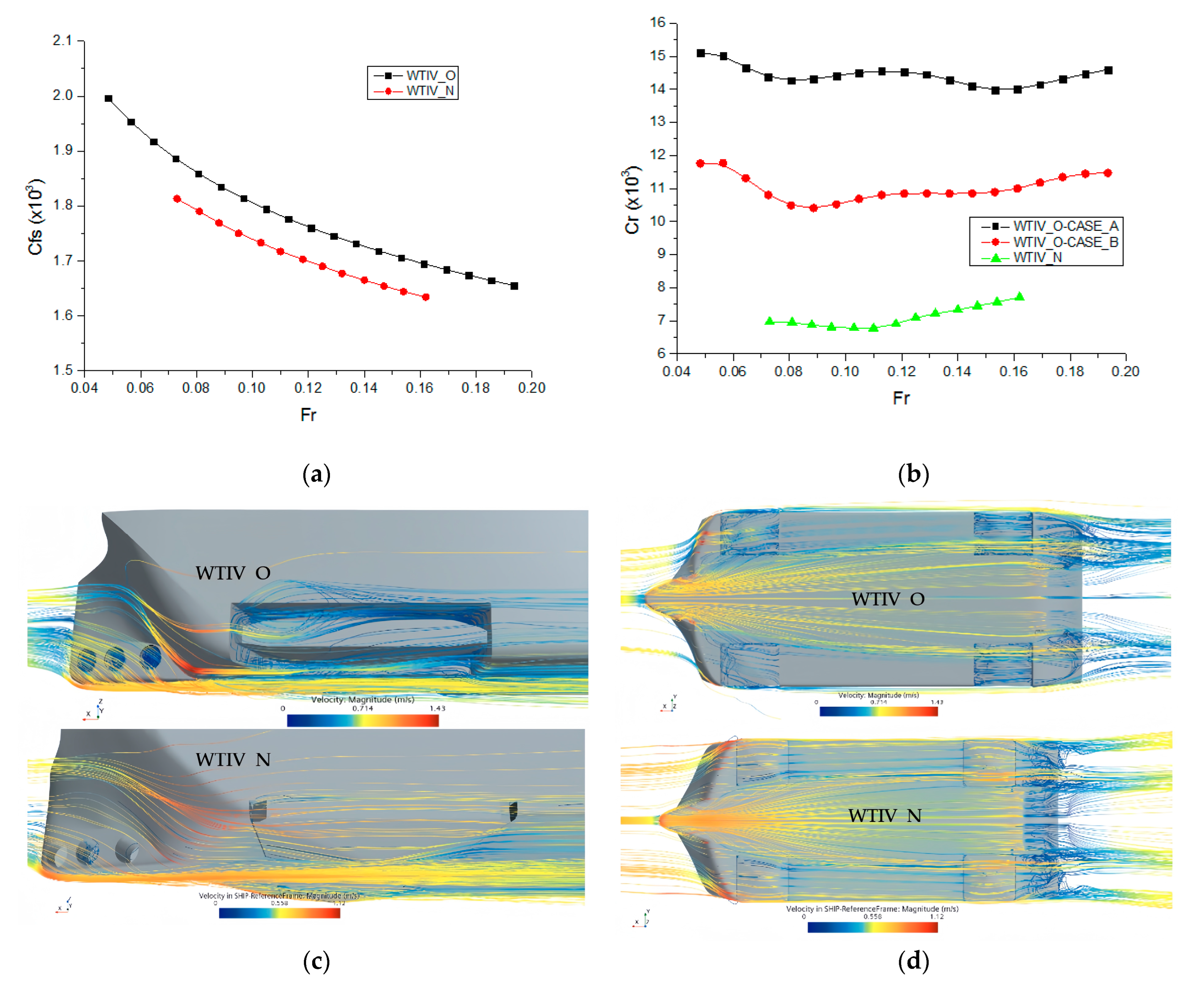
3.3.3. Comparative Analysis of Streamline
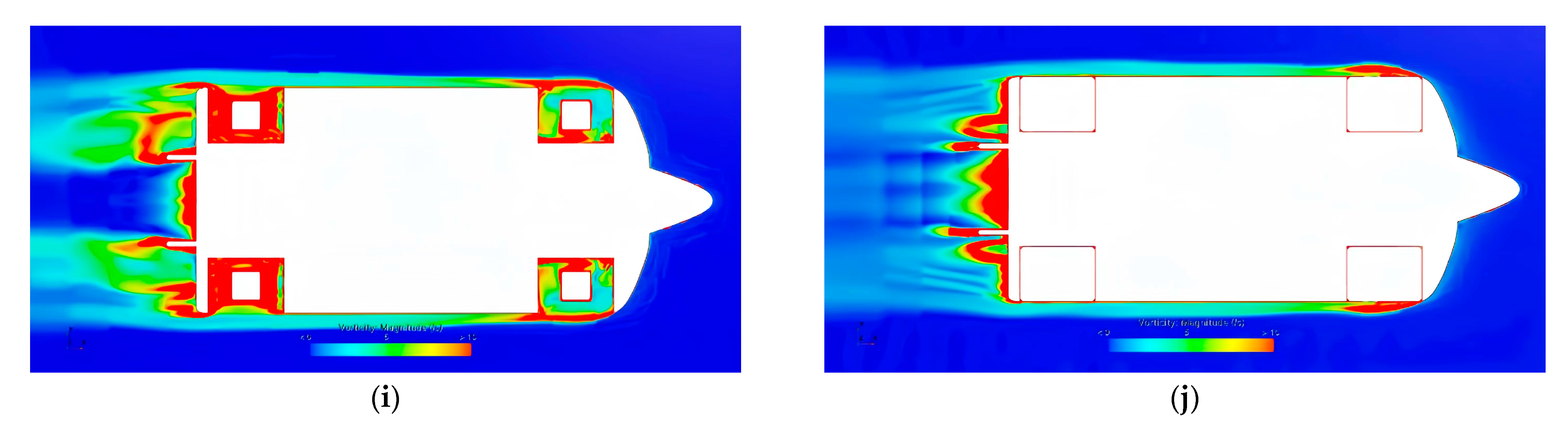
3.4. Generation Mechanism of Resistance
3.4.1. Viscous Pressure Resistance
3.4.2. Wave-Making Resistance
- (1)
- The generation of ship waves by WTIV is primarily due to changes in fluid pressure around the ship while navigating on the water surface, especially as the speed increases, creating a maximum pressure area at the bow shoulders, where the wave-making effect is strongest, as depicted in Figure 10c. Following this are the stern shoulders, where the line type changes abruptly, also producing noticeable stern shoulder waves. Such shoulder waves not only increase the ship’s wave-making resistance but may also cause adverse wave interference.
- (2)
- Analysis shows that the wave-making resistance of the WTIV is related to speed by a power function, with the proportion of wave-making resistance components increasing rapidly when the speed exceeds 9.5 knots.
3.4.3. Appendage Resistance
4. Optimization for Resistance Reduction of Next-Generation WTIV
4.1. Optimization Strategy
- (1)
- Bow structure, particularly the effective transition of line types in the spudcan retraction well area, with the aim to minimize excessive curvature and disturbances to the wave system at the bow shoulders.
- (2)
- Matching design between the spudcan structure and the ship’s bottom and side outer shells in the retraction well area to mitigate the “moonpool additional resistance effect” in the relevant region.
- (3)
- Considering the balance between displacement and weight distribution, the focus should be on the aft body’s flow design to ensure smoother fluid motion, more uniform pressure distribution, and reduced formation of stern vortices and energy loss, consequently lowering viscous pressure resistance.
4.2. Optimization Results
5. Empirical Formulas of WTIV Resistance Estimation Based on Holtrop Method
5.1. Empirical Formulas of Frictional Resistance Estimation
5.2. Empirical Formulas of Viscous Pressure Resistance Estimation
5.3. Empirical Formulas of Wave-Making Resistance Estimation
5.4. Case Study and Verification
6. Conclusions
- (1)
- Resistance Components: The calm water resistance of WTIVs consists of frictional resistance, viscous pressure resistance, and wave-making resistance. Viscous pressure resistance accounts for over 65% of the total, followed by frictional resistance at approximately 12–15%, and wave-making resistance at 1–20%. As speed increases, the coefficients of viscous pressure resistance and frictional resistance decrease, while wave-making resistance increases due to pronounced bow and stern shoulder waves, particularly beyond 9.5 knots, where wave-making resistance rises sharply. The noticeable shoulder waves at the abrupt changes in the hull lines underscore the need to focus on viscous pressure resistance and wave-making resistance at higher design speeds. This observation aligns with the design speeds of 8–9 knots for similarly scaled WTIVs in China.
- (2)
- Impact of Spudcan Retraction Well Area on Resistance: Analysis of the resistance impact with and without spudcan retraction wells reveals a significant “moonpool additional resistance effect”, increasing the total calm water resistance by approximately 30% at design speed. Therefore, the design of such vessels should prioritize the matching of the spudcan structures with the hull shell plate to minimize gaps, maintain flow field continuity, reduce the adverse effects of the spudcan retraction well area on flow, and diminish eddy intensity in this region, thereby improving resistance performance.
- (3)
- Selection of Turbulence Models for Resistance Prediction: The selection of turbulence models for the target vessel at different speeds should be based on Fr = 0.15. For lower speeds (Fr ≤ 0.15), the SST k-ω turbulence model is more suitable for predicting the resistance of low-speed ships. For higher speeds (Fr > 0.15), the Realizable k-ε model with wall functions provides higher accuracy due to the fully developed turbulence around the hull at higher Reynolds numbers.
- (4)
- Modification of Resistance Calculation Based on the Holtrop Method: Compared to model tests and CFD analysis, the empirical formula estimation method, which integrates existing estimation formulas with operational vessel data, offers advantages such as time efficiency and cost-effectiveness. This is particularly beneficial in the preliminary design phase of ships, providing designers with quick resistance estimation results and relatively accurate references for ship propulsion configuration and speed estimation. This study incorporates resistance data from multiple operational WTIVs to modify the Holtrop-based resistance calculation formulas, resulting in empirical formulas suitable for full and blunt hull form self-elevating WTIVs, especially those with spudcan retraction wells.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, P.T.; Wu, Q.; Li, G.A.; Ma, Y.D.; Wang, W. Pratical Handbook for Ship Design; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
- Kline, S. Describing uncertainty in single-sample experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Guo, B.J.; Deng, G.B.; Steen, S. Verification and validation of numerical calculation of ship resistance and flow field of a large tanker. Ships Offshore Struct. 2013, 8, 3–14. [Google Scholar] [CrossRef]
- Nikolov, M.; Judge, C. Uncertainty analysis for calm water tow tank measurements. J. Ship Res. 2017, 61, 177–197. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, J.T.; Chen, W.M.; Ma, X.Q. Uncertainty analysis of calibration ship model single-run resistance tests. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2020, 48, 85–90. [Google Scholar]
- Liu, H.; Ma, N.; Gu, X. Uncertainty analysis for ship-bank interaction tests in a circulating water channel. China Ocean Eng. 2020, 34, 352–361. [Google Scholar] [CrossRef]
- ITTC. Recommended procedures and guidelines, 7.5-03-02-03, Practical guidelines for ship CFD applications. In Proceedings of the International Towing Tank Conference, Virtual, 13–18 June 2021. [Google Scholar]
- Wu, C.S.; Qiu, G.Y.; Wei, Z.; Jin, Z.J. Uncertainty analysis on numerical computation of ship model resistance. J. Ship Mech. 2015, 19, 1197–1208. [Google Scholar]
- Wang, Z.; Liu, X.; Zhang, S.; Xu, L.; Zhou, P. Uncertainty analysis in CFD for resistance. J. Shipp. Ocean Eng. 2017, 7, 192–202. [Google Scholar]
- Islam, H.; Soares, C.G. Uncertainty analysis in ship resistance prediction using OpenFOAM. Ocean Eng. 2019, 191, 105805. [Google Scholar] [CrossRef]
- Tong, S.L.; Chen, Z.G. Uncertainty analysis of ship model resistance measurement in circulating water channel. Chin. J. Ship Res. 2020, 15, 144–152. [Google Scholar]
- Zhang, L.; Chen, W.; Chen, J.; Zhou, C. Verification and validation of CFD un-certainty analysis based on SST k-ω model. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Virtual, 3–7 August 2020; p. V008T008A044. [Google Scholar]
- Zhang, L.; Zhou, C.M.; Chen, W.M.; Chen, J.T. Uncertainty Analysis of CFD Results of Standard Ship Model Resistance. Ship Ocean Eng. 2020, 49, 33–36. [Google Scholar]
- Pena, B.; Huang, L. A review on the turbulence modelling strategy for ship hydrodynamic simulations. Ocean Eng. 2021, 241, 110082. [Google Scholar] [CrossRef]
- Bojovic, P. Resistance of AMECRC systematic series of high speed displacement hull forms. In The IV Symposium on High Speed Marine Vehicles, Naples, Italy, 18–21 March 1997; Australian Maritime Engineering: Launceston, Australia, 1997. [Google Scholar]
- Radojcic, D.; Zgradic, A.; Kalajdzic, M.; Simic, A. Resistance prediction for hard chine hulls in the pre-planing regime. Pol. Marit. Res. 2014, 21, 9–26. [Google Scholar] [CrossRef]
- Xu, C. Optimization and Hydrodynamic Study of Wind Turbine Installation Vessel. Master’s Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
- Huang, Y.N.; Chen, M.L.; Si, M.; Li, F.H.; Feng, J. Optimization of resistance reduction of offshore wind turbine installation vessel based on free-form deformation technique. J. Dalian Univ. Technol. 2023, 63, 61–68. [Google Scholar]
- Kang, Z.; Xu, X.; Ni, W.; Zhang, C. Hydrodynamic Analysis and Model Test Study of Wind Turbine Installation Vessel. In Proceedings of the Twenty-Seventh (2017) International Ocean and Polar Engineering Conference IOPE 2017, San Francisco, CA, USA, 25–30 June 2017; pp. 767–774. [Google Scholar]
- Jing, S.H. Self-Propelled Test and Resistance Numerical Analysis of Jack-Up Platform. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, June 2023. [Google Scholar]
- Kjær, R.B.; Shao, Y.; Walther, J.H. Experimental and CFD analysis of roll damping of a wind turbine installation vessel. Appl. Ocean. Res. 2024, 143, 103857. [Google Scholar] [CrossRef]
- Menter, F.R. Influence of Free stream Values on k-ω Turbulence Model Predictions. Aiaa J. 1992, 30, 1657–1659. [Google Scholar] [CrossRef]
- Xia, G.Z. Ship Fluid Mechanics; Huazhong University of Science and Technology Press: Wuhan, China, 2003. [Google Scholar]
- Yi, W.B.; Wang, Y.S.; Peng, Y.L.; Li, C.J. Resistance and flow field prediction of ship model with consideration of voyage attitude. J. Nav. Univ. Eng. 2016, 28, 26–30. [Google Scholar]
- Holtrop, J.; Mennen, G. An Approximate Power Prediction Method; International Shipbuilding Progress: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Julianto, R.; Prabowo, A.; Muhayat, N.; Putranto, T.; Adiputra, R. Investigation of hull design to quantify resistance criteria using Holtrop’s regression-based method and Savitsky’s mathematical model: A study case of fishing vessels. J. Eng. Sci. Technol. 2021, 16, 1426–1443. [Google Scholar]
- Nikolopoulos, L.; Boulougouris, E. A study on the statistical calibration of the Holtrop and Mennen approximate power prediction method for full hull form, low Froude number vessels. J. Ship Prod. Des. 2019, 35, 41–68. [Google Scholar] [CrossRef]
- Crudu, L.; Bosoancă, R.; Obreja, D. A comparative review of the resistance of a 37,000 dwt Chemical Tanker based on experimental tests and calculations. Tech. Rom. J. Appl. Sci. Technol. 2020, 1, 59–66. [Google Scholar]
- Wang, N.; Zhou, Z. Analysis of Improved Ship Resistance Holtrop Prediction Method. Ship Ocean Eng. 2019, 8, 34–37. [Google Scholar]
- Sheng, Z.B.; Liu, Y.Z. Principles of Ship Design; Shanghai Jiao Tong University Press: Shanghai China, 2017; ISBN 978-7-313-17996-8/U661. [Google Scholar]
- Hu, J.M. Study on Ship Powering Performance Prediction Based on Virtual Experimental Tank of RANS Method. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Deng, R. Numerical Research on Influence of the Interceptor on Catamaran Hydrodynamic Performances. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2010. [Google Scholar]
- Duan, F.; Ma, N.; Zhang, L.J.; Cao, K.; Zhang, Q. Research on the influence of the moonpool scale effect on the navigation resistance of drilling ships. J. Ship Mech. 2020, 24, 1254–1260. [Google Scholar]
- Lin, Y.; He, J.Y. Prediction of Ship Resistance and Free Motion Based on RANS Method. Ship Eng. 2019, 41, 52–57. [Google Scholar]

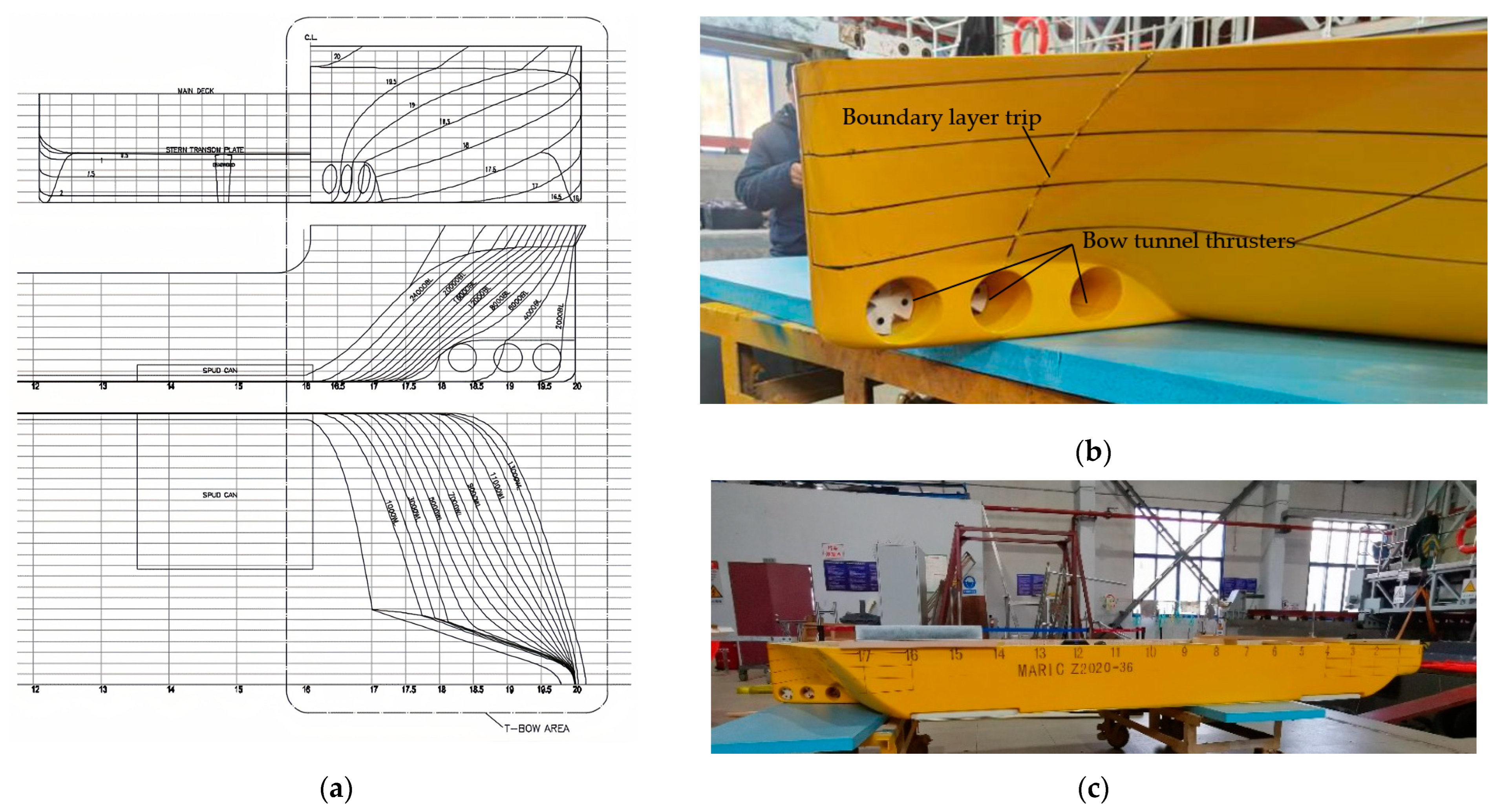






| Property | ZHEN JIANG | TIE JIAN FENG DIAN 01 | HY 78/79 | BAI HE TAN | LAN KUN 01 |
|---|---|---|---|---|---|
| Length on water line, Lwl (m) | 103.8 | 105 | 110.4 | 125 | 136 |
| Breadth, B (m) | 41 | 42 | 42 | 50 | 50 |
| Depth, D (m) | 8.2 | 8.5 | 8.5 | 10 | 10 |
| Block coefficient, CB | 0.822 | 0.824 | 0.834 | 0.801 | 0.816 |
| Draft, T (m) | 5.2 | 5.4 | 5.4 | 6.2 | 6 |
| Speed, V (kn) | 7 | 8 | - | 9 | 8 |
| Azimuth thruster AFT | 3 × 1800 kW | 3 × 1800 kW | 3 × 1800 kW | 3 × 3000 kW | 3 × 2600 kW |
| Bow tunnel thruster | 3 × 750 kW | 3 × 900 kW | 3 × 900 kW | 3 × 1500 kW | 3 × 1600 kW |
| DP class | DP-1 | DP-2 | DP-1 | DP-2 | DP-2 |
| Leg number & Type | 4 × cylindrical shell type | 4 × cylindrical shell type | 4 × cylindrical shell type | 4 × Triangular open truss type | 4 × Triangular open truss type |
| Max. holding Capacity per Leg (t) | 7000 | 7200 | 7200 | 13,500 | 14,000 |
| Single Spudcan size (m2) | 133 | 133 | 131 | 205 | 210 |
| Deadwood number | 2 | 2 | 2 | 2 | 2 |
| Wind turbine installation capacity | 8 MW | 8 MW | 10 MW | 13 MW | 15 MW |
| Property | WTIV_O | WTIV_N | ||
|---|---|---|---|---|
| Full-Scale Vessel | Test Model | Full-Scale Vessel | Test Model | |
| Length overall, Loa (m) | 103.8 | 3.7976 | 126 | 3.6 |
| Length on water line, Lwl (m) | 103.8 | 3.7976 | 125 | 3.5714 |
| Breadth, B (m) | 41 | 1.5 | 50 | 1.4286 |
| Depth, D (m) | 8.2 | 0.3 | 10 | 0.2857 |
| Design draught, d (m) | 5.2 | 0.1902 | 6.2 | 0.1771 |
| Displacement, (ton) | 18,293 | 0.8932 | 32,530 | 0.7403 |
| Vs (kn) | Frm | Vm (m/s) | Case_A | Case_B | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rtm | Ctm | Cfm | Crm | Rtm | Ctm | Cfm | Crm | |||
| (N) | ×103 | ×103 | ×103 | (N) | ×103 | ×103 | ×103 | |||
| 3.0 | 0.048 | 0.295 | 5.72 | 19.97 | 4.86 | 15.10 | 4.76 | 16.61 | 4.86 | 11.75 |
| 3.5 | 0.056 | 0.344 | 7.68 | 19.71 | 4.70 | 15.01 | 6.42 | 16.46 | 4.70 | 11.76 |
| 4.0 | 0.064 | 0.394 | 9.78 | 19.22 | 4.57 | 14.65 | 8.08 | 15.87 | 4.57 | 11.30 |
| 4.5 | 0.073 | 0.443 | 12.13 | 18.83 | 4.45 | 14.37 | 9.82 | 15.25 | 4.45 | 10.79 |
| 5.0 | 0.081 | 0.492 | 14.81 | 18.62 | 4.36 | 14.26 | 11.80 | 14.83 | 4.36 | 10.48 |
| 5.5 | 0.089 | 0.541 | 17.87 | 18.57 | 4.27 | 14.30 | 14.12 | 14.67 | 4.27 | 10.40 |
| 6.0 | 0.097 | 0.590 | 21.30 | 18.60 | 4.19 | 14.40 | 16.84 | 14.70 | 4.19 | 10.51 |
| 6.5 | 0.105 | 0.640 | 25.04 | 18.63 | 4.13 | 14.50 | 19.90 | 14.80 | 4.13 | 10.68 |
| 7.0 | 0.113 | 0.689 | 29.01 | 18.61 | 4.07 | 14.54 | 23.17 | 14.86 | 4.07 | 10.79 |
| 7.5 | 0.121 | 0.738 | 33.17 | 18.53 | 4.01 | 14.53 | 26.57 | 14.85 | 4.01 | 10.84 |
| 8.0 | 0.129 | 0.787 | 37.47 | 18.40 | 3.96 | 14.44 | 30.13 | 14.80 | 3.96 | 10.84 |
| 8.5 | 0.137 | 0.836 | 41.82 | 18.19 | 3.91 | 14.28 | 33.90 | 14.75 | 3.91 | 10.84 |
| 9.0 | 0.145 | 0.886 | 46.28 | 17.96 | 3.87 | 14.09 | 37.91 | 14.71 | 3.87 | 10.84 |
| 9.5 | 0.153 | 0.935 | 51.12 | 17.80 | 3.83 | 13.98 | 42.22 | 14.70 | 3.83 | 10.88 |
| 10.0 | 0.161 | 0.984 | 56.60 | 17.79 | 3.79 | 14.00 | 47.01 | 14.78 | 3.79 | 10.99 |
| 10.5 | 0.169 | 1.033 | 62.75 | 17.89 | 3.75 | 14.14 | 52.33 | 14.92 | 3.75 | 11.17 |
| 11.0 | 0.177 | 1.082 | 69.39 | 18.02 | 3.72 | 14.31 | 57.97 | 15.06 | 3.72 | 11.34 |
| 11.5 | 0.185 | 1.132 | 76.34 | 18.14 | 3.69 | 14.46 | 63.65 | 15.13 | 3.69 | 11.44 |
| 12.0 | 0.193 | 1.181 | 83.60 | 18.25 | 3.66 | 14.59 | 69.26 | 15.12 | 3.66 | 11.46 |
| Grid Scheme | Grid Size (m) | Grid Number (Million) | Numerical Value (N) | Experimental Value (N) | Error (%) | Computational Time (h) |
|---|---|---|---|---|---|---|
| Grid_1 | 0.076 (2.0% Lwl) | 12.14 | 43.79 | 46.28 | −5.38 | 3.8 |
| Grid_2 | 0.106 (2.8% Lwl) | 7.71 | 44.46 | 46.28 | −3.94 | 2.4 |
| Grid_3 | 0.152 (4.0% Lwl) | 5.70 | 43.6 | 46.28 | −5.79 | 1.9 |
| Turbulence Models | Calculation Value (N) | Experimental Value (N) | Error (%) | Computational Time (h) |
|---|---|---|---|---|
| Standard k-ε | 63.71 | 46.28 | 37.63 | 2.5 |
| Realizable k-ε | 44.46 | 46.28 | −3.95 | 2.4 |
| SST k-ω | 48.04 | 46.28 | 3.78 | 2.7 |
| Time Step (s) | Calculation Value (N) | Experimental Value (N) | Error (%) | Computational Time (h) |
|---|---|---|---|---|
| 0.010 | 44.53 | 46.28 | −3.78 | 5.5 |
| 0.020 | 44.46 | 46.28 | −3.93 | 2.3 |
| 0.030 | 44.4 | 46.28 | −4.06 | 1.7 |
| Vs (kn) | Frm | Vm (m/s) | Rtm_EXP. (N) | SST k − ω | Realizable k − ε | Bare Hull | |||
|---|---|---|---|---|---|---|---|---|---|
| Rt_CFD (N) | Error (%) | Rt_CFD (N) | Error (%) | Rt_CFD (N) | Difference with Case_A (%) | ||||
| 3.0 | 0.05 | 0.30 | 5.72 | 5.74 | 0.47 | 4.89 | −14.47 | 3.92 | −31.47 |
| 3.5 | 0.06 | 0.34 | 7.68 | 7.64 | −0.57 | 6.59 | −14.23 | 5.21 | −32.16 |
| 4.0 | 0.06 | 0.39 | 9.78 | 9.93 | 1.44 | 8.62 | −11.90 | 6.68 | −31.70 |
| 4.5 | 0.07 | 0.44 | 12.13 | 12.46 | 2.76 | 10.88 | −10.30 | 8.25 | −31.99 |
| 5.0 | 0.08 | 0.49 | 14.81 | 15.30 | 3.35 | 13.41 | −9.43 | 9.87 | −33.36 |
| 5.5 | 0.09 | 0.54 | 17.87 | 18.12 | 1.40 | 16.06 | −10.13 | 11.64 | −34.86 |
| 6.0 | 0.10 | 0.59 | 21.30 | 21.43 | 0.63 | 19.11 | −10.28 | 13.49 | −36.67 |
| 6.5 | 0.11 | 0.64 | 25.04 | 24.89 | −0.60 | 22.48 | −10.22 | 15.63 | −37.58 |
| 7.0 | 0.11 | 0.69 | 29.01 | 28.87 | −0.49 | 26.1 | −10.03 | 18.00 | −37.95 |
| 7.5 | 0.12 | 0.74 | 33.17 | 33.21 | 0.13 | 29.97 | −9.65 | 20.66 | −37.71 |
| 8.0 | 0.13 | 0.79 | 37.47 | 37.81 | 0.91 | 34.4 | −8.20 | 23.05 | −38.48 |
| 8.5 | 0.14 | 0.84 | 41.82 | 43.01 | 2.84 | 39.06 | −6.61 | 25.88 | −38.12 |
| 9.0 | 0.15 | 0.89 | 46.28 | 48.04 | 3.80 | 44.46 | −3.94 | 29.08 | −37.17 |
| 9.5 | 0.15 | 0.94 | 51.12 | 53.89 | 5.42 | 49.99 | −2.21 | 32.65 | −36.13 |
| 10.0 | 0.16 | 0.98 | 56.60 | 59.47 | 5.07 | 55.81 | −1.40 | 36.77 | −35.04 |
| 10.5 | 0.17 | 1.03 | 62.75 | 66.27 | 5.60 | 62.45 | −0.48 | 41.67 | −33.59 |
| 11.0 | 0.18 | 1.08 | 69.39 | 73.06 | 5.29 | 69.35 | −0.06 | 45.62 | −34.26 |
| 11.5 | 0.19 | 1.13 | 76.34 | 80.96 | 6.06 | 77.06 | 0.95 | 51.18 | −32.96 |
| 12.0 | 0.19 | 1.18 | 83.60 | 89.78 | 7.39 | 85.17 | 1.88 | 55.77 | −33.29 |
| Vs (kn) | Fr | Rtm (N) | Ctm × 103 | Cfm × 103 | Cr × 103 | Cfs × 103 | Cts × 103 | Rts (kN) |
|---|---|---|---|---|---|---|---|---|
| 5 | 0.073 | 6.44 | 11.336 | 4.375 | 6.961 | 1.813 | 8.774 | 236.46 |
| 5.5 | 0.081 | 7.72 | 11.232 | 4.289 | 6.943 | 1.790 | 8.732 | 284.76 |
| 6 | 0.088 | 9.06 | 11.079 | 4.213 | 6.866 | 1.769 | 8.635 | 335.13 |
| 6.5 | 0.095 | 10.50 | 10.943 | 4.144 | 6.799 | 1.750 | 8.549 | 389.38 |
| 7 | 0.103 | 12.08 | 10.855 | 4.082 | 6.773 | 1.733 | 8.506 | 449.32 |
| 7.5 | 0.110 | 13.79 | 10.794 | 4.026 | 6.769 | 1.717 | 8.486 | 514.60 |
| 8 | 0.118 | 15.80 | 10.871 | 3.974 | 6.897 | 1.703 | 8.600 | 593.34 |
| 8.5 | 0.125 | 18.08 | 11.015 | 3.926 | 7.088 | 1.690 | 8.778 | 683.69 |
| 9 | 0.132 | 20.40 | 11.091 | 3.882 | 7.209 | 1.677 | 8.886 | 775.91 |
| 9.5 | 0.140 | 22.89 | 11.166 | 3.841 | 7.325 | 1.665 | 8.990 | 874.68 |
| 10 | 0.147 | 25.54 | 11.246 | 3.802 | 7.444 | 1.654 | 9.098 | 980.84 |
| 10.5 | 0.154 | 28.36 | 11.326 | 3.766 | 7.559 | 1.644 | 9.203 | 1093.86 |
| 11 | 0.162 | 31.44 | 11.439 | 3.733 | 7.706 | 1.634 | 9.340 | 1218.35 |
| VS (kn) | RTPV_EXP (kN) | Rw_EXP (kN) | Rtclam_EXP (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| WTIV_O | WTIV_N | WTIV_3 | WTIV_O | WTIV_N | WTIV_3 | WTIV_O | WTIV_N | WTIV_3 | |
| 3 | 76.46 | - | - | 1.45 | - | - | 91.13 | - | - |
| 3.5 | 100.61 | - | - | 5.55 | - | - | 123.77 | - | - |
| 4 | 127.67 | - | - | 5.51 | - | - | 155.76 | - | - |
| 4.5 | 157.58 | - | - | 3.39 | - | - | 189.09 | - | - |
| 5 | 190.28 | 172.37 | 197.89 | 2.66 | 15.23 | 6.52 | 227.15 | 236.46 | 239.77 |
| 5.5 | 225.71 | 204.46 | 234.74 | 6.07 | 21.95 | 13.36 | 272.64 | 284.76 | 290.34 |
| 6 | 263.83 | 238.98 | 271.75 | 14.85 | 27.50 | 25.25 | 326.74 | 335.13 | 346.68 |
| 6.5 | 304.61 | 275.91 | 307.65 | 27.64 | 33.75 | 44.22 | 388.04 | 389.38 | 409.56 |
| 7 | 348.00 | 315.20 | 351.48 | 41.62 | 42.57 | 66.59 | 453.69 | 449.32 | 484.31 |
| 7.5 | 393.97 | 356.83 | 397.91 | 55.12 | 53.63 | 88.19 | 521.97 | 514.60 | 561.45 |
| 8 | 442.50 | 400.77 | 446.92 | 68.60 | 75.07 | 109.76 | 593.31 | 593.34 | 641.68 |
| 8.5 | 493.55 | 447.00 | 498.49 | 83.33 | 105.11 | 133.34 | 668.95 | 683.69 | 727.01 |
| 9 | 547.10 | 495.49 | 552.57 | 99.86 | 133.98 | 164.77 | 749.40 | 775.91 | 823.26 |
| 9.5 | 603.13 | 546.22 | 609.16 | 120.13 | 166.45 | 204.23 | 836.60 | 874.68 | 930.57 |
| 10 | 661.62 | 599.17 | 661.62 | 147.91 | 203.33 | 248.50 | 934.27 | 980.84 | 1039.08 |
| 10.5 | 722.54 | 654.33 | 715.31 | 184.43 | 244.14 | 302.47 | 1043.62 | 1093.86 | 1159.07 |
| 11 | 785.87 | 711.67 | 770.15 | 224.84 | 293.52 | 370.98 | 1159.78 | 1218.35 | 1295.26 |
| 11.5 | 851.60 | - | 832.86 | 262.97 | - | 447.05 | 1276.56 | - | 1447.40 |
| 12 | 919.71 | - | 892.12 | 296.17 | - | 533.10 | 1391.30 | - | 1606.59 |
| Parameters | ZHAN JIANG WTIV_O | BAI HE TAN WTIV_N | TIE JIAN 01 WTIV_3 | LAN KUN 01 WTIV_4 | HY 78/79 WTIV_5 | HUA XIANG LONG WTIV_6 |
|---|---|---|---|---|---|---|
| L (m) | 103.8 | 125 | 105 | 136 | 110.4 | 130 |
| B (m) | 41 | 50 | 42 | 50 | 42 | 42 |
| T (m) | 5.2 | 6.2 | 5.4 | 6 | 5.4 | 6 |
| CM | 0.9985 | 0.9995 | 0.9994 | 0.9995 | 0.999 | 0.9983 |
| CB | 0.818 | 0.801 | 0.824 | 0.816 | 0.834 | 0.814 |
| CW | 0.925 | 0.801 | 0.923 | 0.816 | 0.928 | 0.855 |
| Target value (m2) | 4832.7 | 7039.2 | 5025 | 7662.2 | 5305.6 | 6322.9 |
| Estimated value (m2) | 4808.84 | 7037.35 | 5026.65 | 7661.84 | 5302.79 | 6322.26 |
| Error (%) | −0.496% | −0.026% | 0.033% | −0.005% | −0.053% | −0.010% |
| VS (kn) | RTPV_EXP. (kN) | Rw_EXP. (kN) | Rtclam_EXP. (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Value__EXP. | Value__HOL. | Error (%) | Value__EXP. | Value__HOL. | Error (%) | Value__EXP. | Value__HOL. | Error (%) | |
| 5 | 149.26 | 153.42 | 2.78% | 11.50 | 11.92 | 3.60% | 212.84 | 217.41 | 2.15% |
| 5.5 | 177.36 | 182.51 | 2.91% | 17.91 | 17.53 | −2.12% | 257.48 | 262.26 | 1.85% |
| 6 | 207.63 | 213.38 | 2.77% | 24.42 | 24.84 | 1.70% | 305.25 | 311.40 | 2.02% |
| 6.5 | 240.06 | 245.83 | 2.41% | 32.81 | 34.11 | 3.97% | 357.85 | 364.93 | 1.98% |
| 7 | 274.60 | 279.68 | 1.85% | 42.60 | 45.62 | 7.10% | 414.81 | 422.91 | 1.95% |
| 7.5 | 311.23 | 314.73 | 1.12% | 55.32 | 59.67 | 7.86% | 477.60 | 485.44 | 1.64% |
| 8 | 349.94 | 350.79 | 0.24% | 70.53 | 76.55 | 8.52% | 545.77 | 552.62 | 1.26% |
| 8.5 | 390.71 | 387.68 | −0.78% | 89.51 | 96.55 | 7.86% | 620.55 | 624.55 | 0.64% |
| 9 | 433.50 | 425.19 | −1.92% | 117.16 | 119.98 | 2.41% | 706.83 | 701.33 | −0.78% |
| 9.5 | 478.31 | 463.14 | −3.17% | 148.23 | 147.16 | −0.73% | 799.33 | 783.08 | −2.03% |
| 10 | 525.12 | 501.34 | −4.53% | 181.41 | 178.39 | −1.67% | 896.73 | 869.91 | −2.99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiahou, M.; Yang, D.; Liu, H.; Shi, Y. Investigation on Calm Water Resistance of Wind Turbine Installation Vessels with a Type of T-BOW. J. Mar. Sci. Eng. 2024, 12, 1337. https://doi.org/10.3390/jmse12081337
Xiahou M, Yang D, Liu H, Shi Y. Investigation on Calm Water Resistance of Wind Turbine Installation Vessels with a Type of T-BOW. Journal of Marine Science and Engineering. 2024; 12(8):1337. https://doi.org/10.3390/jmse12081337
Chicago/Turabian StyleXiahou, Mingsheng, Deqing Yang, Hengxu Liu, and Yuanhe Shi. 2024. "Investigation on Calm Water Resistance of Wind Turbine Installation Vessels with a Type of T-BOW" Journal of Marine Science and Engineering 12, no. 8: 1337. https://doi.org/10.3390/jmse12081337
APA StyleXiahou, M., Yang, D., Liu, H., & Shi, Y. (2024). Investigation on Calm Water Resistance of Wind Turbine Installation Vessels with a Type of T-BOW. Journal of Marine Science and Engineering, 12(8), 1337. https://doi.org/10.3390/jmse12081337







