Containment-Based Distributed Secondary Control for AC Shipboard Microgrids under General Noise

Abstract

This paper investigates the secondary control problem of shipboard microgrids (SMGs) with a high percentage of new energy sources under general noise. Firstly, a polymorphic SMG model is constructed, which enables the software-defined functionality of the control strategy and allows heterogeneous distributed generators (DGs) in AC SMGs to exchange packets of different types. Secondly, due to the presence of highly dynamic and high-power loads in the SMGs, a containment-based distributed secondary control strategy is proposed to improve the flexibility of the DG voltage regulation. Then, considering the complexity and diversity of disturbances during ship navigation, general noise is introduced instead of white noise to describe various disturbances. Furthermore, based on the random differential equations (RDEs), the NOS stability of the proposed strategy is proved using Lyapunov theory, which proves the effectiveness of the containment-based distributed secondary control strategy under general noise. And, the containment error is obtained to prove that the voltage and frequency of the system converge to the convex hull spanned by the virtual leaders, ensuring the high quality of the power supply. Finally, the validity of the proposed containment-based strategy is verified by an AC SMG model with four DGs in three cases.

1. Introduction

With over 80% of global trade now undertaken by shipping, the marine economy has considerably grown [1]. Since diesel and heavy fuel oil remain the main power sources for all maritime applications, marine fleets have become a significant contributor to greenhouse gases [2,3]. In recent years, scholars have become increasingly interested in research to reduce environmental pollution from ships [4,5], which has prompted widespread development for SMGs [6]. The implementation of SMGs can integrate a high proportion of new energy into ships, thereby replacing the use of traditional fuels and greatly reducing greenhouse gas emissions. Depending on the distribution method, SMGs can be classified as DC SMGs, AC SMGs, or DC/AC SMGs [7]. Research in recent years tends to favor DC SMGs due to their simple structure and low energy loss in the configuration of storage devices [8]. However, it should not be overlooked that DC SMGs do not have a current crossing point, which poses a challenge to the safety of SMG systems [9]. Meanwhile, due to the high cost of ships and the fact that existing ships are more likely to use AC power distribution, retrofitting existing ships with AC SMG technology will effectively reduce the cost and realize the integration of new energy. Therefore, this paper investigates the control technique of AC SMGs.

The AC SMG is regarded as a mobile microgrid, operating in grid-connected mode when the ships arrive at the harbor or in islanded mode during ship navigation [10]. In general, SMGs share some similarities with land-based microgrids, such as the presence of various power electronic converters and the need for communication between devices so that the control strategies for land-based microgrids can be extended to SMGs. As a collection of power generation, distribution, and consumption systems, SMGs include distributed power sources, energy storage, electronic conversion elements, loads, and circuit protection devices [11]. SMGs adopt a hierarchical control framework. Primary control stabilizes the SMG systems under load fluctuations at the shortest time scale, and secondary control adjusts the set value for primary control [12], which removes the deviation of primary control to achieve high-quality supply. Tertiary control needs to manage the current of each node [13], which is based on the primary and secondary control and uses an optimization algorithm to improve the economic efficiency. Critical loads on ships, such as propulsion equipment, radar, and navigation systems, have high requirements for power quality [14]. Therefore, this paper investigates a containment-based distributed secondary control strategy to guarantee the power quality of DGs in SMGs.

In recent years, the distributed secondary control problem of microgrids has received attention. According to the communication network, the secondary control method can be categorized into distributed and centralized. Centralized control can achieve high speed and complicated control, which is suitable for small MGs [15]. But, a single point of failure may damage the global control, which reduces reliability [16]. Distributed control utilizes communication networks to realize mutual information exchange, which adopts a distributed local controller; thus, the single point of failure is prevented [17]. Multi-agent system (MAS) consensus algorithms enable message transmission only between neighbors [18,19]. The authors of [20] designed an estimation-dependent false data injection (FDI) attack that may exist in practice and proposed a resilient distributed auxiliary control strategy based on virtual networks to defend against the attack. The authors of [21] developed a high-order fully actuated model and proposed a distributed predictive secondary control strategy, which allows for an arbitrary configuration of closed-loop poles.

The above literature tends to synchronize the state of the DG to that of the same leader, which reduces the flexibility of the SMGs. Under the SMG operating criteria, voltages are often allowed to have a volatility of 10 percent, which means that not all DGs must have the same output voltage. Moreover, the ship propulsion device, as a high-power load in SMGs, needs power supply from the DGs in other regions. At this point, the voltage of the point of common couplings (PCCs) in that region decreases, which is more significant when the ship is accelerating. If the voltage of each DG remains consistent at this time, the AC bus voltage will then drop a lot, which is undesirable. Therefore, this paper studies containment-based distributed secondary control to increase the system’s flexibility in regulating voltage output. The purpose of containment control is to keep the state of each follower within a convex hull [22,23]. Containment control methods are well established [24] and have applications in real-world problems [25]. In the category of distributed secondary control for microgrids, ref. [26] investigated the voltage recovery of distributed AC microgrids under faults. Considering the unknown FDI attack, ref. [27] designed a distributed resilient control strategy.

Due to the high energy density of SMGs [28], there is electromagnetic interference between equipment during SMG operation [29]. The humid sea-surface environment and other disturbances [30] make the noise of SMGs become more of a non-ignorable factor. Disturbances to the receiver front-end in systematic wireless communication can have an impact on the distributed control strategy. Considering the complexity and diversity of disturbances during SMG operation, general noise is used instead of white noise to characterize various disturbances [31], which is uniformly distributed over the frequency spectrum [32], and the state can converge to a vector in the mean square with an expectation of zero using the $It\widehat{o}$ formula [33]. Since noise is unobservable and unrecognizable, and the information that contains noise is difficult to recover [34], it challenges the stability of the system. Therefore, analyzing the influence of the general noise on the containment-based distributed secondary control and designing a reasonable strategy for AC SMGs are important issues.

In order to address the issues of the flexibility of distributed generators in SMGs and stable operation under general noise, a containment-based distributed secondary control strategy is proposed to ensure high-quality power supply under general noise. Taking an electric ship with four generators as an example, the control strategy was simulated in Matlab/Simulink, and the effectiveness of the proposed model and solution was verified in three cases. The following are the contributions:

(1)

A polymorphic SMG was constructed, through which heterogeneous DGs can transfer data to support the implementation of distributed secondary control and software-defined algorithms can be implemented.

(2)

In contrast to the existing research on the distributed consensus-based strategy, this paper investigates the containment-based control strategy for AC SMGs. The containment-based distributed secondary control is proposed to improve the flexibility of the DGs to regulate the voltage at each PCC point of the SMGs and make it available in a wider range of actual situations.

(3)

General noise is introduced to describe the impact of disturbances on the proposed strategy. Based on the RDEs [32], the proposed strategy is proved to be NOS stable, and the mean square of the containment error can converge to a small neighborhood around the origin, which means that the AC SMG achieves containment control under general noise.

The rest of this paper is organized as follows. A polymorphic SMG is established in Section 2. A containment-based distributed secondary control strategy is proposed and a stability analysis is completed in Section 3. Section 4 simulates the effectiveness of the proposed control strategy on new-energy electric ships. Finally, Section 5 presents the conclusions.

2. Problem Statement

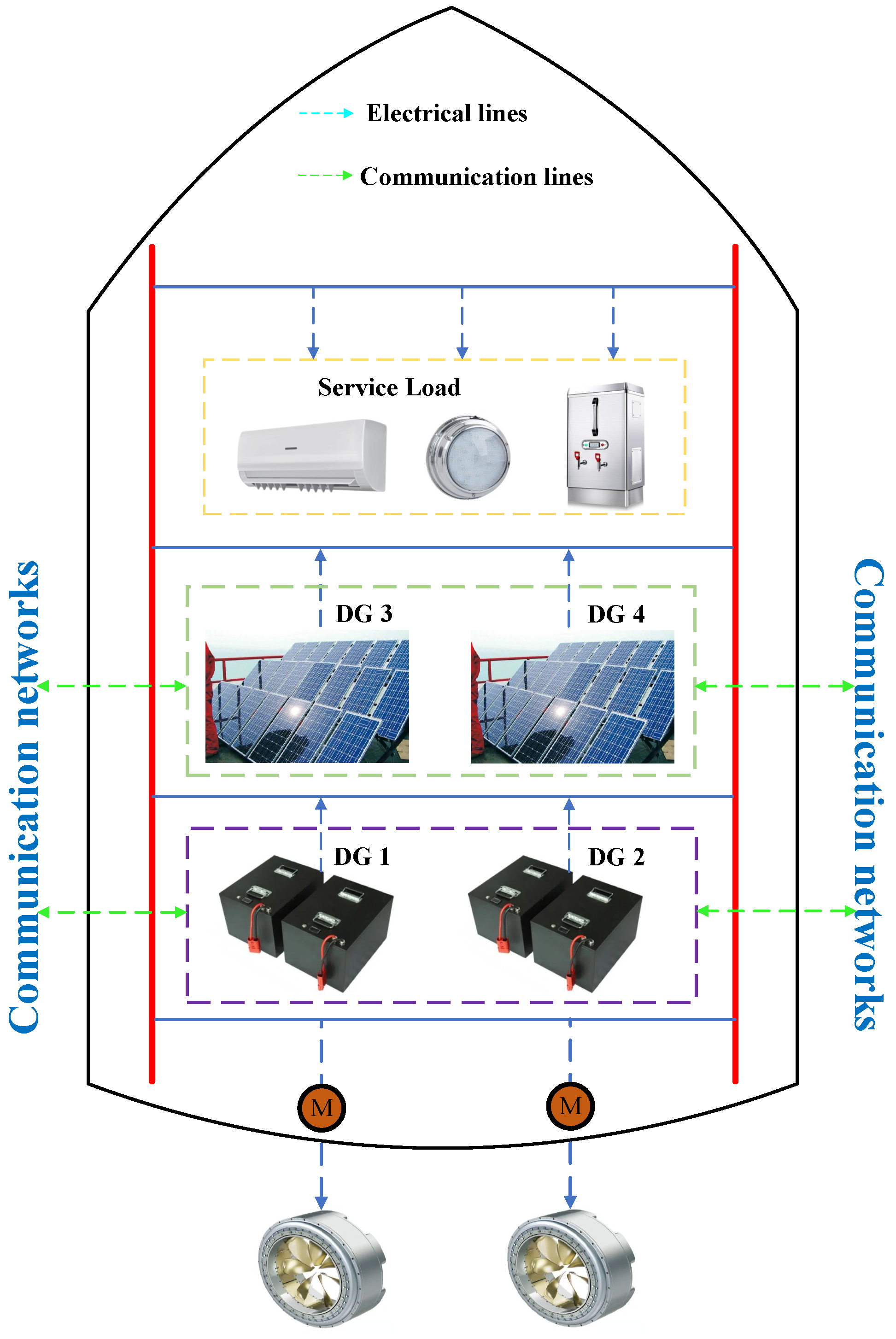
2.1. The Framework of the Polymorphic Shipboard Microgrid

The structure of the SMG consists of DGs, electrical loads, and the control system [35] and is shown in Figure 1. In order to achieve emission reduction, various new energies (fuel cells, photovoltaic arrays, etc.) are integrated into the AC SMG as DGs. The load side of the AC SMGs contains the electric propulsion system, and the frequent start–stop operation of the electric propulsion loads places demands on the power quality of the AC SMG. There are also consumers that operate at different voltage levels, such as radar, lighting systems, and domestic power, most of which require high power quality. Moreover, the control system of SMGs analyzes data and makes decisions. The Supervisory Control And Data Acquisition (SCADA) system collects the data between DGs and transmits them to the energy management system.

Considering the constraints of traditional IP carrier networks, we built a polymorphic SMG model, as shown in Figure 2. The service layer is oriented to the user side and contains data monitoring and energy management processes. Compatibility between the control strategy and various software is accomplished at the control layer, which realizes control over the electrical layer by analyzing and calculating the data. Various types of packets are exchanged between neighboring DGs in the data layer, and polymorphic identification tables are configured to enhance data security. The electrical layer includes the entire DGs and the loads, from which all measured values are obtained. The polymorphic SMG can accomplish communication between heterogeneous DGs from different vendors and facilitate the design of reasonable control strategies for different system characteristics.

2.2. Graph Theory

The communication network between the DGs of SMGs is designed as a directed graph $\mathcal{G}$. The communication weights $a_{ij}$ are involved in a related adjacency matrix $A_{\mathcal{G}}$. $a_{ij}>0$ if agent j can transmit data to neighbor agent i; otherwise, $a_{ij}=0$. $D=diag\left\{d_i\right\}$ is the in-degree matrix, and $d_i={\sum }_{j\in N_i}{a}_{ij}$. The Laplacian matrix $L=D-A_{\varsigma }$ is defined as

$$L=\left\{\begin{array}{c}-a_{ij},i\ne j\hfill \\ \\ \sum _{j=1}^n{a}_{ij},i=j\hfill \end{array}\right.$$

(1)

and $G=diag(g_i)$ is the gain matrix from leaders to the i-th follower.

3. Main Results

In this section, the impact of noise on SMGs is analyzed, and a containment-based distributed secondary control strategy for AC SMGs under general noise is proposed.

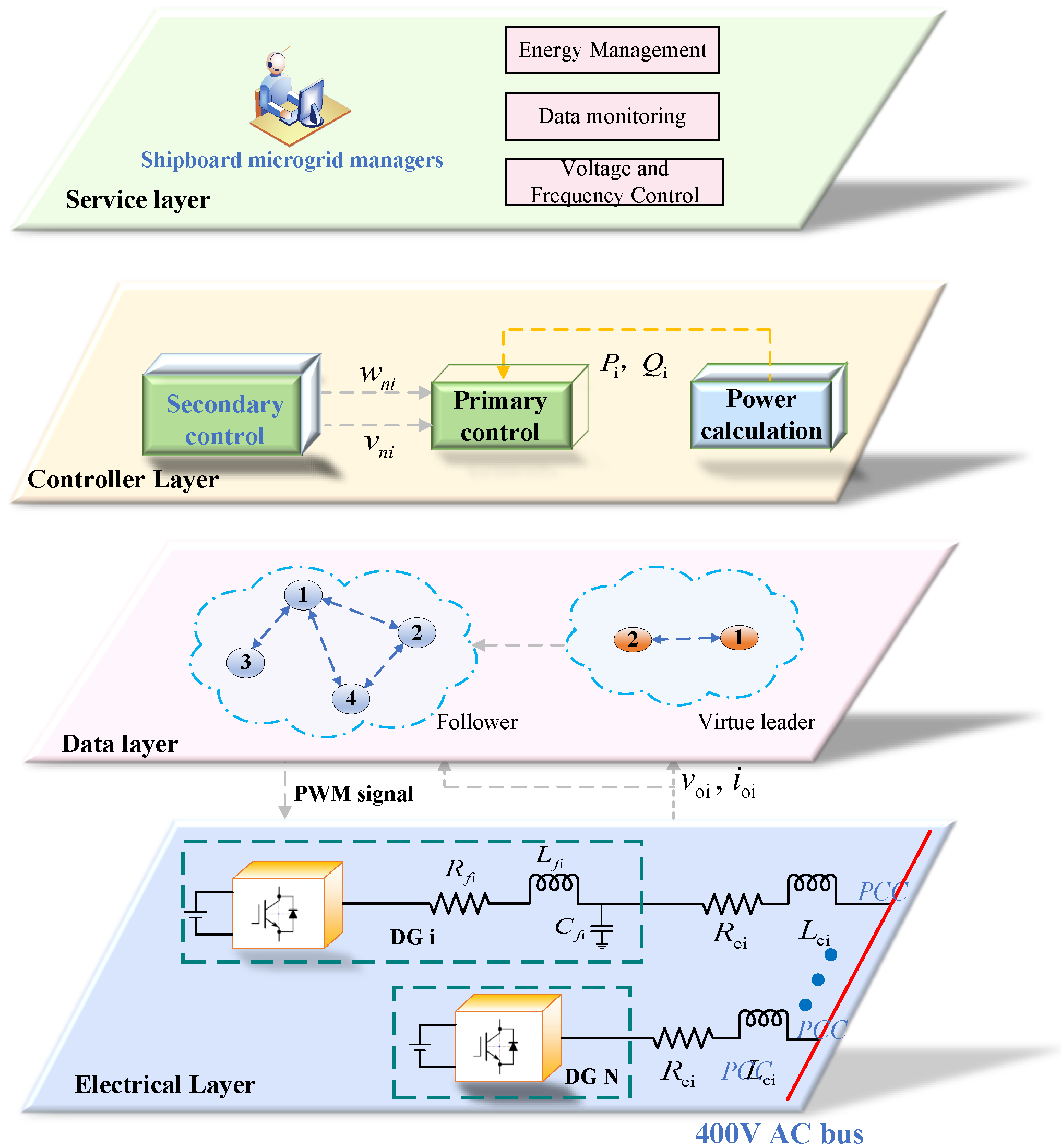
3.1. The Hierarchical Control of AC SMGs

In this paper, the SMG uses hierarchical control with secondary and primary control. Primary control realizes the fast response of individual DGs, while the secondary controller instructs the DGs to recover voltage and frequency based on the data collected by the micro-pmu for primary control. The droop mechanism in [12] is expressed as

$$\begin{array}{c}{w}_i=w_i^{ref}-k_{Pi}{P}_i\hfill \end{array}$$

(2)

$$\begin{array}{c}{V}_i=V_i^{ref}-k_{Qi}{Q}_i,\hfill \end{array}$$

(3)

where $w_i$ and $V_i$ are the frequency and voltage, respectively. $w_i^{ref}$ and $V_i^{ref}$ are the set points. $k_{Pi}$ and $k_{Qi}$ are the droop coefficients of frequency and voltage, respectively. $P_i$ and $Q_i$ are active power and reactive power, respectively.

To maintain the consistent performance of DGs in SMGs, the auxiliary control inputs $u_{wi}$ and $u_{Vi}$ are designed as follows:

$${\dot{w}}_i={\dot{w}}_i^{ref}-k_{Pi}{\dot{P}}_i=u_{wi}$$

(4)

$${\dot{V}}_i={\dot{V}}_i^{ref}-k_{Qi}{\dot{Q}}_i=u_{Vi}.$$

(5)

The containment-based distributed control systems consist of $N+M$ agents. The directed graph is defined as $\mathcal{G}$, which designates $\mathcal{F}=\left\{1,2,\dots ,N\right\}$ and $\mathcal{L}=\left\{N+1,\dots ,N+M\right\}$ to portray the mix of virtual leaders and followers, respectively.

Then, $\mathcal{L}$ is defined as

$$\mathcal{L}=\left[\begin{array}{cc}{0}_{M\times M}& 0_{M\times N}\\ -{\mathcal{L}}_2& {\mathcal{L}}_1,\end{array}\right]$$

(6)

where ${\mathcal{L}}_1\in R^{N\times N}$ and ${\mathcal{L}}_2\in R^{N\times M}$. Each eigenvalue of matrix ${\mathcal{L}}_1$ has a positive real part. Moreover, for matrix ${\mathcal{L}}_1^{-1}{\mathcal{L}}_2$, each row sums to 1, and all of the elements are nonnegative.

Remark 1.

The current always flows from the point with high potential to the point with low potential. To ensure power flow, the voltages at the PCC points are always different. If the output voltage of each DG is controlled at the nominal value, when there are high power and high dynamic response loads, such as propulsion devices in SMGs, the voltage at the PCC point in the corresponding area decreases significantly. Containment control can adjust the voltage of each DG to compensate for the drop in the bus voltage. Containment control keeps the state of each follower within a certain point of the convex packet formed by the virtual leader, instead of guaranteeing the consistency of all DGs, which allows the system to be more flexible in adjusting the state of each DG.

In order to adjust the frequency and voltage of each inverter with its respective reference value to ensure the stability of the SMG, distributed containment-based secondary control is adopted. The local cooperative control strategy with relevant information from neighboring inverters is

$$\begin{array}{c}{\dot{w}}_i=u_{wi}\hfill \\ \\ =-c_w({\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(w_i-w_j)+{\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(k_{Pi}{P}_i-k_{Pj}{P}_j))+{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(w_i-w_k)\hfill \\ \\ =-c_w({\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(w_i^{ref}-w_j^{ref})+{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(w_i^{ref}-w_{nk}))\hfill \end{array}$$

(7)

$$\begin{array}{c}{\dot{V}}_i=u_{Vi}\hfill \\ \\ =-c_V({\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(V_i-V_j)+\sum _{j\in \mathcal{F}}{a}_{ij}(k_{Qi}{Q}_i-k_{Qj}{Q}_j))+{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(V_i-V_k)\hfill \\ \\ =-c_V({\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(V_i^{ref}-V_j^{ref})+{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(V_i^{ref}-V_{nk})),\hfill \end{array}$$

(8)

where $c_w$ and $c_V$ are the controller coefficients. $w_k$ and $V_k$ are reference information.

For convenience, Equations (7) and (8) can be organized as

$$\begin{array}{c}{\dot{v}}_i=u_{vi}\hfill \\ \\ =-c_v({\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(v_i^{ref}-v_j^{ref})+{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(v_i^{ref}-v_{nk})),\hfill \end{array}$$

(9)

where $v_{nk}={\left[w_{nk},V_{nk}\right]}^T$ and $v_i^{ref}={\left[w_i^{ref},V_i^{ref}\right]}^T$ are the references for the frequency and voltage, respectively.

Definition 1

([25]). If a nonnegative constant $p_{ik}(k\in \mathcal{L})$ exists and satisfies ${\sum }_{k=1}^M{p}_{ik}=1$ such that

$$\underset{t\to \infty }{lim}E{\left|v_i-\sum _1^M{p}_{ik}{v}_k\right|}^2\le \delta ,i\in \mathcal{F}$$

(10)

where δ is the upper bound of the mean square containment error, then the followers in (9) are considered to achieve practical containment.

Under Assumption 1, the equation ${\mathcal{L}}_1\mathbf{1}={\mathcal{L}}_2\mathbf{1}$ holds. Then, define

$$Q={\left[p_{ik}\right]}_{N\times M}={\mathcal{L}}_1^{-1}{\mathcal{L}}_2$$

(11)

where $p_{ik}>0$. And, matrix Q is presented as a coefficient in the containment problem.

Assumption 1

([36]). The communication network between the DGs of SMGs is directed. The virtual leader directs at least one state message to all DG terminals.

Assumption 1 is the basic standard assumption of SMG containment control. Under Assumption 1, $-{\mathcal{L}}_1{\mathcal{L}}_2{v}_n$ is within the convex hull spanned by the virtual leaders.

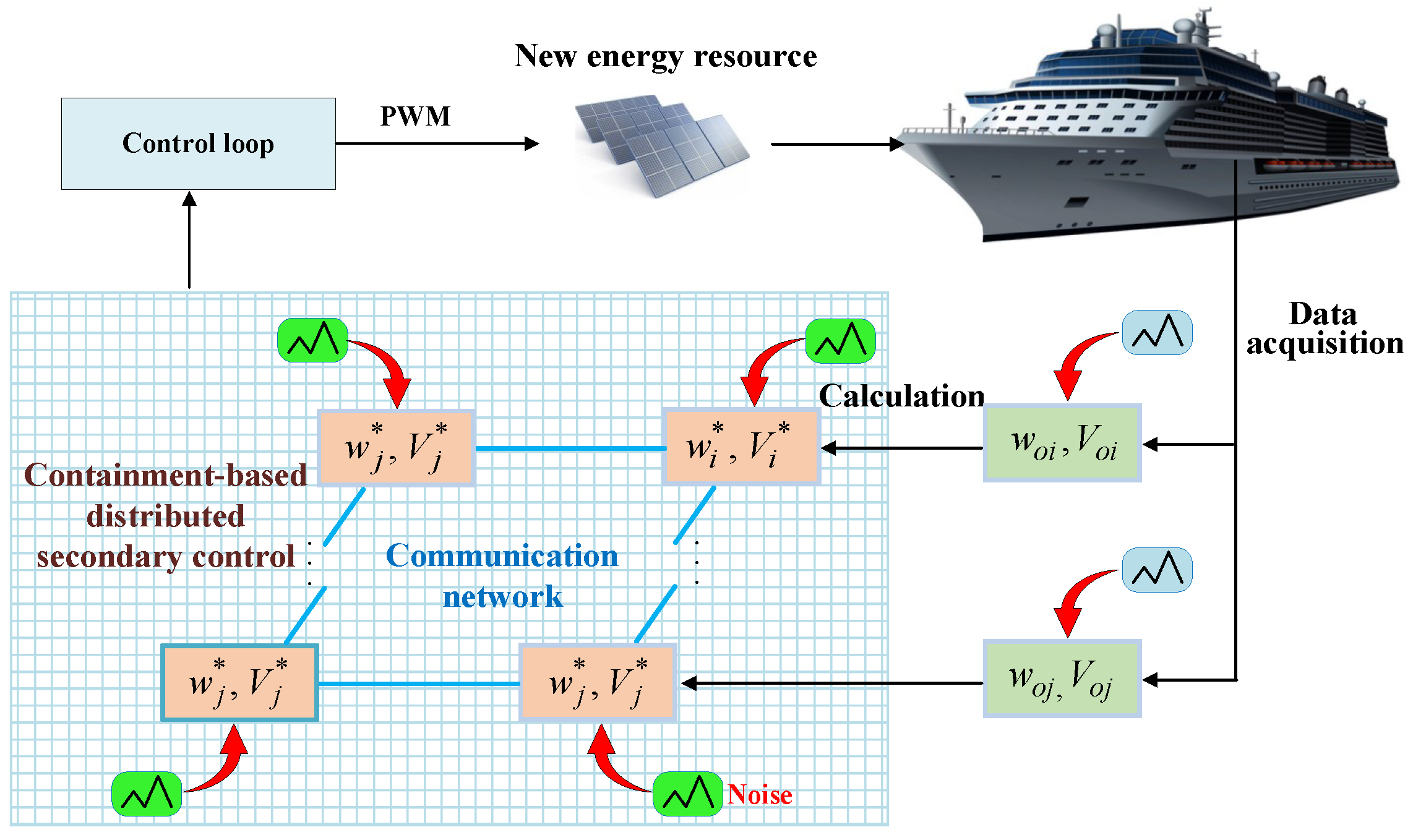
3.2. The Impact of General Noise on Distributed Secondary Control for SMGs

Electric propulsion ships have requirements for power quality; for example, propulsion devices need a fast response from the power supply side, and radar and navigation systems need a stable power supply. At the same time, the power quality affects the efficiency and service life of the equipment, but a large number of low-inertia new-energy devices make the system difficult to stabilize in the marine environment. SMGs need to complete power generation, transmission, transformation, distribution, and consumption in a limited space. But, there are disturbances in limited space, such as electromagnetic interference, communication, and computation noise. And, the marine environment can cause disturbances in the acquisition of SMG data. Thus, there are many types of these disturbances, which cannot be described simply by using white noise. This paper describes these disturbances as general noise, which can be expressed as

$$\dot{\zeta }(t)=-\zeta (t)+\mathrm{\Theta }(t),\zeta (0)=0$$

(12)

where $\mathrm{\Theta }(t)$ represents white noise.

Assumption 2.

The general noise ${\zeta }_{ij}(t)$ is piecewise continuous and $F_t$-adapted during SMG operation, and a positive constant $F>0$ exists such that

$$\underset{t\ge t_0}{sup}E{\left|\zeta (t)\right|}^2<F.$$

(13)

As shown in Figure 3, the frequency of DG in AC SMGs can remain at the reference value without general noise, according to the distributed secondary control strategy (9). At t = 5 s, the general noise is added. Although the SMG is tolerant to voltage fluctuations, the frequency cannot be kept within reasonable limits. Therefore, this paper studies containment-based distributed secondary control under general noise to ensure the stable operation of SMGs.

Remark 2.

During SMG operation, considering the various disturbances described as general noise, it seems reasonable that the solution to the differential Equation (9) has a larger allowable range around the nominal value, which also satisfies the SMG operation criteria. This flexibility means that the containment error bounds $\delta \ne 0$ can be met more easily, which enhances the practicality and versatility of Definition 1. Compared to the asymptotic algorithm, $\delta =0$ may require substantial costs.

3.3. Containment-Based Distributed Secondary Control Strategy under General Noise

Disturbances can affect data acquisition and calculation to disturb distributed secondary control, as shown in Figure 4, which causes the DGs in the electronic layer to not work stably and causes damage to the AC SMGs. A containment-based distributed secondary control strategy is proposed to tolerate the effect of disturbances on AC SMGs and improve the flexibility of the DG voltage, which is expressed as

$$\begin{array}{c}\begin{array}{c}{\dot{v}}_i=u_{vi}\hfill \\ \\ =c_v[{\displaystyle \sum _{j\in \mathcal{F}}}{a}_{ij}(v_j^{ref}-v_i^{ref}+f_{ij}(v_j^{ref},t){\zeta }_{ij})\hfill \\ \\ +{\displaystyle \sum _{k\in \mathcal{L}}}{g}_{ik}(v_{nk}-v_i^{ref}+f_{ii}(v_i^{ref},t){\zeta }_{li})],\hfill \end{array}\hfill \end{array}$$

(14)

where $f_{ij}(v_j,t)$ is the noise intensity, and $c_v$ is the controller coefficient.

Let $\zeta ={({\zeta }_1^T,{\zeta }_{11}^T,{\zeta }_2^T,{\zeta }_{22}^T,\dots ,{\zeta }_n^T,{\zeta }_{nn}^T)}^T\in R^{n(n+m)}$ and ${\zeta }_i={({\zeta }_{i1},\dots ,{\zeta }_{in})}^T\in R^n$ for $i=1,\dots ,n$ and $i\ne j$, $I_2=diag(1,1)$. And, $a(i,·)$ is the ith row of adjacency matrix A, and $k(i,·)$ is described as the ith row of ${\mathcal{L}}_2={(g_{ik})}_{n×m}$. The compact noise intensity matrix is denoted by

$$\tilde{f}=\left(\begin{array}{cccccc}a(1,·)f_1& k(1,·)f_{11}& 0& \dots & 0& 0\\ 0& 0& a(2,·)f_2& k(2,·)f_{22}& 0& 0\\ ⋮& ⋮& & \ddots & ⋮& ⋮\\ 0& 0& 0& \dots & a(n,·)f_n& k(n,·)f_{nn}\end{array}\right)$$

(15)

where $f_i=diag\left\{f_{i1},f_{i2},\dots ,f_{in}\right\}$ and $\tilde{f}\in R^{n\times n(n+m)}$.

Then, Equation (14) is written as

$$\begin{array}{c}\dot{v}=c_v((-{\mathcal{L}}_1\otimes I_2)v+({\mathcal{L}}_2\otimes I_2)v_k+\widehat{f}(v,t)\zeta ),\hfill \end{array}$$

(16)

where $v={(v_1^{ref},\dots ,v_N^{ref})}^T$, $v_k={(v_{n1}^{ref},\dots ,v_{nM}^{ref})}^T$, $\widehat{f}=\tilde{f}\otimes 1_{2\times 1}$.

The containment error $e_i$ for the follower $i(i\in \mathcal{F})$ is defined as

$$e_i=v_i-\sum _{k=1}^M{p}_{ik}{v}_{nk}$$

(17)

The compact form of (17) is

$$e=v-({\mathcal{L}}_1^{-1}{\mathcal{L}}_2\otimes I_2)v_k$$

(18)

Assumption 3.

The noise intensity of different devices in AC SMGs $f_{ij}(e_{ni},t)$ is bounded with respect to $e_{ni}$, and a positive constant ${\rho }_{ij}$ exists such that

$$\left|f_{ij}(e_{ni},t)\right|\le {\rho }_{ij},i=1,2,\dots ,n.$$

(19)

In this paper, general noise is introduced to describe the disturbances in AC SMGs more generally. General noise $\zeta (t)$ is a stationary process, and there is no $E\left\{\zeta (t)\right\}=0$ restriction, so the $It\widehat{o}$ formula is not usable. To analyze the stability of the containment-based strategy (16) under general noise and guarantee the stable power supply of the DGs, the NOS stability of the proposed containment-based strategy under general noise needs to be proven. Some more assumptions and lemmas are given below.

Lemma 1

(Gronwall inequality). The absolutely continuous function $\phi (t)$ for $t\ge t_0$ satisfies the integral inequality

$$\dot{\psi }(t)\le \gamma (t)\psi (t)+\nu (t),$$

(20)

where $\gamma (t)$ and $\nu (t)$ are continuous almost everywhere and integrable for almost all $t\ge t_0$ over every finite interval. Then, over this interval, we have

$$\psi (t)\le \psi (t_0)e^{{\int }_{t_0}^t\gamma (s)ds}+{\int }_{t_0}^t{e}^{{\int }_{t_0}^t\gamma (u)du}\nu (s)ds.$$

(21)

Assumption 4.

There exist constants $L_1$ and $L_2$ such that any $v_{n1}$, $v_{n2}$ ∈ $R^n$, $v_{n1}\ne v_{n2}$, satisfies the following inequality:

$$\begin{array}{c}∥f_{ij}(v_{n2},t)-f_{ij}(v_{n1},t)∥\le L_1\left|v_{n2}-v_{n1}\right|\hfill \end{array}$$

(22)

$$\begin{array}{c}∥f_{ij}(0,t)∥<L_2.\end{array}$$

(23)

Lemma 2

([32]). Assuming that a function V and positive constants $a_1,a_2,a_3,a_4>0$ exist, under Assumption 3, such that

$$\begin{array}{c}{a}_1{\left|e\right|}^2\le V(e)\le a_2{\left|e\right|}^2\\ \\ \dot{V}(e)\le -a_{3}V(e)+{\displaystyle \frac{{\left|\zeta \right|}^2}{4a_4}},\end{array}$$

(24)

then the strategy is NOS stable in the mean square.

By the matrix 2-norm definition, under Assumption 3, we can obtain

$$∥r_i∥=\sqrt{{\lambda }_{max}\left(r_i^T{r}_i\right)}\le {\rho }_i,$$

(25)

where row matrix $r_i=\left(a(i,·)f_i,g_{ik}{f}_{ii}\right)\in R^{1\times (n+m)}$. Then, we can conclude that

$$\begin{array}{c}\parallel \widehat{f}(e,t)\parallel =\sqrt{{\lambda }_{max}\left(\widehat{f}{(e,t)}^T\widehat{f}(e,t)\right)}\hfill \\ \\ \left.=\sqrt{{\lambda }_{max}\left\{diag\left(2r_1^T{r}_1,2r_2^T{r}_2,\dots ,2r_n^T{r}_n\right)\right.}\right\}\hfill \\ \\ =\sqrt{max\left\{{\lambda }_{max}\left(2r_1^T{r}_1\right),{\lambda }_{max}\left(2r_2^T{r}_2\right),\dots ,{\lambda }_{max}\left(2r_n^T{r}_n\right)\right\}}\hfill \\ \\ \le \sqrt{max\left\{2{\rho }_1^2,2{\rho }_2^2,\dots ,2{\rho }_n^2\right\}}\hfill \\ \\ =\rho .\hfill \end{array}$$

(26)

Theorem 1.

Considering the containment-based distributed secondary control strategy (16) under general noise, if there exist positive constants ρ and $a_4$, the symmetric positive definite matrix $P\otimes I_2$ and a function V, satisfying $4{\lambda }_{min}{\mathcal{L}}_1{c}_v-{\rho }^2>0$, then the containment-based distributed secondary control strategy under general noise is NOS stable in the mean square. And, the mean square of containment errors in SMGs can converge to a small neighborhood around the origin.

Proof. 

Choose a Lyapunov function candidate

$$V={\displaystyle \frac{1}{2}}{e}^T(P\otimes I_2)e.$$

(27)

Taking the derivative of function V and using Young’s inequality yields

$$\begin{array}{c}\dot{V}=e^{T}P{c}_v((-{\mathcal{L}}_1\otimes I_2)v+({\mathcal{L}}_2\otimes I_2)v_k+\hat{f}(v,t)\zeta )\hfill \\ \\ =-c_v{e}^{T}P({\mathcal{L}}_1\otimes I_2)e+c_v{e}^{T}P\hat{f}(e,t)\zeta \hfill \\ \le -c_v{e}^{T}P({\mathcal{L}}_1\otimes I_2)e+a_4{c}_v^2{e}^{T}P\hat{f}(e,t){\hat{f}}^T(e,t)P^{T}e+{\displaystyle \frac{1}{4a_4}}{\zeta }^T\zeta \hfill \\ \le -c_v{e}^{T}P({\mathcal{L}}_1\otimes I_2)e+c_v^2{a}_4{e}^{T}P{\parallel \widehat{f}(e,t)\parallel }^2{P}^{T}e+{\displaystyle \frac{{\left|\zeta \right|}^2}{4a_4}}.\hfill \end{array}$$

(28)

Based on the 2-norm of the noise intensity, as shown in (26), which is expressed as $\parallel \widehat{f}(e,t)\parallel \le \rho$, (28) is written as follows:

$$\begin{array}{c}\dot{V}\le c_v{e}^T(-P({\mathcal{L}}_1\otimes I_2)+c_v{a}_{4}P{P}^T{\rho }^2)e+{\displaystyle \frac{{\left|\zeta \right|}^2}{4a_4}}\hfill \\ \\ \le c_v{e}^T(c_v{a}_{4}P{P}^T{\rho }^2-{\lambda }_{min}({\mathcal{L}}_1)P)e+{\displaystyle \frac{{\left|\zeta \right|}^2}{4a_4}}.\hfill \end{array}$$

(29)

Then, the following can be obtained:

$$\begin{array}{c}\dot{V}\le ({\displaystyle \frac{1}{4c_v}}{P}^2{\rho }^2-{\lambda }_{min}({\mathcal{L}}_1)P)V+{\left|c_v\zeta \right|}^2\hfill \\ \\ =-\kappa V+{\displaystyle \frac{{\left|\zeta \right|}^2}{4a_4}},\hfill \end{array}$$

(30)

where $a_4=1/4c_v^2$. When $c_v>{\displaystyle \frac{{\rho }^{2}P}{4{\lambda }_{min}({\mathcal{L}}_1)}}$, there exists a positive constant $\kappa$, and it is easy to derive that ${\lambda }_{min}(P){\left|e\right|}^2\le V\le {\lambda }_{max}(P){\left|e\right|}^2.$ Thus, strategy (16) for AC SMGs is NOS stable within the mean square based on Lemma 2.

Furthermore, the containment error can satisfy the following inequality based on Lemma 1:

$$\begin{array}{c}V(e)\le V(e_0)e^{{\int }_{t_0}^t-\kappa ds}+{\int }_{t_0}^t{e}^{{\int }_s^t-\kappa du}{\displaystyle \frac{{\left|\zeta \right|}^2}{4d}}ds\hfill \\ \\ =V(e_0)e^{-\kappa (t-t_0)}+{\int }_{t_0}^t{e}^{-\kappa (t-s)}{\displaystyle \frac{{\left|\zeta \right|}^2}{4d}}ds\hfill \\ \\ =V(e_0)e^{-\kappa (t-t_0)}+{\displaystyle \frac{{\left|\zeta \right|}^2}{4d\kappa }}(1-e^{-\kappa (t-t_0)}).\hfill \end{array}$$

(31)

Taking integral expectations on both sides, the inequality $V(e_0)\le e_0^T{\lambda }_{max}{e}_0={\lambda }_{max}{\left|e_0\right|}^2$ holds. The mean square of the containment error is

$$\begin{array}{c}E{\left|e\right|}^2\le {\displaystyle \frac{{\lambda }_{max}(P)}{{\lambda }_{min}(P)}}{\left|e_0\right|}^2{e}^{-\kappa (t-t_0)}\hfill \\ \\ +{\displaystyle \frac{1-e^{-\kappa (t-t_0)}}{4d\kappa {\lambda }_{min}(P)}}\underset{t_0\le s\le t}{sup}E{\left|\zeta \right|}^2.\hfill \end{array}$$

(32)

For $t\to \infty$, the following can be obtained:

$$\underset{t\to \infty }{lim}E{\left|e\right|}^2\le {\displaystyle \frac{1}{4d\kappa {\lambda }_{min}(P)}}\underset{t_0\le s\le t}{sup}E{\left|\zeta \right|}^2.$$

(33)

Under Assumption 1, the second-order moments of frequency and voltage deviation are obtained as

$$\underset{t\to \infty }{lim}E{\left|e\right|}^2\le {\displaystyle \frac{F}{4d\kappa {\lambda }_{min}(P)}}.$$

(34)

It can be adapted to the neighbors of the origin. Finally, it can be derived that

$$\underset{t\to \infty }{lim}E{\left|v_i-\sum _{k=1}^M{p}_{ik}{v}_k\right|}^2=\underset{t\to \infty }{lim}E{\left|e_i\right|}^2\le \underset{t\to \infty }{lim}E{\left|e\right|}^2\le \delta$$

(35)

It can be concluded that the voltage and frequency of the DGs can converge to the convex hull spanned by the virtual leaders based on the proposed strategy, which means that the goal of containment control [25] is achieved. At the same time, the upper bound of the second-order moment of the containment errors is obtained, satisfying Definition 1. Meanwhile, according to the law of large numbers, we can estimate the actual containment errors and thus design controller parameters based on the different parameters and characteristics of the DGs. □

4. Case Study

A test SMG with four DGs and loads is used to demonstrate the validity of the proposed containment-based distributed secondary control under general noise. The transmission lines on the AC SMG between the DGs are inductive. The DGs exchange information through communication networks, and the simulation model of the SMG is shown in Figure 5. The nominal voltage of the SMG is 380V, and the frequency is 50 Hz. The rated parameters of the test SMG are shown in

Table 1. Settings of test SMG.

Symbol	Parameters
DG1, DG2	20 KW
DG3, DG4	8 KW
Lines	R = 0.25 $\mathsf{\Omega }$, L = 0.0035 H
$w_i^{ref}$	50 Hz
$v_i^{ref}$	380 V
$R_f$	0.1 $\mathsf{\Omega }$
$L_f$	0.023 H
$C_f$	0.0004 F
$R_c$	0.03 $\mathsf{\Omega }$
$L_c$	0.005 H

. Loads 1–4 represent the bow thruster motor, ballast pump, radar, and equivalent living load, which can be connected to the AC bus through transformers. Through the following simulation cases, the efficacy of the proposed containment-based strategy can be verified.

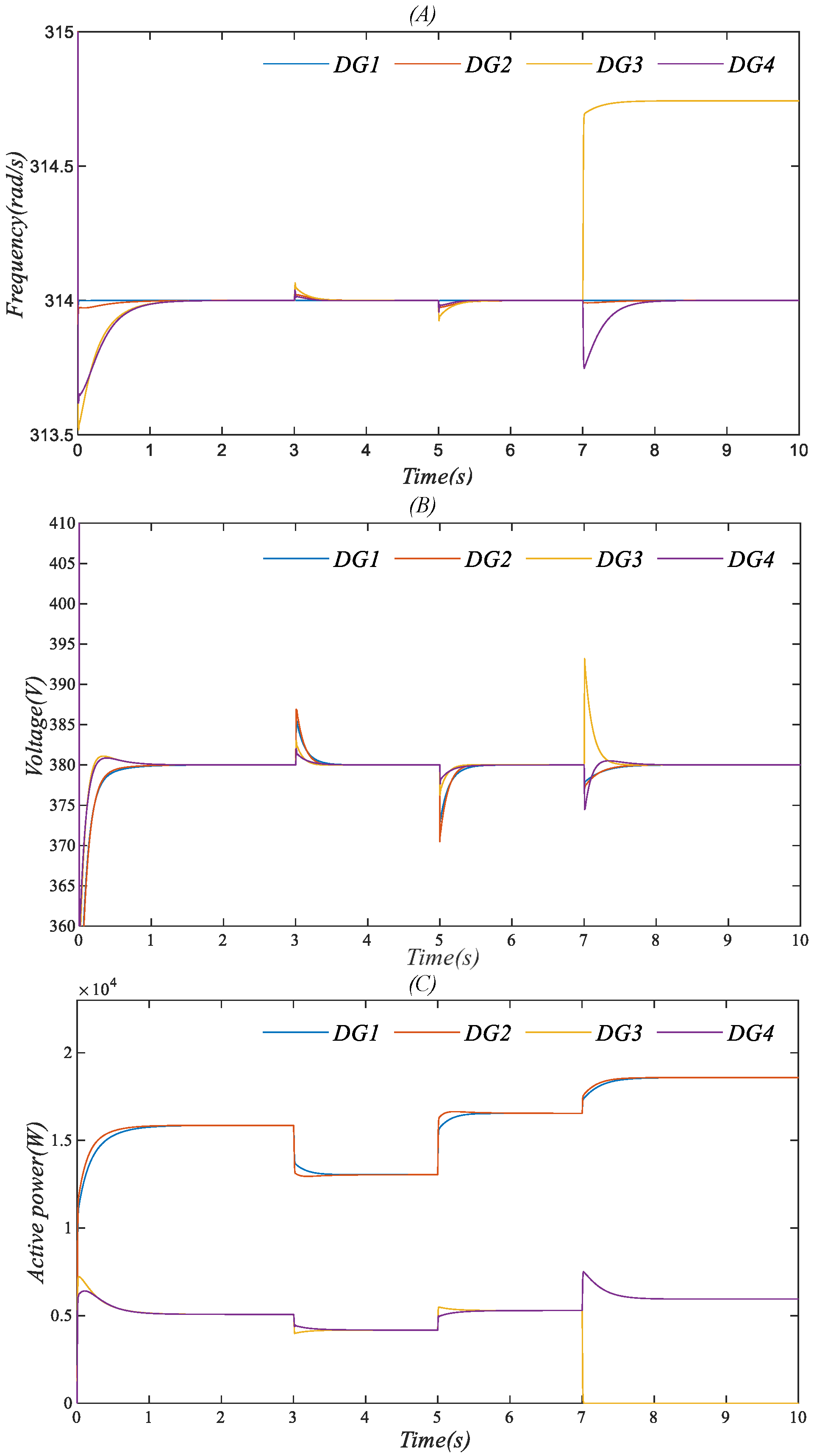
4.1. Case 1: The Effectiveness of the Consensus-Based Distributed Secondary Control Strategy under Load Disturbance and No General Noise

The applicability of the distributed secondary control strategy for AC SMGs in the presence of load fluctuations and a generator fault without general noise is demonstrated through this simulation case. The ship accelerates and decelerates at t = 3 and t = 5. At t = 7, a PV array fails and disconnects from the AC bus. It can be seen in Figure 6 that the state of the DGs can be stabilized after a short fluctuation, whether the load increases or decreases, with or without engine failure. In this state, DGs can satisfy the power demand of high-power loads and other loads with high-quality power demands during ship navigation.

4.2. Case 2: The Effectiveness of the Distributed Containment Control Strategy under Load Disturbance and No General Noise

This case study demonstrates the effect of the containment control strategy on voltage regulation. Due to the presence of high-power loads in the SMG, it is necessary for the DGs in other regions to supply it with power to meet the energy demand, which leads to a voltage reduction at the PCC nodes. Flexible adjustment of the output voltage of the DGs is often expected due to the greater variation in the bus voltage at this PCC point during acceleration. The parameter matrix is used as follows:

$${\mathcal{L}}_1^{-1}{\mathcal{L}}_2=\left[\begin{array}{cc}0.3939& 0.6061\\ 0.7273& 0.2727\\ 0.4545& 0.5455\\ 0.3636& 0.6364\end{array}\right]$$

(36)

As shown in Figure 7A, the output voltage of each DG is stable within the range formed by each virtual leader with consideration of the limits allowed by SMGs. As shown in Figure 7B, the output voltage of the DGs is appropriately adjusted by the containment control strategy, after which a better range can be achieved for each PCC point. Meanwhile, Figure 7C shows the containment error $e_i$, and the output voltage of each DG stays within the convex hull. This case indicates that the containment control strategy can be achieved, which means that the voltage of DGs can converge to the convex hull without general noise.

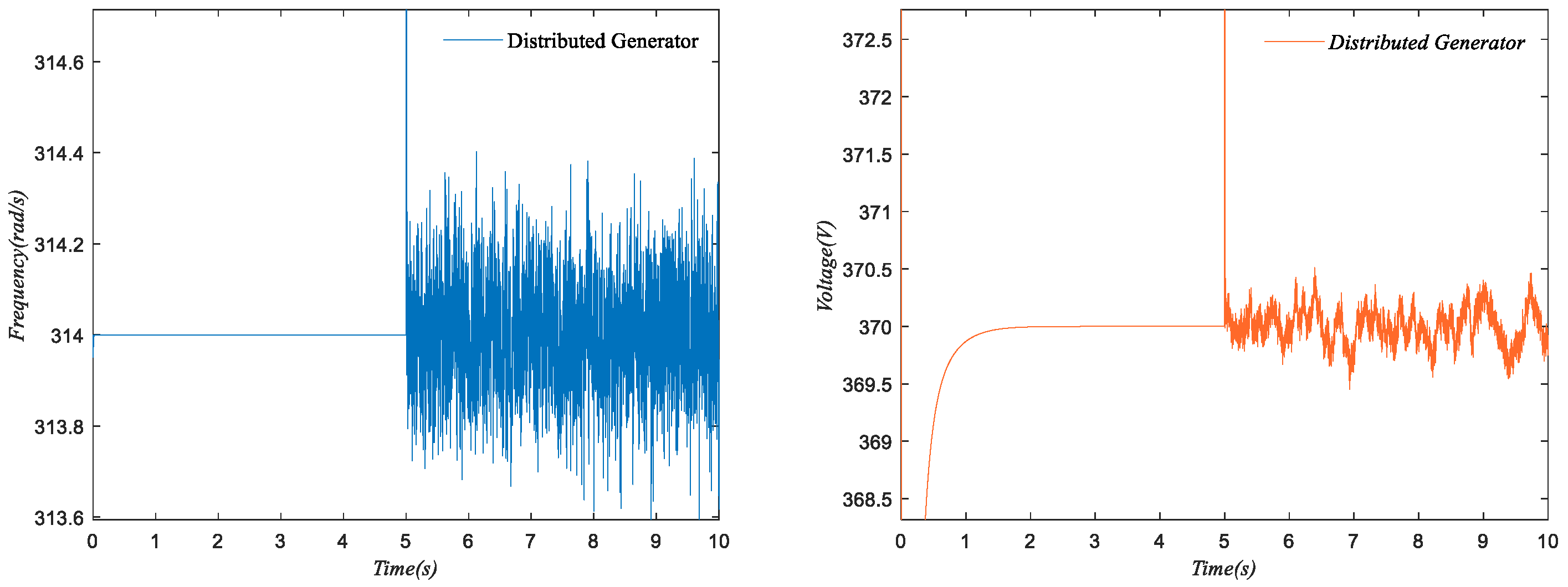
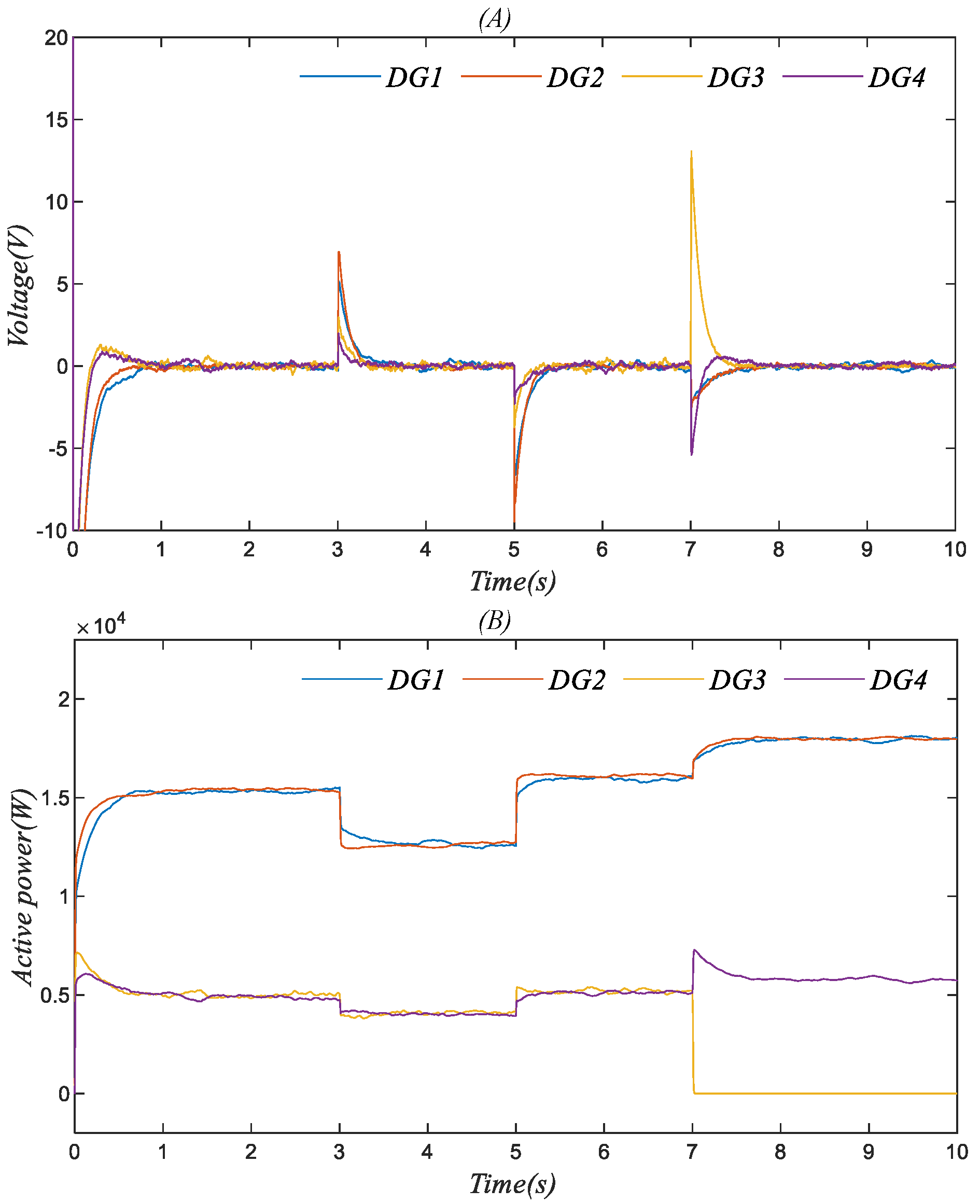
4.3. Case 3: The Effectiveness of the Containment-Based Distributed Secondary Control Strategy under General Noise

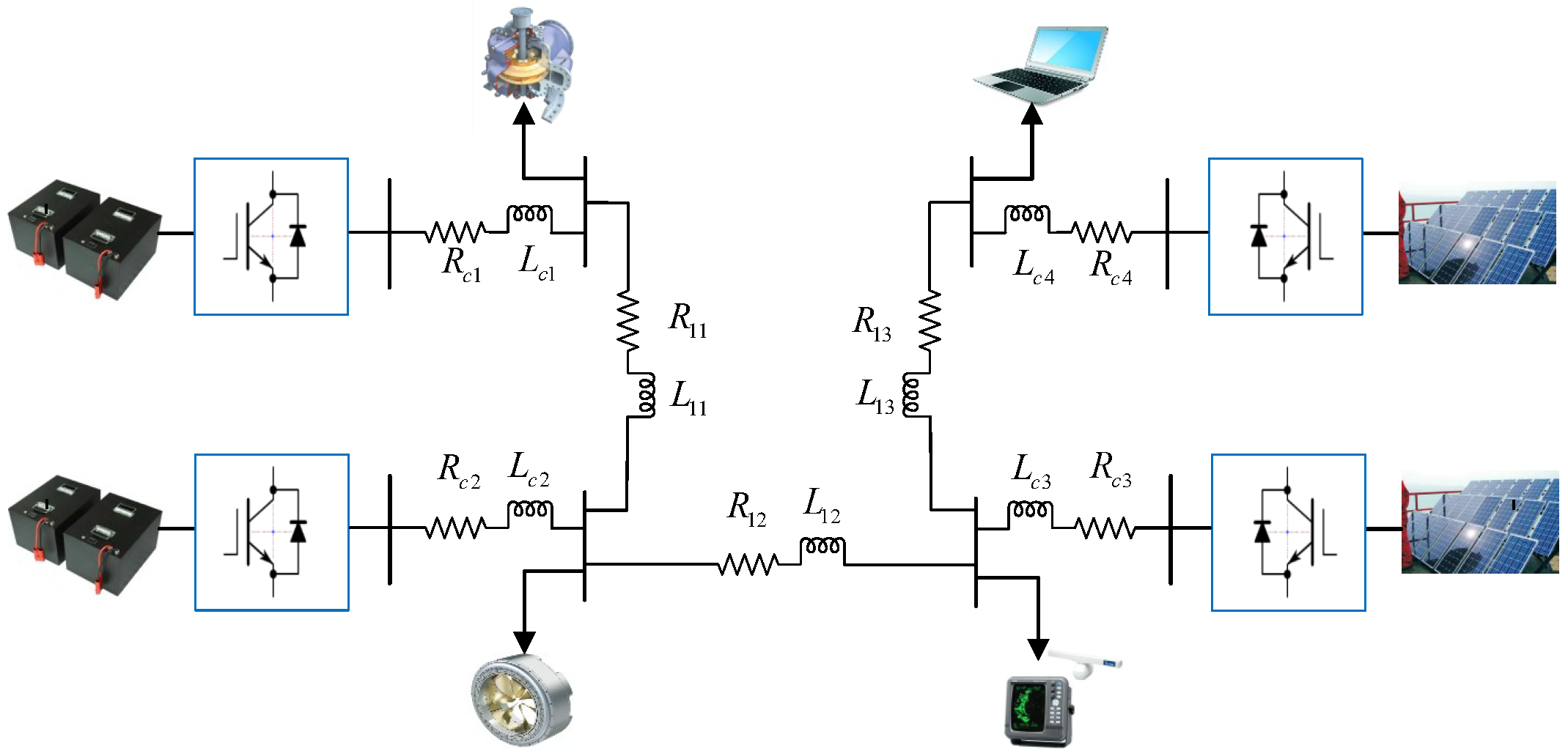
This case demonstrates the effectiveness of the proposed strategy in a noisy environment. With the introduction of general noise, as shown in (12), Figure 8A shows that the containment error of voltage of the DGs can be guaranteed to be within a stable range when the system parameters are designed to satisfy NOS stability. Figure 8B demonstrates that the DGs can maintain stability and accurate power sharing while changing states under general noise, which guarantees the stability of SMGs’ energy supply. More importantly, the proposed containment-based distributed secondary control strategy improves the flexibility of the system, enabling the system to adjust the DG output voltage for bus voltage regulation under high-power load fluctuations.

5. Conclusions

This article proposes a containment-based distributed secondary control strategy for SMGs under general noise to ensure the high-quality power demand of AC SMGs, which provides assistance for the integration of new energy into electric ships. In order to achieve the collaborative control of heterogeneous DGs from different manufacturers, a polymorphic SMG framework has been established. Considering the problem of the drop in bus voltage in the SMG with high-power loads such as ship propulsion equipment, a containment-based distributed secondary control strategy is proposed to improve the flexibility of DG voltage regulation to increase the voltage of some key nodes. Due to the disturbances of the SMG in the marine environment, general noise is introduced to describe complex marine disturbances, which is more accurate than white noise. The stability of the NOS system is analyzed using the Lyapunov function based on RDEs, and the control parameters are designed to ensure a reliable power supply. Finally, several SMG simulation cases verify the effectiveness of the containment-based distributed secondary control strategy under general noise with four DGs.