Hyperbolic Paraboloid Free-Surface Breakwaters: Hydrodynamic Study and Structural Evaluation
Abstract
:1. Introduction
2. Methodology
2.1. Smoothed Particle Hydrodynamics Principle
2.2. Governing Equations and Boundary Treatment
2.3. Wave Generation
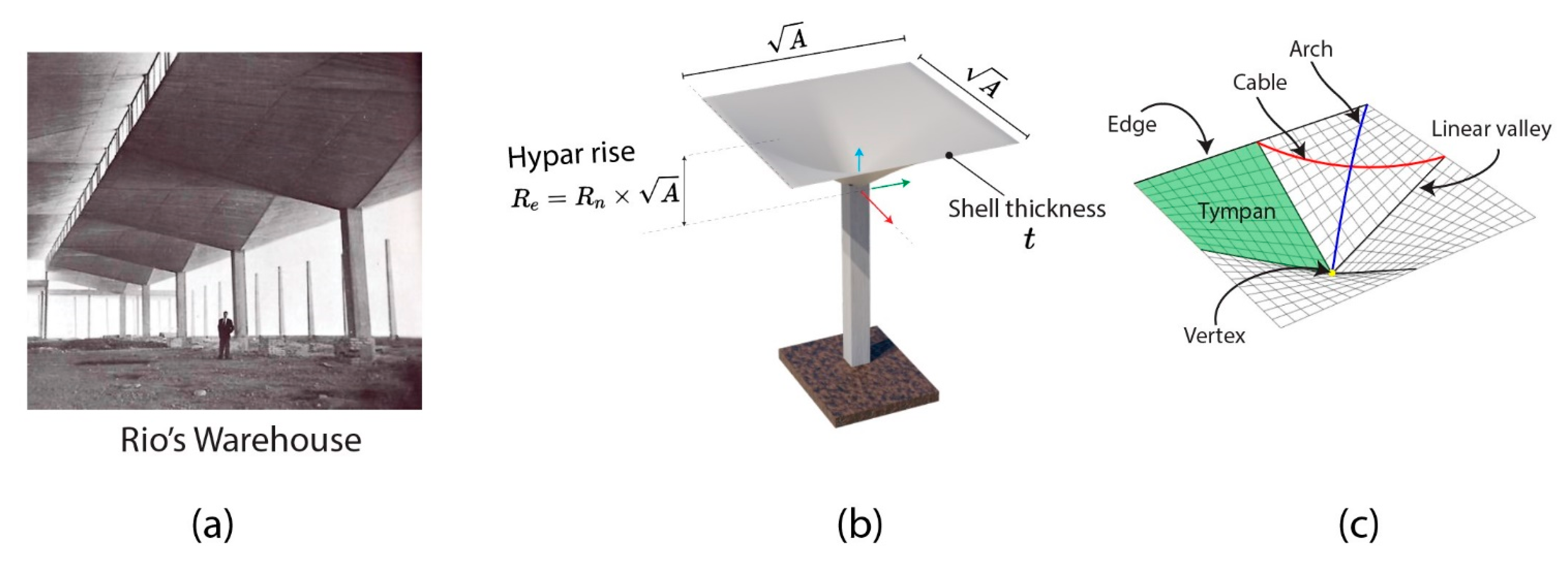
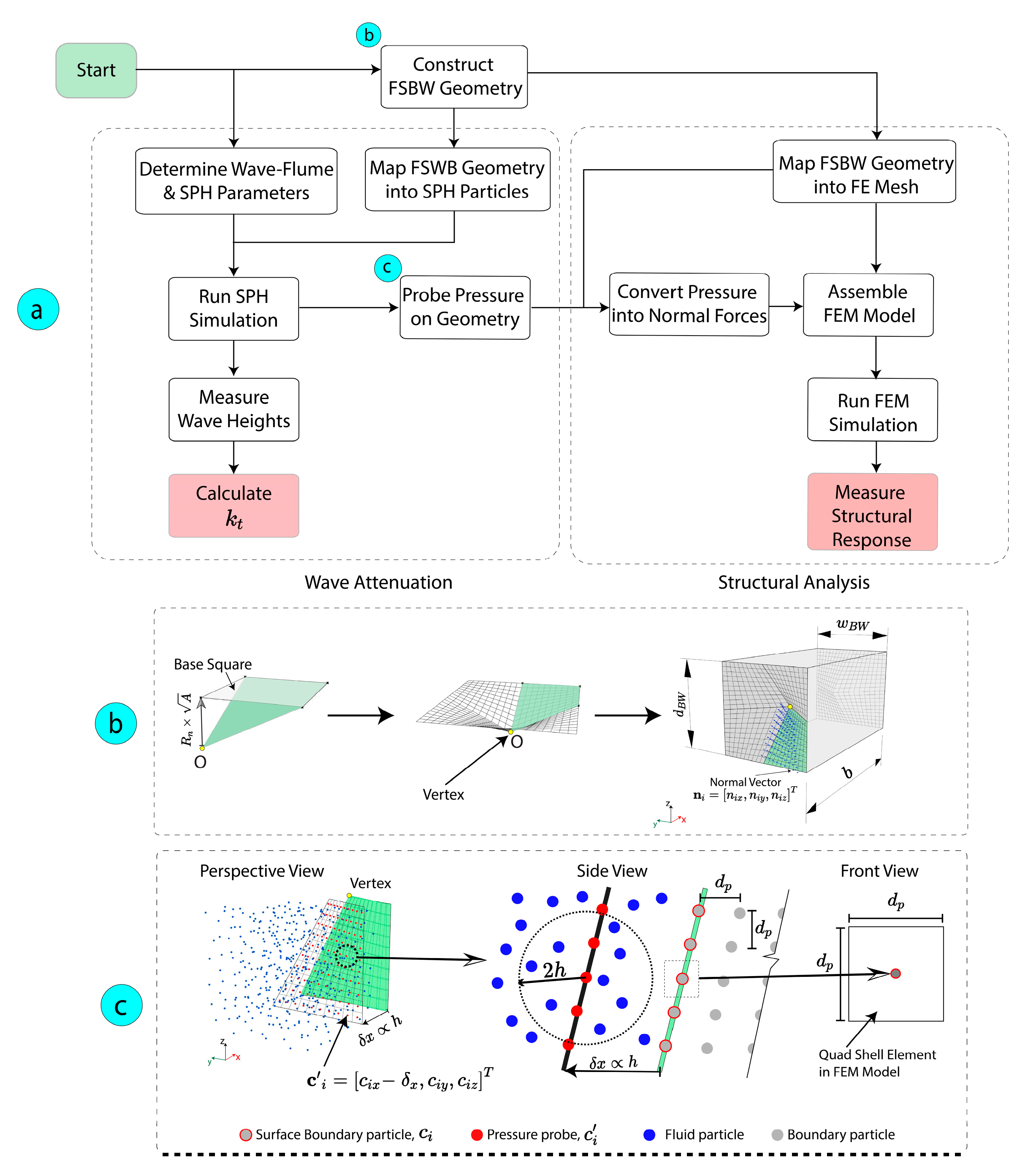
2.4. Geometric Modeling and SPH-FEM Mapping
2.5. Wave Attenuation
2.6. Static and Dynamic Structural Analysis
3. SPH Validation for Hypar FSBW
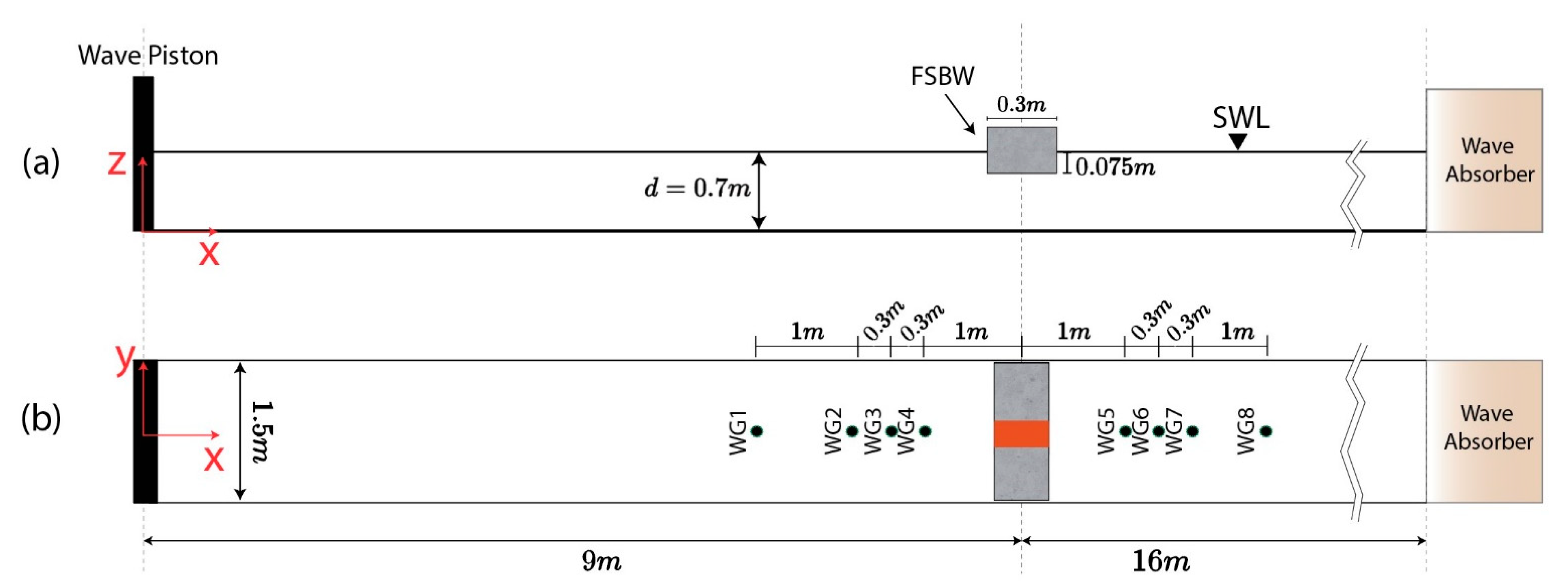
3.1. Experiment Setup
3.2. SPH Numerical Model
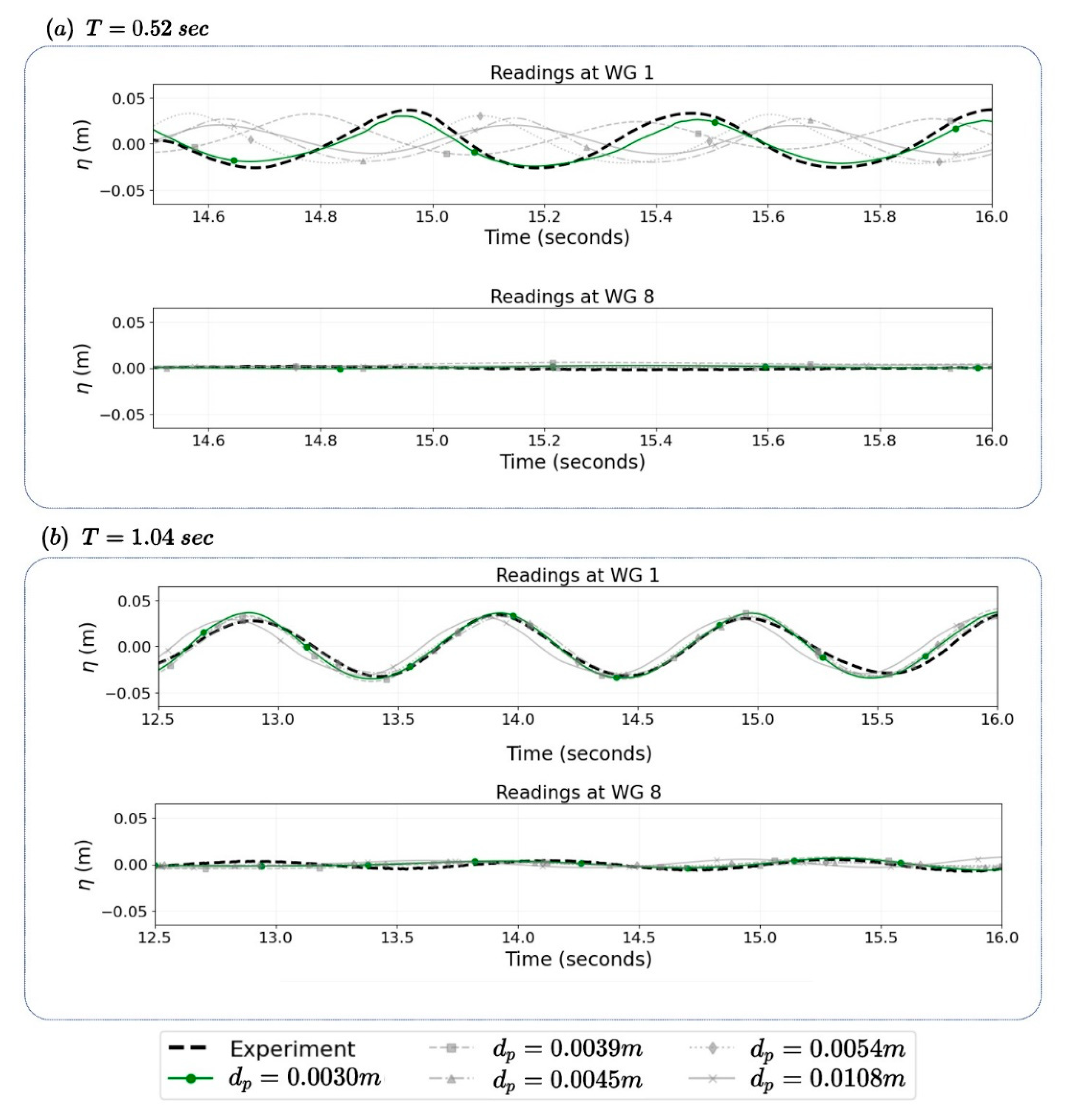
3.3. Model Validation Study
4. Parametric Study
4.1. Parameters of the Study
4.2. Parametric Study Results
4.2.1. Wave Attenuation Performance
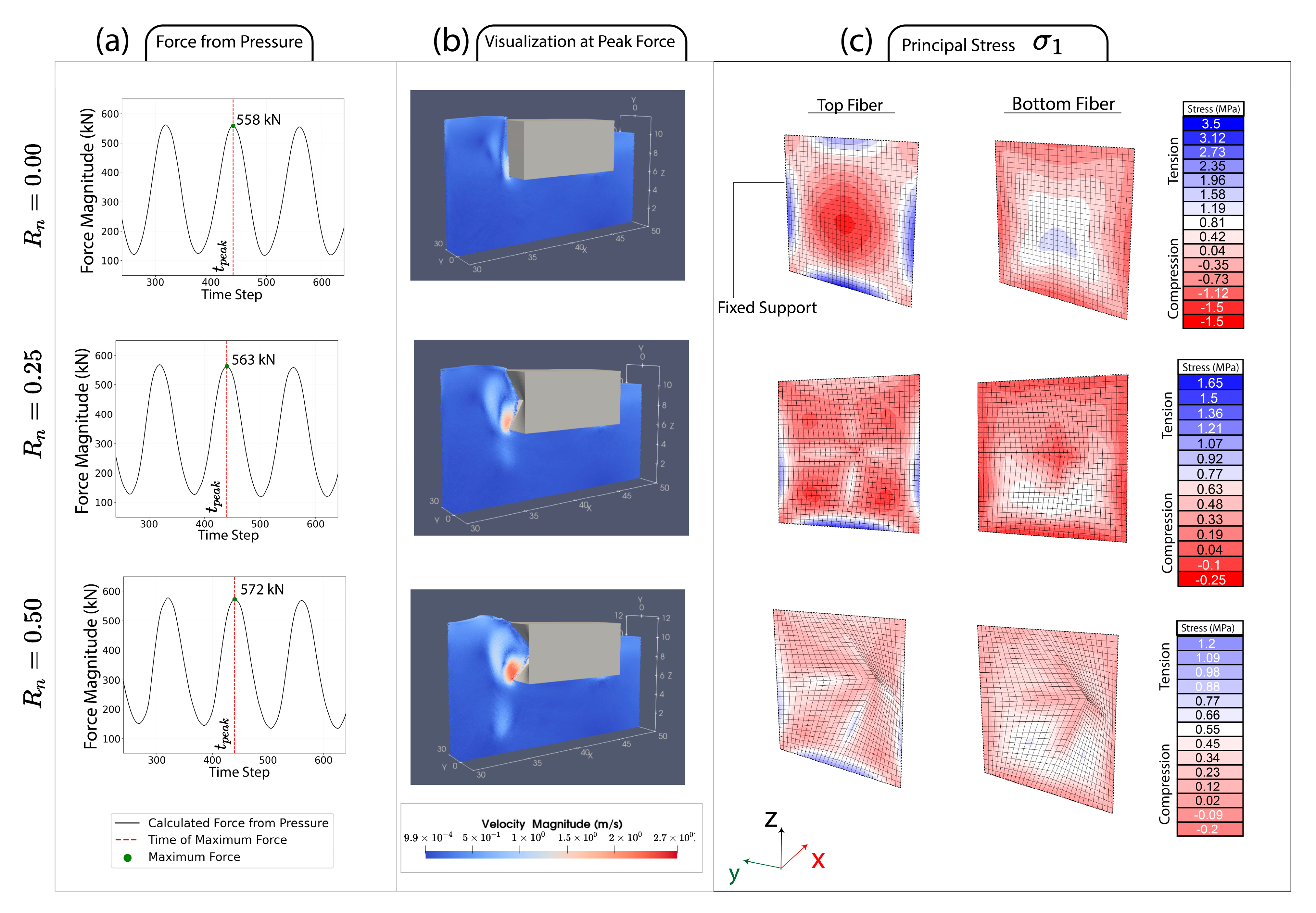
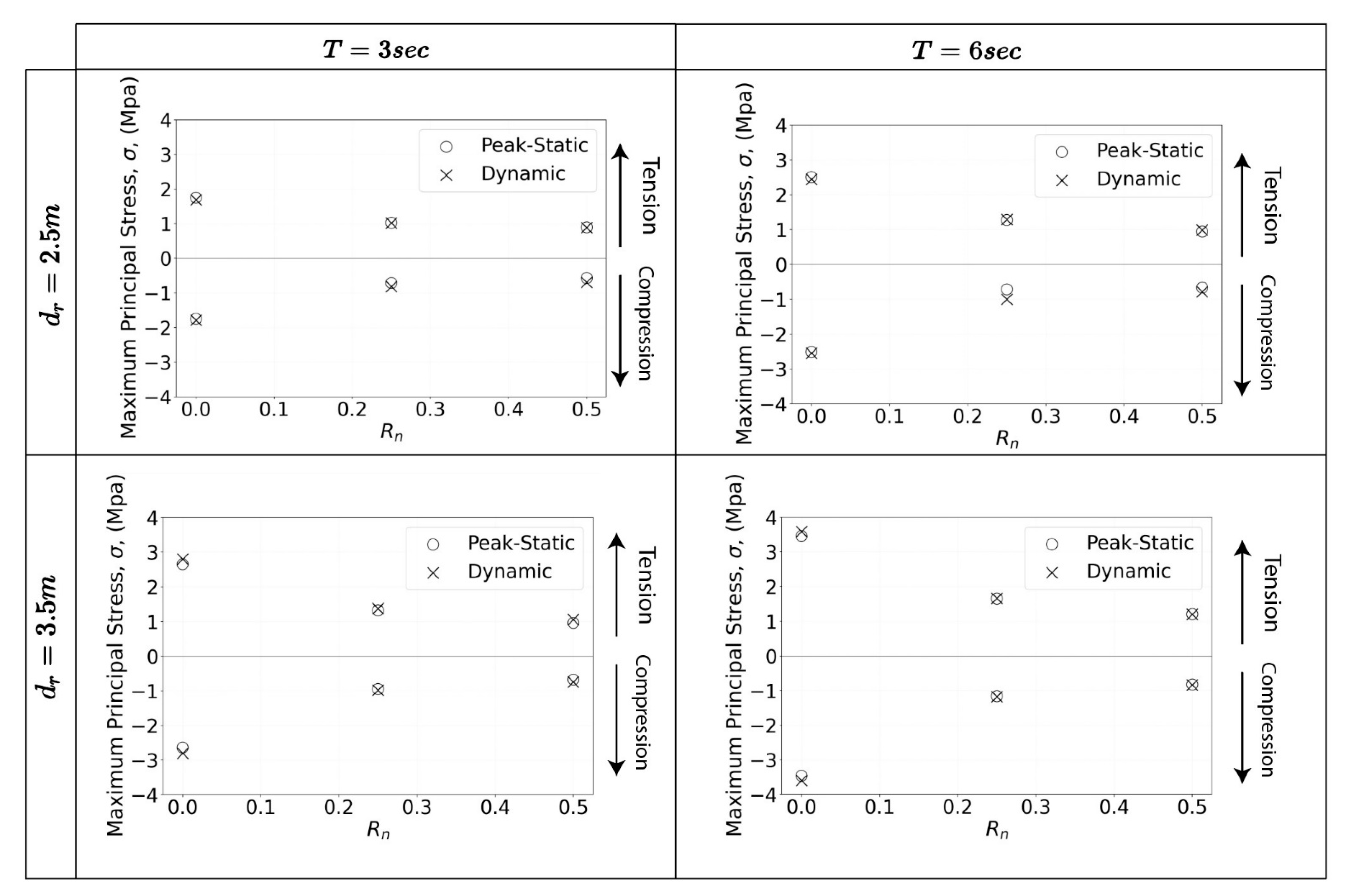
4.2.2. Structural Response
5. Summary and Conclusions
- Hypar-faced FSBW designs improve wave attenuation performance compared to flat-faced designs, primarily through wave dissipation. The improved performance is more pronounced for shorter wave periods and lower draft values.
- Hypar geometry significantly reduces maximum principal stress values compared to flat designs. This effect is most pronounced for FSBWs with thinner shell walls.
- Peak-static analysis provides a reasonable approximation for the structural stresses of hypar FSBW under regular wave conditions, with less than 6% difference from dynamic analysis results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vardy, M.; Oppenheimer, M.; Dubash, N.K.; O’Reilly, J.; Jamieson, D. The intergovernmental panel on climate change: Challenges and opportunities. Annu. Rev. Environ. Resour. 2017, 42, 55–75. [Google Scholar] [CrossRef]
- Pérez-Alarcón, A.; Fernández-Alvarez, J.C.; Coll-Hidalgo, P. Global Increase of the Intensity of Tropical Cyclones Under Global Warming Based on Their Maximum Potential Intensity and CMIP6 Models. Environ. Process. 2023, 10, 36. [Google Scholar] [CrossRef]
- Rambabu, N.; Srineash, V. A Review on Methodologies to Upgrade the Coastal Structures to Enhance the Coastal Resilience. In Proceedings of the OCEANS 2022-Chennai, Chennai, India, 21–24 February 2022; pp. 1–9. [Google Scholar]
- Teh, H. Hydraulic performance of free surface breakwaters: A review. Sains Malays. 2013, 42, 1301–1310. [Google Scholar]
- Lorenzoni, C.; Soldini, L.; Brocchini, M.; Mancinelli, A.; Postacchini, M.; Seta, E.; Corvaro, S. Working of defense coastal structures dissipating by macroroughness. J. Waterw. Port Coast. Ocean. Eng. 2010, 136, 79–90. [Google Scholar] [CrossRef]
- He, F. Experimental Investigation of Pile-Supported/Floating Breakwaters Integrated with Oscillating-Water-Column Converters. Ph.D. Thesis, Nanyang Technological University, Singapore, 2013. [Google Scholar]
- Isaacson, M.; Whiteside, N.; Gardiner, R.; Hay, D. Modelling of a circular-section floating breakwater. Can. J. Civ. Eng. 1995, 22, 714–722. [Google Scholar] [CrossRef]
- Elchahal, G.; Lafon, P.; Younes, R. Design optimization of floating breakwaters with an interdisciplinary fluid–solid structural problem. Can. J. Civ. Eng. 2009, 36, 1732–1743. [Google Scholar] [CrossRef]
- Brossard, J.; Jarno-Druaux, A.; Marin, F.; Tabet-Aoul, E. Fixed absorbing semi-immersed breakwater. Coast. Eng. 2003, 49, 25–41. [Google Scholar] [CrossRef]
- Günaydın, K.; Kabdaşlı, M. Performance of solid and perforated U-type breakwaters under regular and irregular waves. Ocean. Eng. 2004, 31, 1377–1405. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, G.; Li, G. Experimental study on the performance of the multiple-layer breakwater. Ocean. Eng. 2006, 33, 1829–1839. [Google Scholar] [CrossRef]
- Sundar, V. Hydrodynamic pressures and forces on quadrant front face pile supported breakwater. Ocean. Eng. 2002, 29, 193–214. [Google Scholar] [CrossRef]
- Koutandos, E.; Prinos, P. Hydrodynamic characteristics of semi-immersed breakwater with an attached porous plate. Ocean. Eng. 2011, 38, 34–48. [Google Scholar] [CrossRef]
- Lv, C.; Zhao, X.; Zheng, K.; Zong, Y.; Zheng, S.; Jiang, H.; Yao, S.; Luan, H. Hydrodynamic performance of a floating fluid-filled membrane breakwater: Experimental and numerical study. J. Fluid Mech. 2024, 1001, A21. [Google Scholar] [CrossRef]
- Elchahal, G.; Younes, R.; Lafon, P. Optimization of coastal structures: Application on detached breakwaters in ports. Ocean. Eng. 2013, 63, 35–43. [Google Scholar] [CrossRef]
- Cebada-Relea, A.J.; López, M.; Claus, R.; Aenlle, M. Short-term analysis of extreme wave-induced forces on the connections of a floating breakwater. Ocean. Eng. 2023, 280, 114579. [Google Scholar] [CrossRef]
- Wang, S.; Garlock, M.; Glisic, B. Geometric and area parameterization of N-edged hyperbolic paraboloidal umbrellas. Eng. Struct. 2022, 250, 113499. [Google Scholar] [CrossRef]
- ElDarwich, H.; Mansouri, I.; Garlock, M.; Wang, S. Predicting Maximum Deflection of N-Edged Thin-Shelled Hyperbolic-Paraboloid Umbrella Using Machine Learning Techniques. Thin-Walled Struct. 2024, 205, 112412. [Google Scholar] [CrossRef]
- Gergely, P.; Banavalkar, P.V.; Parker, J.E. The Analysis and Behavior of Thin-Steel Hyperbolic Paraboloid Shells; Report No. 338; Wei-Wen Yu Center for Cold-Formed Steel Structures, Civil, Architectural and Environmental Engineering Department, Missouri University of Science and Technology: Rolla, MO, USA, 1971. [Google Scholar]
- Garlock, M.E.M.; Billington, D.P. Félix Candela: Engineer, Builder, Structural Artist; Princeton University Art Museum: Princeton, NJ, USA; Yale University Press: New Haven, CT, USA, 2008. [Google Scholar]
- Wang, S.; Garlock, M.; Deike, L.; Glisic, B. Feasibility of Kinetic Umbrellas as deployable flood barriers during landfalling hurricanes. J. Struct. Eng. 2022, 148, 04022047. [Google Scholar] [CrossRef]
- Wang, S.; Garlock, M.; Glisic, B. Kinematics of deployable hyperbolic paraboloid umbrellas. Eng. Struct. 2021, 244, 112750. [Google Scholar] [CrossRef]
- Wang, S.; Notario, V.; Garlock, M.; Glisic, B. Parameterization of hydrostatic behavior of deployable hypar umbrellas as flood barriers. Thin-Walled Struct. 2021, 163, 107650. [Google Scholar] [CrossRef]
- Wu, G.; Garlock, M.; Wang, S. A decoupled SPH-FEM analysis of hydrodynamic wave pressure on hyperbolic-paraboloid thin-shell coastal armor and corresponding structural response. Eng. Struct. 2022, 268, 114738. [Google Scholar] [CrossRef]
- ElDarwich, H.S.; Pawitan, K.A.; Garlock, M.E. Conceptual Investigation on the Effectiveness of Hyperbolic Paraboloid Surfaces for Floating Breakwaters. In Proceedings of the IASS 2022 Symposium Affiliated with APCS 2022 Conference, Beijing, China, 19–23 September 2022. [Google Scholar]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid–structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- McNeel, R. Rhinoceros 3D, Version 7 2020. Robert McNeel & Associates, Seattle, WA, USA, 2015. Available online: https://www.rhino3d.com.
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- CSI. SAP2000 CSI Analysis Reference Manual 2014; Computers and Structures, Inc.: Walnut Creek, CA, USA, 2014; Available online: https://www.csiamerica.com.
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.; Crespo, A.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Martínez-Estévez, I.; Tagliafierro, B.; El Rahi, J.; Domínguez, J.; Crespo, A.; Troch, P.; Gómez-Gesteira, M. Coupling an SPH-based solver with an FEA structural solver to simulate free surface flows interacting with flexible structures. Comput. Methods Appl. Mech. Eng. 2023, 410, 115989. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Fourtakas, G.; Vacondio, R.; Alonso, J.D.; Rogers, B.D. Improved Density Diffusion Term for Long Duration Wave Propagation. In Proceedings of the 2020 SPHERIC Harbin International Workshop, Harbin, China, 13 January–16 September 2020. [Google Scholar]
- Grubmüller, H.; Heller, H.; Windemuth, A.; Schulten, K. Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions. Mol. Simul. 1991, 6, 121–142. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Cas, R.A.; Kos, A.; Hallworth, M. Gravity currents descending a ramp in a stratified tank. J. Fluid Mech. 1999, 379, 39–69. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y. Numerical studies of submerged moored box-type floating breakwaters with different shapes of cross-sections using SPH. Coast. Eng. 2020, 158, 103687. [Google Scholar] [CrossRef]
- Wu, G.; Garlock, M. Investigating the effects of box girder bridge geometry on solitary wave force using SPH modeling. Coast. Eng. 2024, 187, 104430. [Google Scholar] [CrossRef]
- Cabrera Crespo, A.J.; Gómez Gesteira, R.; Dalrymple, R.A. Boundary conditions generated by dynamic particles in SPH methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Estevez, I.M. Coupling Between the DualSPHysics Solver and Multiphysics Libraries: Implementation, Validation and Real Engineering Applications. Ph.D. Thesis, Universidade of Vigo, Pontevedra, Spain, 2024. [Google Scholar]
- Pawitan, K.A. Wave Loadings and Scaling Effects on, and Within, an Oscillating Water Column (OWC) Caisson Breakwater. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2019. [Google Scholar]
- Zago, V.; Schulze, L.J.; Bilotta, G.; Almashan, N.; Dalrymple, R. Overcoming excessive numerical dissipation in SPH modeling of water waves. Coast. Eng. 2021, 170, 104018. [Google Scholar] [CrossRef]
- Mathisen, J.; Bitner-Gregersen, E. Joint distributions for significant wave height and wave zero-up-crossing period. Appl. Ocean. Res. 1990, 12, 93–103. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. Coast. Eng. 1976, 1976, 828–845. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering, 7th ed.; World Scientific: Singapore, 1993. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fundamentals of Fluid Mechanics, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Reis, C.; Barbosa, A.R.; Figueiredo, J.; Clain, S.; Lopes, M.; Baptista, M.A. Smoothed particle hydrodynamics modeling of elevated structures impacted by tsunami-like waves. Eng. Struct. 2022, 270, 114851. [Google Scholar] [CrossRef]
- Domínguez, J.; Fourtakas, G.; Cercós-Pita, J.; Vacondio, R.; Rogers, B.D.; Crespo, A. Evaluation of reliability and efficiency of different boundary conditions in a SPH code. In Proceedings of the 10th International SPHERIC Workshop, Parma, Italy, 16–18 June 2015. [Google Scholar]
- Ferrand, M.; Laurence, D.R.; Rogers, B.D.; Violeau, D.; Kassiotis, C. Unified semi-analytical wall boundary conditions for inviscid, laminar or turbulent flows in the meshless SPH method. Int. J. Numer. Methods Fluids 2013, 71, 446–472. [Google Scholar] [CrossRef]
- Dai, J.; Wang, C.M.; Utsunomiya, T.; Duan, W. Review of recent research and developments on floating breakwaters. Ocean. Eng. 2018, 158, 132–151. [Google Scholar] [CrossRef]
- Wang, S.; Garlock, M.; Glisic, B. Hydrostatic Response of Deployable Hyperbolic-Paraboloid Umbrellas as Coastal Armor. J. Struct. Eng. 2020, 146, 04020096. [Google Scholar] [CrossRef]
- Robutti, G.; Ronzoni, E.; Ottosen, N. Failure Strength and Elastic Limit for Concrete: A Comparative Study. In Proceedings of the 5th International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, 12–16 August 1979. [Google Scholar]
- Le Méhauté, B.; Koh, R.C.Y. On the Breaking of Waves Arriving at an Angle to the Shore. J. Hydraul. Res. 1967, 5, 67–88. [Google Scholar] [CrossRef]
- Martin, W.; Adee, B.H. Theoretical Analysis of Floating Breakwater Performance. In Proceedings of the Fifth Indian National Conference on Harbour and Ocean Engineering, Goa, India, 4–6 February 1974. [Google Scholar]
- Macagno, E. Fluid mechanics: Experimental study of the effects of the passage of a wave beneath an obstacle. In Proceedings of the Academic Des Sciences, Paris, France, 28 February 1953. [Google Scholar]


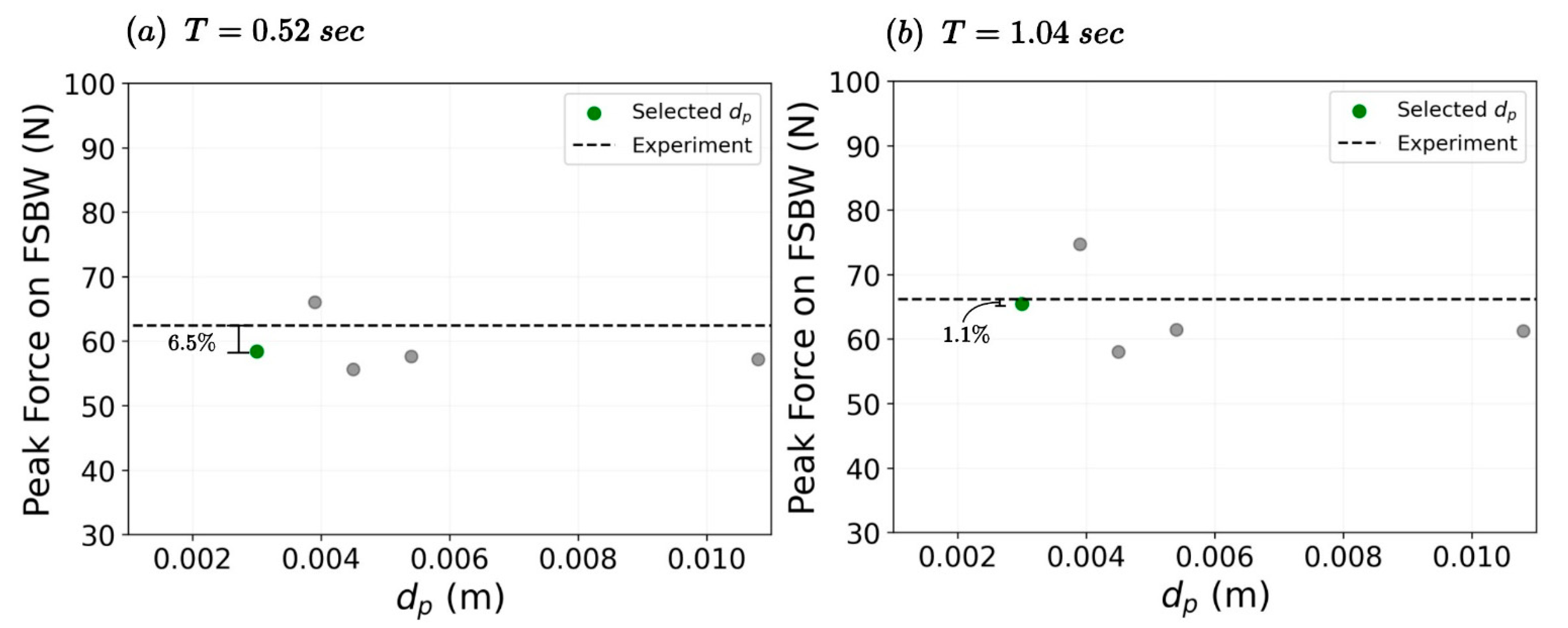
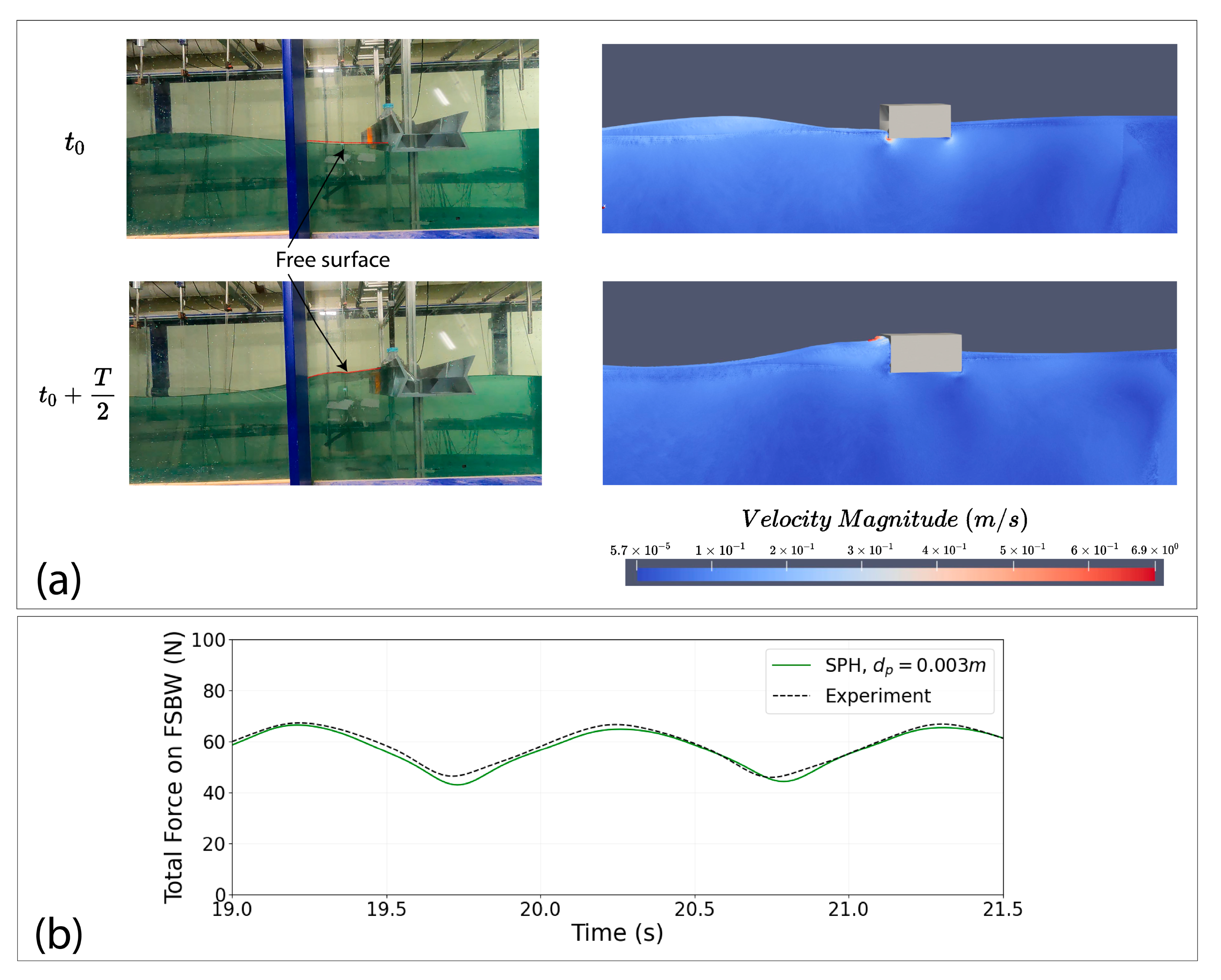
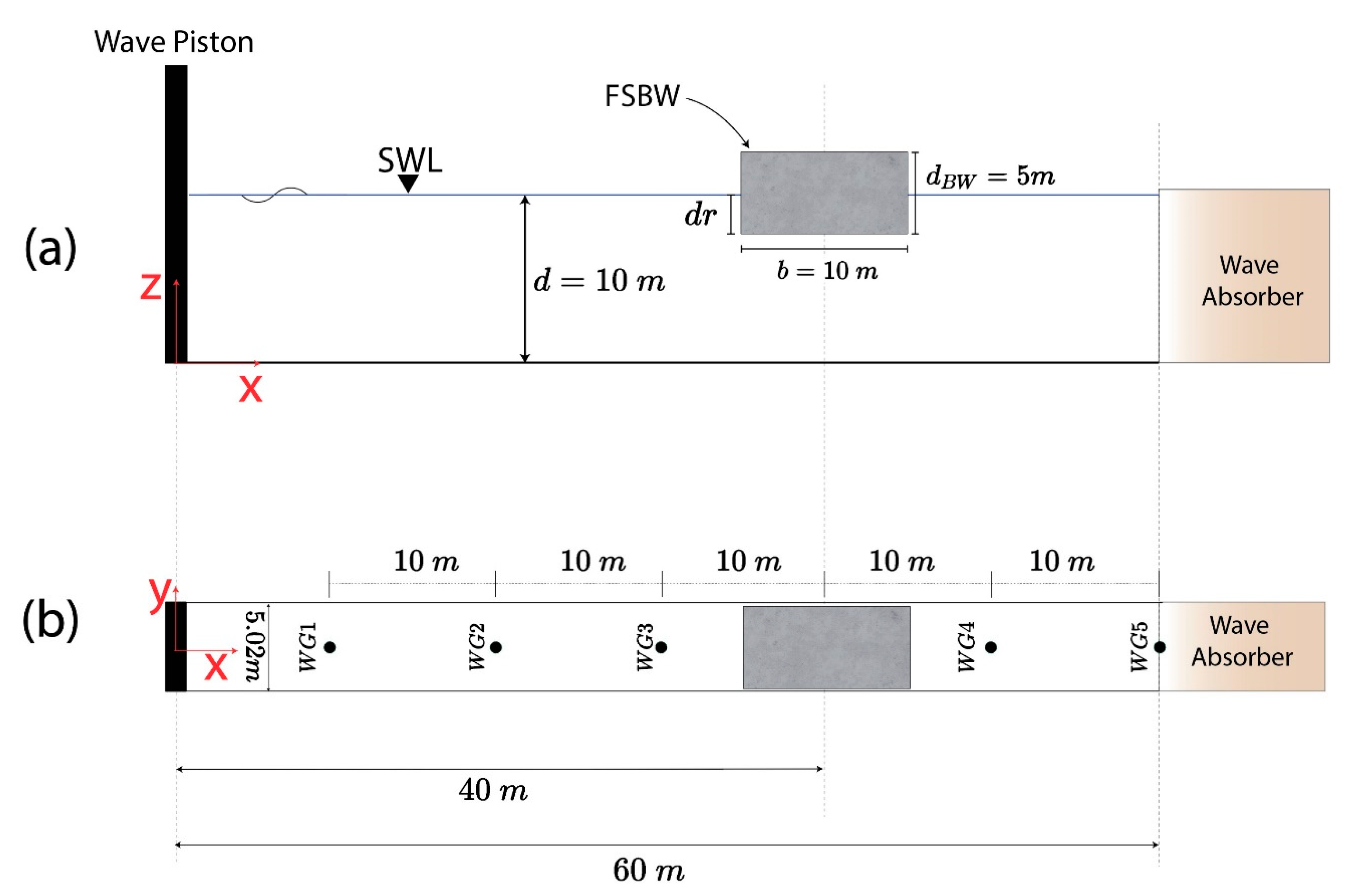
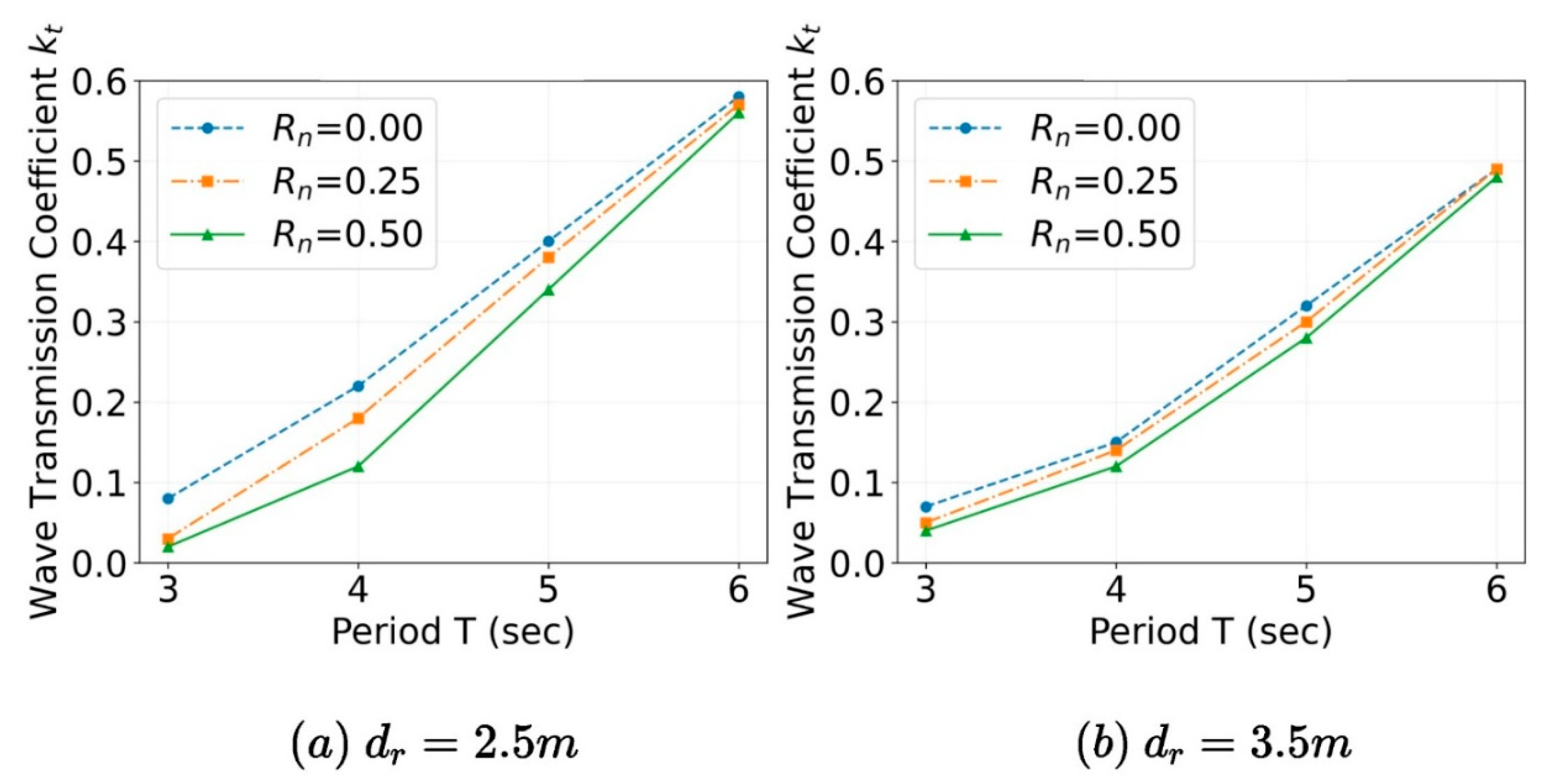

| Parameter (Units) | Full-Scale Value | Model Scale Value |
|---|---|---|
| (s) | 3, 6 | 0.52, 1.04 |
| Wave Height, H (m) | 1.8 | 0.054 |
| (m) | 2.5 | 0.075 |
| Attribute | Values |
|---|---|
| Kernal type | Quintic Wendland kernel |
| Boundary Method | Dynamic Boundary Condition |
| Artificial viscosity coefficient | 0.01 (near irrotational flows) |
| Time per second | ~600 |
| GPU | NVIDIA A100 |
| CPU | Intel(R) Xeon(R) Platinum 8380 |
| Parameter | Values | |
|---|---|---|
| Geometric Properties (See Figure 3) | 0, 0.25, 0.5 | |
| Breakwater length, b (m) | 10 | |
| (m) | 5 | |
| (m) | 5 | |
| (m) | 0.25 | |
| Wave and Bathymetry (See Figure 9) | (s) | 3, 4, 5, 6 |
| Wave Height, H (m) | 1.8 | |
| (m) | 2.5, 3.5 |
| Wave Scenario | Parameter | |||
|---|---|---|---|---|
| , | 0.22 | 0.18 | 0.12 | |
| 0.76 | 0.60 | 0.40 | ||
| 0.61 | 0.78 | 0.91 | ||
| , | 0.15 | 0.14 | 0.12 | |
| 0.75 | 0.61 | 0.43 | ||
| 0.64 | 0.78 | 0.89 | ||
| , | 0.40 | 0.38 | 0.34 | |
| 0.10 | 0.10 | 0.08 | ||
| 0.91 | 0.92 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ElDarwich, H.; Wu, G.; Pawitan, K.A.; Garlock, M. Hyperbolic Paraboloid Free-Surface Breakwaters: Hydrodynamic Study and Structural Evaluation. J. Mar. Sci. Eng. 2025, 13, 245. https://doi.org/10.3390/jmse13020245
ElDarwich H, Wu G, Pawitan KA, Garlock M. Hyperbolic Paraboloid Free-Surface Breakwaters: Hydrodynamic Study and Structural Evaluation. Journal of Marine Science and Engineering. 2025; 13(2):245. https://doi.org/10.3390/jmse13020245
Chicago/Turabian StyleElDarwich, Hamid, Gaoyuan Wu, Krisna A Pawitan, and Maria Garlock. 2025. "Hyperbolic Paraboloid Free-Surface Breakwaters: Hydrodynamic Study and Structural Evaluation" Journal of Marine Science and Engineering 13, no. 2: 245. https://doi.org/10.3390/jmse13020245
APA StyleElDarwich, H., Wu, G., Pawitan, K. A., & Garlock, M. (2025). Hyperbolic Paraboloid Free-Surface Breakwaters: Hydrodynamic Study and Structural Evaluation. Journal of Marine Science and Engineering, 13(2), 245. https://doi.org/10.3390/jmse13020245






