A Time-Delay Overlapping Modulation-Based Maritime High-Speed and High-Spectral-Efficiency Communication Technology
Abstract
1. Introduction
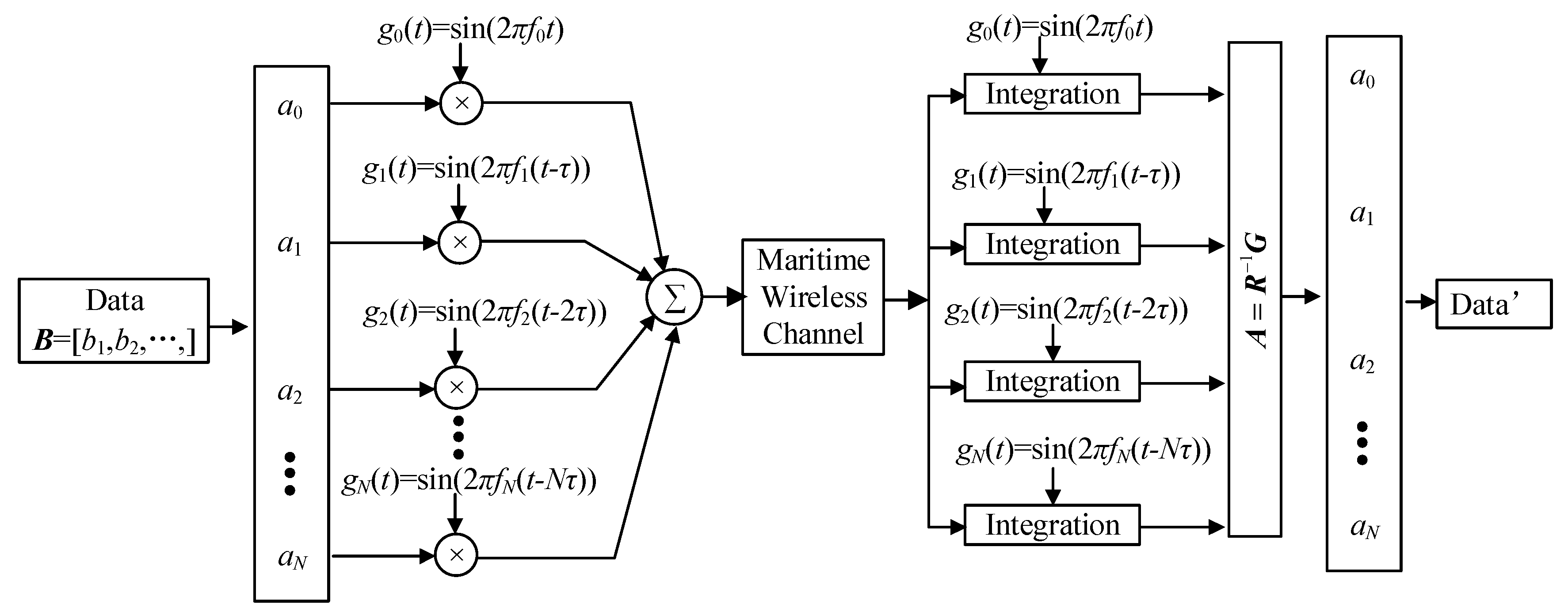
2. System Architecture
2.1. Transmitter
2.2. Receiver
2.3. Maritime Channel
3. Performance Analysis
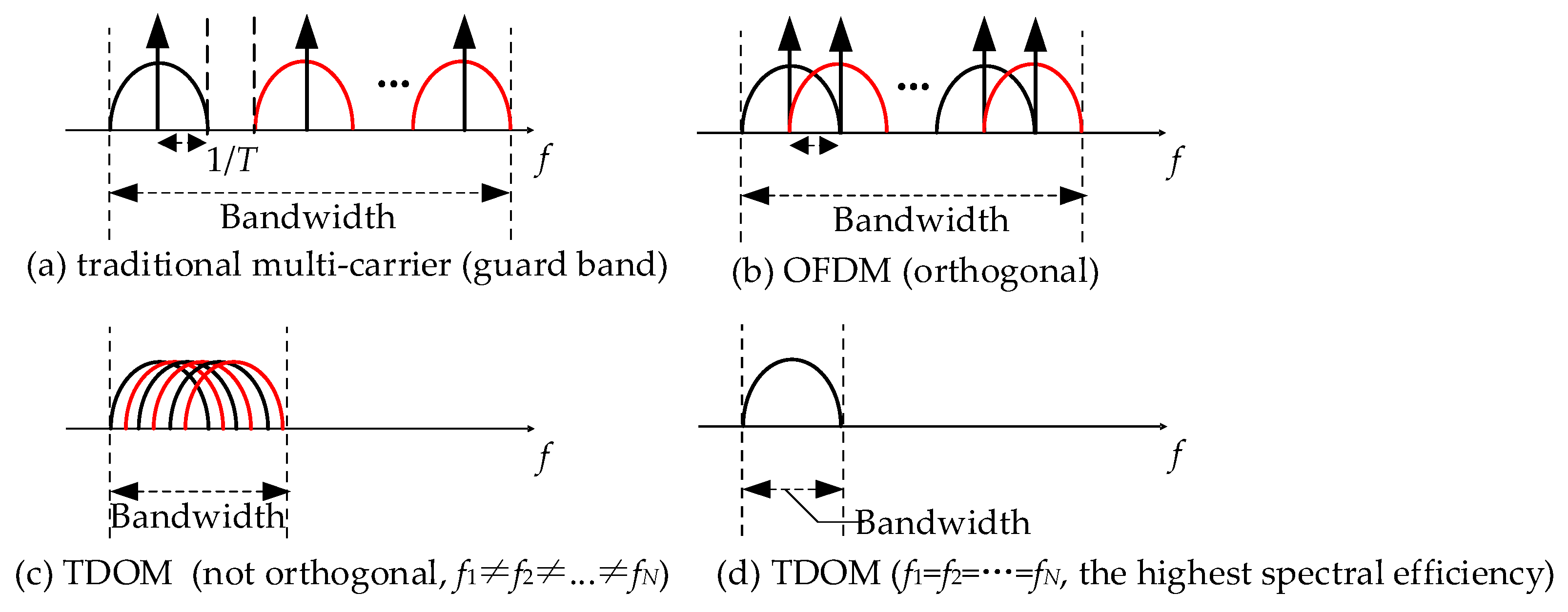
3.1. Spectral Efficiency
3.2. Complexity
3.3. BER Source Analysis
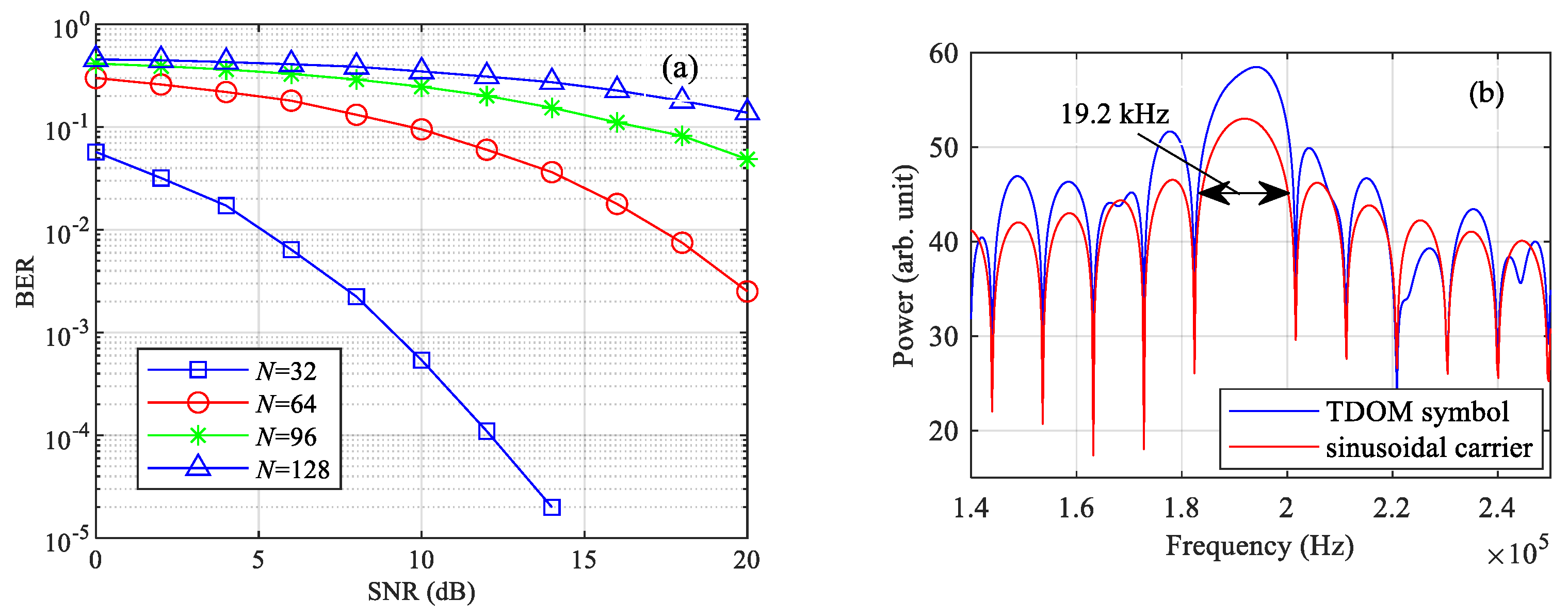
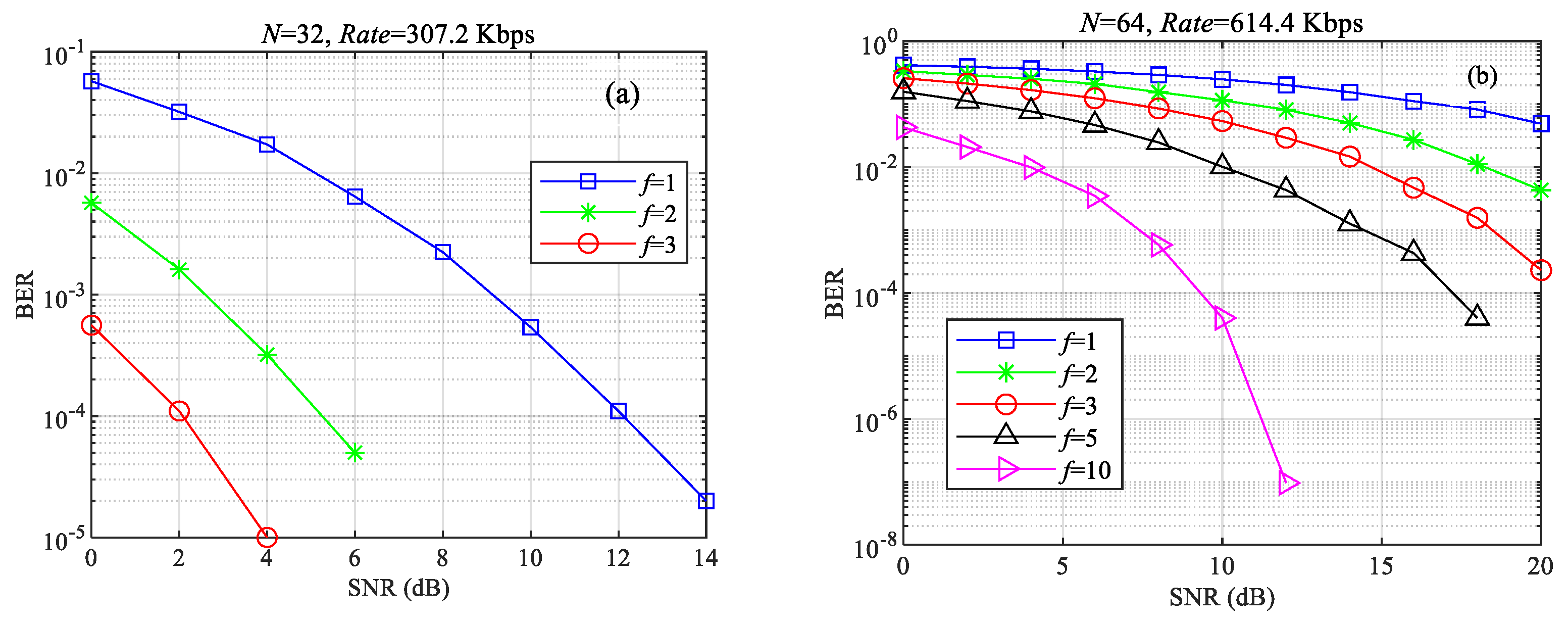
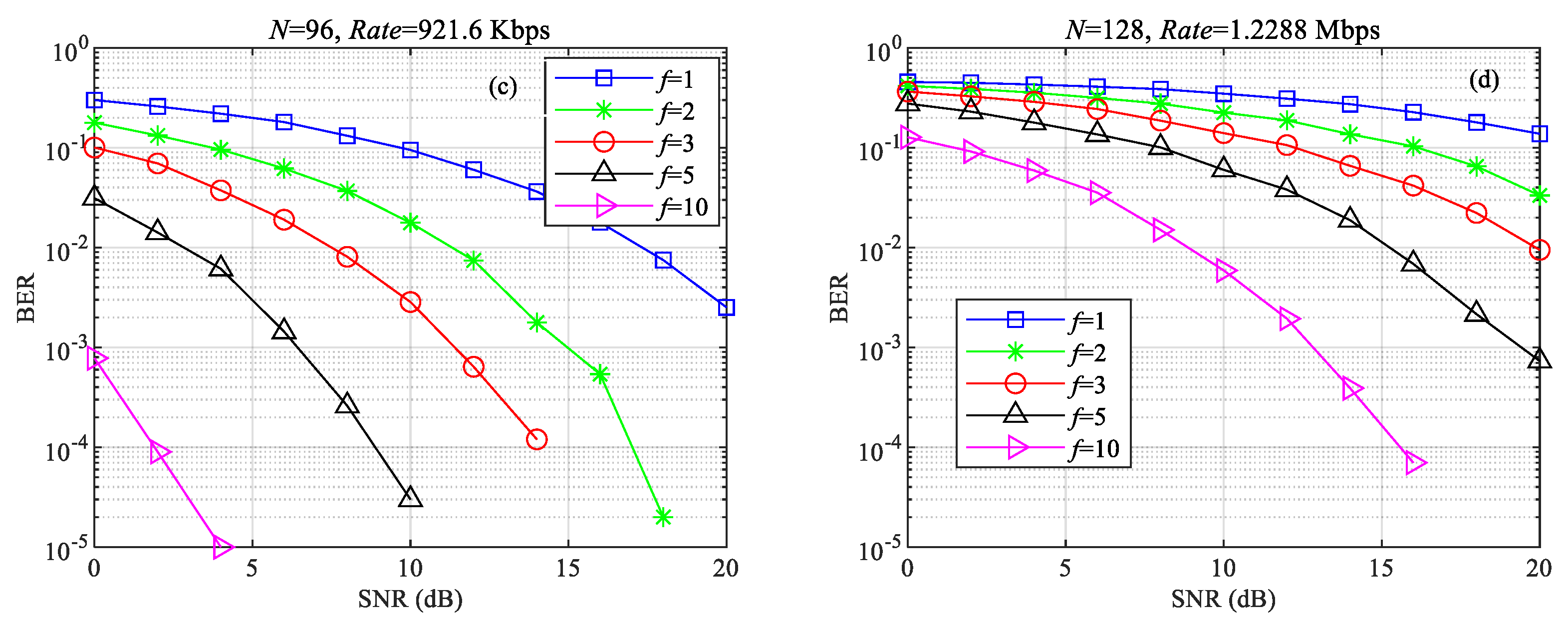
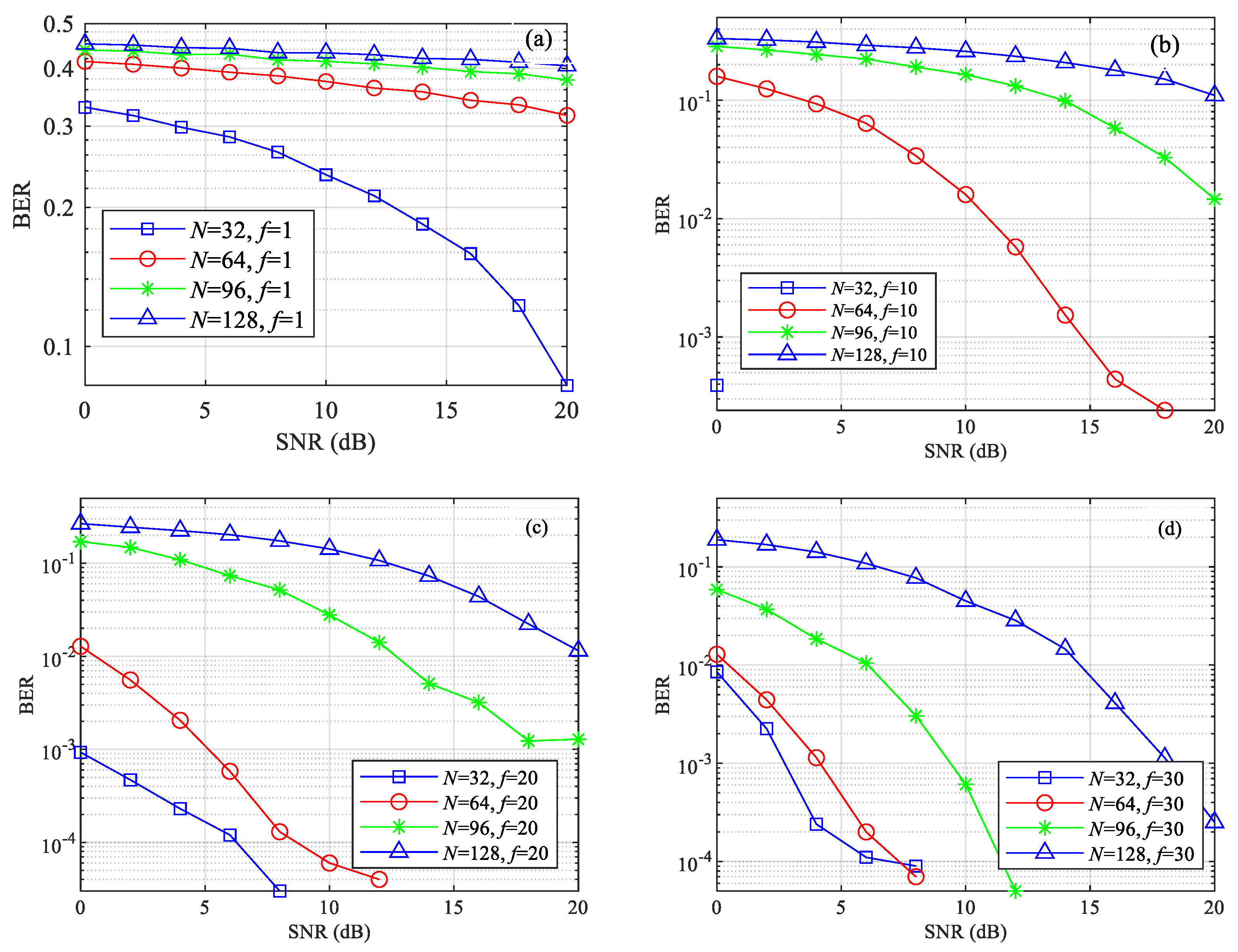
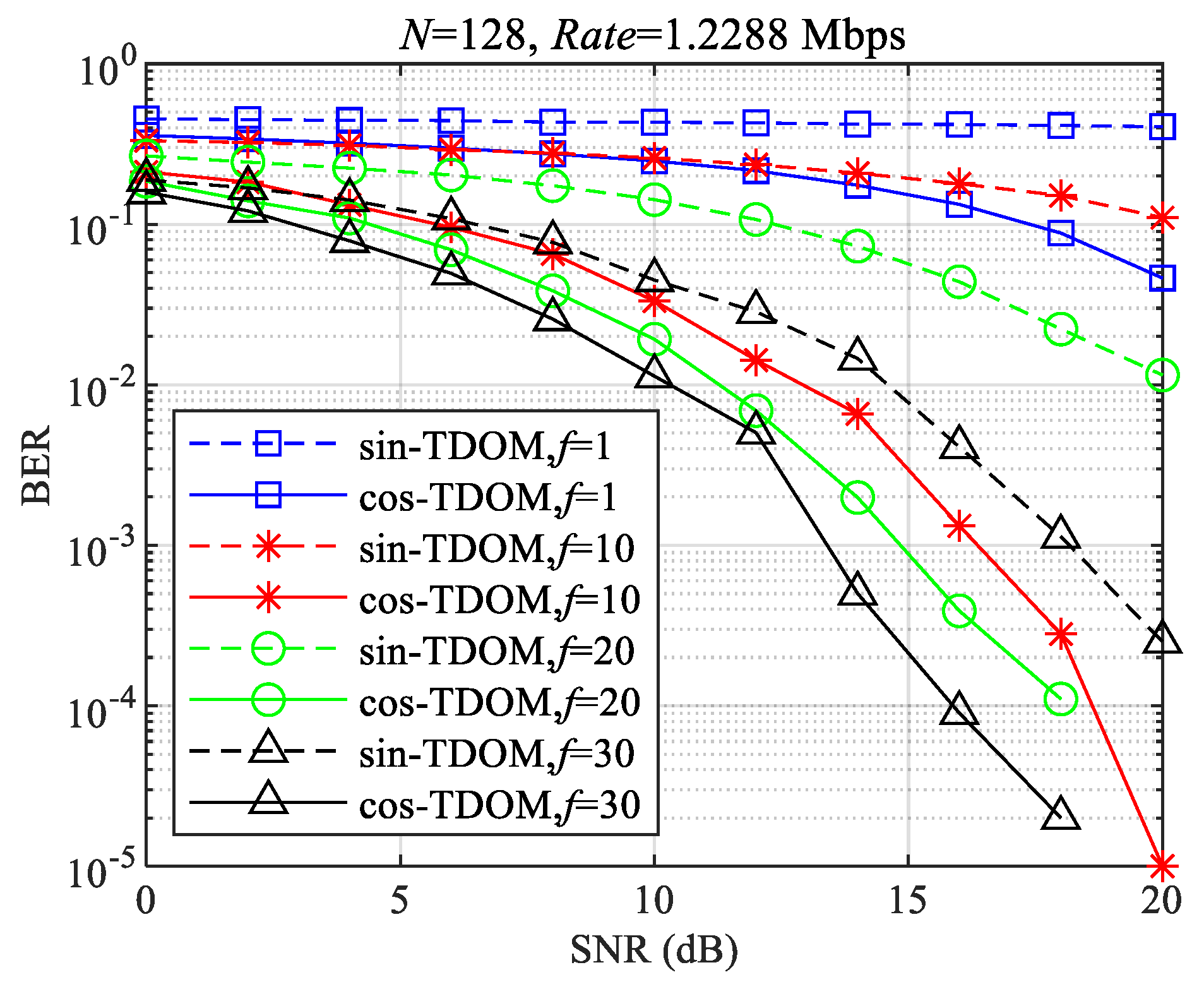
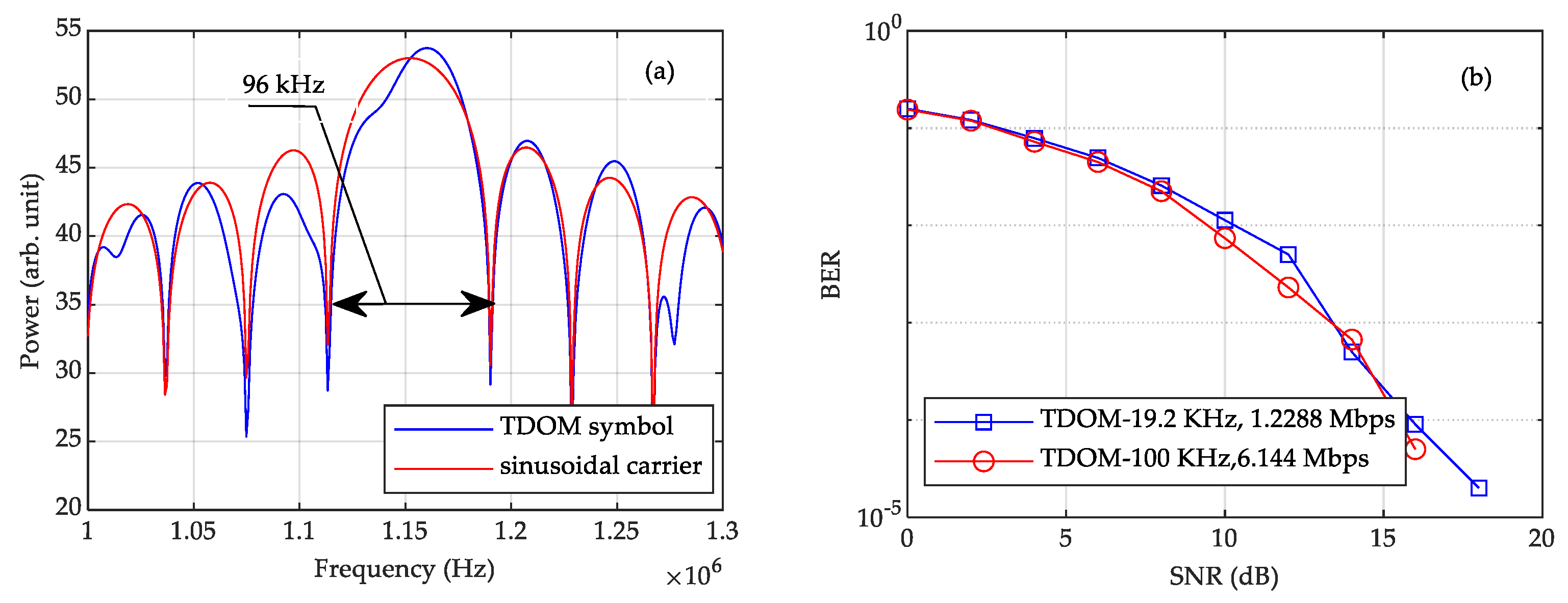
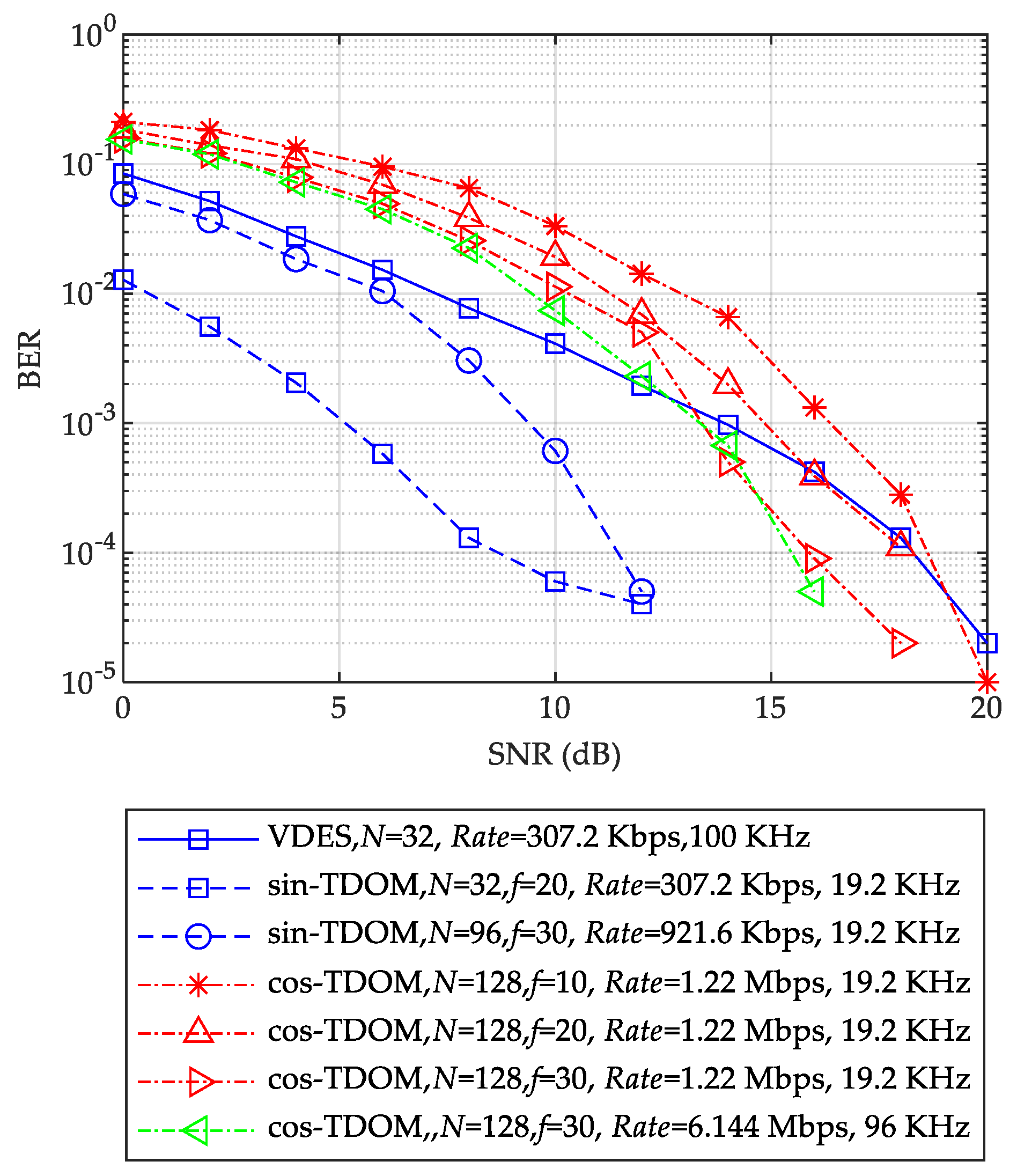
4. Simulation Results
4.1. System Performance
4.2. Peak Communication Rate When the Bandwidth of TDOM Is Nearly 100 KHz
4.3. Comparison Between TDOM and Other Maritime Communications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Orabi, M.; Khalife, J.; Kassas, Z.M. Opportunistic navigation with doppler measurements from Iridium next and orbcomm LEO satellites. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021. [Google Scholar]
- Surekha, T.P.; Ananthapadmanabha, T.; Puttamadappa, C. Performance evaluation of VSAT-QPSK system. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 726–730. [Google Scholar]
- Zhuang, Q.; Zheng, C. Research on INMARSAT based on Ka band and applications. In Proceedings of the 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS), Dalian, China, 24–26 July 2017; pp. 127–129. [Google Scholar]
- Koulikova, Y.; Roberti, L. Global Xpress Broadband. Available online: https://www.itu.int/dms_pub/itu-r/md/12/iturka.band/c/R12-ITURKA.BAND-C-0002!!PDF-E.pdf (accessed on 1 September 2012).
- ITU-R M.1084-5; Interim Solutions for Improved Efficiency in the Use of the Band 156–174 MHz by Stations in the Maritime Mobile Service. International Telecommunication Union: Geneva, Switzerland, 2012.
- ITU-R M.2092-0; Technical Characteristics for a VHF Data Exchange System in the VHF Maritime Mobile Band. International Telecommunication Union: Geneva, Switzerland, 2015.
- Zhou, M.-T.; Hoang, V.D.; Harada, H.; Pathmasuntharam, J.S.; Wang, H.; Kong, P.-Y.; Ang, C.-W.; Ge, Y.; Wen, S. TRITON: High-speed maritime wireless mesh network. IEEE Wirel. Commun. 2013, 20, 134–142. [Google Scholar] [CrossRef]
- Bekkadal, F.; Yang, K. Novel maritime communications technologies. In Proceedings of the 2010 10th Mediterranean Microwave Symposium (MMS), Ankara, Türkiye, 25–27 August 2010; pp. 338–341. [Google Scholar]
- Kim, Y.; Kim, J.; Wang, Y.; Chang, K.; Park, J.W.; Lim, Y. Application scenarios of nautical Ad-Hoc network for maritime communications. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; pp. 1–4. [Google Scholar]
- Campos, R.; Oliveira, T.; Cruz, N.; Matos, A.; Almeida, J.M. BLUECOM+: Cost-effective broadband communications at remote ocean areas. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016. [Google Scholar]
- Teixeira, F.B.; Oliveira, T.; Lopes, M.; Leocadio, C.; Salazar, P.; Ruela, J.; Campos, R.; Ricardo, M. Enabling broadband internet access offshore using tethered balloons: The BLUECOM+ experience. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017. [Google Scholar]
- Lopes, M.J.; Teixeira, F.; Mamede, J.B.; Campos, R. Wi-Fi broadband maritime communications using 5.8 GHz band. In Proceedings of the 2014 Underwater Communications and Networking (UComms), Sestri Levante, Italy, 3–5 September 2014. [Google Scholar]
- Garroppo, R.G.; Giordano, S.; Iacono, D.; Cignoni, A.; Falzarano, M. WiMAX testbed for interconnection of mobile navy units in operational scenarios. In Proceedings of the MILCOM 2008—2008 IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; p. 3907. [Google Scholar]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Quek, T.Q.S.; Xu, C. Wireless channel models for maritime communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Garroppo, R.G.; Giordano, S.; Iacono, D. Experimental and simulation study of a WiMAX system in the sea port scenario. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 4729–4733. [Google Scholar]
- Choi, M.S.; Park, S.; Lee, Y.; Lee, S.R. Ship to ship maritime communication for e-Navigation using WiMAX. Int. J. Multimed. Ubiquitous Eng. 2014, 9, 171–178. [Google Scholar] [CrossRef]
- Anwar, S.M.; Goron, E.; Toutain, Y.; Peronne, J.P.; Hethuin, S. LTE terminal for maritime applications. In Proceedings of the 2013 Military Communications and Information Systems Conference, Saint-Malo, France, 7–9 October 2013. [Google Scholar]
- Kim, H.-J.; Choi, J.-K.; Yoo, D.-S.; Jang, B.-T.; Chong, K.-T. Implementation of MariComm bridge for LTE-WLAN maritime heterogeneous relay network. In Proceedings of the 2015 17th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 1–3 July 2015; pp. 230–234. [Google Scholar]
- Xu, Y.; Jiang, S.; Liu, F. An LTE-based communication architecture for coastal networks. In Proceedings of the 11th International Conference on Underwater Networks & Systems (WUWNET ’16), Shanghai, China, 24–26 October 2016. [Google Scholar]
- ITU-R M.1842-1; Characteristics of VHF Radio Systems and Equipment for the Exchange of Data and Electronic Mail in the Maritime Mobile Service RR Appendix 18 Channels. International Telecommunication Union: Geneva, Switzerland, 2009.
- Liang, C.; Jin, Y.; Hu, Q. Multipath time delay in maritime VHF data exchange system. J. Shanghai Marit. Univ. 2016, 37, 55–58. [Google Scholar]
- Qu, F.; Li, Z.; Zhang, M.; Tu, X.; Wei, Y. A Carrier-Based Gardner Timing Synchronization Algorithm for BPSK Signal in Maritime Communication. J. Mar. Sci. Eng. 2023, 11, 829. [Google Scholar] [CrossRef]
- Huang, F.; Liao, X.; Bai, Y. Multipath channel model for radio propagation over sea surface. Wirel. Pers. Commun. 2016, 90, 245–257. [Google Scholar] [CrossRef]


| B | a |
|---|---|
| [0,0] | −1.05 |
| [0,1] | −0.35 |
| [1,1] | 0.35 |
| [1,0] | 1.05 |
| N | |
|---|---|
| 32 | 0.0489 |
| 64 | 0.3967 |
| 96 | 1.3427 |
| 128 | 3.1839 |
| N & f | ||
|---|---|---|
| f = 1 | 0.0489 | |
| f = 2 | 0.0119 | |
| 32 | f = 3 | 0.0051 |
| f = 5 | 0.0016 | |
| f = 10 | 1.8127 × 10−4 | |
| f = 1 | 0.3967 | |
| f = 2 | 0.0986 | |
| 64 | f = 3 | 0.0434 |
| f = 5 | 0.0151 | |
| f = 10 | 0.0032 | |
| f = 1 | 1.3427 | |
| f = 2 | 0.3348 | |
| 96 | f = 3 | 0.1482 |
| f = 5 | 0.0526 | |
| f = 10 | 0.0123 | |
| f = 1 | 3.1839 | |
| f = 2 | 0.7948 | |
| 128 | f = 3 | 0.3524 |
| f = 5 | 0.1259 | |
| f = 10 | 0.0903 | |
| f | Carrier Form | |
|---|---|---|
| 1 | sine | 3.1839 |
| 20 | cosine | 0.0019 |
| 30 | cosine | 0.0018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, X.; Ma, T.; Liang, D. A Time-Delay Overlapping Modulation-Based Maritime High-Speed and High-Spectral-Efficiency Communication Technology. J. Mar. Sci. Eng. 2025, 13, 345. https://doi.org/10.3390/jmse13020345
Dou X, Ma T, Liang D. A Time-Delay Overlapping Modulation-Based Maritime High-Speed and High-Spectral-Efficiency Communication Technology. Journal of Marine Science and Engineering. 2025; 13(2):345. https://doi.org/10.3390/jmse13020345
Chicago/Turabian StyleDou, Xinyu, Teng Ma, and Dequn Liang. 2025. "A Time-Delay Overlapping Modulation-Based Maritime High-Speed and High-Spectral-Efficiency Communication Technology" Journal of Marine Science and Engineering 13, no. 2: 345. https://doi.org/10.3390/jmse13020345
APA StyleDou, X., Ma, T., & Liang, D. (2025). A Time-Delay Overlapping Modulation-Based Maritime High-Speed and High-Spectral-Efficiency Communication Technology. Journal of Marine Science and Engineering, 13(2), 345. https://doi.org/10.3390/jmse13020345






