Structural Failure Modes of Single-Story Timber Houses Under Tsunami Loads Using ASCE 7’S Energy Grade Line Analysis
Abstract
1. Introduction
1.1. Impacts of Tsunamis on Buildings
1.2. Methods Used to Compute the Structural Response of Buildings
1.3. The ASCE 7′s EGLA
2. The 27 February 2010 Tsunami in San Juan Bautista
3. Methodology
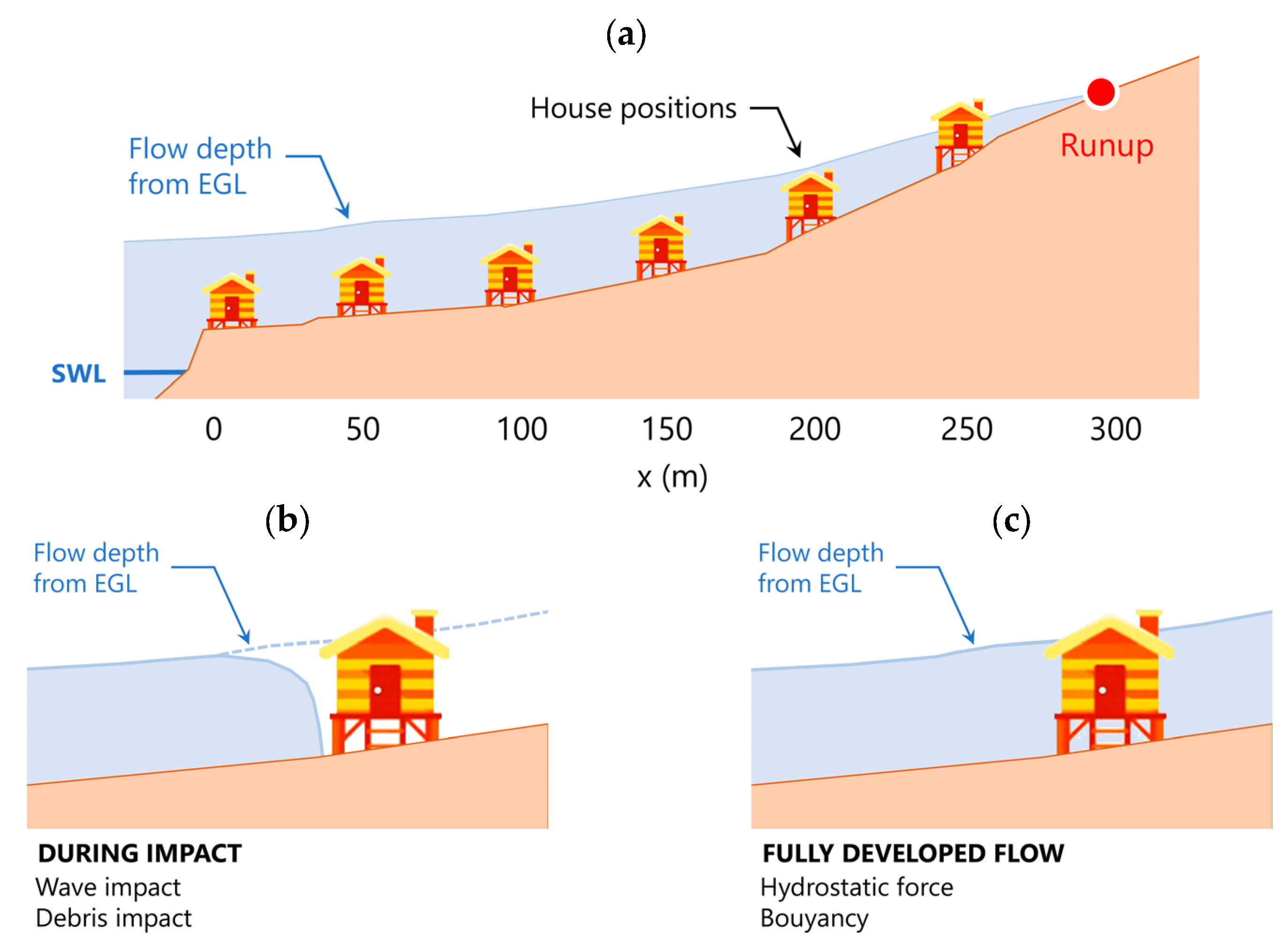
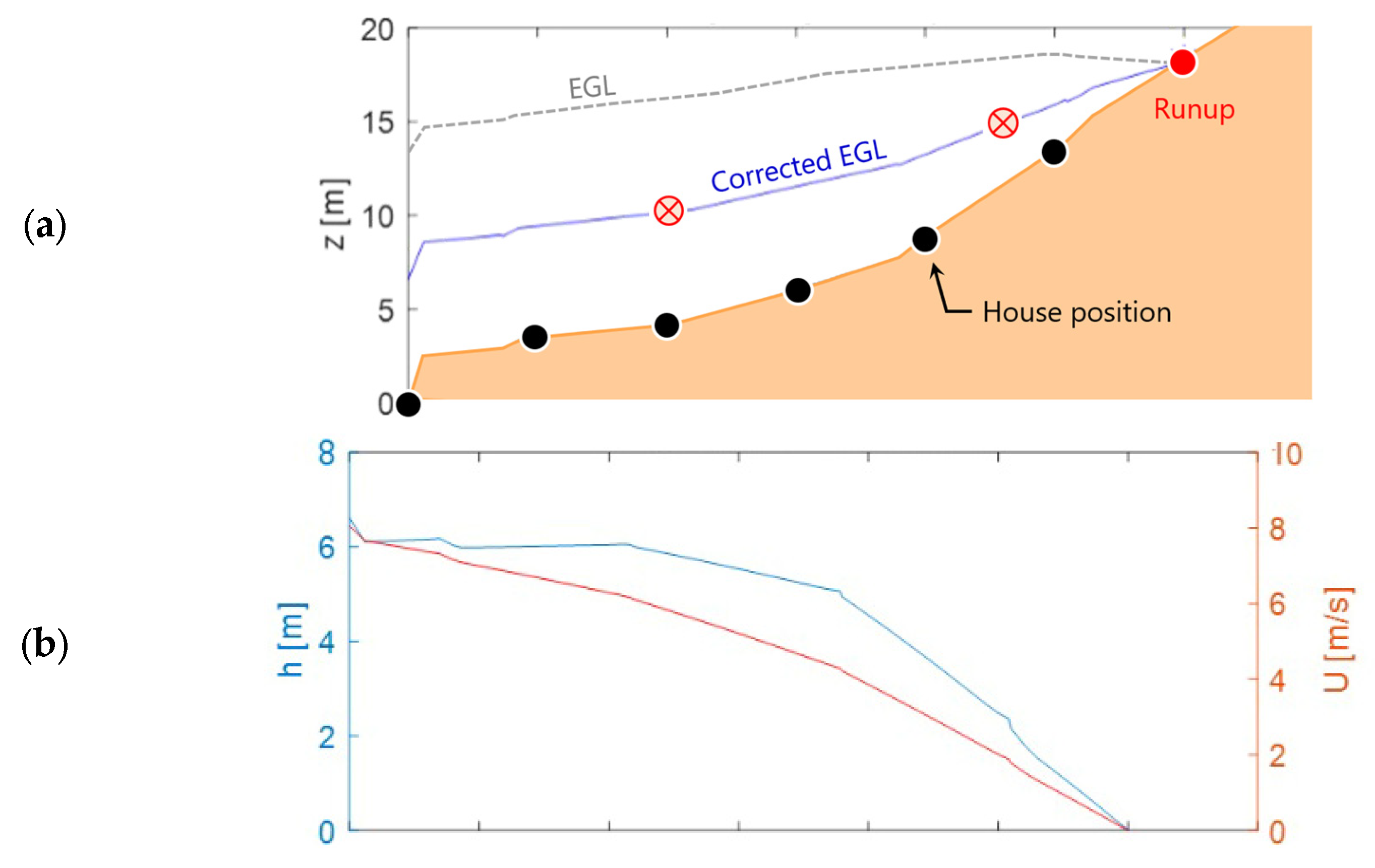
3.1. EGLA of Maximum Inundation Depths and Flow Velocity
3.2. Tsunami Hydrodynamic Loads
3.2.1. Buoyancy Force
3.2.2. Unbalanced Lateral Hydrostatic Force
3.2.3. Drag Force
3.2.4. Impact of Wood Logs
3.2.5. Load Cases
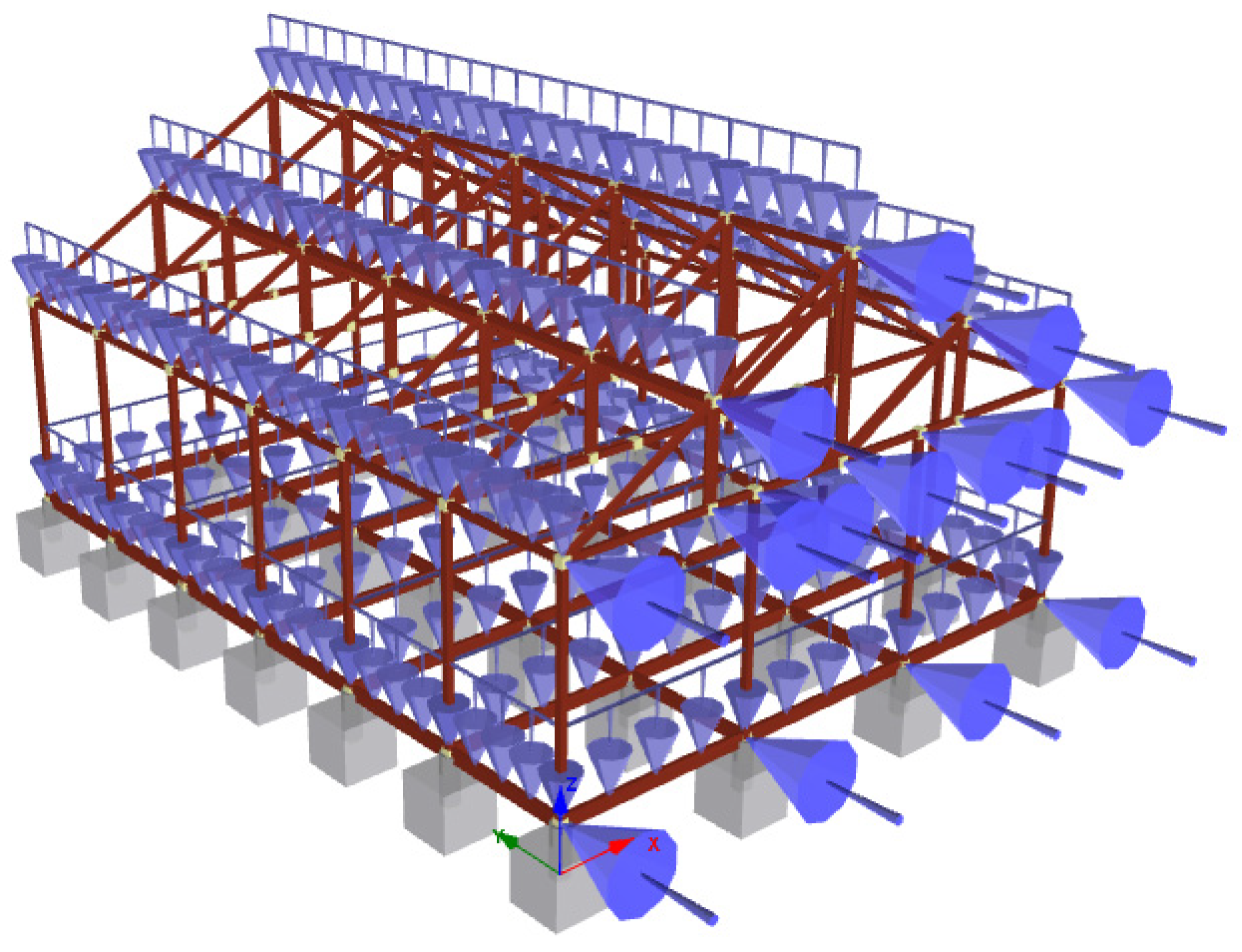
3.3. Structural Modeling of a Timber Single-Story House
3.4. Load Combinatios
3.5. Nonlinear Analysis
4. Results
4.1. EGLA of Maximum Inundation Depths and Flow Velocities
4.2. Relative Displacements
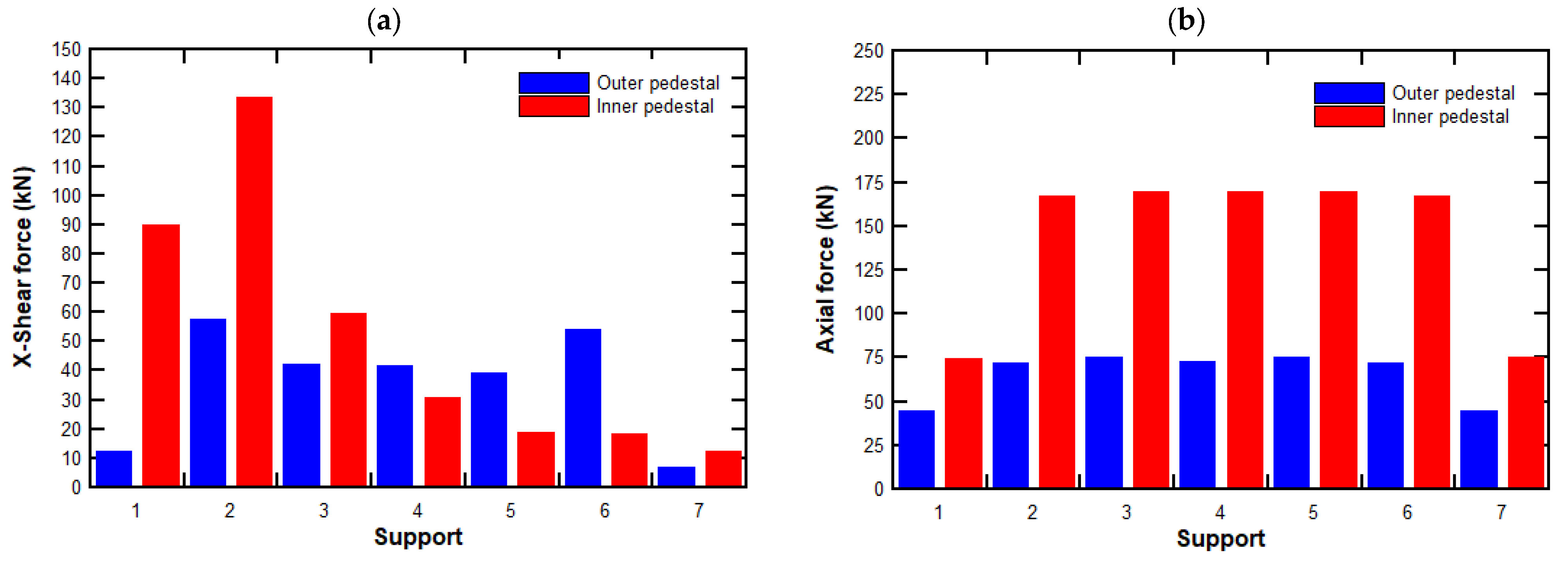
4.3. Supports Reactions
5. Discussion
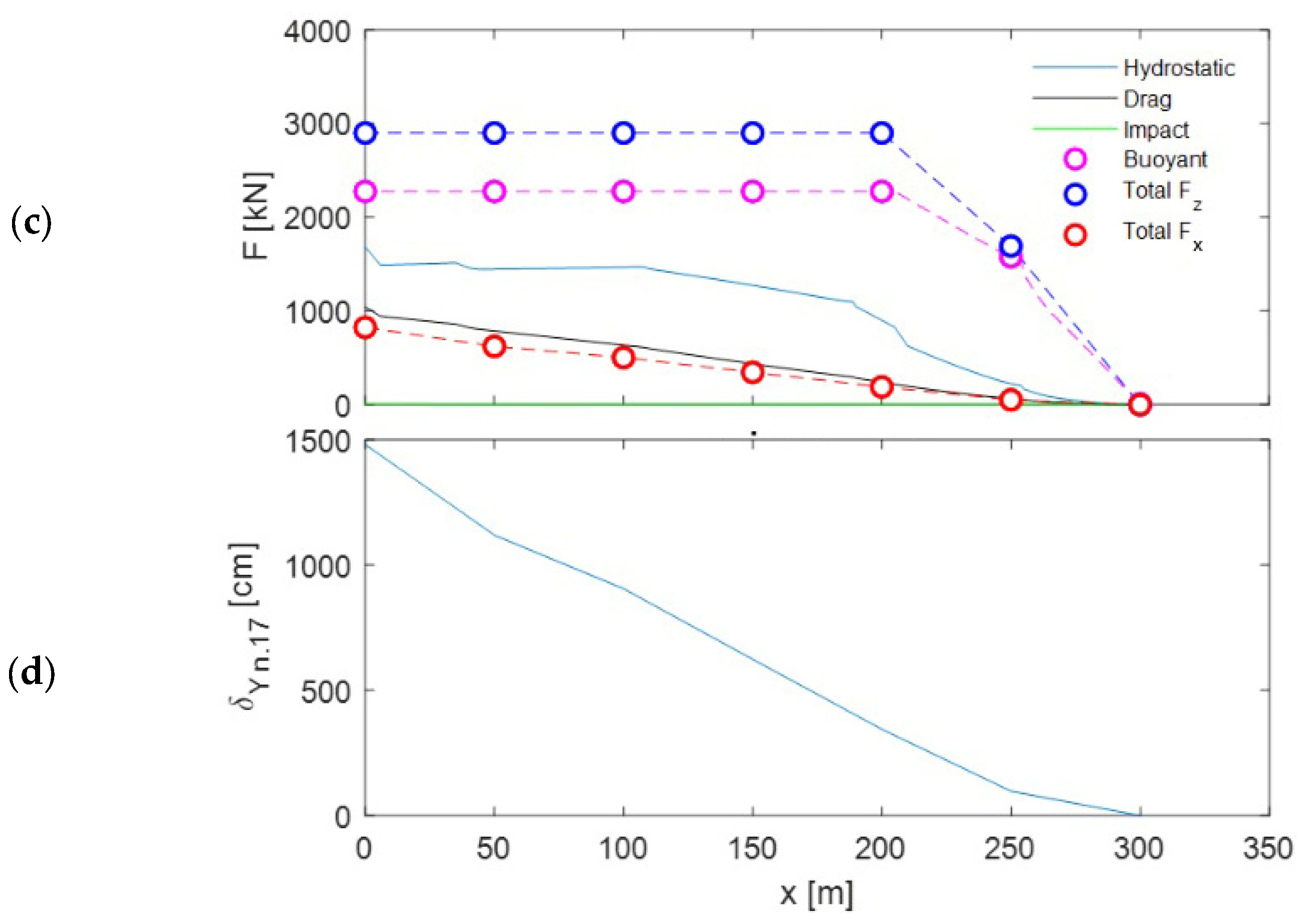
5.1. Hydrodynamic Loads Using the EGLA
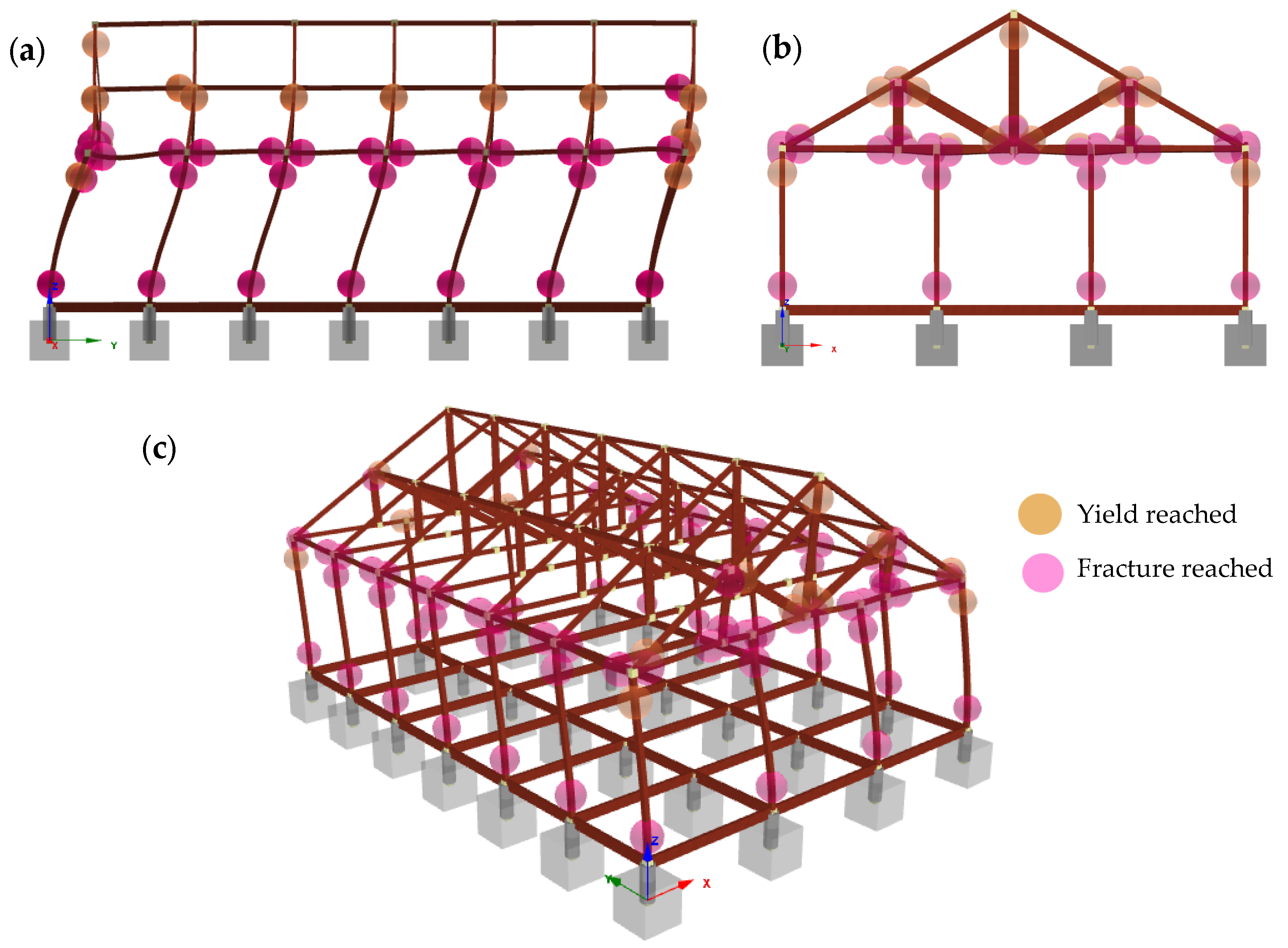
5.2. Structural Analysis Using the EGLA
5.3. Failure Due to Buoyancy
5.4. Contribution to the Resilience of Coastal Communities
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Impact of Wood Logs Using ASCE 7-22
| Parameter | Symbol | Dimension | Value |
|---|---|---|---|
| Effective stiffness of the impacting logs | k | kN/m | 1.39 × 106 |
| Maximum velocity at depths of debris | m/s | 8.05 | |
| Mass of debris object | kg | 500 | |
| Orientation coefficient | - | 0.65 |
References
- Stolle, J.; Takabatake, T.; Nistor, I.; Mikami, T.; Nishizaki, S.; Hamano, G.; Ishii, H.; Shibayama, T.; Goseberg, N.; Petriu, E. Experimental investigation of debris damming loads under transient supercritical flow conditions. Coast. Eng. 2018, 139, 16–31. [Google Scholar] [CrossRef]
- Aguiniga, F.; Jaiswal, M.; Sai, J.; Cox, D.; Gupta, R.; Lindt, J. Experimental study of tsunami forces on structures. In Coastal Hazards; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 111–118. [Google Scholar] [CrossRef]
- Bremm, G.; Goseberg, N.; Schlurmann, T.; Nistor, I. Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach. J. Mar. Sci. Eng. 2015, 3, 821–844. [Google Scholar] [CrossRef]
- Goseberg, N.; Schlurmann, T. Non-stationary Flow around Buildings during Run-up of Tsunami Waves on a Plain Beach. Coast. Eng. Proc. 2014, 1, 21. [Google Scholar] [CrossRef]
- Goseberg, N.; Wurpts, A.; Schlurmann, T. Laboratory-Scale Generation of Tsunami and Long Waves. Coast. Eng. 2013, 79, 57–74. [Google Scholar] [CrossRef]
- Ghobarah, A.; Saatcioglu, M.; Nistor, I. The Impact of the 26 December 2004 Earthquake and Tsunami on Structures and Infrastructure. Eng. Struct. 2006, 28, 312–326. [Google Scholar] [CrossRef]
- Fritz, H.; Petroff, C.; Catalán, P.; Cienfuegos, R.; Winckler, P.; Kalligeris, N.; Weiss, R.; Barrientos, S.; Meneses, G.; Valderas-Bermejo, C.; et al. Field Survey of the 27 February 2010 Chile Tsunami. Pure Appl. Geophys. 2011, 168, 1989–2010. [Google Scholar] [CrossRef]
- Robertson, I.; Chock, G.; Morla, J. Structural Analysis of Selected Failures Caused by the 27 February 2010 Chile Tsunami. Earthq. Spectra 2012, 28, 215–243. [Google Scholar] [CrossRef]
- Zareian, F.; Aguirre, C.; Beltran, J.; Cruz, E.; Herrera, R.; Leon, R.; Millan, A.; Verdugo, A. Reconnaissance Report of Chilean Industrial Facilities Affected by the 2010 Chile Offshore Bío-Bío Earthquake. Earthq. Spectra 2012, 28, 513–532. [Google Scholar] [CrossRef]
- Jayaratne, M.; Premaratne, B.; Adewale, A.; Mikami, T.; Matsuba, S.; Shibayama, T.; Esteban, M.; Nistor, I. Failure Mechanisms and Local Scour at Coastal Structures Induced by Tsunami. Coast. Eng. J. 2016, 58, 1640017-1–1640017-38. [Google Scholar] [CrossRef]
- Koshimura, S.; Hayashi, S.; Gokon, H. The Impact of the 2011 Tohoku Earthquake Tsunami Disaster and Implications to the Reconstruction. Soils Found. 2014, 54, 560–572. [Google Scholar] [CrossRef]
- Amakuni, K.; Terazono, N.; Yamamoto, T.; Enomoto, T. Basic Analysis on Building Damages by Tsunami Due to the 2011 Great East Japan Earthquake Disaster Using GIS. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Charvet, I.; Suppasri, A.; Imamura, F. Empirical Fragility Analysis of Building Damage Caused by the 2011 Great East Japan Tsunami in Ishinomaki City Using Ordinal Regression, and Influence of Key Geographical Features. Stoch. Environ. Res. Risk Assess. 2014, 28, 1853–1867. [Google Scholar] [CrossRef]
- Chock, G.; Robertson, I.N. Tsunami Design Criteria and Load Cases of the ASCE 7-16 Chapter 6, Tsunami Loads and Effects. In Proceedings of the 16th World Conference on Earthquake Engineering, 16WCEE, Santiago de Chile, Chile, 9–13 January 2017. [Google Scholar]
- Robertson, I.N.; Thomas, S.A. Prototype Building Tsunami Design Examples. In Proceedings of the 16th World Conference on Earthquake Engineering, 16WCEE, Santiago de Chile, Chile, 9–13 January 2017. [Google Scholar]
- Charvet, I.; Macabuag, J.; Rossetto, T. Estimating Tsunami-Induced Building Damage through Fragility Functions: Critical Review and Research Needs. Front. Built Environ. 2017, 3, 36. [Google Scholar] [CrossRef]
- Kihara, N.; Kaida, H.; Shibayama, A.; Miyagawa, Y. Responses of Concrete Vertical Walls to Tsunami Wave Pressures and Debris Impact. Coast. Eng. Proc. 2018, 1, 38. [Google Scholar] [CrossRef]
- Kihara, N.; Niida, Y.; Takabatake, D.; Kaida, H.; Shibayama, A.; Miyagawa, Y. Large-Scale Experiments on Tsunami-Induced Pressure on a Vertical Tide Wall. Coast. Eng. 2015, 99, 46–63. [Google Scholar] [CrossRef]
- Naito, C.J.; Riggs, H.R.; Wei, Y.; Cercone, C. Shipping-Container Impact Assessment for Tsunamis. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 05016003. [Google Scholar] [CrossRef]
- Naito, C.J.; Cercone, C.; Riggs, H.R.; Cox, D. Procedure for Site Assessment of the Potential for Tsunami Debris Impact. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 223–232. [Google Scholar] [CrossRef]
- Linton, D.; Gupta, R.; Cox, D.; van de Lindt, J.; Oshnack, M.E.; Clauson, M. Evaluation of Tsunami Loads on Wood-Frame Walls at Full Scale. J. Struct. Eng. 2013, 139, 1318–1325. [Google Scholar] [CrossRef]
- Krautwald, C.; von Häfen, H.; Niebuhr, P.; Vögele, K.; Stolle, J.; Schimmels, S.; Schürenkamp, D.; Sieder, M.; Goseberg, N. Collapse Processes and Associated Loading of Square Light-Frame Timber Structures Due to Bore-Type Waves. Coast. Eng. 2022, 177, 104178. [Google Scholar] [CrossRef]
- Suppasri, A.; Mas, E.; Charvet, I.; Gunasekera, R.; Imai, K.; Fukutani, Y.; Abe, Y.; Imamura, F. Building Damage Characteristics Based on Surveyed Data and Fragility Curves of the 2011 Great East Japan Tsunami. Nat. Hazards 2013, 66, 319–341. [Google Scholar] [CrossRef]
- Baiguera, M.; Rossetto, T.; Robertson, I.N.; Petrone, C. Towards a Tsunami Nonlinear Static Analysis Procedure for the ASCE 7 Standard. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure 2019, Chania, Greece, 23–26 June 2019. [Google Scholar]
- Aegerter, D.W.; Robertson, I.N. Push-over Tsunami Analysis Using ETABS. In Proceedings of the Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems, Proceedings of the 8th International Conference on Structural Engineering, Mechanics and Computation 2022, Cape Town, South Africa, 5–7 September 2022; CRC Press/Balkema: Boca Raton, FL, USA, 2023; pp. 221–227. [Google Scholar]
- McKenna, F.; Fenves, G.L.; Scott, M.H.; Jeremic, B. Open system for earthquake engineering simulation (OpenSees). In Computer Program; University of California: Berkeley, CA, USA, 2000; Available online: https://opensees.berkeley.edu/ (accessed on 15 June 2024).
- CSI (Computers and Structures, Inc.). ETABS Integrated Building Design Software, Version 2018; CSI: Walnut Creek, CA, USA, 2018; Available online: https://www.csiamerica.com/products/etabs (accessed on 1 December 2024).
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE7-22: Reston, VA, USA, 2022; ISBN 9780784415788. [Google Scholar]
- Kriebel, D.L.; Lynett, P.J.; Cox, D.T.; Petroff, C.; Robertson, I.N.; Chock, G.Y.K. Energy method for approximating overland tsunami flows. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 1–19. [Google Scholar] [CrossRef]
- Wiebe, D.M. Tsunami Inundation: Estimating Damage and Predicting Flow. Properties. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2013. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures; ASCE 7-16: Reston, VA, USA, 2017. [Google Scholar]
- Carden, L.; Chock, G.; Yu, G.; Robertson, I. The New ASCE Tsunami Design Standard Applied to Mitigate Tohoku Tsunami Building Structural Failure Mechanisms. In Handbook of Coastal Disaster Mitigation for Engineers and Planners; Shibayama, T., Esteban, M., Takagi, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 461–490. [Google Scholar] [CrossRef]
- Chock, G.; Yu, G.; Thio, H.; Lynett, P. Target Structural Reliability Analysis for Tsunami Hydrodynamic Loads of the ASCE 7 Standard. J. Struct. Eng. 2016, 142, 04016092. [Google Scholar] [CrossRef]
- Chock, G. Design for Tsunami Loads and Effects in the ASCE 7-16 Standard. J. Struct. Eng. 2016, 142, 04016093. [Google Scholar] [CrossRef]
- Tada, T.; Miyata, Y.; Bathurst, R. Energy Grade Line Analysis of Tsunami Run-up on the Sendai Plain after the 2011 Tohoku Earthquake. Coast. Eng. 2018, 140, 306–315. [Google Scholar] [CrossRef]
- Breuer, W.A.; Igualt, F.; Contreras-López, M.; Winckler, P.; Zambra, C. Tsunami Impact and Resilience Cycle in an Insular Town: The Case of Robinson Crusoe Island, Chile. Ocean Coast. Manag. 2021, 209, 105714. [Google Scholar] [CrossRef]
- Contreras, M.; Winckler, P. Pérdidas de vidas, viviendas, infraestructura y embarcaciones por el Tsunami del 27 de Febrero de 2010 en la costa central de Chile. Obras Proy. 2013, 14, 6–19. [Google Scholar] [CrossRef]
- UV. El Sonido de Robinson. Escuela de Ingeniería Civil Oceánica, Universidad de Valparaíso and Mosca Films. 2010. Available online: https://www.youtube.com/watch?v=pWtCDsXpWcE (accessed on 1 November 2023).
- Chock, G.; Carden, L.; Robertson, I.; Olsen, M.; Yu, G. Tohoku tsunami-induced building failure analysis with implications for US tsunami and seismic design codes. Earthq. Spectra 2013, 29 (Suppl. S1), 99–126. [Google Scholar] [CrossRef]
- Chock, G.; Robertson, I.; Kriebel, D.; Francis, M.; Nistor, I. Tohoku, Japan, Earthquake and Tsunami of 2011: Performance of Structures under Tsunami Loads; Book Set: Tohoku Earthquake; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- Winckler, P.; Reyes, M.; Sepúlveda, I.; Molina, M. El Tsunami del 27-02-2010 en Isla Robinson Crusoe, Archipiélago Juan Fernández. Preparado Para la Ilustre Municipalidad de Juan Fernández. Technical Report. 2010. Available online: http://ingenieriaoceanica3.uv.cl/sitio/index.php/documentos-ico/84-el-tsunami-del-27-02-2010-en-isla-robinsoncrusoe-archipielago-juan-fernandez (accessed on 1 November 2023).
- Autodesk. Robot Structural Analysis Professional; Version 2024; Autodesk, Inc.: San Rafael, CA, USA, 2024; Available online: https://www.autodesk.com/products/robot-structural-analysis/overview (accessed on 1 July 2023).
- FEMA (Federal Emergency Management Agency). Guidelines for Design of Structures for Vertical Evacuation from Tsunamis, 3rd ed.; US Department of Homeland Security, Federal Emergency Management Agency: Washington, DC, USA, 2019. [Google Scholar]
- INN (Instituto Nacional de Normalización). NCh 3363 of. 2015. Diseño Estructural-Edificaciones en Áreas de Riesgo de Inundación Por Tsunami o Seiche; INN: Santiago, Chile, 2015. [Google Scholar]
- CMPC Maderas SpA, Pino Radiata. Available online: www.cmpcmaderas.com (accessed on 5 February 2024).
- INN (Instituto Nacional de Normalización). NCh 1198 of. 2014. Madera-Construcción en Madera-Cálculo; INN: Santiago, Chile, 2014. [Google Scholar]
- INN (Instituto Nacional de Normalización). NCh 1537 of. 2009. Diseño Estructural-Cargas Permanentes y Cargas de Uso; INN: Santiago, Chile, 2009. [Google Scholar]
- Vielma-Quintero, J.C.; Carvallo, J.; Vielma, J.C. Comparative assessment of performance-based design methodologies applied to a R.C. shear-wall building. Buildings 2023, 13, 1492. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and nonelastic behavior of elements under combined normal force and bending. In Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, International Association for Bridge and Structural Engineering; IABSE: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Perez, A. Comparison of Compression Tests on Structural Wood Using UNE and ASTM Standards. Master Thesis, University of Valladolid, Valladolid, Spain, 2014. (In Spanish). [Google Scholar]
- Seismosoft Ltd. SeismoStruct 2024 User Manual—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures; Seismosoft Ltd.: Pavia, Italy, 2021; Available online: https://seismosoft.com/ (accessed on 11 December 2024).
- Ariete, N. Characterization of Pinus radiata D. Don wood subjected to a thermal modification process using an immersion environment. Bachelor Thesis, Austral University of Chile, Valdivia, Chile, 2010. (In Spanish). [Google Scholar]
- van de Lindt, J.W.; Pei, S.; Pang, W.; Rosowsky, D.V. IDA Comparison of IBC-Designed and DDD-Designed Six-Story Light-Frame Wood Buildings. J. Perform. Constr. Facil. 2011, 25, 138–142. [Google Scholar] [CrossRef]
- Namba, T.; Nakagawa, T.; Isoda, H.; Kado, Y.; Odani, R.; Takino, A. Seismic Response Comparison of Full-Scale Moment-Resisting Timber Frame and Joint Test Result. J. Struct. Eng. 2023, 149, 04023079. [Google Scholar] [CrossRef]
- Yeh, H.; Barbosa, A.; Ko, H.; Cawley, J. Tsunami loadings on structures: Review and analysis. Int. Conf. Coastal. Eng. 2014, 1, 4. [Google Scholar] [CrossRef]
- del Zoppo, M.; Rossetto, T.; Ludovico, M.d.; Prota, A. Effect of buoyancy loads on the tsunami fragility of reinforced concrete frames including consideration of blow-out slabs. Res. Sq. 2022, preprint. [Google Scholar] [CrossRef]
- Yeh, H.; Sato, S.; Tajima, Y. The 11 March 2011 East Japan Earthquake and Tsunami: Tsunami Effects on Coastal Infrastructure and Buildings. Pure Appl. Geophys. 2013, 170, 1019–1031. [Google Scholar] [CrossRef]
- Manawasekara, C.; Mizutani, N.; Nakamura, T.; Aoki, S. Failure of concrete structure under tsunami loading. J. JSCE 2014, 2, 214–223. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Harati, M.; Van De Lindt, J.W. Community-Level Resilience Analysis Using Earthquake-Tsunami Fragility Surfaces. Resilient Cities Struct. 2024, 3, 101–115. [Google Scholar] [CrossRef]
- Villagra, P.; Herrmann, M.G.; Quintana, C.; Sepúlveda, R.D. Community Resilience to Tsunamis along the Southeastern Pacific: A Multivariate Approach Incorporating Physical, Environmental, and Social Indicators. Nat. Hazards 2017, 88, 1087–1111. [Google Scholar] [CrossRef]
- Frucht, E.; Salamon, A.; Rozelle, J.; Levi, T.; Calvo, R.; Avirav, V.; Burns, J.N.; Zuzak, C.; Gal, E.; Trapper, P.; et al. Tsunami Loss Assessment Based on Hazus Approach–The Bat Galim, Israel, Case Study. Eng. Geol. 2021, 289, 106175. [Google Scholar] [CrossRef]
- Mebarki, A.; Jerez, S.; Prodhomme, G.; Reimeringer, M. Natural Hazards, Vulnerability and Structural Resilience: Tsunamis and Industrial Tanks. Geomat. Nat. Hazards Risk 2016, 7, 5–17. [Google Scholar] [CrossRef]
- Attary, N.; Unnikrishnan, V.U.; Van De Lindt, J.W.; Cox, D.T.; Barbosa, A.R. Performance-Based Tsunami Engineering Methodology for Risk Assessment of Structures. Eng. Struct. 2017, 141, 676–686. [Google Scholar] [CrossRef]
- León, J.; March, A. Urban Morphology as a Tool for Supporting Tsunami Rapid Resilience: A Case Study of Talcahuano, Chile. Habitat Int. 2014, 43, 250–262. [Google Scholar] [CrossRef]
- Petrone, C.; Rossetto, T.; Goda, K. Fragility assessment of a RC structure under tsunami actions via nonlinear static and dynamic analyses. Eng. Struct. 2017, 136, 36–53. [Google Scholar] [CrossRef]
- Petrone, C.; Rossetto, T.; Baiguera, M.; Bustamante, C.; Ioannou, I. Fragility functions for a reinforced concrete structure subjected to earthquake and tsunami in sequence. Eng. Struct. 2020, 205, 110120. [Google Scholar] [CrossRef]
- Tagle, S.J.; Jünemann, R.; Vásquez, J.; de la Llera, J.C.; Baiguera, M. Performance of a reinforced concrete wall building subjected to sequential earthquake and tsunami loading. Eng. Struct. 2021, 238, 111995. [Google Scholar] [CrossRef]
- Karafagka, S.; Fotopoulou, S.; Pitilakis, K. Analytical tsunami fragility curves for seaport RC buildings and steel light frame warehouses. Soil Dyn. Earthq. Eng. 2018, 112, 118–137. [Google Scholar] [CrossRef]







| Parameter | Symbol | Dimension | Value |
|---|---|---|---|
| Overall building width | B | m | 6.6 |
| Manning’s roughness coefficient | - | 0.025 | |
| Height of wall | m | 2.4 | |
| Width subject to force | m | 6.6 | |
| Minimum fluid specific weight density | kN/m3 | 11 | |
| Minimum fluid mass density | g/cm3 | 1.1 | |
| Importance factor | - | 1 | |
| Drag coefficient | Cd | - | 1.25 |
| Proportion of closure coefficient | - | 4.42 | |
| Story height of story x | m | 4.35 | |
| Time interval | s | 1 |
| x m | m | m | m | kPa | kPa | kPa | kN |
|---|---|---|---|---|---|---|---|
| 250 | 2.48 | 2.15 | 1.81 | 27.31 | 13.66 | 2.27 | 1.01 |
| 200 | 4.55 | 4.36 | 4.16 | 47.85 | 31.40 | 8.34 | 1.93 |
| 150 | 5.54 | 5.48 | 5.41 | 47.85 | 44.37 | 15.20 | 2.61 |
| 100 | 6.05 | 6.02 | 6.00 | 47.85 | 51.10 | 22.14 | 3.14 |
| 50 | 5.99 | 6.00 | 6.00 | 47.85 | 50.38 | 27.42 | 3.50 |
| 0 | 6.62 | 6.37 | 6.12 | 47.85 | 58.64 | 36.35 | 4.03 |
| Load Case | ||||||
|---|---|---|---|---|---|---|
| C1 | 1.4 | - | - | - | - | - |
| C2 | 1.2 | 1.6 | - | - | - | - |
| C3 | 1.2 | - | - | - | - | - |
| C4 | 1.2 | 0.5 | - | - | - | - |
| C5 | 0.9 | - | - | - | - | - |
| C6 (I) | 1.2 | 0.5 | 1 | 1 | - | - |
| C7 (I) | 1.2 | - | 1 | 1 | - | - |
| C8 (I) | 1.2 | 0.5 | −1 | −1 | - | - |
| C9 (I) | 1.2 | - | −1 | −1 | - | - |
| C10 (I) | 0.9 | - | 1 | 1 | - | - |
| C11 (I) | 0.9 | - | −1 | −1 | - | - |
| C6 (F) | 1.2 | 0.5 | - | - | 1 | 1 |
| C7 (F) | 1.2 | - | - | - | 1 | 1 |
| C8 (F) | 1.2 | 0.5 | - | - | −1 | −1 |
| C9 (F) | 1.2 | - | - | - | −1 | −1 |
| C10 (F) | 0.9 | - | - | - | 1 | 1 |
| C11 (F) | 0.9 | - | - | - | −1 | −1 |
| Parameter | Dimensions | Value |
|---|---|---|
| Compression strength | MPa | 4.26 |
| Strength lower bound | MPa | 3.7 |
| Bending strength | MPa | 8.6 |
| Modulus of elasticity | MPa | 8829 |
| Specific weight | kN/m3 | 4.9 |
| Parameter | Dimensions | Value |
|---|---|---|
| Compression strength | MPa | 33 |
| Strength lower bound | MPa | 25 |
| Tension strength | MPa | 2.6 |
| Modulus of elasticity | MPa | 26,999 |
| Specific weight | kN/m3 | 24 |
| Parameter | Dimensions | Value |
|---|---|---|
| Modulus of elasticity | MPa | 200,000 |
| Yield strength | MPa | 490 |
| Strain hardening parameter | - | 0.005 |
| Transition curve initial shape parameter | - | 20 |
| Coefficient A1 | - | 18.5 |
| Coefficient A2 | - | 0.15 |
| Coefficient A3 | - | 0 |
| Coefficient A4 | - | 1 |
| Fracture/buckling strain | - | 1 |
| Specific weight | kN/m3 | 78 |
| Load Case | kN | kN | kN | kNm | kNm | kNm |
|---|---|---|---|---|---|---|
| C1 | 0 | 0 | 18.2 | 0 | 0 | 0 |
| C2 | 0 | 0 | 241.5 | 0 | 0.01 | 0 |
| C3 | 0 | 0 | 15.6 | 0 | 0 | 0 |
| C4 | 0 | 0 | 86.2 | 0 | 0 | 0 |
| C5 | 0 | 0 | 11.7 | 0 | 0 | 0 |
| C6 (I) | −825.5 | 0 | 86.2 | 0 | 540.2 | 0 |
| C7 (I) | −825.5 | 0 | 15.6 | 0 | 540.2 | 0 |
| C8 (I) | 825.5 | 0 | 86.2 | 0 | −540.2 | 0 |
| C9 (I) | 825.5 | 0 | 15.6 | 0 | −540.2 | 0 |
| C10 (I) | −825.5 | 0 | 11.7 | 0 | 540.2 | 0 |
| C11 (I) | 825.5 | 0 | 11.7 | 0 | −540.2 | 0 |
| C6 (F) | 0 | 0 | −2727.6 | 0 | 0 | 0 |
| C7 (F) | 0 | 0 | −2798.2 | 0 | −0.01 | 0 |
| C8 (F) | 0 | 0 | 2900.1 | 0 | 0.01 | 0 |
| C9 (F) | 0 | 0 | 2829.5 | 0 | 0.01 | 0 |
| C10 (F) | 0 | 0 | −2802.2 | 0 | −0.01 | 0 |
| C11 (F) | 0 | 0 | 2825.6 | 0 | 0.01 | 0 |
| Load Case | kN | kN | kN | kNm | kNm | kNm |
|---|---|---|---|---|---|---|
| C1 | 0 | 0 | 18.23 | 0 | 0 | 0 |
| C2 | 0 | 0 | 241.53 | 0 | 0.01 | 0 |
| C3 | 0 | 0 | 15.63 | 0 | 0 | 0 |
| C4 | 0 | 0 | 86.22 | 0 | 0 | 0 |
| C5 | 0 | 0 | 11.72 | 0 | 0 | 0 |
| C6 (I) | −52.32 | 0 | 86.22 | 0 | 34.42 | 0 |
| C7 (I) | −52.32 | 0 | 15.63 | 0 | 34.41 | 0 |
| C8 (I) | 52.32 | 0 | 86.22 | 0 | −34.41 | 0 |
| C9 (I) | 52.32 | 0 | 15.63 | 0 | −34.41 | 0 |
| C10 (I) | −52.32 | 0 | 11.72 | 0 | 34.41 | 0 |
| C11 (I) | 52.32 | 0 | 11.72 | 0 | −34.41 | 0 |
| C6 (F) | 0 | 0 | −1520 | 0 | 0 | 0 |
| C7 (F) | 312.36 | 0 | −1590.6 | 0 | 0 | 0 |
| C8 (F) | −312.36 | 0 | 52.32 | 0 | 0.01 | 0 |
| C9 (F) | 0 | 0 | 1621.86 | 0 | 0.01 | 0 |
| C10 (F) | 0 | 0 | −1594.51 | 0 | 0 | 0 |
| C11 (F) | 0 | 0 | 1617.95 | 0 | 0.01 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otey, D.; Vielma, J.C.; Winckler, P. Structural Failure Modes of Single-Story Timber Houses Under Tsunami Loads Using ASCE 7’S Energy Grade Line Analysis. J. Mar. Sci. Eng. 2025, 13, 484. https://doi.org/10.3390/jmse13030484
Otey D, Vielma JC, Winckler P. Structural Failure Modes of Single-Story Timber Houses Under Tsunami Loads Using ASCE 7’S Energy Grade Line Analysis. Journal of Marine Science and Engineering. 2025; 13(3):484. https://doi.org/10.3390/jmse13030484
Chicago/Turabian StyleOtey, Darko, Juan Carlos Vielma, and Patricio Winckler. 2025. "Structural Failure Modes of Single-Story Timber Houses Under Tsunami Loads Using ASCE 7’S Energy Grade Line Analysis" Journal of Marine Science and Engineering 13, no. 3: 484. https://doi.org/10.3390/jmse13030484
APA StyleOtey, D., Vielma, J. C., & Winckler, P. (2025). Structural Failure Modes of Single-Story Timber Houses Under Tsunami Loads Using ASCE 7’S Energy Grade Line Analysis. Journal of Marine Science and Engineering, 13(3), 484. https://doi.org/10.3390/jmse13030484







