A Multi-Resolution Sequence Method with Strong Constraints for Marine Gravity Matching Navigation

Abstract

The navigation and positioning of underwater vehicles is challenging work, especially when there is already a large initial position error, and there is an increasing concern about how to quickly correct the position error. To enhance positioning accuracy under large initial positioning errors, this paper proposes a multi-resolution sequence method with a strong constraint marine gravity-matching navigation algorithm and validates it through field experiments. First, the fundamental principles and common optimization approaches of the standard Terrain Contour Matching (TERCOM) and Iterative Closest Contour Point (ICCP) algorithms are introduced, the limitations of the sequence-matching algorithms are analyzed, and a multi-resolution sequence-matching fusion framework is designed. Then, the constrained models incorporating positional, navigational, and gravitational parameters are designed, and a strongly constrained multi-resolution sequence-matching algorithm is proposed. Finally, the performance of the method is verified by three field test trajectories with an initial position error of about 6 nautical miles. The field test results show that the proposed method has better accuracy and reliability under large initial position errors.

1. Introduction

The marine gravity field reflects information about Earth’s internal structure, material migration, density distribution, etc. The magnitude of the gravity value establishes a nonlinear functional relationship with a geospatial location (longitude, latitude, and altitude) and is stable on the milligal scale (1 mGal = 1 × 10⁻⁵ m/s²), so the marine gravity field is a continuous and stable fundamental physical field [1,2,3].

Navigation and positioning serve as crucial guarantees for underwater vehicles to accomplish designated missions and are essential prerequisites for underwater formation coordination [4]. Common underwater navigation and positioning methods primarily include: (1) velocity integration between the Doppler Velocity Log (DVL) and Inertial Navigation System (INS) for suppressing INS errors; (2) positioning and INS calibration through underwater acoustic positioning systems; and (3) geophysics-aided inertial navigation, among others [5,6,7]. The inertial navigation system, characterized by complete autonomy, passivity, and high short-term accuracy while providing comprehensive navigation parameters, generally serves as a foundation for underwater vehicle navigation. This is typically implemented through an INS-based integrated navigation scheme supplemented by auxiliary navigation methods. Among these, the Gravity-Aided Inertial Navigation System (GAINS) represents a typical passive navigation modality. Its gravity data acquisition requires neither signal transmission nor reception, endowing it with advantages, including all-weather capabilities, high autonomy, strong concealment, superior precision, and anti-interference performance. Consequently, the GAINS has emerged as a vital research direction for autonomous underwater vehicle navigation [8].

As shown in Figure 1, the GAINS primarily comprises the INS, gravimeter, gravity anomaly background field, navigation computer, and gravity-matching algorithms [9]. The INS provides comprehensive navigation parameters, including raw outputs from gyroscopes and accelerometers, angular velocity and acceleration, as well as attitude (pitch, roll, and heading), velocity (easterly, northerly, and up), and position (longitude, latitude, and altitude), which is a piece of essential navigation equipment for underwater vehicles. Gravimeters enable real-time measurements of gravitational values at the vehicle’s location, supporting both gravity database construction and matching navigation implementation. High-precision and high-resolution marine gravity anomaly background fields constitute fundamental infrastructure for marine exploration and applications. These datasets also serve as critical technical enablers for practical implementations in domains such as GAINS technology, demonstrating significant economic value and military strategic importance. In addition, matching algorithms represent a critical technical component within the GAINS. This paper primarily focuses on the improvement and innovation of matching algorithms.

Gravity-matching algorithms can be primarily categorized into two classes based on the number of gravimetric measurement points required for a single matching process. The first category comprises sequence-matching algorithms employing correlation extremum criteria [10], which require underwater vehicles to follow predefined trajectories to collect sequential data points. These measured profiles are then matched with the gravity background field to determine the positioning information. The second category involves single-point-matching algorithms based on filtering frameworks [11,12], which perform an INS position error correction at each epoch by integrating current gravimetric measurements, IMU outputs, and gravity background field. Additionally, hybrid matching navigation techniques combining multiple algorithms, as well as intelligent optimization and machine learning-based approaches, have been developed [13,14,15].

Among these methods, single-point-matching algorithms enable real-time INS error corrections but demand high-precision initial navigation parameters prior to implementation. Consequently, underwater vehicles must surface or acquire such information through acoustic positioning systems, potentially compromising mission covertness and limiting the application’s scope. This underscores the necessity to develop sequence-matching algorithms that are tolerant of large initial position errors.

With advancements in marine gravimeter accuracy and gravity anomaly background field reliability, sequence-matching algorithms have undergone significant optimization in recent years, achieving enhanced precision and stability. Common sequence-matching algorithms include (ICCP) [16], (TERCOM) [17], and their related improved variants [18].

• TERCOM estimates underwater vehicle trajectories through correlation analysis between gravity measurement sequences and reference maps. While demonstrating high accuracy and robustness to initial position errors, it exhibits sensitivity to heading deviations. To address the trajectory shape constraints in conventional TERCOM, Wu et al. [19] proposed a Relative Positions-Constrained Pattern Matching (RPCM) method. Han et al. [20] reduced computational burden through algorithmic refinements, while Li and Zhao et al. enhanced computational efficiency via a Novel Hierarchical Neighborhood Threshold Search [21], Soft-Margin Local Semicircular Domain Research Model [22], and Domain-Center Adaptive-Transfer Matching Method (DAMM) [23].
• The ICCP obtains optimal trajectory transformations through iterative objective function minimization, offering high precision but sensitivity to the initial position errors. Liu et al. [24] developed a real-time ICCP algorithm with an Optimized Matching Sequence Length (OMSL-ICCP). By employing a golden section search for sequence length optimization and a Hausdorff distance-based contour point search range determination, this method addresses the limitations of existing real-time ICCP implementations. Wang et al. [25] improved underwater vehicle matching accuracy through a Sliding Window ICCP-based Filtered Marine Map Matching method. Zhang et al. [26] proposed an enhanced ICCP algorithm resolving mismatch issues under large initial position errors, validated through simulations and field tests across flat and rugged terrains.
• Common variants include the Correlation Method (COR), Mean Absolute Differences (MAD), and Mean Square Differences (MSD). Xie et al. [27] employed Taylor’s first-order expansion to establish geomagnetic information relationships between matching and reference points, adopting the MSD for optimal trajectory identification. Gao et al. [28] integrated the MSD with Extended Kalman Filter algorithms to mitigate the initial position error impacts through novel observation equations.

In summary, sequence-matching constitutes a localization method based on contour point sequence analysis, where the quantity and quality of contour points directly determine positioning accuracy. Consequently, accuracy enhancement generally involves two strategies: (1) eliminating invalid contour points and (2) selecting reliable contour points. However, the current study does not adequately consider these.

This study, therefore, focuses on developing universal contour point selection and constraint methodologies through a systematic analysis of sequence-matching characteristics. The proposed approaches aim to improve algorithmic precision and stability and ultimately enhance underwater vehicle navigation performance.

In this paper, Section 2 introduces the basic principles and common optimization methods of the standard TERCOM and ICCP algorithms while analyzing the limitations of existing sequence-matching approaches. Section 3 presents a multi-resolution sequence-matching fusion solution, constructing constraint metric models for position, navigation, and gravity parameters and proposing a multi-resolution sequence method with a strong constraint-matching algorithm. Section 4 validates the proposed method’s performance under large initial position errors through field experiments with comparative analyses. Discussions and conclusions are provided in Section 5.

2. Optimized TERCOM and ICCP Algorithm

The fundamental principle of sequence matching lies in the nonlinear functional relationship between the gravity value and geographic location, enabling the determination of an underwater vehicle’s position based on gravity data. The real-time gravity measurement sequence acquired by gravimeters is compared with the gravity search sequences generated within a predefined background field using INS positions. By applying evaluation criteria, the optimal matching position sequence is identified. Representative algorithms include the TERCOM and ICCP. This section outlines their principles and common optimizations and analyzes their limitations through simulations.

2.1. TERCOM

As shown in Figure 2, the TERCOM algorithm comprises four steps:

Step 1: Acquire the INS-indicated position sequence $P_{ins}=\left\{p_{ins}^i,p_{ins}^{i+1},\cdots ,p_{ins}^{i+N-1}\right\}$ and gravity measurement sequence $G_m=\left\{g_m^i,g_m^{i+1},\cdots ,g_m^{i+N-1}\right\}$ of the $i$-th time sequence $t_i,t_{i+1},\cdots ,t_{i+N-1}$. Synchronize the INS and gravimeter sampling timestamps.

Step 2: Generate reference gravity sequences $G_{sj}=\left\{g_{sj}^i,g_{sj}^{i+1}\cdots g_{sj}^{i+N-1}\right\}$ by translating, rotating, or scaling $P_{ins}$ within the background field, $j=1,2,\cdots ,K$ means there are $K$ reference gravity sequences.

Step 3: Perform a correlation extremum analysis between $G_m$ and $G_{sj}$ to identify the optimal reference sequence $G_{\mathrm{ref}}^{\mathrm{opt}}$, which yields the best-matched trajectory sequence $P_{match}=\left\{p_{match}^i,p_{match}^{i+1},\cdots ,p_{match}^{i+N-1}\right\}$.

Step 4: Correct INS errors using $P_{match}$.

Correlation analysis is a key step in the TERCOM matching algorithm, which aims to calculate the degree of correlation between the trajectory gravity measurement sequence $G_m$ and the reference gravity sequence $G_{sj}$. The COR, MAD, and MSD correlation analysis models for the $i$-th time series can be expressed as follows:

$$J_{COR}(j)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{x=i}^{i+N-1}{g}_m^x\times g_s^x(j)},\begin{array}{c}\end{array}j=1,2,\cdots ,K$$

(1)

$$J_{MAD}(j)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{x=i}^{i+N-1}\left|g_m^x-g_s^x(j)\right|},\begin{array}{c}\end{array}j=1,2\cdots K$$

(2)

$$J_{MSD}(j)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{x=i}^{i+N-1}{\left|g_m^x-g_s^x(j)\right|}^2},\begin{array}{c}\end{array}j=1,2\cdots K$$

(3)

where $g_m^x$ represents the $x$-th measured gravity anomaly and $g_s^x(j)$ is the $x$-th gravity anomaly on the $j$-th matching trajectory.

The optimal matching trajectory corresponds to the reference gravity sequence that maximizes the performance metric $J_{COR}$ or minimizes the performance metrics $J_{MAD}$ and $J_{MSD}$. In practical applications, $J_{MSD}$ exhibits superior accuracy and is commonly adopted as the primary indicator for evaluating the correlation between the matching gravity anomaly profiles and measured gravity anomaly profiles.

To mitigate the excessive computational load and ensure algorithmic real-time performance, the TERCOM algorithm analyzes the INS output data and derives the position error bounds (i.e., confidence interval) of the INS-indicated trajectory point $P_{ins}^i$ using Rayleigh distribution [29]. Subsequently, it defines a contour point search threshold ${\sigma }_g$ based on gravimeter measurement accuracy and gravity background field precision. The algorithm then identifies all contour points satisfying $[g_m^i-{\sigma }_g,g_m^i+{\sigma }_g]$ within the confidence interval, thereby generating the reference gravity sequence set $G_{sj}$.

The standard TERCOM algorithm typically selects the potential drift distance $R_{\max }$ of point $p_{ins}^{i+N-1}$ (i.e., the final point in the INS-indicated position sequence) as the radius of the confidence interval. As shown in Figure 3a, the standard mode suffers from excessive search scope, high computational complexity, and the proliferation of false candidate points. Notably, the INS horizontal position errors accumulate over time, with the divergence rates being dependent on inertial sensor accuracy, initial alignment precision, and vehicle maneuvering trajectories. Consequently, the confidence interval radius can be dynamically adjusted based on the INS drift rates and the underwater vehicle’s navigation duration, thereby reducing the search space and improving matching efficiency, as demonstrated in Figure 3b.

Based on the above analysis, the optimized TERCOM algorithm described in this section enhances the standard TERCOM framework by incorporating rotation and scaling operations on the INS-indicated position sequence $P_{ins}$. Additionally, a dynamic adjustment mechanism for confidence intervals is implemented as follows: (1) Set the initial confidence interval radius $R_0$ based on the position error of the starting matching point $p_{ins}^i$; (2) determine the radius increment $\Delta R$ based on the time difference $\Delta t$ between consecutive matching points and the INS drift rate $\mu$, $\Delta R=\mu \cdot \Delta t$; and (3) calculate the subsequent confidence interval radii as $R_0+x\Delta R$, where $x=1,2,\cdots ,N-1$.

The aforementioned analysis demonstrates that TERCOM imposes no requirement on the INS initial position errors, and under ideal conditions, it can be positioned to the grid point closest to the true location. However, the matched trajectory remains parallel or approximately parallel to the INS-indicated trajectory, rendering the correlation-based positioning results highly susceptible to heading errors in the INS-indicated trajectory.

2.2. ICCP

Similar to TERCOM, ICCP requires measurements of multiple gravity anomaly points along the underwater vehicle’s trajectory to form a polyline. Through iterative rigid transformations (including rotation and translation), the algorithm progressively aligns the polyline with the nearest contour trajectory, thereby achieving INS error correction. The search iteration process of a standard ICCP is shown in Figure 4, with the key steps as follows:

Step 1: Acquire the INS position sequence $P_{ins}=\left\{p_{ins}^i,p_{ins}^{i+1},\cdots ,p_{ins}^{i+N-1}\right\}$ and gravity measurement sequence $G_m=\left\{g_m^i,g_m^{i+1},\cdots ,g_m^{i+N-1}\right\}$.

Step 2: Extract gravity anomaly contour lines $C=\left\{c^i,c^{i+1},\cdots ,c^{i+N-1}\right\}$ within the INS error bounds.

Step 3: Identify the nearest contour points $y^i$ to $p_{ins}^i$ by searching the contour line $c^i$ for the nearest contour points and obtain one iteration trajectory $Y=\left\{y^i,y^{i+1},\cdots ,y^{i+N-1}\right\}$.

Step 4: Compute the rigid transformation rotation parameter $R_{\theta }$ and translation parameter $T$ according to $P_{ins}$ and $Y$, as shown in (4), and then use $T$ and $R_{\theta }$ to rigidly transform $P_{ins}$ to obtain one iteration of estimated trajectory ${\tilde{P}}_{ins}$.

$$\eta =\arg \underset{{\Psi }_r}{\min }{\displaystyle \sum _{i=1}^N{‖y^i-{\mathcal{I}}_{{\Psi }_r}(p_{ins}^i)‖}^2}=\arg \underset{\theta ,T}{\min }{\displaystyle \sum _{i=1}^N{‖y^i-(R_{\theta }{p}_{ins}^i+T)‖}^2}$$

(4)

where ${\Psi }_r\triangleq (\theta , T)$ is the optimal rigidity transformation parameter, ${\mathcal{I}}_{{\Psi }_r}(p_{ins})=R{p}_{ins}+T$ is the rigidity transformation, and $R_{\theta }$ is the rotation matrix corresponding to $\theta$.

Step 5: Assign the estimated trajectory sequence ${\tilde{P}}_{ins}$ to the INS sequence $P_{ins}$, repeat steps 2~4 until the convergence criteria are met and the final matching track is $P_{match}$.

In step 3, the search for the nearest contour point $y^i$ to the INS-indicated position $p_{ins}^i$ necessitates the prerequisite that the true position of the underwater vehicles lies near $p_{ins}^i$ and resides on the contour corresponding to the measured gravity anomaly value. This implies that a standard ICCP exclusively searches for $y^i$ along contour $c^i$, neglecting the impact of gravity anomaly measurement accuracy and background field precision. However, in practical applications, the integrated error ${\sigma }_g$ arising from gravimeter measurements and background field inaccuracies cannot be disregarded. Consequently, the search domain must be expanded to a gravity anomaly equivalence band centered at $c^i$ with a bandwidth of $2{\sigma }_g$, within which the nearest contour point $y^i$ to $p_{ins}^i$ is identified, as shown in Figure 5.

In step 4, the rigid transformation parameters $T$ and $R_{\theta }$ are determined based on the INS-indicated position sequence $P_{ins}$ and the corresponding nearest contour point sequence $Y$. These parameters must satisfy the optimization criterion of minimizing the sum of the squared Euclidean distances between $P_{ins}$ and $Y$, which is:

$$\min \left(\mathrm{D}\right)=\underset{R_{\theta },T}{\arg \min }{\displaystyle \sum _{x=i}^{i+N-1}{‖R_{\theta }{p}_{ins}^x+T-y^x‖}^2}$$

(5)

In step 5, establishing the appropriate iterative termination criteria is critical for enhancing the navigation accuracy of the standard ICCP algorithm. In practical implementations, multiple cascaded termination conditions can be serially integrated into the matching algorithm, where iteration terminates upon meeting any single criterion. Common termination criteria include:

• $\left|T\right|<T_{th}$ or $\left|R_{\theta }\right|<R_{\theta (\mathrm{th})}$, where $T_{th}$ and $R_{\theta (\mathrm{th})}$ are thresholds set in advance;
• The increments $\left|T_{j+1}-T_j\right|$ and $\left|R_{\theta (j+1)}-R_{\theta (j)}\right|$ of $T$ and $R_{\theta }$ between two neighboring iterations are less than the set thresholds $\Delta T$ and $\Delta R_{\theta }$;
• The distance between the estimated track points obtained from two adjacent iterations $D_j$ is less than the set threshold $D_{th}$;
• The number of iterations reaches a set maximum value $k_{\max }$.

The aforementioned analysis demonstrates that the ICCP algorithm features simple principles and imposes no constraints on underwater vehicle trajectories, with minimal sensitivity to heading errors in the INS-indicated path. However, its implementation requires that the true position resides near the INS-indicated position and exactly on the contour corresponding to the measured gravity anomaly value. Consequently, this method demands higher accuracy in both the gravimeter and gravity background fields.

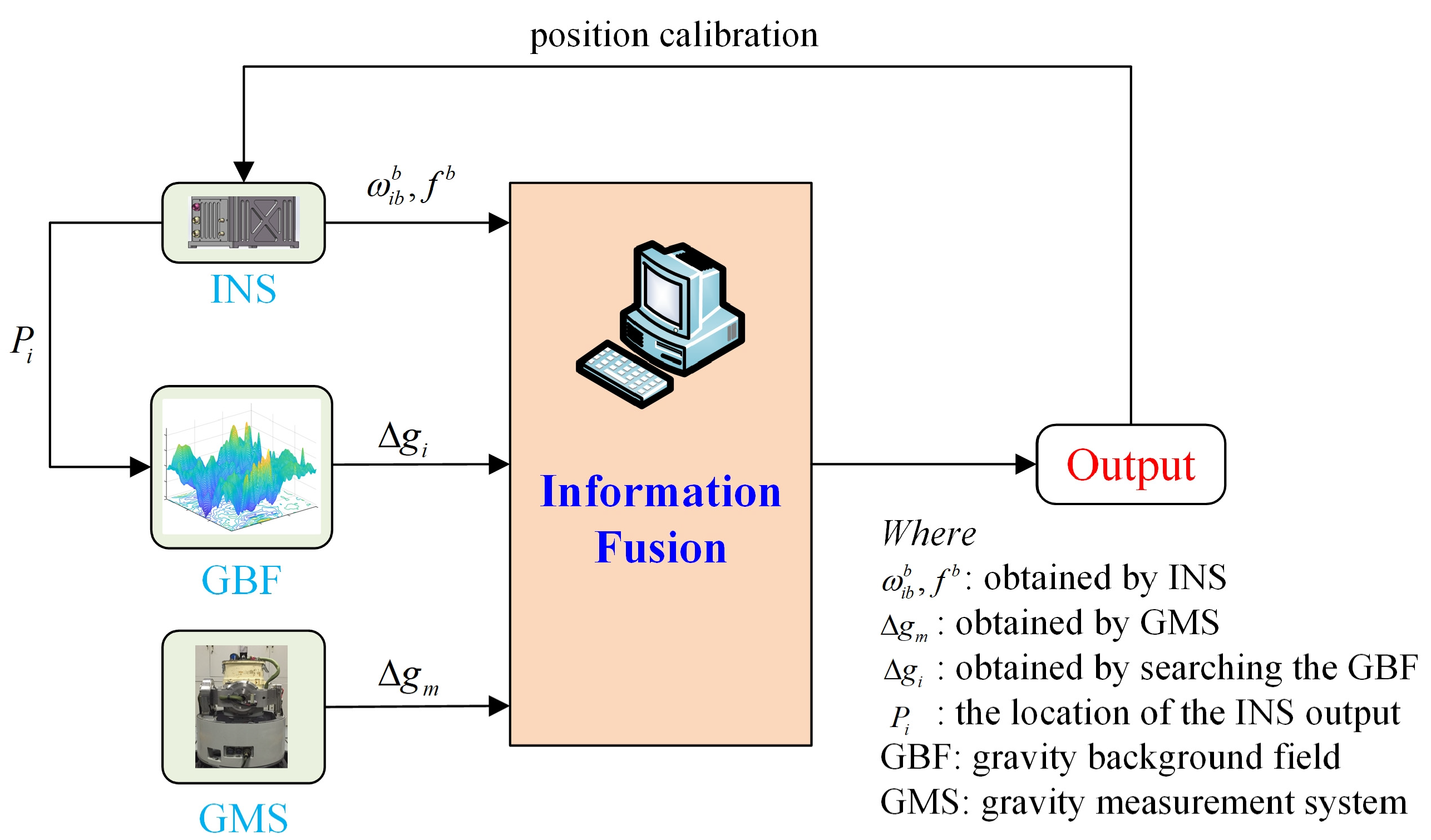
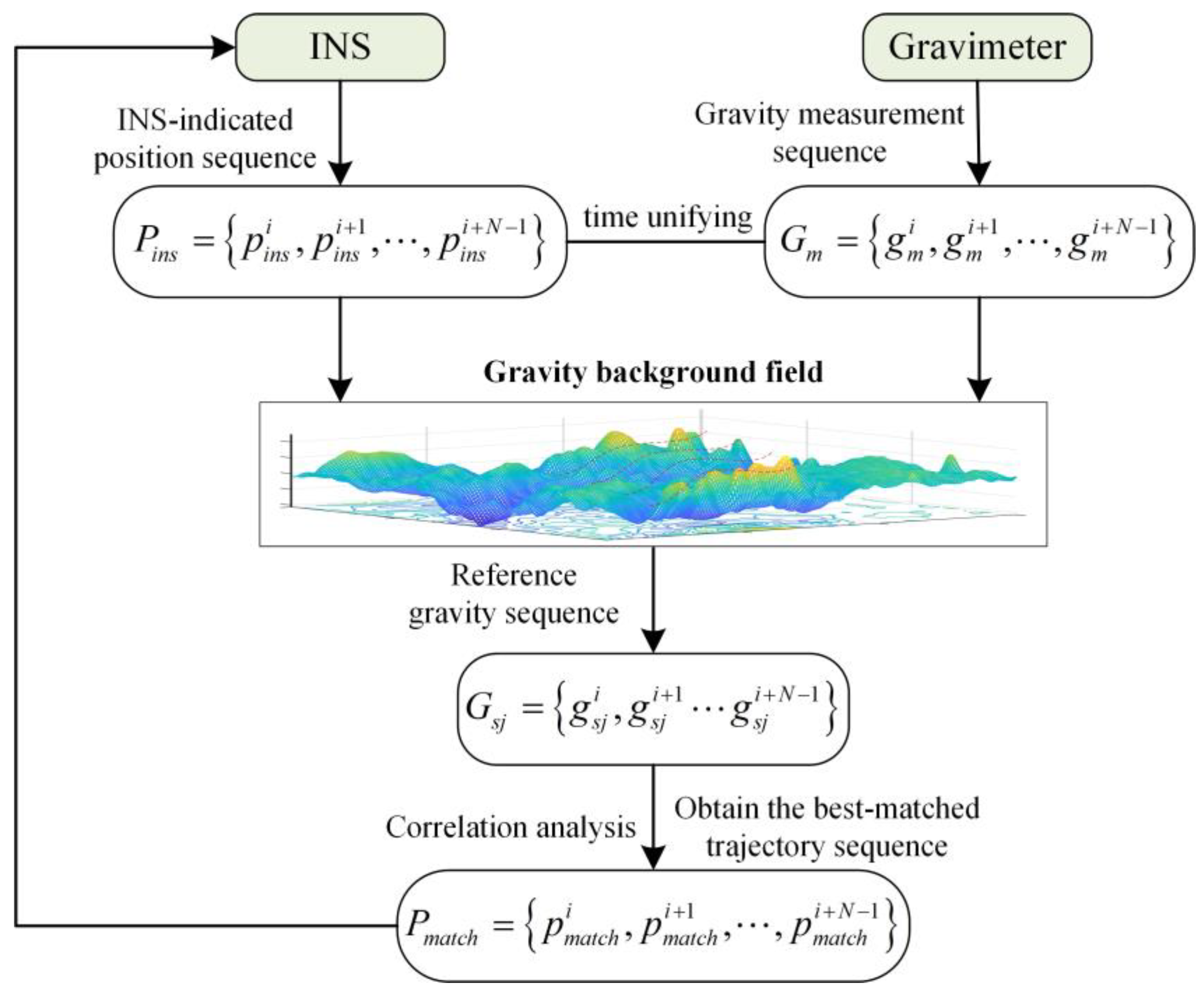
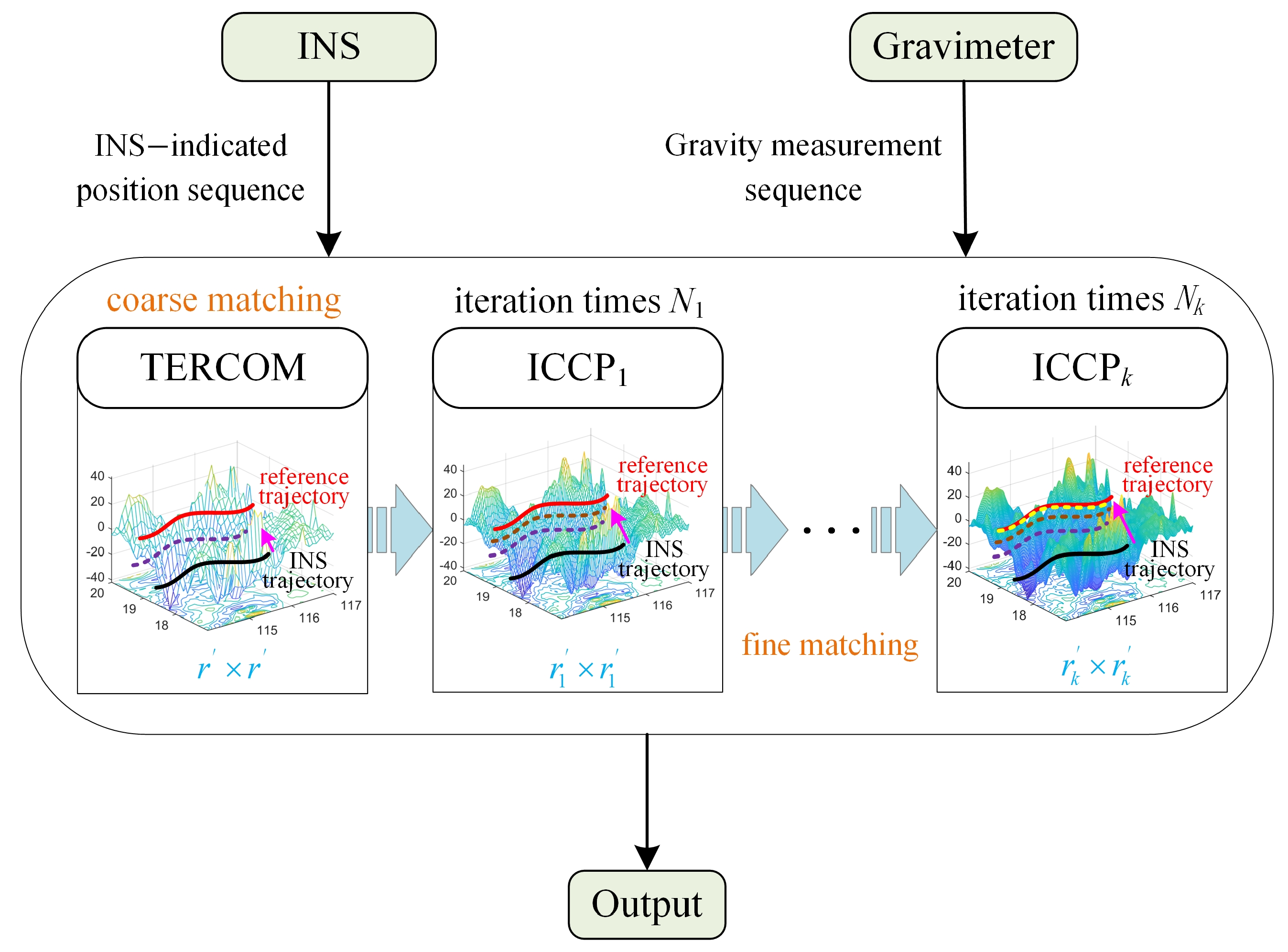
3. mRSMSC Model for Marine Gravity Matching

Conventional sequence-matching algorithms fail to fully exploit the inherent characteristics of gravity information and INS, resulting in limited practical performance. To address this limitation, this section develops a multi-resolution sequence method with strong constraint (mRSMSC) by integrating multi-constraint conditions, synergizing the complementary strengths of TERCOM and ICCP (introduced in Section 2), and rigorously incorporating the inherent properties of the gravity fields and INS. The proposed framework establishes a strongly constrained multi-resolution fusion mechanism to enhance matching accuracy and robustness.

3.1. Multi-Resolution Sequence-Matching Fusion Algorithm

As analyzed in Section 2, the TERCOM and ICCP algorithms exhibit complementarity advantages, and their fusion can synergistically leverage the strengths of both methods while minimizing the mismatch risk inherent to individual algorithms. To fully exploit this complementary advantage and enhance the compatibility between the optimized ICCP algorithm and background field resolution, this section proposes a multi-resolution sequence-matching (mRSM) fusion algorithm specifically designed for scenarios with large initial position errors.

As shown in Figure 6, the mRSM algorithm integrates the optimized TERCOM and ICCP sequence-matching methods. The workflow consists of two primary phases:

(1) TERCOM-based Coarse Matching suppresses large initial position errors using a low-resolution background field.

(2) ICCP-based Iterative Fine Alignment sequentially enhances positioning accuracy through high-resolution refinement. Let $r_i^{\prime }\times r_i^{\prime }$ denote the background field resolution for the $i$-th ICCP fine matching, $K$ is the total number of fine matching, and $N_k$ is the iteration count of the $K$-th fine matching. The pseudo-code of the mRSM algorithm is structured as follows in

Table 1. Pseudo-code for the mRSM algorithm.

Algorithm:	mRSM
Input	$\mathrm{INS}\text{-}\mathrm{indicated} \mathrm{sequence} P_{ins}=\left\{p_{ins}^i,p_{ins}^{i+1},\cdots ,p_{ins}^{i+N-1}\right\}$, $\mathrm{gravity} \mathrm{measurement} \mathrm{sequence} G_m=\left\{g_m^i,g_m^{i+1},\cdots ,g_m^{i+N-1}\right\}$, $\mathrm{gravity} \mathrm{background} \mathrm{field} GBF$$, \mathrm{number} \mathrm{of} \mathrm{fine} \mathrm{matching} \mathrm{iterations} N_{ICCP}, \mathrm{and} \mathrm{number} \mathrm{of} \mathrm{fine} \mathrm{matching} K$.
Output	$\mathrm{Position} \mathrm{sequence} P_{mRSM}$ after mRSM matching.
Step 1	$\mathrm{Coarse} \mathrm{matching}. \mathrm{The} \mathrm{TERCOM} \mathrm{algorithm} \mathrm{is} \mathrm{used} \mathrm{to} \mathrm{perform} \mathrm{sequence} \mathrm{matching} \mathrm{in} r_i^{\prime }\times r_i^{\prime }$$(\mathrm{typically} 1^{\prime }\times 1^{\prime }$) background field, and the large initial position error is quickly suppressed;
Step 2	$\mathrm{Fine} \mathrm{matching}. \mathrm{The} \mathrm{background} \mathrm{field} \mathrm{is} \mathrm{interpolated} \mathrm{from} r^{\prime }\times r^{\prime }$$\mathrm{to} r_1^{\prime }\times r_1^{\prime }$, $\mathrm{and} \mathrm{then} \mathrm{one} \mathrm{sequence} \mathrm{matching} \mathrm{is} \mathrm{performed} \mathrm{using} \mathrm{the} \mathrm{ICCP} \mathrm{algorithm}, \mathrm{where} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{iterations} \mathrm{is} N_1$;
Step 3	$\mathrm{Iterate} \mathrm{fine} \mathrm{matching}. \mathrm{Repeat} \mathrm{step} 2 \mathrm{until} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{fine} \mathrm{matches} \mathrm{is} \mathrm{reached} K$.

:

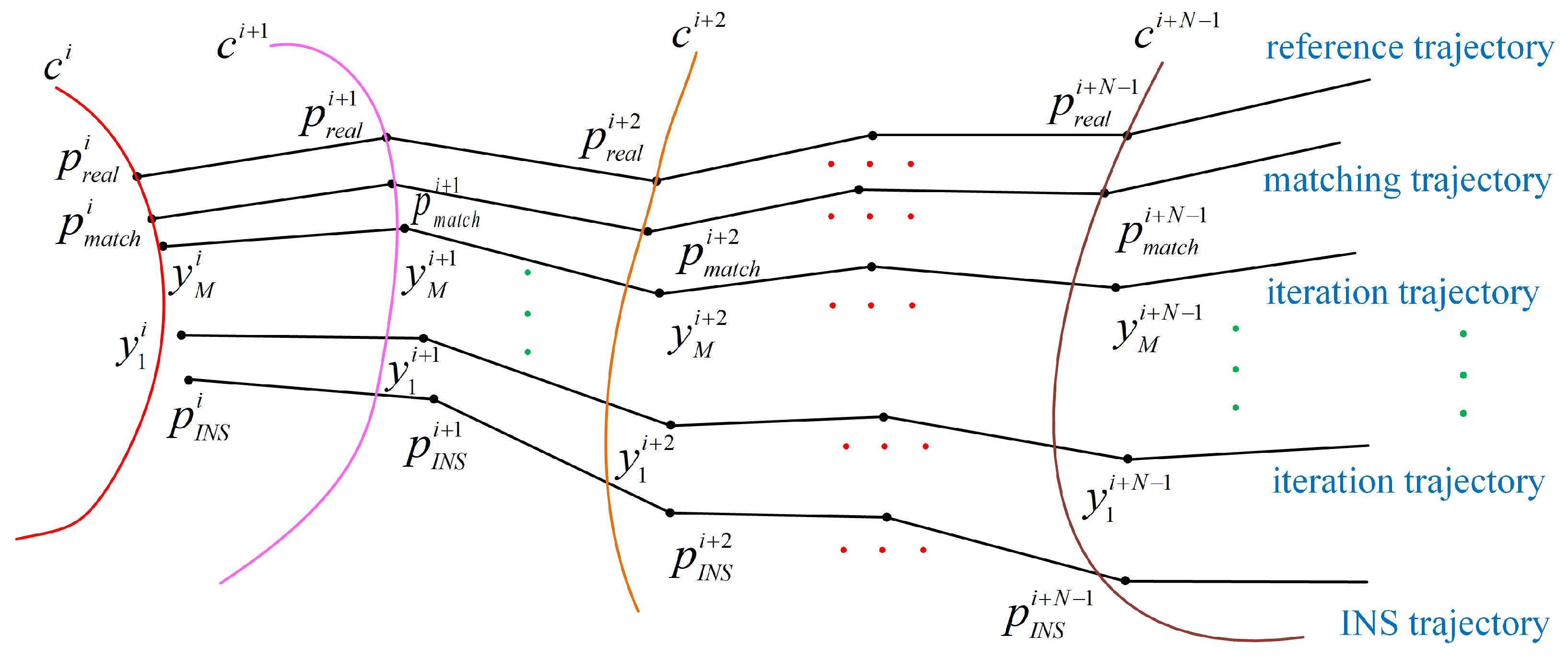
3.2. Analysis and Modeling of Strong Constraints

This section leverages the inherent characteristics of the INS—including minimal short-term trajectory distortion, high heading accuracy, and low relative position drift—to design multiple correlation-based constraints, thereby further eliminating invalid contour points.

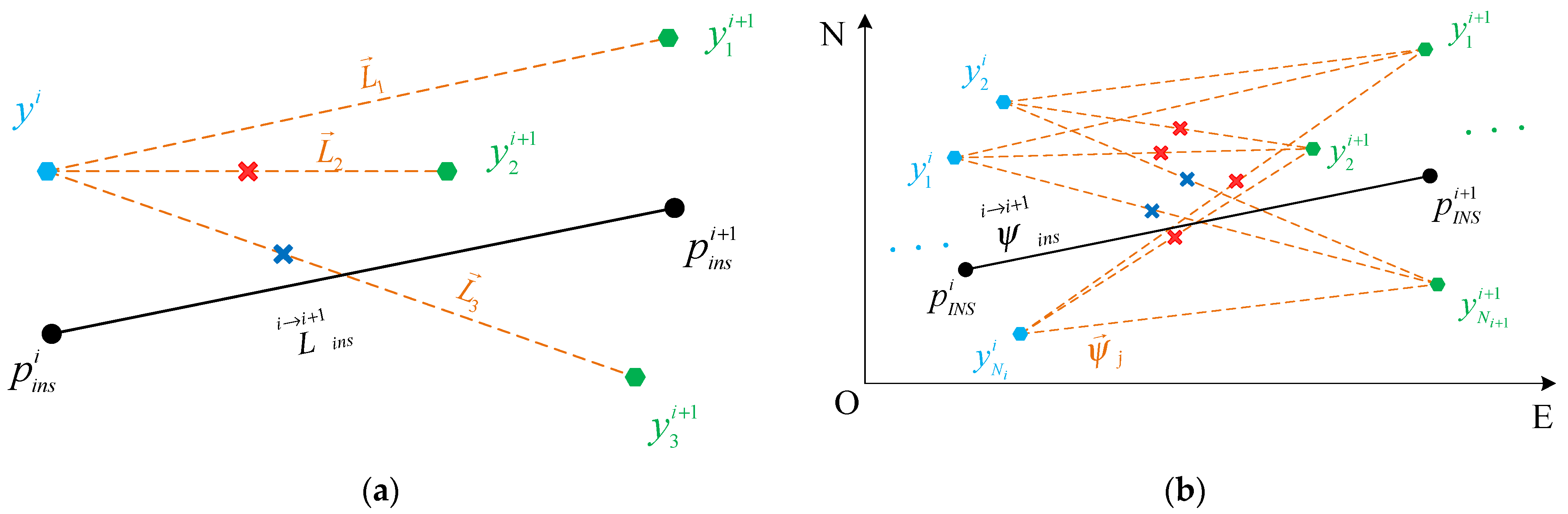
3.2.1. Positional Correlation Constraint

As shown in Figure 7, let $p_{ins}^i$ and $p_{ins}^{i+1}$ denote the INS-indicated position sequences at adjacent sampling epochs $i$ and $i+1$, respectively. The contour point sets corresponding to these sequences are $\left\{y_1^i,y_2^i,\cdots ,y_{N_i}^i\right\}$ and $\left\{y_1^{i+1},y_2^{i+1},\cdots ,y_{N_{i+1}}^{i+1}\right\}$, with the spacing between adjacent contour points represented as ${\overrightarrow{L}}_j,j=1,2,\cdots ,N_i\times N_{i+1}$. A total of $N_i\times N_{i+1}$ candidate connections (depicted as dashed lines) are generated. The distance between $p_{ins}^i$ and $p_{ins}^{i+1}$ is denoted as ${\stackrel{i\to i+1}{L}}_{ins}$. During sequence-matching navigation, the spacing ${\overrightarrow{L}}_j$ should approximate the actual travel distance within the sampling interval, i.e., the discrepancy $\Delta L_j=\left|{\stackrel{i\to i+1}{L}}_{ins}-{\overrightarrow{L}}_j\right|$ must remain minimal. Notably, a higher INS accuracy results in a smaller $\Delta L_j$. The dashed lines marked in red crosses in Figure 7 highlight the adjacent contour point pairs violating this positional correlation constraint.

Therefore, a positional drift threshold $\Delta d$ can be established based on the INS accuracy level. By comparing the magnitude of $\Delta L_j$ with $\Delta d$, adjacent contour points are evaluated against the positional constraint. Specifically, a contour point $y^i$ at epoch $i$ is retained only if it satisfies the following condition:

$$\left|{\stackrel{i\to i+1}{L}}_{ins}-D\left(y^i,y_k^{i+1}\right)\right|\le \Delta d, k=1,2,\cdots ,N_{i+1}$$

(6)

where $D\left(\right)$ represents the Euclidean distance between two points; if $y^i$ fails to meet this criterion for all $y_k^{i+1}$, it is eliminated from the candidate set.

By applying (6) to all contour points at epochs $i$ and $i+1$, invalid contour points within the candidate sets $\left\{y_1^i,y_2^i,\cdots ,y_{N_i}^i\right\}$ and $\left\{y_1^{i+1},y_2^{i+1},\cdots ,y_{N_{i+1}}^{i+1}\right\}$ can be effectively eliminated. Furthermore, positional correlation constraints can be extended to non-adjacent contour points by proportionally scaling the drift threshold $\Delta d$. Then, it yields:

$$\left|{\stackrel{i\to i+\kappa }{L}}_{ins}-D\left(y^i,y_k^{i+\kappa }\right)\right|\le {\kappa }_1\Delta d$$

(7)

where ${\kappa }_1$ is the interval between the constraint points.

3.2.2. Heading Correlation Constraint

While the positional correlation constraints for the adjacent contour points were analyzed in the previous section, certain candidate pairs (e.g., ${\overrightarrow{L}}_1$ and ${\overrightarrow{L}}_3$ in Figure 8a) that satisfy positional thresholds may still exhibit significant heading deviations that are incompatible with the high-precision heading characteristics of the INS. Although ${\overrightarrow{L}}_1$ and ${\overrightarrow{L}}_3$ comply with the positional constraints, the heading of ${\overrightarrow{L}}_2$ substantially deviates from the INS-indicated trajectory, necessitating its elimination.

Let ${\overrightarrow{\Psi }}_j$ denote the heading magnitude between the adjacent contour points and ${\stackrel{i\to i+1}{\Psi }}_{ins}$ represent the heading magnitude between $p_{ins}^i$ and $p_{ins}^{i+1}$. It is critical to note that only the absolute heading magnitudes are considered so as to eliminate the influence of the negative directional values introduced by navigation orientation. During sequence-matching navigation, the heading of the adjacent contour points should closely align with the underwater vehicle’s trajectory, i.e., the discrepancy $\Delta {\Psi }_j=\left|{\stackrel{i\to i+1}{\Psi }}_{ins}-{\overrightarrow{\Psi }}_j\right|$ must remain minimal. A higher INS accuracy inherently reduces $\Delta {\Psi }_j$. As shown in Figure 8b, adjacent contour point pairs violating this heading correlation constraint are marked with blue crosses.

A heading drift threshold $\Delta m$ is established based on the INS accuracy level. By comparing the magnitude of $\Delta {\Psi }_j$ and $\Delta m$, the algorithm evaluates whether the adjacent contour points satisfy the heading constraint. Specifically, a contour point $y^i$ at epoch $i$ is retained only if it satisfies:

$$\left|{\stackrel{i\to i+1}{\Psi }}_{ins}-H\left(y^i,y_k^{i+1}\right)\right|\le \Delta m, k=1,2,\cdots ,N_{i+1}$$

(8)

where $H\left(\right)$ denotes the heading between two points. This criterion eliminates invalid contour points from the sets $\left\{y_1^i,y_2^i,\cdots ,y_{N_i}^i\right\}$ and $\left\{y_1^{i+1},y_2^{i+1},\cdots ,y_{N_{i+1}}^{i+1}\right\}$.

In addition to the heading correlation constraints for neighboring contour points, similar heading correlation constraints can be designed between non-neighboring contour points, which yields:

$$\left|{\stackrel{i\to i+\kappa }{\Psi }}_{ins}-H\left(y^i,y_k^{i+\kappa }\right)\right|\le {\kappa }_2\Delta m$$

(9)

where ${\kappa }_2$ is the interval between the constraint points.

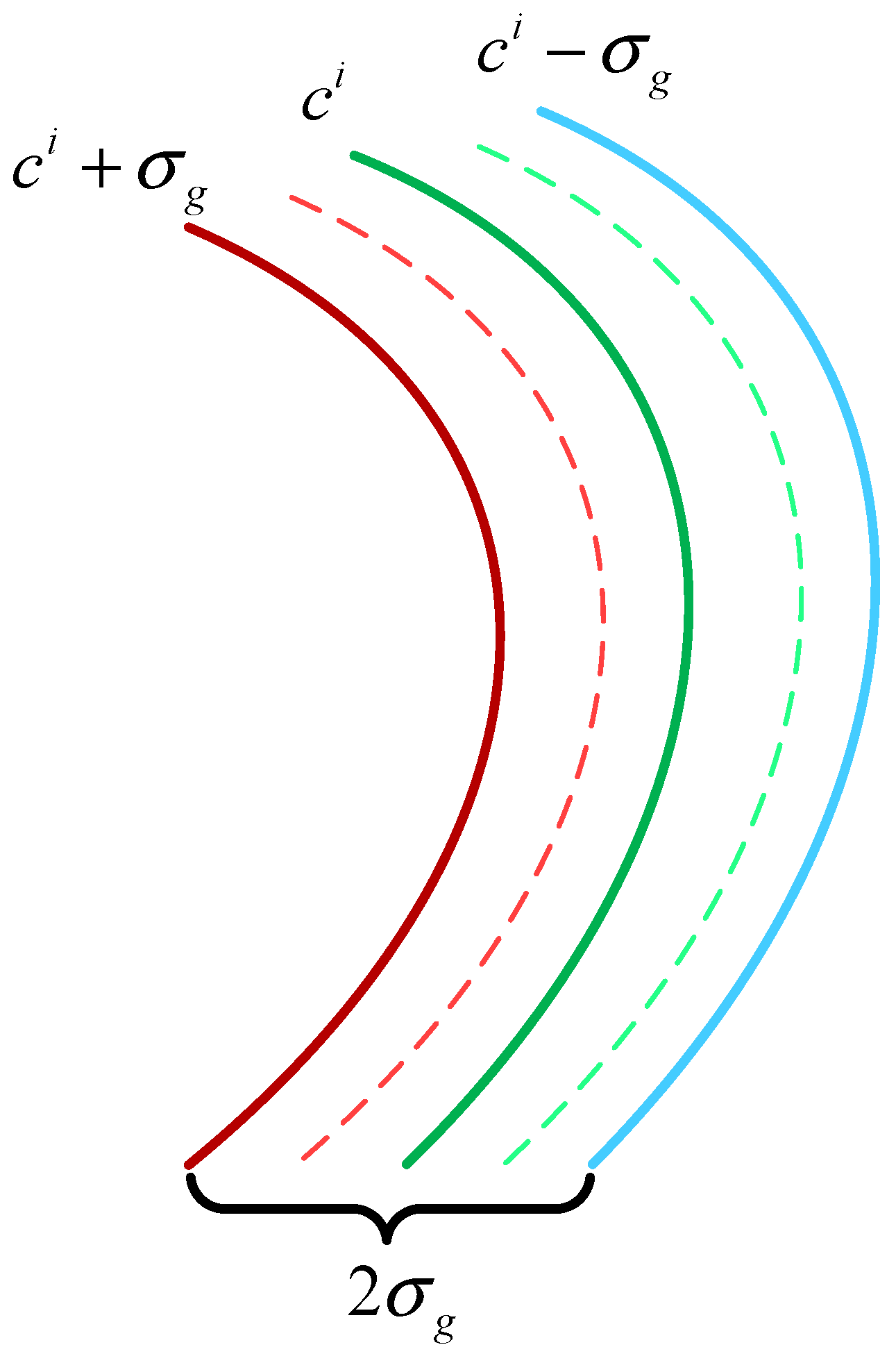
3.2.3. Gravity Correlation Constraint

The gravity field is a continuous potential field, and gravity anomalies generally exhibit no abrupt changes at small scales. Consequently, during sequence-matching navigation, the magnitude of the gravity anomaly differences ${\stackrel{i\to i+1}{\Delta g}}_{gra}$ measured by gravimeters at adjacent sampling points should correlate with the gravity anomaly differences $\Delta g_j$ derived from adjacent contour point searches. Leveraging this property, a gravity correlation constraint is designed for adjacent sequence points, as shown in Figure 9, where the circles represent gravity anomalies at the measurement points, and the pentagrams denote the contour point search results.

The measured gravity anomaly difference between adjacent epochs is defined as

$${\stackrel{i\to i+1}{\Delta g}}_{gra}=\left|g_{gra}^i-g_{gra}^{i+1}\right|$$

(10)

where $g_{gra}^i$ and $g_{gra}^{i+1}$ denote the gravity anomaly measurements at epochs $i$ and $i+1$, respectively. This differencing operation mitigates the impact of gravimeter measurement errors on ${\stackrel{i\to i+1}{\Delta g}}_{gra}$, thereby accentuating the true variation trend of gravity anomalies.

Similarly, the gravity anomaly difference for the contour point searches is expressed as

$$\Delta g_j=\left|g_u^i-g_w^{i+1}\right|$$

(11)

where $g_u^i$ is the search gravity anomaly values at $y_u^i$, $u=1,2,\cdots ,N_i$, which is the contour point at $i$; $g_w^{i+1}$ is the search gravity anomaly values at $y_w^{i+1}$, $w=1,2,\cdots ,N_{i+1}$, which is the contour point at $i+1$. The above equation reduces the influence of the gravity background field errors on $\Delta g_j$, emphasizing the variation characteristics of the search-based gravity anomalies.

Next, compare the magnitude discrepancy between ${\stackrel{i\to i+1}{\Delta g}}_{gra}$ and $\Delta g_j$, evaluating the contour points against a gravity variation threshold $\Delta q$. A contour point $y^i$ is retained only if

$$\left|{\stackrel{i\to i+1}{\Delta g}}_{gra}-\Delta g_j\right|\le \Delta q$$

(12)

It should be noted that the threshold $\Delta q$ must be adaptively configured based on local gravity gradient variations around the underwater vehicle’s position. This requirement introduces limitations in operational flexibility. To ensure algorithmic stability, the weight of gravity correlation constraints is reduced relative to the positional and heading constraints.

In practical sequence-matching navigation, uncertainties in INS-indicated position errors, heading errors, gravity search anomalies, and true gravity anomalies often prevent the precise construction of the constraints defined in (6), (8), and (12). Consequently, residual contour points can only be qualitatively assessed as “likely valid” or “likely invalid” through conventional deterministic methods. To address this ambiguity, a fuzzy mathematical model is introduced to compute the probabilistic validity evaluations for the remaining contour points [30].

Membership functions and membership degrees constitute the core components of fuzzy mathematics. In this section, three key factors—INS-indicated travel distance, INS-indicated heading, and gravimeter measurements within the sampling interval—are utilized to construct fuzzy membership functions for evaluating the error magnitude of each contour point. The membership degrees are computed individually for each factor and then aggregated to derive a comprehensive evaluation of the contour point’s error magnitude. Then, it yields:

$$\left(\begin{array}{cc}{\mu }_1& {\mu }_2\end{array}\right)=\left(\begin{array}{ccc}{\rho }_1& {\rho }_2& {\rho }_3\end{array}\right)\left(\begin{array}{cc}{\mu }_d\left(l\right)& {\tilde{\mu }}_d\left(l\right)\\ {\mu }_m\left(h\right)& {\tilde{\mu }}_m\left(h\right)\\ {\mu }_q\left(a\right)& {\tilde{\mu }}_q\left(a\right)\end{array}\right)$$

(13)

where ${\mu }_1$ and ${\mu }_2$ represent the membership degrees for the “small error” and “large error”, respectively.

During algorithm execution, invalid contour points are sequentially eliminated based on the positional, heading, and gravity correlation constraints. The remaining contour points are then ranked, with higher probability candidates prioritized as optimal matches for sequence alignment. Notably, the positional and heading constraints are equally significant, whereas the gravity constraints are less critical due to their susceptibility to gravimeter measurement errors, background field inaccuracies, and interpolation errors. Consequently, the weighting coefficients are typically set as ${\rho }_1=0.4$, ${\rho }_2=0.4$, ${\rho }_3=0.2$.

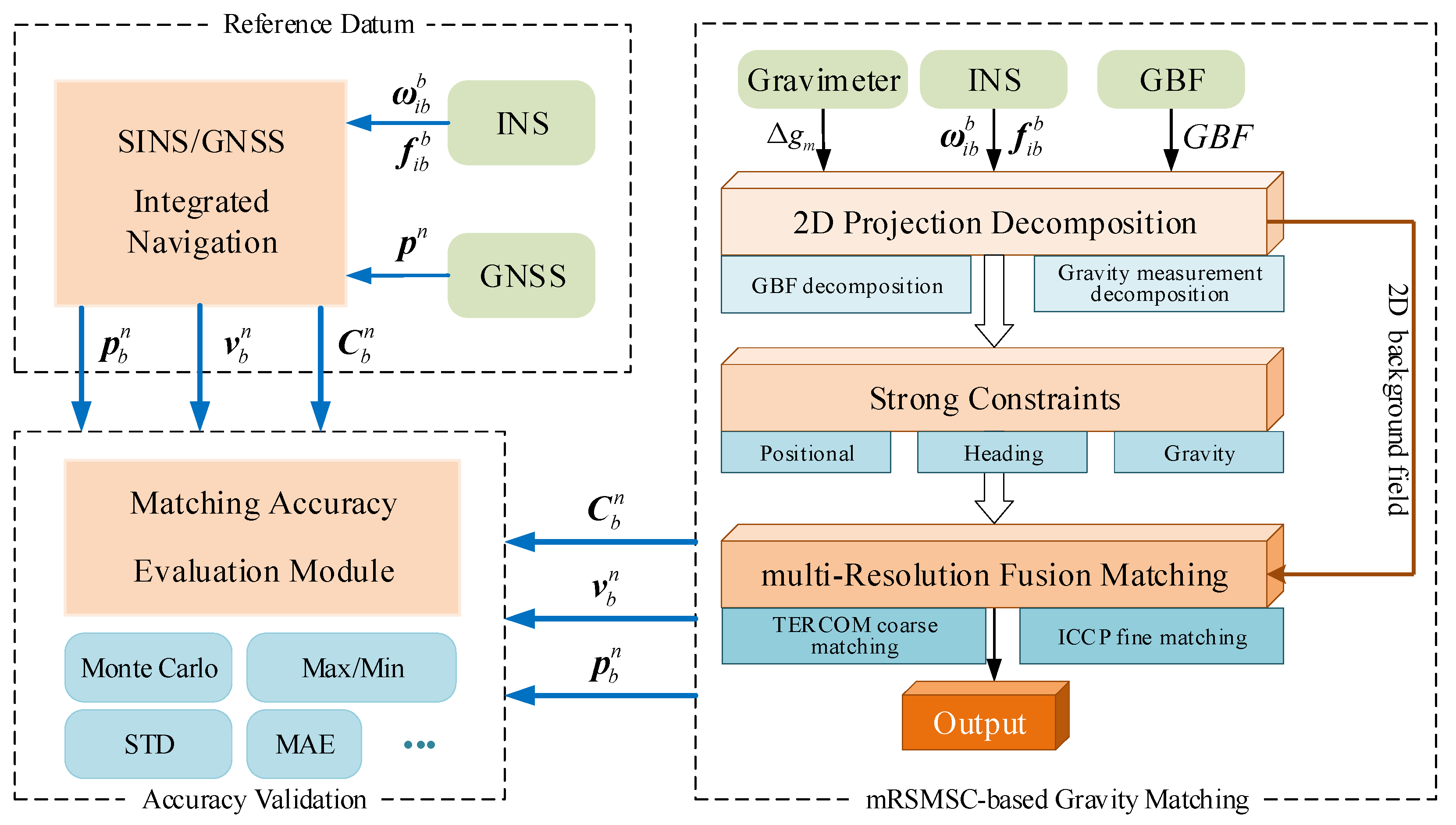
3.3. Algorithm Flow

As shown in Figure 10, the proposed mRSMSC algorithm comprises three core modules: (1) 2D projection decomposition (detailed in the authors’ prior work [31]), (2) multi-criteria strong constraints, and (3) 2D multi-resolution fusion matching. The main steps are as follows:

Step 1: This module performs gravity background field decomposition and gravimetric measurement decomposition based on geodetic axis projection. The 2D gravity background field is preprocessed offline once the target matching area is defined, imposing no real-time computational burden. Real-time gravimeter measurements are projected onto the 2D plane using the INS-indicated position, enabling subsequent contour point searches within the decomposed gravity field.

Step 2: This phase eliminates invalid contour points through positional, heading, and gravity correlation constraints and ranks the remaining candidates. A fuzzy synthetic metric is designed by constructing fuzzy membership functions for positional, heading, and gravity error magnitudes. The fuzzy membership function of the error size of each contour point is established, respectively. Its membership degree is calculated and then the fuzzy evaluation of each contour point is obtained by synthesizing the influence degree of three factors.

Step 3: This final stage achieves stable positioning by integrating the constrained contour point set with the projected 2D gravity field and INS-indicated positions. The mRSM fusion algorithm estimates INS position errors through iterative coarse-to-fine resolution matching.

The proposed mRSMSC algorithm is an optimized extension of the standard TERCOM and ICCP, incorporating multi-resolution fusion and projection-based strong constraints to eliminate invalid contour points and refine the search scopes. As shown in Figure 10, the mRSMSC-based navigation framework comprises three modules:

• Reference Datum: Provided by SINS/GNSS integrated navigation;
• Matching Positioning: Executes mRSMSC-based gravity matching;
• Accuracy Validation: Evaluates reliability by comparing the mRSMSC outputs with SINS/GNSS references.

4. Experimental Study

In this section, to evaluate the performance of the proposed mRSMSC algorithm in practical applications, shipboard gravity-matching experiments were conducted. In addition, the experimental results of the optimized TERCOM and ICCP, which are described in Section 2, as well as the two-dimensional projection decomposition of TERCOM and ICCP (denoted as DTERCOM and DICCP) and the mRSMSC proposed in this paper, are compared and analyzed.

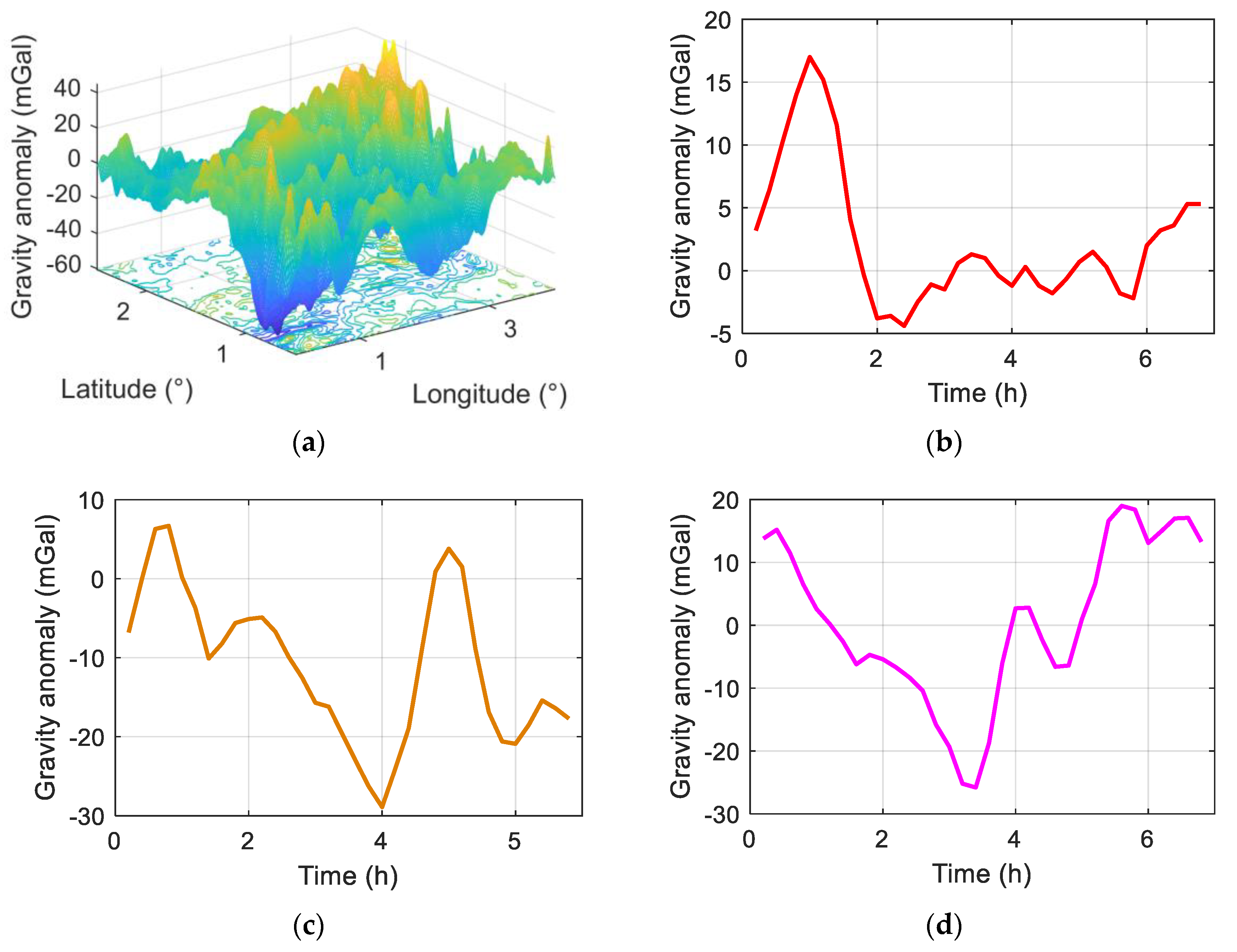
4.1. Field Test

The shipboard experiments were carried out in the Western Pacific Ocean; the experimental setups are shown in Figure 11. The GNSS information is provided by OEM 628 GPS receiver from NovAtel, Canada (update rate: 1 Hz; velocity accuracy: 0.1 m/s; position accuracy: 10 m), and the reference trajectory is obtained through the NovAtel combined navigation post-processing software Inertial Explorer 8.90 (IE). The IMU is equipped with a triad of ring laser gyroscopes (bias stability: <0.003°/h; angular random walk: <0.0003°/$\sqrt{h}$) and three quartz accelerometers (bias: <20 μg; random walk: <2 μg/$\sqrt{h}$), with an update rate of 400 Hz. The CHZ-II marine gravity meter measures gravity values (update rate: 1 Hz; accuracy: 1 mGal), and the matching algorithm update period is 300 s [32].

In the test, the sampling interval is 300 s, the number of matching points is 21, and all sampling points on the track are matched by the fixed interval sliding method, with one sampling point sliding each time.

Three trajectories (trajectories 1, 2, and 3) were tested at ~10 knots, heading northeast, with a total voyage of 70 nautical miles. The gravity anomaly reference map, derived from satellite altimetry data (Scripps Institution of Oceanography, V32.1), has a resolution of 1′ × 1′ and an accuracy of 3~5 mGal [33,34,35]. Figure 12 shows the gravity anomaly variations along the trajectories, which are ranked by gradient intensity: Trajectory 1 < trajectory 2 < trajectory 3. To evaluate the effectiveness, an initial position error of about 6 nautical miles was injected into the SINS.

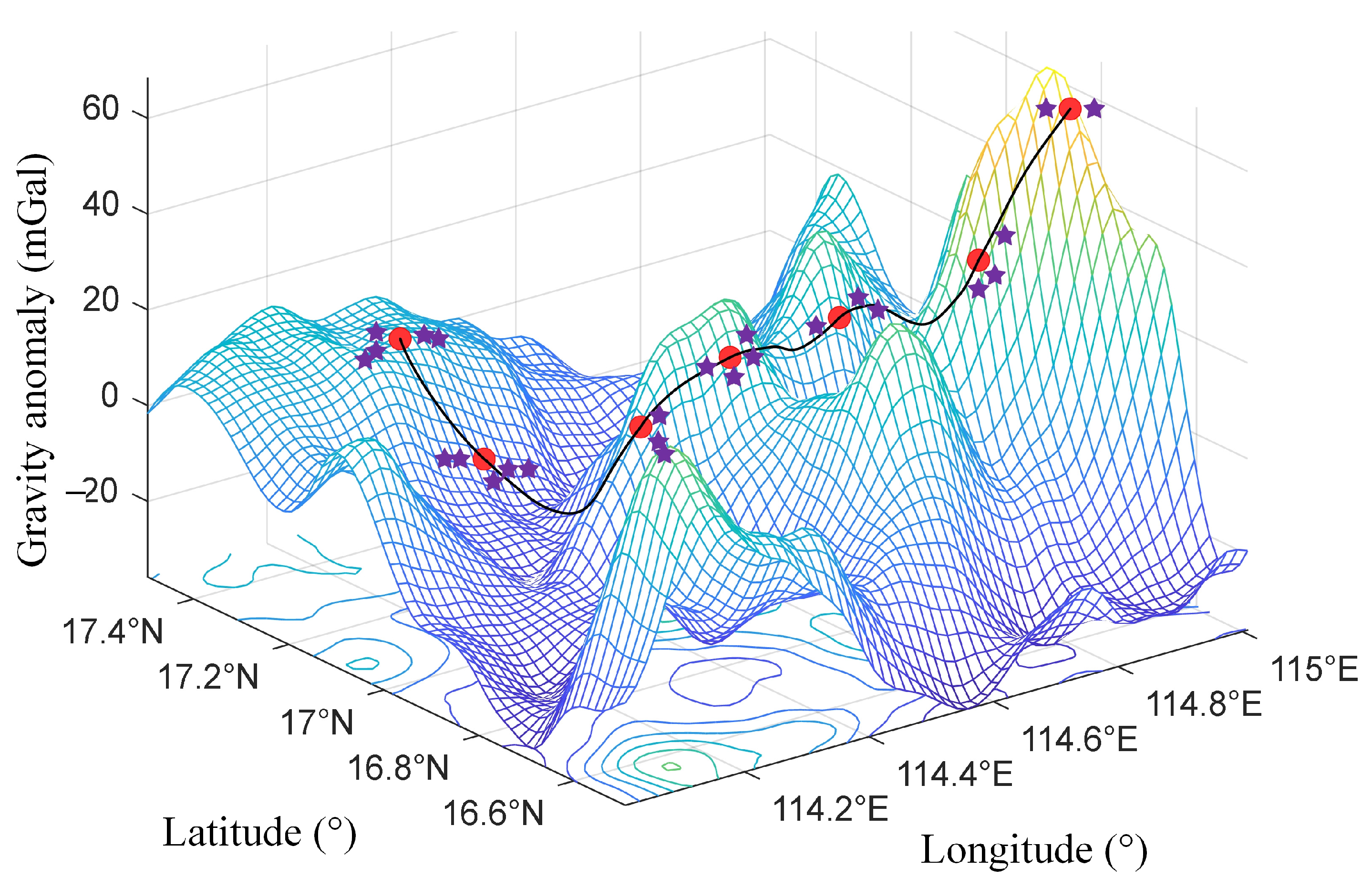
4.2. Results and Analysis

To verify the matching accuracy and reliability of the proposed algorithm, each trajectory underwent 1000 Monte Carlo tests. The performance metrics included the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE). Figure 13 shows the Cumulative Distribution Function (CDF) of the positioning errors for 1000 Monte Carlo trials for each of the five matching algorithms for the three trajectories, and the corresponding error statistics are given in

Table 2. Statistics of the average positioning error of the different algorithms (unit: nautical miles).

Algorithm	Flight Path 1		Flight Path 2		Tracks 3
	MAE	RMSE	MAE	RMSE	MAE	RMSE
SINS	9.6001	9.6253	9.6416	9.6667	9.5993	9.6241
TERCOM	0.7773	0.8383	0.4952	0.5245	0.4240	0.4564
ICCP	0.7389	0.7978	0.4621	0.4983	0.4328	0.4667
DTERCOM	0.5949	0.6417	0.4074	0.4380	0.3362	0.3620
DICCP	0.5600	0.6038	0.3757	0.4051	0.3580	0.3842
mRSMSC	0.3507	0.3770	0.2776	0.2986	0.2276	0.2444
Improvement *	37.4%	37.5%	26.1%	26.3%	32.3%	32.5%

* Accuracy improvement of the mRSMSC compared to the results of the matching error minimization algorithm (blue in the table).

, which yields the following:

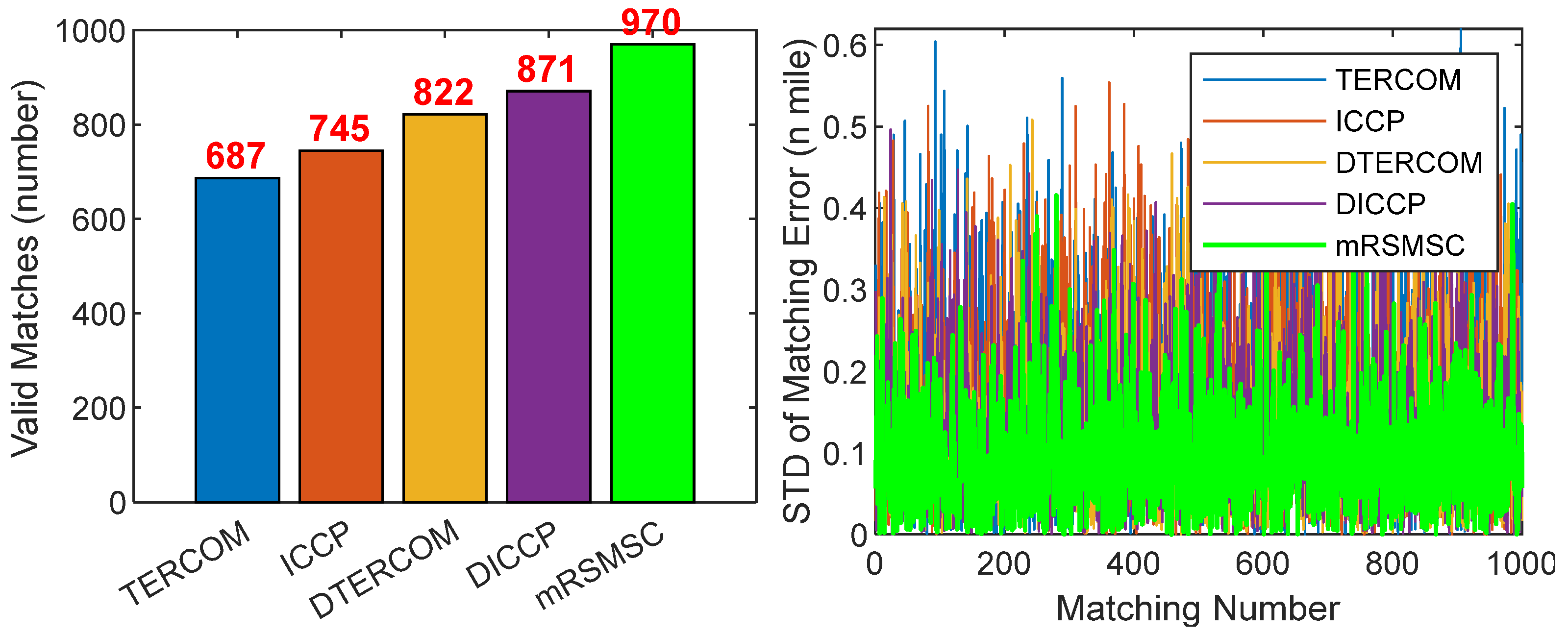
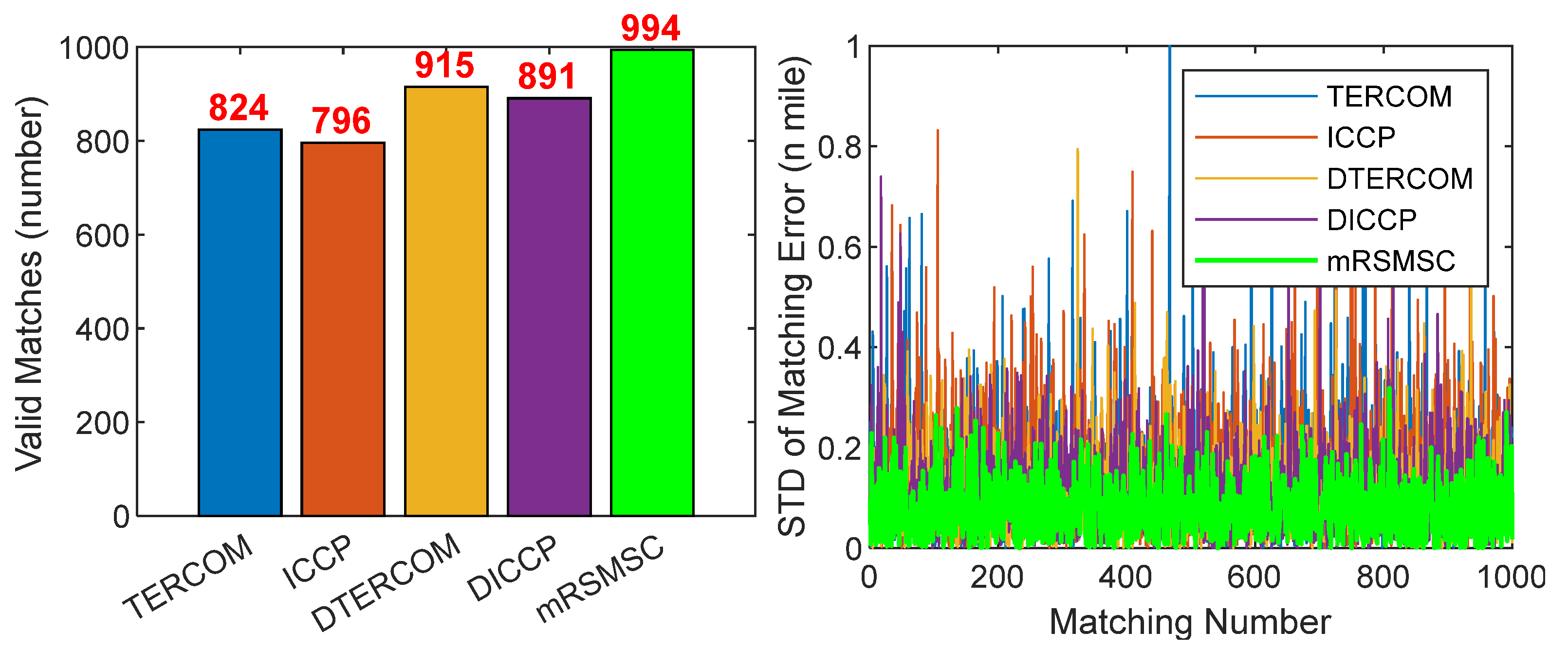
• The average horizontal position errors are positively correlated with the intensity of the gravity anomaly changes on the trajectories, i.e., the more intense the gravity anomaly changes (trajectory 1 < trajectory 2 < trajectory 3), the smaller the average horizontal position error (trajectory 1 > trajectory 2 > trajectory 3) of the matching results;
• The MAE of the mRSMSC is 0.3507 nautical miles (Traj.1), 0.2776 nautical miles (Traj.2), and 0.2276 nautical miles (Traj.3), respectively, which outperformed the TERCOM, ICCP, DTERCOM, and DICCP across all trajectories. Compared with the matching results with the smallest error among the other four algorithms (blue in the table), the mRSMSC improved by about 37.4%, 26.1%, and 32.3%, respectively, with an average improvement of about 31.9%;
• Compared with the remaining four algorithms, the MAE of mRSMSC in the three trajectories improved by about 48.4%, 46.6%, 35.1%, and 33.3%, on average. Combining and comparing the MAE and RMSE of the experimental results, the mRSMSC algorithm shows a better overall performance by having better accuracy and reliability on the three trajectories.

Considering the marine gravity anomaly reference map resolution ($1\prime \times 1\prime$), gravimeter measurement accuracy (about 1 mGal), and safety requirements for underwater vehicles, a matching result is classified as valid only if all matched points exhibit errors below one grid cell. Matching results exceeding this threshold are deemed mismatches. This stringent criterion rigorously validates algorithm reliability. Additionally, the standard deviation of positioning errors quantifies matching stability—smaller values indicate more consistent error distributions and higher trajectory stability.

The statistics of the matching results of trajectory 1 are shown in Figure 14. Among 1000 trials, valid matches for the TERCOM, ICCP, DTERCOM, DICCP, and mRSMSC are 430, 471, 596, 620, and 886, respectively. Compared to the baselines, the mRSMSC achieves valid match rate improvements of 51.5%, 46.8%, 32.7%, and 30.0%.

The statistics of the trajectory 2 matching results are shown in Figure 15. Among 1000 trials, the valid matches are 687, 745, 822, 871, and 970, respectively, and the mRSMSC achieves valid match rate improvements of 29.2%, 23.2%, 15.3%, and 10.2%.

The statistics of the matching results of trajectory 3 are shown in Figure 16. Among 1000 trials, the valid matches are 824, 796, 915, 891, and 994, respectively, and the mRSMSC achieves valid match rate improvements of 17.1%, 19.9%, 7.9%, and 10.4%.

As evidenced by Table 2 and Figure 14, Figure 15 and Figure 16, the valid match rates of all algorithms increase proportionally with the gravity anomaly gradient intensity along trajectories. An analysis of 1000 Monte Carlo matching trials across three trajectories demonstrates that the proposed mRSMSC achieves average valid match rate improvements of 32.6%, 30.0%, 18.6%, and 16.9% compared to the TERCOM, ICCP, DTERCOM, and DICCP, respectively, under varying anomaly gradient conditions. Notably, the DTERCOM and DICCP exhibit superior performance relative to the TERCOM and ICCP, though still underperforming the mRSMSC. Overall, without introducing additional restrictive conditions, the mRSMSC realizes strongly constrained multi-resolution 2D sequence matching, significantly enhancing both positioning accuracy and operational reliability. This framework provides a novel methodology for addressing sequence-matching challenges in underwater navigation.

5. Conclusions

In this paper, the mRSMSC matching algorithm is proposed to address the instability of sequence-matching algorithms under varying initial navigation parameter errors. Firstly, to overcome the limitations of the two sequence-matching algorithms, the TERCOM and ICCP, a multi-resolution sequence-matching fusion framework is developed by synergizing the TERCOM and ICCP with multi-scale gravity anomaly background fields. Then, to refine contour point selection and enhance search quality, a strongly constrained multi-resolution sequence-matching algorithm based on strong constraints is proposed by designing three correlation constraint models (positional, heading, and gravity). Finally, the performance of the mRSMSC is verified using three field test trajectories with an initial position error of about 6 nautical miles. Furthermore, 1000 Monte Carlo simulation validations for each of the three trajectories show that, compared with the TERCOM, ICCP, DTERCOM, and DICCP, the mRSMSC improves the MAE by an average of about 48.4%, 46.6%, 35.1%, and 33.3% and the effective matching rate by an average of about 32.6%, 30.0%, 18.6%, and 16.9%.

We are convinced that the proposed algorithms have great potential in matching navigation. Future work is as follows.

• Collecting more extensive field datasets to facilitate a more comprehensive assessment of the algorithm’s performance;
• Explore the combination of the sequence-matching algorithm and filter matching to further improve matching accuracy.