Cooperative Formation Control of Multiple Ships with Time Delay Conditions
Abstract
:1. Introduction
- (1)
- Development of a consensus-based formation control algorithm capable of handling various communication topologies, ensuring stability in dynamic environments.
- (2)
- Extension of the control strategy to accommodate communication delays, with rigorous proof of its stability through Lyapunov’s stability theory.
2. Literature Review
3. Problem Statement and Formulation
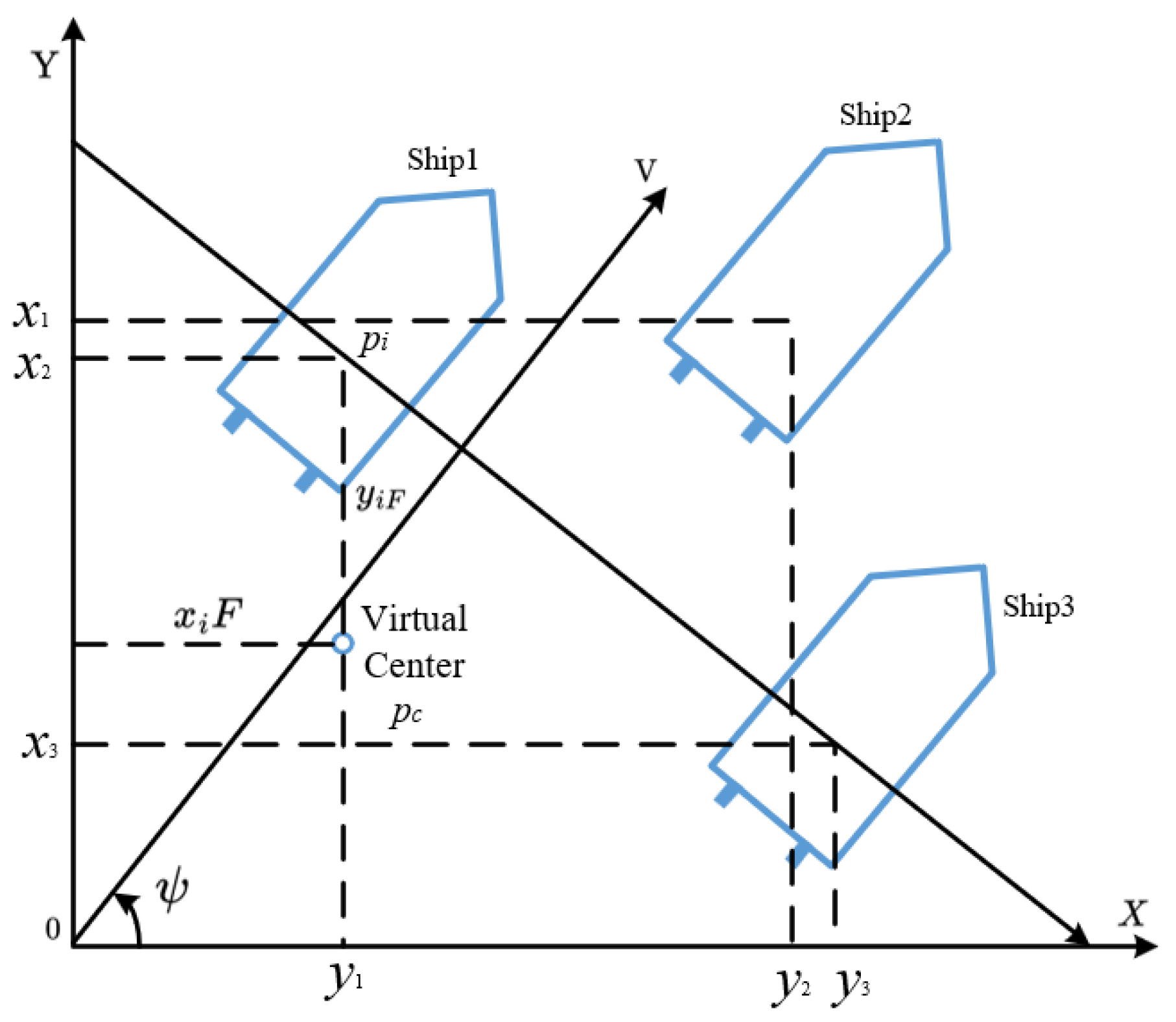
3.1. Formation Matrix Description for Ship Formation
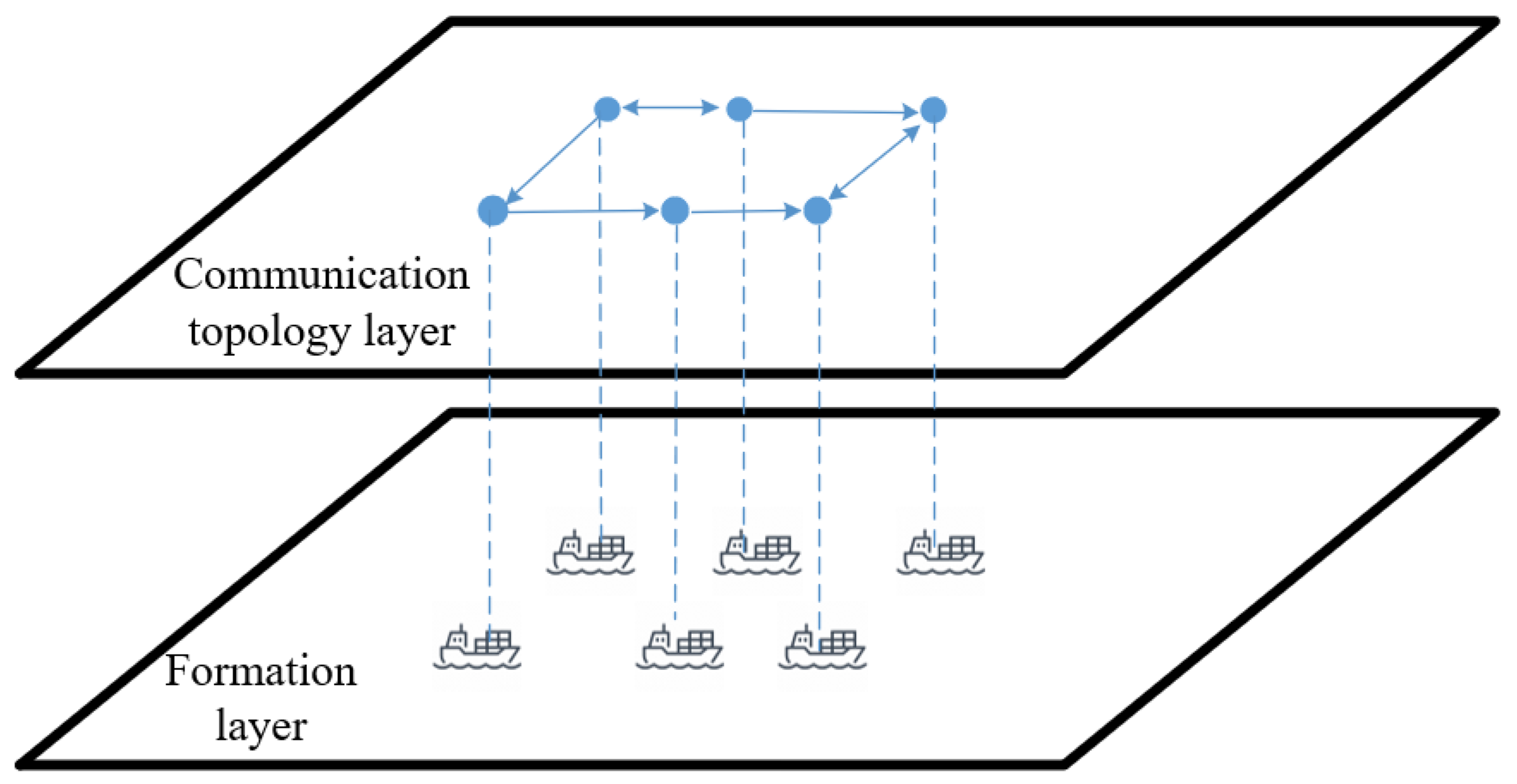
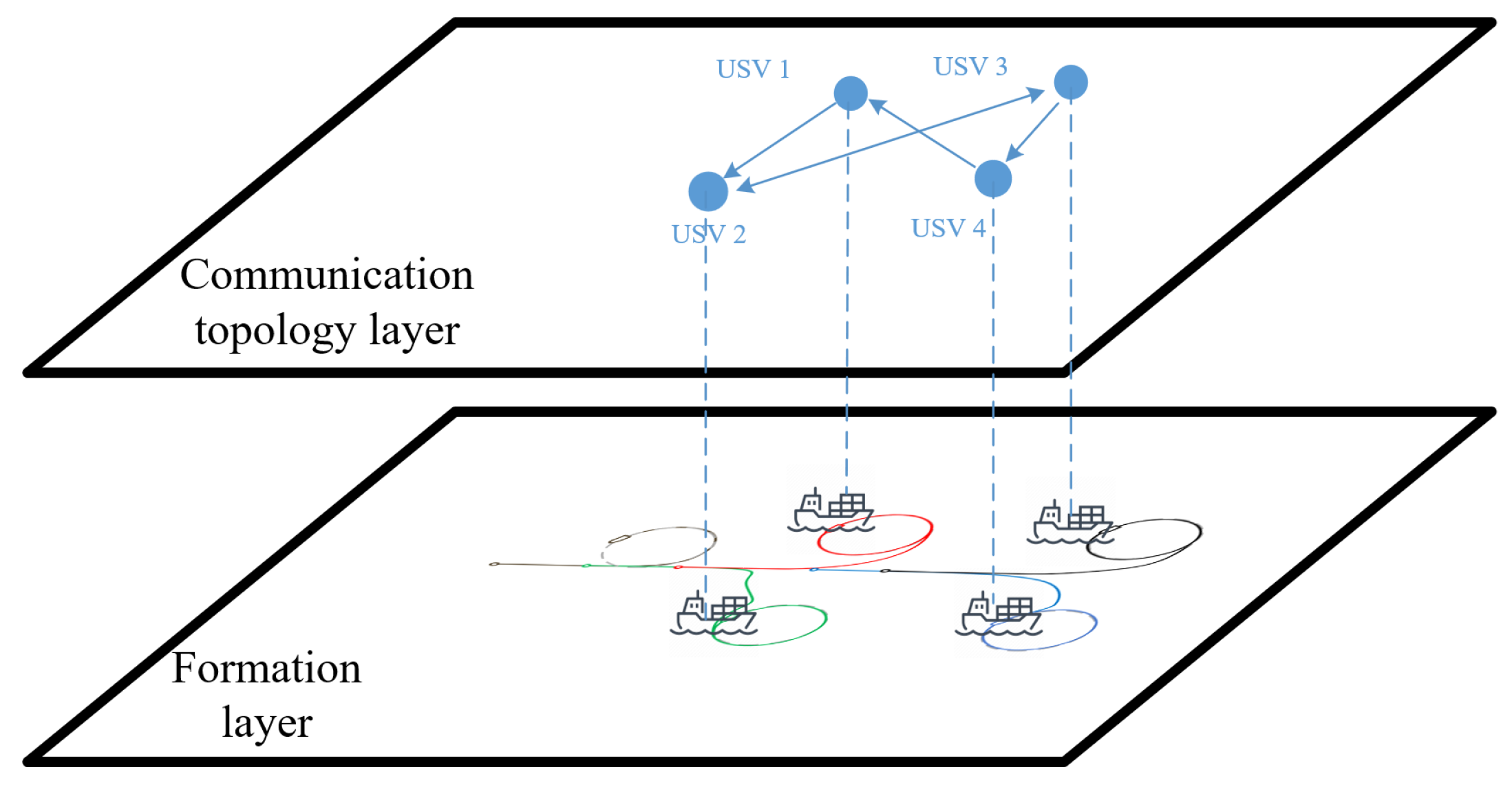
3.2. Construction of Communication Topology Models
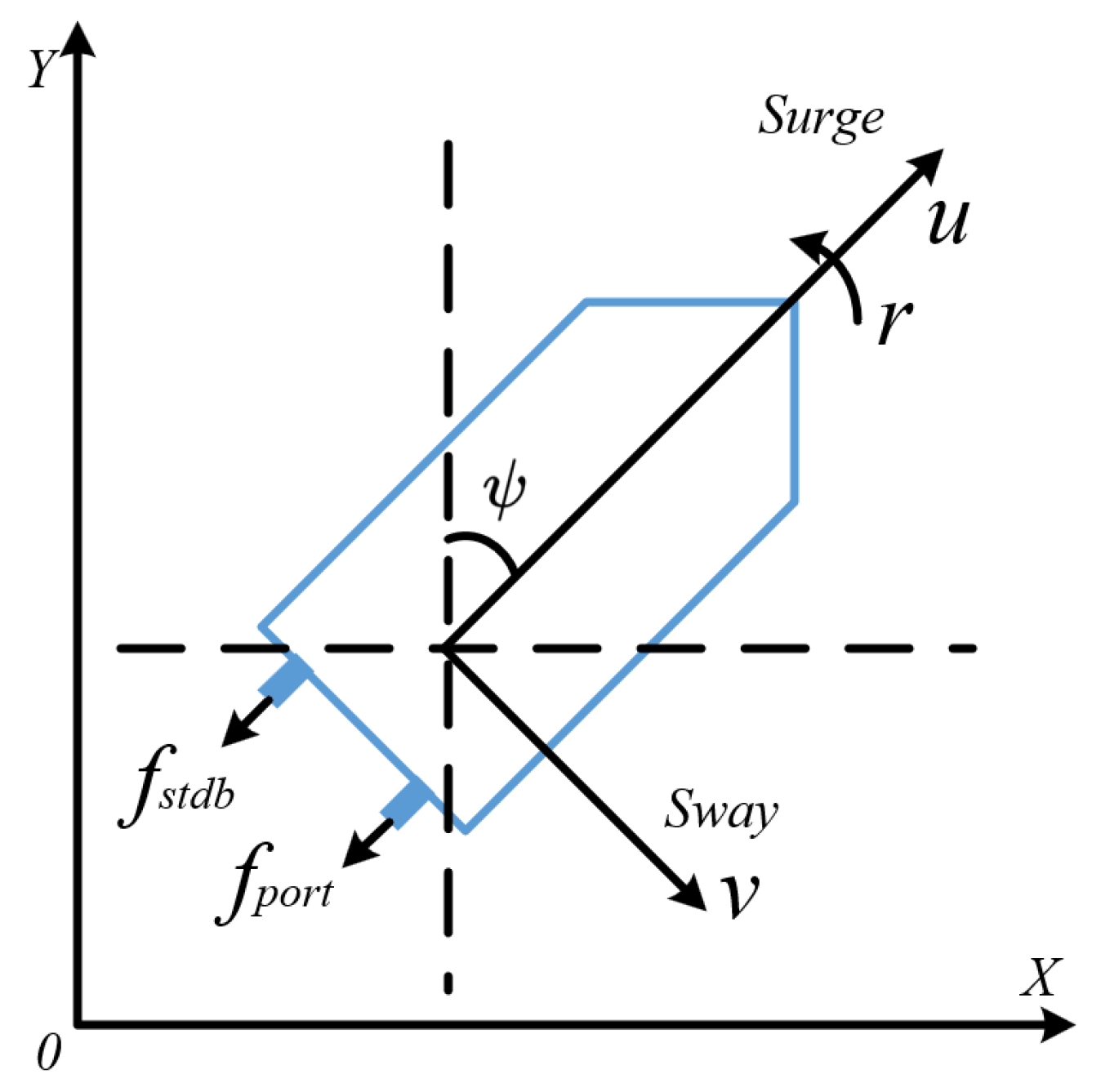
3.3. Dynamic Model
4. Cooperative Formation Control Strategies for Autonomous Surface Vehicles
4.1. Cooperative Formation Control Strategy
4.1.1. Stability Analysis of Consensus Control Strategy
4.1.2. State Control for Cooperative Motion
4.1.3. Cooperative Formation Control Strategy Based on Consensus Theory
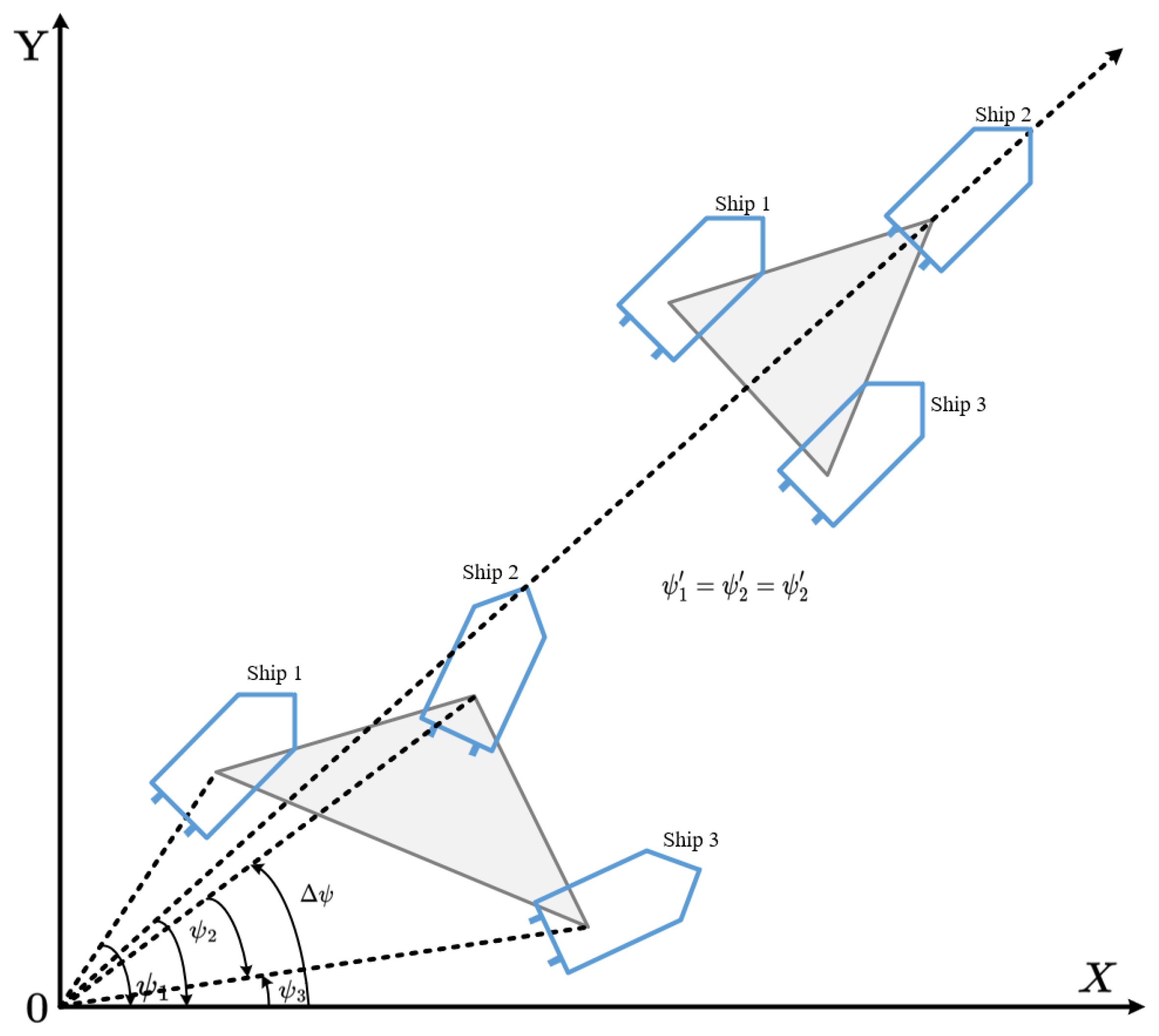
4.1.4. Formation Maintenance and Transformation of ASV Formations
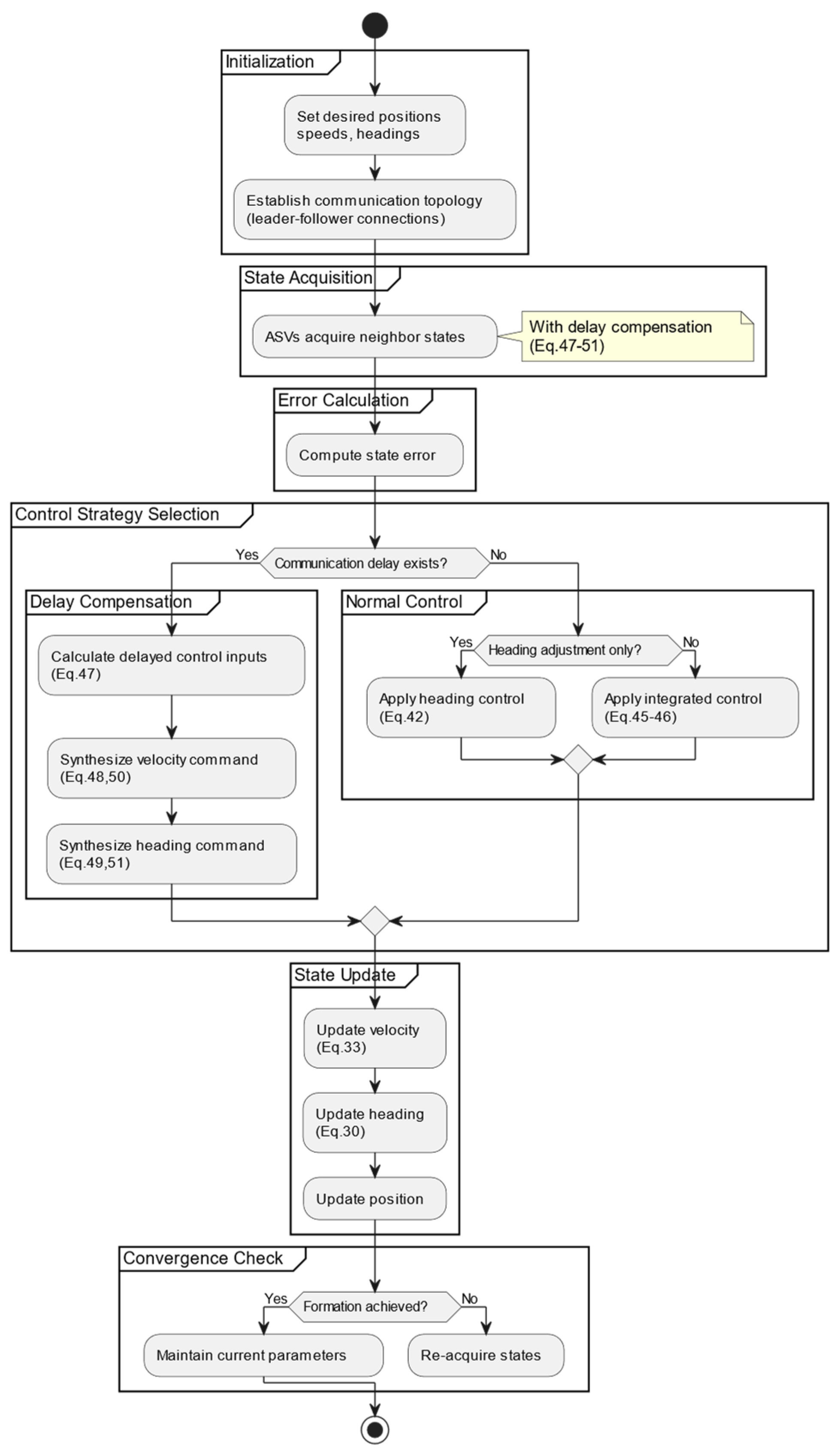
4.2. Cooperative Control Strategies for Formations Under Delay
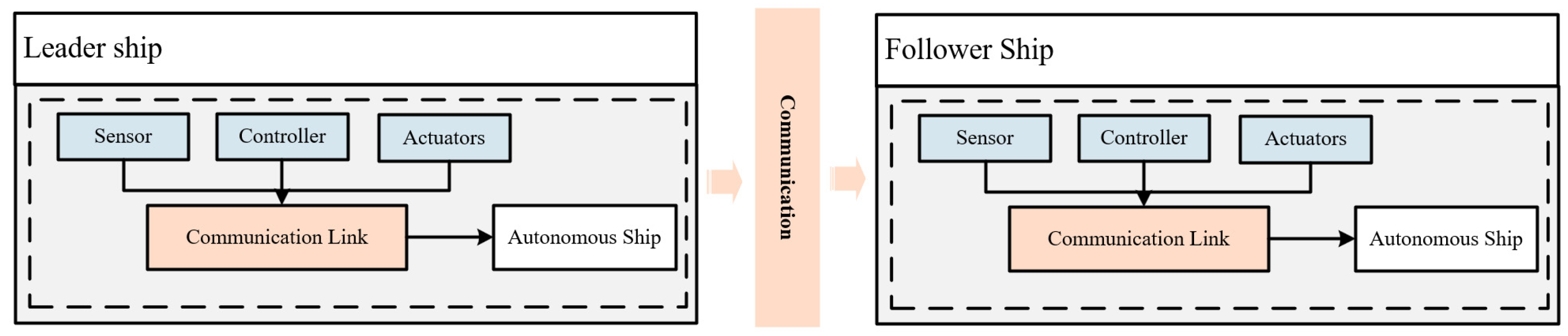
4.2.1. Sources of Communication Delays
4.2.2. Control Strategies for Delayed Formations Based on Consensus Theory
4.2.3. Stability Proof of Cooperative Control Strategies Under Delay
5. Simulation Verification of Multi-ASV Cooperative Formation Control Strategy
5.1. Parameter Selection
5.2. Results and Analysis
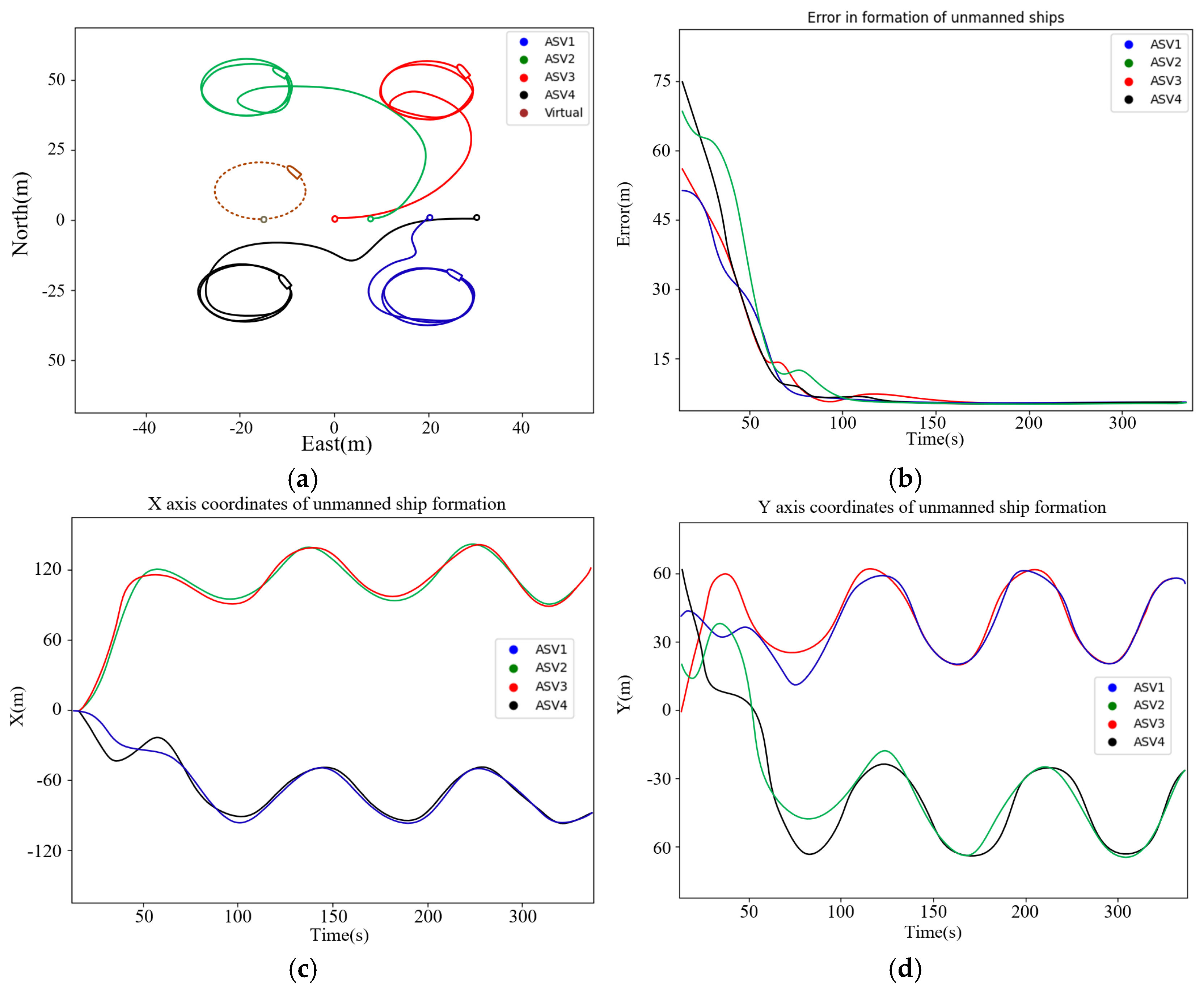
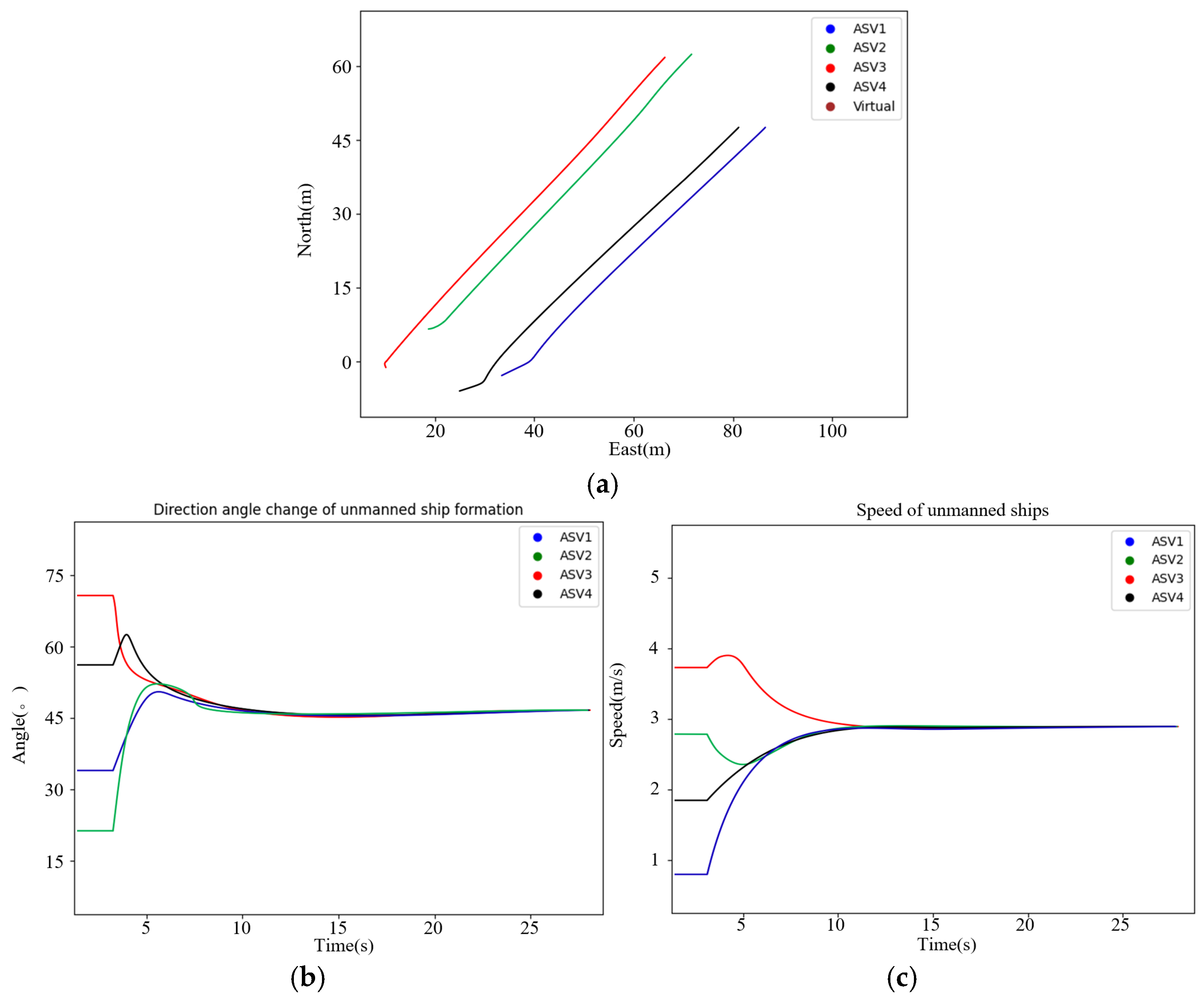
5.2.1. Case I: Circular Cooperative Formation Control
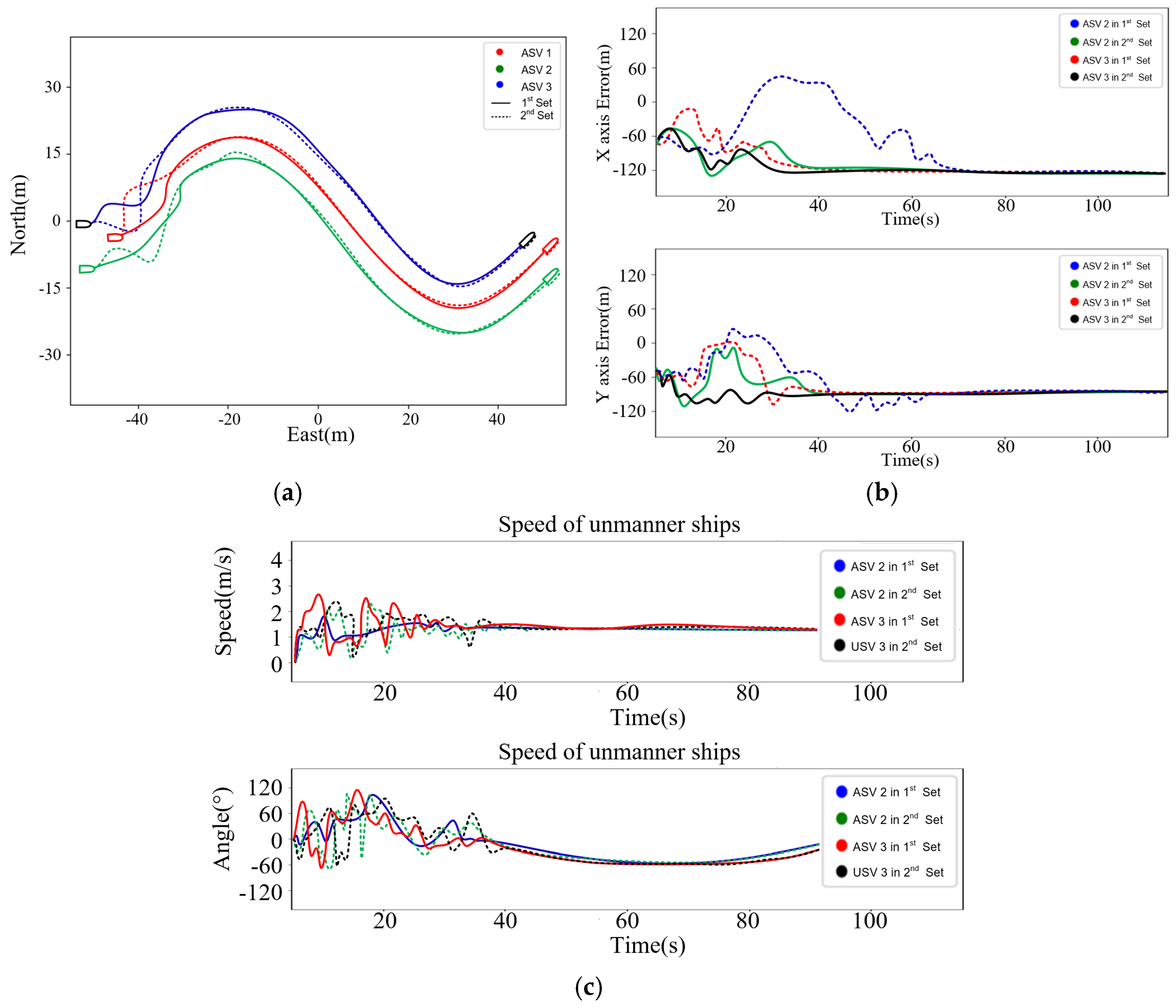
5.2.2. Case II: Cooperative Control Strategy Under Delays
5.2.3. Case III: Sinusoidal Cooperative Formation Control
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Main Symbol | Definition/Description |
| Spatial coordinates of ASV i | |
| The desired relative position between ASV i and the virtual center of the formation | |
| The position and heading vector of the ASV | |
| The velocity vector of the ASV | |
| The heading angle of the ASV | |
| The standard rotation matrix of the ASV | |
| The state information of the i-th ASV | |
| The control input for the i-th ASV | |
| The state variable of information which is the l-th order derivative of xi | |
| The weights of the state variables | |
| The open-loop transfer function matrix of the system | |
| The closed-loop transfer function matrix of the system | |
| Variable gains that measure the influence of the desired formation spacing on the control commands |
References
- Wen, Y.; Tao, W.; Sui, Z.; Piera, M.A.; Song, R. Dynamic model-based method for the analysis of ship behavior in marine traffic situation. Ocean Eng. 2022, 257, 111578. [Google Scholar] [CrossRef]
- Du, B.; Xie, W.; Zhang, W.; Chen, H. A target tracking guidance for unmanned surface vehicles in the presence of obstacles. IEEE Trans. Intell. Transp. Syst. 2023, 25, 4102–4115. [Google Scholar] [CrossRef]
- Zhang, M.; Du, L.; Wen, Y.; Guo, L.; Wu, B. Optimization of ship transport capacity structure for traffic congestion alleviation on inland waterways. Ocean Eng. 2024, 311, 118841. [Google Scholar] [CrossRef]
- Granado, I.; Hernando, L.; Galparsoro, I.; Gabiña, G.; Groba, C.; Prellezo, R.; Fernandes, J.A. Towards a framework for fishing route optimization decision support systems: Review of the state-of-the-art and challenges. J. Clean. Prod. 2021, 320, 128661. [Google Scholar] [CrossRef]
- Bae, I.; Hong, J. Survey on the developments of unmanned marine vehicles: Intelligence and cooperation. Sensors 2023, 23, 4643. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, W.; Zhang, X. Robust control for cooperative path following of marine surface-air vehicles with a constrained inter-vehicles communication. Ocean Eng. 2024, 308, 118240. [Google Scholar] [CrossRef]
- Tao, W.; Zhu, M.; Chen, S.; Cheng, X.; Wen, Y.; Zhang, W.; Negenborn, R.R.; Pang, Y. Coordination and optimization control framework for vessels platooning in inland waterborne transportation system. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15667–15686. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, D.; Han, Q.-L. An overview of recent advances in coordinated control of multiple autonomous surface vehicles. IEEE Trans. Ind. Inform. 2020, 17, 732–745. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A. Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Bunic, M.; Bogdan, S. Potential Function Based Multi-Agent Formation Control in 3D Space. IFAC Proc. Vol. 2012, 45, 682–689. [Google Scholar] [CrossRef]
- Chang, D.; Shadden, S.; Marsden, J.; Olfati-Saber, R. Collision Avoidance for Multiple Agent Systems. In Proceedings of the 42nd IEEE International Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003. [Google Scholar]
- Do, K. Formation Control of Mobile Agents Using Local Potential Functions. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Anh, D.; La, H.; Nguyen, T.; Horn, J. Formation Control for Autonomous Robots with Collision and Obstacle Avoidance Using a Rotational and Repulsive Force–Based Approach. Int. J. Adv. Robot. Syst. 2019, 16, 172988141984789. [Google Scholar]
- Piet, B.; Ablak, M.; Strub, G.; Changey, S.; Petit, N. Experiments of High-Level Formation Flight of a Medium-Scaled Swarm of Micro UAVs in a Confined Environment with Obstacles. In Proceedings of the 2025 AIAA SciTech, Orlando, FL, USA, 6–10 January 2025. [Google Scholar]
- Abbasi, M.; Marquez, H.J. Dynamic Event-Triggered Formation Control of Multi-Agent Systems With Non-Uniform Time-Varying Communication Delays. IEEE Trans. Autom. Sci. Eng. 2024; early access. [Google Scholar]
- Lodhi, Z.A.; Zhang, K. Formation Control of Multi-agent Systems Over Directed Topologies: A Sliding Mode Control Approach With Prescribed-time Convergence. Int. J. Control Autom. Syst. 2024, 22, 3177–3190. [Google Scholar] [CrossRef]
- Cao, X.; Li, K.; Li, Y. Robust adaptive formation control for nonlinear multi-agent systems with range constraints. Nonlinear Dyn. 2024, 112, 1917–1929. [Google Scholar] [CrossRef]
- Epp, M.; Molinari, F.; Raisch, J. Exploiting Over-The-Air Consensus for Collision Avoidance and Formation Control in Multi-Agent Systems. arXiv 2024, arXiv:2403.14386. [Google Scholar]
- Onuoha, O.; Kurawa, S.; Tang, Z.; Dong, Y. Discrete-time stress matrix-based formation control of general linear multi-agent systems. arXiv 2024, arXiv:2401.05083. [Google Scholar]
- Moeurn, S.K. Distributed Cooperative Formation Control of Nonlinear Multi-Agent System (UGV) Using Neural Network. arXiv 2024, arXiv:2403.13473. [Google Scholar]
- Liu, G.-P. Predictive control of networked nonlinear multiagent systems with communication constraints. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4447–4457. [Google Scholar] [CrossRef]
- Zhang, D.-W.; Liu, G.-P.; Cao, L. Proportional integral predictive control of high order fully actuated networked multiagent systems with communication delays. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 801–812. [Google Scholar] [CrossRef]
- Psillakis, H.E. Adaptive NN cooperative control of unknown nonlinear multiagent systems with communication delays. IEEE Access 2021, 51, 5311–5321. [Google Scholar] [CrossRef]
- Qi, T.; Lu, R.; Chen, J. Consensus of continuous-time multiagent systems via delayed output feedback: Delay versus connectivity. IEEE Trans. Autom. Control 2021, 66, 1329–1336. [Google Scholar] [CrossRef]
- Pang, Z.H.; Luo, W.C.; Liu, G.P.; Han, Q.L. Observer-based incremental predictive control of networked multi-agent systems with random delays and packet dropouts. IEEE Trans. Circ. Syst. II Express Briefs 2021, 68, 426–430. [Google Scholar] [CrossRef]
- Liu, G.P. Coordinated control of networked multiagent systems via distributed cloud computing using multistep state predictors. IEEE Trans. Cybern. 2022, 52, 810–820. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Chen, J.; Chen, X.; He, H. Adaptive observer-based output regulation of multiagent systems with communication constraints. IEEE Trans. Cybern. 2021, 51, 5259–5268. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, G.; Zhang, X. DVSL guidance-based composite neural path following control for underactuated cable-laying vessels using event-triggered inputs. Ocean Eng. 2021, 238, 109713. [Google Scholar] [CrossRef]
- Chen, C.; Zou, W.; Xiang, Z. Event-triggered connectivity-preserving formation control of heterogeneous multiple USVs. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7746–7755. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, X.; Luo, G.; Liu, G. A formation control method for AUV group under communication delay. Front. Bioeng. Biotechnol. 2022, 10, 848641. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Li, Y.; Xu, G. Distributed robust prescribed performance 3-D time-varying formation control of underactuated AUVs under input saturations and communication delays. IEEE J. Ocean. Eng. 2023, 48, 649–662. [Google Scholar] [CrossRef]
- Li, J.; Tian, Z.; Zhang, H. Discrete-time AUV formation control with leader-following consensus under time-varying delays. Ocean Eng. 2023, 286, 115678. [Google Scholar] [CrossRef]
- Sadeghzadeh-Nokhodberiz, N.; Meskin, N. Consensus-based distributed formation control of multi-quadcopter systems: Barrier Lyapunov function approach. IEEE Access 2023, 11, 142916–142930. [Google Scholar] [CrossRef]
- Du, Z.; Qu, X.; Shi, J.; Lu, J. Formation control of fixed-wing UAVs with communication delay. ISA Trans. 2024, 146, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Bucknall, R. A survey of formation control and motion planning of multiple unmanned vehicles. Robotica 2018, 36, 1019–1047. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, W.; Zhang, X. ASV formation navigation decision-making through hybrid deep reinforcement learning using self-attention mechanism. Expert Syst. Appl. 2024, 256, 124906. [Google Scholar] [CrossRef]
- Liu, H.; Weng, P.; Tian, X.; Mai, Q. Distributed adaptive fixed-time formation control for UAV-ASV heterogeneous multi-agent systems. Ocean Eng. 2023, 267, 113240. [Google Scholar] [CrossRef]
- Lee, J.H.; Jeong, S.K.; Ji, D.H.; Park, H.Y.; Kim, D.Y.; Choo, K.B.; Jung, D.W.; Kim, M.J.; Oh, M.H.; Choi, H.S. Unmanned surface vehicle using a leader–follower swarm control algorithm. Appl. Sci. 2023, 13, 3120. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L. Coordination control for multiple autonomous surface vehicles using hybrid behavior-based method. Ocean Eng. 2021, 232, 109147. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, M.; Wen, Y.; Sun, W.; Zhang, W.; Lei, T. Formation tracking control for networked heterogeneous MSV systems with actuator faults: A distributed optimal event-triggered fixed-time sliding mode fault-tolerant control approach. Ocean Eng. 2024, 313, 119370. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach. Neurocomputing 2022, 481, 322–332. [Google Scholar] [CrossRef]
- Meng, C.; Zhang, W.; Du, X. Finite-time extended state observer based collision-free leaderless formation control of multiple AUVs via event-triggered control. Ocean Eng. 2023, 268, 113605. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wen, Y.; Tao, W.; Zhu, M.; Zhou, J.; Xiao, C. Characteristic model-based path following controller design for the unmanned surface vessel. Appl. Ocean Res. 2020, 101, 102293. [Google Scholar] [CrossRef]

| Research Article | Type of Vehicles | Number of Vehicles | Communication Constraints | Method | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ASV | AUV | UAV | 3 | 4 | 5 | 6 | Time-Delay | Packet Dropouts | ||
| [22] | ● | ● | ● | ● | Auto-regressive model | |||||
| [23] | ● | ● | ● | Proportional–integral (PI) predictive control | ||||||
| [24] | ● | ● | ● | RBF neural networks | ||||||
| [25] | ● | ● | ● | Rational approximation, based on the Hermite–Feje’r tangential interpolation condition | ||||||
| [26] | ● | ● | ● | Luenberger observer | ||||||
| [27] | ● | ● | ● | Radial basis function (RBF) neural networks, event-triggered | ||||||
| [28] | ● | ● | ● | Consensus theory, adaptive control | ||||||
| [29] | ● | ● | ● | Consensus theory | ||||||
| [30] | ● | ● | ● | ● | Consensus theory | |||||
| [31] | ● | ● | ● | Robust control, observer | ||||||
| [32] | ● | ● | ● | Consensus theory | ||||||
| [33] | ● | ● | ● | ● | Consensus theory | |||||
| Parameter | Value | ||
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| 1 | 0.73, 1.02 | 1st 0.73, 1.02; 2nd 0.93, 1.42. | |
| initial position of ASV 1 | [19, 0] | [36, −5] | [−53, −13, 0] |
| initial position of ASV 2 | [8, 0] | [20, 8] | [−5, −5] |
| initial position of ASV 3 | [0, 0] | [7, −2] | [−53, −2, 0] |
| initial position of ASV 4 | [32, 0] | [23, −8] | [−5, 5] |
| Error | Proposed | DEFSMFC | NONNS | NOETC |
|---|---|---|---|---|
| ea(m) | 7.605 | 10.895 | 10.0975 | 13.3825 |
| eAsv1(m) | 9.73 | 11.91 | 11.39 | 13.51 |
| eAsv2 (m) | 8.60 | 10.63 | 17.6 | 14.38 |
| eAsv3 (m) | 5.31 | 9.81 | 10.31 | 10.73 |
| eAsv4 (m) | 6.78 | 11.23 | 1.090 | 14.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, W.; Tan, J.; Sui, Z.; Wang, L.; Xiong, X. Cooperative Formation Control of Multiple Ships with Time Delay Conditions. J. Mar. Sci. Eng. 2025, 13, 549. https://doi.org/10.3390/jmse13030549
Tao W, Tan J, Sui Z, Wang L, Xiong X. Cooperative Formation Control of Multiple Ships with Time Delay Conditions. Journal of Marine Science and Engineering. 2025; 13(3):549. https://doi.org/10.3390/jmse13030549
Chicago/Turabian StyleTao, Wei, Jian Tan, Zhongyi Sui, Lizheng Wang, and Xin Xiong. 2025. "Cooperative Formation Control of Multiple Ships with Time Delay Conditions" Journal of Marine Science and Engineering 13, no. 3: 549. https://doi.org/10.3390/jmse13030549
APA StyleTao, W., Tan, J., Sui, Z., Wang, L., & Xiong, X. (2025). Cooperative Formation Control of Multiple Ships with Time Delay Conditions. Journal of Marine Science and Engineering, 13(3), 549. https://doi.org/10.3390/jmse13030549






