Optimizing Stack-Yard Positioning in Full Shoreline Loading Operations
Abstract
:1. Introduction
- This paper develops a full-quay container ship loading yard location selection model to dynamically address the location selection problem during the loading process.
- By integrating the COGA and GRASP algorithms, an improved COGA-GRASP algorithm is designed to enhance both solution efficiency and quality.
- Through comparative analysis of different weightings and algorithms, the robustness of the proposed algorithm is validated.
2. Literature Review
2.1. Instruction Optimization
2.2. Scheduling Optimization
2.3. Summary
3. Mathematical Model
3.1. Assumptions
3.2. Symbol Specifications
3.2.1. Dimensions
3.2.2. Model Parameter
3.2.3. Decision Variables
3.3. Objective Function
3.3.1. Yard Channel Instruction Balancing
3.3.2. Quay Crane Instruction Balancing
3.3.3. Model Objective Function
- Normalization of Sub-Objective Functions
- 2.
- Total Objective Function
3.4. Constraint Condition
4. GOGA-GRASP Algorithm
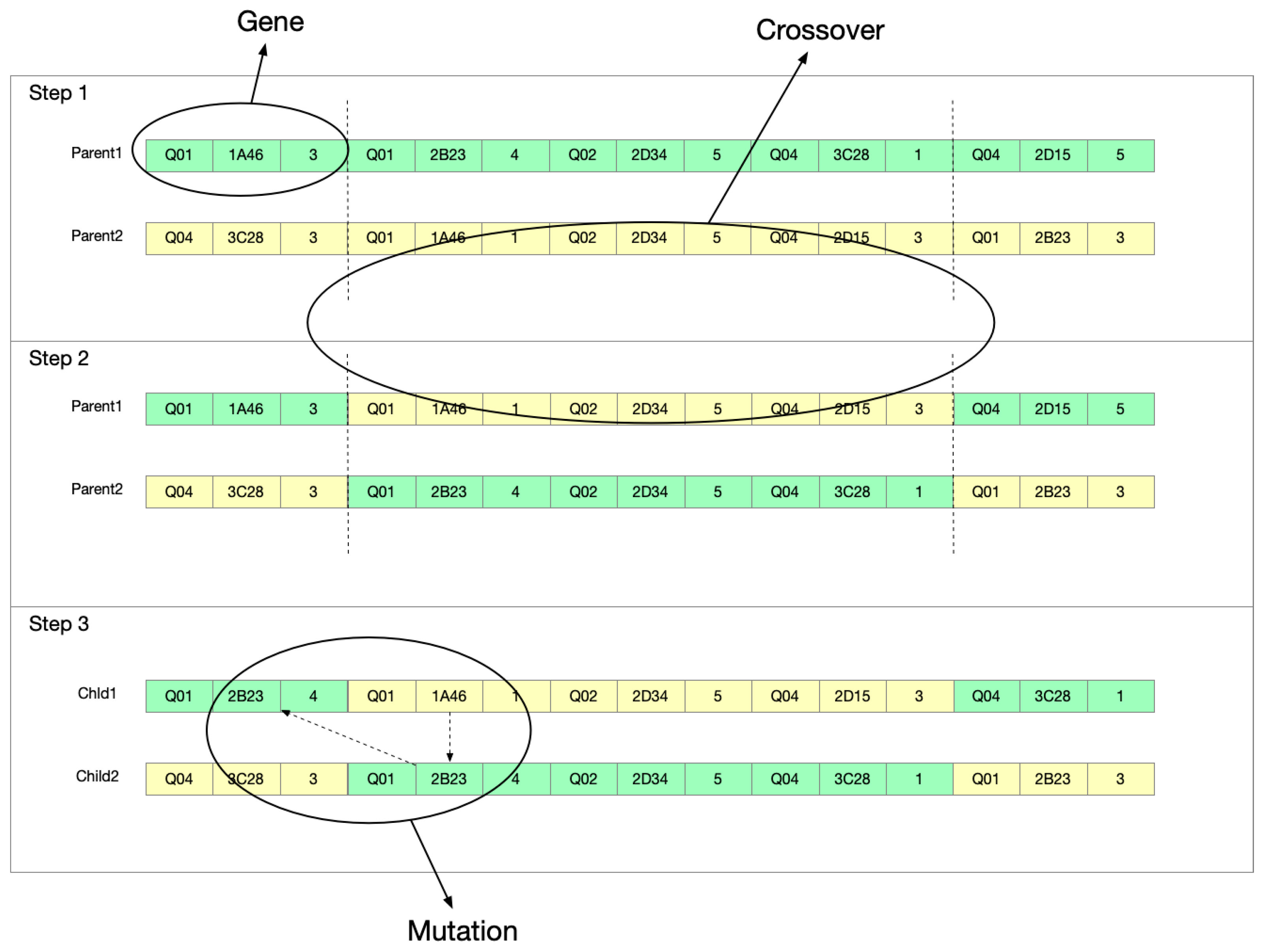
4.1. Gene Coding
4.2. Initial Solution Generation
4.3. Fitness Value
4.4. Select, Crossover and Mutation
5. Experiment
5.1. Experiment Description
5.2. Experiment Analysis
- Using Tournament Selection and Self-adaptive Mutation algorithms, with 100 iterations and population sizes of 50 and 100, the convergence curves are shown in Figure 6. In this example, the fitness function values are calculated with the parameters for loading and unloading instructions in Equations (3) and (6) set to For the total objective function in Equation (9), the parameter values are set to .
- 2.
- Due to the varying emphasis placed on quay crane balance and yard balance by different container terminals, the importance of loading and unloading instructions differs. Therefore, the parameters are set differently. To analyze the impact of different parameters on the algorithm’s convergence, several experiments were conducted, and some of the results are summarized below.
- Experiment 1: The parameters are set as . The fitness value is 0.11975, as shown in Figure 7a.
- Experiment 2: The parameters are set as . The fitness value is 0. 08304 as shown in Figure 7b.
- Experiment 3: The parameters are set as . The fitness value is 0. 07185, as shown in Figure 7c.
- Experiment 4: The parameters are set as . The fitness value is 0. 07185, as shown in Figure 7d.
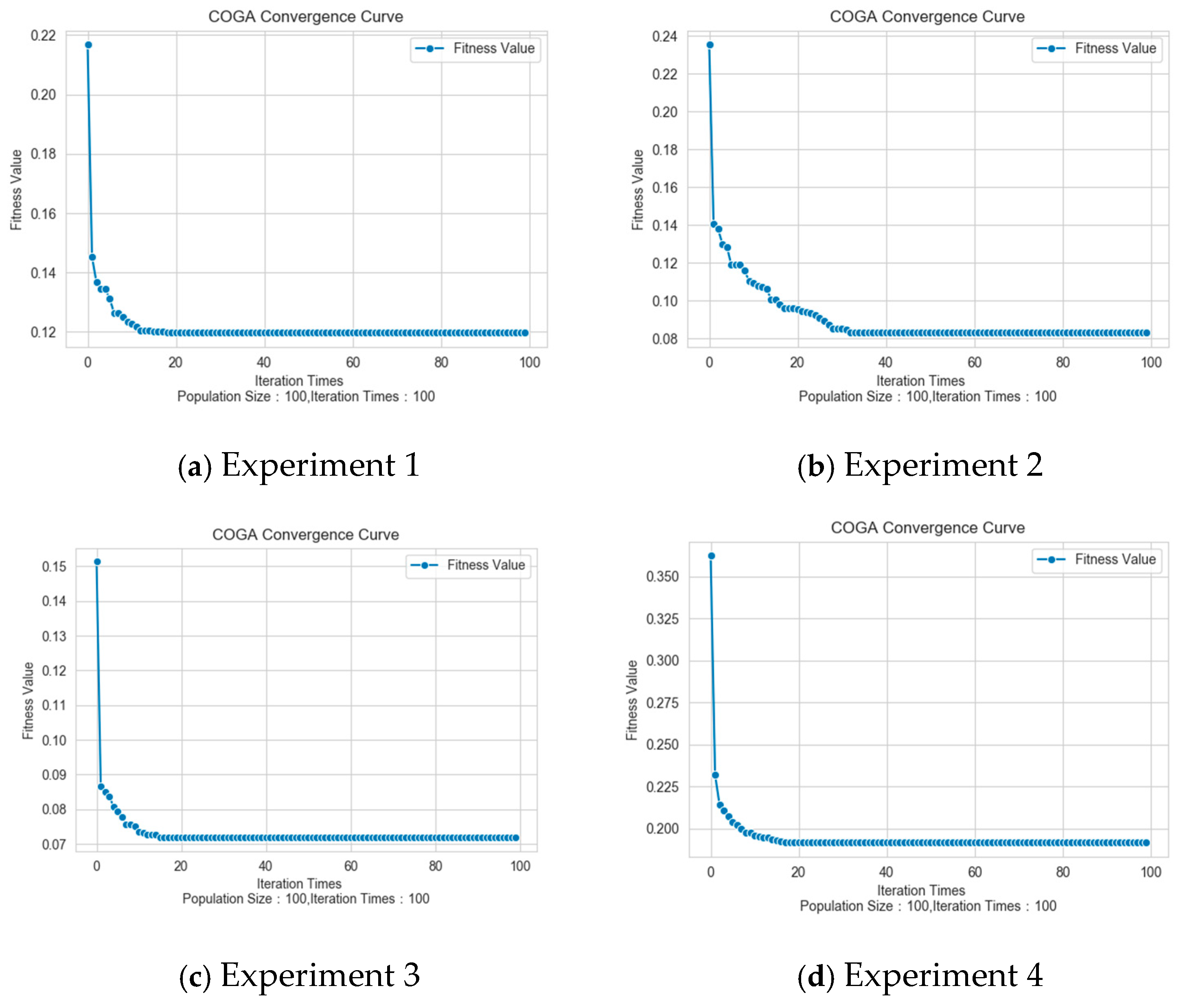
- 3.
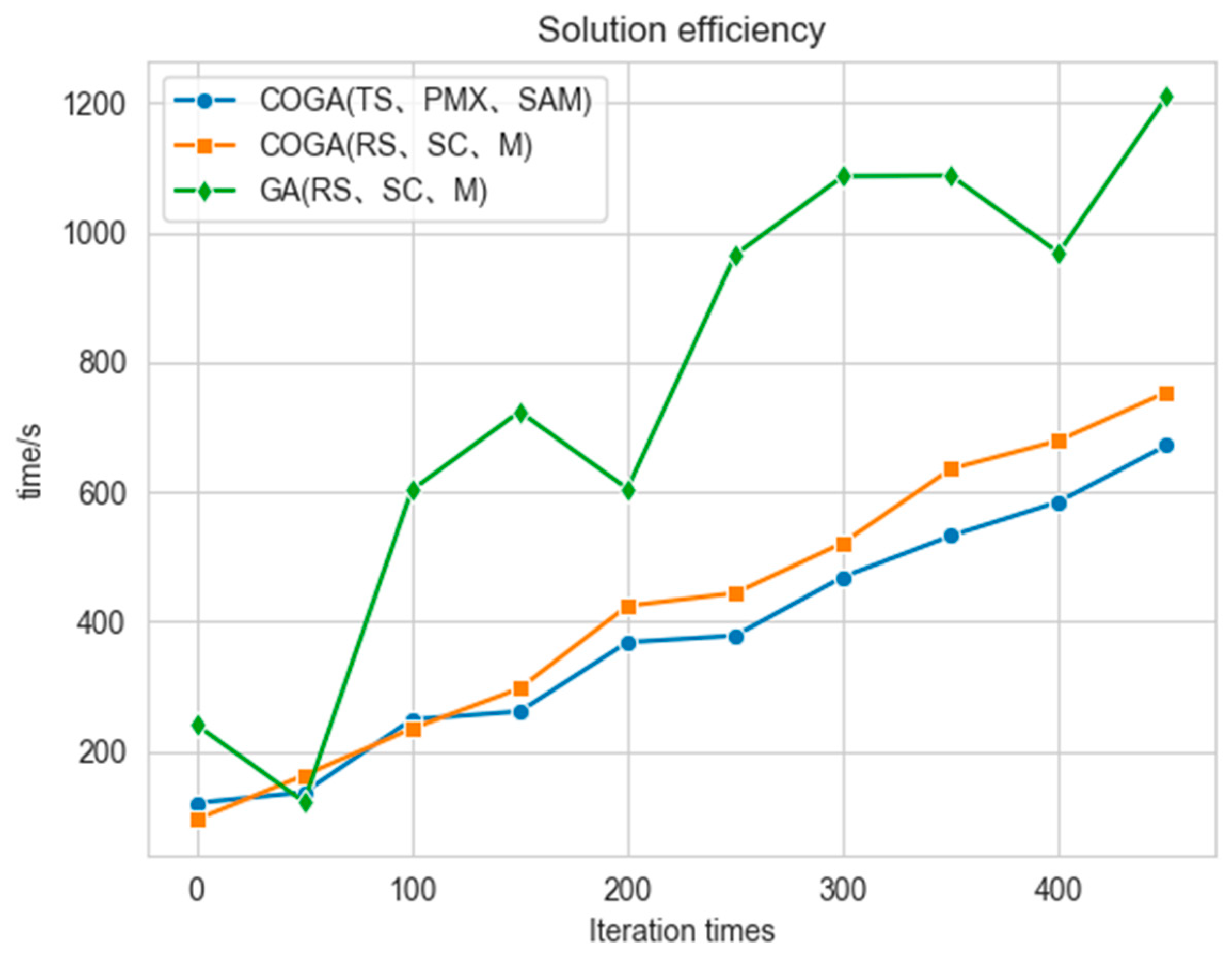
- This paper presents a statistical analysis of different strategies and population sizes, as shown in Figure 8. It can be observed that the COGA algorithm, utilizing Tournament Selection (TS), Partially Matched Crossover (PMX), and Self-Adaptive Mutation (SAM), achieves faster solution speeds and higher solution quality. A comparison between the COGA and GA algorithms indicates that COGA offers higher solving efficiency and greater stability, which is of significant importance for practical production.
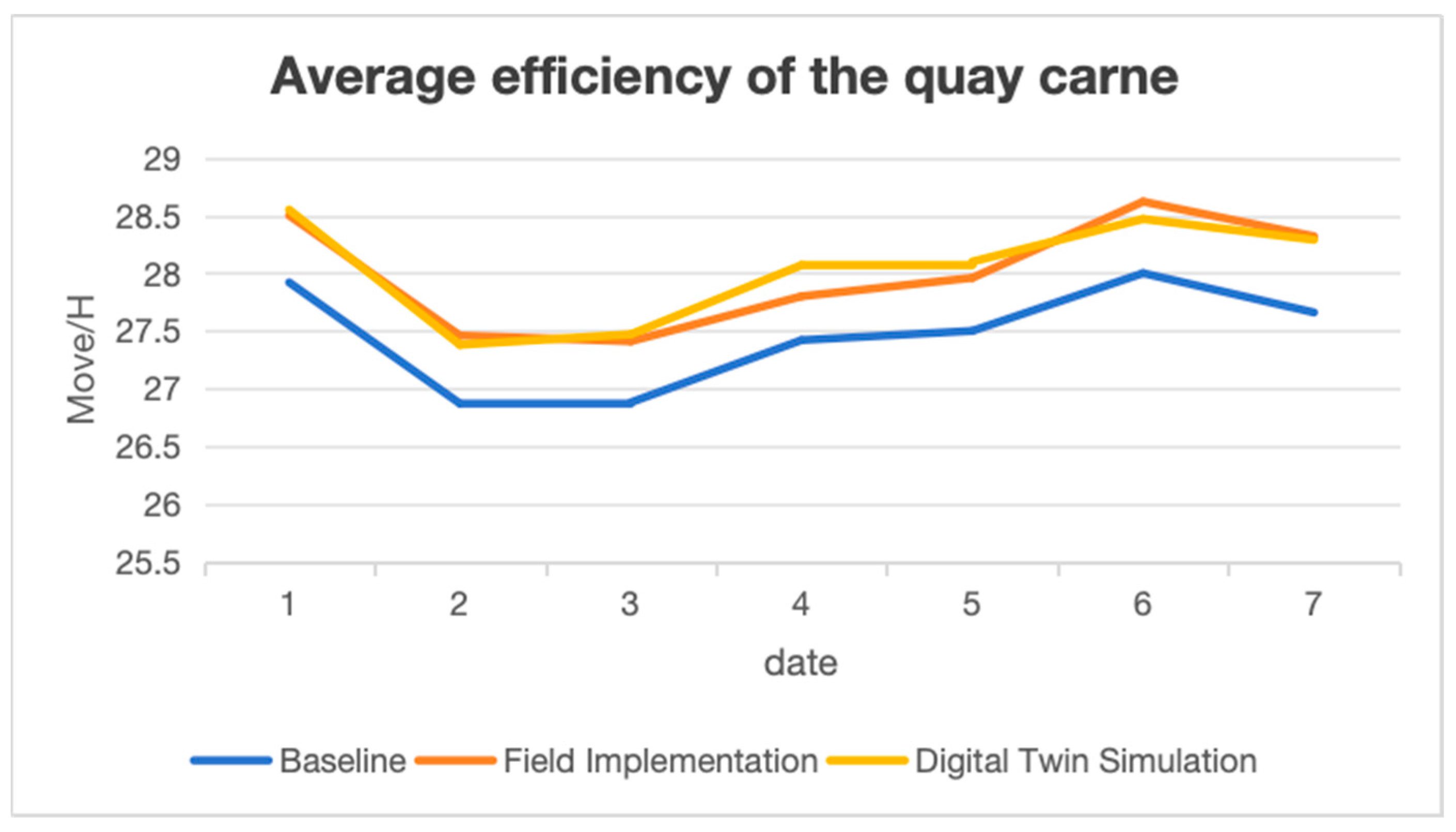
5.3. Applicationt Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wen, B.; Kim, K.H.; Feng, X. Sequencing ship operations considering the trajectory of the quay crane spreader. Transp. Res. Part B Methodol. 2024, 186, 102987. [Google Scholar] [CrossRef]
- Zhou, C.; Yuan, M.; Zhang, J.; Zhang, W. A tree search algorithm for uncertainty-considered consecutive discharging and loading operations between ship and offshore platform. Eur. J. Oper. Res. 2024, 315, 729–749. [Google Scholar] [CrossRef]
- Rahman, M.M.; Jahin, M.A.; Islam, M.S.; Mridha, M.F. Optimizing Container Loading and Unloading through Dual-Cycling and Dock-yard Rehandle Reduction Using a Hybrid Genetic Algorithm. arXiv 2024, arXiv:2406.08534. [Google Scholar]
- Yan, Q.; Song, R.; Kim, K.H.; Wang, Y.; Feng, X. Optimizing container relocation operations by using deep reinforcement learning. Marit. Policy Manag. 2024, 1–23. [Google Scholar] [CrossRef]
- Zhang, Z.; Tan, K.C.; Qin, W.; Chew, E.P.; Li, Y. A data-driven approach to solving the container relocation problem with uncertainties. Adv. Eng. Inform. 2025, 65, 103112. [Google Scholar] [CrossRef]
- Parreño-Torres, C.; Alvarez-Valdes, R.; Ruiz, R.; Tierney, K. Minimizing crane times in pre-marshalling problems. Transp. Res. Part E Logist. Transp. Rev. 2020, 137, 101917. [Google Scholar] [CrossRef]
- Xia, M.; Li, Y.; Shen, Y.; Zhao, N. Loading sequencing problem in container terminal with deep Q-learning. J. Coast. Res. 2020, 103, 817–821. [Google Scholar] [CrossRef]
- Cai, M.D. Intelligent Decision-Making for Multi-Bay Container Loading in Yards Based on Inverse Reinforcement Learning. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2023. [Google Scholar] [CrossRef]
- Xia, M.J. Research on Sequential Decision-Making for Intelligent Ship Control in Container Terminals. Ph.D. Thesis, Shanghai Maritime University, Shanghai, China, 2021. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H. Dynamic scheduling and path planning of automated guided vehicles in automatic container terminal. IEEE/CAA J. Autom. Sin. 2022, 9, 2005–2019. [Google Scholar] [CrossRef]
- Fibrianto, H.Y.; Kang, B.; Hong, S. A job sequencing problem of an overhead shuttle crane in a rail-based automated container terminal. IEEE Access 2020, 8, 156362–156377. [Google Scholar] [CrossRef]
- Oladugba, A.O.; Gheith, M.; Eltawil, A. A new solution approach for the twin yard crane scheduling problem in automated container terminals. Adv. Eng. Inform. 2023, 57, 102015. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Yan, B.; Zhang, X. Optimization approach for yard crane scheduling problem with uncertain parameters in container terminals. J. Adv. Transp. 2021, 2021, 5537114. [Google Scholar] [CrossRef]
- Yu, M.; Liang, Z.; Teng, Y.; Zhang, Z.; Cong, X. The inbound container space allocation in the automated container terminals. Expert Syst. Appl. 2021, 179, 115014. [Google Scholar] [CrossRef]
- Yang, X.; Hu, H.; Jin, J.; Luo, N. Joint optimization of space allocation and yard crane deployment in container terminal under uncertain demand. Comput. Ind. Eng. 2022, 172, 108425. [Google Scholar] [CrossRef]
- Gulić, M.; Maglić, L.; Krljan, T.; Maglić, L. Solving the container relocation problem by using a metaheuristic genetic algorithm. Appl. Sci. 2022, 12, 7397. [Google Scholar] [CrossRef]
- Yang, X.; Hu, H.; Cheng, C.; Wang, Y. Automated guided vehicle (agv) scheduling in automated container terminals (acts) focusing on battery swapping and speed control. J. Mar. Sci. Eng. 2023, 11, 1852. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Zhou, Y.; Wang, H.; Fan, H. A hybrid dynamic method for conflict-free integrated schedule optimization in U-shaped automated container terminals. J. Mar. Sci. Eng. 2022, 10, 1187. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q. A branch-and-bound approach for AGV dispatching and routing problems in automated container terminals. Comput. Ind. Eng. 2022, 166, 107968. [Google Scholar] [CrossRef]
- Lu, Y. The Three-Stage Integrated Optimization of Automated Container Terminal Scheduling Based on Improved Genetic Algorithm. Math. Probl. Eng. 2021, 2021, 67921. [Google Scholar] [CrossRef]
- Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2021, 20, 89–104. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Scheduling of container-handling equipment during the loading process at an automated container terminal. Comput. Ind. Eng. 2020, 149, 106848. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Hong, S. An exact algorithm for multiple-equipment integrated scheduling in an automated container terminal using a double-cycling strategy. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103565. [Google Scholar] [CrossRef]
- Yin, Y.Q.; Zhong, M.; Wen, X.; Ge, Y.E. Scheduling quay cranes and shuttle vehicles simultaneously with limited apron buffer capacity. Comput. Oper. Res. 2023, 151, 106096. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Ma, M. Optimizing configuration and scheduling of double 40 ft dual-trolley quay cranes and AGVs for improving container terminal services. J. Clean. Prod. 2021, 292, 126019. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, M.; He, J.; Tan, C. Choice of loading clusters in container terminals. Adv. Eng. Inform. 2020, 46, 101190. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, M.; Wang, Z.; Xiao, Y. A Genetic Algorithm for Integrated Scheduling of Container Handing Systems at Container Terminals from a Low-Carbon Operations Perspective. Sustainability 2023, 15, 6035. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Tan, C.; Yu, H. Modeling berth allocation and quay crane assignment considering QC driver cost and operating efficiency. Adv. Eng. Inform. 2021, 47, 101252. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Yang, Y.; Wen, F.; Song, H. Integrated scheduling optimization of U-shaped automated container terminal under loading and unloading mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, N.; de Waal, A.; Negenborn, R.R. Coordinated optimization of equipment operations in a container terminal. Flex. Serv. Manuf. J. 2021, 33, 281–311. [Google Scholar] [CrossRef]
- Lu, Y. The optimization of automated container terminal scheduling based on proportional fair priority. Math. Probl. Eng. 2022, 2022, 7889048. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, C.H.; Chang, D. A machine learning-based approach for multi-agv dispatching at automated container terminals. J. Mar. Sci. Eng. 2023, 11, 1407. [Google Scholar] [CrossRef]
- Cahyono, R.T.; Kenaka, S.P.; Jayawardhana, B. Simultaneous allocation and scheduling of quay cranes, yard cranes, and trucks in dynamical integrated container terminal operations. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8564–8578. [Google Scholar] [CrossRef]
- Shouwen, J.; Di, L.; Zhengrong, C.; Dong, G. Integrated scheduling in automated container terminals considering AGV conflict-free routing. Transp. Lett. 2021, 13, 501–513. [Google Scholar] [CrossRef]
- Hsu, H.P.; Wang, C.N.; Fu, H.P.; Dang, T.T. Joint scheduling of yard crane, yard truck, and quay crane for container terminal considering vessel stowage plan: An integrated simulation-based optimization approach. Mathematics 2021, 9, 2236. [Google Scholar] [CrossRef]
- Gong, L.; Huang, Z.; Xiang, X.; Liu, X. Real-time AGV scheduling optimisation method with deep reinforcement learning for energy-efficiency in the container terminal yard. Int. J. Prod. Res. 2024, 62, 7722–7742. [Google Scholar] [CrossRef]
- Xin, J.; Meng, C.; D’Ariano, A.; Wang, D.; Negenborn, R.R. Mixed-integer nonlinear programming for energy-efficient container handling: Formulation and customized genetic algorithm. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10542–10555. [Google Scholar] [CrossRef]
- Wang, T.; Gao, G.; Wang, K.; Shi, J. Integrated operation models with quay crane maintenance in a container terminal. Ocean Coast. Manag. 2024, 251, 107101. [Google Scholar] [CrossRef]
- Shen, Z.; Liang, C.; Gen, M. Scheduling of AGV with group operation area in automated terminal by hybrid genetic algorithm. In Proceedings of the Fifteenth International Conference on Management Science and Engineering Management, Toledo, Spain, 2–3 August 2021; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; Volume 115, pp. 427–442. [Google Scholar]
- Fan, H.; Peng, W.; Ma, M.; Yue, L. Storage space allocation and twin automated stacking cranes scheduling in automated container terminals. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14336–14348. [Google Scholar] [CrossRef]
- Jian, W.; Zhu, J.; Zeng, Q. An Optimization Model of Integrated AGVs Scheduling and Container Storage Problems for Automated Container Terminal Considering Uncertainty. Symmetry 2021, 13, 1904. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Wang, S. Multiple equipment scheduling and AGV trajectory generation in U-shaped sea-rail intermodal automated container terminal. Measurement 2023, 206, 112262. [Google Scholar] [CrossRef]
- Hsu, H.P.; Wang, C.N.; Nguyen, T.T.T.; Dang, T.T.; Pan, Y.J. Hybridizing WOA with PSO for coordinating material handling equipment in an automated container terminal considering energy consumption. Adv. Eng. Inform. 2024, 60, 102410. [Google Scholar] [CrossRef]
- Fontes, D.B.M.M.; Homayouni, S.M. A bi-objective multi-population biased random key genetic algorithm for joint scheduling quay cranes and speed adjustable vehicles in container terminals. Flex. Serv. Manuf. J. 2023, 35, 241–268. [Google Scholar]
- Hsu, H.P.; Tai, H.H.; Wang, C.N.; Chou, C.C. Scheduling of collaborative operations of yard cranes and yard trucks for export containers using hybrid approaches. Adv. Eng. Inform. 2021, 48, 101292. [Google Scholar] [CrossRef]




| Algorithm Type | Literature | Key Features |
|---|---|---|
| Genetic Algorithm (GA) and Variants | [1,3,8,11,12,13,14,16,17,18,20,22,23,25,27,29,31,34,37,38,39,40,41,44] | Includes standard GA, hybrid GA (e.g., embedded tabu search), adaptive GA, multi-objective GA (e.g., NSGA-III), etc. |
| Swarm Intelligence Algorithms | [21] (MOBCO), [30] (Simulated Annealing), [35] (PSO/MGPSO), [36] (MADDPG), [43] (WOA+PSO), [45] (GA/PSO/SGPSO) | Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), Bacterial Colony Optimization (BCO), etc., often used for multi-objective problems. |
| Deep Reinforcement Learning (DRL) | [4,7,36] | Combines deep learning and reinforcement learning for dynamic decision-making (e.g., container loading sequences, AGV scheduling). |
| Tree Search Algorithms | [2] (tabu-based tree search), [5] (Monte Carlo Tree Search) | Tree-structured search strategies with heuristic rules or probabilistic extensions. |
| Exact Algorithms and Decomposition Methods | [6] (Branch-and-Bound)], [19] (Branch-and-Bound), [23] (Benders Decomposition), [28] (Mixed-Integer Programming)] | Suitable for small-scale problems or model decomposition (e.g., accelerated convergence). |
| Hybrid Heuristic Algorithms | [10] (Dijkstra + Q-Learning), [15] (tabu list), [24] (sequence insertion+ greedy insertion), [33] (Model Predictive Control), [42] (Spatiotemporal Greedy Strategy) | Integrates rules, graph theory, or simulation optimization to address complex constraints (e.g., path conflicts, dynamic scheduling). |
| other | [9] (sequential decision), [26] (not explicitly mentioned), [32] (Gurobi solver) |
| Symbol | Description |
|---|---|
| ; | |
| Symbol | Description |
|---|---|
| (−1: unloading, 0: simultaneous, 1: loading) | |
| ; | |
| belong to the same vessel bay | |
| Total number of containers requiring operations | |
| Total number of quay cranes | |
| Total number of channels | |
| in the same column | |
| belong to the same channel |
| ...Function GreedyRandomInitializePopulation() ← Empirical design S ← S + While S.size ≤ Initial population size do n ← GreedyRandomSelection(seed) If n Satisfy constraint S ← S + n End While Return S Function GreedyRandomSelection(seed) Based on seed, generate a list of potential solutions in a greedy manner Randomly select a solution from the list Return selected solution |
| Function PMX () random select 2 individual random select 2 index remove duplication Return |
| Population Size:50 | Population Size: 100 | ||||
|---|---|---|---|---|---|
| Quay INS | Yard INS | Fitness Value | Quay INS | Yard INS | Fitness Value |
| Q01:21: 19 | 3B:18:45 | 0.0958 | Q01:20:19 | 3B:22:45 | 0.0944 |
| Q02:21: 14 | 3A:36:20 | Q02:20: 14 | 3A:36: 20 | ||
| Q03:21: 15 | 2B:38: 30 | Q03:20: 15 | 2B:38: 30 | ||
| Q04:21: 15 | 1A:34:19 | Q04:20: 15 | 1A:22: 19 | ||
| Q05: 21: 0 | 2A:42:34 | Q05: 20: 0 | 2A:35: 34 | ||
| Q06:21: 12 | 1C:26: 46 | Q06:20: 12 | 1C:26: 46 | ||
| Q07:21: 15 | 3C:38: 32 | Q07:20: 15 | 3C:39: 32 | ||
| Q08:21: 15 | 2C:29: 24 | Q08:20: 15 | 1B:33: 39 | ||
| Q09: 21: 4 | 1B:27: 39 | Q09: 20: 4 | 2C:22: 24 | ||
| Q10: 21: 16 | Q10: 20: 16 | ||||
| Q11: 21: 4 | Q11: 20: 4 | ||||
| Q12: 21: 10 | Q12: 20: 10 | ||||
| Q13: 21: 6 | Q13: 20: 6 | ||||
| Q14: 21: 5 | Q14: 20: 5 | ||||
| Q15: 21: 4 | Q15: 20: 4 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Luo, B.; Wang, J.; Zhao, J.; Li, D.; Sun, Q.; Li, H. Optimizing Stack-Yard Positioning in Full Shoreline Loading Operations. J. Mar. Sci. Eng. 2025, 13, 593. https://doi.org/10.3390/jmse13030593
Du X, Luo B, Wang J, Zhao J, Li D, Sun Q, Li H. Optimizing Stack-Yard Positioning in Full Shoreline Loading Operations. Journal of Marine Science and Engineering. 2025; 13(3):593. https://doi.org/10.3390/jmse13030593
Chicago/Turabian StyleDu, Xueqiang, Bencheng Luo, Jing Wang, Jieting Zhao, Dahai Li, Qian Sun, and Haobin Li. 2025. "Optimizing Stack-Yard Positioning in Full Shoreline Loading Operations" Journal of Marine Science and Engineering 13, no. 3: 593. https://doi.org/10.3390/jmse13030593
APA StyleDu, X., Luo, B., Wang, J., Zhao, J., Li, D., Sun, Q., & Li, H. (2025). Optimizing Stack-Yard Positioning in Full Shoreline Loading Operations. Journal of Marine Science and Engineering, 13(3), 593. https://doi.org/10.3390/jmse13030593





