Mechanical Evaluation of Casing in Multiple Thermal Recovery Cycles for Offshore Heavy Oil Wells
Abstract
1. Introduction
2. Materials and Experiments
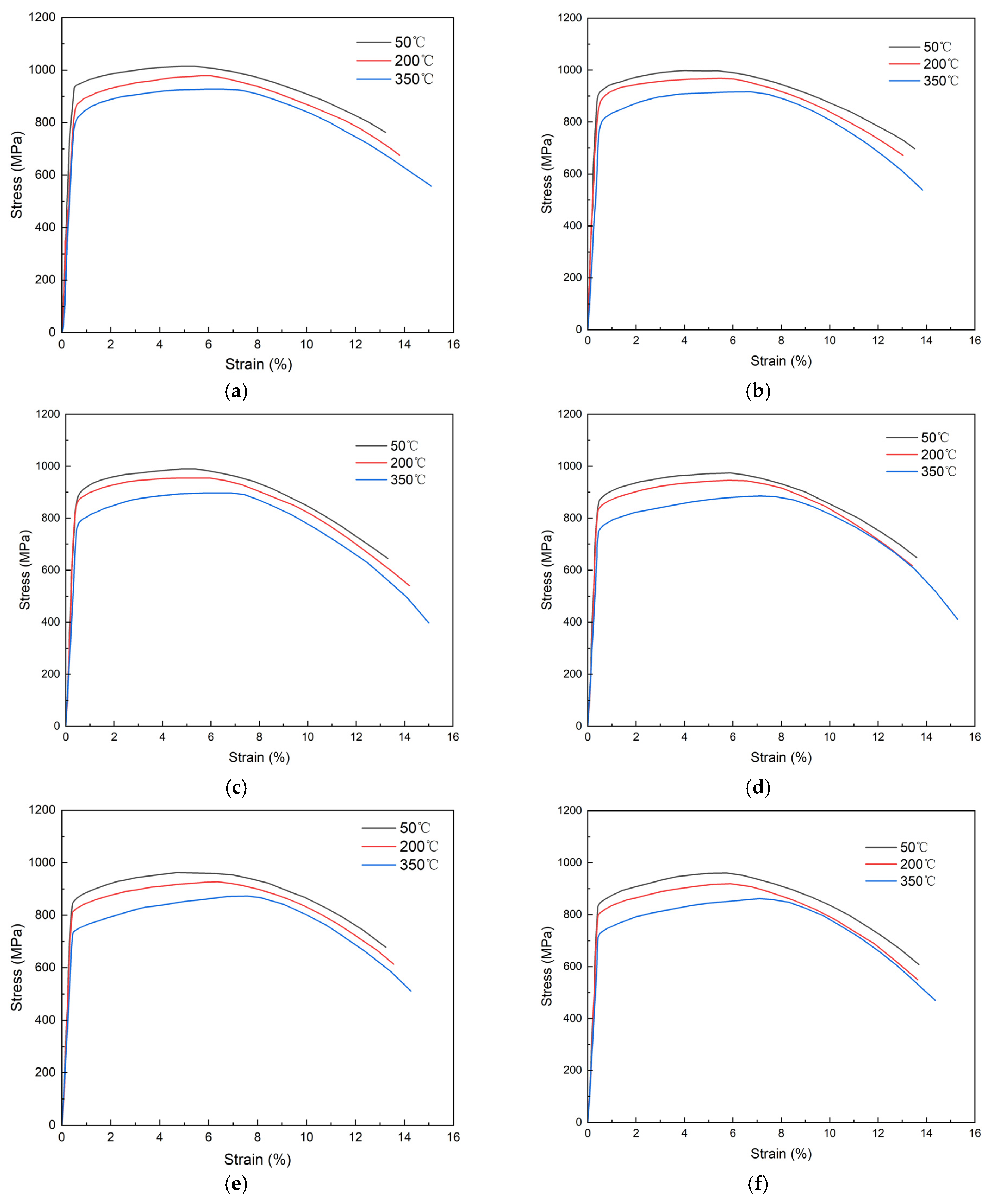
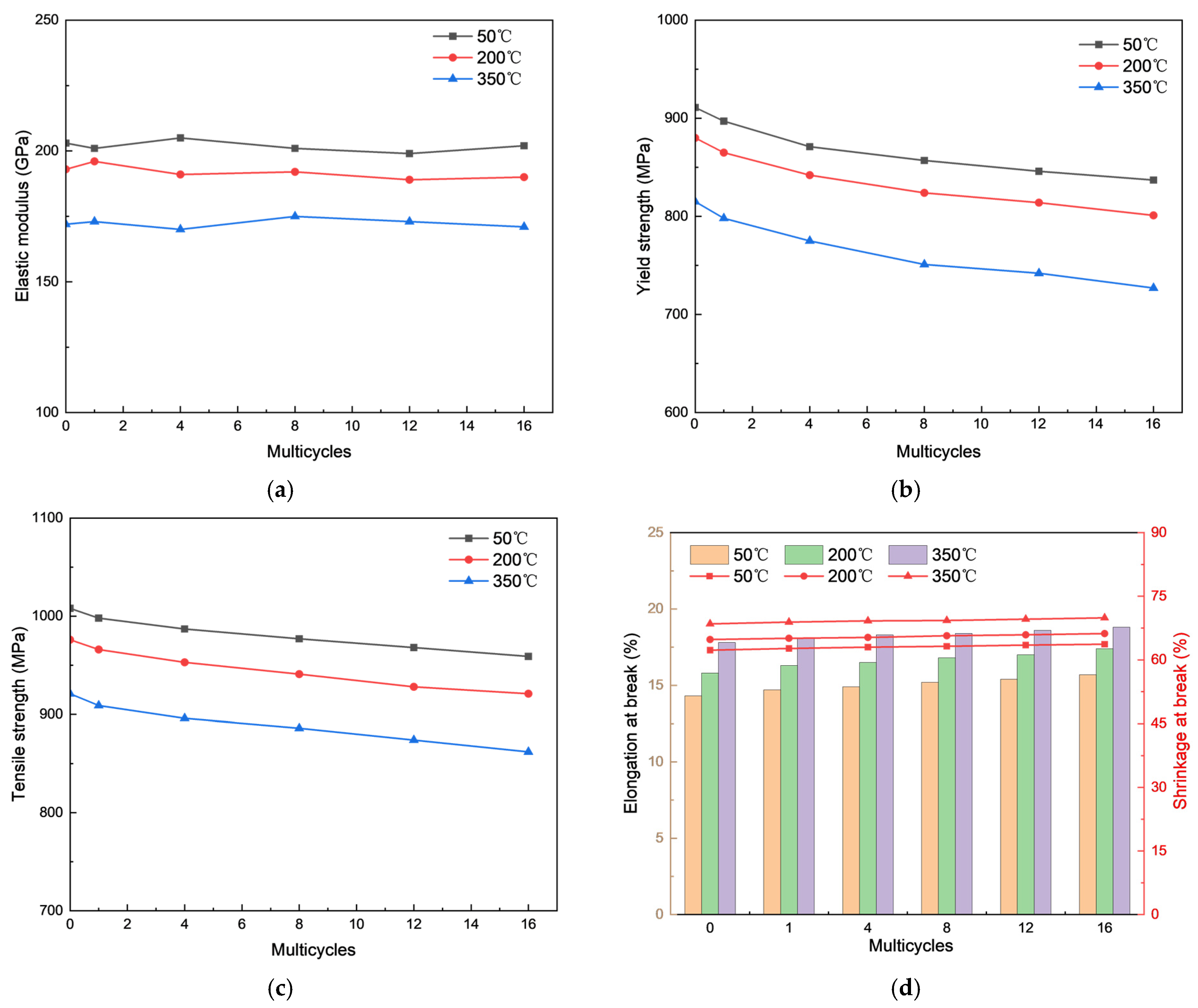
2.1. Tensile Experiment
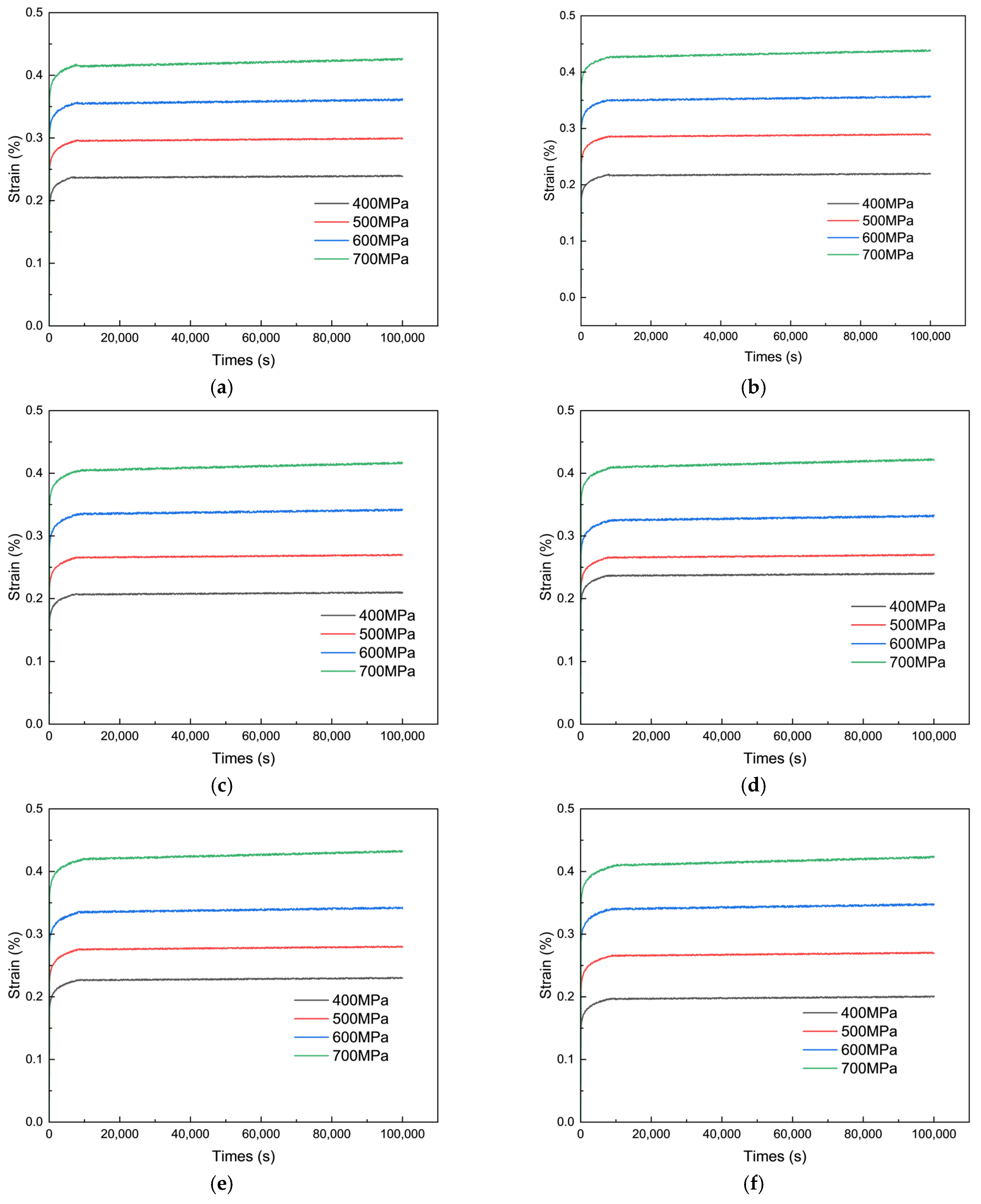
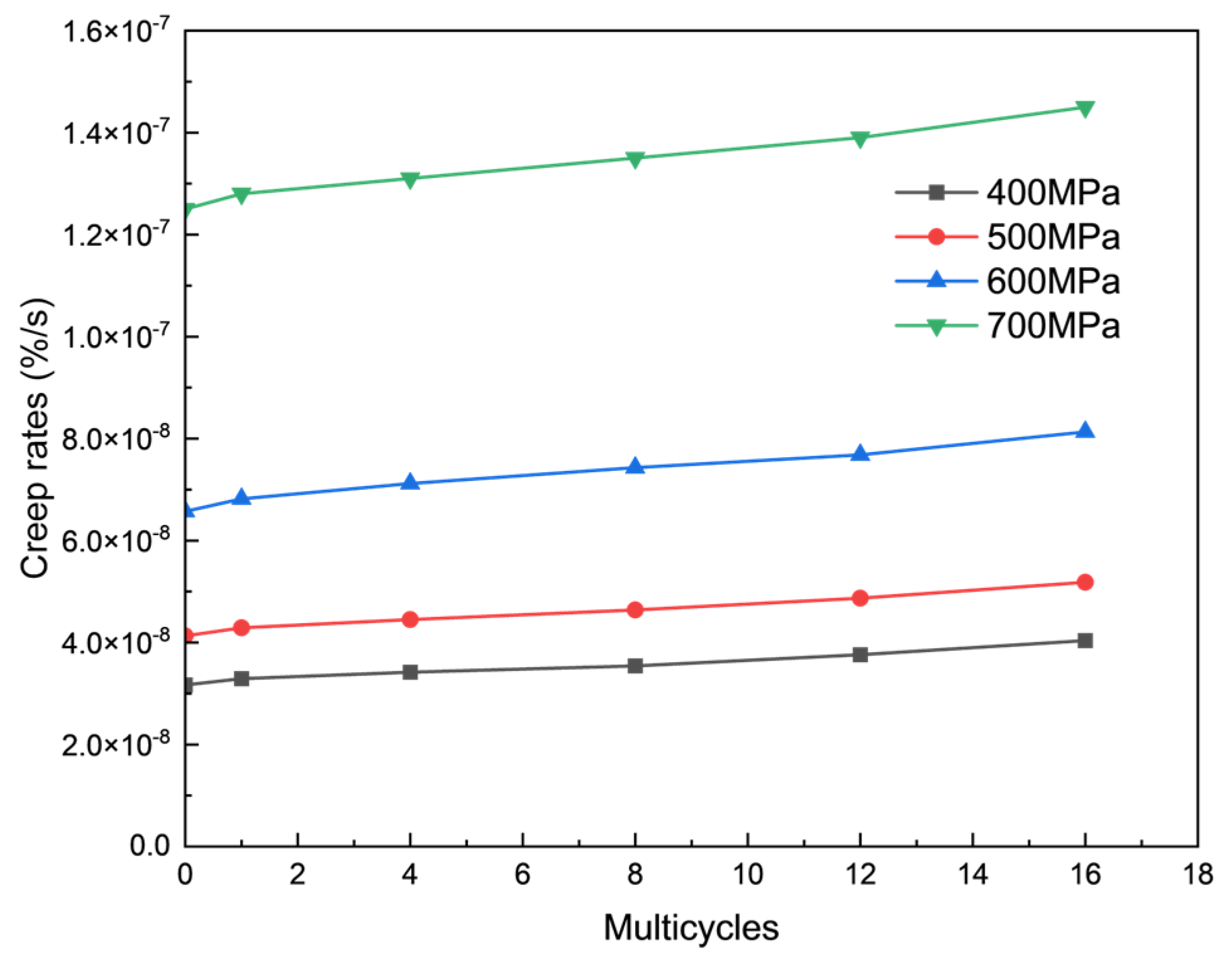
2.2. Creep Experiment
3. Temperature Stress Analysis of Wellbore in Thermal Wells
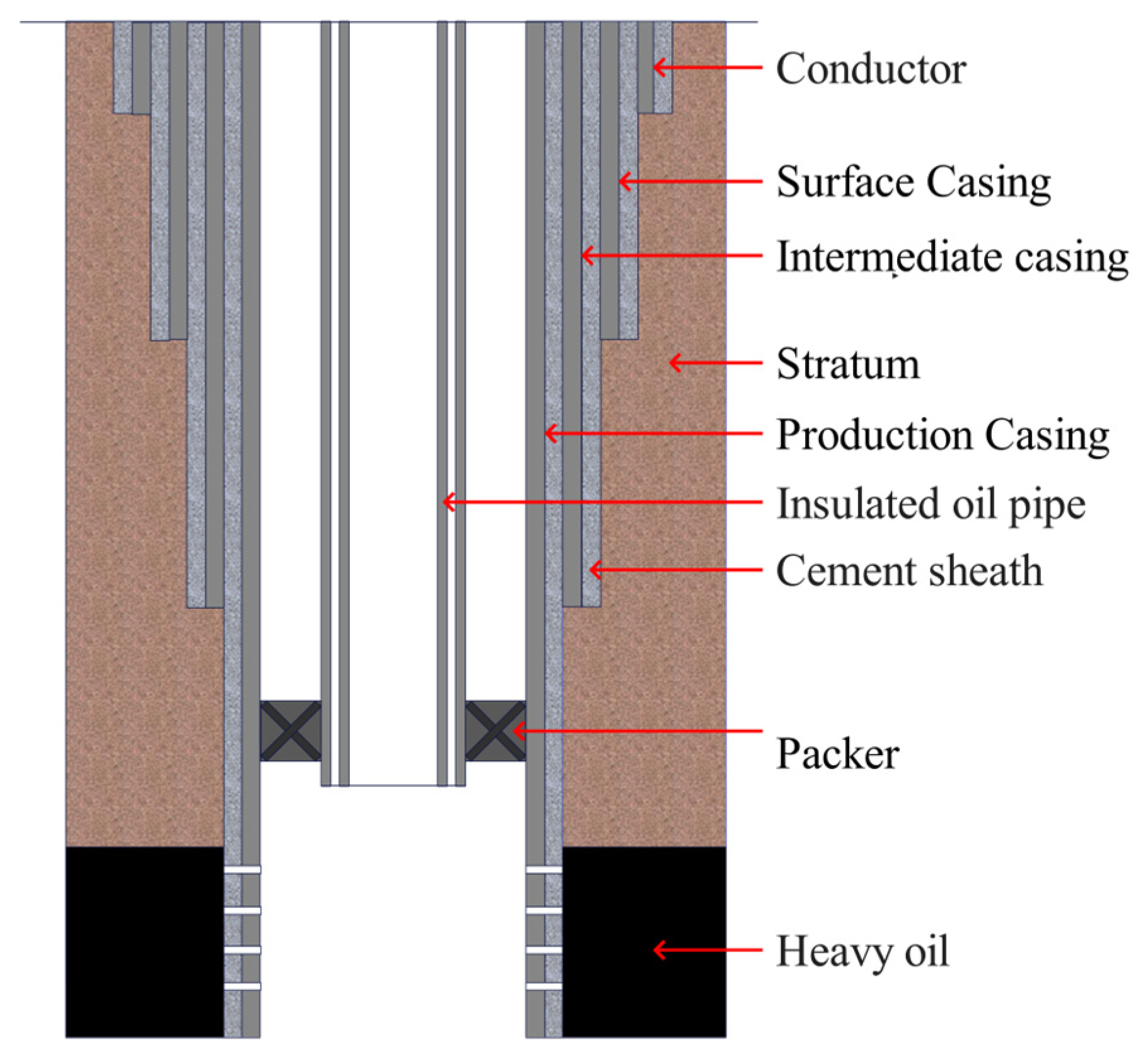
3.1. Well Structure
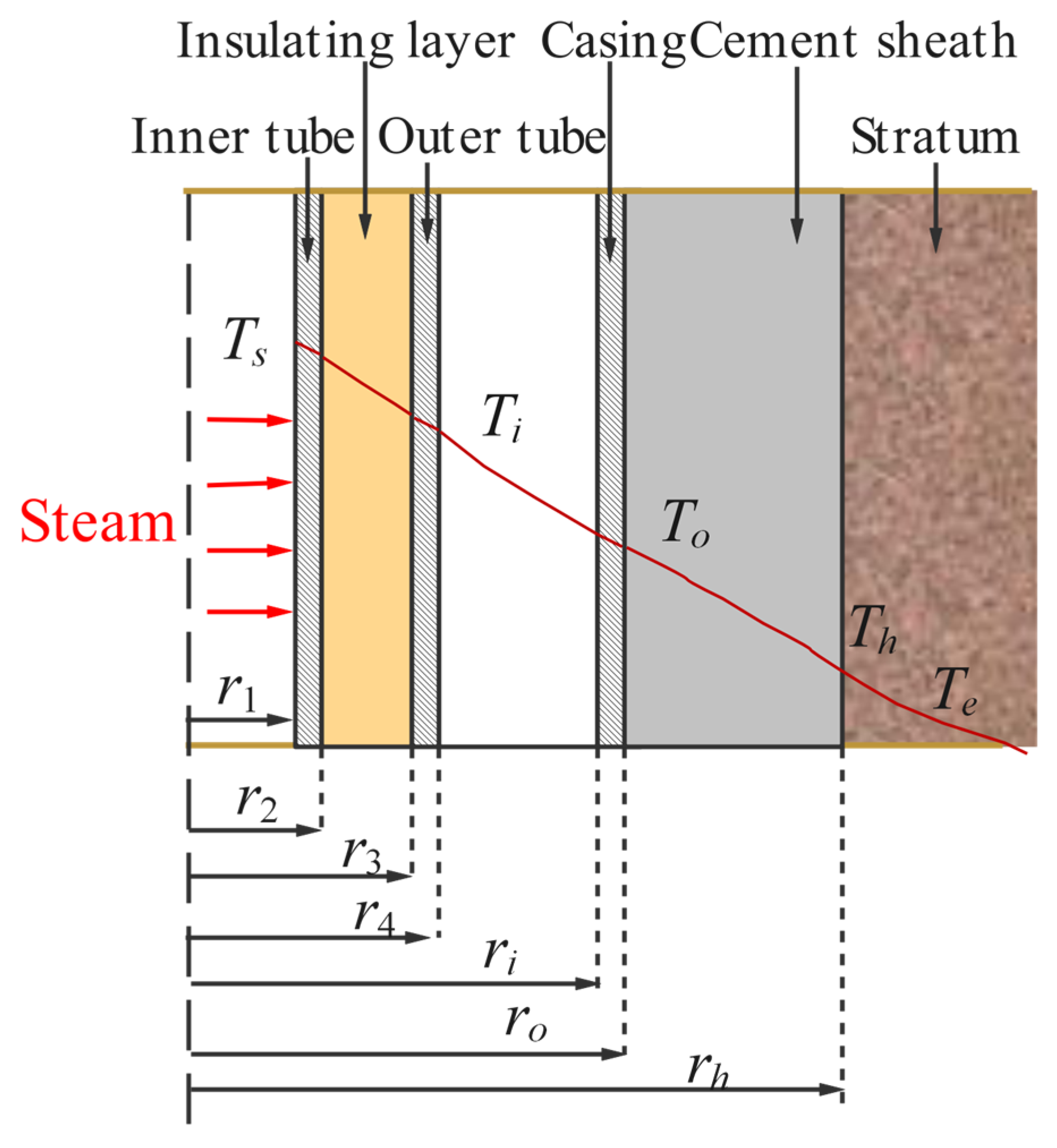
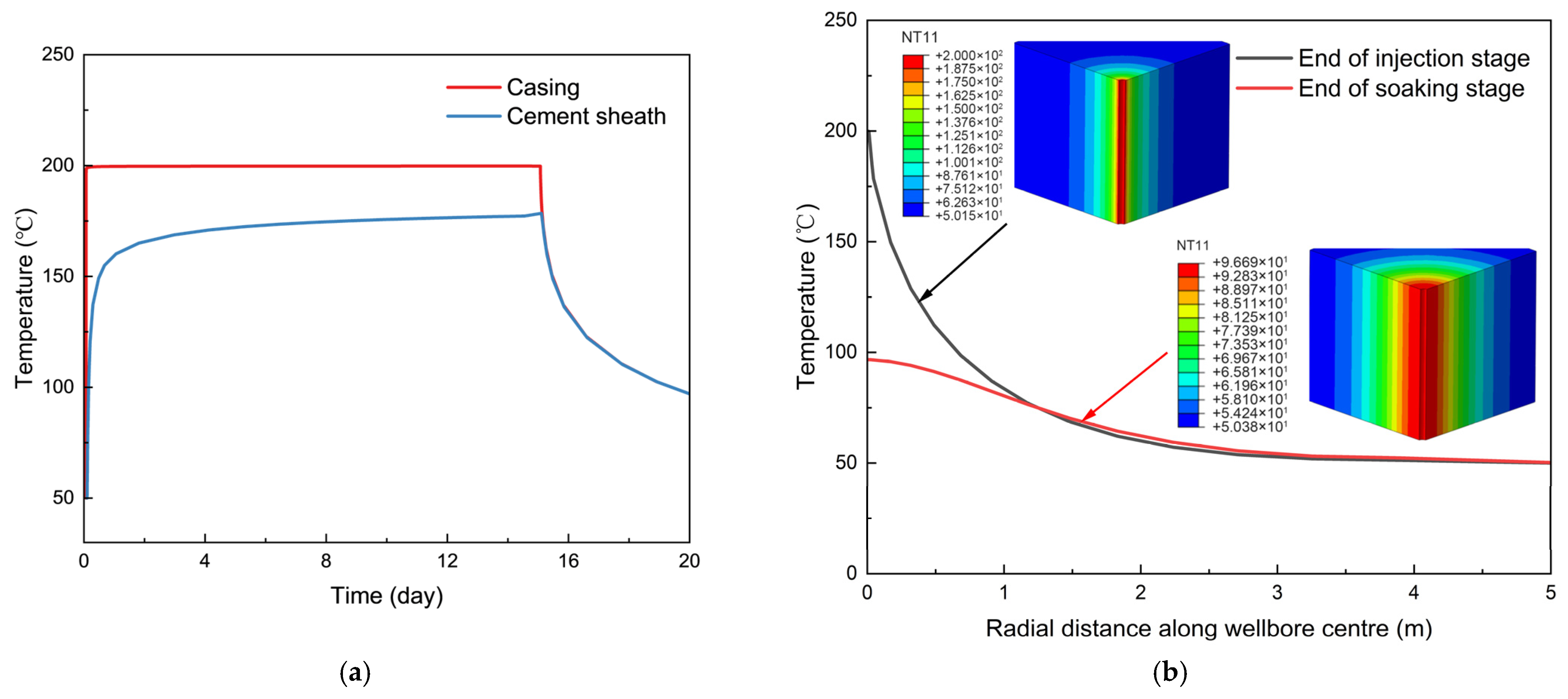
3.2. Temperature Analysis of Wellbore
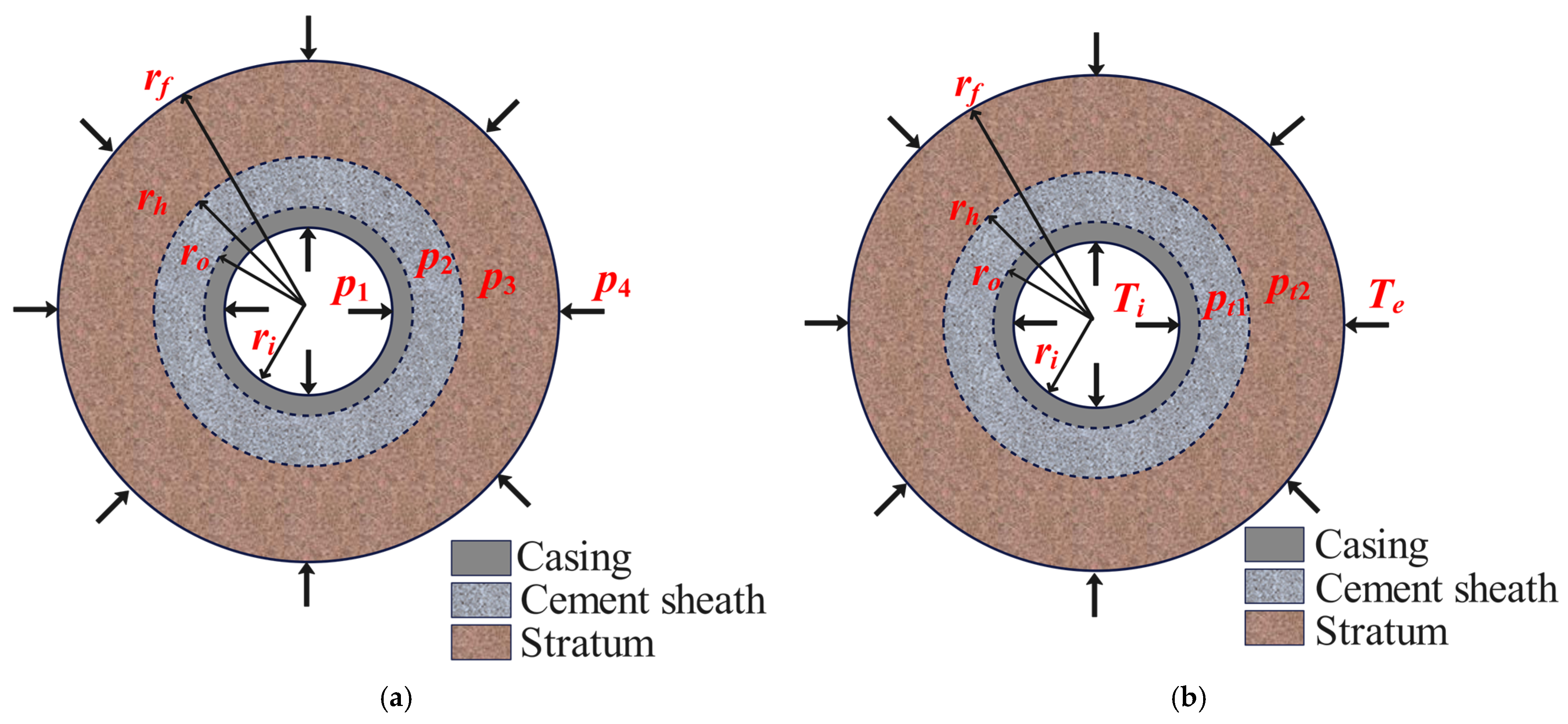
3.3. Stress Analysis of Casing
3.3.1. Stress and Displacement of the Casing Under Internal and External Pressures
3.3.2. Stress and Displacement of the Casing Under Thermal Loading
3.4. Casing Strain Design Method
3.5. Numerical Simulation of Casing Under Thermal Recovery Cycles
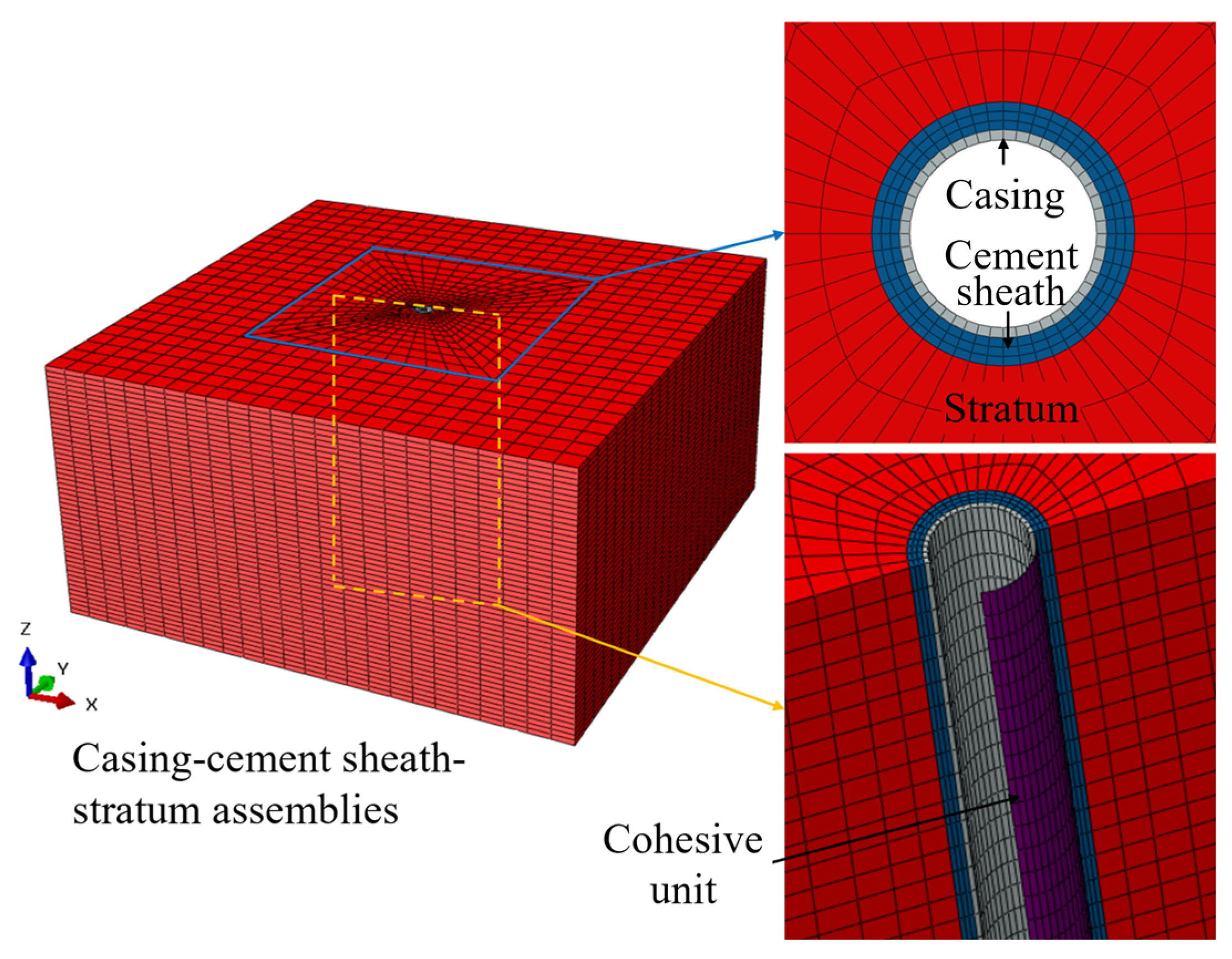
3.5.1. Basic Information on the Finite Element Model
3.5.2. Boundary Conditions
3.5.3. Model Validation
4. Results and Discussion
4.1. Analysis of the Upper Well Section Above the Packer
4.1.1. Conventional Straight Well Section
4.1.2. Inclined Well Section
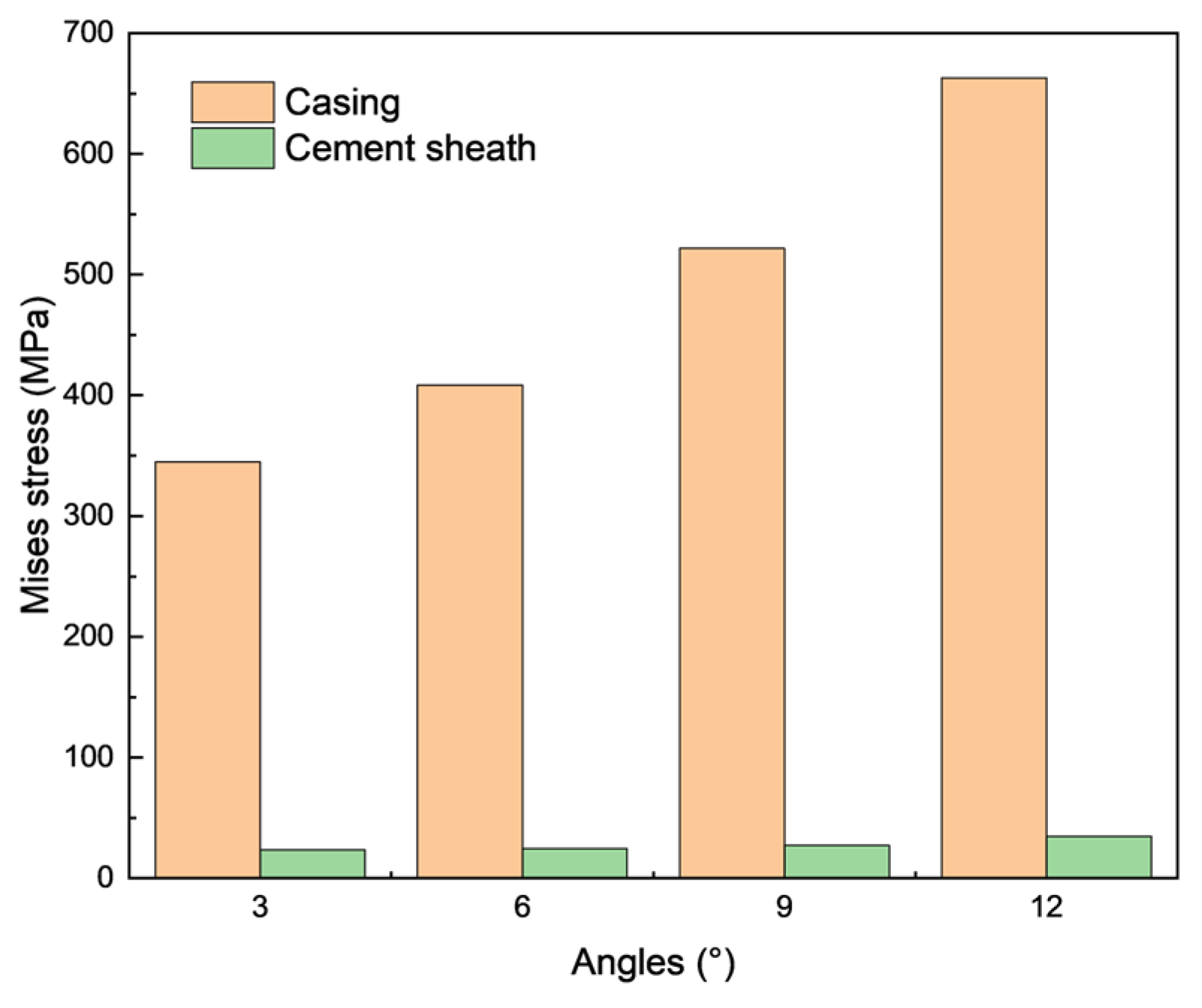
4.1.3. Side Drilling Branch Points
4.2. Analysis of the Well Section Below the Packer
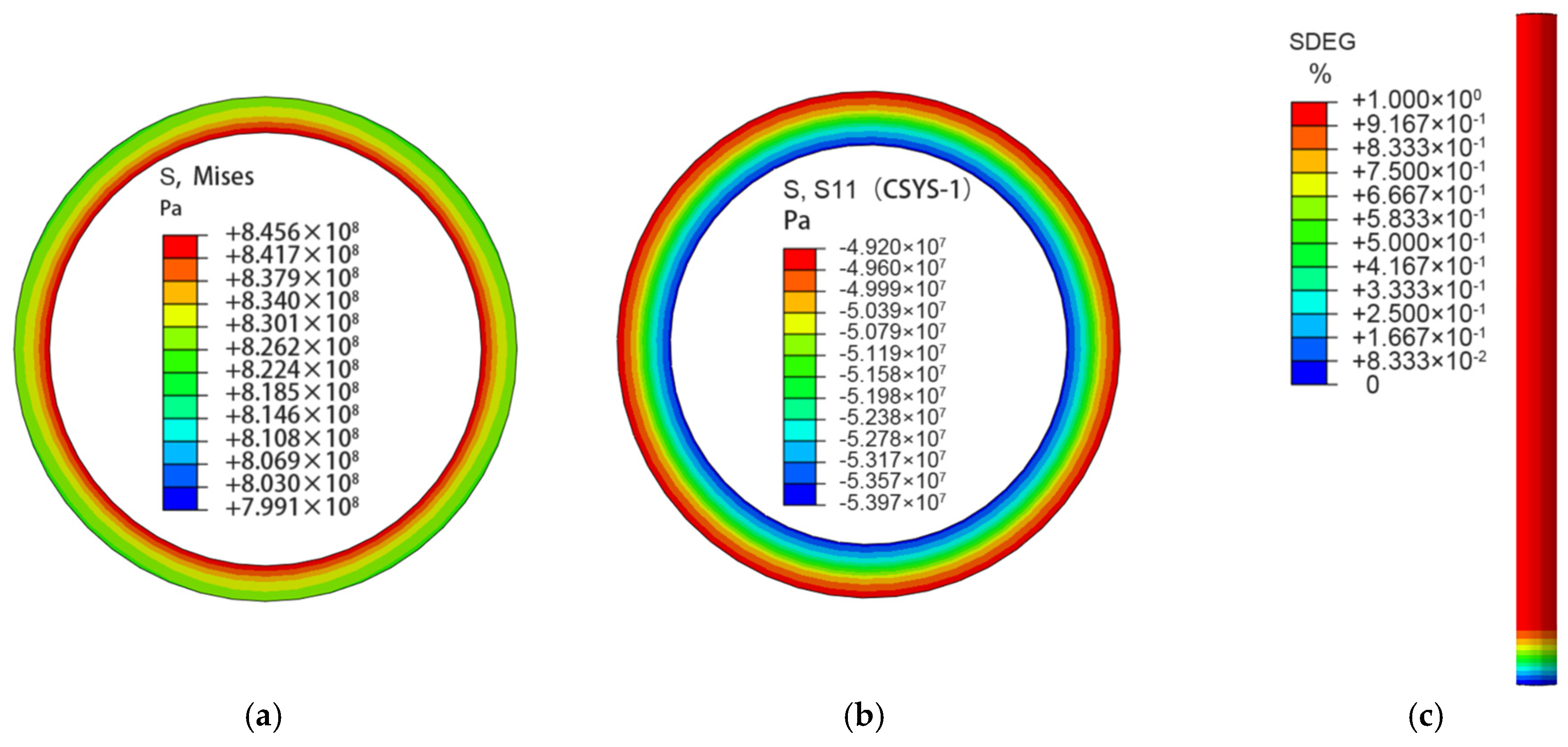
4.2.1. Stress Analysis of Casing and Cement Sheath
4.2.2. Influence of Steam Injection Pressure
4.2.3. Influence of In Situ Stress
4.2.4. Influence of Cement Elastic Modulus
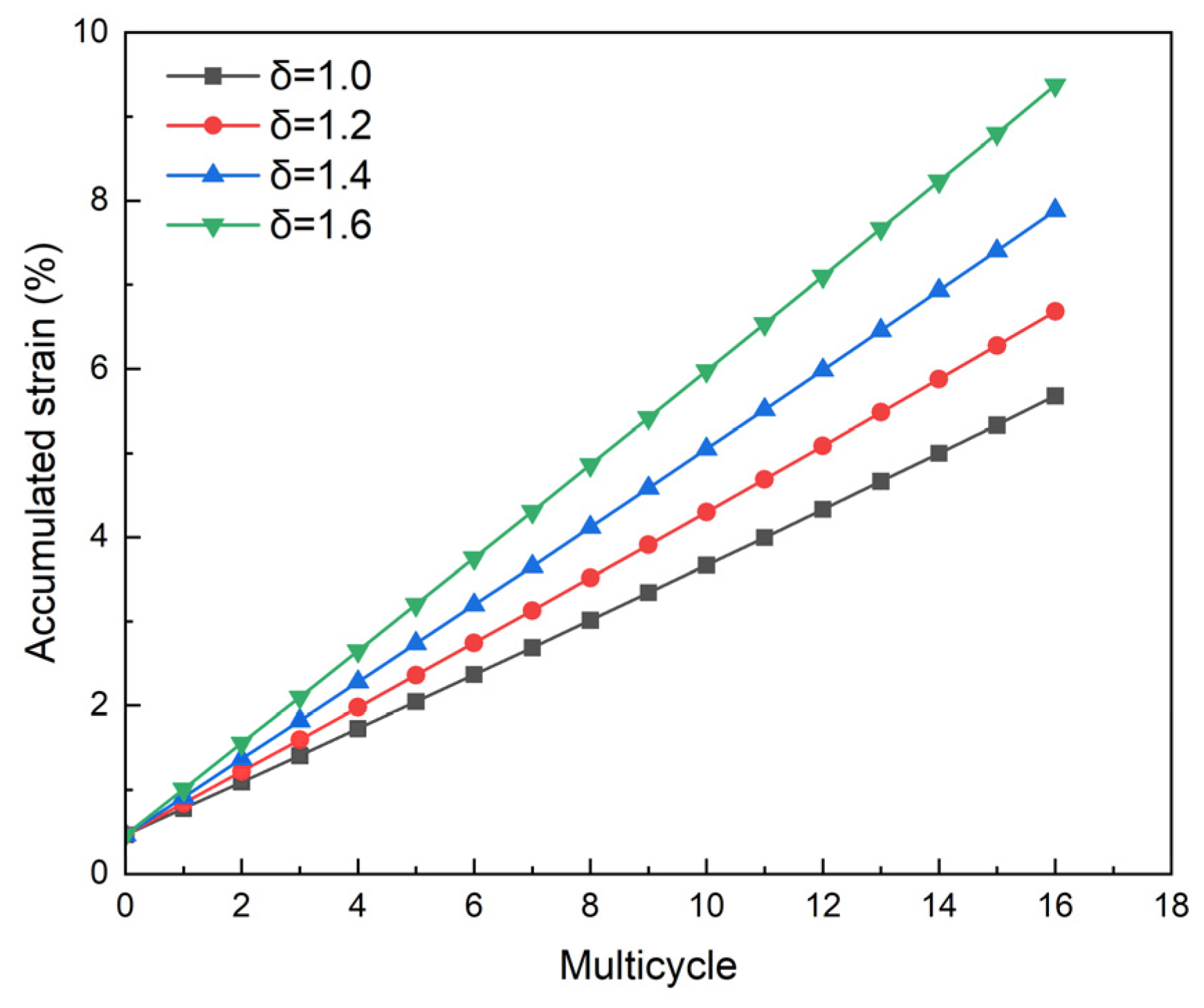
4.2.5. Influence of Prestressing
5. Conclusions and Future Work
- (1)
- Tensile and creep experiments on TP110H casing indicate that high- and low-temperature cycles significantly degrade casing performance, making their effects essential to consider. Higher temperatures impact casing properties more than thermal cycles. As temperature increases, the elastic modulus, yield strength, and tensile strength decrease, while elongation at break and section shrinkage increase. At 350 °C, after 16 thermal cycles, the elastic modulus, yield strength, and tensile strength decrease by 15.3%, 13.1%, and 10.1%, respectively. In contrast, elongation at break and section shrinkage increase by 18.8% and 69.9%, respectively. Creep rates rise with the number of thermal cycles, especially under higher stress levels (700 MPa), accelerating the process. At 350 °C, after 16 cycles, the maximum creep rate reaches 1.45 × 10−7%/s.
- (2)
- Utilizing heat transfer theory, a calculation method for the steam injection process in wellbores is proposed. Furthermore, based on thick-walled cylinder theory and thermoelastic principles, formulas for stress and displacement in the casing-cement sheath-formation system were derived under internal and external pressures as well as thermal loading. These formulas were obtained using individual solutions and finally combined through the superposition principle.
- (3)
- To simulate the thermally coupled steam injection and soaking cycles in production order, the well section above the packer, equipped with heat-insulating tubing, showed that casing temperatures remained below 200 °C. In the conventional straight, inclined, and side-drilled well sections, both the casing and cement sheath exhibited elastic behavior without plastic deformation. In practice, it is important to minimize the inclined section and to be mindful of the stress concentration effects on the casing around the side-drilling point. The strain design method was used to evaluate casing safety in steam-stimulated thermal recovery wells. Results indicate that TP110H casing can fundamentally meet the production requirements for 16 cycles in the lower section of the packer. Increasing steam injection pressure, using low-modulus cement, and applying prestress lifting can effectively reduce cumulative casing strain, thereby decreasing casing damage rates and extending wellbore service life. However, under conditions of uneven in situ stress, cumulative casing strain rises sharply, significantly impacting casing service life.
- (4)
- There are several aspects of this study that warrant further investigation, including thermal cycling test parameters, extreme operating conditions, and cement sealing performance. Future research should focus on multi-cycle high- and low-temperature thermal cycling tests and conduct in-depth analyses of the “casing-cement-stratum” system to evaluate cement–casing interface integrity and cement sheath sealing performance under thermal cycling. Additionally, in real-world applications, cementing quality issues—such as casing eccentricity, partial cement loss, and exposure to harsh environments with combined loads and corrosive media—can cause severe wear and corrosion. These pre-existing defects alter wellbore stress conditions and impact the service life of offshore heavy oil thermal recovery wells. Future studies should incorporate these factors to improve the accuracy and practical relevance of research in this field.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Symbol | Definition | unit |
| a | Stratum’s thermal diffusivity | m2/d |
| C1 | Solution constants | |
| C2 | Solution constants | |
| Ec | Elastic modulus of the casing | Pa |
| F | Strain design safety factor | |
| f(t) | A time-dependent function of the stratum’s thermal conductivity | / |
| h1 | Convective heat transfer coefficient between high-temperature steam and the inner pipe wall | W/(m2·k) |
| h2 | Convective heat transfer coefficient between the annular space and the casing wall | W/(m2·k) |
| h3 | Radiative heat transfer coefficient between the annular space and the casing wall | W/(m2·k) |
| kA | Thermal conductivity of the tubing | W/(m·k) |
| kB | Thermal conductivity of the insulation | W/(m·k) |
| kC | Thermal conductivity of the casing | W/(m·k) |
| kD | Thermal conductivity of the cement sheath | W/(m·k) |
| kE | Thermal conductivity of the stratum | W/(m·K) |
| L | Vertical depth | m |
| p1 | Internal pressure on the casing’s inner wall | Pa |
| p2 | Contact pressure between the casing and the cement sheath | Pa |
| R | Total thermal resistance | K/W |
| r1 | Inner radius of the inner pipe | m |
| r2 | Outer radius of the inner pipe | m |
| r3 | Inner radius of the outer pipe | m |
| r4 | Outer radius of the outer pipe | m |
| ri | Inner radius of the casing | m |
| ro | Outer radius of the casing | m |
| rh | Outer radius of the cement sheath | m |
| T | Radial temperature distribution function within the cylinder | °C |
| T0 | Mean annual surface temperature | °C |
| Ts | Injected steam temperature | °C |
| Th | Cement sheath’s outer boundary temperature | °C |
| t | Steam injection duration | days |
| ur | Radial displacement of the casing under internal and external pressure | m |
| αT | geothermal gradient | °C/m |
| σr | Radial stress of the casing under internal and external pressure | Pa |
| σθ | Circumferential stress of the casing under internal and external pressure | Pa |
| α | Linear thermal expansion coefficient of the material | °C−1 |
| μc | Poisson’s ratio of the casing | |
| Uniform elongation of the casing | % | |
| Cumulative strain in the casing | % | |
| Cumulative strain increment in the casing after the i-th cycle | % | |
| Permissible strain of the casing | % |
References
- Han, X.; Feng, F.; Zhang, J. Study on the Whole Life Cycle Integrity of Cement Interface in Heavy Oil Thermal Recovery Well under Circulating High Temperature Condition. Energy 2023, 278, 127873. [Google Scholar] [CrossRef]
- Haugan, J.A.; Jenssen, E.S.; Hatlem, S. Challenges in Heavy Crude Oil-Grane, an Overview. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar]
- Hein, F.J. Heavy Oil and Oil (Tar) Sands in North America: An Overview & Summary of Contributions. Nat. Resour. Res. 2006, 15, 67–84. [Google Scholar] [CrossRef]
- Omoregbe, O.; Hart, A. Global Trends in Heavy Oil and Bitumen Recovery and In-Situ Upgrading: A Bibliometric Analysis during 1900–2020 and Future Outlook. J. Energy Resour. Technol. 2022, 144, 123007. [Google Scholar] [CrossRef]
- Trindade, W.L.; Branco, C.C.M. The Offshore Heavy Oil Development Challenges in Brazil. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 20 June 2005; SPE: Rio de Janeiro, Brazil, 2005; p. SPE-97381-MS. [Google Scholar]
- Sun, H.; Wang, H.; Cao, X.; Shu, Q.; Fan, Z.; Wu, G.; Yang, Y.; Wu, Y. Innovations and Applications of the Thermal Recovery Techniques for Heavy Oil. Energy Geosci. 2024, 5, 100332. [Google Scholar] [CrossRef]
- Cui, G.; Niu, Z.; Hu, Z.; Feng, X.; Chen, Z. The Production Analysis and Exploitation Scheme Design of a Special Offshore Heavy Oil Reservoir—First Offshore Artificial Island with Thermal Recovery. J. Mar. Sci. Eng. 2024, 12, 1186. [Google Scholar] [CrossRef]
- Wang, L.; Guo, J.; Li, C.; Xiong, R.; Chen, X.; Zhang, X. Advancements and Future Prospects in In-Situ Catalytic Technology for Heavy Oil Reservoirs in China: A Review. Fuel 2024, 374, 132376. [Google Scholar] [CrossRef]
- Li, Y.; Qian, Y.; Lu, H.; Dai, P.; Zhu, H.; Yang, Q.; Liu, Y. High-Efficiency Pre-Treatment Core Tube for Produced Water in the Main Cavity Coupled with Secondary Cavities and Its Application in the Bohai Heavy Oilfield. J. Mar. Sci. Eng. 2023, 11, 93. [Google Scholar] [CrossRef]
- Liu, Y.; Zou, J.; Meng, X.; Zhou, F.; Liu, H.; Wang, Q.; Qi, Z.; Fan, J. Experimental Study on Horizontal-Well Multi-Thermal Fluid Stimulation Process in Offshore Heavy Oil Reservoirs. J. Pet. Explor. Prod. Technol. 2020, 10, 3057–3068. [Google Scholar] [CrossRef]
- Temizel, C.; Canbaz, C.H.; Tran, M.; Abdelfatah, E.; Jia, B.; Putra, D.; Irani, M.; Alkouh, A. A Comprehensive Review Heavy Oil Reservoirs, Latest Techniques, Discoveries, Technologies and Applications in the Oil and Gas Industry. In Proceedings of the PE International Heavy Oil Conference and Exhibition, Roma, Italy, 10 December 2018; SPE: Kuwait City, Kuwait, 2018; p. D012S024R001. [Google Scholar]
- Tan, J.; Wang, Z.; Chen, S.; Hu, H. Progress and Outlook of Supercritical CO2 —Heavy Oil Viscosity Reduction Technology: A Minireview. Energy Fuels 2023, 37, 11567–11583. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, Y.; Lu, N.; Xu, T.; Zhu, G.; Wang, K. A Review on Upgrading and Viscosity Reduction of Heavy Oil and Bitumen by Underground Catalytic Cracking. Energy Rep. 2021, 7, 4249–4272. [Google Scholar] [CrossRef]
- Guo, K.; Li, H.; Yu, Z. In-Situ Heavy and Extra-Heavy Oil Recovery: A Review. Fuel 2016, 185, 886–902. [Google Scholar] [CrossRef]
- Yang, M.; Chai, M.; Yuan, S.; Feng, T.; Wang, S.; Zhang, J.; Feng, Q.; Chen, Z.; Wei, T.; Wu, G.; et al. In-Situ Combustion for Heavy Oil and Oil Sands Recovery: Recent Progress, Field Applications, and Future Perspectives. Energy Fuels 2024, 38, 10395–10420. [Google Scholar] [CrossRef]
- Telmadarreie, T.; Berton, P.; Bryant, S.L. Treatment of Water-in-Oil Emulsions Produced by Thermal Oil Recovery Techniques: Review of Methods and Challenges. Fuel 2022, 330, 125551. [Google Scholar] [CrossRef]
- Dong, X.; Liu, H.; Chen, Z.; Wu, K.; Lu, N.; Zhang, Q. Enhanced Oil Recovery Techniques for Heavy Oil and Oilsands Reservoirs after Steam Injection. Appl. Energy 2019, 239, 1190–1211. [Google Scholar] [CrossRef]
- Neshat Ghojogh, J.; Noruzi-Masir, B.; Bakhshi, P.; Keyvan, P.; Salehipour-Bavarsad, A. Application of Horizontal Wells for Cyclic Steam Stimulation (CSS) in Bitumen Recovery: Production Optimization through Reservoir Simulation. Arab. J. Geosci. 2020, 13, 150. [Google Scholar] [CrossRef]
- Xu, A.Z.; Wu, X.H.; Fan, Z.F.; Zhao, L.; Wang, C.G. Improvements of Superheated Steam Stimulation in Secondary Development of Heavy Oil Reservoir. Adv. Mater. Res. 2012, 524–527, 1450–1455. [Google Scholar] [CrossRef]
- Gil′manov, A.Y.; Shevelev, A.P.; Lagunov, P.S.; Gulyaev, P.N.; Petukhov, A.S.; Lyutoev, P.A. Influence of the Thermophysical Properties of the Reservoir and Fluid on the Technological Parameters of the Cyclic Steam Stimulation. J. Eng. Phys. Thermophys. 2023, 96, 1311–1319. [Google Scholar] [CrossRef]
- Gil’manov, Y.A.; Arazov, A.R.; Shevelyov, A.P. Influence of Convective Processes on Technological Parameters of Cyclic Steam Stimulation of Oil Reservoirs. J. Eng. Phys. Thermophys. 2022, 95, 1172–1179. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, J.; Gates, I.D. On the Physics of Cyclic Steam Stimulation. Energy 2016, 115, 969–985. [Google Scholar] [CrossRef]
- Pratama, R.A.; Babadagli, T. A Review of the Mechanics of Heavy-Oil Recovery by Steam Injection with Chemical Additives. J. Pet. Sci. Eng. 2022, 208, 109717. [Google Scholar] [CrossRef]
- Hein, F.J. Geology of Bitumen and Heavy Oil: An Overview. J. Pet. Sci. Eng. 2017, 154, 551–563. [Google Scholar] [CrossRef]
- He, C.; Xu, A.; Fan, Z.; Zhao, L.; Bo, B. A New Mathematical Model For Heat Radius of Cyclic Superheated Steam Stimulation with Horizontal Wellbore. Math. Probl. Eng. 2018, 2018, 7601702. [Google Scholar] [CrossRef]
- Li, Z. Casing Cementing with Half Warm-up for Thermal Recovery Wells. J. Pet. Sci. Eng. 2008, 61, 94–98. [Google Scholar] [CrossRef]
- Geng, L.; Liu, D.; Han, L.; Feng, S. Numerical Analysis of Casing Damage in Heavy Oil Thermal Recovery Wells. IOP Conf. Ser. Earth Environ. Sci. 2021, 726, 012011. [Google Scholar] [CrossRef]
- Loiseau, A. Thermal Expansion of Cement and Well Integrity of Heavy Oil Wells. In Proceedings of the PE Latin America and Caribbean Heavy and Extra Heavy Oil Conference, Medellin, Colombia, 24 September 2014; SPE: Medellín, Colombia, 2014; p. D011S004R003. [Google Scholar]
- Wang, Z.; Wen, Y.; Li, Y.; Wang, J.; Liu, W. Effect of Poroelasticity on the Integrity of Cement Sheath in Heavy Oil Wells. Chem. Technol. Fuels Oils 2022, 58, 851–861. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, S.; Tong, H. Plastic Limit Analysis of Defective Casing for Thermal Recovery Wells. Eng. Fail. Anal. 2013, 27, 340–349. [Google Scholar] [CrossRef]
- Hou, D.; Zhang, Z.; Geng, Y.; Yue, J.; Wu, Z. Study on Channeling-Leakage Pressure of Casing-Cement Sheath-Stratum Assembly in Thermal Recovery Wells. Fuel 2024, 356, 129592. [Google Scholar] [CrossRef]
- Li, F.; Yan, W.; Kong, X.; Li, J.; Zhang, W.; Kang, Z.; Yang, T.; Tang, Q.; Wang, K.; Tan, C. Study on Multi-Factor Casing Damage Prediction Method Based on Machine Learning. Energy 2024, 296, 131044. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Zhao, Q.; Hao, W.; Zhang, H.; Li, Y.; Huang, P.; Zou, Y. Study on Casing Safety Evaluation in High-Temperature Wells with Annular Pressure Buildup. Processes 2023, 11, 1915. [Google Scholar] [CrossRef]
- Xu, J.; Deng, J.; Chen, Y.; Jia, L.; Xiao, Y.; Liu, W. Analysis of Casing Instability and Factors Influencing It in Thermal Production Oil Wells. Chem. Technol. Fuels Oils 2021, 57, 804–812. [Google Scholar] [CrossRef]
- Choi, W.; Fujiyama, K.; Kim, B.; Song, G. Development of Thermal Stress Concentration Factors for Life Assessment of Turbine Casings. Int. J. Press. Vessel. Pip. 2012, 98, 1–7. [Google Scholar] [CrossRef]
- Xu, A.; Mu, L.; Fan, Z.; Wu, X.; Zhao, L.; Bo, B.; Xu, T. Mechanism of Heavy Oil Recovery by Cyclic Superheated Steam Stimulation. J. Pet. Sci. Eng. 2013, 111, 197–207. [Google Scholar] [CrossRef]
- Hua, W.; Michael, F.; Aimé, F. Assessing Leak Paths in the Cement Sheath of a Cased Borehole by Analysis of Monopole Wavefield Modes. Commun. Comput. Phys. 2020, 28, 424–441. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, H.; Zhang, J.; Guo, L. Analytical Modeling on the Geo-Stress and Casing Damage Prevention with the Thermo-Hydro-Mechanical (THM) Coupling of Multi-Field Physics. J. Therm. Anal. Calorim. 2020, 139, 2719–2737. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, Q.; Lian, Z.; Ding, L.; Wan, Z. A Calculation Method for Ultimate and Allowable Loads in High-Pressure Thick-Walled Worn Casing. Ocean Eng. 2024, 313, 119448. [Google Scholar] [CrossRef]
- Gruben, G.; Dillingh, B.; Kaldal, G.S.; Hoang, N.-H.; Wollenweber, J.; Rørvik, G.; Thorbjornsson, I.; Nyhus, B. Thermo-Mechanical Tensile Testing of Geothermal Casing Materials. Geothermics 2021, 89, 101944. [Google Scholar] [CrossRef]
- Peng, J.; Li, R. Implementation of Method a in GB/T 228.1-2010 by Using Crosshead Displacement Rate. Phys. Test. Chem. Anal. Part A: Phys. Test. 2021, 57, 19–21+24. [Google Scholar]
- GB/T 34907-2017; Technical Specifications and Fitness for Service Evaluation Method for Thermal Well Casing under Cyclic Steam Stimulation Process. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2017.
- Liu, W.; Zhou, Z.; Li, Z.; Li, M.; Li, Q.; Ye, Z.; Yao, J.; Zhong, X. The High-Temperature Mechanical Properties of HS110S Steel and Its Corrosion Behaviors in Harsh Downhole Environment. Anti Corros. Methods Mater. 2022, 69, 550–560. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, X.; Zhang, F.; Ge, T.; Wang, D.; Zhang, C.; Liu, D. The Study on Classification Methods for Low Production Wells of Thermal Recovery and Its Applications. J. Pet. Explor. Prod. Technol. 2019, 9, 469–481. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Martyushev, N.V.; Kukartsev, V.V.; Tynchenko, V.S.; Bukhtoyarov, V.V.; Wu, X.; Tyncheko, Y.A.; Kukartsev, V.A. Overview of Methods for Enhanced Oil Recovery from Conventional and Unconventional Reservoirs. Energies 2023, 16, 4907. [Google Scholar] [CrossRef]
- Mokheimer, E.M.A.; Hamdy, M.; Abubakar, Z.; Shakeel, M.R.; Habib, M.A.; Mahmoud, M. A Comprehensive Review of Thermal Enhanced Oil Recovery: Techniques Evaluation. J. Energy Resour. Technol. 2019, 141, 030801. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; He, M.; Xu, M.; Dai, B. Coupled Modeling Circulating Multi-Layer Wellbore Temperature and Stress Field during Deepwater High-Temperature and High-Pressure Gas Well Testing. Therm. Sci. Eng. Prog. 2024, 47, 102356. [Google Scholar] [CrossRef]
- Brown, C.S.; Falcone, G. Investigating Heat Transmission in a Wellbore for Low-Temperature, Open-Loop Geothermal Systems. Therm. Sci. Eng. Prog. 2024, 48, 102352. [Google Scholar] [CrossRef]
- Gu, H.; Cheng, L.; Huang, S.; Li, B.; Shen, F.; Fang, W.; Hu, C. Steam Injection for Heavy Oil Recovery: Modeling of Wellbore Heat Efficiency and Analysis of Steam Injection Performance. Energy Convers. Manag. 2015, 97, 166–177. [Google Scholar] [CrossRef]
- Fuentes-Ibarra, D.; Cazarez-Candia, O.; Aguilar-Madera, C.G. Local Thermal Equilibrium Constraints for Energy Transport Equations for Thermal Oil Recovery Processes. Int. J. Therm. Sci. 2024, 197, 108782. [Google Scholar] [CrossRef]
- Kolawole, F.; Evenick, J.C. Global Distribution of Geothermal Gradients in Sedimentary Basins. Geosci. Front. 2023, 14, 101685. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Wang, X. Wellbore Two-Phase Flow and Heat Transfer during Transient Testing. SPE J. 1998, 3, 174–180. [Google Scholar] [CrossRef]
- Li, P.; Wang, X.; Zhang, Y. Thermal Recovery of Heavy Oil Reservoirs: Modeling of Flow and Heat Transfer Characteristics of Superheated Steam in Full-Length Concentric Dual-Tubing Wells. Geoenergy Sci. Eng. 2025, 244, 213432. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Liang, W. Casing Safety Evaluation for Setting Liner Hanger. J. Nat. Gas Sci. Eng. 2014, 19, 58–61. [Google Scholar] [CrossRef]
- Jiang, X.; Dong, X.; Xu, W.; Liu, H.; Chen, Z. Mathematical Modeling for the Production Performance of Cyclic Multi-Thermal Fluid Stimulation Process in Layered Heavy Oil Reservoirs. Geoenergy Sci. Eng. 2024, 243, 213350. [Google Scholar] [CrossRef]
- Han, L.; Wang, H.; Wang, J.; Xie, B.; Tian, Z.; Wu, X. Strain-Based Casing Design for Cyclic-Steam-Stimulation Wells. SPE Prod. Oper. 2018, 33, 409–418. [Google Scholar] [CrossRef]
- Lihong, H.; Jianjun, W.; Hang, W.; Changyi, Q.; Yaorong, F.; Bin, X.; Xuelu, Z.; Zhihua, T. Strain Based Design and Material Selection Technology for Thermal Well Casing. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26 March 2013; IPTC: Beijing, China, 2013; p. IPTC-16739-Abstract. [Google Scholar]
- Wang, J.; Li, D.; Du, X.; Li, H.; Yang, S. Development of a Design Method for Casing and Tubing Strings under Complex Alternating Loads. Processes 2023, 11, 2582. [Google Scholar] [CrossRef]
- Han, L.; Wang, H.; Wang, J.; Zhu, L.; Xie, B.; Tian, Z. Strain Based Design and Field Application of Thermal Well Casing String for Cyclic Steam Stimulation Production. In Proceedings of the SPE Canada Heavy Oil Conference, Calgary, AB, Canada, 7 June 2016; SPE: Calgary, AB, Canada, 2016; p. D011S001R003. [Google Scholar]
- Zhang, J. Performance of High Temperature Steam Injection in Horizontal Wells of Heavy Oil Reservoirs. Energy 2023, 282, 128863. [Google Scholar] [CrossRef]
- Tang, K.; Wang, X.; Peng, J.; Yang, H.; Zhang, Y. Development of Grade 110SH-1 Thermal Recovery Casing for Heavy Oil Thermal Recovery Well. Steel Specif. 2020, 41, 43–47. [Google Scholar] [CrossRef]





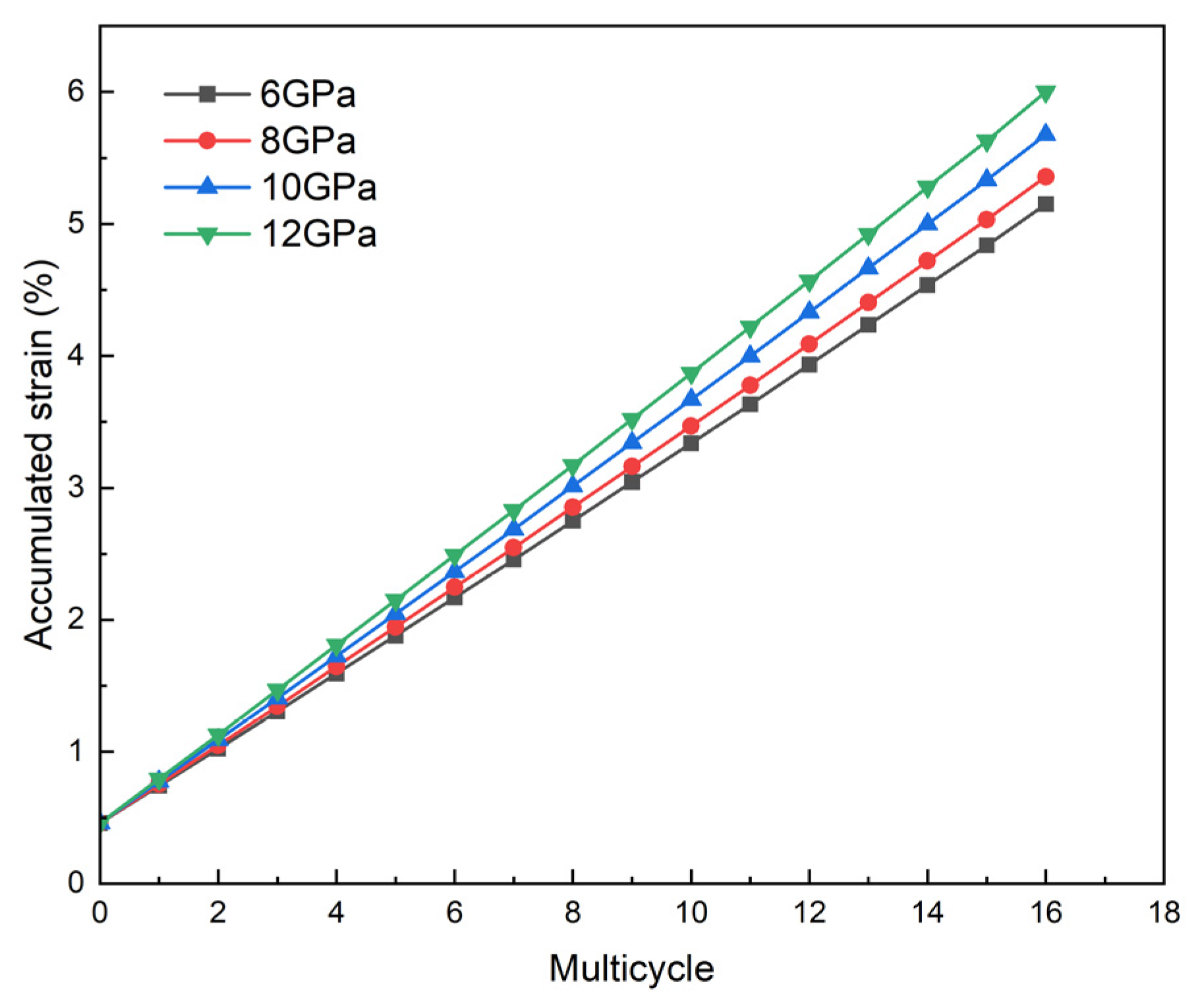
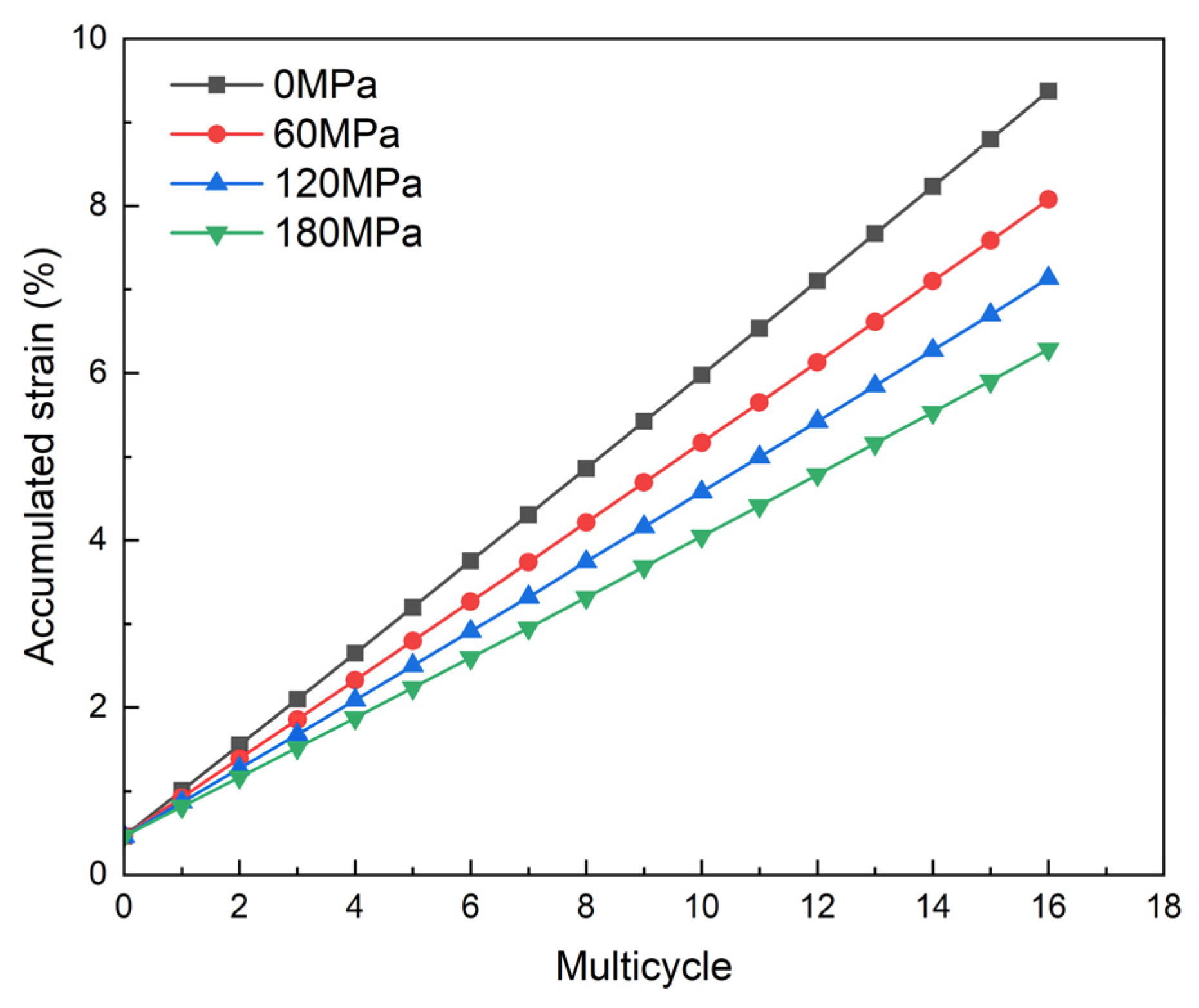
| Temperature | Number of Thermal Cycles | Yield Strength /% | Tensile Strength /% | GB/T 34907-2017 Permissible Strength Limits/% | Assessment Results |
|---|---|---|---|---|---|
| 50 | 1 | 1.5 | 1.0 | 20 | Compliance |
| 4 | 4.4 | 2.1 | 20 | Compliance | |
| 8 | 5.9 | 3.1 | 20 | Compliance | |
| 12 | 7.1 | 4.0 | 20 | Compliance | |
| 16 | 8.1 | 4.9 | 20 | Compliance | |
| 200 | 1 | 1.7 | 1.0 | 20 | Compliance |
| 4 | 4.3 | 2.4 | 20 | Compliance | |
| 8 | 6.4 | 3.6 | 20 | Compliance | |
| 12 | 7.5 | 4.9 | 20 | Compliance | |
| 16 | 9.0 | 5.6 | 20 | Compliance | |
| 350 | 1 | 2.1 | 1.3 | 20 | Compliance |
| 4 | 4.9 | 2.7 | 20 | Compliance | |
| 8 | 7.9 | 3.8 | 20 | Compliance | |
| 12 | 9.0 | 5.1 | 20 | Compliance | |
| 16 | 10.8 | 6.4 | 20 | Compliance |
| Materials | Density kg/m3 | Expansion Coefficient 10−5/°C | Specific Heat Capacity J/kg/°C | Thermal Conductivity W/m/°C |
|---|---|---|---|---|
| Casing | 7800 | 1.36 | 460 | 46.0 |
| Cement sheath | 1900 | 1.10 | 837 | 0.98 |
| Stratum | 2300 | 1.03 | 896 | 1.6 |
| Assemblies | Outer Diameter/mm | Wall Thickness/mm | Inner Diameter/mm | Stress/MPa | |
|---|---|---|---|---|---|
| Wellbore in Reference [31] | Casing | 246 | 11.5 | 223 | 15.18–131.74 |
| Cement-sheath | 311 | 32.5 | 246 | 1.72–9.35 | |
| stratum | 389 | 40 | 309 | 1.66–37.35 | |
| Model in Reference [31] | Casing | 114.3 | 6.6 | 101.1 | 15.54–116.33 |
| Cement-sheath | 164.3 | 25 | 114.3 | 1.69–9.03 | |
| stratum | 206.3 | 21 | 164.3 | 2.27–43.08 | |
| Model in this study | Casing | 244.48 | 11.99 | 220.5 | 14.98–136.46 |
| Cement-sheath | 330.48 | 43 | 244.48 | 1.71–9.51 | |
| stratum | 10,000 | 4834.76 | 330.48 | 0.94–32.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Song, Y.; Hu, S.; Liu, H.; Ge, X. Mechanical Evaluation of Casing in Multiple Thermal Recovery Cycles for Offshore Heavy Oil Wells. J. Mar. Sci. Eng. 2025, 13, 597. https://doi.org/10.3390/jmse13030597
He Y, Song Y, Hu S, Liu H, Ge X. Mechanical Evaluation of Casing in Multiple Thermal Recovery Cycles for Offshore Heavy Oil Wells. Journal of Marine Science and Engineering. 2025; 13(3):597. https://doi.org/10.3390/jmse13030597
Chicago/Turabian StyleHe, Yuxian, Yongpeng Song, Shenghua Hu, Hangming Liu, and Xianchi Ge. 2025. "Mechanical Evaluation of Casing in Multiple Thermal Recovery Cycles for Offshore Heavy Oil Wells" Journal of Marine Science and Engineering 13, no. 3: 597. https://doi.org/10.3390/jmse13030597
APA StyleHe, Y., Song, Y., Hu, S., Liu, H., & Ge, X. (2025). Mechanical Evaluation of Casing in Multiple Thermal Recovery Cycles for Offshore Heavy Oil Wells. Journal of Marine Science and Engineering, 13(3), 597. https://doi.org/10.3390/jmse13030597






