Predictive Study on the Cutting Energy Efficiency of Dredgers Based on Specific Cutting Energy
Abstract
1. Introduction
2. Effective Specific Cutting Energy Estimation Method
2.1. Working Process of the Dredger
2.2. Dredging Construction Evaluation Parameters
2.3. Specific Cutting Energy
2.4. Effective Specific Cutting Energy
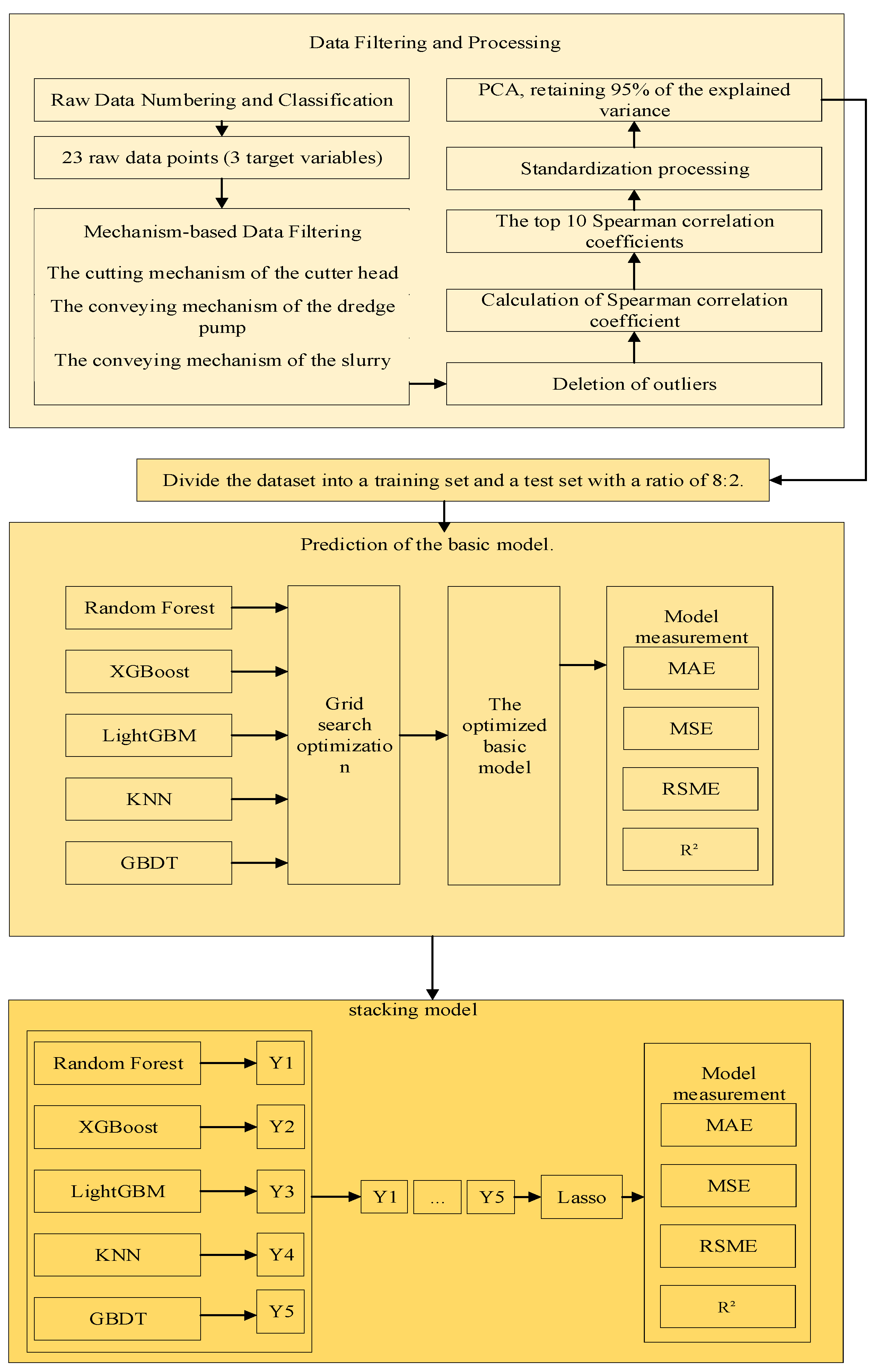
3. Methods and Models
3.1. Key Theoretical Models of the Dredger
- Suction Inlet Slurry Formation Model
- Soil and Sand Particle Motion Model
- Slurry Pump Models: Clear Water and Slurry Characteristics
3.2. Feature Engineering
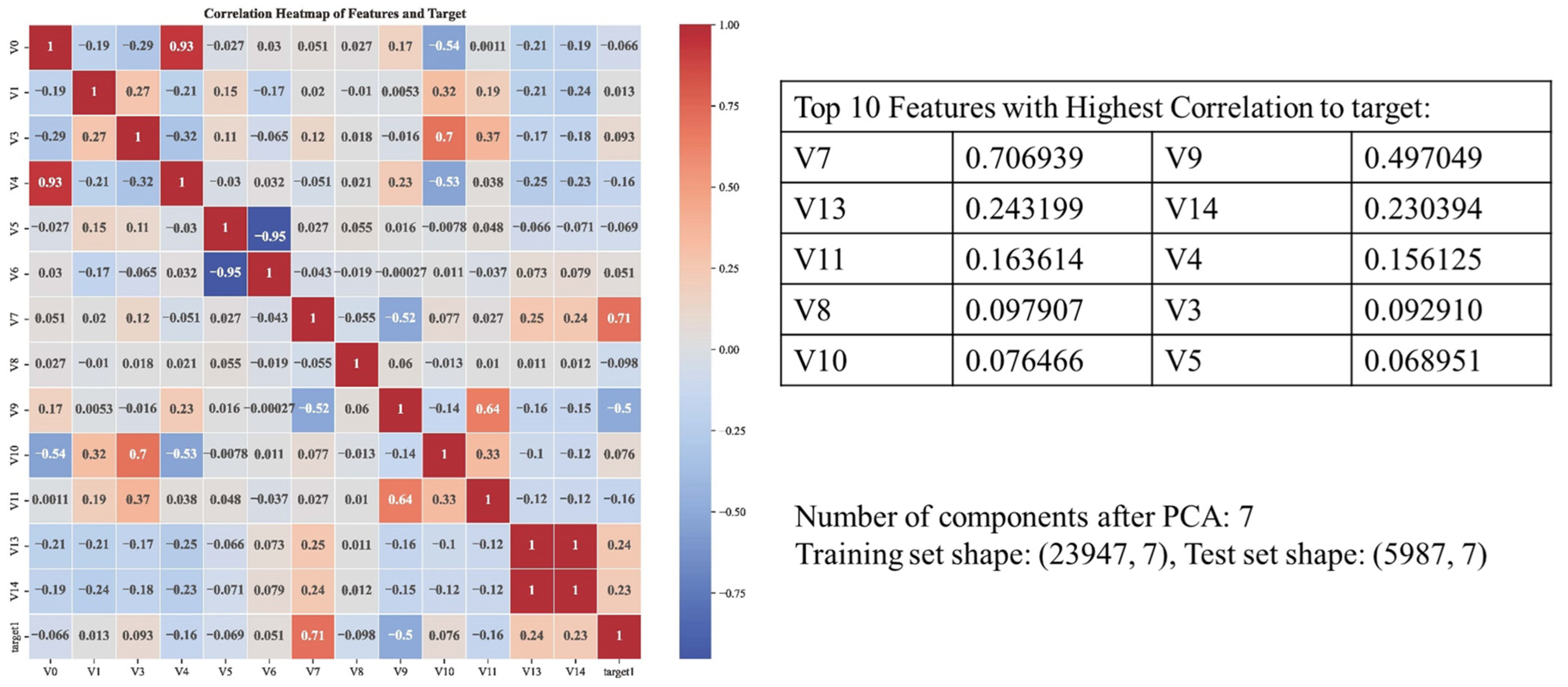
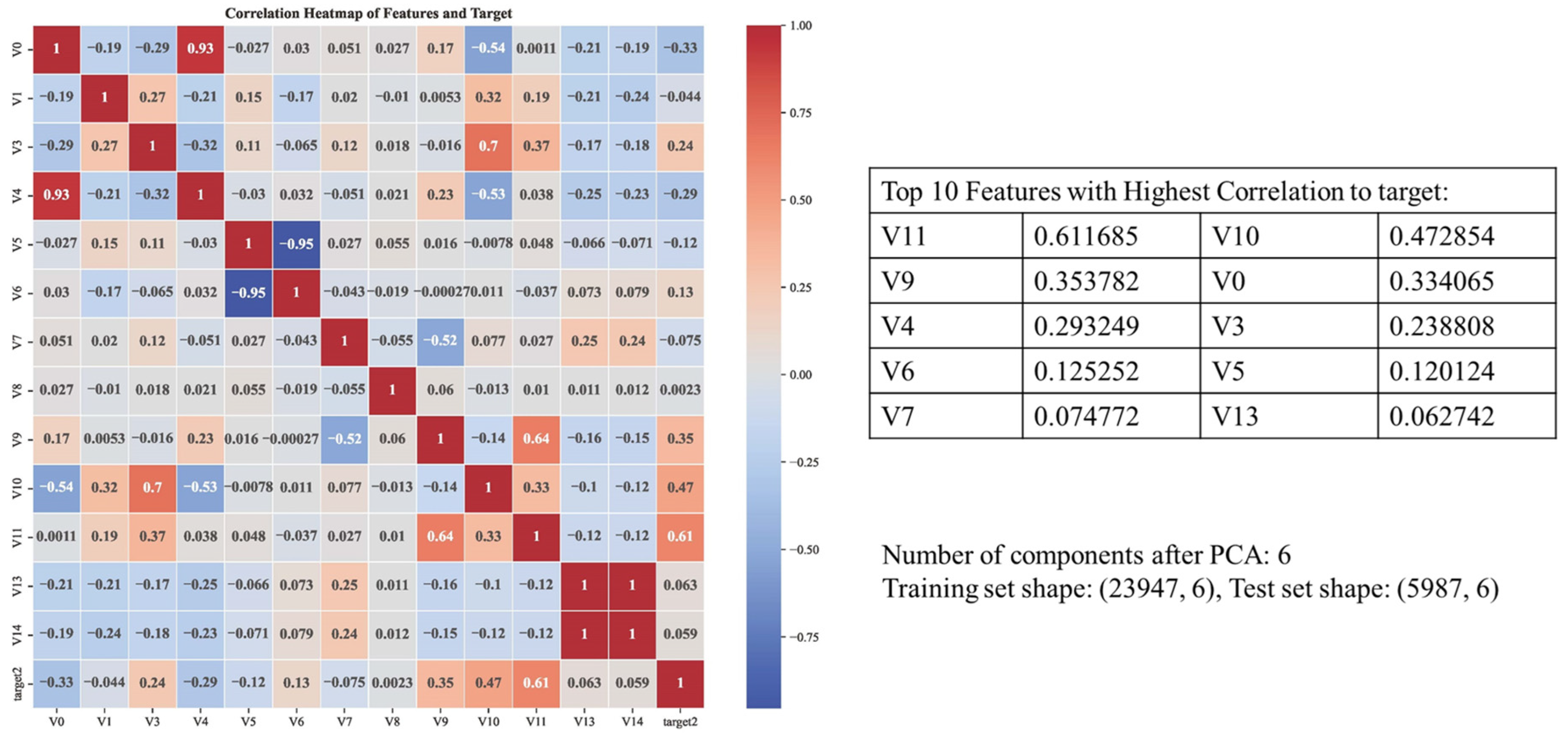
- Spearman Rank Correlation Coefficient
- Principal Component Analysis (PCA)
3.3. Prediction Algorithms
3.4. Model Evaluation
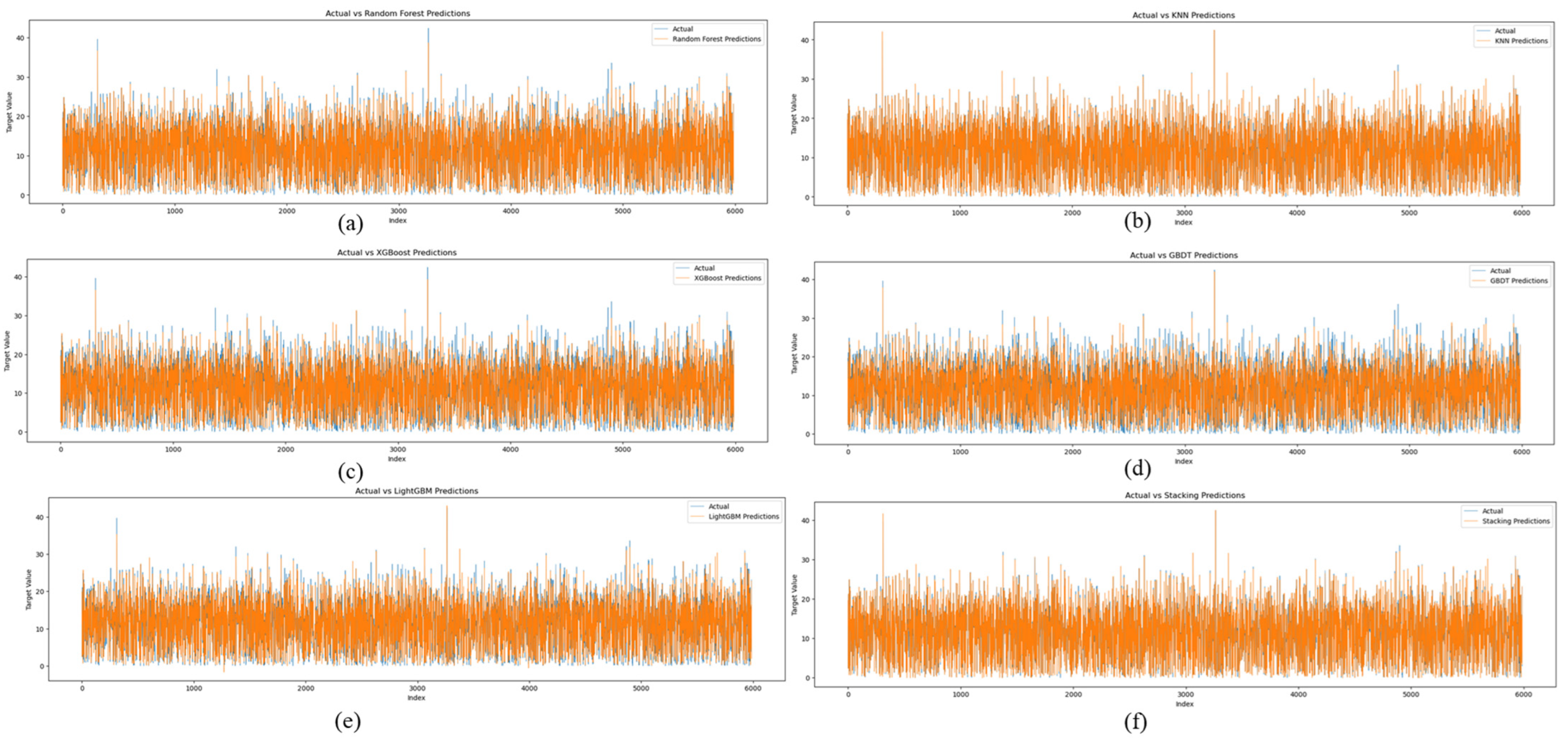
4. Results and Discussion
4.1. Ship Introduction
4.2. Data Selection and Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSD | Cutter Suction Dredger |
| PCA | Principal Component Analysis |
| RF | Random Forest |
| KNN | K-Nearest Neighbor |
| XGBoost | eXtreme Gradient Boosting |
| GBDT | Gradient Boosting Decision Tree |
| LightGBM | Light Gradient Boosting Machine |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| RSME | Root Mean Squared Error |
| R2 | Coefficient of Determination |
References
- Ouyang, Y.P.; Yang, Q.; Chen, X.Q.; Xu, Y.F. An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger. J. Mar. Sci. Eng. 2020, 8, 806. [Google Scholar] [CrossRef]
- Reddy, N.V.K.; Pothal, J.K.; Barik, R.; Senapati, P.K. Pipeline Slurry Transportation System: An Overview. J. Pipel. Syst. Eng. Pract. 2023, 14, 15. [Google Scholar] [CrossRef]
- Miedema, S.A. A head loss model for slurry transport in the heterogeneous regime. Ocean Eng. 2015, 106, 360–370. [Google Scholar] [CrossRef]
- Miedema, S.A. An overview of theories describing head losses in slurry transport a tribute to some of the early researchers. In Proceedings of the 32nd ASME International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Bai, S.; Li, M.C.; Kong, R.; Han, S.; Li, H.; Qin, L. Data mining approach to construction productivity prediction for cutter suction dredgers. Autom. Constr. 2019, 105, 13. [Google Scholar] [CrossRef]
- Yue, P.; Zhong, D.H.; Miao, Z.J.; Yu, J. Prediction of Dredging Productivity Using a Rock and Soil Classification Model. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 7. [Google Scholar] [CrossRef]
- Li, J.Y.; Shi, Y.Y.; Rao, K.P.; Zhao, K.Y.; Xiao, J.F.; Xiong, T.; Huang, Y.Z.; Huang, Q.B. The Design and Analysis of Double Cutter Device for Hinge and Suction Dredger Based on Feedback Control Method. Appl. Sci. 2022, 12, 3793. [Google Scholar] [CrossRef]
- Fu, J.K.; Tian, H.J.; Song, L.G.; Li, M.C.; Bai, S.; Ren, Q.B. Productivity estimation of cutter suction dredger operation through data mining and learning from real-time big data. Eng. Constr. Archit. Manag. 2021, 28, 2023–2041. [Google Scholar] [CrossRef]
- Tang, H.Z.; Wang, Q.F.; Bi, Z.Y. Expert system for operation optimization and control of cutter suction dredger. Expert Syst. Appl. 2008, 34, 2180–2192. [Google Scholar] [CrossRef]
- Tang, J.Z.; Wang, Q.F.; Zhong, T.Y. Automatic monitoring and control of cutter suction dredger. Autom. Constr. 2009, 18, 194–203. [Google Scholar] [CrossRef]
- Wei, C.Y.; Ni, F.S.; Chen, X.J. Obtaining Human Experience for Intelligent Dredger Control: A Reinforcement Learning Approach. Appl. Sci. 2019, 9, 1769. [Google Scholar] [CrossRef]
- Wei, C.Y.; Wei, Y.; Ji, Z. Model predictive control for slurry pipeline transportation of a cutter suction dredger. Ocean Eng. 2021, 227, 11. [Google Scholar] [CrossRef]
- Wei, C.Y.; Wang, H.; Bai, H.A.; Ji, Z.; Liu, Z.H. PPLC: Data-driven offline learning approach for excavating control of cutter suction dredgers. Eng. Appl. Artif. Intell. 2023, 125, 13. [Google Scholar] [CrossRef]
- Li, M.C.; Kong, R.; Han, S.; Tian, G.P.; Qin, L. Novel Method of Construction-Efficiency Evaluation of Cutter Suction Dredger Based on Real-Time Monitoring Data. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 14. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Jiang, P.; Chen, Y.; Zhu, H.H.; Xiong, T. Cutting state estimation and time series prediction using deep learning for Cutter Suction Dredger. Appl. Ocean Res. 2023, 134, 9. [Google Scholar] [CrossRef]
- Yang, K.; Yuan, J.L.; Xiong, T.; Wang, B.; Fan, S.D. A Novel Principal Component Analysis Integrating Long Short-Term Memory Network and Its Application in Productivity Prediction of Cutter Suction Dredgers. Appl. Sci. 2021, 11, 8159. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Chen, Y.; Zheng, L.Y.; Zhu, H.H.; Fang, Z.L.; Zhang, M. The replacement of dysfunctional sensors based on the digital twin method during the cutter suction dredger construction process. Measurement 2022, 189, 14. [Google Scholar] [CrossRef]
- Wang, B.; Zio, E.; Fan, S.D. Reliability evaluation of the hybrid-redundancy sensor fault tolerate system in the dredging perception system. Ocean Eng. 2023, 281, 16. [Google Scholar] [CrossRef]
- Han, S.; Li, H.; Li, M.C.; Tian, H.J.; Qin, L.; Yu, Y.; Ma, J. Intelligent short-term forecasting for mud concentration in CSD dredging construction. Ocean Eng. 2022, 266, 17. [Google Scholar] [CrossRef]
- Chen, Y.; Ren, Q.B.; Li, M.C.; Tian, H.J.; Qin, L.; Wu, D.C. Prediction of submarine soil dredging difficulty scale in cutter suction dredger construction with clustering-based deep learning. Eng. Appl. Artif. Intell. 2025, 147, 110370. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, Q.R.; Kang, H.R.; Fan, Z.Y.; Bai, S. Productivity Prediction and Analysis Method of Large Trailing Suction Hopper Dredger Based on Construction Big Data. Buildings 2022, 12, 1505. [Google Scholar] [CrossRef]
- Jiang, P.; Yang, Y.K.; Cao, C.H.; Dong, X.Y. Implementation of Constant Power Control for a Reamer Using a Fuzzy PID Algorithm. Mathematics 2025, 13, 647. [Google Scholar] [CrossRef]
- Wang, W.; Shen, Y.C.; Wang, L.Y.; Wang, D.S.; Bai, Y.M. Design of Dredging Process Control System for Cutter Suction Dredger. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 5932–5937. [Google Scholar]
- Xin, C.H.; Yue, S.H.; Yang, L. Feedback Control System in Dredging Engineering Based on Convolutional Neural Network Prediction. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021. [Google Scholar]
- Zhou, B.L.; Yu, M.H.; Guo, J. Hybrid optimization algorithm for estimating soil parameters of spoil hopper deposition model for trailing suction hopper dredgers. J. Intell. Fuzzy Syst. 2024, 46, 1813–1831. [Google Scholar] [CrossRef]
- Balogun, V.A.; Edem, I.F.; Adekunle, A.A.; Mativenga, P.T. Specific energy based evaluation of machining efficiency. J. Clean Prod. 2016, 116, 187–197. [Google Scholar] [CrossRef]
- Cho, J.W.; Jeon, S.; Jeong, H.Y.; Chang, S.H. Evaluation of cutting efficiency during TBM disc cutter excavation within a Korean granitic rock using linear-cutting-machine testing and photogrammetric measurement. Tunn. Undergr. Space Technol. 2013, 35, 37–54. [Google Scholar] [CrossRef]
- He, X.Q.; Xu, C.S. Specific Energy as an Index to Identify the Critical Failure Mode Transition Depth in Rock Cutting. Rock Mech. Rock Eng. 2016, 49, 1461–1478. [Google Scholar] [CrossRef]
- Nieuwboer, B.J.; van Rhee, C.; Keetels, G.H. Towards simulating flow induced spillage in dredge cutter heads using DEM-FVM. Ocean Eng. 2023, 275, 13. [Google Scholar] [CrossRef]
- Mahgoub, M.; Keetels, G.H.; Alhaddad, S. Impact of operational parameters on turbidity generation in cutter suction dredging: Insights from a numerical model and sensitivity analysis. Appl. Ocean Res. 2025, 154, 104312. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, M.H.; Liu, Q.Y.; Chen, S.H.; Liu, Y.C.; Zhang, C.H.; Liu, R.H. XGBoost-Based Algorithm Interpretation and Application on Post-Fault Transient Stability Status Prediction of Power System. IEEE Access 2019, 7, 13149–13158. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.L.; Meng, Q.; Finley, T.; Wang, T.F.; Chen, W.; Ma, W.D.; Ye, Q.W.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ma, X.J.; Sha, J.L.; Wang, D.H.; Yu, Y.B.; Yang, Q.; Niu, X.Q. Study on a prediction of P2P network loan default based on the machine learning LightGBM and XGboost algorithms according to different high dimensional data cleaning. Electron. Commer. Res. Appl. 2018, 31, 24–39. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Saul, L.K. Distance Metric Learning for Large Margin Nearest Neighbor Classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Wu, X.D.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.H. ML-KNN: A lazy learning approach to multi-label leaming. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]




| System | Description | Unit | Original Data Number |
|---|---|---|---|
| Cutter | Angle of the cutter ladder | ° | V0 |
| Distance of the swing movement | m | V1 | |
| Power of the cutter | kW | V2 (target1) | |
| Rotation speed of the cutter | rpm | V3 | |
| Depth of the dredging | m | V4 | |
| Left horizontal movement speed | m/s | V5 | |
| Right horizontal movement speed | m/s | V6 | |
| Pump | Vacuum | kPa | V7 |
| Rotation speed of the submersible pump | rpm | V8 | |
| Discharge pressure of the underwater pump | kPa | V9 | |
| Rotation speed of the No. 1 slurry pump | rpm | V10 | |
| Discharge pressure of the No. 1 slurry pump | kPa | V11 | |
| Rotation speed of the No. 2 slurry pump | rpm | V16 | |
| Discharge pressure of the No. 2 slurry pump | kPa | V17 | |
| Pipeline | Flow | m3/h | V18 |
| Flow rate | m/s | V12 (target2) | |
| Slurry density | kg/m3 | V19 | |
| Environment | Water density | kg/m3 | V20 |
| Soil density | kg/m3 | V21 | |
| Ship | Trolley trip | m | V13 |
| Angle of the swing | ° | V14 | |
| Production Rate | m3 | V22 | |
| Slurry concentration | % | V15 (target) |
| MAE | MSE | RMSE | R2 | ||
|---|---|---|---|---|---|
| RF | max_depth:None, min_samples_split: 2, n_estimators: 200 | 0.4333 | 0.8975 | 0.9474 | 0.9782 |
| XGBoost | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 1.0316 | 2.2521 | 1.5007 | 0.9453 |
| LightGBM | learning_rate: 0.1, max_depth: −1, min_child_samples: 10, n_estimators: 200, num_leaves: 100 | 0.7034 | 1.1492 | 1.0720 | 0.9721 |
| KNN | n_neighbors: 3, p: 1 | 0.1862 | 0.2832 | 0.5322 | 0.9931 |
| GBDT | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 1.1244 | 2.6352 | 1.6233 | 0.9360 |
| Stacking Model | 0.2664 | 0.3868 | 0.6219 | 0.9906 |
| MAE | MSE | RMSE | R2 | ||
|---|---|---|---|---|---|
| RF | max_depth:None, min_samples_split: 2, n_estimators: 200 | 74.0720 | 16,144.1292 | 127.0595 | 0.8633 |
| XGBoost | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 85.3572 | 18,969.0241 | 137.7281 | 0.8393 |
| LightGBM | learning_rate: 0.1, max_depth: −1, min_child_samples: 10, n_estimators: 200, num_leaves: 100 | 78.5289 | 16,466.1618 | 128.3205 | 0.8605 |
| KNN | n_neighbors: 3, p: 2 | 75.6162 | 17,669.2174 | 132.9256 | 0.8503 |
| GBDT | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 90.0801 | 20,982.5755 | 144.8536 | 0.8223 |
| Stacking Model | 74.8949 | 16,320.4874 | 127.7517 | 0.8618 |
| MAE | MSE | RMSE | R2 | ||
|---|---|---|---|---|---|
| RF | max_depth:None, min_samples_split: 2, n_estimators: 200 | 0.0193 | 0.0019 | 0.0436 | 0.9696 |
| XGBoost | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 0.0365 | 0.0035 | 0.0593 | 0.9435 |
| LightGBM | learning_rate: 0.1, max_depth: −1, min_child_samples: 10, n_estimators: 200, num_leaves: 100 | 0.0291 | 0.0025 | 0.0501 | 0.9598 |
| KNN | n_neighbors: 3, p: 2 | 0.0102 | 0.0010 | 0.0309 | 0.9847 |
| GBDT | learning_rate: 0.1, max_depth: 7, n_estimators: 200 | 0.0389 | 0.0039 | 0.0623 | 0.9378 |
| Stacking Model | 0.0375 | 0.0029 | 0.0536 | 0.9539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Yang, K.; Yang, T.; Xu, H.; Xiong, T.; Fan, S. Predictive Study on the Cutting Energy Efficiency of Dredgers Based on Specific Cutting Energy. J. Mar. Sci. Eng. 2025, 13, 598. https://doi.org/10.3390/jmse13030598
Yuan J, Yang K, Yang T, Xu H, Xiong T, Fan S. Predictive Study on the Cutting Energy Efficiency of Dredgers Based on Specific Cutting Energy. Journal of Marine Science and Engineering. 2025; 13(3):598. https://doi.org/10.3390/jmse13030598
Chicago/Turabian StyleYuan, Junlang, Ke Yang, Taiwei Yang, Haoran Xu, Ting Xiong, and Shidong Fan. 2025. "Predictive Study on the Cutting Energy Efficiency of Dredgers Based on Specific Cutting Energy" Journal of Marine Science and Engineering 13, no. 3: 598. https://doi.org/10.3390/jmse13030598
APA StyleYuan, J., Yang, K., Yang, T., Xu, H., Xiong, T., & Fan, S. (2025). Predictive Study on the Cutting Energy Efficiency of Dredgers Based on Specific Cutting Energy. Journal of Marine Science and Engineering, 13(3), 598. https://doi.org/10.3390/jmse13030598






