Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure
Abstract
:1. Introduction
- Composite Fault Modeling and Control Method: A novel composite fault modeling framework is introduced, capable of handling complex combinations of actuator faults and external disturbances. This approach effectively accommodates various fault scenarios, thereby markedly improving the robustness and stability of the control system under fault conditions.
- Innovative Sliding Mode Control Design: Building on conventional sliding mode control, this paper develops a new sliding mode surface and convergence law. The refined convergence law decelerates the initiation of the arrival phase to reduce chattering, while simultaneously accelerating the system’s response as it moves away from the sliding mode surface. This dual effect enhances both the dynamic performance and responsiveness of the system.
- Combination of Nonlinear Saturation Fitting and Event-Triggered Mechanism: To address issues related to saturation filtering and communication resource constraints, a nonlinear saturation fitting function is designed and integrated with an event-triggered mechanism. This combined solution effectively reduces the communication overhead, mitigates potential communication problems during fault events, and maintains system stability and precision under adverse fault conditions.
2. Problem Formulation
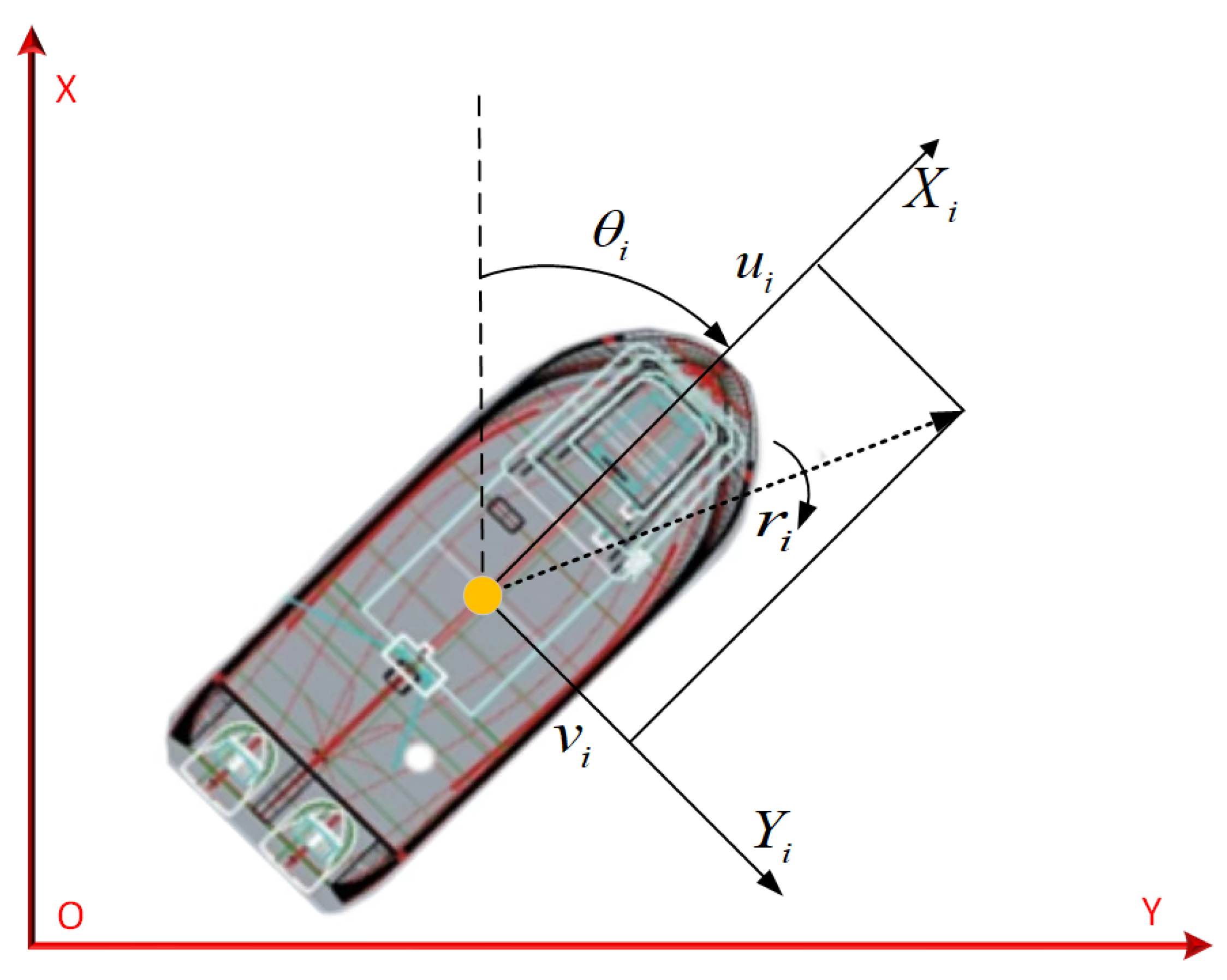
2.1. Mathematical Model
2.2. Fault Model
2.3. Cooperative Formation Model
3. Basic Control Design
3.1. Non-Singular Terminal Sliding Mode Surface Design and Analysis
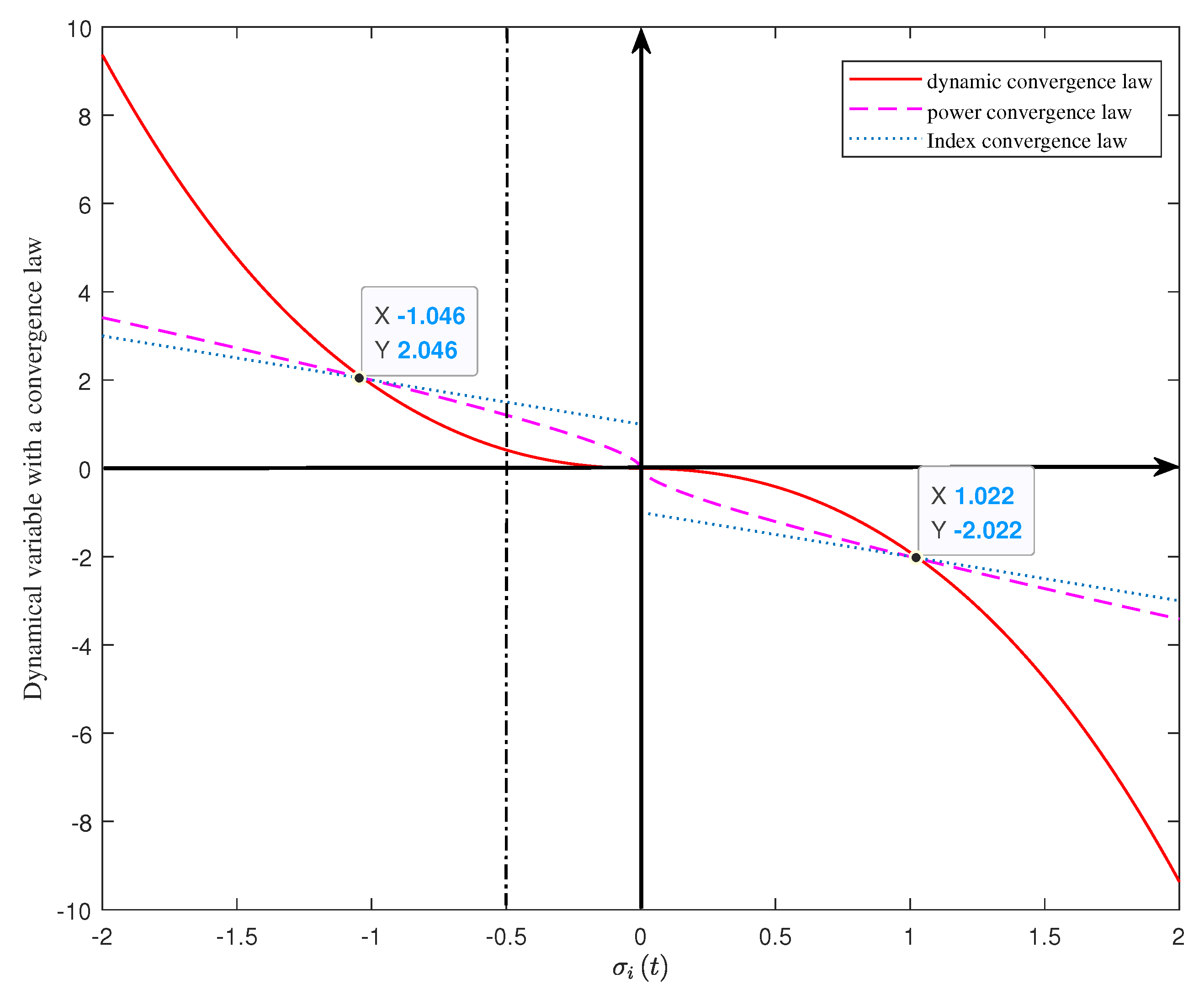
3.2. Dynamically Regulated Convergence Law Design and Analysis
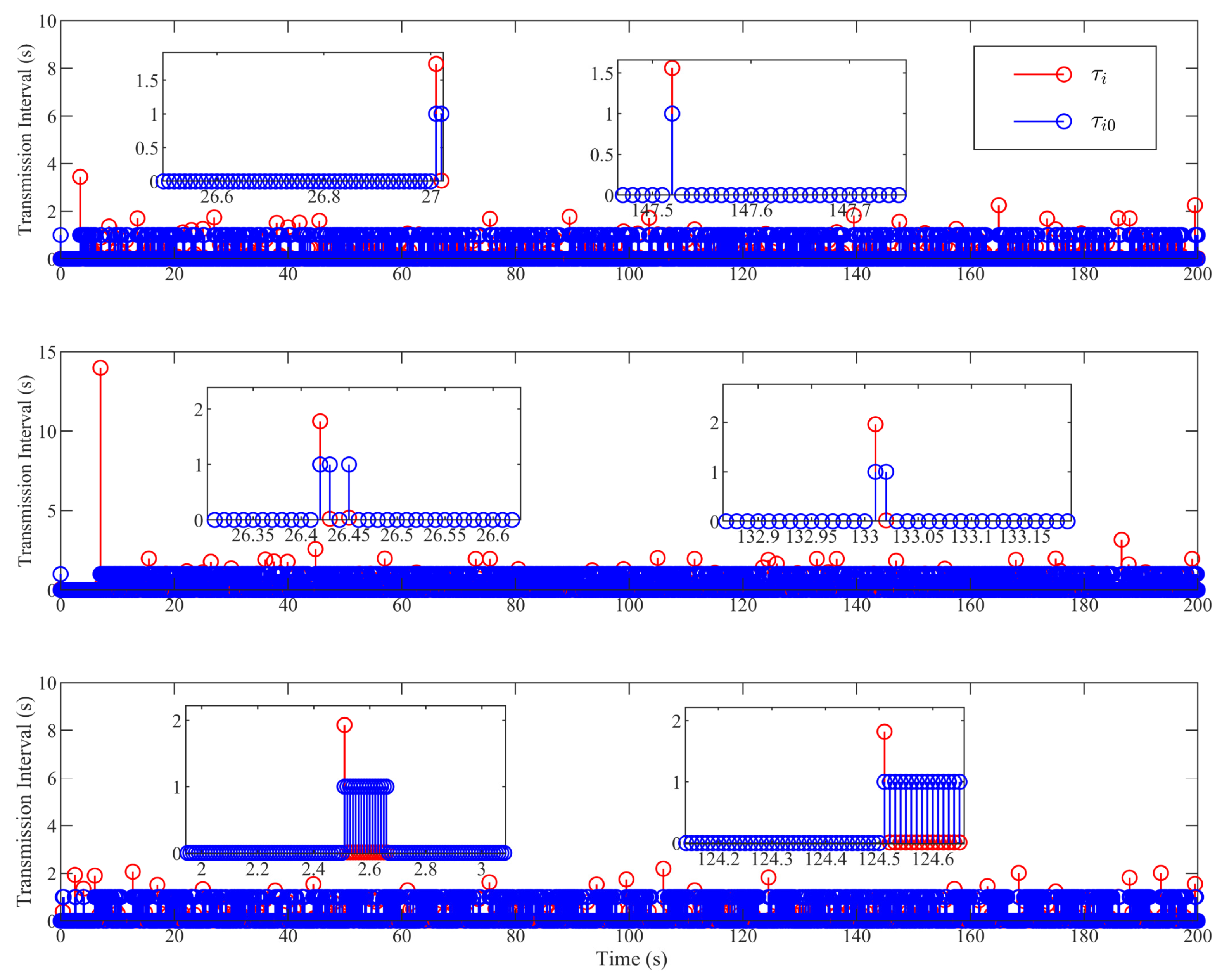
3.3. Event-Triggering Mechanism Design and Stability Analysis
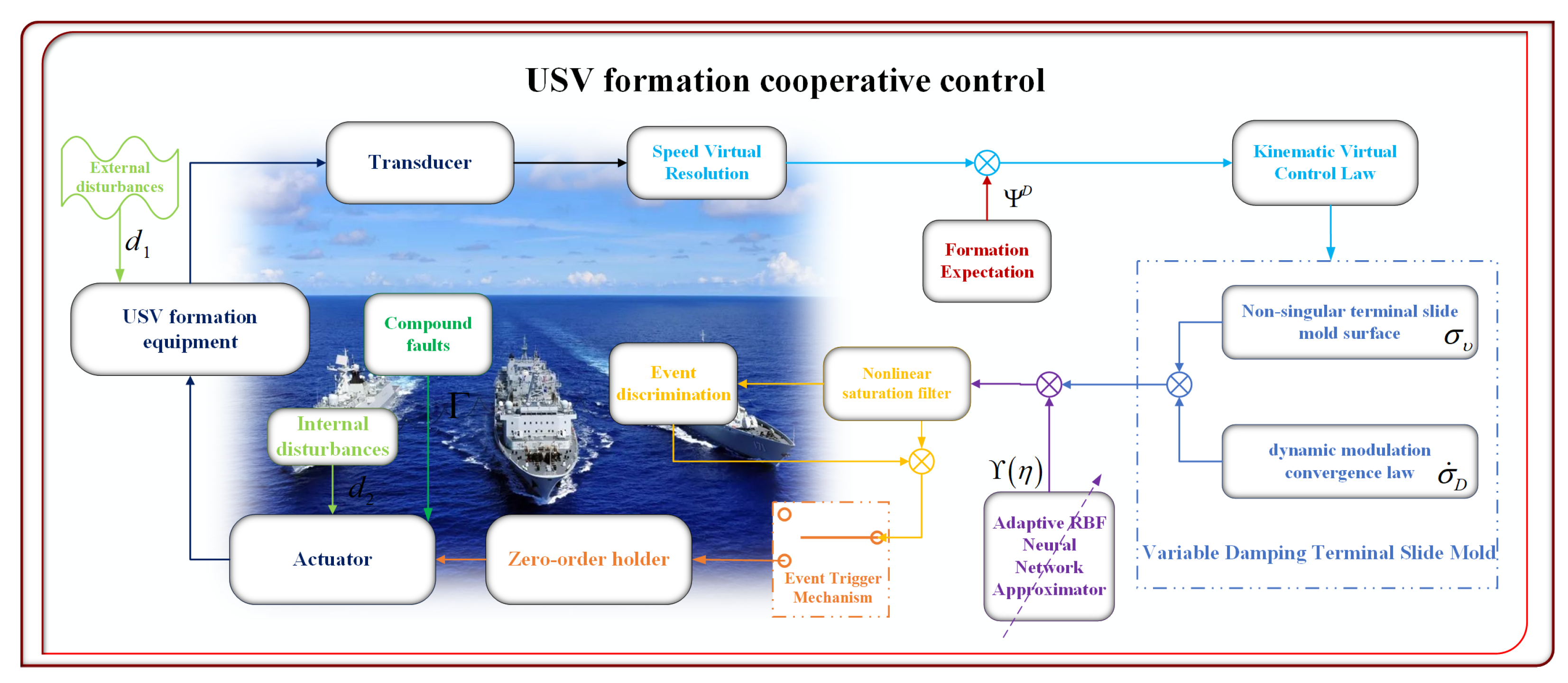
3.4. Controller Design
3.5. Stability Analysis
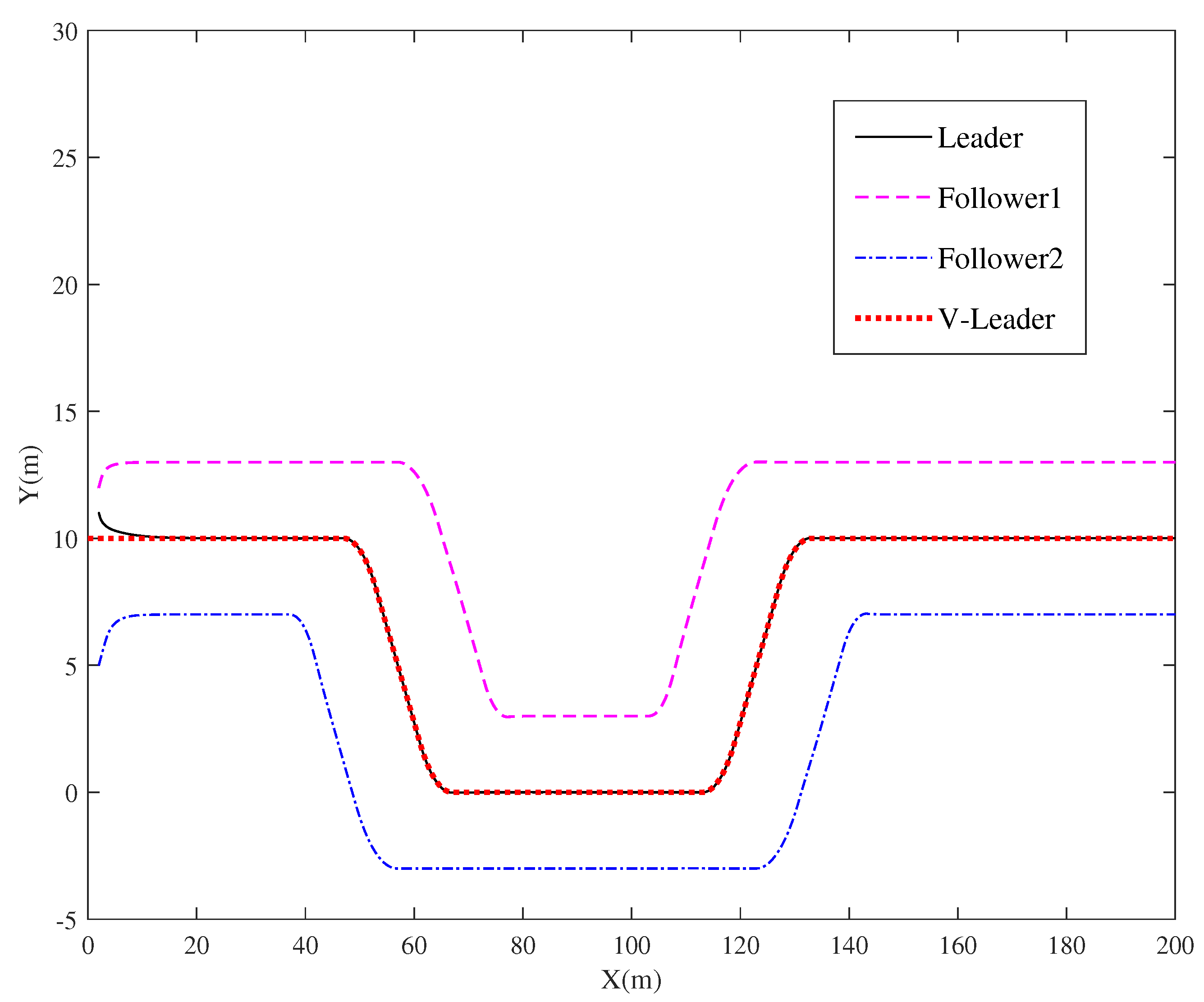
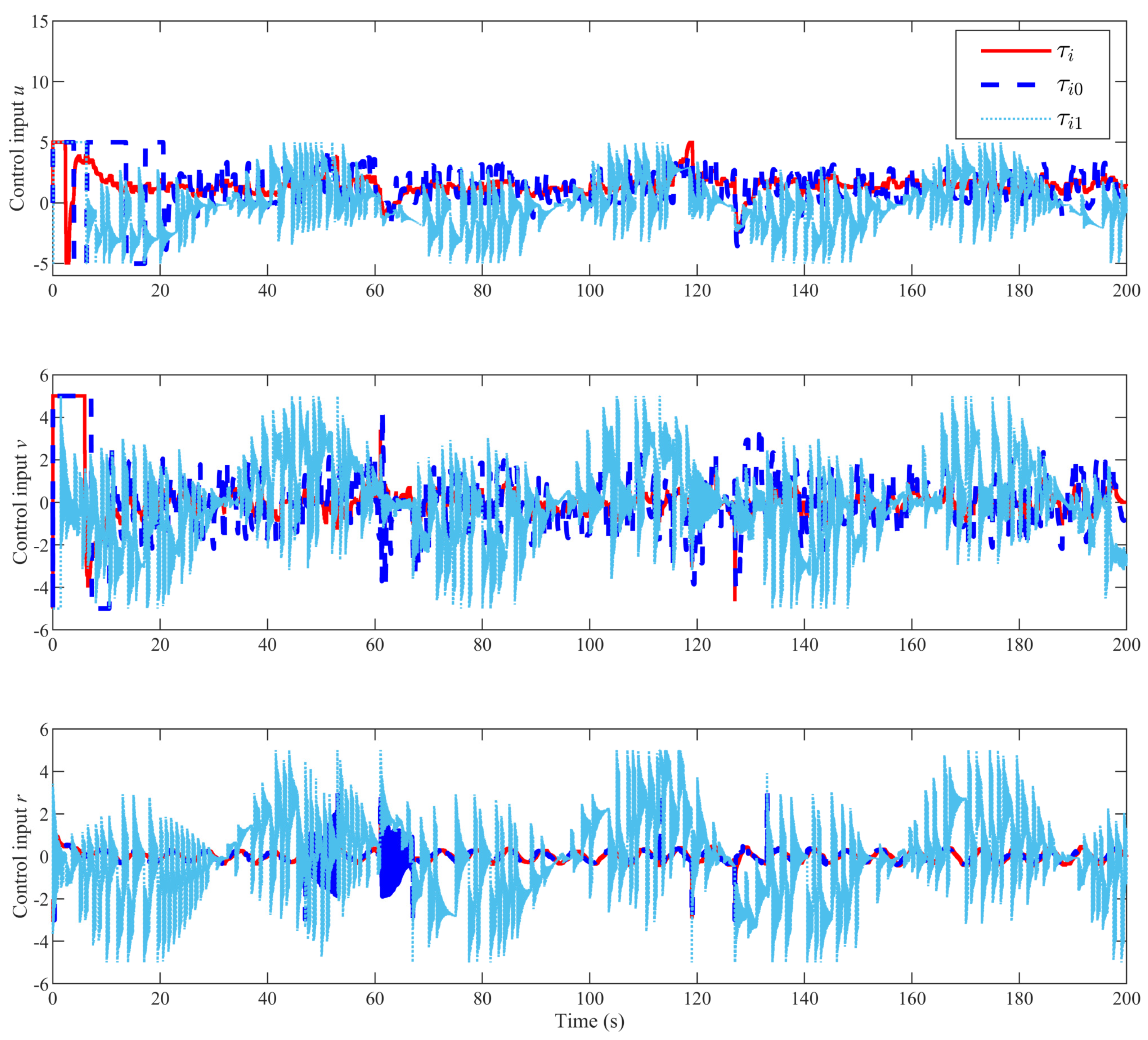
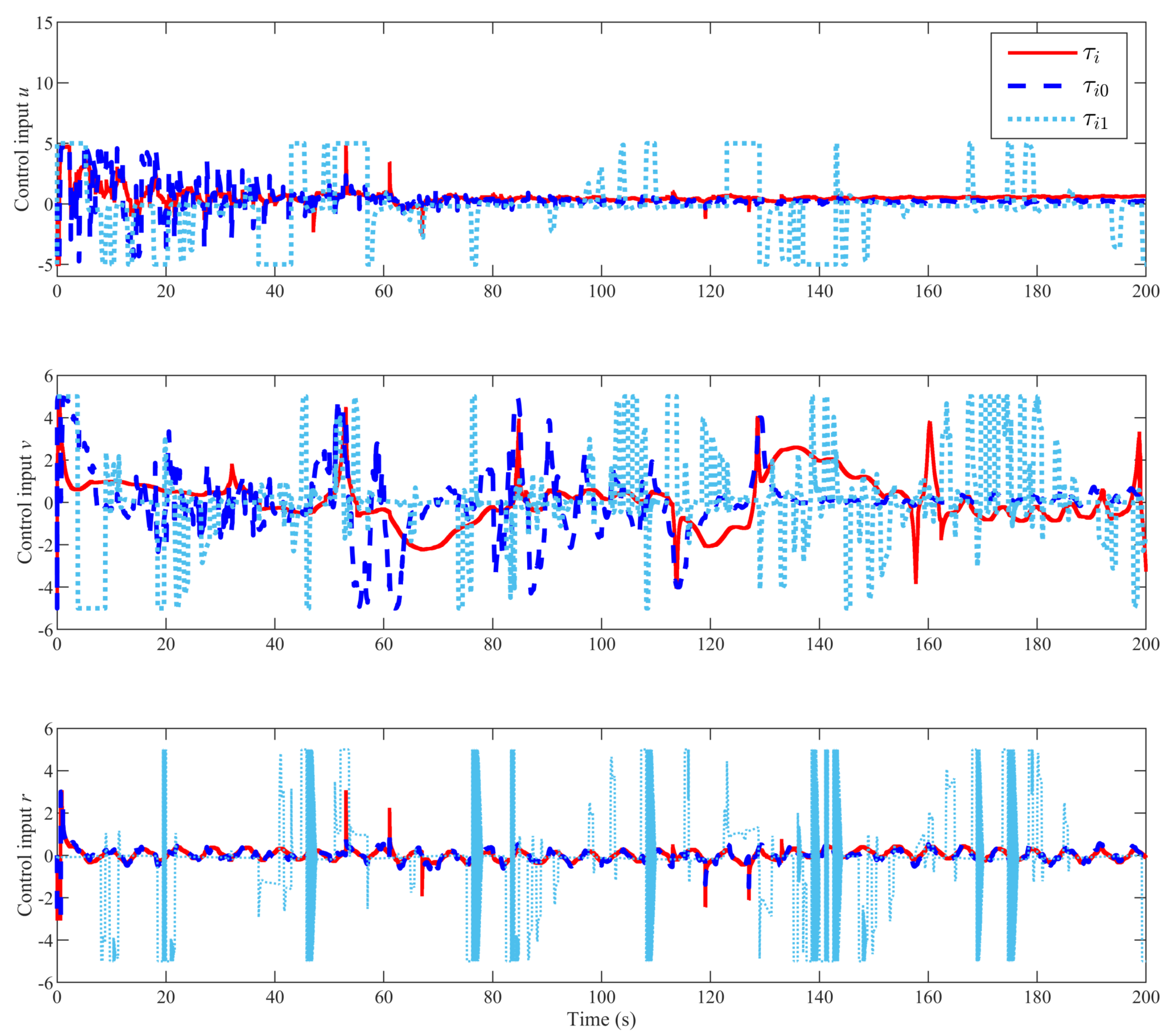
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, H.; Cui, G.; Ma, Q.; Li, Z.; Hao, W. Fixed-time disturbance observer-based distributed formation control for multiple QUAVs. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2181–2185. [Google Scholar] [CrossRef]
- Zou, Z.; Yang, S.; Zhao, L. Dual-loop control and state prediction analysis of QUAV trajectory tracking based on biological swarm intelligent optimization algorithm. Sci. Rep. 2024, 14, 19091. [Google Scholar]
- Mirzaee Kahagh, A.; Pazooki, F.; Etemadi Haghighi, S.; Asadi, D. Real-time formation control and obstacle avoidance algorithm for fixed-wing UAVs. Aeronaut. J. 2022, 126, 2111–2133. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, W.; Shan, Q.; Zhang, W. Cooperative path following control of USV-UAVs considering low design complexity and command transmission requirements. IEEE Trans. Intell. Veh. 2024, 9, 715–724. [Google Scholar]
- Najafi, A.; Vu, M.T.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics 2022, 10, 3009. [Google Scholar] [CrossRef]
- Lai, G.; Tao, G.; Zhang, Y.; Liu, Z.; Wang, J. Adaptive Actuator Failure Compensation Control Schemes for Uncertain Noncanonical Neural-Network Systems. IEEE Trans. Cybern. 2022, 52, 2635–2648. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Xuan Mung, N.; Hong, S.K. Actuator fault detection and fault-tolerant control for hexacopter. Sensors 2019, 19, 4721. [Google Scholar] [CrossRef]
- Ruiz-Carcel, C.; Starr, A. Data-based detection and diagnosis of faults in linear actuators. IEEE Trans. Instrum. Meas. 2018, 67, 2035–2047. [Google Scholar]
- Vizentin, G.; Vukelic, G.; Murawski, L.; Recho, N.; Orovic, J. Marine propulsion system failures—A review. J. Mar. Sci. Eng. 2020, 8, 662. [Google Scholar] [CrossRef]
- Kuperman, A.; Zhong, Q. Robust control of uncertain nonlinear systems with state delays based on an uncertainty and disturbance estimator. Int. J. Robust Nonlinear Control 2011, 21, 79–92. [Google Scholar]
- Chen, F.; Zhang, S.; Jiang, B.; Tao, G. Multiple model–based fault detection and diagnosis for helicopter with actuator faults via quantum information technique. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 228, 182–190. [Google Scholar] [CrossRef]
- Alattas, K.A.; Vu, M.T.; Mofid, O.; El-Sousy, F.F.M.; Alanazi, A.K.; Awrejcewicz, J.; Mobayen, S. Adaptive Nonsingular Terminal Sliding Mode Control for Performance Improvement of Perturbed Nonlinear Systems. Mathematics 2022, 10, 1064. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, B.; Tao, G. An intelligent self-repairing control for nonlinear MIMO systems via adaptive sliding mode control technology. J. Frankl. Inst. 2014, 351, 399–411. [Google Scholar] [CrossRef]
- Veluvolu, K.C.; Defoort, M.; Soh, Y.C. High-gain observer with sliding mode for nonlinear state estimation and fault reconstruction. J. Frankl. Inst. 2014, 351, 1995–2014. [Google Scholar] [CrossRef]
- Zou, Y. Nonlinear robust adaptive hierarchical sliding mode control approach for quadrotors. Int. J. Robust Nonlinear Control 2017, 27, 925–941. [Google Scholar] [CrossRef]
- Mofid, O.; Amirkhani, S.; ud Din, S.; Mobayen, S.; Vu, M.T.; Assawinchaichote, W. Finite-time convergence of perturbed nonlinear systems using adaptive barrier-function nonsingular sliding mode control with experimental validation. J. Vib. Control 2023, 29, 3326–3339. [Google Scholar] [CrossRef]
- Witkowska, A.; Śmierzchalski, R. Adaptive dynamic control allocation for dynamic positioning of marine vessel based on backstepping method and sequential quadratic programming. Ocean Eng. 2018, 163, 570–582. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Yang, S.X. A novel tracking controller for autonomous underwater vehicles with thruster fault accommodation. J. Navig. 2016, 69, 593–612. [Google Scholar] [CrossRef]
- Huang, H.; Wan, L.; Chang, W.-T.; Pang, Y.-J.; Jiang, S.-Q. A fault-tolerable control scheme for an open-frame underwater vehicle. Int. J. Adv. Robot. Syst. 2014, 11, 77. [Google Scholar]
- Qin, H.; Yang, H.; Sun, Y.; Zhang, Y. Adaptive interval type-2 fuzzy fixed-time control for underwater walking robot with error constraints and actuator faults using prescribed performance terminal sliding-mode surfaces. Int. J. Fuzzy Syst. 2021, 23, 1137–1149. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach. Neurocomputing 2022, 481, 322–332. [Google Scholar] [CrossRef]
- Wang, Y.; Wilson, P.A.; Liu, X. Adaptive neural network-based backstepping fault tolerant control for underwater vehicles with thruster fault. Ocean Eng. 2015, 110, 15–24. [Google Scholar]
- Chen, H.; Ren, H.; Gao, Z.; Yu, F.; Guan, W.; Wang, D. Disturbance observer-based finite-time control scheme for dynamic positioning of ships subject to thruster faults. Int. J. Robust Nonlinear Control 2021, 31, 6255–6271. [Google Scholar]
- Hao, L.Y.; Zhang, H.; Li, T.S.; Lin, B.; Chen, C.P. Fault tolerant control for dynamic positioning of unmanned marine vehicles based on TS fuzzy model with unknown membership functions. IEEE Trans. Veh. Technol. 2021, 70, 146–157. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Wang, Y.; Rogers, E. Design and experimental validation of an adaptive sliding mode observer-based fault-tolerant control for underwater vehicles. IEEE Trans. Control Syst. Technol. 2018, 27, 2655–2662. [Google Scholar] [CrossRef]
- Huang, Y.; Dai, S.L. Similarity-Based Rigidity Formation Maneuver Control of Underactuated Surface Vehicles Over Directed Graphs. IEEE Trans. Control Netw. Syst. 2024, 12, 461–473. [Google Scholar] [CrossRef]
- Wang, B.; Nersesov, S.G.; Ashrafiuon, H. Robust formation control and obstacle avoidance for heterogeneous underactuated surface vessel networks. IEEE Trans. Control Netw. Syst. 2022, 9, 125–137. [Google Scholar]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances. Ocean Eng. 2018, 167, 36–44. [Google Scholar]
- Wang, P.; Yu, C.; Pan, Y.J. Finite-time output feedback cooperative formation control for marine surface vessels with unknown actuator faults. IEEE Trans. Control Netw. Syst. 2022, 10, 887–899. [Google Scholar]
- Shojaei, K. Leader–follower formation control of underactuated autonomous marine surface vehicles with limited torque. Ocean Eng. 2015, 105, 196–205. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.L.; Luo, F. Leader–follower formation control of USVs with prescribed performance and collision avoidance. IEEE Trans. Ind. Inform. 2018, 15, 572–581. [Google Scholar]
- Chen, F.; Dimarogonas, D.V. Leader–follower formation control with prescribed performance guarantees. IEEE Trans. Control Netw. Syst. 2020, 8, 450–461. [Google Scholar]
- Fan, Y.; Liu, B.; Wang, G.; Mu, D. Adaptive fast non-singular terminal sliding mode path following control for an underactuated unmanned surface vehicle with uncertainties and unknown disturbances. Sensors 2021, 21, 7454. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Du, J. Global robust adaptive trajectory tracking control for surface ships under input saturation. IEEE J. Ocean. Eng. 2018, 45, 442–450. [Google Scholar]
- Chen, Z.; Sulem, A. An integral representation theorem of g-expectations. Risk Decis. Anal. 2011, 2, 245–255. [Google Scholar]
- Chen, Q.; Zhang, Q.; Hu, Y.; Liu, Y.; Wu, H. Euclidean distance damping–based adaptive sliding mode fault-tolerant event-triggered trajectory-tracking control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2023, 237, 551–567. [Google Scholar]
- Wang, H.; Zhou, X.; Tian, Y. Robust adaptive fault-tolerant control using RBF-based neural network for a rigid-flexible robotic system with unknown control direction. Int. J. Robust Nonlinear Control 2022, 32, 1272–1302. [Google Scholar]
- Min, H.; Xu, S.; Zhang, Z. Adaptive finite-time stabilization of stochastic nonlinear systems subject to full-state constraints and input saturation. IEEE Trans. Autom. Control 2020, 66, 1306–1313. [Google Scholar]
- Shi, J.; Zhou, D.; Yang, Y.; Sun, J. Fault tolerant multivehicle formation control framework with applications in multiquadrotor systems. Sci. China. Inf. Sci. 2018, 61, 124201. [Google Scholar]
- Zhang, G.; Liu, S.; Zhang, X. Adaptive distributed fault-tolerant control for underactuated surface vehicles with bridge-to-bridge event-triggered mechanism. Ocean Eng. 2022, 262, 112205. [Google Scholar]
- Chen, Q.; Hu, Y.; Zhang, Q.; Jiang, J.; Chi, M.; Zhu, Y. Dynamic damping-based terminal sliding mode event-triggered fault-tolerant pre-compensation stochastic control for tracked ROV. J. Mar. Sci. Eng. 2022, 10, 1228. [Google Scholar] [CrossRef]

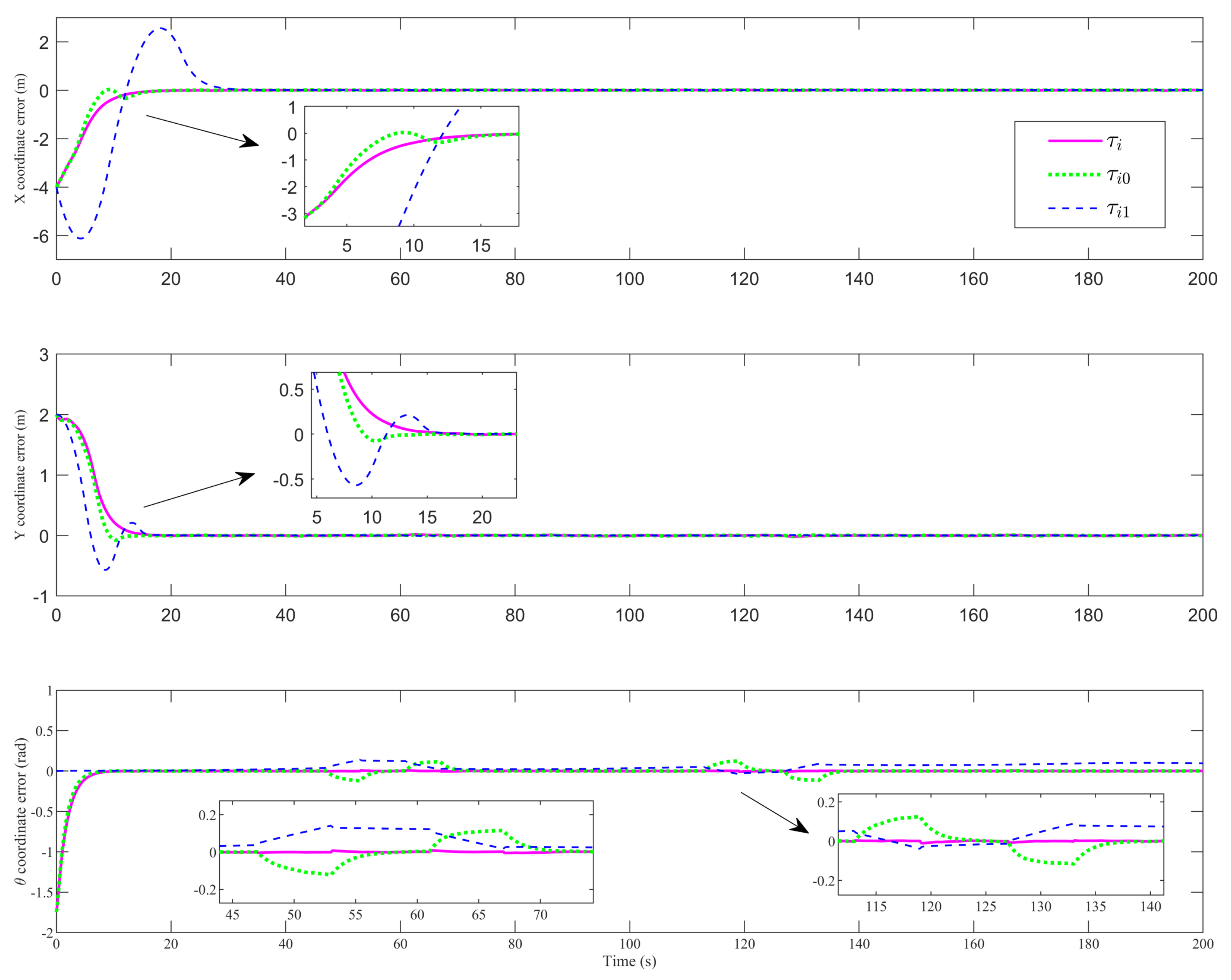
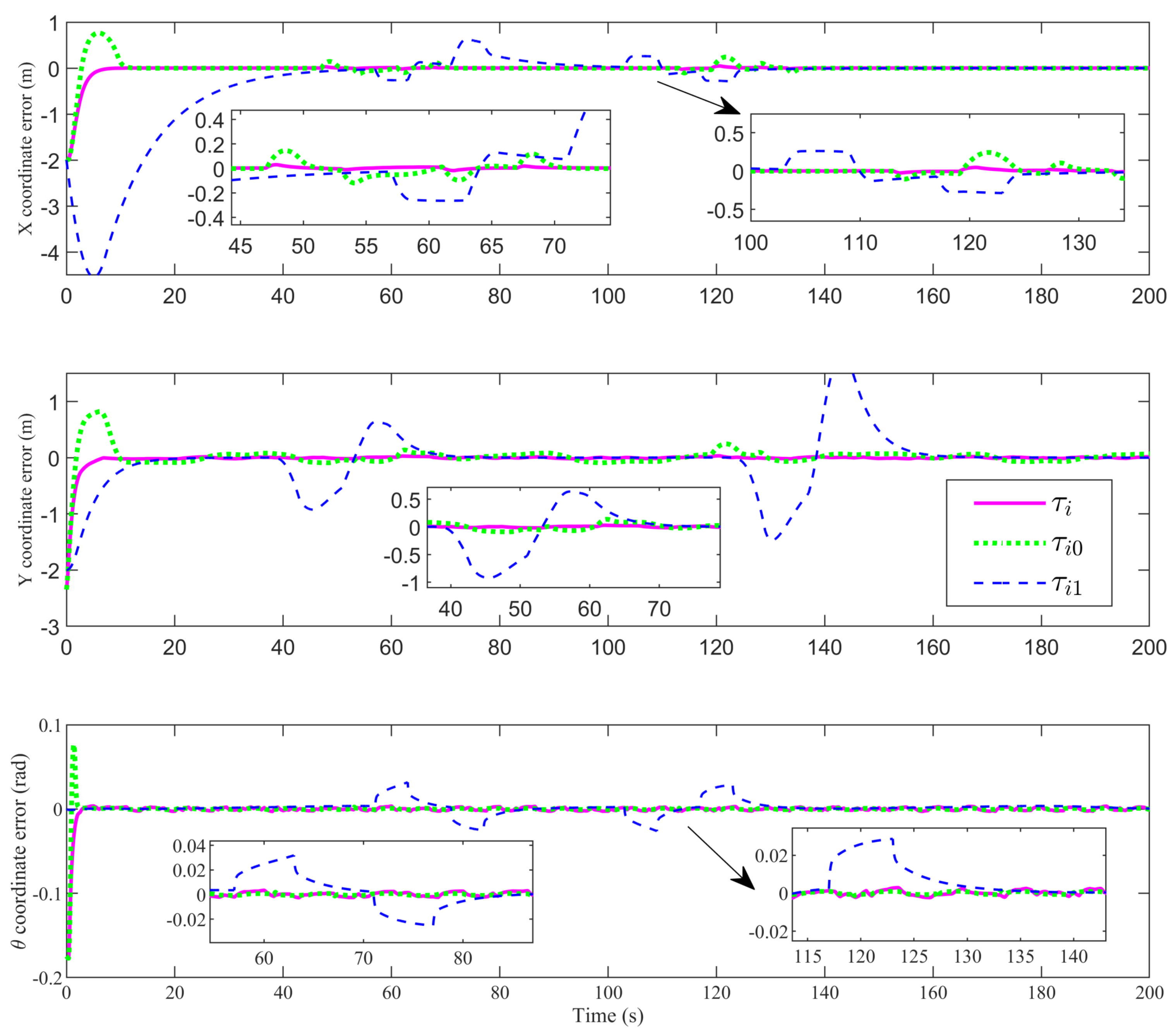

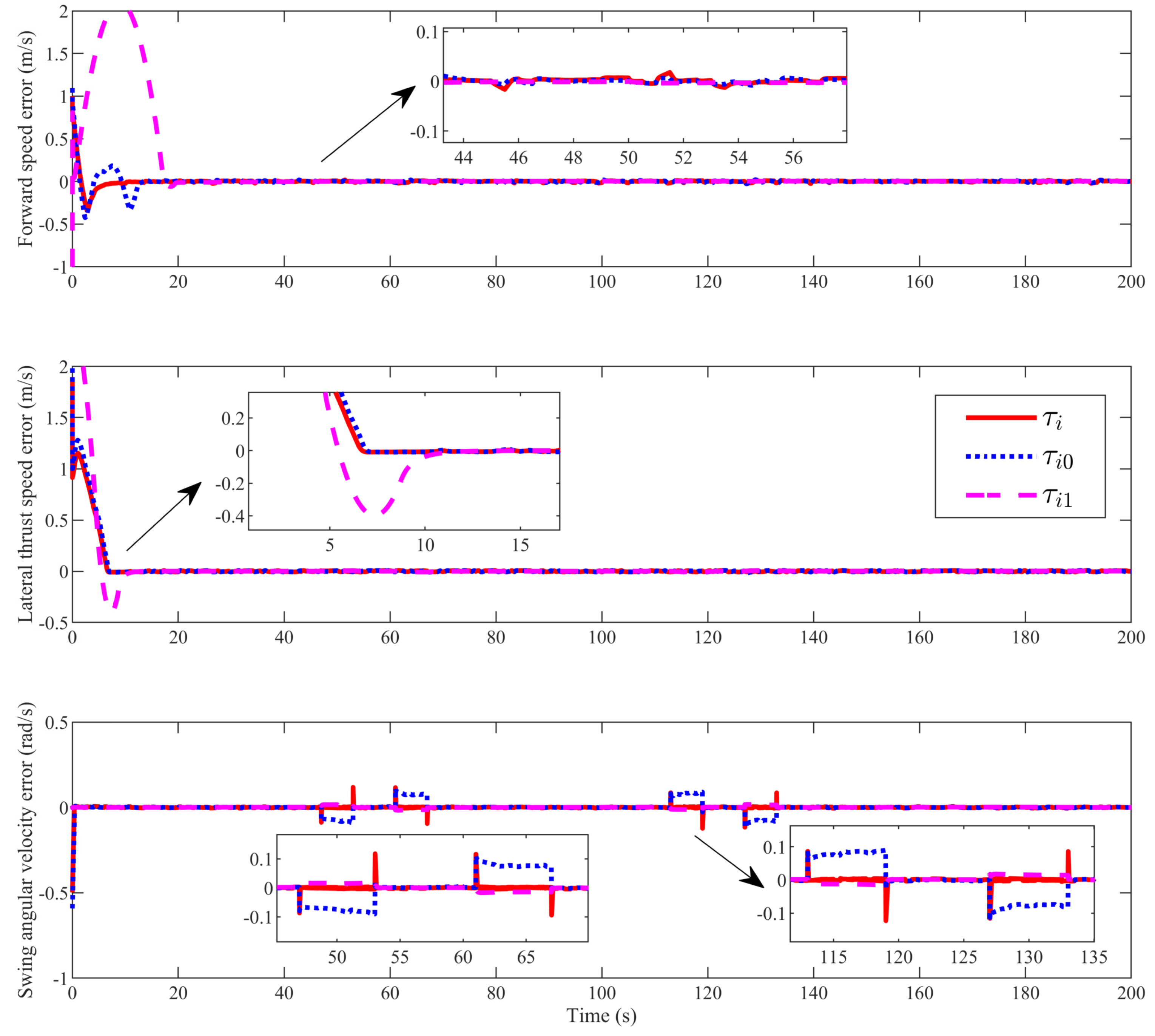
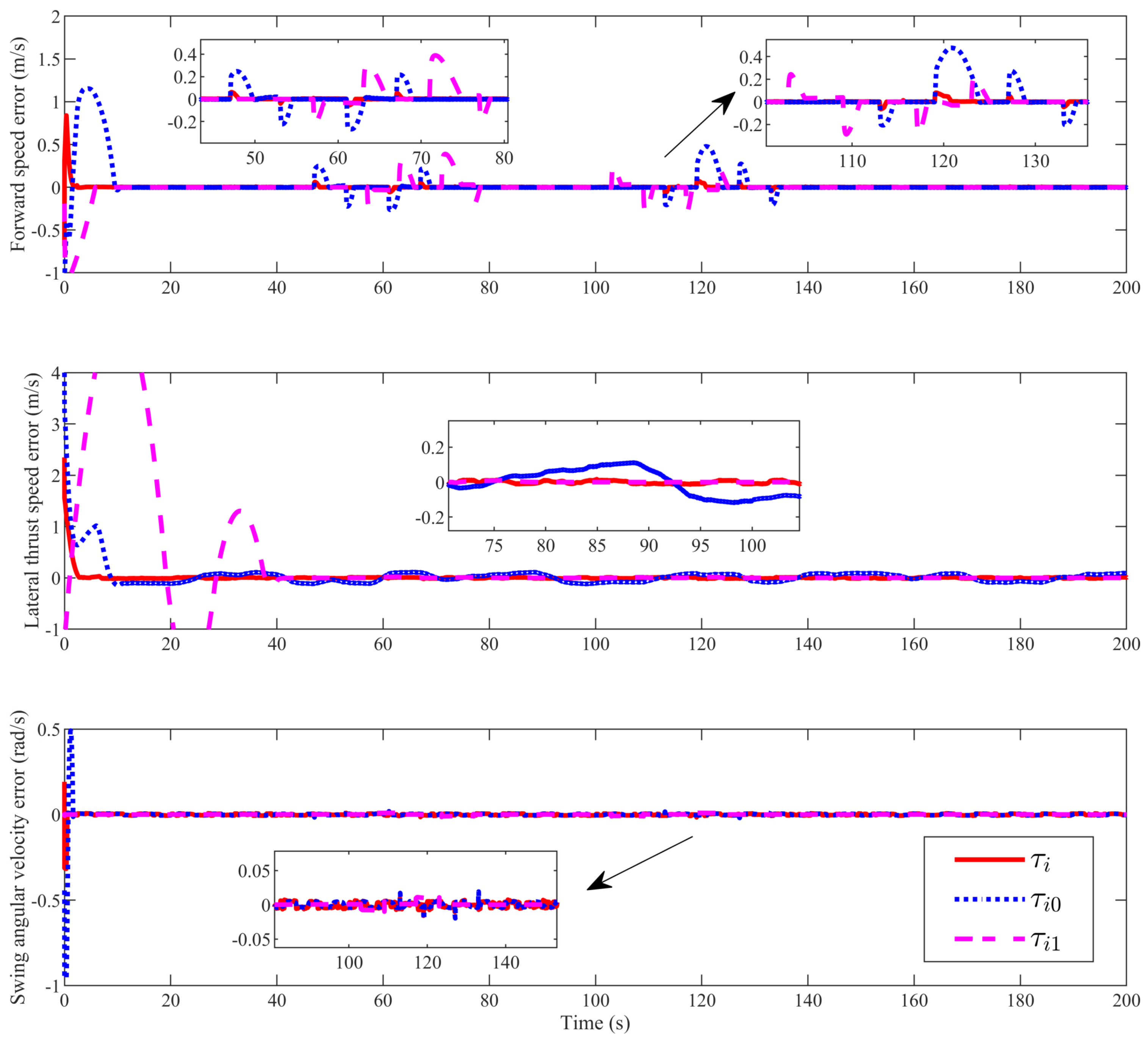
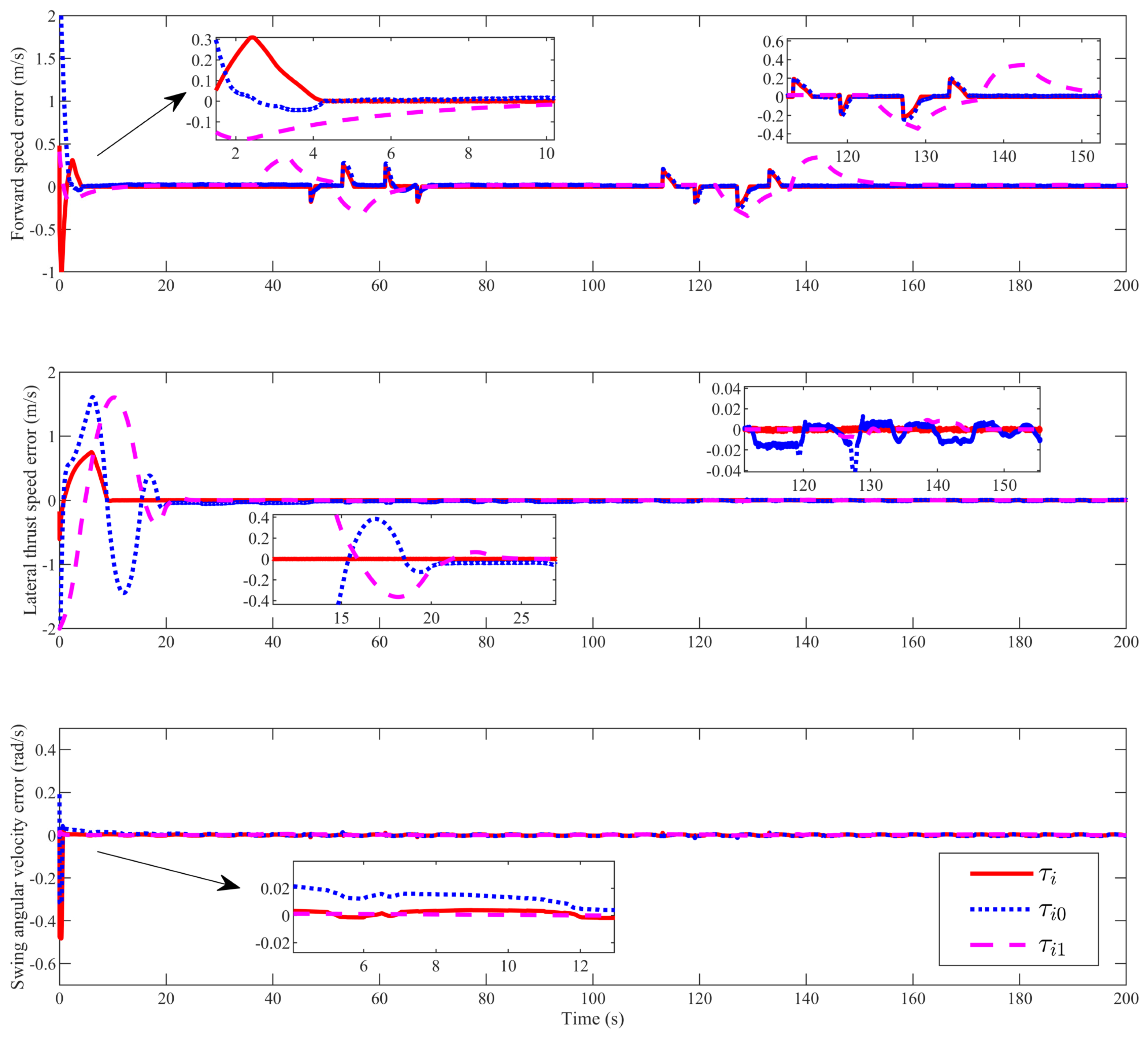
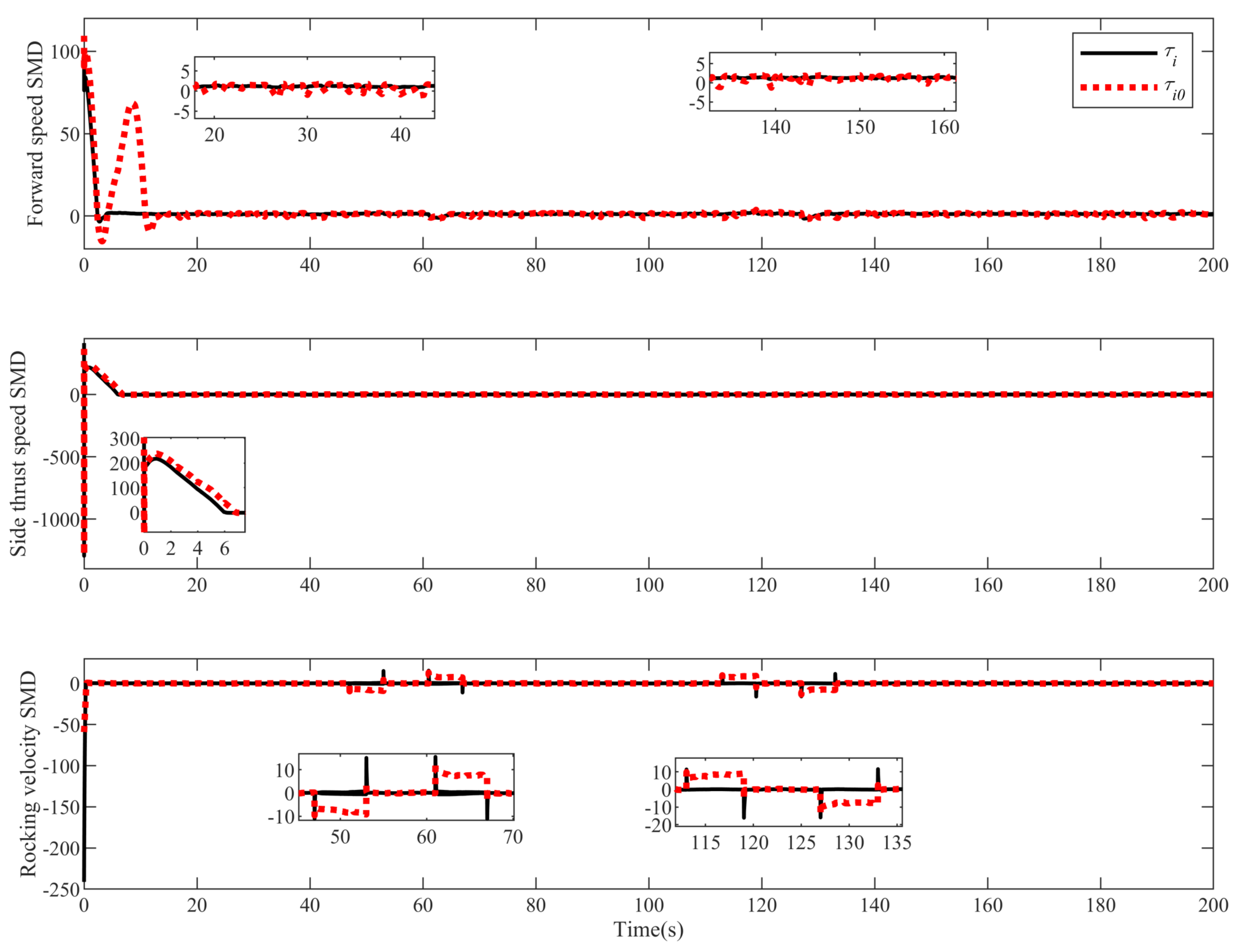
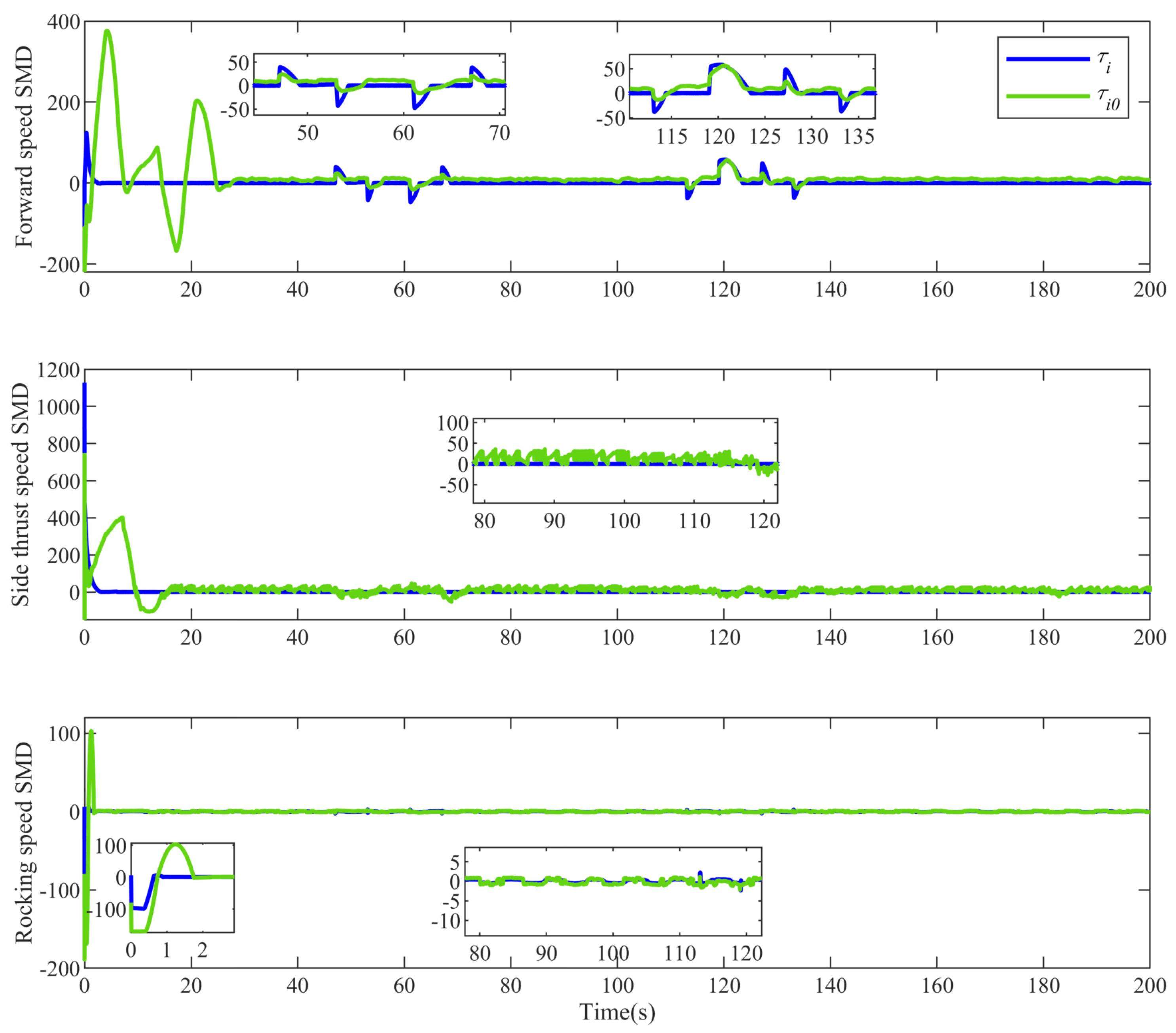
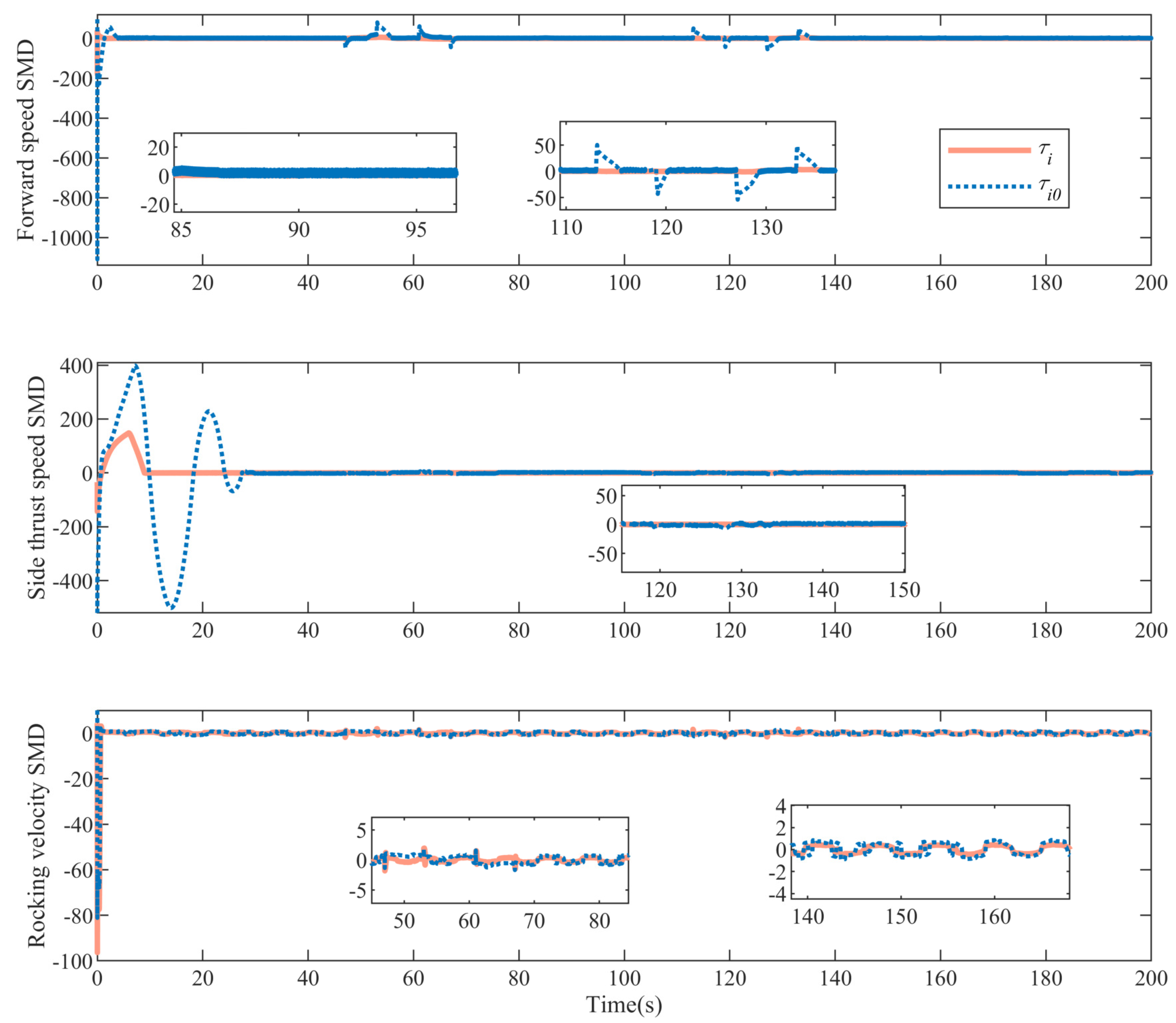

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 10 | |||
| 1 | 25 | ||
| 17 | |||
| 15 | |||
| 180 | |||
| 130 | |||
| 2 | 40 | ||
| 1 | |||
| 1 | |||
| Evaluation Criterion | MIAC | MISE | Number of Transmissions |
|---|---|---|---|
| Leader | |||
| Follower 1 | |||
| Follower 2 |
| Evaluation Criterion | MIAC | MISE | Number of Transmissions |
|---|---|---|---|
| Leader | 20,000 | ||
| Follower 1 | 20,000 | ||
| Follower 2 | 20,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, Q.; Xu, L.; Xu, S.; Zhang, Y.; Hu, Y. Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure. J. Mar. Sci. Eng. 2025, 13, 657. https://doi.org/10.3390/jmse13040657
Zhang S, Zhang Q, Xu L, Xu S, Zhang Y, Hu Y. Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure. Journal of Marine Science and Engineering. 2025; 13(4):657. https://doi.org/10.3390/jmse13040657
Chicago/Turabian StyleZhang, Sihang, Qiang Zhang, Ligangao Xu, Sheng Xu, Yan Zhang, and Yancai Hu. 2025. "Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure" Journal of Marine Science and Engineering 13, no. 4: 657. https://doi.org/10.3390/jmse13040657
APA StyleZhang, S., Zhang, Q., Xu, L., Xu, S., Zhang, Y., & Hu, Y. (2025). Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure. Journal of Marine Science and Engineering, 13(4), 657. https://doi.org/10.3390/jmse13040657







