A Numerical Simulation Study on Hydrogen-Enriched Gas Explosions on Hydrogen Fuel Cell Ships Based on OpenFOAM
Abstract
1. Introduction
1.1. Current Status of Safety Research on Hydrogen Fuel Cell Ships
1.2. Application of Numerical Simulations in Hydrogen Explosion Research
2. Materials and Methods
2.1. Theoretical Basis
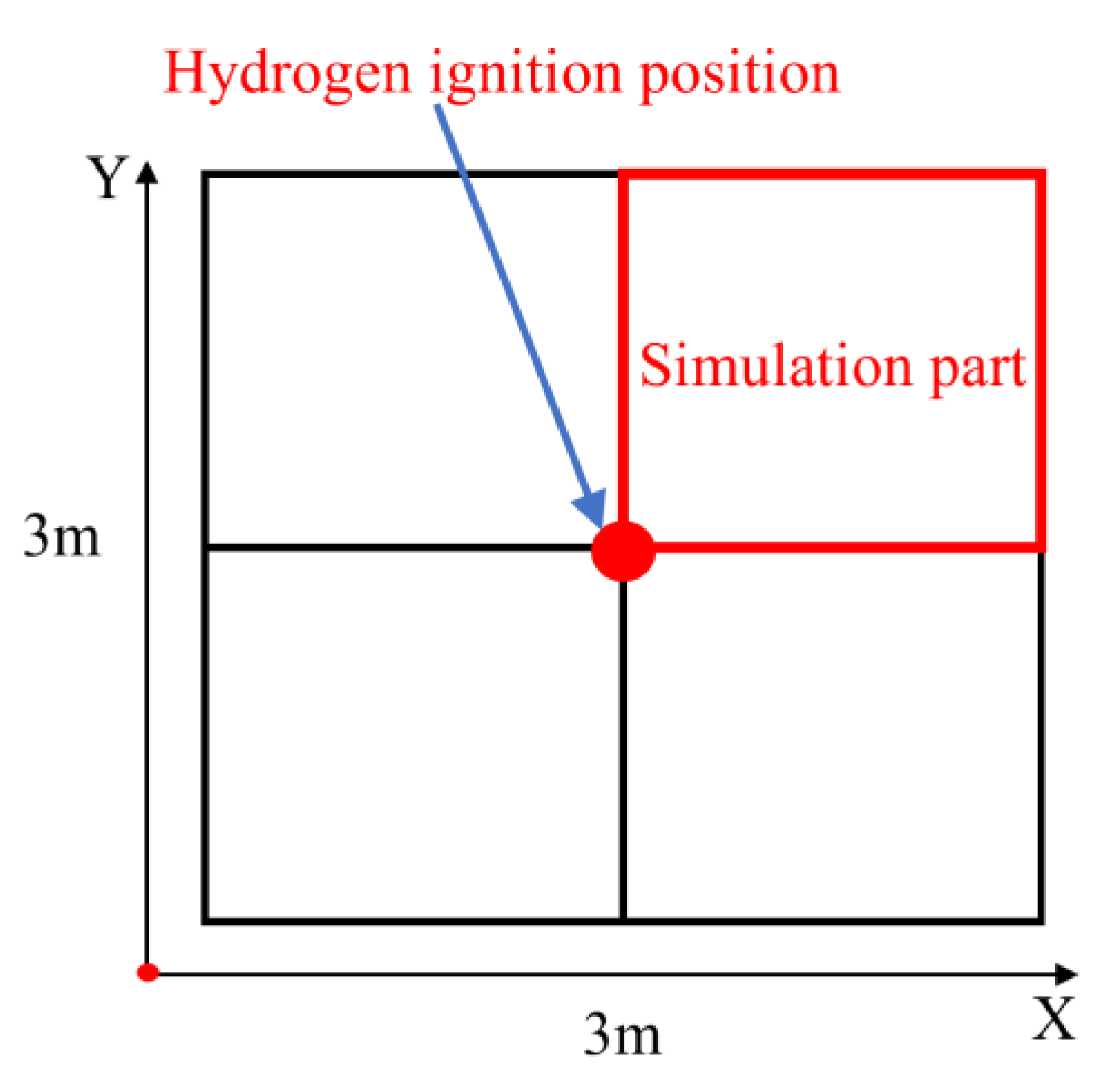
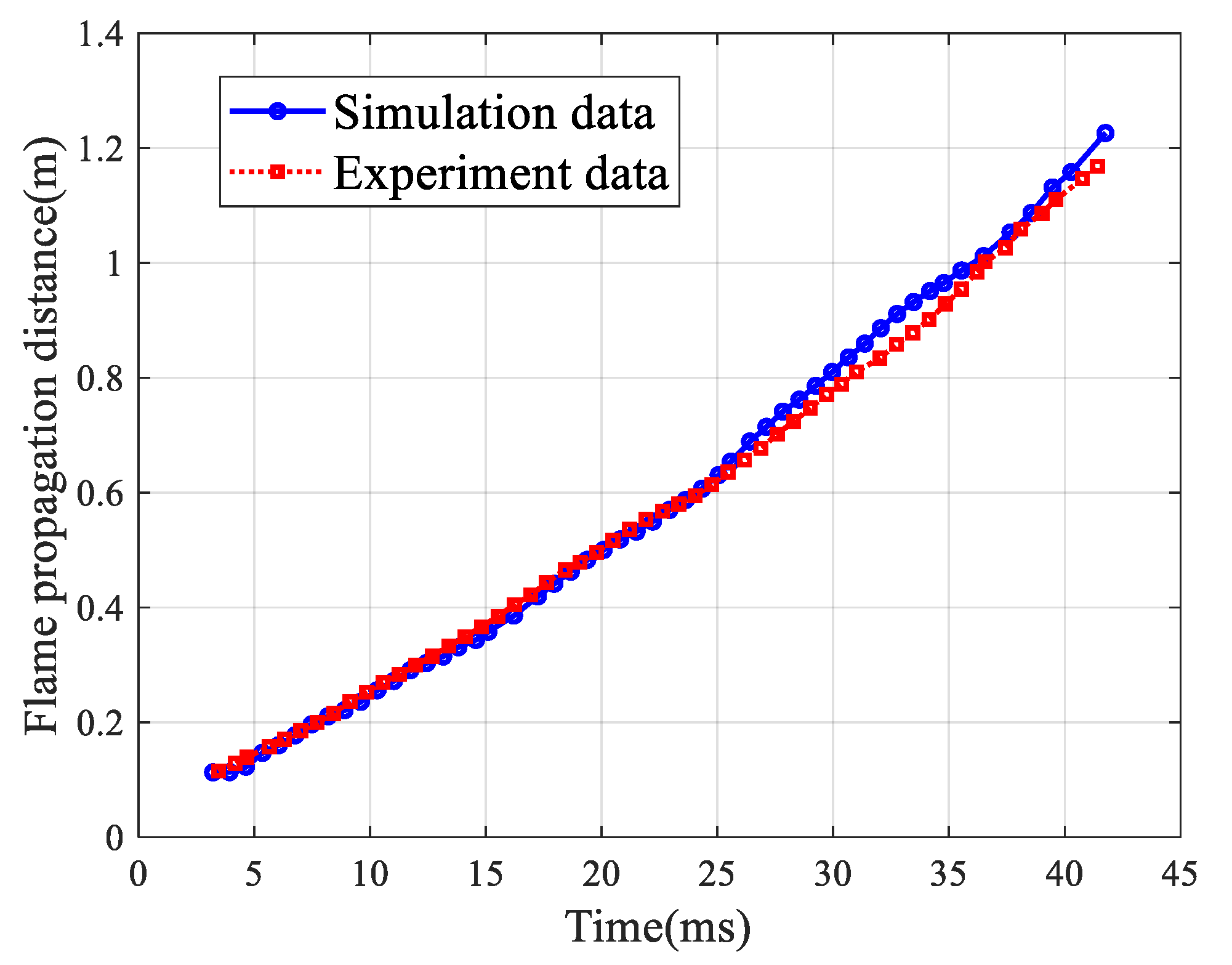
2.2. Computational Model Validation
2.3. Numerical Configuration
3. Results
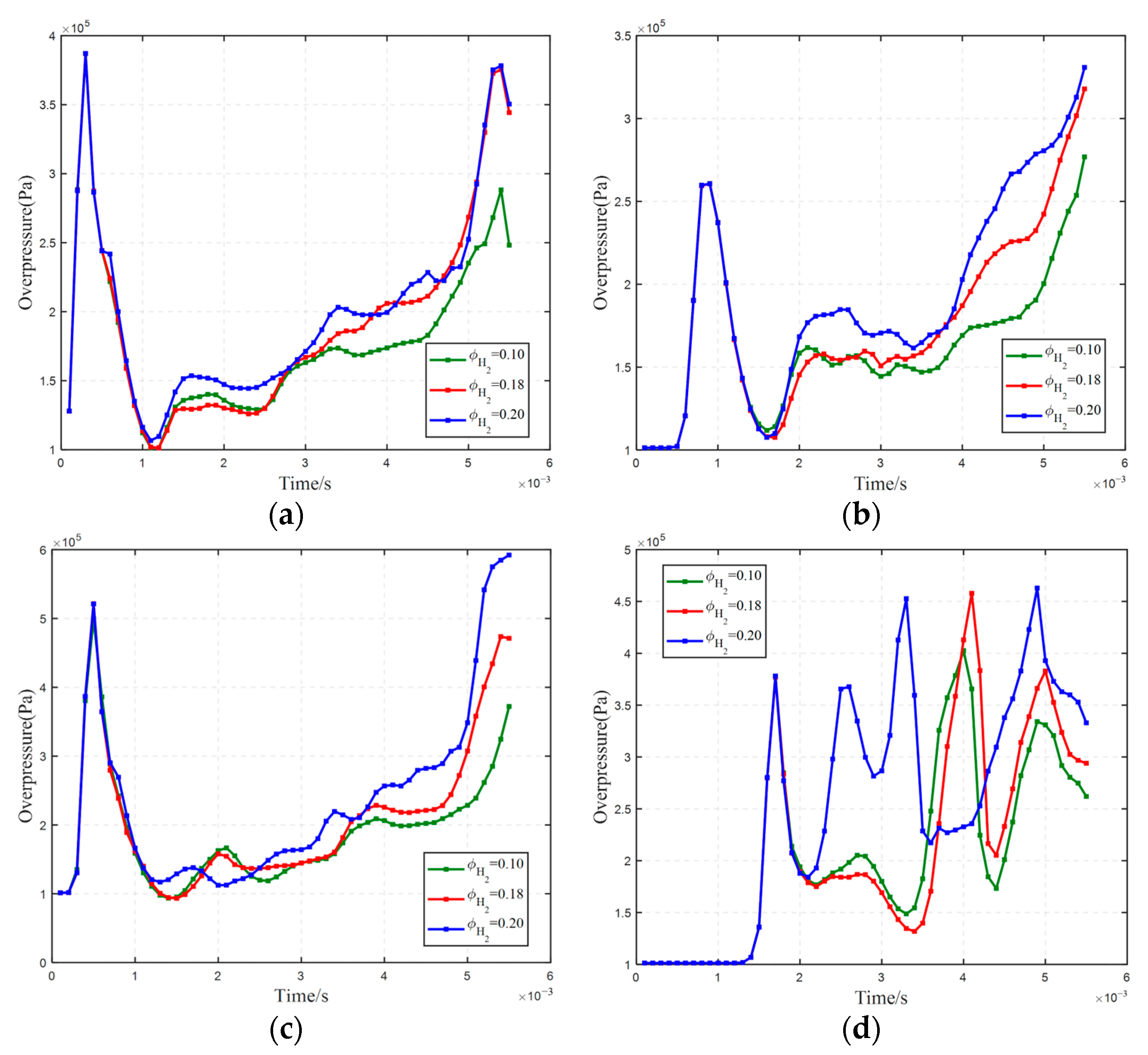
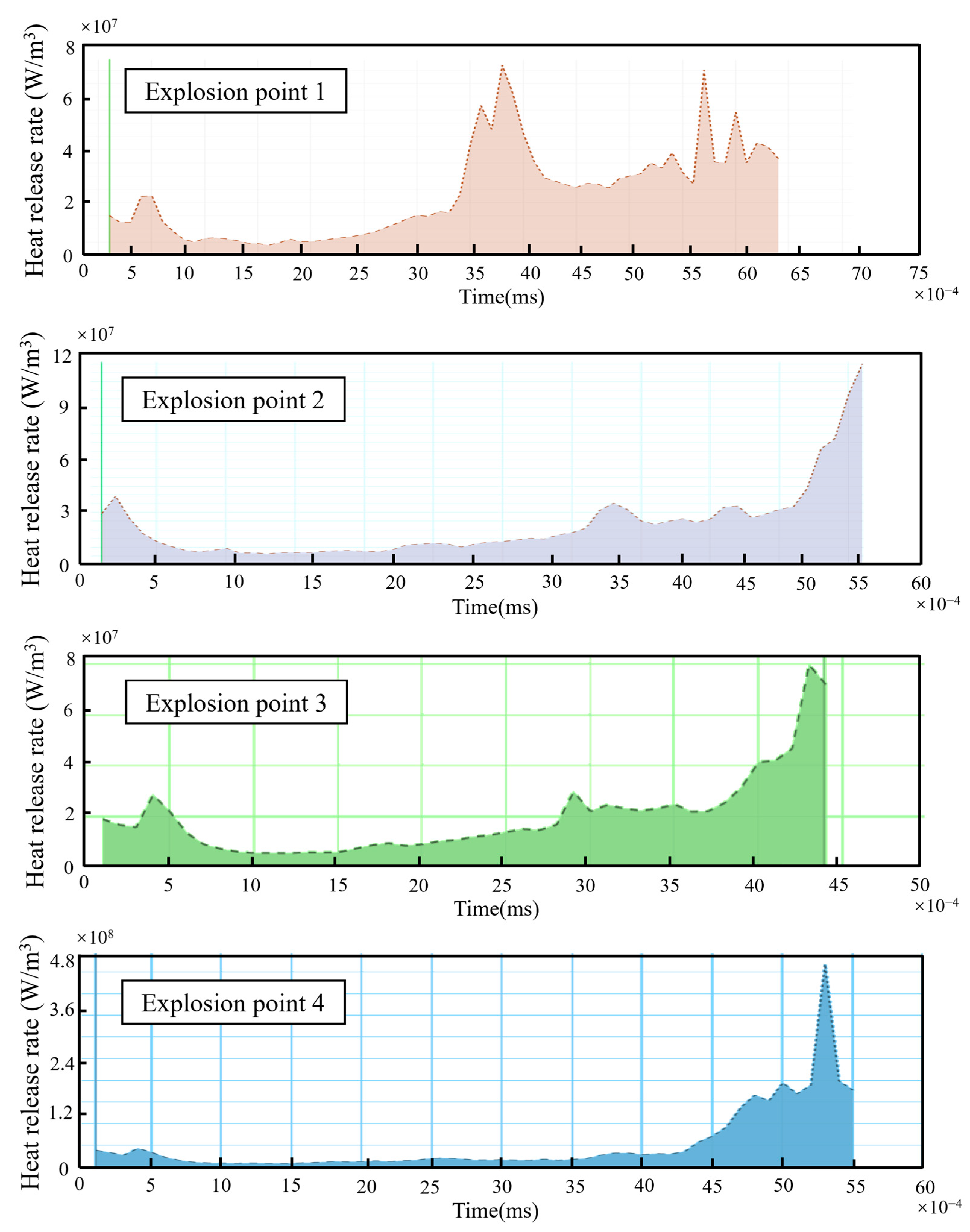
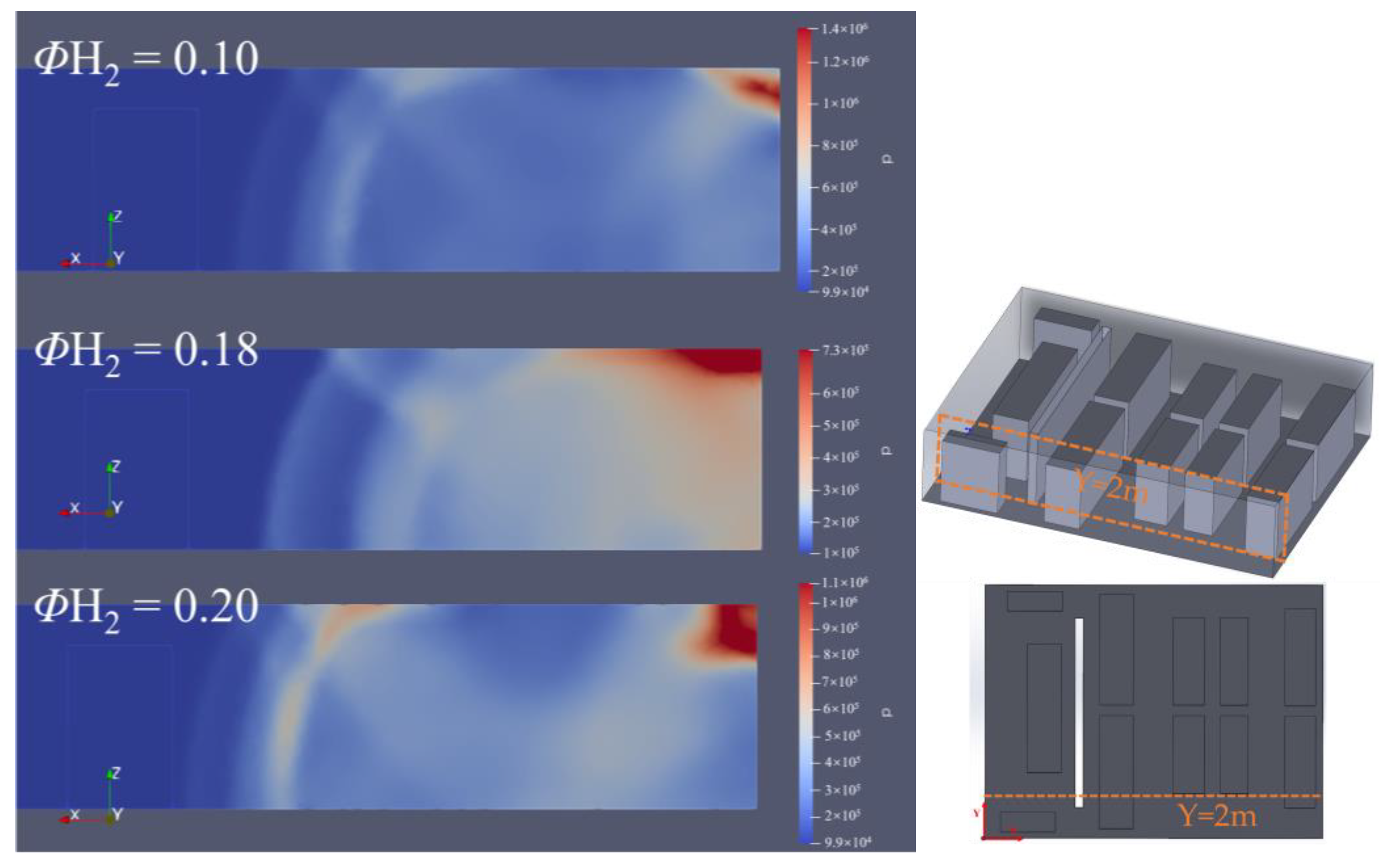
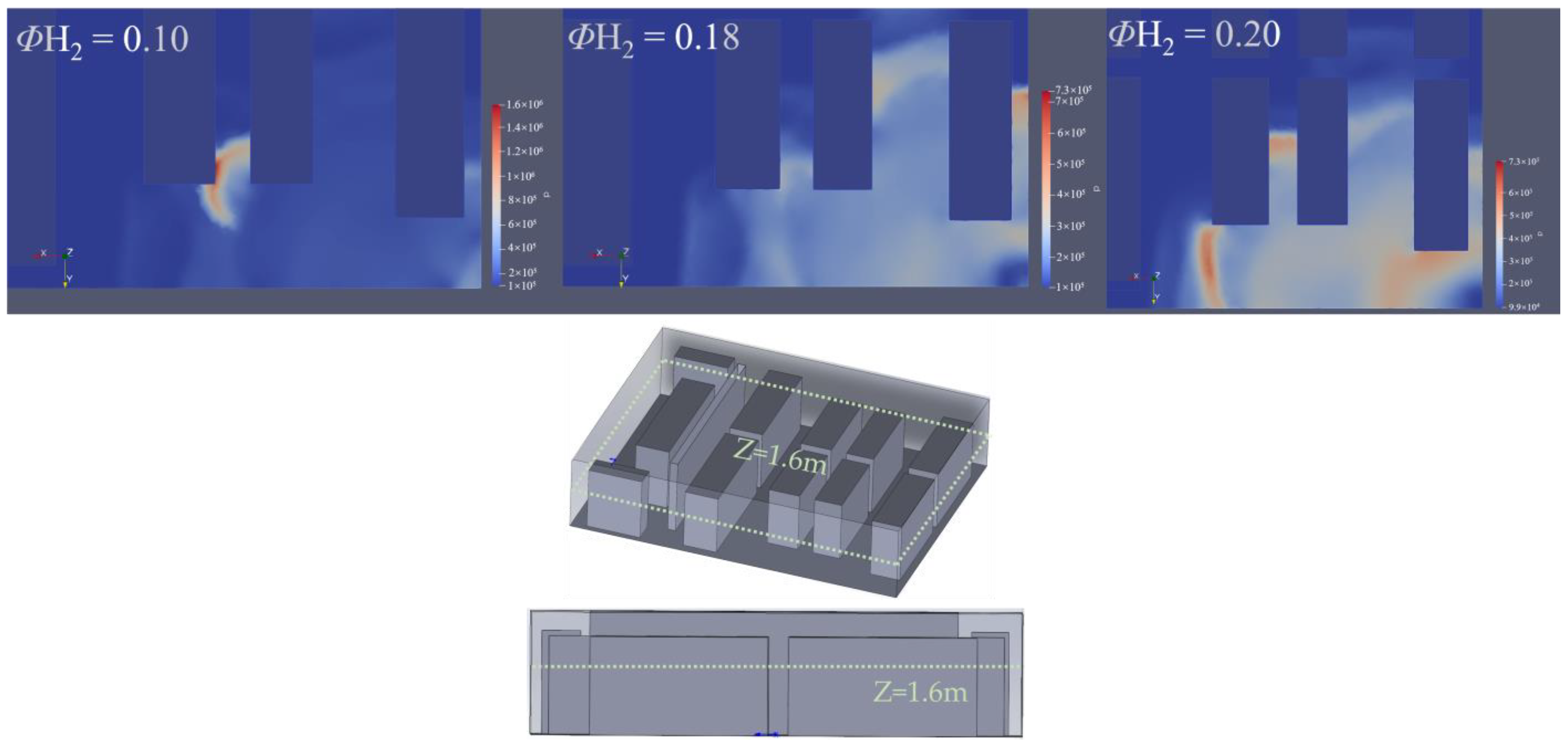
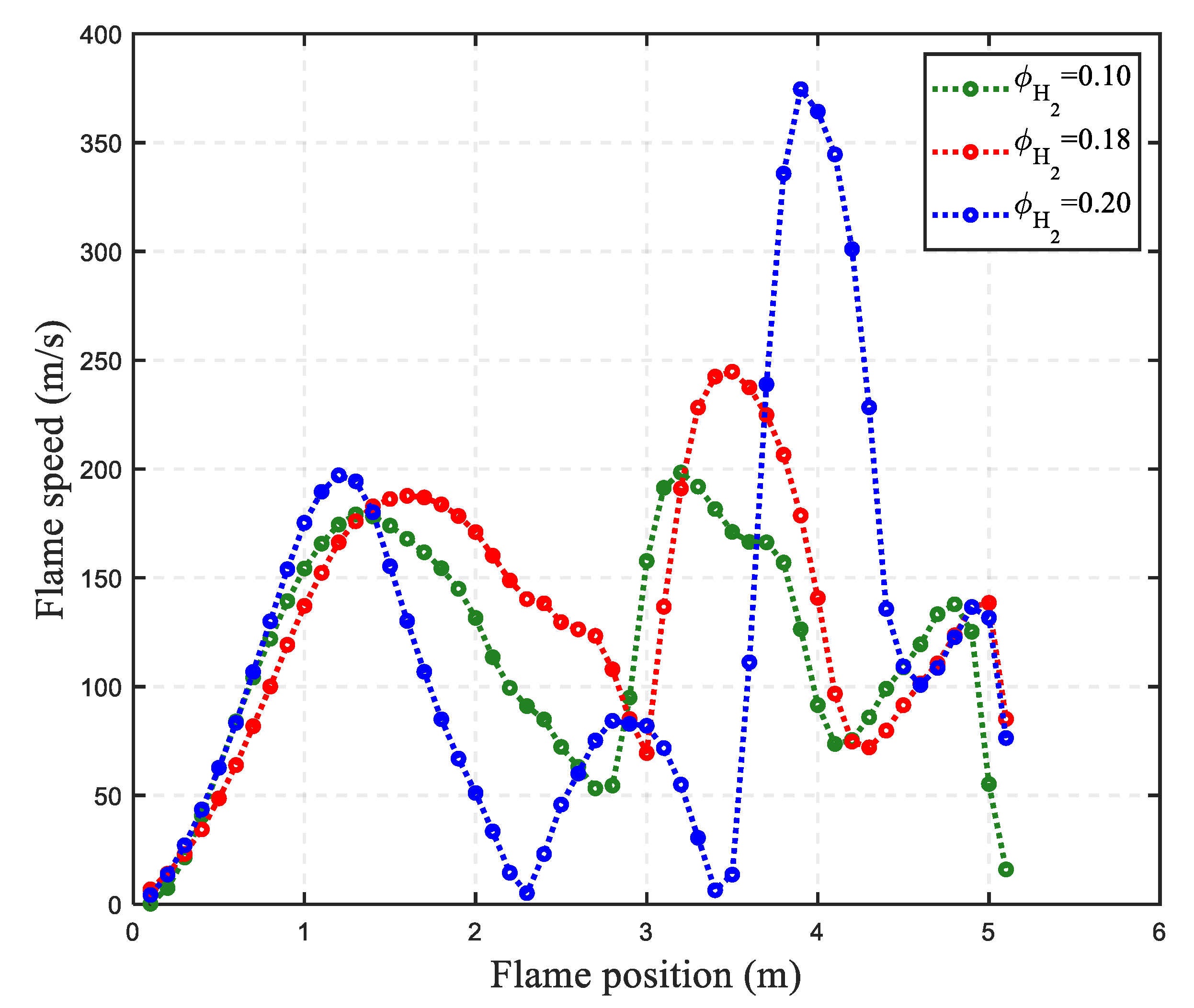
3.1. Effect of Hydrogen Concentration on Hydrogen Explosion
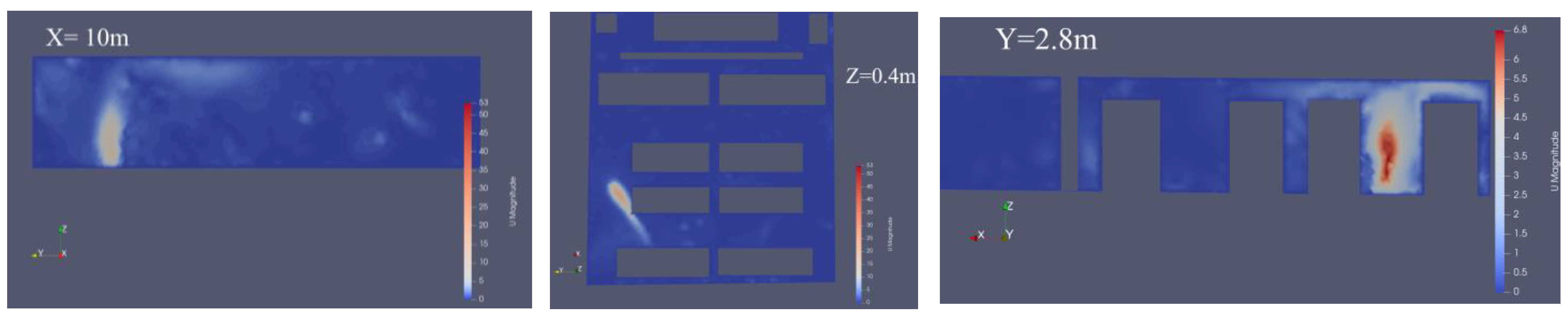
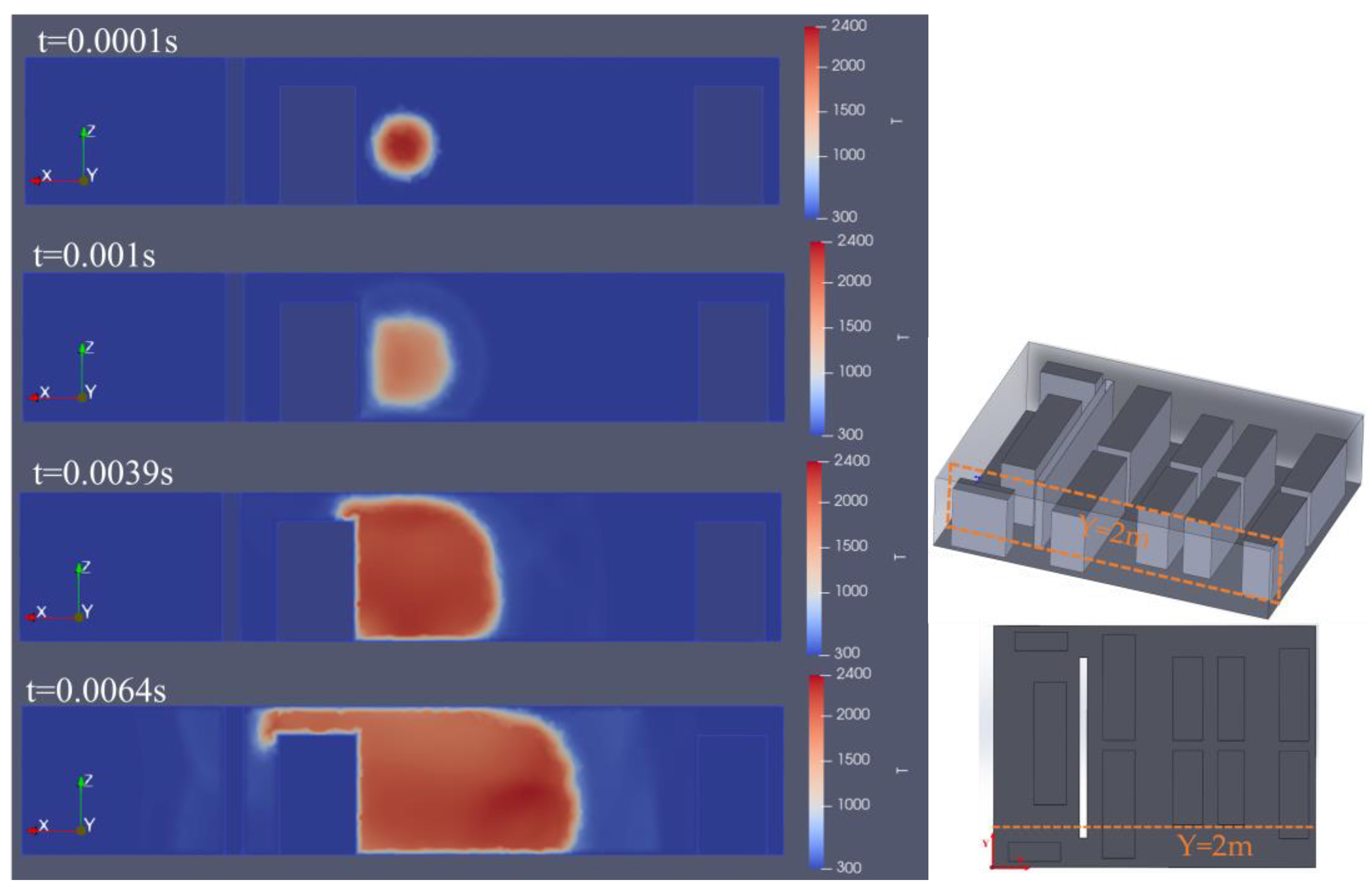
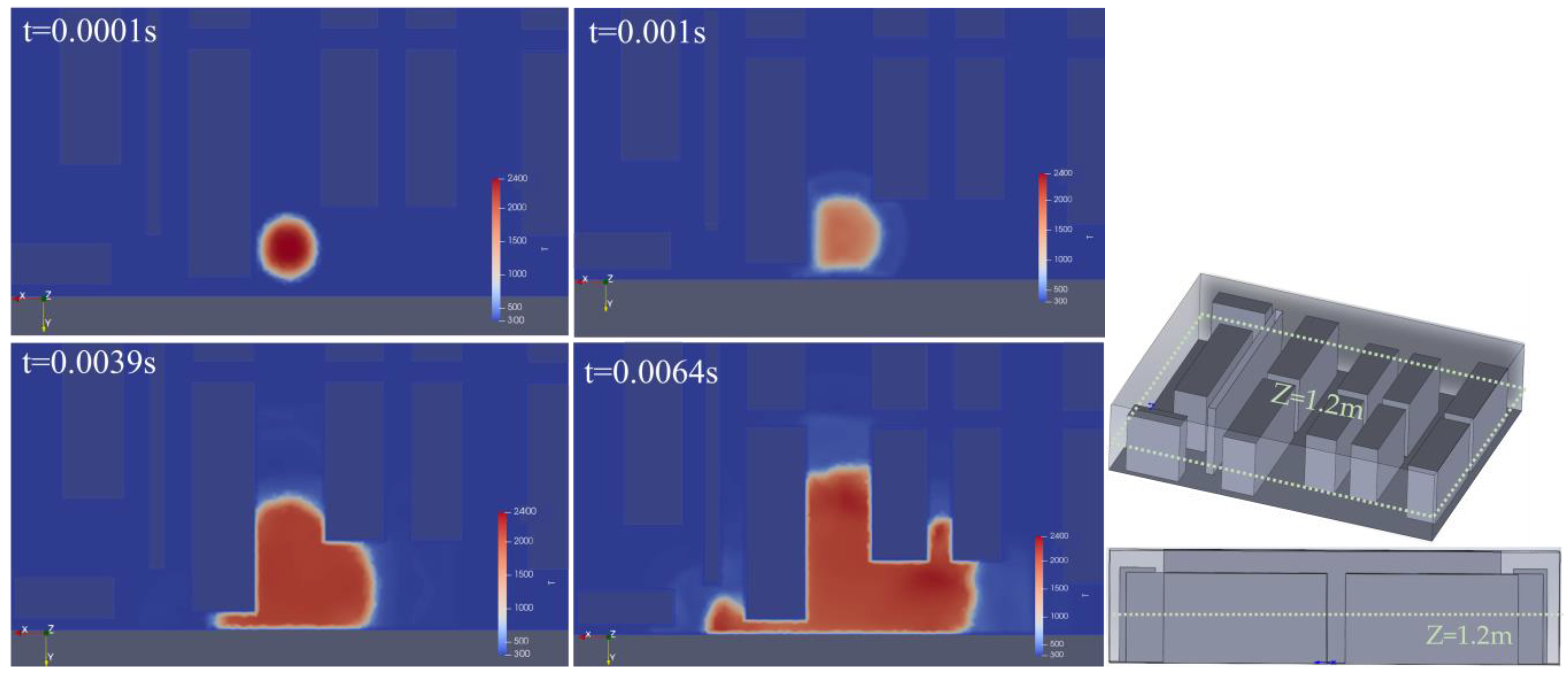
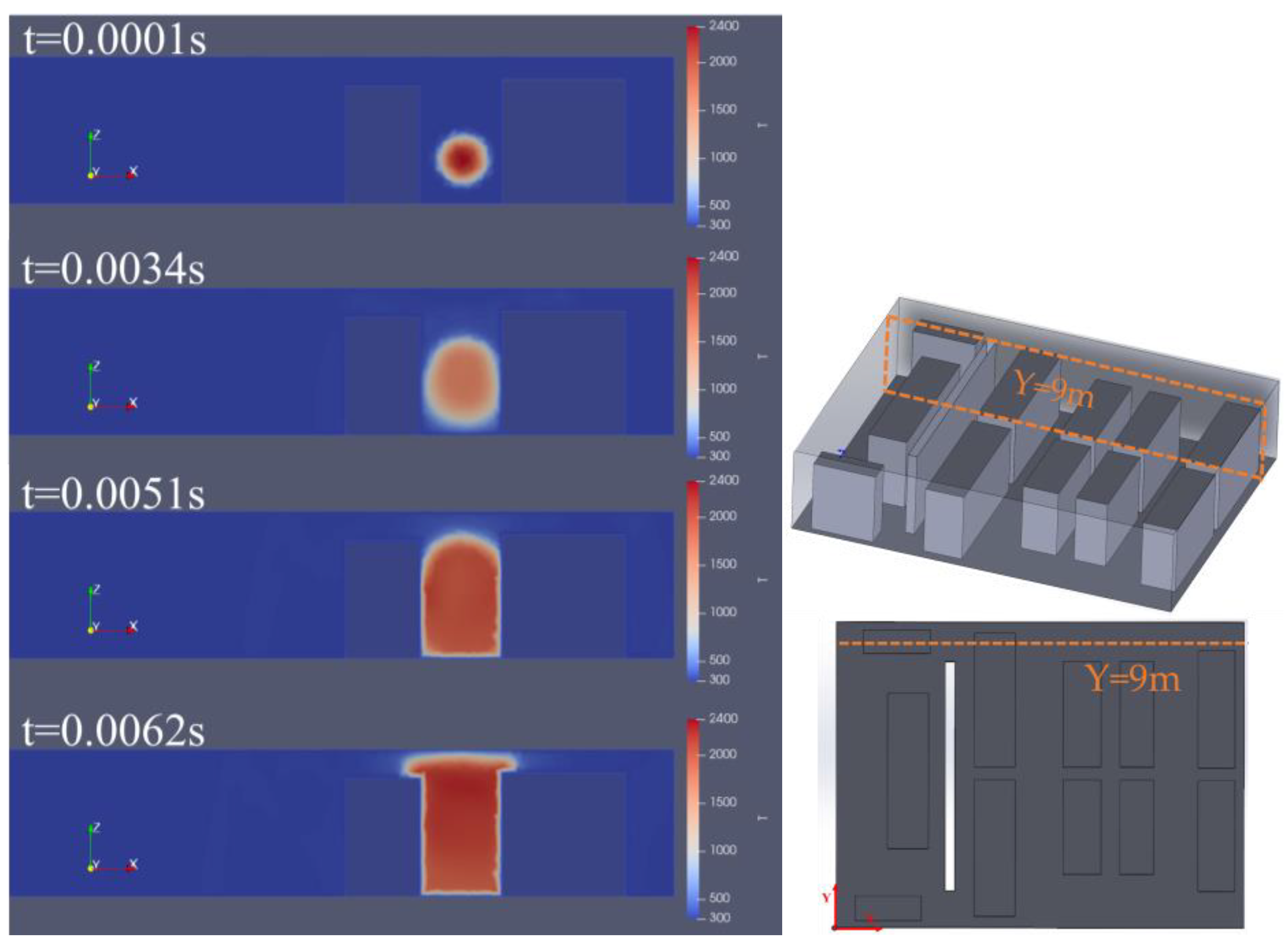
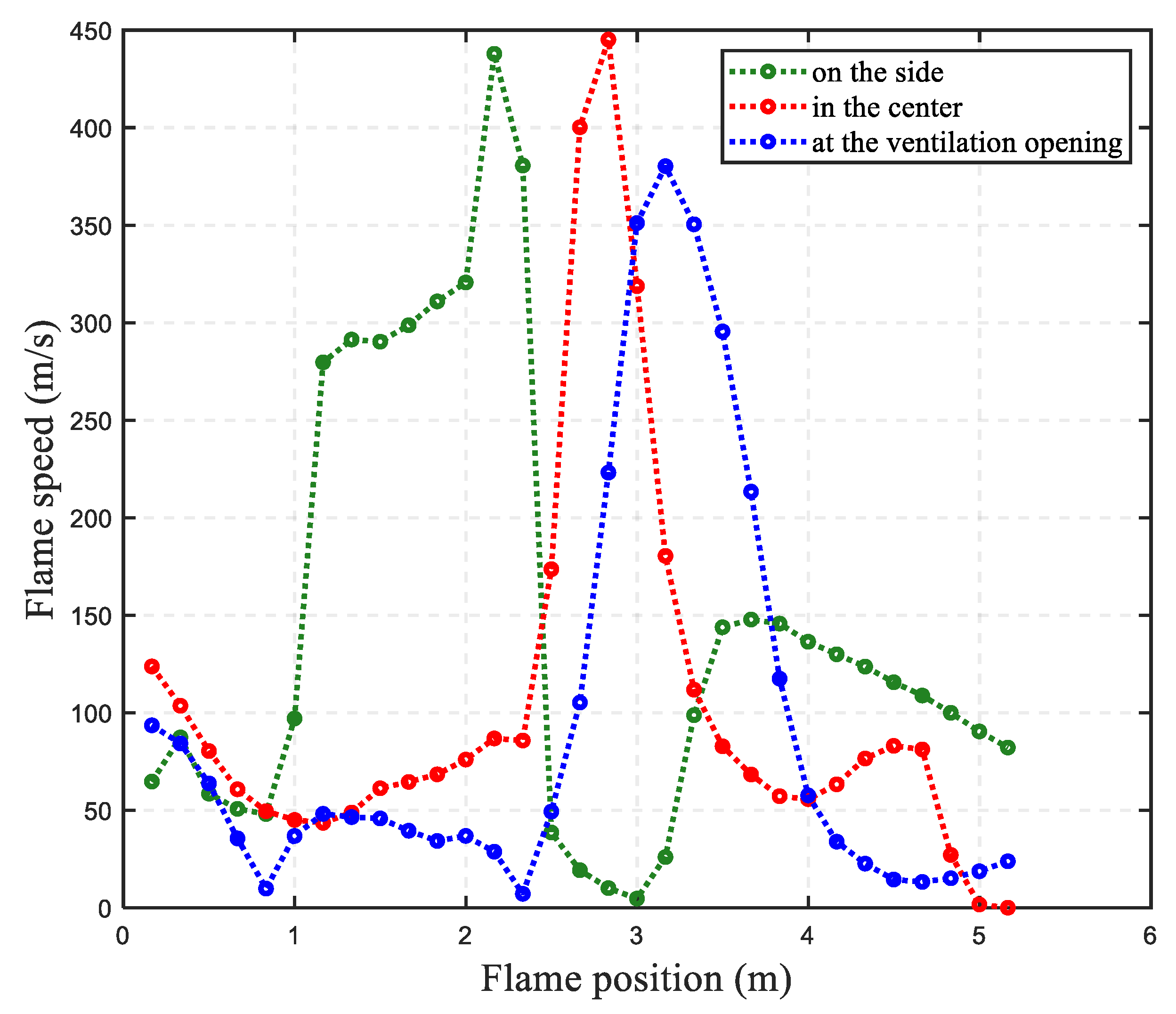
3.2. The Impact of Hydrogen Leak Explosion Location
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| OpenFOAM | Open field operation and manipulation |
| DDT | Deflagration to detonation transition |
| STAR-CCM | Simulation of turbulent flow in arbitrary regions—computational continuum mechanics |
| CFD-ACE | Computational fluid dynamics—advanced computational environment |
| CFX | Computational fluid dynamics eXtreme—ANSYS CFX |
| PEM | Polymer electrolyte membrane |
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes |
References
- Styhre, L.; Winnes, H.; Black, J.; Lee, J.; Le-Griffin, H. Greenhouse Gas Emissions from Ships in Ports—Case Studies in Four Continents. Transp. Res. Part D Transp. Environ. 2017, 54, 212–224. [Google Scholar] [CrossRef]
- Tollefson, J. Hydrogen Vehicles: Fuel of the Future. Nature 2010, 464, 1262–1264. [Google Scholar]
- Dodds, P.E.; Staffell, I.; Hawkes, A.D.; Li, F.; Grünewald, P.; McDowall, W.; Ekins, P. Hydrogen and Fuel Cell Technologies for Heating: A Review. Int. J. Hydrogen Energy 2015, 40, 2065–2083. [Google Scholar]
- Grove, W.R., XXIV. On Voltaic Series and the Combination of Gases by Platinum. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1839, 14, 127–130. [Google Scholar]
- Radojčić, D.; Simić, A.; Momčilović, N.; Motok, M.; Friedhoff, B. Concepts of Contemporary and Innovative Vessels. In Design of Contemporary Inland Waterway Vessels: The Case of the Danube River; Radojčić, D., Simić, A., Momčilović, N., Motok, M., Friedhoff, B., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 269–325. ISBN 978-3-030-77325-0. [Google Scholar]
- Fuel Cell Ferry Water Go Round Finds Fleet Investment—Electrive.Com. Available online: https://www.electrive.com/2019/06/13/fuel-cell-ferry-water-go-round-finds-fleet-investment/ (accessed on 18 March 2025).
- Garancini, C. Water Go Round, il Traghetto Passeggeri a Idrogeno. Available online: https://www.lifegate.it/traghetto-idrogeno (accessed on 18 March 2025).
- AAM and Switch Launch Hydrogen Fuel Cell-Driven Ferry ‘Sea Change’. Available online: https://www.ship-technology.com/news/aam-switch-launch-hydrogen-ferry/ (accessed on 18 March 2025).
- 70′ Hydrogen Fuel Cell Passenger Ferry for Switch Maritime. Available online: https://www.allamericanmarine.com/vessels-gallery/sea-change-hydrogen/ (accessed on 18 March 2025).
- Johansson, S. Norwegian Hydra Is the First Ship to Run on Liquid Hydrogen. MannTek 2023. Available online: https://www.manntek.se/hydra/ (accessed on 22 September 2023).
- Ragland, K.W.; Bryden, K.M.; Kong, S.-C. Combustion Engineering; CRC Press: Boca Raton, FL, USA, 2011; ISBN 1-4200-9250-2. [Google Scholar]
- Herath, I.; Madeley, D.; Bradshaw, B. Hydrogen Fuel Cell Taxi: Safety Analysis Experiences. In Proceedings of the 4th IET International Conference on Systems Safety 2009. Incorporating the SaRS Annual Conference, London, UK, 26–28 October 2009; pp. 1–6. [Google Scholar]
- Dorofeev, S.; Kuznetsov, M.; Alekseev, V.; Efimenko, A.; Breitung, W. Evaluation of Limits for Effective Flame Acceleration in Hydrogen Mixtures. J. Loss Prev. Process Ind. 2001, 14, 583–589. [Google Scholar]
- Groethe, M.; Colton, J.; Chiba, S. Hydrogen Deflagration Safety Studies in a Semi-Open Space. In Proceedings of the 14th World Hydrogen Energy, Montreal, QC, Canada, 9–13 June 2002. [Google Scholar]
- Kuznetsov, M.; Alekseev, V.; Yankin, Y.; Dorofeev, S. Slow and Fast Deflagrations in Hydrocarbon-Air Mixtures. Combust. Sci. Technol. 2002, 174, 157–172. [Google Scholar]
- Breitung, W.; Dorofeev, S.; Kotchourko, A.; Redlinger, R.; Scholtyssek, W.; Bentaib, A.; L’Heriteau, J.-P.; Pailhories, P.; Eyink, J.; Movahed, M. Integral Large Scale Experiments on Hydrogen Combustion for Severe Accident Code Validation-HYCOM. Nucl. Eng. Des. 2005, 235, 253–270. [Google Scholar]
- Molkov, V. Hydrogen Safety Research: State-of-the-Art. In Proceedings of the 5th International Seminar on Fire and Explosion Hazards, Edinburgh, UK, 23–27 April 2007; Volume 23, p. 27. [Google Scholar]
- Ng, H.D.; Lee, J.H. Comments on Explosion Problems for Hydrogen Safety. J. Loss Prev. Process Ind. 2008, 21, 136–146. [Google Scholar]
- Dorofeev, S.B. Flame Acceleration and Explosion Safety Applications. Proc. Combust. Inst. 2011, 33, 2161–2175. [Google Scholar]
- Xiao, H. Experimental and Numerical Study of Dynamics of Premixed Hydrogen-Air Flames Propagating in Ducts; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 3-662-48379-3. [Google Scholar]
- McConnell, V.P. Now, Voyager? The Increasing Marine Use of Fuel Cells. Fuel Cells Bull. 2010, 2010, 12–17. [Google Scholar]
- Choi, C.H.; Yu, S.; Han, I.-S.; Kho, B.-K.; Kang, D.-G.; Lee, H.Y.; Seo, M.-S.; Kong, J.-W.; Kim, G.; Ahn, J.-W.; et al. Development and Demonstration of PEM Fuel-Cell-Battery Hybrid System for Propulsion of Tourist Boat. Int. J. Hydrogen Energy 2016, 41, 3591–3599. [Google Scholar] [CrossRef]
- Takeno, K.; Okabayashi, K.; Kouchi, A.; Nonaka, T.; Hashiguchi, K.; Chitose, K. Dispersion and Explosion Field Tests for 40 MPa Pressurized Hydrogen. Int. J. Hydrogen Energy 2007, 32, 2144–2153. [Google Scholar] [CrossRef]
- Mao, X.; Ying, R.; Yuan, Y.; Li, F.; Shen, B. Simulation and Analysis of Hydrogen Leakage and Explosion Behaviors in Various Compartments on a Hydrogen Fuel Cell Ship. Int. J. Hydrogen Energy 2021, 46, 6857–6872. [Google Scholar] [CrossRef]
- Seyam, S.; Dincer, I.; Agelin-Chaab, M. An Innovative Study on a Hybridized Ship Powering System with Fuel Cells Using Hydrogen and Clean Fuel Blends. Appl. Therm. Eng. 2023, 221, 119893. [Google Scholar] [CrossRef]
- Sato, Y.; Iwabuchi, H.; Groethe, M.; Merilo, E.; Chiba, S. Experiments on Hydrogen Deflagration. J. Power Sources 2006, 159, 144–148. [Google Scholar] [CrossRef]
- Middha, P.; Hansen, O.R.; Storvik, I.E. Validation of CFD-Model for Hydrogen Dispersion. J. Loss Prev. Process Ind. 2009, 22, 1034–1038. [Google Scholar]
- Lipatnikov, A.N.; Chomiak, J. Turbulent Flame Speed and Thickness: Phenomenology, Evaluation, and Application in Multi-Dimensional Simulations. Prog. Energy Combust. Sci. 2002, 28, 1–74. [Google Scholar] [CrossRef]
- Kang, H.-S.; Kim, S.-M.; Kim, J. Safety Issues of a Hydrogen Refueling Station and a Prediction for an Overpressure Reduction by a Barrier Using OpenFOAM Software for an SRI Explosion Test in an Open Space. Energies 2022, 15, 7556. [Google Scholar] [CrossRef]
- Aung, T.T.; Terada, A.; Ryutaro, H.; Nagaishi, R.; Kadowaki, S. Simulation of the Self-Propagating Hydrogen-Air Premixed Flame in a Closed-Vessel by an Open-Source CFD Code. J. Nucl. Sci. Technol. 2022, 59, 573–579. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, H.; Xiao, J.; Wen, J.; Usmani, A.S. Numerical Investigation of the Effect of Riser Spacing on Gas Explosion from Semi-Submersible Platform. Process Saf. Environ. Prot. 2024, 188, 239–250. [Google Scholar] [CrossRef]
- Blaylock, M.; Klebanoff, L. Hydrogen Gas Dispersion Studies for Hydrogen Fuel Cell Vessels I: Vent Mast Releases. Int. J. Hydrogen Energy 2022, 47, 21506–21516. [Google Scholar]
- Choi, S.; Jeong, B. CFD Simulation of Gas Dispersion at Hydrogen Bunkering Station. J. Int. Marit. Saf. Environ. Aff. Shipp. 2023, 7, 2261350. [Google Scholar]
- Kim, B.; Hwang, K.-I. Numerical Validation of a Hydrogen Leakage and Dispersion Experiment Considering Ship Kinetic Characteristics. J. Adv. Mar. Eng. Technol. (JAMET) 2023, 47, 352–359. [Google Scholar]
- Pasculescu, V.M.; Ghicioi, E.; Vlasin, N.I.; Suvar, M.C.; Morar, M.S. Numerical Modelling as a Tool for Investigating Hydrogen Explosions. Inżynieria Miner. 2024, 1, 71–76. [Google Scholar]
- Bédard-Tremblay, L.; Fang, L.; Bauwens, L.; Cheng, Z.; Tchouvelev, A.V. Numerical Simulation of Hydrogen–Air Detonation for Damage Assessment in Realistic Accident Scenarios. J. Loss Prev. Process Ind. 2008, 21, 154–161. [Google Scholar] [CrossRef]
- Swain, M.R.; Filoso, P.; Grilliot, E.S.; Swain, M.N. Hydrogen Leakage into Simple Geometric Enclosures. Int. J. Hydrogen Energy 2003, 28, 229–248. [Google Scholar]
- Schefer, R.W.; Groethe, M.; Houf, W.G.; Evans, G. Experimental Evaluation of Barrier Walls for Risk Reduction of Unintended Hydrogen Releases. Int. J. Hydrogen Energy 2009, 34, 1590–1606. [Google Scholar] [CrossRef]
- Venetsanos, A.; Baraldi, D.; Adams, P.; Heggem, P.; Wilkening, H. CFD Modelling of Hydrogen Release, Dispersion and Combustion for Automotive Scenarios. J. Loss Prev. Process Ind. 2008, 21, 162–184. [Google Scholar]
- Rigas, F.; Sklavounos, S. Evaluation of Hazards Associated with Hydrogen Storage Facilities. Int. J. Hydrogen Energy 2005, 30, 1501–1510. [Google Scholar]
- Wilkening, H.; Baraldi, D. CFD Modelling of Accidental Hydrogen Release from Pipelines. Int. J. Hydrogen Energy 2007, 32, 2206–2215. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Y.; Sheng, S.; Chen, H.; Wang, B. Numerical Investigation on Dispersion of Hydrogen in Hydrogen Powered Automobile. J. Saf. Sci. Technol. 2009, 5, 5–8. [Google Scholar]
- Li, J.; Zhao, Y.; Zheng, J. Simulation and Analysis on Leakage and Explosion of High Pressure Hydrogen in Hydrogen Refueling Station. Eng. Sci. 2015, 49, 1389–1394. [Google Scholar]
- Li, J.-C.; Xu, H.; Zhou, K.; Li, J.-Q. A Review on the Research Progress and Application of Compressed Hydrogen in the Marine Hydrogen Fuel Cell Power System. Heliyon 2024, 10, e25304. [Google Scholar] [CrossRef]
- Dongxing, W.; Zhe, W.; Fan, Z.; Fenghui, H.; Yulong, J. State-of-the-Art and Prospect of Technical Standards for the Ships Powered by Hydrogen Fuel Cells. J. Transp. Inf. Saf. 2023, 41, 157–167. [Google Scholar]
- Inal, O.B.; Deniz, C. Assessment of Fuel Cell Types for Ships: Based on Multi-Criteria Decision Analysis. J. Clean. Prod. 2020, 265, 121734. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Han, M. Industrial Development Status and Prospects of the Marine Fuel Cell: A Review. J. Mar. Sci. Eng. 2023, 11, 238. [Google Scholar] [CrossRef]
- Elkafas, A.G.; Rivarolo, M.; Gadducci, E.; Magistri, L.; Massardo, A.F. Fuel Cell Systems for Maritime: A Review of Research Development, Commercial Products, Applications, and Perspectives. Processes 2022, 11, 97. [Google Scholar] [CrossRef]
- Bauwens, C.R.; Chao, J.; Dorofeev, S.B. Effect of Hydrogen Concentration on Vented Explosion Overpressures from Lean Hydrogen–Air Deflagrations. Int. J. Hydrogen Energy 2012, 37, 17599–17605. [Google Scholar] [CrossRef]
- Rui, S.; Wang, C.; Guo, S.; Jing, R.; Li, Q. Hydrogen-Air Explosion with Concentration Gradients in a Cubic Enclosure. Process Saf. Environ. Prot. 2021, 151, 141–150. [Google Scholar] [CrossRef]
- Ma, X.; Nie, B.; Wang, W.; Zhao, D.; Zhang, Y.; Yang, Y.; Ma, C.; Hu, B.; Chang, L.; Yang, L. Effect of Hydrogen Concentration, Initial Pressure and Temperature on Mechanisms of Hydrogen Explosion in Confined Spaces. Combust. Flame 2024, 269, 113696. [Google Scholar] [CrossRef]
- Yasari, E.; Runsten, J.; Andric, J. Tutorial XiFoam; Chalmers University of Technology: Gothenburg, Sweden, 2010. [Google Scholar]
- Zhou, Y.; Li, Y.; Gao, W. Experimental Investigation on Unconfined Hydrogen Explosion with Different Ignition Height. Int. J. Hydrogen Energy 2023, 48, 20112–20123. [Google Scholar] [CrossRef]
- Pratt, J.W.; Klebanoff, L.E. Feasibility of the SF-BREEZE: A Zero-Emission, Hydrogen Fuel Cell, High-Speed Passenger Ferry; U.S. Department of Transportation: Washington, DC, USA, 2016. [Google Scholar]
- Klebanoff, L. Hydrogen and Fuel Cells for Maritime Applications: From Sandia Feasibility Studies to First Demonstrations; Sandia National Lab. (SNL-CA): Livermore, CA, USA, 2022. [Google Scholar]








| Mesh Size | Points | Faces | Cells | Meshing Method |
|---|---|---|---|---|
| 0.08 m | 71,498 | 200,880 | 64,800 | Block Mesh |
| Configuration Name | Parameter |
|---|---|
| Overall length | 33 m |
| Molded breadth | 10 m |
| Load draught | 1.4 m |
| Overall displacement | 135 t |
| Specified fuel consumption | 2400 kg LH2 per day |
| Total installed power | 4.92 MW |
| Standard passenger capacity | 150 |
| Range | 100 nautical miles (NM) |
| Service speed | 35 knots |
| Endurance time | 4 h |
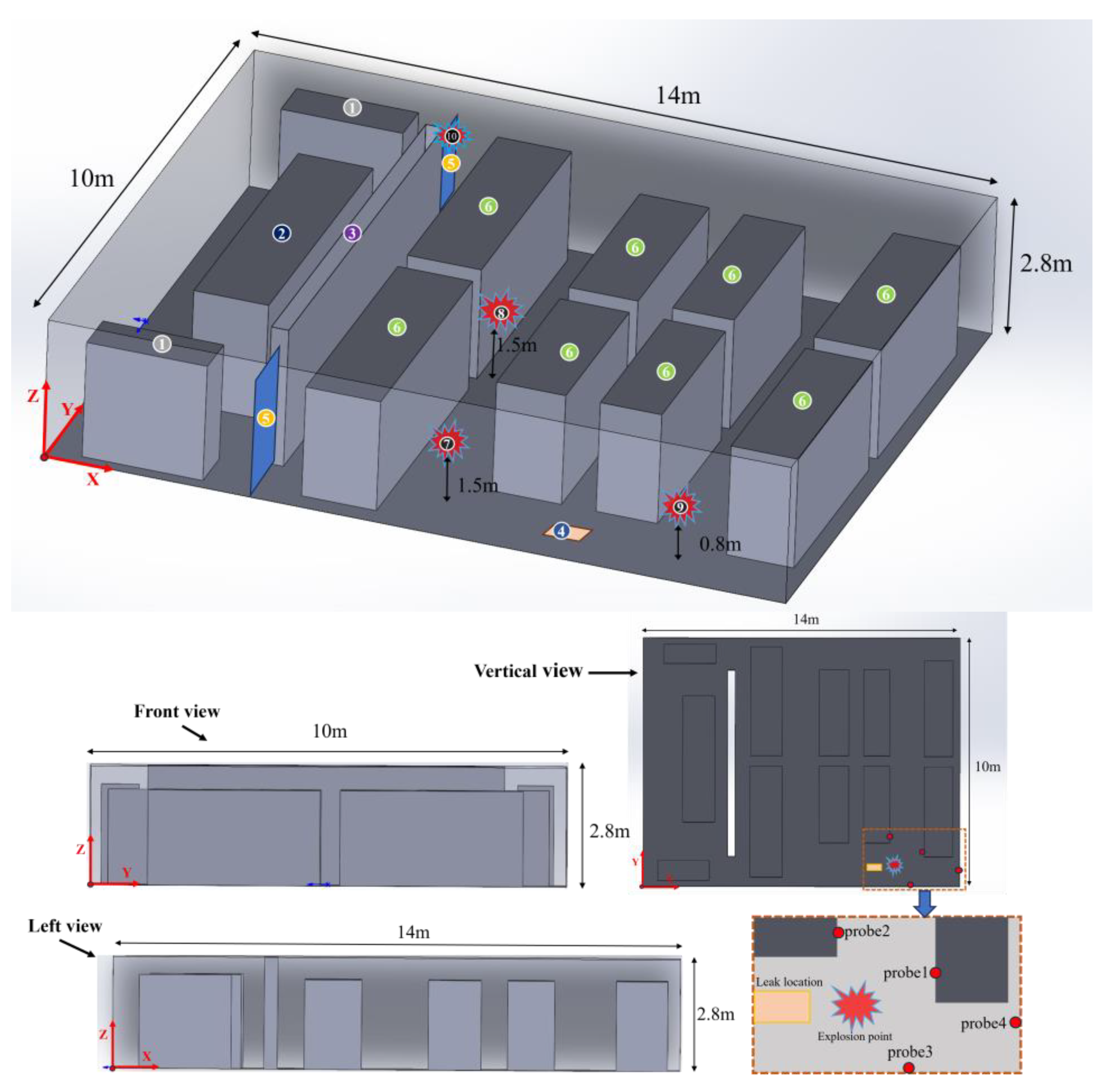
| No. | Position |
|---|---|
| 1 | DC–DC converter and DC–AC inverter |
| 2 | Switchboard |
| 3 | Control room and fuel cell room partition wall |
| 4 | Leak location |
| 5 | Vents |
| 6 | Hydrogen fuel cells |
| 7 | Explosion point 1 |
| 8 | Explosion point 2 |
| 9 | Explosion point 3 |
| 10 | Explosion point 4 |
| Mesh Size | Points | Faces | Cells | Meshing Method |
|---|---|---|---|---|
| 0.08 m | 7,202,048 | 74,723,712 | 567,992 | Tetrahedral mesh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Miao, Z.; Li, Y.; Ai, D.; Wang, Q. A Numerical Simulation Study on Hydrogen-Enriched Gas Explosions on Hydrogen Fuel Cell Ships Based on OpenFOAM. J. Mar. Sci. Eng. 2025, 13, 667. https://doi.org/10.3390/jmse13040667
Zhao Y, Miao Z, Li Y, Ai D, Wang Q. A Numerical Simulation Study on Hydrogen-Enriched Gas Explosions on Hydrogen Fuel Cell Ships Based on OpenFOAM. Journal of Marine Science and Engineering. 2025; 13(4):667. https://doi.org/10.3390/jmse13040667
Chicago/Turabian StyleZhao, Yuechao, Zeya Miao, Yubo Li, Dihao Ai, and Qifei Wang. 2025. "A Numerical Simulation Study on Hydrogen-Enriched Gas Explosions on Hydrogen Fuel Cell Ships Based on OpenFOAM" Journal of Marine Science and Engineering 13, no. 4: 667. https://doi.org/10.3390/jmse13040667
APA StyleZhao, Y., Miao, Z., Li, Y., Ai, D., & Wang, Q. (2025). A Numerical Simulation Study on Hydrogen-Enriched Gas Explosions on Hydrogen Fuel Cell Ships Based on OpenFOAM. Journal of Marine Science and Engineering, 13(4), 667. https://doi.org/10.3390/jmse13040667








