A Review on Research of Load Reduction and Ballistic Stability During Cross-Media Water Entry Processes
Abstract
1. Introduction
- Air-dropped torpedoes are designed with a blunt-nosed thin-shell structure (approximately 100 mm in diameter [4]) housing integrated precision electronics. They typically enter water at speeds of tens of meters per second [4]. During water entry, the head const sustains severe impact loads, often leading to structural deformation and damage to internal electronic components [5]. Additionally, unstable hydrodynamic loads frequently induce body whip phenomena.
- Supercavitating vehicles employ large-scale thin-shell structures (approximately 100 mm in diameter [6]) and enter water at high speeds of hundreds of meters per second with small water entry angles [7]. Rapid maneuvering flatting after entering the water makes the tail of the vehicle suffer intense intermittent tail-slapping loads, potentially causing structural damage or even fractures in the slender structure [8].
- High-speed projectiles feature conical compact rigid-body designs (approximately 10 mm in diameter [9]) and enter water at ultra-high speeds ranging from hundreds to thousands of meters per second with minimal entry angles [9]. The coupling effects of extreme speed and small water entry angles often trigger dynamic issues such as structural bending, ricochet, and ballistic instability [10].
2. Water Entry Load and Load Reduction Strategies
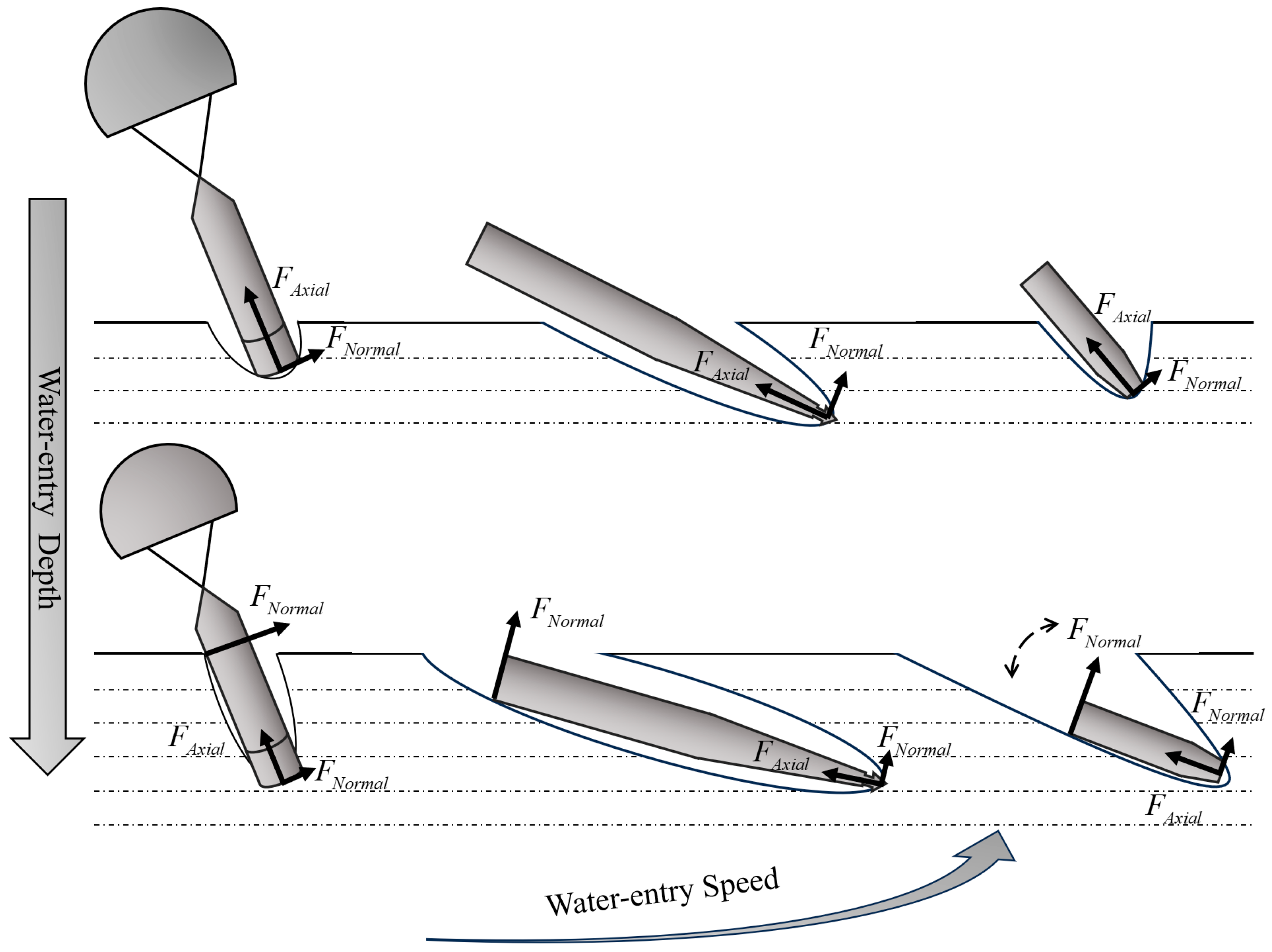
- Surface impact stage: During this stage, the head of the vehicle experiences a significant water entry impact load. Factors such as the head shape of the vehicle, water entry speed, and water entry angle have a substantial influence on the peak load [12,13,14]. The characteristics of the impact load in this stage include a high peak value and short duration [15]. The intense and instantaneous impact load can damage stress concentration points in the vehicle’s structure, potentially affecting the normal operation of electronic equipment in the vehicle’s head. According to Von Karman’s flat plate water entry impact model [16], the dynamic load peak aimpcat caused by the impact load is:where Fimpcat is the axial impact load; ρ is the density of the fluid; v is the relative velocity between the vehicle and the free surface of the water; c is the speed of sound in water; A is the wet area of the bow inlet surface; m is the mass of the vehicle.
- 2.
- Liquid flow stage: The water is compressed and rapidly diffuses outward, causing the fluid pressure around the vehicle to drop sharply, which leads to cavitation [17]. During this stage, the vehicle is subjected to continuous hydrodynamic loads. The peak load is significantly smaller than in the surface impact stage, but the duration is longer, and the head wet area is also larger. As a result, the loads experienced during this stage can have a notable impact on the vehicle’s structure and its subsequent ballistic stability. The overload ahydrodynamic caused by the continuous hydrodynamic load can be expressed as:where Fhydrodynamic is the axial hydrodynamic load; ρ is the density of the fluid; v is the relative velocity between the vehicle and the free surface of the water; A is the wet area of the bow inlet surface; m is the mass of the vehicle; Cd is the drag coefficient.
- 3.
- Cavity formation stage: As the depth of the vehicle entering the water increases, cavitation flow gradually forms. During this stage, an open cavity is created if the speed of the vehicle is fast enough, meaning the interior of the cavity is connected to the outside atmosphere, and air is continuously entrained into the cavity. At this stage, a slamming effect may occur between the vehicle and the cavity wall, generating normal impact loads and pitching moments [18]. This can easily lead to transient changes in the pitch angular velocity of the vehicle.
- 4.
- Cavity closure stage: As the vehicle continues to move forward, the volume of the cavity increases, and the vehicle becomes fully enveloped by the cavity. The cavity closure stage begins when the tail of the cavity starts to close under fluid pressure and surface tension. Due to various initial disturbance factors, the vehicle will repeatedly hit the upper and lower walls of the cavity after the initial slapping action. This results in periodic changes in the vehicle’s angular velocity, known as the tail-slapping phenomenon [19].
2.1. Shape-Based Load Reduction
2.2. Structural Load Resistance
2.3. Active Load Reduction
3. Water Entry Ballistic Stability
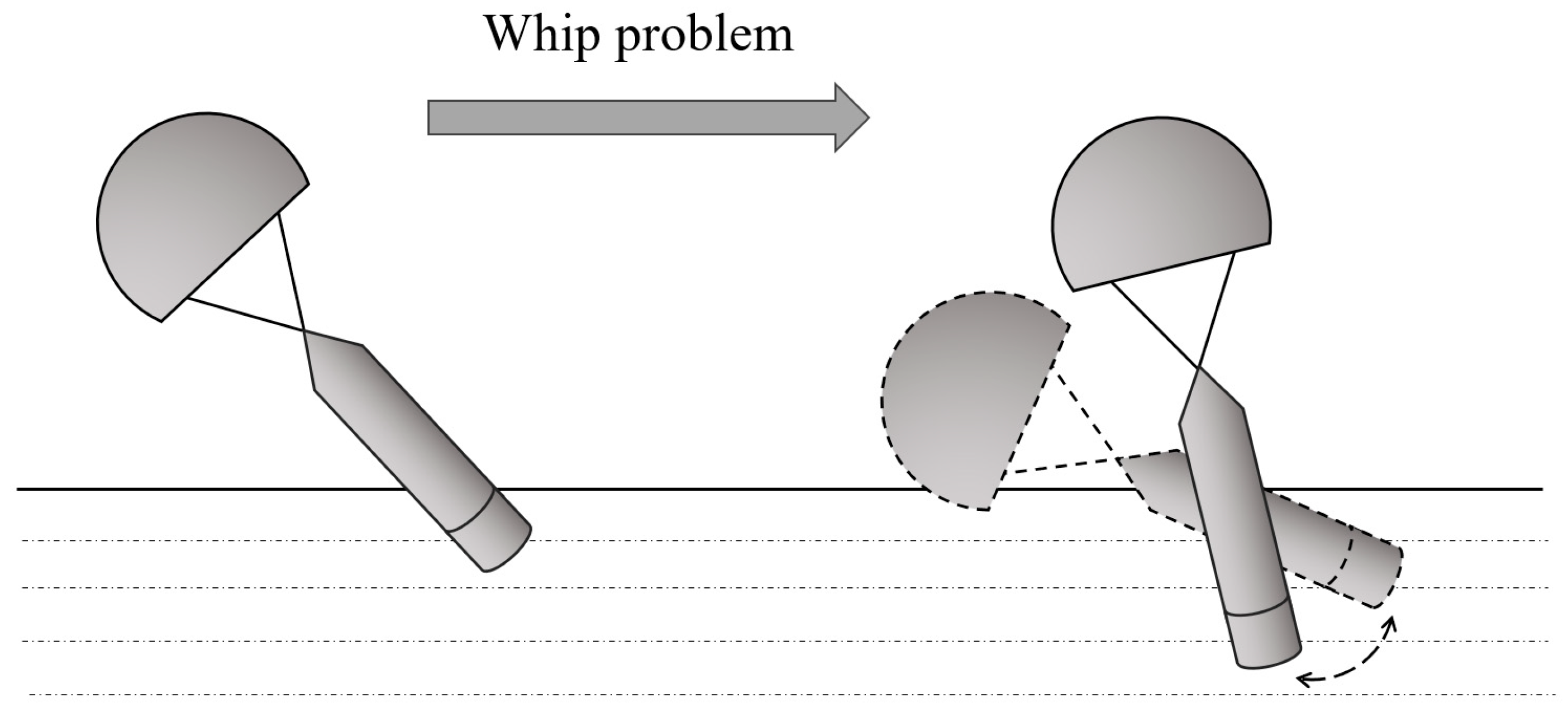
3.1. Whip Problem of Air-Dropped Torpedoes
3.2. Flat-Turning Problem of Supercavitating Vehicles
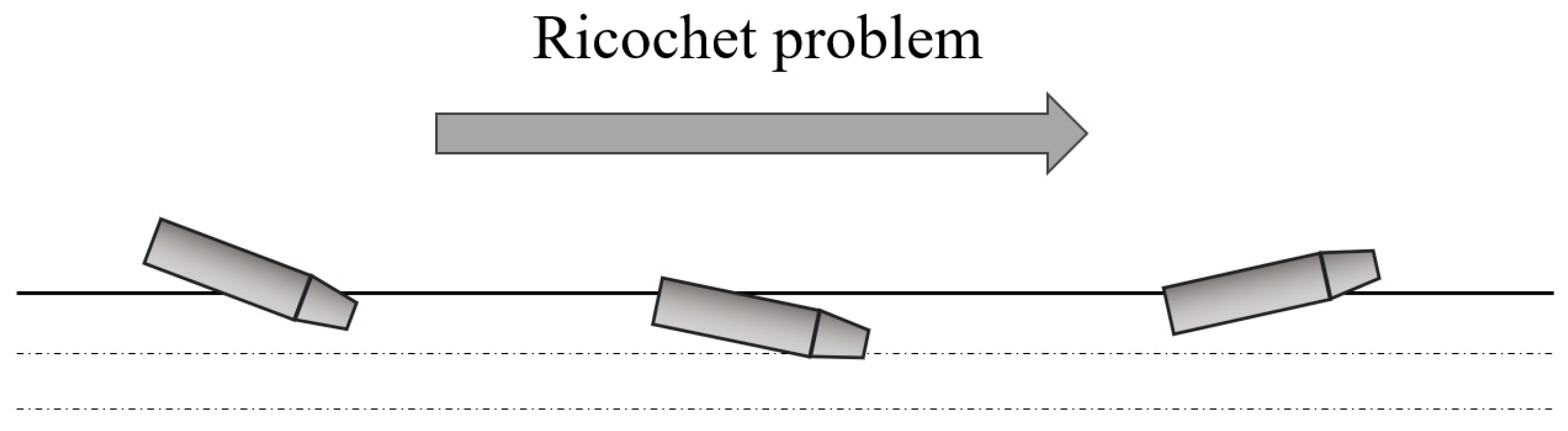
3.3. Ricochet Problem of High-Speed Projectiles
4. Research Methods for Cross-Media Water Entry
4.1. Theoretical Research
4.2. Experimental Research
4.3. Numerical Simulation
4.4. Artificial Intelligence in Cross-Media Problems
5. Summary and Prospects
- Water entry impact load and load reduction strategies: Current load reduction strategies primarily focus on the damage caused by axial impact loads to the head structure and internal components during the surface impact stage. However, when the vehicle enters the water at a small angle or with an angle of attack, or when the cavity asymmetrically closes around the vehicle structure, the negative effects of normal loads on the mid-section or aft section of the vehicle cannot be ignored. At present, research on normal load characteristics and load reduction strategies is insufficient and requires further development.
- Water entry ballistic stability: Current research on ballistic stability primarily focuses on the whip phenomenon of air-dropped torpedoes, the flat-turning problem of supercavitating vehicles, and the ricochet phenomenon of high-speed projectiles. However, theoretical research on motion stability has rarely been reported, and the mechanism of complex phenomena such as whip remain unclear. Further research can also explore efficient methods for enhancing stability.
- Research methods for cross-media water entry: Due to the complexity of cross-media water entry problems, current theoretical studies mostly simplify complex scenarios, and it is difficult to summarize a universally applicable theoretical model that accurately describes the entire physical phenomenon, so further in-depth research is needed. The development of scaled-down test technology has provided a deeper understanding of the complex physical phenomenon of small-size vehicles during high-speed water entry. However, considering the limitations of scaled-down test, it cannot truly restore the real physical phenomenon of full-size model entering water. At present, there are few reports on cross-media water entry tests for full-size models, that can be further improved in the future. In terms of numerical simulation, the monolithic approach can provide high-precision results but faces high computational costs in solving complex and strongly coupled fluid–structure interaction problems. The partitioned approach may also face accuracy and stability issues when dealing with strong coupling and large deformation problems due to its staged iteration process. Future research can focus on improving simulation accuracy, stability, and computational scale.
- Artificial intelligence in cross-media problems: Artificial intelligence has been preliminarily applied to solving cross-media problems, offering efficient computational speed and high accuracy, thereby providing a novel approach to addressing complex challenges. Currently, AI can predict the load and hydrodynamic properties of vehicles during cross-media processes. In the future, it can be integrated with image recognition technology to further predict flow characteristics, such as the evolution of cavities, in cross-media processes. With the continuous advancement of AI technology, its application prospects in cross-media problems will expand, and it is expected to play an increasingly significant role in fields such as aerospace and ocean engineering.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| FSI | Fluid–Structure Interaction |
| ALE | Arbitrary Lagrangian-Eulerian |
| OLM | Original Logvinovich Method |
| MLM | Modified Logvinovich Method |
| CFD | Computational Fluid Dynamics |
| CSD | Computational Structural Dynamics |
| SMPC | Shape Memory Polymer Composite |
| SMP | Shape Memory Polymer |
| AI | Artificial Intelligence |
| ML | Machine Learning |
| DNN | Deep Neural Network |
| PNN | Parallel Neural Network |
References
- Wang, H.; Huang, Z.; Huang, D.; Hou, Y.; Chen, Z.; Guo, Z.; Sun, S.; Xue, R. Influences of floating ice on the vertical water entry process of a trans-media projectile at high speeds. Ocean Eng. 2022, 265, 112548. [Google Scholar] [CrossRef]
- Ming, F.; Wang, J.; Liu, W.; Liu, X.; Zhang, A.M. Review of multiphase flow and fluid-structure interaction of high-speed water entry. Acta Aerodyn. Sin. 2024, 42, 68–85. [Google Scholar] [CrossRef]
- Qi, X.; Liu, X.; Wang, R.; Miao, P.; Li, R. Numerical Simulation of Water Entry for High-Speed Projectile at Small Angle. Shipbuild. China 2022, 63, 31–39. [Google Scholar] [CrossRef]
- Li, S. Numerical Simulation of Torpedo Water-Entry Impact. Master’s Thesis, North University of China, Taiyuan, China, 2015. [Google Scholar]
- Pan, G.; Yang, K. Impact force encountered by waterentry airborne torpedo. Explos. Shock Waves 2014, 34, 521–526. [Google Scholar] [CrossRef]
- Sun, S. Study on Trajectory Stability Mechanism of Supercavitating Projectile in Highspeed Water Entry with Small Incident Angle. Ph.D. Dissertation, China Ship Research & Development Academy, Wuxi, China, 2023. [Google Scholar] [CrossRef]
- Wei, P.; Hou, J.; Yang, K. Summary of Supercavitating Projectile Researches. Ship Electron. Eng. 2008, 28, 13–17,128. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, Z.; Liu, J.; Gu, J. Research development of high-speed super-cavitating flow of the high-speed underwater vehicle. Ship Ocean Eng. 2006, 35, 26–29. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, R.; Xu, B. Research on Current Application State of Supercavitation Projectile Artillery Weapons. J. Gun Launch Control. 2017, 38, 92–96. [Google Scholar] [CrossRef]
- Qian, C.; Yu, C.; Mu, Q.; Yi, W.; Guan, J. Numerical Research of Effects of Launch Speed and Launch Angle on Water Entry of High-Speed Projectile. J. Ordnance Equip. Eng. 2019, 40, 35–39, 50. [Google Scholar] [CrossRef]
- Qi, H.; Guo, J.; Chu, F.; Wu, H.; Yang, X.; Zhao, H.; Fu, H.; Wang, P. Review on the Fluid-structure Coupling Characteristicsin the Water Entry of Cross-media Vehicles. Aerosp. Shanghai 2024, 41, 74–86. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, C.; Xu, H.; Xia, W.; Ma, X.; Zhao, J. Impact Load Characteristics of Large-Scale Trans-Medium Vehicles during High-Speed Oblique Water Entry. J. Unmanned Undersea Syst. 2024, 32, 426–433. [Google Scholar] [CrossRef]
- Zhu, Z.; Yuan, X. High-Speed Water-entry Impact and Cavity Characters of Cylinder. Comput. Simul. 2014, 31, 29–33,82. [Google Scholar] [CrossRef]
- Qi, X.; Li, X.; Shi, Y.; Wang, R.; Yuan, X. Analysis of Trajectory Characteristics of Shallow Angle Water Entry for High-speed Projectile. Digit. Ocean Underw. Warf. 2023, 6, 293–299. [Google Scholar] [CrossRef]
- Yuan, K.; Yu, J.; He, Z.; Yu, H.; Meng, F. Numerical study on the dynamic response of liquid-filled closed hollow cylinder under water impact. Ocean Eng. 2023, 288, 116157. [Google Scholar] [CrossRef]
- von Kármán, T. The Impact on Seaplane Floats During Landing; National Advisory Committee for Aeronatics: Washington, DC, USA, 1929. [Google Scholar]
- Mirzaei, M.; Taghvaei, H.; Golneshan, A.A. Improvement of cavity shape modeling in water-entry of circular cylinders by considering the cavity memory effect. Appl. Ocean Res. 2020, 97, 102073. [Google Scholar] [CrossRef]
- Zheng, C. Study on Trajectory and Load Characteristics of Supercavitating Vehicle During High-Speed Oblique Entry into Water. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2023. [Google Scholar]
- Yuan, X.; Li, M.; Ding, X.; Wei, R.; Zhou, F. Impact Load Characteristics of a Trans-media Vehicle during High-speed Water-entry. Acta Armamentarii 2021, 42, 1440–1449. [Google Scholar] [CrossRef]
- Bodily, K.G.; Carlson, S.J.; Truscott, T.T. The water entry of slender axisymmetric bodies. Phys. Fluids 2014, 26, 072108. [Google Scholar] [CrossRef]
- Shafaghat, R.; Hosseinalipour, S.M.; Lashgari, I.; Vahedgermi, A. Shape optimization of axisymmetric cavitators in supercavitating flows, using the NSGA II algorithm. Appl. Ocean Res. 2011, 33, 193–198. [Google Scholar] [CrossRef]
- Lu, B.; Zhu, Z. Numerical research on load of a super-cavity vehicle with cone-shaped segment at high-speed water-entry. Ship Sci. Technol. 2017, 39, 119–123. [Google Scholar] [CrossRef]
- Sharker, S.I.; Holekamp, S.; Mansoor, M.M.; Fish, F.E.; Truscott, T.T. Water entry impact dynamics of diving birds. Bioinspiration Biomim. 2019, 14, 056013. [Google Scholar] [CrossRef]
- Wang, T.M.; Yang, X.B.; Liang, J.H.; Yao, G.C.; Zhao, W.D. CFD based investigation on the impact acceleration when a gannet impacts with water during plunge diving. Bioinspiration Biomim. 2013, 8, 036006. [Google Scholar] [CrossRef]
- Wu, Z. Bionic Configuration Design and Water Entry Performance of Aquatic UAV Based on Water Entry Strategy of Kingfisher. Ph.D. Dissertation, Jilin University, Changchun, China, 2021. [Google Scholar]
- Chen, Y.; Sun, J.; Liu, Y.; Leng, J. Variable stiffness property study on shape memory polymer composite tube. Smart Mater. Struct. 2012, 21, 094021. [Google Scholar] [CrossRef]
- Gong, M.; Tao, C.; Zhang, C.; Ji, H.; Qiu, J. A method for regulating negative Poisson’s ratio by a reentrant anti-tetrachiral structure. Mech. Adv. Mater. Struct. 2022, 29, 7399–7414. [Google Scholar] [CrossRef]
- Huang, X.; Liu, B. Current situation and development of warship structure material. Ship Boat 2004, 3, 21–24. [Google Scholar] [CrossRef]
- Huang, D. Application and Development of New Material in Modern Torpedo Technology. Torpedo Technol. 2004, 12, 1–3. [Google Scholar]
- Zhang, M.; Sun, S.; Feng, D. Application and Development of New Materials in Torpedo Designs. Torpedo Technol. 2015, 23, 86–89,118. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Chao, Q.; Bian, M.; Tian, S. Modeling and Simulation Analysis of Torpedo’s Water-Entry Impact Based on CEL Algorithm. J. Unmanned Undersea Syst. 2020, 28, 75–80. [Google Scholar] [CrossRef]
- He, Z.; Gao, Z.; Gu, X.; Gao, Z. Numerical simulation on the structural response of a torpedo at the moment of vertical water entry. Explos. Shock Waves 2023, 43, 144–158. [Google Scholar] [CrossRef]
- Han, M. Vibration Analysis of Supercavitating Body with Tail Slap and Damping Structural Design. Master’s Thesis, Harbin Engineering University, Harbin, China, 2014. [Google Scholar]
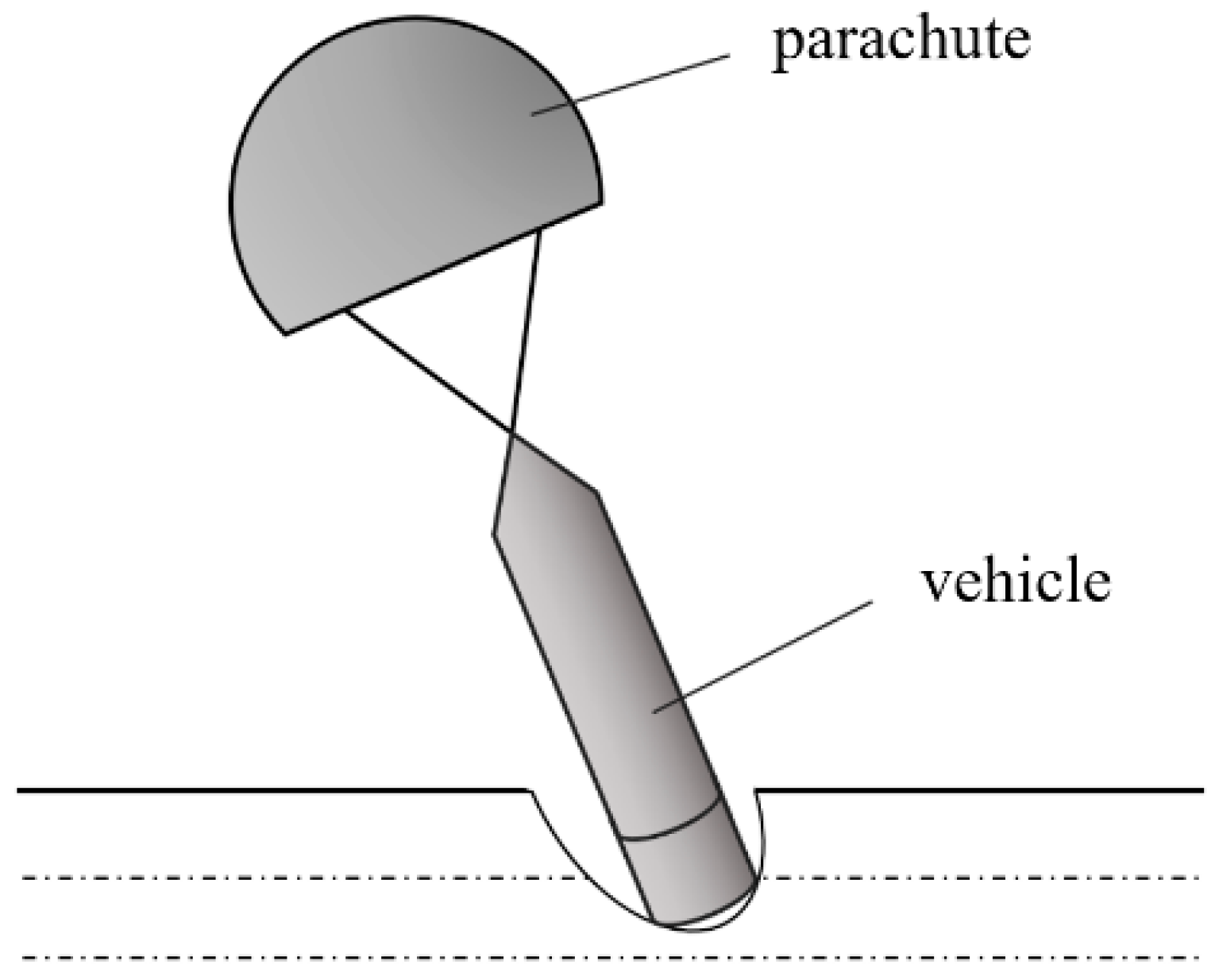
- Guo, J.; Han, J.; Li, X.; Lu, C.; Jiang, P.; Lv, Z. Reseach of Modeling and Simulation of Airdrop Torpedo Parachute System Based on Six Free Degrees. Ship Electron. Eng. 2022, 42, 124–128. [Google Scholar] [CrossRef]
- Li, B. Preliminary Discussion of Torpedo Parachute. Torpedo Technol. 2004, 12, 37–40. [Google Scholar]
- Jiang, L.; Jia, H.; Xu, X.; Rong, W.; Wang, Q.; Chen, G.; Fan, J.; Xue, X. Effect of Different Geometric Porosities on Aerodynamic Characteristics of Supersonic Parachutes. Space Sci. Technol. 2023, 3, 0062. [Google Scholar] [CrossRef]
- Pan, L.; Wang, H.; Yao, E.; Wang, X. Mechanism Research on the Water-Entry Impact of the Head-Jetting Flat Cylinder. J. Eng. Thermophys. 2015, 36, 1691–1695. [Google Scholar]
- Gao, Z. Numerical Study on the Buffering Characteristics of Low-Speed Water Entry for the Head-Jetting Vehicle. Master’s Thesis, Harbin Engineering University, Harbin, China, 2023. [Google Scholar]
- Liu, H.; Yu, F.; Han, B.; Zhang, Y.; Liu, G.; Chen, H. Numerical Simulation Study on Influence of Top Jet in Object Water Entering Impact. J. Eng. Thermophys. 2019, 40, 300–305. [Google Scholar]
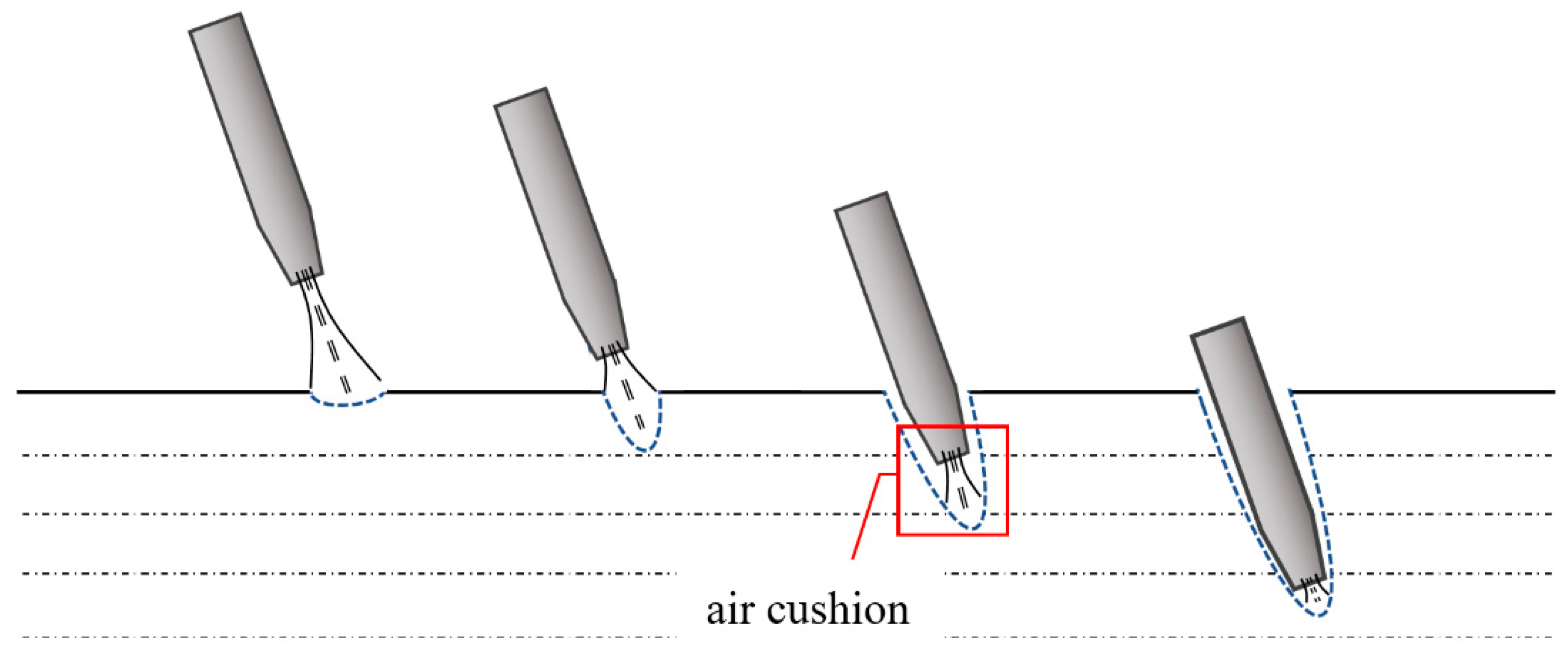
- Zou, Z.; Li, J.; Yang, M.; Liu, H.; Jiang, Y. Experimental Investigation on Cavity Flow Characteristics of Water Entry of Vehicle With Gas Jet Cavitator. J. Ballist. 2022, 34, 1–8,97. [Google Scholar] [CrossRef]
- Wei, H.; Xin, W.; Liu, H.; Liu, Y. Research on the Influence of Different Nozzle Structures on the Impact of High-Speed Water-Entry Vehicles. Astronaut. Syst. Eng. Technol. 2021, 5, 41–46,53. [Google Scholar]
- Peng, R.; Feng, H.; Xiang, M.; Peng, Y. Effect of head jet on load characteristics of a transdielectric vehicle during water entry. Ship Sci. Technol. 2024, 46, 59–66. [Google Scholar] [CrossRef]
- Shi, Y.; Gao, X.-F.; Pan, G. Design and load reduction performance analysis of mitigator of AUV during high speed water entry. Ocean Eng. 2019, 181, 314–329. [Google Scholar] [CrossRef]
- Zheng, W.; Li, Q.; Fan, X.; Lv, X. Review of the Development on Load Reduction Methods for Water Entry of High-Speed Vehicles. J. Unmanned Undersea Syst. 2024, 32, 411–425. [Google Scholar] [CrossRef]
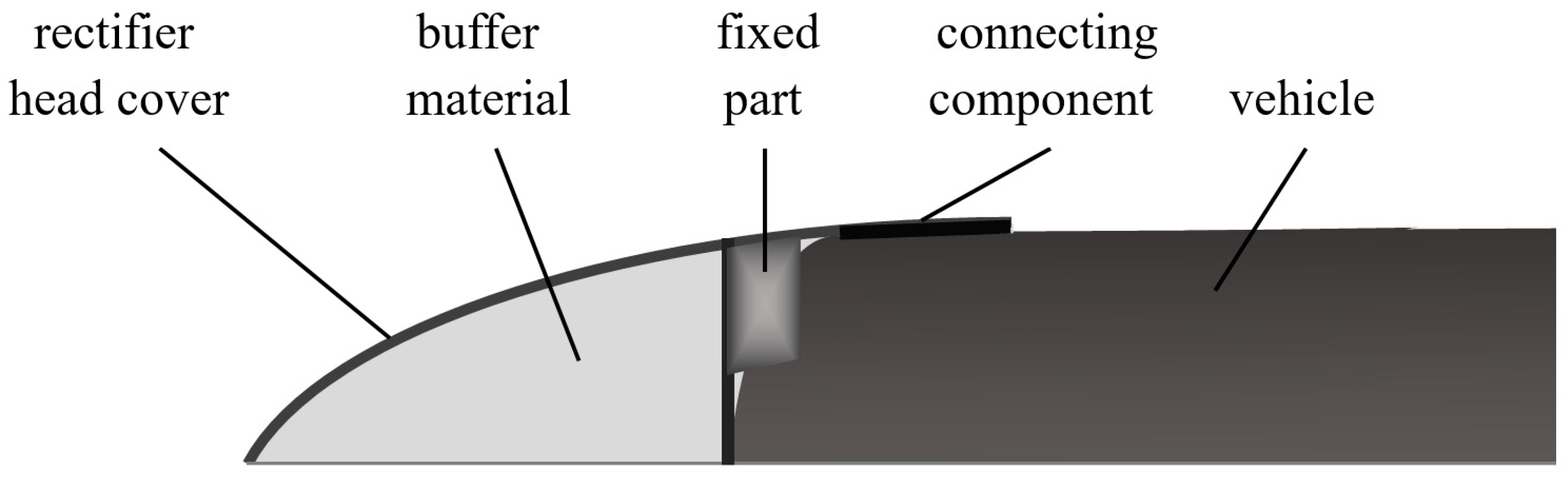
- Xu, X.; Li, J.; Cao, X.-J. Water-Entry Impact Performance of Torpedo′s Cushion Nose Cap. Torpedo Technol. 2012, 20, 161–165,170. [Google Scholar] [CrossRef]
- Yan, Z. An Approach to the Behavior of water-entry missile’s mitigator. Chin. J. Hydrodyn. 1987, 1, 112–121. [Google Scholar]
- Wang, Y.; Shi, X.; Wang, P. Exploring Analysis of Dynamic Cushioning Properties of Water-Entry Missile’s Shock Mitigator. J. Northwestern Polytech. Univ. 2009, 27, 707–712. [Google Scholar] [CrossRef]
- Wei, H.; Shi, C.; Sun, T.; Bao, W.; Zhang, G. Numerical study on load-shedding performance of a high-speed water-entry vehicle based on an ALE method. Explos. Shock Waves 2021, 41, 112–123. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Z.; Pan, G.; Gao, X. Structural design and load reduction performance analysis of gradient density head cap of vehicle. Chin. J. Theor. Appl. Mech. 2022, 54, 939–953. [Google Scholar] [CrossRef]
- Yao, X.; Yang, Z.; Ma, G.; Chen, Y.; Yin, Q.; Kong, D.; Sun, L.; Fan, S.; Fang, M. Research on the characteristics and similarity relationships of impact load reduction of a vehicle entering water. Appl. Ocean Res. 2024, 142, 103814. [Google Scholar] [CrossRef]
- Li, Y.; Zong, Z.; Sun, T. Crushing behavior and load-reducing performance of a composite structural buffer during water entry at high vertical velocity. Compos. Struct. 2021, 255, 112883. [Google Scholar] [CrossRef]
- Li, Y.; Zong, Z.; Sun, T. Classification of the collapse of a composite fairing during the oblique high-speed water entry. Thin-Walled Struct. 2023, 182, 110260. [Google Scholar] [CrossRef]
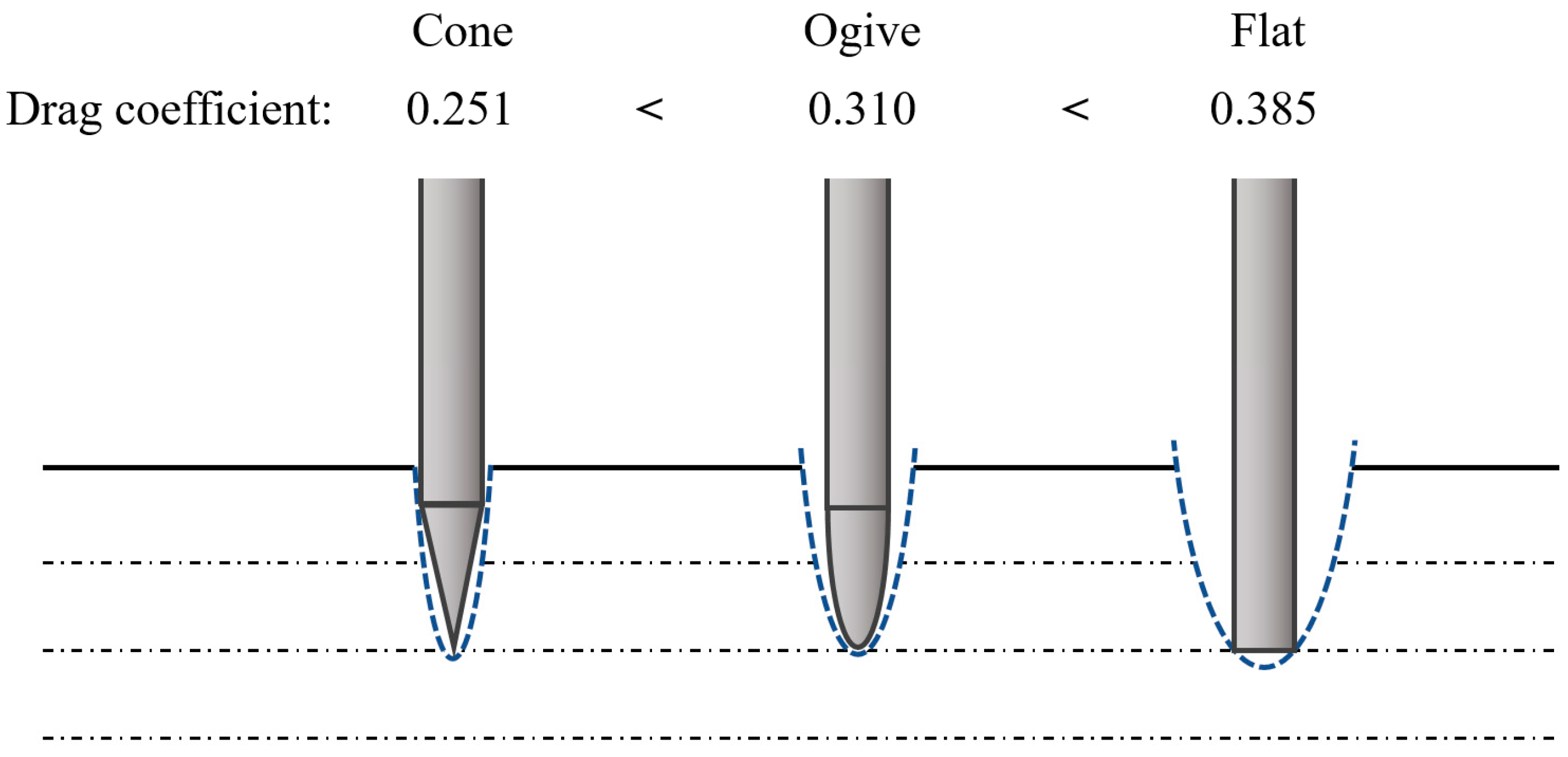
- Sui, Y. Study on the Fluid-Structure Coupling Load Characteristics of the Water Entry of the Projectiles with Different Nose Shapes. Ph.D. Dissertation, Harbin Engineering University, Harbin, China, 2023. [Google Scholar]
- Liu, H. Study on Load Reduction of Revolved Body Entering Water at High Speed. Master’s Thesis, Harbin Engineering University, Harbin, China, 2021. [Google Scholar]
- Sui, Y.-T.; Ming, F.-R.; Wang, S.-P.; Han, R. Experimental investigation on the impact force of the oblique water entry of a slender projectile with spring buffer. Appl. Ocean Res. 2023, 138, 103631. [Google Scholar] [CrossRef]
- Fu, Z.; Sun, L.; Zhi, M.; Wang, P.; Wang, D. Numerical study on the dynamic characteristics of a vehicle with a multistage load reduction structure during oblique water entry. Ocean Eng. 2024, 295, 116778. [Google Scholar] [CrossRef]
- Zhi, M.; Li, Z.; Sun, L.; Wang, D. Investigation and optimization of load characteristics of a multi-stage load-reduction structure for vehicles during high-speed vertical water entry. Ocean Eng. 2023, 289, 116183. [Google Scholar] [CrossRef]
- Wang, Y. Study on Load Reduction of Projectile with High Speed. Master’s Thesis, Harbin Engineering University, Harbin, China, 2022. [Google Scholar]
- May, A. Water Entry and the Cavity-Running Behavior of Missiles. J. Fluid Mech. 1975, 1, 123–145. [Google Scholar] [CrossRef]
- Zhou, K.; Huang, Z.; Chen, Z.; Liu, X.; Wang, H. Ricochet Phenomenon of Tans-media Vehicle at High-speed Oblique Water-entry. Equip. Environ. Eng. 2022, 19, 39–48. [Google Scholar] [CrossRef]
- Liu, X.; Luo, K.; Yuan, X.; Ren, W. Influence of Expansion Sterns on the Flattening Trajectory Characteristics of a Trans-Media Vehicle During High-Speed Water Entry. Chin. J. Theor. Appl. Mech. 2023, 55, 343–354. [Google Scholar] [CrossRef]
- Yu, F. The Numerical Simulation Study of Whipping Performance in Water Entry of Navigation Body. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Yan, Z. The Technology of Stabilization of Initial Trajectory of Water-entry Torpedoes. Chin. J. Hydrodyn. 1990, 5, 117–126. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, X. Numerical Analysis for Initial Hydroballistics of Airborne Missile During Oblique Water-entry Impact. J. Ballist. 2012, 24, 92–95. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, W.; Li, J.; Li, Z.; Pang, D. Simulation on Whip Phenomenon of Torpedo during Oblique Water Entry. J. Unmanned Undersea Syst. 2018, 26, 146–151. [Google Scholar] [CrossRef]
- Xu, X. Investigation of Water Entry Trajectory of Torpedo. Torpedo Technol. 2004, 12, 29–31. [Google Scholar]
- Ruzzene, M.; Kamada, R.; Bottasso, C.L.; Scorcelletti, F. Trajectory Optimization Strategies for Supercavitating Underwater Vehicles. J. Vib. Control. 2008, 14, 611–644. [Google Scholar] [CrossRef]
- Kirschner, I.N.; Rosenthal, B.J.; Uhlman, J.S. Simplified Dynamical Systems Analysis of Supercavitating High-Speed Bodies. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Yuan, X.; Zhu, Z. Influence of preset rudder angle on trajectory and hydro-dynamic at high-speed water-entry. Chin. J. Appl. Mech. 2015, 1, 11–16. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, X.; Luo, K.; Qi, X. Experimental Investigation of the Influence of Preset Rudder Angle on Tail-slapping of a Transmedia Vehicle during Water Entry. Acta Armamentarii 2023, 44, 1632–1642. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, X.; Luo, K.; Lu, N. Experiments and Simulation of Continuous Water Entry and Exit Trajectories of a Trans-media Vehicle. Acta Armamentarii 2023, 44, 1225–1236. [Google Scholar] [CrossRef]
- Huang, B.; Li, D.; Huang, C.; Gu, J.; Luo, K. Effect of Material Density on the Tail-slapping Characteristics of Supercavitating Projectiles. J. Unmanned Undersea Syst. 2023, 31, 211–220. [Google Scholar] [CrossRef]
- Miloh, T.; Shukron, Y. Ricochet Off Water of Spherical Projectiles. J. Ship Res. 1991, 35, 91–100. [Google Scholar] [CrossRef]
- Hutchings, I.M. The ricochet of spheres and cylinders from the surface of water. Int. J. Mech. Sci. 1976, 18, 243–247. [Google Scholar] [CrossRef]
- Park, M.-S.; Jung, Y.-R.; Park, W.-G. Numerical study of impact force and ricochet behavior of high speed water-entry bodies. Comput. Fluids 2003, 32, 939–951. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, P.; Liu, G.; Zhao, X.; Qin, X. Load and motion behaviors of ogive-nosed projectile during high-speed water entry with angle of attack. Ocean Eng. 2022, 266, 112937. [Google Scholar] [CrossRef]
- Li, Q.; Lu, L.; Cai, T. Numerical investigations of trajectory characteristics of a high-speed water-entry projectile. AIP Adv. 2020, 10, 095107. [Google Scholar] [CrossRef]
- Qi, X.; Shi, Y.; Liu, X.; Pan, G. Study on trajectory characteristics of stepped cylindrical projectile entering water at small angle. Chin. J. Theor. Appl. Mech. 2023, 55, 2468–2479. [Google Scholar] [CrossRef]
- Sui, Y.-T.; Li, S.; Ming, F.-R.; Zhang, A.M. An experimental study of the water entry trajectories of truncated cone projectiles: The influence of nose parameters. Phys. Fluids 2022, 34, 052102. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, H.; Wei, J.; Zhang, F. Stability Analysis of High-Speed Water Entry of Different Structure Projectiles. J. Ordnance Equip. Eng. 2019, 40, 50–54. [Google Scholar] [CrossRef]
- Song, B.; Du, X.; Meng, R.; Li, J.; Shao, C. Numerical Simulation of Water-entry Impact Force for Air-launched Mine. Torpedo Technol. 2008, 16, 6–8,12. [Google Scholar] [CrossRef]
- Wagner, H. Phenomena associated with impacts and sliding on liquid surfaces. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Logvinovich, G.V. Hydrodynamics of Flows with Free Boundaries; Institute for Physical Science and Technology: College Park, MD, USA, 1969. [Google Scholar]
- Korobkin, A. Analytical models of water impact. Eur. J. Appl. Math. 2004, 15, 821–838. [Google Scholar] [CrossRef]
- Dobrovol’skaya, Z.N. On some problems of similarity flow of fluid with a free surface. J. Fluid Mech. 1969, 36, 805–829. [Google Scholar] [CrossRef]
- Chen, C.; Sun, T.; Wei, Y.; Wang, C. Computational analysis of compressibility effects on cavity dynamics in high-speed water-entry. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 495–509. [Google Scholar] [CrossRef]
- Li, G.; You, T.; Kong, D.; Li, J.; Zhou, W. Effect of Fluid Compressibility on High-speed Water-entry of Revolutionary Body. Acta Armamentarii 2020, 41, 720–729. [Google Scholar] [CrossRef]
- Egorov, L.T. Impact on a Compressible Fluid; National Advisory Committee for Aeronautics: Washington, DC, USA, 1958. [Google Scholar]
- Borg, S.F. Initial Wedge Impact on a Compressible Fluid. J. Appl. Phys. 1959, 30, 1432–1436. [Google Scholar] [CrossRef]
- Korobkin, A.A. Asymptotic Theory of Liquid--Solid Impact. Philos. Trans. Math. Phys. Eng. Sci. 1997, 355, 507–522. [Google Scholar] [CrossRef]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Plesset, M.S. The Dynamics of Cavitation Bubbles. J. Appl. Mech. 2021, 16, 277–282. [Google Scholar] [CrossRef]
- Garabedian, P.R. Calculation of axially symmetric cavities and jets. Pac. J. Math. 1956, 6, 611–684. [Google Scholar] [CrossRef]
- Truscott, T.T. Cavity Dynamics of Water Entry for Spheres and Ballistic Projectiles. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Aldape, K.; Zadeh, G.; Mansouri, S.; Reifenberger, G.; von Deimling, A. Glioblastoma: Pathology, molecular mechanisms and markers. Acta Neuropathol. 2015, 129, 829–848. [Google Scholar] [CrossRef]
- Lundstrom, E.A.; Fung, W.K. Fluid Dynamic Analysis of Hydraulic Ram III (Result of Analysis); NASA STI/Recon Technical Report N: Washington, DC, USA, 1976. [Google Scholar]
- Lee, M.; Longoria, R.G.; Wilson, D.E. Cavity dynamics in high-speed water entry. Phys. Fluids 1997, 9, 540–550. [Google Scholar] [CrossRef]
- Zhang, W. Study on Fluid-structure Interactions Characteristics and Similarity Analysis of HighSpeed Navigation Body Enter Water. Master’s Thesis, Harbin Engineering University, Harbin, China, 2023. [Google Scholar]
- Stinebring, D.; Billet, M.; Lindau, J.; Kunz, R. Developed Cavitation-Cavity Dynamics. VKI Spec. Course Supercavitating Flows 2001, 29. [Google Scholar]
- Xu, H.; Luo, K.; Huang, C.; Zuo, Z.; Gu, J. Variation Characteristics of Formation and Development of Ventilated Supercavity at Low Froude Numbers. J. Shanghai Jiaotong Univ. 2021, 55, 934–941. [Google Scholar] [CrossRef]
- Waugh, J.G. Water-entry pitch modeling (Water entry pitch modeling using Froude and cavitation number scaling with and without gas density scaling, using dummy Mk 25 aircraft torpedoes). J. Hydronautics 1968, 2, 87–92. [Google Scholar] [CrossRef]
- Qi, D.; Feng, J.; Xu, B.; Zhang, J.; Li, Y. Investigation of water entry impact forces on airborne-launched AUVs. Eng. Appl. Comput. Fluid Mech. 2016, 10, 473–484. [Google Scholar] [CrossRef]
- Korobkin, A.; Guéret, R.; Malenica, Š. Hydroelastic coupling of beam finite element model with Wagner theory of water impact. J. Fluids Struct. 2006, 22, 493–504. [Google Scholar] [CrossRef]
- Hao, C.; Dang, J.; Chen, C.; Huang, C. Numerical study on water entry process of supercavitating projectile by considering bidirectional fluid structure interaction effect. Chin. J. Theor. Appl. Mech. 2022, 54, 678–687. [Google Scholar] [CrossRef]
- Wu, Q. Physical and Numerical Investigation of Cavitating Flow-Induced Vibrations. Ph.D. Dissertation, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Ryzhakov, P.B.; Rossi, R.; Idelsohn, S.R.; Oñate, E. A monolithic Lagrangian approach for fluid–structure interaction problems. Comput. Mech. 2010, 46, 883–899. [Google Scholar] [CrossRef]
- Deng, C. The Algorithm Study of Weak Coupling in Fluid-Structure Interaction. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2012. [Google Scholar]
- Xu, Y.; Tan, D.; Yang, C. Study on tail-slap load characteristics of high-speed projectile based on CFD/CSD coupling. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 2539–2546. [Google Scholar] [CrossRef]
- Gao, Y. Numerical Analysis of Impact Load and Flow Characteristics of High Speed Water-Entry for a Revolution Body Based on a Fluid-Structure Interaction Method. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Shi, Y.; Pan, G.; Yim, S.C.; Yan, G.; Zhang, D. Numerical investigation of hydroelastic water-entry impact dynamics of AUVs. J. Fluids Struct. 2019, 91, 102760. [Google Scholar] [CrossRef]
- Wei, T.; Li, J.; Zeng, Z.; Lian, L. Trans-media resistance investigation of hybrid aerial underwater vehicle base on hydrodynamic experiments and machine learning. Ocean Eng. 2022, 266, 112808. [Google Scholar] [CrossRef]
- Lv, K.; Lin, E.; Liu, Y.; Chen, Z.; Wang, Y.; He, M.; Yan, J.; Lv, P.; Yang, Y.; Li, H.; et al. Data-driven optimization of nose profiles for water entry impact load reduction. Ocean Eng. 2025, 315, 119851. [Google Scholar] [CrossRef]
- Huang, X.; Li, Z.; Dai, Y.; Zhu, X. Application of parallel neural networks (PNN) in predicting and analyzing vehicle attitude during the water exit process. Ocean Eng. 2025, 323, 120602. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, H.; Sun, T.; Duan, J. Water-exit dynamics of a ventilated underwater vehicle in wave environments with a combination of computational fluid dynamics and machine learning. Phys. Fluids 2024, 36, 023312. [Google Scholar] [CrossRef]



| Types | Structural Characteristics | Water Entry States | Load Impact Problem | Ballistic Stability Problem |
|---|---|---|---|---|
| Air-dropped torpedoes | Blunt-nosed thin-shell structure (~100 mm diameter [4]) with integrated precision electronics. | Speed: Tens of m/s; Large water entry angle: usually >70° [4]. | The problems of head structural damage and internal electronics damage. | The whip problem. |
| Supercavitating vehicles | Large-scale thin-shell structure (~100 mm diameter [6]) in conical shape with cavitator. | Speed: Hundreds of m/s; Small water entry angle: usually 10°~45° [7]. | The problems of thin body structure fracture. | The flat-turning problem. |
| High-speed projectiles | Conical compact rigid-body design (~10 mm diameter [8]). | Speed: Hundreds to thousands of m/s; Minimal water entry angle [9]. | The problems of structural bending. | The ricochet problem. |
| Active Load Reduction Methods | Load Reduction Mechanisms | Types of Applicable Vehicles |
|---|---|---|
| Parachute | Opening the parachute increases the drag force, reduces the water entry speed, and prolongs the water impact time. | Air-dropped torpedoes |
| Air jet | The air jet creates an air cushion effect, making the peak pressure far away from the bow of the vehicle and prolonging the water impact action time. | High-speed projectiles, supercavitating vehicles |
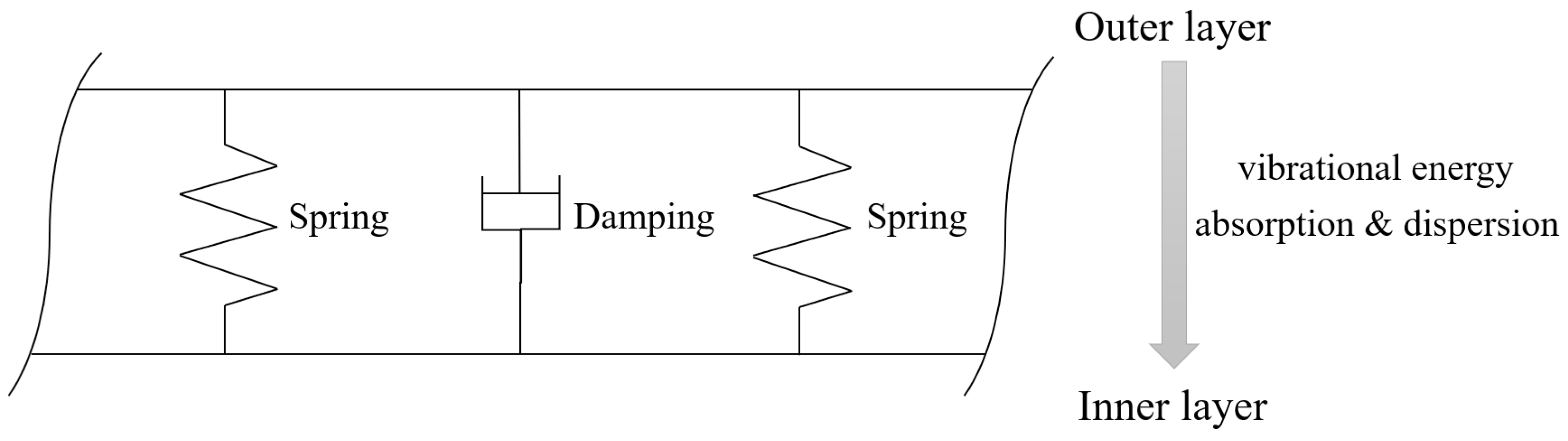
| Buffer headcap | The elastic material prolongs the water impact action time, absorbs strong impact energy and undergoes gradual compression, failure, and destruction until it detaches from the vehicle. | Air-dropped torpedoes |
| Spring, air chamber, and its composite structures | The buffer structure prolongs the water impact action time, absorbs the impact energy, and slowly releases it to the vehicle. | High-speed projectiles, supercavitating vehicles |
| Research Aspects | Research Phase | Main Theoretical Researchers | Research Achievements and Contributions |
|---|---|---|---|
| Water- entry impact load | Early Studies | Von Karman | Introduced the “added mass” concept and applied momentum conservation to calculate water impact pressure during seaplane landings. |
| Wagner | Developed approximate flat-plate theory by considering free surface elevation and introducing a correction factor for small deadrise angles. Extended the model for wedge-shaped bodies. | ||
| Egorov, Borg | Investigated blunt-body impacts on compressible fluids, proposed time-scale formulas for compressibility effects (related to sound speed in water). | ||
| Subsequent Developments | Logvinovich | Proposed the Original Logvinovich Method (OLM), incorporating nonlinear terms in the Bernoulli equation and added velocity terms at solid–liquid contact points. Improved modeling of shockwave propagation and liquid separation. | |
| Dobrovol’skaya | Applied self-similarity theory to transform free surface flow problems into nonlinear singular integral equations, providing tools for solving complex free surface flows. | ||
| Further improvement | Korobkin | Developed the Modified Logvinovich Method (MLM), refining nonlinear terms and velocity treatments. Enabled simulations for complex geometries, motions, and flow conditions. Refined the cross-media water entry process into five stages: supersonic, transonic, subsonic, inertial, and developed flow stages. | |
| Evolution of water- entry cavity | Early Studies | Rayleigh & Plesset | Formulated the Rayleigh–Plesset equation, describing the kinetic behavior of cavitation bubbles under the influence of pressure changes, viscosity, and surface tension. |
| Garabedian | Derived asymptotic expressions for cavity width, length, and parameters (Garabedian formula) using perturbation methods for axisymmetric free surface flows. | ||
| Logvinovich | Proposed the “independence principle of cavity section expansion”, enabling theoretical calculations of unsteady cavity evolution by decomposing cavity morphology. | ||
| Subsequent development | Lundstrom | Derived an empirical formula for cavity radius based on energy conservation, summarizing cavity shape evolution laws for cross-media water entry vehicles. | |
| Lee | Proposed a universal cavity evolution model applicable to arbitrary shapes and velocities, predicting closure time and position accurately. | ||
| Further improvement | Truscott | Improved Logvinovich’s model with full-scale experiments, analyzing effects of velocity, geometry, and angle of attack on cavity formation. Optimized vehicle shape design. | |
| Vasin | Applied Logvinovich’s theory to analyze unsteady cavity dynamics and external pressure changes, including gravity effects on cavity shape. |
| Similarity Parameter | Expression | Physical Meaning | Explicit Value |
|---|---|---|---|
| Froude Number (Fr) | Ratio of inertial forces to gravitational forces | 71.4 | |
| Cavitation Number (σ) | Ratio of static pressure to dynamic pressure | 0.0198 | |
| Reynolds Number (Re) | Ratio of inertial forces to viscous forces | 2.0 × 107 | |
| Weber Number (We) | Ratio of inertial forces to surface tension forces , the surface tension coefficient) | 2.74 × 107 | |
| Capillary Number (Ca) | Ratio of viscous forces to surface tension forces , the surface tension coefficient) | 1.376 | |
| Mach Number (Ma) | Ratio of fluid velocity to speed of sound , the speed of sound in water) | 0.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Ma, X.; Zhao, J.; Shen, L. A Review on Research of Load Reduction and Ballistic Stability During Cross-Media Water Entry Processes. J. Mar. Sci. Eng. 2025, 13, 703. https://doi.org/10.3390/jmse13040703
Lu Q, Ma X, Zhao J, Shen L. A Review on Research of Load Reduction and Ballistic Stability During Cross-Media Water Entry Processes. Journal of Marine Science and Engineering. 2025; 13(4):703. https://doi.org/10.3390/jmse13040703
Chicago/Turabian StyleLu, Qingxia, Xiaojian Ma, Jing Zhao, and Lin Shen. 2025. "A Review on Research of Load Reduction and Ballistic Stability During Cross-Media Water Entry Processes" Journal of Marine Science and Engineering 13, no. 4: 703. https://doi.org/10.3390/jmse13040703
APA StyleLu, Q., Ma, X., Zhao, J., & Shen, L. (2025). A Review on Research of Load Reduction and Ballistic Stability During Cross-Media Water Entry Processes. Journal of Marine Science and Engineering, 13(4), 703. https://doi.org/10.3390/jmse13040703




