Tramp Ship Routing and Scheduling with Integrated Carbon Intensity Indicator (CII) Optimization

Abstract

In response to growing environmental concerns and regulatory pressures, reducing carbon emissions in maritime transport has become a priority. Shipping companies face the challenge of balancing profitability objectives with the imperative to minimize their environmental footprint. This study addresses the tramp ship routing and scheduling problem by incorporating the carbon intensity indicator (CII) into the optimization framework. A bi-objective optimization model is developed, with two objective functions aimed at maximizing fleet profit and improving CII ratings. The Gale–Shapley algorithm is employed to achieve stable vessel–cargo matching, and the genetic algorithm is adopted for iterative optimization. This computational study, based on real historical data, verifies the effectiveness of the proposed model and algorithm. The results demonstrate notable improvements in fleet efficiency and environmental performance, increasing profitability by 4.38% while maintaining favorable CII ratings. The findings provide valuable theoretical guidance for shipping companies navigating increasingly stringent CII regulations.

1. Introduction

As an important mode of freight transportation, maritime shipping accounts for more than 80% of the global freight trade [1]. In 2022, the international seaborne trade volume reached 12,027 million tons, with a world fleet capacity of 2273 million deadweight tons [2]. According to Clarkson’s statistics, in 2022, the international trade in dry bulk cargoes was 5252 million tons, making up about 50% of seaborne trade and occupying an important position in the shipping market. Additionally, because of its uncertainties, including uncertain cargoes, calling ports, routes, timetables, and freight rates, the schedule of tramp shipping is more complex compared with liner shipping and industrial shipping, and research on tramp ship scheduling remains relatively rare [3].

Although maritime shipping plays a crucial role in boosting world trade and connecting the global economy, it is also a major energy consumer, one of the main sources of greenhouse gas (GHG) emissions, accounting for 3% of total global GHG emissions [4]. With the rapid growth in seaborne trade volume, shipping CO₂ emissions have increased from 977 million tons in 2012 to 1056 million tons in 2018, and international shipping emissions are likely to increase by 40% based on the 2008 level by 2050 [4].

In response to climate change, the IMO has established GHG reduction targets. In 2018, the IMO adopted the “Initial Strategy on Reduction of GHG Emissions from Ships”, which sets out quantified targets for emission reductions in the short, medium, and long term [5]. Each ship receives a CII rating annually based on its carbon emissions intensity for that year. CII is a metric that evaluates the carbon emissions intensity of a ship engaged in transport work. Ships with poor ratings may face challenges in obtaining a CII compliance statement. This could adversely affect their normal operations. This implies that ships need to strike a balance between increasing profits and reducing carbon emissions. There are several methods shipping companies can use to improve their ships’ CII ratings, thereby avoiding incurring penalties. These methods can be divided into technical and operational aspects.

One effective technical measure is to switch from fossil fuel to alternative low-carbon or zero-carbon fuel, although high investment costs may make this a long-term goal [6]. Chemical absorption has been identified as the commercially viable mainstream approach despite challenges in high energy consumption, low regeneration efficiency, and spatial constraints. The development and application of carbon capture and storage (CCS) technology will provide more possibilities to achieve carbon reduction targets for the shipping industry [7]. The IMO lists several applications that can improve vessel energy efficiency, such as energy-saving devices (ESDs), engine power limitation (EPL), waste heat recovery systems (WHRS), solid-oxide fuel cells (SOFCs), and improvements to marine equipment, such as propellers and rudder blades [8,9,10,11]. Regular maintenance and timely inspections also help optimize mechanical performance and reduce energy consumption. Adland et al. [12] pointed out that periodic hull cleaning and dry-docking can significantly reduce fuel consumption. Different emission allowance allocation policies significantly influence shipowners’ adoption of emission reduction technologies, with grandfathering effectively reducing emissions but potentially hindering advanced technology adoption, while non-free allocation, though cost-neutral, impedes low-carbon technology uptake, emphasizing the need for adaptive policymaking to optimize emission reductions in evolving market and technological landscapes [13,14]. Operational solutions are generally more cost-effective and easier to implement than most technical measures [15]. Controlling sailing speed and optimizing routes are key strategies for reducing carbon emissions. Slow steaming is widely used in commercial shipping to lower fuel consumption, but it could result in cargo delivery delays and reduced transport commitments, thereby impacting costs and reputation [16]. Wang et al. [17] developed a mixed-integer linear programming model to optimize ship deployment, sailing speed, and fuel selection, balancing cost minimization with compliance through the strategic use of traditional and renewable fuels in designated areas. These practices cut operational costs and align with sustainability goals.

In these circumstances, maximizing economic benefits while meeting the rating requirements of CII is a crucial concern in the current marine transportation industry. The main contribution of this paper is the bi-objective mixed-integer programming model, aiming to increase the profits of the entire fleet while simultaneously achieving high CII ratings. The model also includes self-owned ships, chartered ships, and cargo time windows. As vessel–cargo matching involves both shipowners and cargo owners, matching must be performed after considering and selecting options for both sides. Gale and Shapley [18] introduced a stable matching model that enables agents from both sides to achieve optimal pairing. Furthermore, the genetic algorithm (GA) has been widely recognized as an effective solution for vehicle routing problems [19]. This paper uses the Gale–Shapley algorithm for vessel–cargo matching, followed by iterative speed optimization using the GA to output the final fleet scheduling plan. The effectiveness of the method is demonstrated through a case study.

The remainder of this paper is organized as follows. Section 2 presents the literature review, detailing previous research and methodologies related to ship routing and scheduling, along with carbon intensity metrics in maritime operations. Section 3 describes the specific problem of tramp ship routing and scheduling with consideration of CII. We propose a mathematical optimization model and outline methods for solving this problem based on the Gale–Shapley algorithm and the GA. Section 5 provides a detailed case study to assess the applicability and effectiveness of the proposed model. Section 6 concludes this paper by summarizing the findings and suggesting potential directions for future research.

2. Literature Review

The optimization of ship routing and scheduling is a typical operations research problem and a complex dynamic issue. Carriers must allocate their own ships rationally based on shippers’ transport demands and shipping capabilities, creating transport plans for cargo assignments. This study focuses on two aspects of the research literature: ship routing and scheduling and the integration of carbon emissions, including CII considerations.

Traditional ship routes and schedules are manually planned based on past experience. Recently, there has been in-depth research on this issue. Researchers have explored more sophisticated approaches dealing with carrier selection, many-to-many matching, and two-sided matching. These studies aim to optimize the allocation of vessels to cargoes, considering the preferences and constraints of shipowners and cargo owners. Since 1995, the dry bulk transportation market has faced an overcapacity of vessels, leading to a continuous decline in vessel freight rates in the shipping market. This situation prompted Kim and Lee [20] to develop a ship scheduling decision-making system based on a generalized elastic ship capacity segmentation model. The intention was to optimize the static one-stage decision-making optimization problem for a single voyage or a limited number of voyages, a single ship’s scheduling, and a cargo-determined ship-model-based DSS in Ship Scheduling (MoDiss). On this basis, Fagerholt [21] established a corresponding model for tramp ship scheduling, using a hybrid heuristic algorithm, adding a search engine interface to help shipowners and cargo owners search in the system for the ships or cargoes of direct interest to them. The aims were to increase the chances of reaching a cooperative deal between the two parties, to reduce the voyage time of empty ships and the waiting time of ships in line at ports, to shorten the voyage mileage of empty ships, and to reduce the additional costs incurred by empty ships. Fagerholt and Christiansen [22] presented a bulk ship scheduling problem that is a combined multi-ship pickup and delivery problem with time windows (m-PDPTW) and a multi-allocation problem. Zeng et al. [23] developed an integer linear programming model to improve coal transportation efficiency and designed a two-stage heuristic tabu search algorithm to optimize fleet planning and route selection. Numerical experiments showed that the proposed method could reduce unit transportation costs and average ship delays and improve the reliability of the coal transport system.

Compared with liner shipping, tramp shipping needs to find cargo sources in a highly uncertain market. Bronmo et al. [24] considered variable cargo sizes and quantities, introducing flexible cargo sizes into tramp ship scheduling and routing problems. They proposed a realistic mixed-integer programming model and used a set partitioning method to solve multi-vessel loading and unloading problems with time windows and flexible cargo sizes, aiming to maximize profits. Lin and Liu [25] simultaneously addressed the problems of ship allocation, freight assignment, and ship routing in tramp shipping. They constructed sub-networks for transportation and navigation based on the port locations and transportation time of cargoes, transforming the ship routing problem into a network arc flow problem in operations research. Vilhelmsen et al. [26] combined the voyage separation requirements to minimize the time intervals between voyages, designed a dynamic programming algorithm, and created a time window branching scheme. Computational results showed that this algorithm converged better and could find optimal solutions more effectively compared with previous ship routing optimizations. In addition to the uncertainty of cargo demand, seasonal fluctuations and weather-related unseaworthy conditions are difficulties in tramp ship scheduling. Yu et al. [27] considered all the factors, constructed a mixed-integer programming model to maximize profits and proposed a heuristic method. Zhao et al. [28] proposed a robust multi-objective optimization model, integrating chance-constrained programming and NSGA-II to address voyage duration uncertainties for ore transportation, demonstrating enhanced robustness.

The sailing speed of ships is a crucial parameter in ship design and operation, determining the time window, affecting fuel consumption, and thereby determining emissions. Consequently, it considerably impacts shipping companies’ ship scheduling and routing, operational efficiency, and profitability. In recent years, increasing concerns about carbon emissions and continuous fluctuations in fuel prices, mean that speed optimization has become a vital cost-control decision for shipping companies. Ma et al. [29] considered emission control areas (ECA) regulations and weather conditions, investigating the optimization of ship routes and speed solved by the Non-dominated Sorting Genetic Algorithm (NSGA-II), minimizing sailing cost and time. Carbon emissions are directly affected by fuel consumption. Wang et al. [30] considered factors including ship carbon emissions, as well as demurrage, dispatch in voyage chartering, and proposed speed decision models under three forms of carbon emission taxation. Addressing a multiple-ship scenario, Wen et al. [31] derived ship scheduling plans and optimal speeds under different objective functions, such as the shortest sailing time, minimum total cost, and lowest carbon emissions. As the IMO enforces increasingly stringent regulations on ship emissions, more scholars believe that a comprehensive analysis of ship emissions is a critical step in devising effective strategies to reduce air pollution. Weng et al. [32] estimated the emissions from vessels in the Yangtze River Estuary based on AIS data, examining the impact of vessel type, operational mode, emission equipment, time, and location on emissions. Based on noon report data, Yan et al. [33] proposed a two-stage model for predicting and reducing ship fuel consumption. In the first stage, a random forest regression model was developed to predict fuel consumption for dry bulk carriers under different conditions, such as sailing speed, cargo load, sea state, and weather. In the second stage, a mixed-integer programming model was built based on the prediction model to optimize sailing speed and minimize total fuel consumption over a voyage segment. Numerical experiments demonstrated that this model could effectively reduce fuel consumption by 2–7%, thereby reducing CO₂ emissions. Increasingly stringent regulations on ship energy-saving and emission-reduction technologies promoted Sun et al. [34] to consider wind-assisted devices such as rotors and sails to harness renewable wind energy. They proposed an improved ship weather routing optimization framework based on the A* algorithm, using ship design, weather forecasts, and historical navigation information to determine the optimal route and operation of ships equipped with wind-assisted rotors. Several improvements to the classic A* algorithm, including directional search and three-dimensional expansion, have been introduced to enhance optimization efficiency and effectiveness. Considering ship speed and payload, Li et al. [35] proposed a mixed-integer nonlinear programming model, introducing a discretized speed variable and employing a branch-and-price algorithm, the research successfully solves large-scale problem instances, demonstrating the model’s effectiveness in reducing ship fuel consumption. Yuan et al. [36] proposed an optimization method that integrates speed and route planning to enhance the operational efficiency of ship fleets while ensuring compliance with CII regulations. Focusing on the Northeast Passage, Tsai et al. [37] found that the CII system could significantly influence future shipping routes as it aligns with global efforts to reduce carbon emissions in maritime shipping.

Although an increasing number of scholars have proposed various models and algorithms for optimizing ship routing and scheduling, much of the existing research focuses on maximizing economic benefits. While prior studies have incorporated sailing speed and carbon emissions into optimization models, few studies have taken the CII into account. This study addresses this gap by integrating the CII as both one of the objective functions and a constraint in the research framework. In contrast to conventional manual matching, this study introduces a two-sided matching mechanism that explicitly balances the interests of shipowners and cargo owners. Furthermore, rather than focusing on individual vessels, the research adopts a fleet-centric perspective, ensuring that each vessel remains profitable and meets carbon intensity standards, thereby achieving overall fleet optimization. In short, the main objective of this study is to develop a bi-objective optimization framework for tramp ship scheduling that simultaneously maximizes the fleet’s overall profit and optimizes the CII rating, which can provide guidance for operational decision-making.

3. Mathematical Model

The tramp shipping market, characterized by the extensive presence of numerous carriers and shippers, exhibits a perfectly competitive market structure. Within this environment, the scheduling problem, taking carbon emission intensity into account, is a complex task that requires strategic consideration. The problem has two objectives: to maximize the total operational profit and to reduce the unit carbon emission. These objectives are often in conflict. In this section, we examine the specifics of the bi-objective optimization model, exploring the mathematical formulations and potential solutions for addressing tramp ship routing and scheduling, taking profit and CII objectives into consideration.

The first objective is to optimize the fleet schedule to increase the total operational profits. The shipping company must strategically allocate ships in a manner commensurate with cargo demands to optimize operational efficiency and enhance service quality. The second objective is to improve the CII rating. Sailing speed determines fuel consumption, fuel cost, and carbon emissions. However, lower energy consumption may reduce economic benefits. Therefore, when executing freight tasks, it is necessary to adjust the speed to maximize fleet profits while achieving optimal CII ratings for the vessels. Striking a balance between economic objectives and environmental responsibilities is a challenging prospect. Therefore, this paper focuses on improving the profit of a fleet and achieving a higher CII rating.

3.1. Problem Description

A voyage charter is commonly used in tramp shipping, particularly for meeting one-time or short-term cargo transportation needs. The flexibility of a voyage charter makes it a crucial option for shippers when dealing with volatile market conditions and fluctuating cargo demands. Shipping companies and cargo owners frequently enter into contracts of affreightment (COAs), which are long-term agreements between the carrier and shipper. These contracts provide both parties with enhanced certainty and stability, facilitating more predictable and secure operational planning over extended periods. A COA stipulates the carrier’s commitment to transport specified quantities of cargo between designated ports for the shipper. The specific details regarding the routes, time window, and freight rate are usually agreed upon in the contract. For carriers, COAs provide a steady source of cargo volume, allowing for better planning and utilization of the fleet. Shippers can secure transportation capacity at a known cost, thereby reducing exposure to freight rate volatility.

Let us take the example of a shipping company operating a heterogeneous fleet of ships consisting of dry bulk carriers with specific ship characteristics, including ship capacity, cost structure, and original location. As a carrier, the shipping company is obligated to execute designated transportation tasks within the planning period. The company must carefully assign vessels to each shipment, taking into account cargo volume, destination, and the time windows for loading and unloading. Several types of dry bulk cargo are scheduled for transport, including COA cargo and spot cargo. Each vessel within the fleet is limited to carrying a single shipment per voyage, precluding the possibility of loading or unloading additional cargo en route. If the capacity of the fleet is insufficient to handle all cargoes during the planning horizon, additional vessels may be chartered on the spot market to meet transportation demand. The revenue generated from these shipments is determined by the quantity of cargo and the negotiated freight rate.

3.2. Model Assumptions

To facilitate the process of calculation, the following assumptions are made:

• The tramp ships in the fleet are heterogeneous in terms of size, loading capacity, cruising speed, draft, fuel efficiency, and some other indicators;
• Each ship can only transport one cargo on one voyage, and each cargo can only be transported by one ship on one voyage; there are no split loads or trans-shipments;
• The shipping company can choose its own ships or charter ships on the spot market if necessary;
• There are no unforeseen delays due to weather conditions or port congestion. Details of each cargo demand, including its specific weight, loading port, discharging port, and time window, are fixed and known in advance;
• Ships sail at a specific constant speed on each leg;
• Ships have enough fuel to reach their destinations, and fuel prices do not change over time;
• Carriers and shippers are rational.

3.3. Model Formulation

3.3.1. Cost Calculation

When making informed decisions regarding freight assignments, cost is one of the key factors that needs to be considered. Because tramp ships do not have fixed sailing routes and schedules, each voyage has different costs and revenues based on known information, such as cargo quantities, ports of call, sailing distances, and ship parameters. In addition, if the current fleet capacity is insufficient to meet all transportation needs, there will be extra expenses for chartering ships on the spot market. The freight assignments must be carefully analyzed and calculated to ensure higher profits.

Voyage costs are mainly made up of two components: fuel cost and port cost. The specific calculation methods are as follows:

Fuel Cost:

The daily fuel consumption of the ship is given by a function $f\left(v,w\right)(tons/day)$. We use the realistic closed-form solution of Psaraftis and Kontovas [38].

$$f\left(v,w\right)=\mu v_{ijk}^3{\left(w_k+A_k\right)}^{{\displaystyle \frac{2}{3}}}$$

(1)

where $v$ is the ship speed, $w$ is the ship payload, $A$ is the lightship weight, and $\mu$ is a constant.

Let $p_f$ be heavy fuel price. The shipping cost for ship $k$ between nodes $i$ and $j$ can be defined as

$$C_{ijk}^s=p_f\mu v_{ijk}^3{\left(w_k+A_k\right)}^{{\displaystyle \frac{2}{3}}}{\displaystyle \frac{d_{ijk}}{24v_{ijk}}}$$

(2)

Port Cost:

During operation and berthing at port, ships will load and discharge cargoes, inevitably queuing at anchorages or ports, incurring fuel costs at port $C_{ik}^{pf}$:

$$C_{ik}^{pf}=p_f\gamma \left\{t_{ik}+\max \left[\left(T_{i\min }-T_{ik}\right),0\right]\right\}$$

(3)

where $\gamma$ is the fuel consumption of the ship at port(ton/h), $t_{ik}$ is the total berth time at node $i$ for ship $k$, $T_{i\min }$ and $T_{ik}$ denote the real times for arriving at node $i$ for ship $k$ and the earliest arrival time for the ship at node $i$ expected by the shipper, respectively.

Ships also need to use channels, berths, docks, and anchorages and apply for various services provided by the port authority, such as pilotage and tug assistance. Port disbursement is a crucial component of the voyage cost for tramp ships. It consists of port charges, stevedoring charges, cleaning holds, and other items. In this paper, let $P_{ik}$ be the port disbursement, and let $C_{ik}^p$ denote the port cost of ship $k$ at node $i$.

$$C_{ik}^p=p_f\gamma \left\{t_{ik}+\max \left[\left(T_{i\min }-T_{ik}\right),0\right]\right\}+P_{ik}$$

(4)

3.3.2. CII Calculation Method

According to the IMO, the CII determines the annual reduction factor needed to ensure continuous improvement of a ship’s operational carbon intensity within a specific rating level. The actual annual operational CII achieved must be documented and verified against the required annual operational CII. This enables the operational carbon intensity rating to be determined.

A ship rated D for three consecutive years, or E for one year, has to submit a corrective action plan to show how the required index of C or above will be achieved [39].

According to the IMO, the steps for CII rating of ships are as follows [40,41,42,43,44]:

• Calculation of CII (G1 CII calculation methods)

The attained annual operational CII is a measure used to evaluate the efficiency of a ship’s CO₂ emissions over a certain period, typically on an annual basis. This is calculated by dividing the total amount of CO₂ emitted by the ship (M) by the transport work completed (W):

$$Attained CII={\displaystyle \frac{M}{W}}={\displaystyle \frac{{\displaystyle \sum _{j}F{C}_j\times C_{Fj}}}{Capacity\times D_t}}$$

(5)

where $M$ is the sum of CO₂ emissions, $j$ is the fuel type, $F{C}_j$ is the total mass(in grams) fuel consumption of type $j$, $C_{Fj}$ represents the fuel oil mass of type $j$ to CO₂ mass conversion factor, $D_t$ is the total distance traveled (in nautical miles), and $W$ is the transport work completed by the ship, defined as the product of the ship’s capacity and $D_t$. For bulk carriers, deadweight tonnage should be used as $Capacity$.

2.

Reference Lines for CII (G2 reference lines guideline)

The 2023 IMO Strategy on Reduction of GHG Emissions from Ships set a goal of reducing the CO₂ emission intensity of shipping by 40% relative to 2008. Because of the unavailability of data in 2008, the IMO decided to base the development on fuel consumption data of operating ships in 2019. The reference guideline of CII, $CI{I}_{ref}$, is a function of capacity. Equation (6) indicates the computation of $CI{I}_{ref}$.

$$CI{I}_{ref}=aCapacit{y}^{-c}$$

(6)

G2 gives the values of parameters $a$ and $c$ for each ship type. In this paper, for bulk carriers, $a$ equals 4745 and $c$ equals 0.622.

3.

Operational Carbon Intensity Reduction Factors Relative to Reference Lines (G3 reduction factors)

The required CII can be calculated using $CI{I}_{ref}$ and reduction factor $Z$. The annual operational carbon intensity reduction rate is defined as the percentage by which the required annual operational CII value for a given year is lower than the baseline value.

$$\mathrm{Re}quired CII=\left(1-{\displaystyle \frac{Z}{100}}\right)\times CI{I}_{ref}$$

(7)

$Z$ is determined as 5, 7, 9, and 11 from 2023 to 2026, respectively. The values for the years beyond 2026 will be further studied and strengthened.

4.

Operational Carbon Intensity Rating of Ships (G4 rating guidelines)

The CII rating is determined by comparing the Attained CII with the Required CII. It can be classified into one of the five performance levels (A, B, C, D, E), representing excellent, good, average, fair, or unsatisfactory, respectively. There are four boundaries to separate the levels: superior, lower, upper, and inferior. The formulas for the four boundary values are as follows:

$$\begin{gathered} \mathrm{Superior} \mathrm{boundary}=\exp \left(d_1\right)\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Lower} \mathrm{boundary}=\exp \left(d_2\right)\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Upper} \mathrm{boundary}=\exp \left(d_3\right)\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Inferior} \mathrm{boundary}=\exp \left(d_4\right)\times \mathrm{Required} \mathrm{CII} \end{gathered}$$

(8)

The value of exp(d_i) is different for each ship type. For bulk carriers,

$$\begin{gathered} \mathrm{Superior} \mathrm{boundary}=0.86\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Lower} \mathrm{boundary}=0.94\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Upper} \mathrm{boundary}=1.06\times \mathrm{Required} \mathrm{CII} \\ \mathrm{Inferior} \mathrm{boundary}=1.18\times \mathrm{Required} \mathrm{CII} \end{gathered}$$

(9)

The ship’s rating is determined by the range of its Attained CII value for the corresponding year, as Figure 1 shows.

3.3.3. Optimization Model

This section presents the mathematical formulation of the optimization model for the tramp ship scheduling problem considering CII rating issues.

Table 1. Indices and sets.

Sets	Description
$N$	The set of loading ports, discharge ports, and the initial position of each ship in the fleet.
$K$	The set of ships, each element is denoted as $k$$. K=\left\{1,2,\dots ,k,\dots ,m\right\}$.
$I$	The set of cargoes, each element is denoted as $i$$. I=\left\{1,2,\dots ,i,\dots ,n\right\}$.
$N_L$	The set of loading ports associated with cargo $i$ is a loading port $i$$. N_L=\left\{1,2,3\dots ,n\right\}$.
$N_D$	The set of discharge ports associated with cargo $i$ is a discharge port $n+i$$. N_D=\left\{n+1,n+2,n+3\dots ,2n\right\}$.
$N_k$	The set of nodes that can be visited by ship $k$.
$N_k^L$	The set of loading ports that ship $k$ may visit.
$N_k^D$	The set of discharge ports that ship $k$ may visit.
${\Omega }_k$	The set of arcs that are traversable by ship $k$$. {\Omega }_k=\left\{\left(i,j\right):i,j\in N_L\cup N_D,i\ne j\right\}$.

,

Table 2. Parameters.

Parameters	Description
$o\left(k\right)$	The origin node of the ship $k$.
$d\left(k\right)$	The artificial destination node of ship $k$.
$Q_k$	The load capacity of ship $k$ (tons).
$D_i$	The total quantity of cargo $i$ (tons).
$q_i$	The quantity of cargo $i$ that has been actually transported (tons).
$t_{ik}$	The total berth time at node $i$ for ship $k$, including loading and discharging time, waiting for service time, etc (days).
$T_{ik}$	The time for arrival node $i$ for ship $k$ (days).
$T_{i\min }$	The earliest arrival time for the ship at node $i$ expected by the shipper.
$T_{i\max }$	The latest time for the start of service at node $i$.
$\left[T_{i\min },T_{i\max }\right]$	The expected time window associated with node $i$.
$d_{ij}$	The sailing distance from node $i$ to node $j$ (n miles).
γ	The amount of fuel consumption when the ship is at port (tons/hour)

and

Table 3. Decision variables.

Decision Variables	Description
$w_{ik}$	The exact load on board at node $i$.
$x_{ijk}$	If ship $k$ sails from node $i$ to node $j$, $x_{ijk}=1$; otherwise, $x_{ijk}=0$.
$y_i$	If cargo $i$ is transported by a charter ship in the spot market, $y_i=1$; otherwise, $y_i=0$.
$v_{ijk}$	The sailing speed of ship $k$ from node $i$ to node $j$.

show the notations used in the model.

Based on these, the model can be stated as follows:

The objective functions are as follows:

$$\max {\displaystyle \sum _{i\in I}{R}_i{q}_i}-{\displaystyle \sum _{k\in K}{\displaystyle \sum _{\left(i.j\right)\in {\Omega }_k}{x}_{ijk}{C}_{ijk}^s}}-{\displaystyle \sum _{k\in K}{\displaystyle \sum _{\left(i.j\right)\in {\Omega }_k}{x}_{ijk}{C}_{ik}^p}}-{\displaystyle \sum _{i\in I}{y}_i{C}_i}$$

(10)

$$\min AttainedCII={\displaystyle \frac{{\displaystyle \sum _{j}F{C}_j\times C_{Fj}}}{C\times D_t}}$$

(11)

The constraint conditions are as follows:

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{j\in N_k}{x}_{ijk}+}}{y}_i=1,\forall i\in I$$

(12)

$${\displaystyle \sum _{k\in K}{x}_{i\left(n+i\right)k}}\le 1,\forall i\in I$$

(13)

$${\displaystyle \sum _{i\in I}{x}_{ijk}}\le 1, \forall k\in K, j\in N_k$$

(14)

$$x_{ijk}=0,\forall k\in K,i\in N_k^L,j\in N_k^L$$

(15)

$$x_{ijk}=0,\forall k\in K,i\in N_k^D,j\in N_k^D$$

(16)

$${\displaystyle \sum _{j\in N_k^L\cup \left\{d\left(k\right)\right\}}{x}_{o\left(k\right)jk}}=1, \forall k\in K$$

(17)

$${\displaystyle \sum _{j\in N_k^D\cup \left\{o\left(k\right)\right\}}{x}_{id\left(k\right)k}}=1, \forall k\in K$$

(18)

$${\displaystyle \sum _{j\in N_k}{x}_{ijk}}-{\displaystyle \sum _{j\in N_k}{x}_{jik}}=0,\forall k\in K,i\in N_k\backslash \left\{o\left(k\right),d\left(k\right)\right\}$$

(19)

$${\displaystyle \sum _{j\in N_k}{x}_{ijk}}-{\displaystyle \sum _{j\in N_k}{x}_{j\left(n+i\right)k}}=0,\forall k\in K,i\in N_k^L$$

(20)

$$x_{i\left(n+i\right)k}{w}_{\left(n+i\right)k}=0,\forall k\in K,i\in N_k^L,\left(i,n+i\right)\in {\Omega }_k$$

(21)

$$x_{\left(n+i\right)jk}\left(q_j-w_{jk}\right)=0,\forall k\in K,i,j\in N_k^L,\left(n+i,j\right)\in {\Omega }_k$$

(22)

$${\displaystyle \sum _{j\in N_k}{x}_{ijk}{D}_i\left(1-\mu \right)}\le q_i\le {\displaystyle \sum _{j\in N_k}{x}_{ijk}{D}_i\left(1+\mu \right)},\forall i\in N_k^L$$

(23)

$$0\le w_{ik}\le Q_k,\forall k\in K,i\in N_k$$

(24)

$$x_{ijk}\left[\max \left(T_{ik},T_{i\min }\right)+t_{ik}+{\displaystyle \frac{d_{ij}}{24v_{ijk}}}-T_{jk}\right]=0,\forall k\in K,\left(i,j\right)\in {\Omega }_k$$

(25)

$$\max \left(T_{ik},T_{i\min }\right)+t_{ik}+{\displaystyle \frac{d_{i\left(n+i\right)}}{24v_{i\left(n+i\right)k}}}=T_{\left(n+i\right)k},\forall k\in K,\left(i,j\right)\in {\Omega }_k$$

(26)

$$T_{i\min }\le T_{ik}\le T_{i\max },\forall k\in K,i\in N_k$$

(27)

$${\displaystyle \frac{AttainedCII}{\mathrm{Re}quiredCII}}\le 1.06$$

(28)

$$\underset{¯}{v_{bk}}\le v_{ijk}\le \overline{v_{bk}},\forall k\in K,i\in N_k\backslash N_k^L,j\in N_k^L$$

(29)

$$\underset{¯}{v_{lk}}\le v_{i\left(n+i\right)k}\le \overline{v_{lk}},\forall k\in K,i\in N_k^L$$

(30)

$$x_{ijk}\in \left\{0,1\right\},\forall k\in K,\left(i,j\right)\in {\Omega }_k$$

(31)

$$y_i\in \left\{0,1\right\},\forall i\in I$$

(32)

Objective (10) is to maximize the total profit of the fleet over the planning period. The total cost includes fuel cost, port cost, and charter cost.

Objective (11) is to minimize Attained CII, which means optimizing the CII rating.

Constraint (12) guarantees that each consignment should be transported by a ship in the fleet or by a charter ship.

Constraints (13) and (14) indicate that each consignment should be shipped in the whole ship transport and cannot be mixed.

Constraints (15) and (16) indicate that the ship cannot consecutively dock at two loading ports or two discharging ports, respectively.

Constraint (17) ensures the ship leaves its initial position only once.

Constraint (18) ensures that the ship arrives at the virtual destination only once.

Constraints (19) and (20) describe the flow of the sailing route for ship $k$. Constraint (19) indicates that the number of ships arriving and leaving any port is the same. Constraint (20) ensures the consistency of the scheduling plan for ship $k$ when transporting cargo $i$, ship $k$ must visit loading node $i$ before discharging at node $n+i$.

Constraints (21) and (22) describe the relationship between the quantity of cargo $i$ on board and loading and discharging ports, respectively.

Constraint (23) indicates that the actual quantity of cargo $i$ on board should be within the specified range.

Constraint (24) ensures that the load on board cannot exceed the capacity of ship $k$.

Constraint (25) states the relationship between the sailing route and the sailing time.

Constraint (26) indicates that the discharging node for cargo $i$ must be visited after its loading node.

Constraint (27) ensures that the ship must meet the time window of cargo $i$.

Constraint (28) ensures that the CII rating can be C and above.

Constraints (29) and (30) are the lower and upper bounds for ballast and loading speed variables, respectively.

Constraints (31) and (32) are binary restrictions.

4. Algorithm Design

In this paper, the Gale–Shapley algorithm is used to solve the stable vessel–cargo matching problem. Shipowners evaluate available cargoes, and cargo owners compile preference lists for vessels, leading to multiple vessel–cargo matches. The one-to-one matching result is obtained by using the dynamic bilateral matching of ship and cargo. Then, through the iteration of the GA, ship scheduling and sailing speed are optimized, resulting in the fleet’s optimal transportation scheduling scheme.

4.1. Gale–Shapley Algorithm

The Gale–Shapley algorithm, also known as the deferred-acceptance algorithm and originally developed for the stable marriage problem, is a method used to solve the problem of finding stable matching between sets of elements [18]. In vessel–cargo matching, considering attributes such as cargo type, volume, port specification, and time window, each vessel has a ranking of cargoes based on their preferences, and each cargo ranks vessels similarly. Vessels propose to their most preferred cargo or to one that prefers them over their current match. Cargoes can reject proposals except for those from their most preferred vessel. This process continues until no vessel or cargo would benefit from switching partners, achieving stable matching where all preferences are optimally aligned. This algorithm can be applied to efficiently match vessels with available cargo in a way that maximizes overall efficiency, satisfaction, and profitability.

When applying the Gale–Shapley algorithm to the problem of vessel–cargo matching, the steps can be summarized as follows:

• Initialize vessel data and cargo data.
• For each vessel, call the vessel-to-cargo matching algorithm to obtain the result set of matches sorted by voyages; this could be the preference list ranking the potential matches.
• Extract the optimal solution for each vessel to form an initial array of solutions.
• Extract the part of the initial solution that does not have conflicting cargoes and save it to the final result set.
• Extract the cargo involved to eliminate unlikely candidates before the next round of the cycle.
• Remove from backward to forward the initial solution that has entered the final set of matching results.
• Rank the corresponding solutions according to their profits for the optimal set of outcomes where multiple ships are present simultaneously for one cargo.
• Add the conflicting scenario with the best net benefit to the final matching result and list the other conflicting scenarios as deletions.
• Loop steps 5, 6, 7, and 8 until the initial solution is empty.
• For the set of vessels that have not yet been matched, a new initial result set is formed by selecting the suboptimal solution with no cargo conflicts based on the gains from the initial matching results.
• Output the final stable matching scheme.

4.2. Genetic Algorithm

GAs are adaptive search heuristics that mimic the process of natural selection and genetic recombination. They are used to generate optimal solutions to optimization and search problems by iteratively evolving a potential population solution continuously optimizing the fitness of individuals. In GA, each potential solution is represented as an individual, called a chromosome, within a population of possible solutions. The algorithm starts with a randomly generated initial population. Each individual is then evaluated based on a fitness function, which assigns a fitness value based on how well the individual satisfies the objective of the optimization problem. Operations such as selection, crossover, and mutation are applied to evolve and improve these solutions iteratively. In short, they solve problems by simulating the survival of the fittest among individuals of consecutive generations.

When applied to ship routing and scheduling problems, GAs are effective because of their ability to handle large search spaces and multiple constraints efficiently. To solve the bi-objective optimization model proposed in this paper, considering the total profit of the fleet and the CII, the GA iteratively improves the allocation of cargo to vessels while simultaneously optimizing the speed of each sailing leg.

The specific steps of the GA are as follows:

• Initialization:

Generate a set of chromosomes to form an initial population of solutions randomly or by using heuristics. Each individual in the population represents a potential scheduling solution, including a sequence of ports to visit, the allocation of cargo to ships, and sailing speed.

2.

Evaluation:

Develop a fitness function to calculate and evaluate the fitness value of each individual in the population, potentially reflecting the performance of each scheme. The fitness function should be based on multiple criteria. In this paper, the values of the fleet profit and Attained CII are deformed and weighted as the fitness function. We have assigned them equal weights (1:1) in the fitness function to reflect their operational parity.

3.

Selection:

Select chromosomes with higher fitness values from the current generation to be parents for the next generation. There are several selection methods, such as roulette wheel selection, tournament selection, or rank selection. In this paper, roulette wheel selection is employed.

4.

Crossover:

Crossover is a genetic operator used to combine the genes of parents to generate new offspring. This could involve swapping segments of two different routes to create a new one.

5.

Mutation:

Introduce random mutations to some chromosomes to maintain the diversity of the population, thereby avoiding becoming stuck in local optima.

6.

Replacement:

Repeat steps 2 to 5 to generate the new offspring, which will replace some individuals with lower fitness scores in the previous population, ensuring the population size remains constant. This can help preserve diversity and improve scheduling schemes.

7.

Termination:

Set an appropriate termination condition, such as reaching a preset maximum number of iterations, reaching a satisfactory solution, and running out of computational resources. Repeat the selection, crossover, mutation, and replacement steps until the termination condition is met. The algorithm halts and outputs the optimal scheme for the current population.

5. Computational Study

A computational study was conducted in this section to validate the effectiveness of the proposed mathematical model and evaluate the performance of the algorithms for considering carbon intensity in the tramp ship scheduling problem. We applied the proposed model and algorithm to a historical instance, comparing the optimal solution with actual operational data from past tramp ship voyages for a comprehensive evaluation. This study used Python 3.10 to simulate a dry bulk shipping fleet, thereby providing a robust framework for analyzing performance and efficiency under real-world conditions.

5.1. Data Source and Description

To conduct a comparative analysis with the optimized results, this study constructs an empirical analysis case based on accessible historical operational data, selecting actual freight data from a specific period in China’s coastal region as the research sample. Data for the computational study were sourced from AIS and COSCO Shipping Technology Co., Ltd. The dataset mainly covers details on 30 cargo bookings along the coastal regions of China and information on a fleet of 15 bulk carriers transporting dry bulk commodities, such as iron ore, coal, and grain.

The fleet is composed of 15 ships with varying specifications, as

Table 4. Information on 15 ships.

Ship ID	MMSI	Deadweight Tonnage (ton)	Lightship Weight (ton)	Min Speed (kn)	Max Speed (kn)	Initial Location		Fuel Consumption (ton/day)
						Longitude (°)	Latitude (°)	Anchoring	Berthing
1	354643000	76,546	40,896	10.239	15.359	4.049	51.937	6.114	2.867
2	354879000	55,676	30,953	9.888	14.900	113.486	23.082	5.080	3.099
3	356760000	56,907	33,044	10.765	16.084	73.907	7.153	7.030	4.120
4	412343000	55,566	30,963	9.888	14.900	127.735	34.907	4.408	2.995
5	412523920	32,034	19,995	11.510	17.201	140.670	35.922	4.553	2.998
6	412775000	57,617	33,511	11.063	16.594	123.337	34.771	5.121	1.987
7	413219590	52,818	29,995	10.481	15.660	102.003	2.170	6.396	3.271
8	414139000	64,542	38,384	12.529	18.793	118.012	38.386	6.719	2.892
9	414166000	49,998	31,893	11.312	16.968	118.455	38.987	5.625	2.582
10	414775000	49,256	28,714	10.981	16.407	122.471	31.273	5.514	2.510
11	414783000	49,281	28,714	10.981	16.407	118.188	38.950	5.232	2.454
12	477043400	63,261	36,378	10.732	16.189	121.374	31.501	6.610	3.423
13	477595900	76,364	40,896	10.239	15.359	−43.930	−23.128	5.185	2.698
14	477961500	56,687	32,899	10.765	16.084	29.458	40.763	5.976	2.785
15	563023600	52,395	30,053	8.117	13.529	171.427	41.853	7.411	3.836

Source: Compiled by the authors from data provided by COSCO Shipping Technology Co., Ltd.

shows. We numbered these 15 ships from 1 to 15 as Ship ID. The second column, MMSI, is the acronym for Maritime Mobile Service Identity; it is a unique nine-digit numerical assigned to a vessel for digital identification and communication in maritime tracking systems to ensure safety, navigation, and emergency coordination. Deadweight tonnage is the maximum weight a ship can safely carry, including cargo, fuel, ballast water, crew, and supplies, while maintaining its designated draft and structural integrity. Lightship weight is the total weight of a ship in its empty operational state, including its hull, machinery, and permanent equipment but excluding all cargo, fuel, crew, and consumable supplies. The Min speed and Max speed columns define the lower and upper bounds of the vessel’s navigational speed. The initial location column refers to the vessel’s location at the start of the planning period, expressed in longitude and latitude coordinates. Positive values denote east longitude or north latitude, while negative values indicate west longitude or south latitude. The last two columns represent the daily fuel consumption of the vessel during port anchoring and berthing.

Table 5. Information on cargoes.

Cargo ID	Quantity (ton)	Loading Port	Discharging Port	LAN/CAN
1	49,000	CNQHD	CNZHE	1–3 July 2022
2	47,500	CNQHD	CNZJG	4–6 July 2022
3	57,000	CNQHD	CNNBO	4–6 July 2022
4	58,500	CNTJN	CNZHE	5–7 July 2022
5	76,550	CNHUA	CNNJG	5–7 July 2022
6	44,500	CNJIT	CNZJG	6–8 July 2022
7	59,000	CNHUA	CNDAL	6–8 July 2022
8	47,000	CNQHD	CNYZH	6–8 July 2022
9	57,200	CNQHD	CNGUA	6–8 July 2022
10	46,600	CNJIT	CNZJG	6–8 July 2022
11	46,600	CNJIT	CNZJG	6–8 July 2022
12	47,500	CNZHA	CNJIA	7–9 July 2022
13	47,000	CNCFD	CNNJG	7–9 July 2022
14	43,500	CNJIT	CNZHE	8–10 July 2022
15	53,000	CNJIT	CNTZH	8–10 July 2022
16	47,000	CNHUA	CNNJG	8–10 July 2022
17	70,500	CNQHD	CNGUA	9–11 July 2022
18	70,500	CNQHD	CNGUA	9–11 July 2022
19	47,000	CNCFD	CNYZH	10–12 July 2022
20	50,000	CNJIT	CNZJG	10–12 July 2022
21	47,800	CNCFD	CNYZH	10–12 July 2022
22	47,000	CNHUA	CNYZH	10–12 July 2022
23	45,000	CNZHA	CNJIJ	10–12 July 2022
24	65,000	CNHUA	CNZHA	11–13 July 2022
25	57,500	CNCFD	CNGUA	12–14 July 2022
26	49,300	CNJIT	CNZJG	12–14 July 2022
27	58,300	CNJIT	CNZJG	12–14 July 2022
28	70,000	CNHUA	CNMEZ	12–14 July 2022
29	69,000	CNCFD	CNGUA	12–14 July 2022
30	46,000	CNJIT	CNNJG	15–17 July 2022

Source: Compiled by the authors from data provided by COSCO Shipping Technology Co., Ltd.

provides information on transportation volumes, loading and discharging ports, time windows, and other cargo information. We numbered these 30 cargos from 1 to 30 as Cargo ID. The quantity column refers to the specific shipment volume assigned to each task. Columns 3 and 4 represent the loading port and discharging port for each freight task, respectively. The last column indicates the lay days of each shipment; the vessel must arrive at the designated port and be ready to load within the period.

Table 6. Port code cross-reference table.

Port Code	Port Name
CNCFD	Caofeidian Port
CNDAL	Dalian Port
CNGUA	Guangzhou Port
CNHUA	Huangpu Port
CNJIA	Jiangyin Port
CNJIJ	Jingjiang Port
CNJIT	Jingtang Port
CNMEZ	Meizhou Port
CNNBO	Ningbo Port
CNNJG	Nanjing Port
CNQHD	Qinhuangdao Port
CNTJN	Tianjin Port
CNTZH	Taizhou Port
CNYZH	Yangzhou Port
CNZHA	Zhanjiang Port
CNZHE	Zhenjiang Port
CNZJG	Zhangjiagang Port

provides full names corresponding to the port code used in Table 5.

The freight rate in this paper is based on the freight rate of several important coal shipping routes along China’s coast over the past three months. The fuel price is $589.6/ton.

5.2. Computational Results and Analysis

Cargo owners compile preference lists for ships, and shipowners evaluate available cargoes, leading to multiple cargo–vessel matches. Transitioning from one-to-many matching, where one party has multiple options, to many-to-many matching, where both parties have several options, requires reconciling potential conflicts. A comprehensive assessment of preference ranking lists for shipowners and cargo owners is crucial for a stable, mutually beneficial outcome. First, the original dataset is preprocessed to generate a preference list based on the characteristics of the ships and cargoes. Second, this list is inputted into the model for computational analysis. We leverage the Gale–Shapley algorithm to output the final stable matching scheme, as Figure 2 shows.

In Figure 2, the left column represents the cargo, the width of the blocks, and the thickness of the connecting lines indicate the volume of the cargo; thicker lines denote a larger volume of the respective cargo. Each shipment is linked to the matching vessel; the right column represents the destination ports of the cargo. Upon reviewing the calculation results, it was consistently observed that not all self-owned ships in the fleet were assigned to cargo transport tasks. Additionally, a few of the 30 shipments required the chartering of external ships. Specifically, Ships 1, 3, 4, 5, 7, 12, 13, 14, and 15 have no cargo to transport; Ship 2 transports Cargoes 14, 16, and 25; Ship 6 transports Cargoes 1, 7, 9, 15, and 26; Ship 8 transports Cargoes 4, 6, 18, 24, 27, and 28; Ship 9 transports Cargoes 2, 19, 21, 22, and 23; Ship 10 transports Cargoes 8, 10, 11, and 12; Ship 11 transports Cargoes 13, 20, and 30. Unfortunately, there is no suitable ship for Cargoes 3, 5, 17, and 29.

Factors contributing to these outcomes include the following:

• A mismatch between ship capabilities and cargo requirements: The type, capacity, or other characteristics of some ships may not align with cargo needs.
• Distance to departure ports: Certain ships were too far from the departure ports to meet the time windows, making chartering ships necessary to avoid time constraint violations.
• Impact on CII ratings: Some voyages may increase unit carbon emissions, thereby lowering the CII rating below acceptable levels.
• Flexibility of chartering on the spot market: Charter shipping possesses considerable flexibility and enables rapid adjustment of shipping capacity and routes. In some cases, charter shipping can be more economical and efficient.

The results indicate that ships in the fleet have been partially laid up, while several cargoes are proposed to be transported by chartered ships. The ships assigned to transportation tasks have been renumbered for clarity, with the original Ship 2 now designated as 001, Ship 6 as 002, Ship 8 as 003, Ship 9 as 004, Ship 10 as 005, and Ship 11 as 006.

Based on the vessel–cargo matching results, we take Ship 2 as an example to evaluate the performance of the Genetic Algorithm (GA), Simulated Annealing (SA), and Particle Swarm Optimization (PSO) for optimizing profit and CII rating. The comparative outcomes are presented in

Table 7. Performance comparison of GA, SA, and PSO.

Metric	Genetic Algorithm (GA)	Simulated Annealing (SA)	Particle Swarm Optimization (PSO)
Profit (USD)	205,001.19	183,200.45 (−10.6%)	192,450.70 (−6.1%)
CII Rating	A (0.69)	A (0.82)	C (0.95)
Convergence Iterations	430	680	590
Speed Optimization Strategy	Dynamic speed adjustment	Single-speed optimization	Locally Optimal Speed Combinations
Time Window Satisfaction Rate	100%	92%	88%

.

As summarized in Table 7, the GA outperforms SA and PSO in economic efficiency, environmental performance, and computational effectiveness.

• Economic efficiency: The profit achieved by GA is $205,001.19, exhibiting 10.6% and 6.1% improvements over SA ($183,200.45) and PSO ($192,450.70), respectively. By dynamically optimizing sailing speeds, GA balances fuel costs and transportation efficiency. In contrast, SA and PSO fail to identify superior speed combinations because of insufficient local search capabilities.
• CII rating: GA achieves an A-level CII rating with the Attained CII to Required CII ratio of 0.69, significantly better than the A rating (0.82) of SA and the C rating (0.95) of PSO. The speed strategies of SA and PSO result in higher carbon emissions per transport work, failing to meet the IMO’s stringent standards.
• Convergence Efficiency and Global Search Capability: GA converges after 430 iterations, which is faster than PSO (590 iterations), while also delivering superior solution quality. SA requires 680 iterations because of its conservative cooling strategy and is prone to local optima. GA’s crossover and mutation mechanisms effectively maintain population diversity, preventing premature convergence.
• Practical Constraint Satisfaction: The transportation schedules optimized by GA achieve full compliance with time window constraints (100%), whereas SA and PSO exhibit lower compliance rates of 92% and 88%, respectively, which significantly escalates operational risks.

This validation confirms the superior performance of GA in addressing complex ship scheduling challenges, attributed to its global search capabilities and effective multi-objective optimization strategies.

Based on the aforementioned results, the final fleet routing and scheduling plan is determined by the GA. We set the maximum number of iterations as 1000, the crossover probability as 0.8, and the mutation probability as 0.003.

Table 8. Optimized tramp ship routing and scheduling scheme.

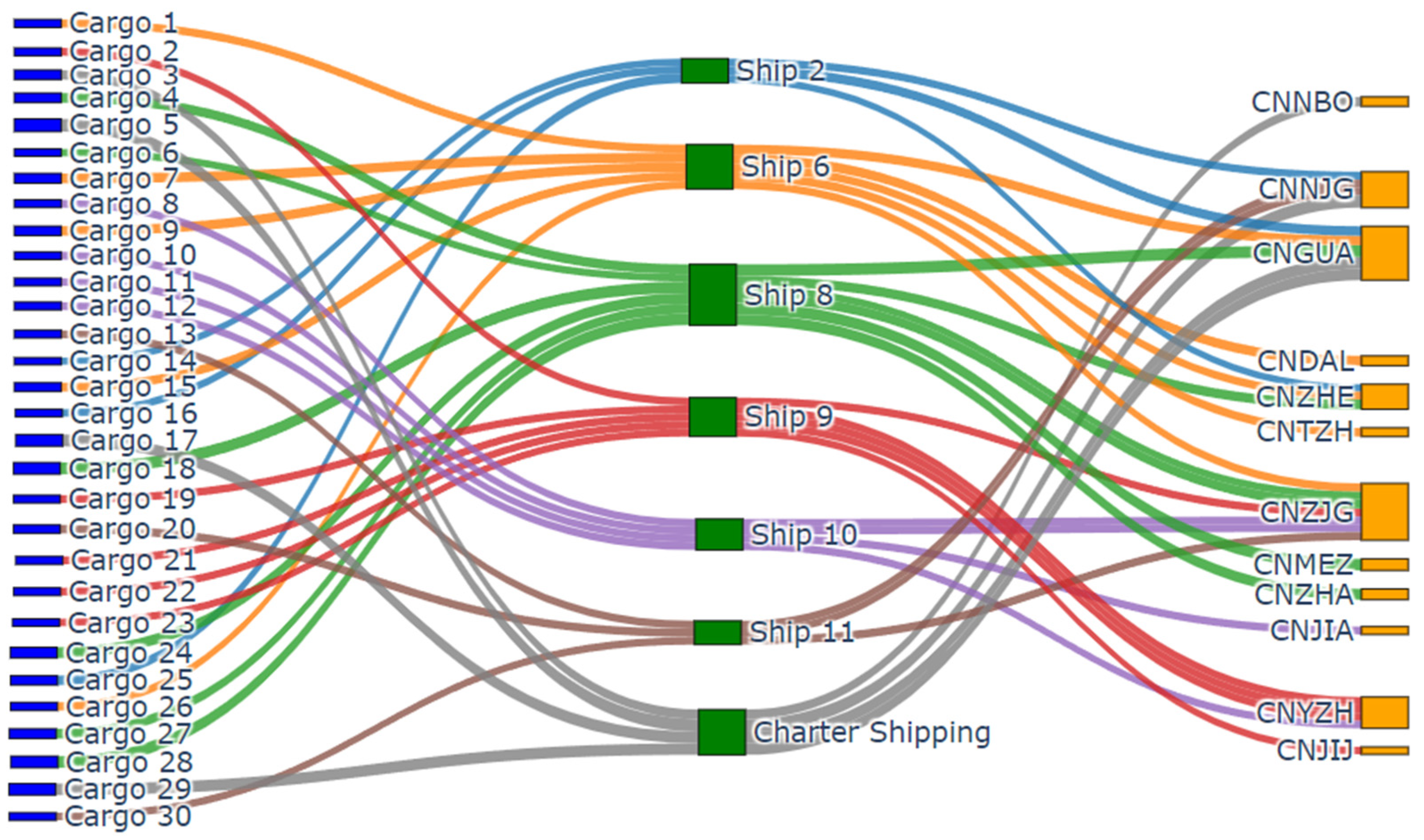
Ship	MMSI	Route	Attained CII/ Required CII	CII Rating	Profit ($)	Speed (Knot)
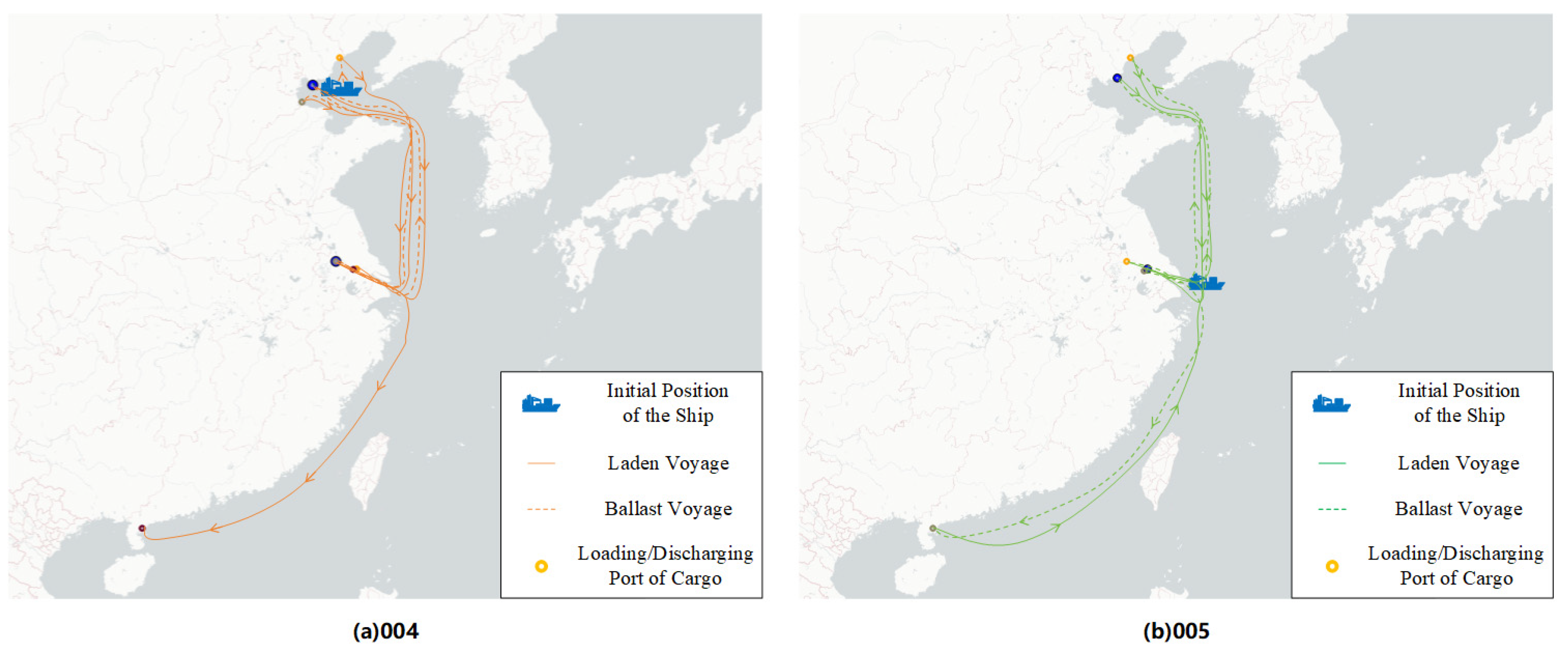
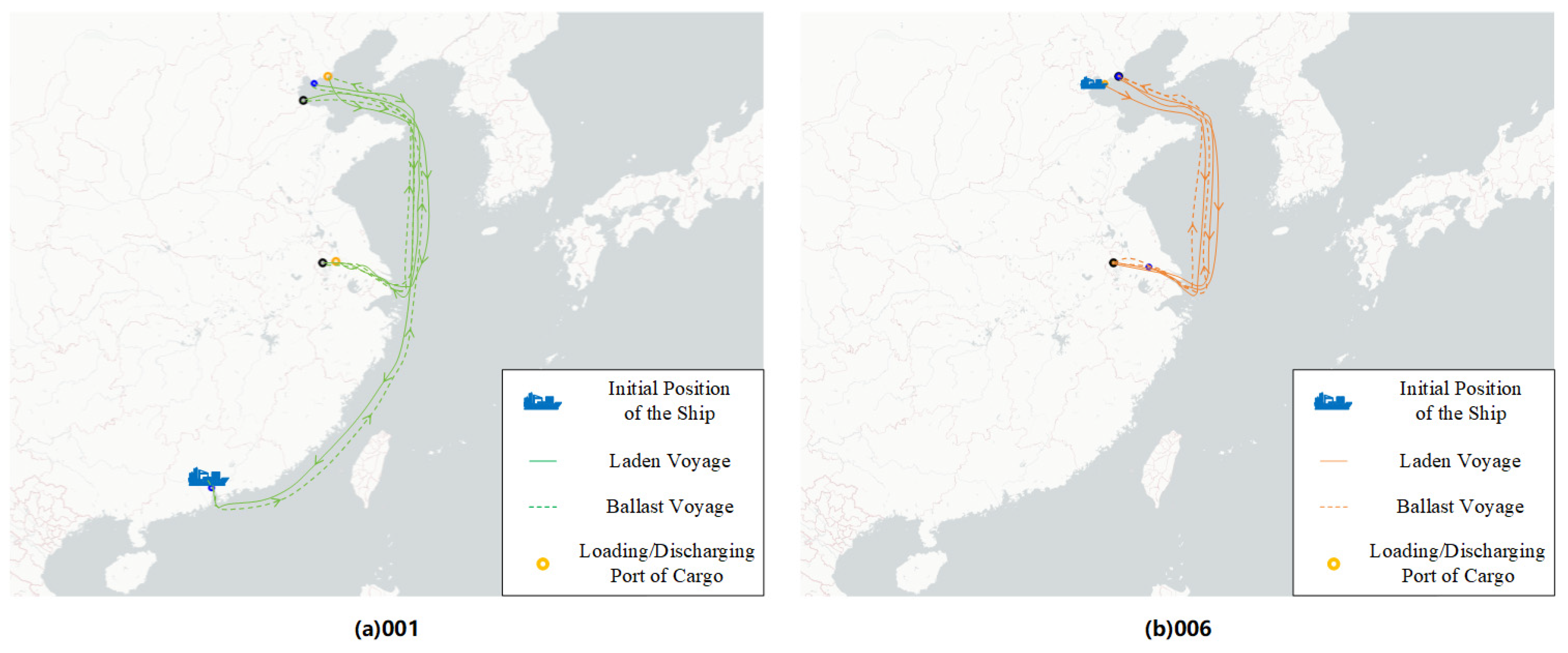
001	354879000	14-16-25	0.69	A	205,001.19	[11.86, 14.32]-[14.21, 10.10]-[12.28, 10.72]
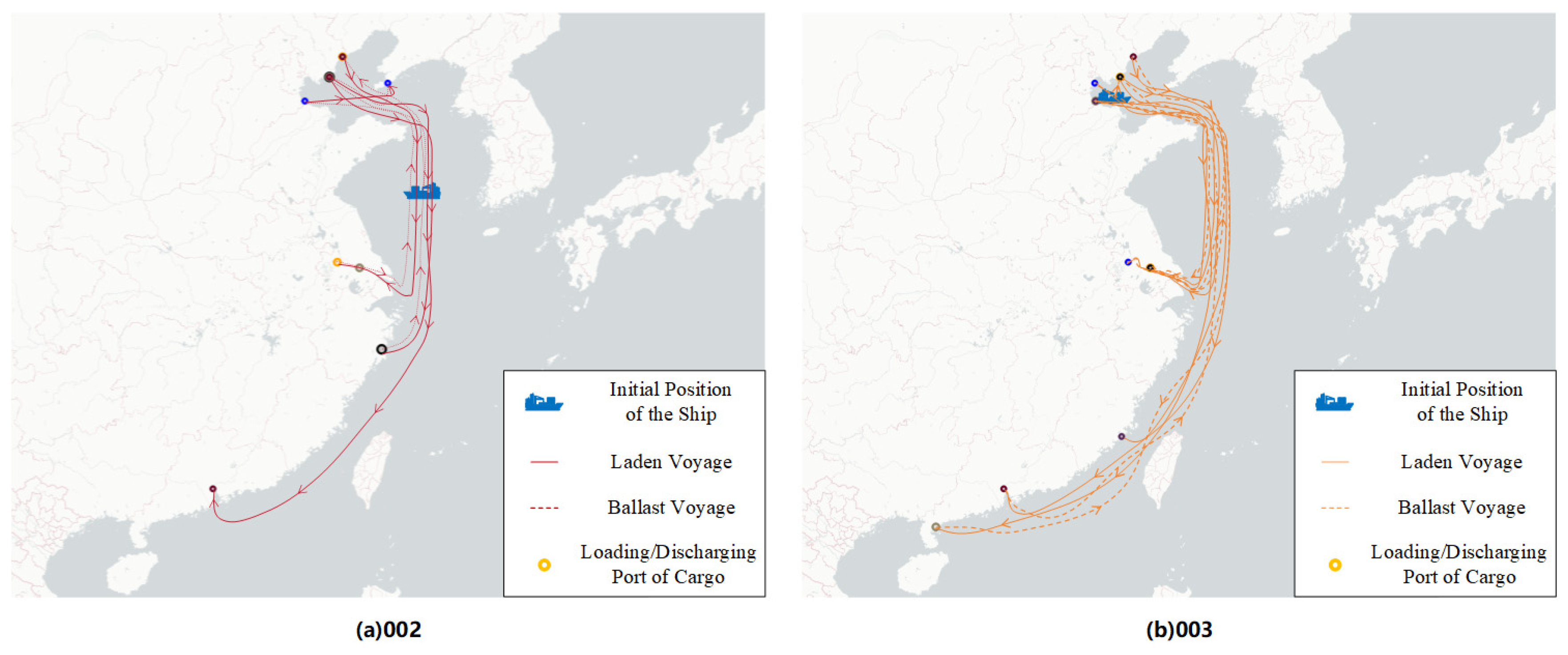
002	412775000	1-15-7-26-9	1.05	C	429,955.47	[14.36, 16.49]-[14.71, 16.55]-[13.88, 13.75]-[11.94, 15.04]-[15.61, 14.69]
003	414139000	6-27-4-24-18-28	0.90	B	259,211.12	[16.94, 13.64]-[14.90, 13.97]-[17.36, 17.85]-[18.50, 18.17]-[12.82, 15.39]-[14.18, 15.58]
004	414166000	2-21-19-22-23	0.87	B	290,509.53	[14.30, 12.34]-[11.88, 13.18]-[13.09, 13.14]-[15.46, 16.44]-[14.03, 14.62]
005	414775000	8-10-11-12	0.79	A	294,967.22	[16.17, 11.91]-[14.92, 11.42]-[11.57, 12.15]-[13.06, 13.25]
006	414783000	13-30-20	0.90	B	220,333.49	[15.57, 11.21]-[13.26, 13.74]-[14.84, 13.68]
C	-	3-5-17-29	-	-	-	-

shows the scheme and calculation results.

In Table 8, the first column is the updated ship number. The Route column specifies the cargo assignment and transport sequence for each ship. For example, Ship 001 is scheduled to first load Cargo 14 and transport it to the destination port, followed by Cargo 16, and finally, to complete its tasks by delivering Cargo 25. The Attained CII/Required CII column represents the ratio of the Attained CII to the Required CII. The CII Rating column provides the ship’s CII rating result after optimizing. The Profit column reflects the net profit for each ship within the planning period, calculated as the difference between the revenue earned from completing transportation tasks and the associated operational costs. The Speed column shows the sailing speed of each ship in each leg. In this context, we refer to both the voyage for picking up cargo and delivering it as a leg. Similarly, using Ship 001 as an example, the optimized results show that the ship sails at a speed of 11.86 knots from its initial position to the loading port of Cargo 14 and at 14.32 knots to the discharge port. The sailing speed of the leg to pick up Cargo 16 is 14.21 knots, while the loaded transport speed is 10.10 knots. From the discharge port of Cargo 16 to the next Cargo 25, the speeds are 12.28 knots and 10.72 knots for the respective legs.

Lowering sailing speed is a prevalent strategy for cutting fuel consumption and enhancing energy efficiency, thereby directly lowering the numerator in the CII calculation formula. Some carriers also curtail fuel expenditure by idling their ships or selecting shorter routes; this is indeed the case with Ship 004 and Ship 005. Figure 3 illustrates the optimized shipping routes of these two vessels, where green and orange lines denote CII ratings of A and B, respectively. Ship 004 has completed five shipments and achieved a B rating; Ship 005 has transported four shipments with an A rating.

However, simply slowing down or reducing voyage frequency does not necessarily optimize the CII rating. Although higher speed increases fuel consumption, it also raises the transport workload of the ship. This corresponds to the denominator in the formula by allowing the ship to complete more cargo tasks efficiently, thereby potentially improving overall CII performance.

Taking Ship 002 and Ship 003 as examples, Ship 002 has undertaken five cargo shipments, with a ratio of Attained CII to Required CII being 1.05, resulting in the CII rating of C, indicated by red lines. Meanwhile, Ship 003 has completed six tasks with a ratio of 0.90, achieving a B rating. This indicates that, despite increased transportation tasks, optimizing scheduling and improving operational efficiency can effectively reduce carbon intensity and improve the CII rating. Figure 4 illustrates the optimized shipping routes of these two vessels.

Similarly, as Figure 5 shows, Ship 001 and Ship 006 both transport three batches of cargo. Ship 001 achieves an A rating, while Ship 006 is rated B. The cargo volume transported by these two ships is similar, but the sailing routes of 006 are much shorter. This requires attention to the relationship between route length, transportation efficiency, and ship scheduling. The results validate the model’s effectiveness, demonstrating that reasonable scheduling and route optimization can achieve reduced carbon intensity and improved CII ratings.

After optimization, all six ships achieve a CII rating of C or higher. A comparative analysis between actual data and optimized outcomes is presented in

Table 9. Changes in CII ratings and profit before and after optimization.

Ship	Actual CII Rating	Optimized CII Rating	Actual Profit ($)	Optimized Profit ($)	Optimized Profit Change
001	D	A	244,058.00	205,001.19	−16.00%
002	B	C	320,563.99	429,955.47	+34.12%
003	E	B	290,911.29	259,211.12	−10.90%
004	C	B	257,488.50	290,509.53	+12.82%
005	C	A	317,483.07	294,967.22	−7.09%
006	C	B	198,159.95	220,333.49	+11.19%
Total	-	-	1,628,664.80	1,699,978.02	+4.38%

. Five of the six ships show improvements in their CII ratings. Specifically, Ship 001 and Ship 003 see considerable upgrades, transitioning from noncompliant D and E ratings to A and B, respectively. However, these environmental enhancements are accompanied by trade-offs in profitability, with profit margins decreasing by 16.00% and 10.90% for Ship 001 and Ship 003, respectively. Additionally, Ship 004 and Ship 006 both upgrade from C to B, achieving profit increases of 12.82% and 11.19%, respectively. While Ship 005 improves from C to A, with a 7.09% reduction in profit. These results suggest that through reasonable allocation and optimization of routing and speed, these ships achieve improvements in transportation efficiency and CII ratings, validating the effectiveness of the proposed methodology. In contrast, the rating of Ship 002 decreases from B to C while exhibiting a 34.12% profit surge. After optimization using the proposed model and algorithm, the total fleet profit has increased by 4.38% compared with actual operational data. This result indicates that achieving greater economic efficiency may involve trade-offs in which some environmental benefits are sacrificed while compliance with carbon intensity standards is still ensured.

Furthermore, by monitoring and updating the real-time ship position, the proposed method effectively matches ships with nearby cargoes, allowing for the timely allocation of new transportation assignments. This approach improves ship utilization and accelerates cargo flow and delivery. These enhancements result in a more reliable service, fostering greater satisfaction among cargo owners and strengthening the shipping company’s competitiveness.

6. Conclusions

The increasing global emphasis on sustainability and stringent regulations on carbon emissions make it imperative to integrate CII into the optimization problem. While considerable research efforts have been dedicated to optimizing ship routing and scheduling, and some have considered carbon emissions, there remains a notable gap in integrating CII into these problems. This paper has introduced CII into the tramp ship routing and scheduling problem. We aimed to address the dual objectives of maximizing economic benefits and improving the CII rating while comprehensively considering the complex relationships between sailing speed, CII ratings, fleet operating costs, and shipment revenues. As a result, we established a bi-objective mixed-integer programming model. The model effectively balances economic returns and environmental impacts by optimizing resource allocation and operational strategies. The Gale–Shapley algorithm was employed to solve the cargo–vessel matching problem, ensuring optimal matching between cargoes and vessels. This approach enhances scheduling efficiency and resource utilization, avoiding unnecessary empty voyages and resource wastage and achieving a win–win situation for shippers and carriers. A GA was also used to optimize ship routing and scheduling and sailing speed, further improving operational efficiency and CII ratings.

The computational results validate the effectiveness of our methodology, demonstrating a 4.38% increase in the fleet’s overall profit through model and algorithmic optimizations, with all vessels achieving CII compliance and significant improvements in environmental performance. This assists stakeholders in evaluating the trade-offs between economic returns and CII regulations. In an increasingly competitive market with stringent low-carbon requirements, the proposed model provides critical insights for tramp shipping operations, demonstrating considerable practical implications.

However, this study has limitations that could be considered in future studies. The current research results are mainly focused on coastal routes in China. Expanding the scope of this study to include a broader range of routes could yield more comprehensive conclusions. Additionally, shipowners need to ensure that their vessels meet CII standards to avoid penalties. In future research, it would be valuable to incorporate the CII requirements of chartered vessels into the optimization model.