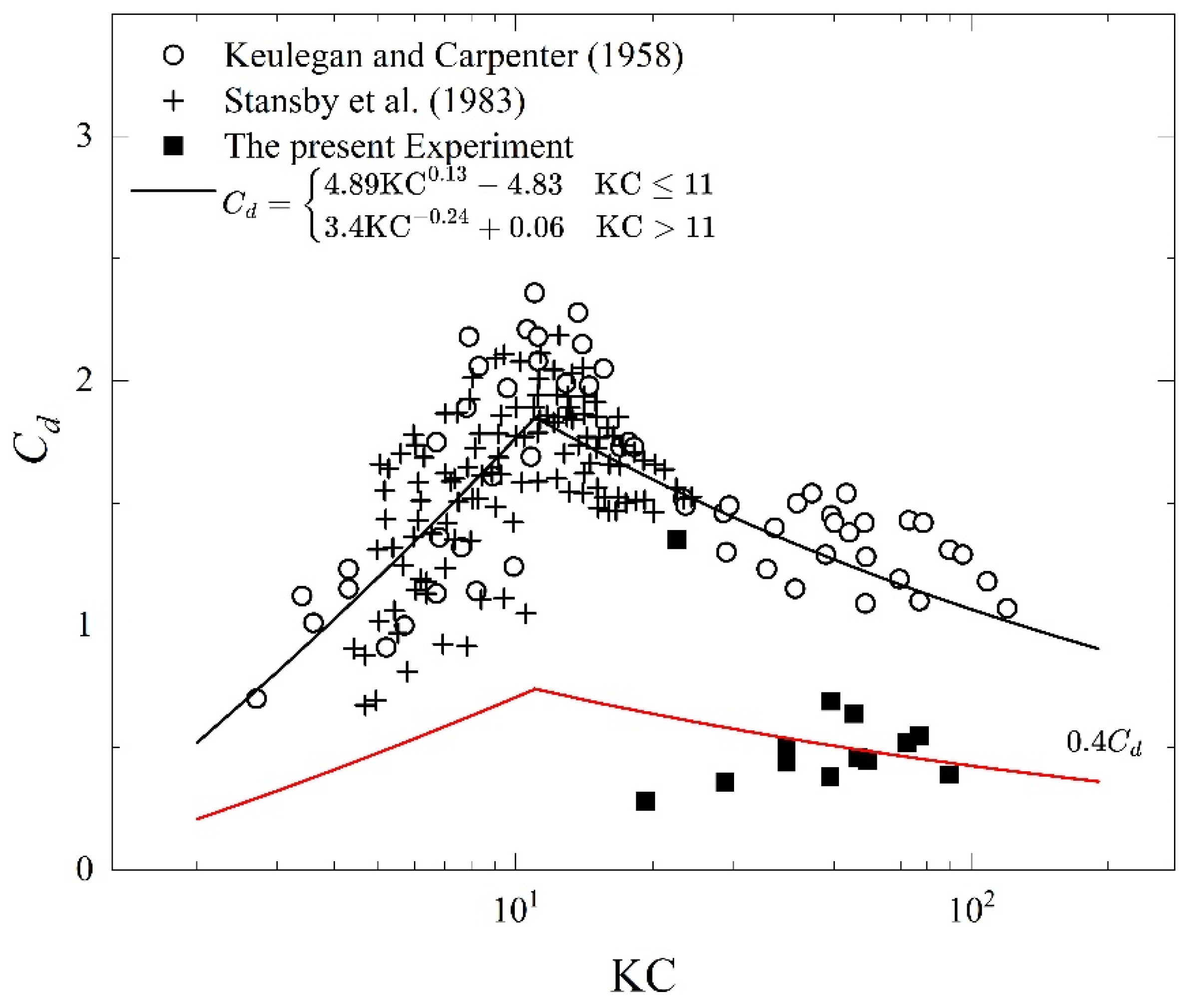
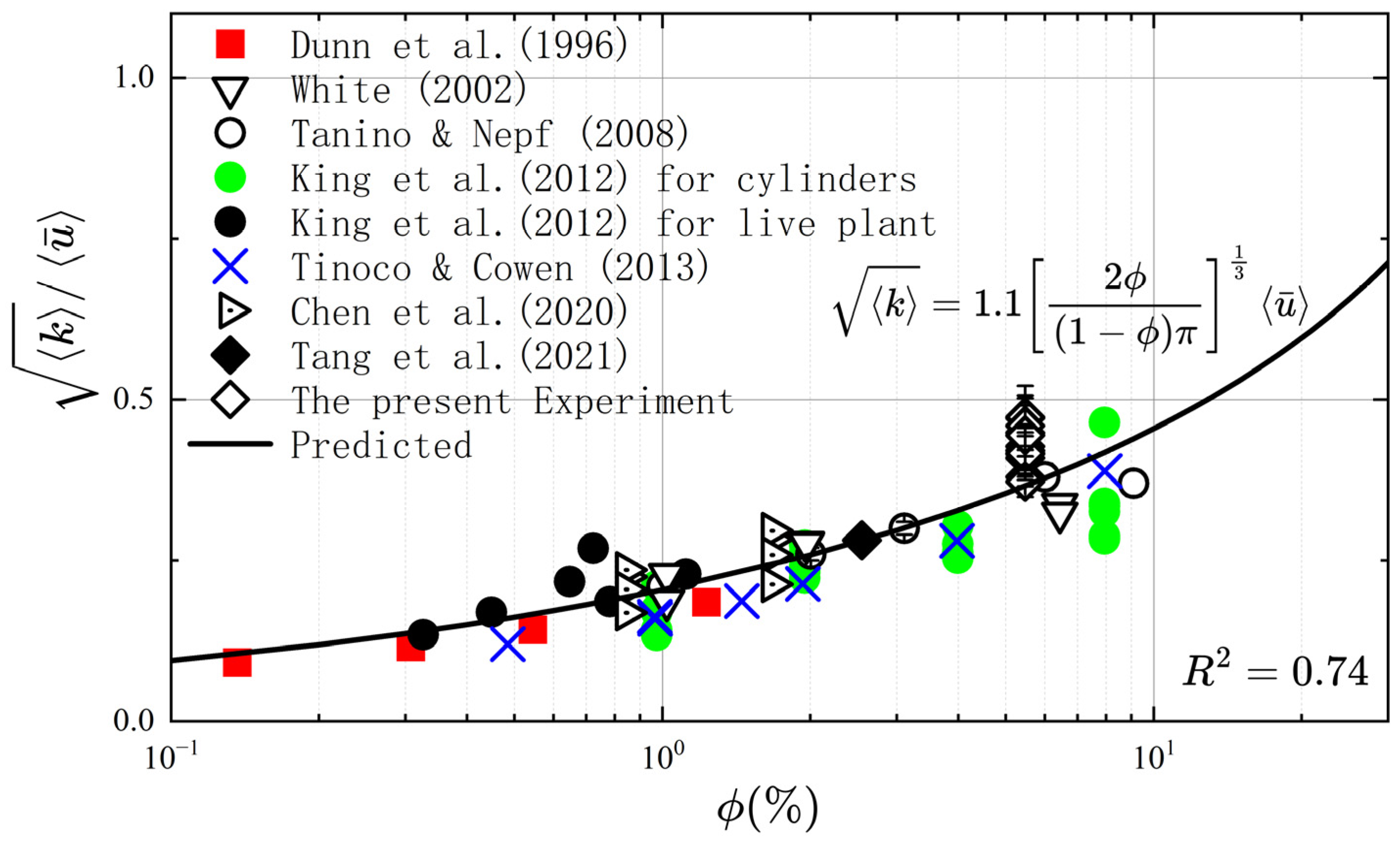
Parameterizing the Tip Effects of Submerged Vegetation in a VARANS Solver
Abstract
:1. Introduction
2. Numerical Model
2.1. Hydrodynamic Model
2.2. Turbulence Model
2.3. Analysis of Wake-Scale Turbulence
2.4. Boundary Conditions and Numerical Scheme
3. Laboratory Experiments
3.1. Experimental Setup
3.2. Data Analysis
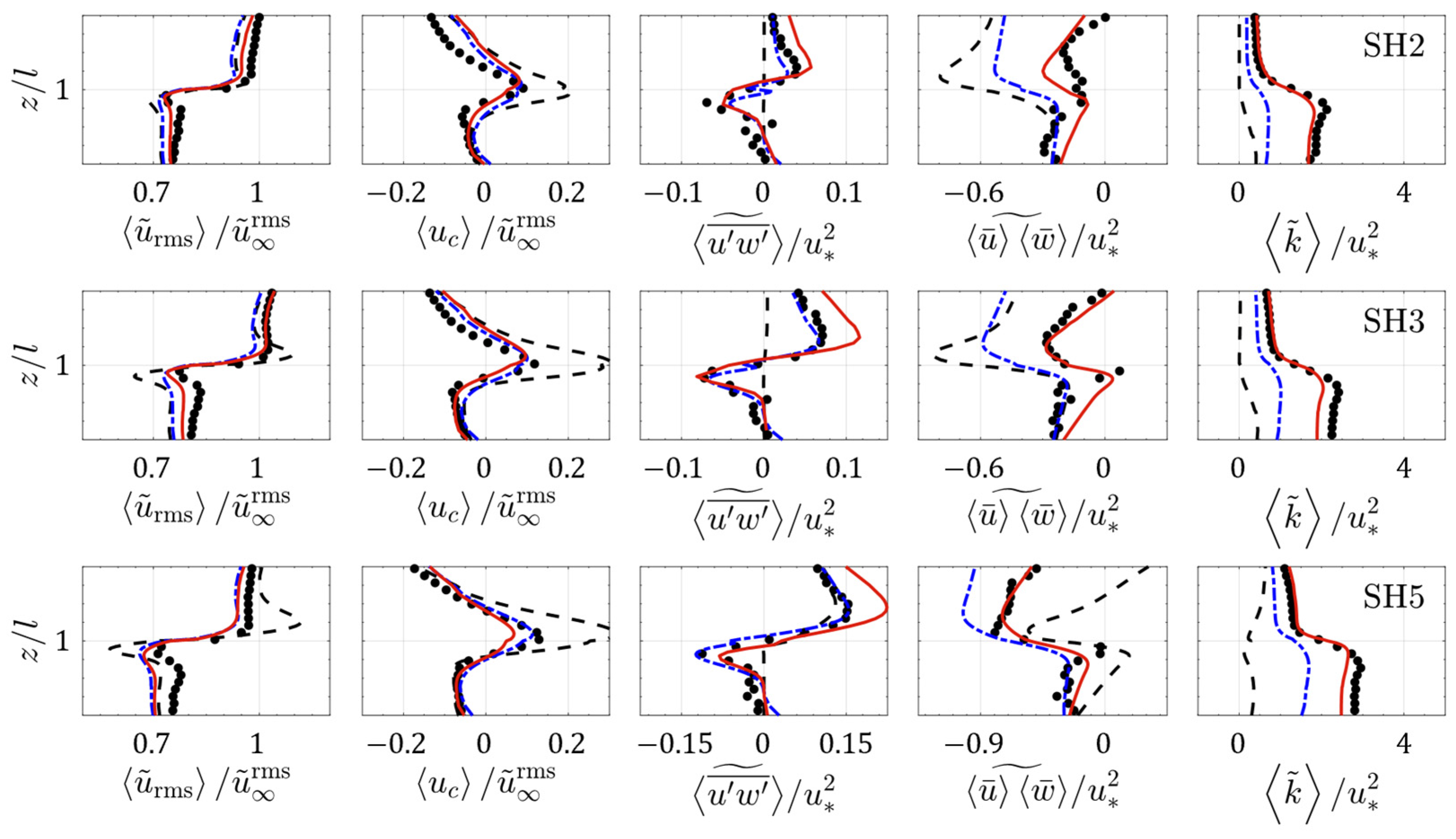
4. Results
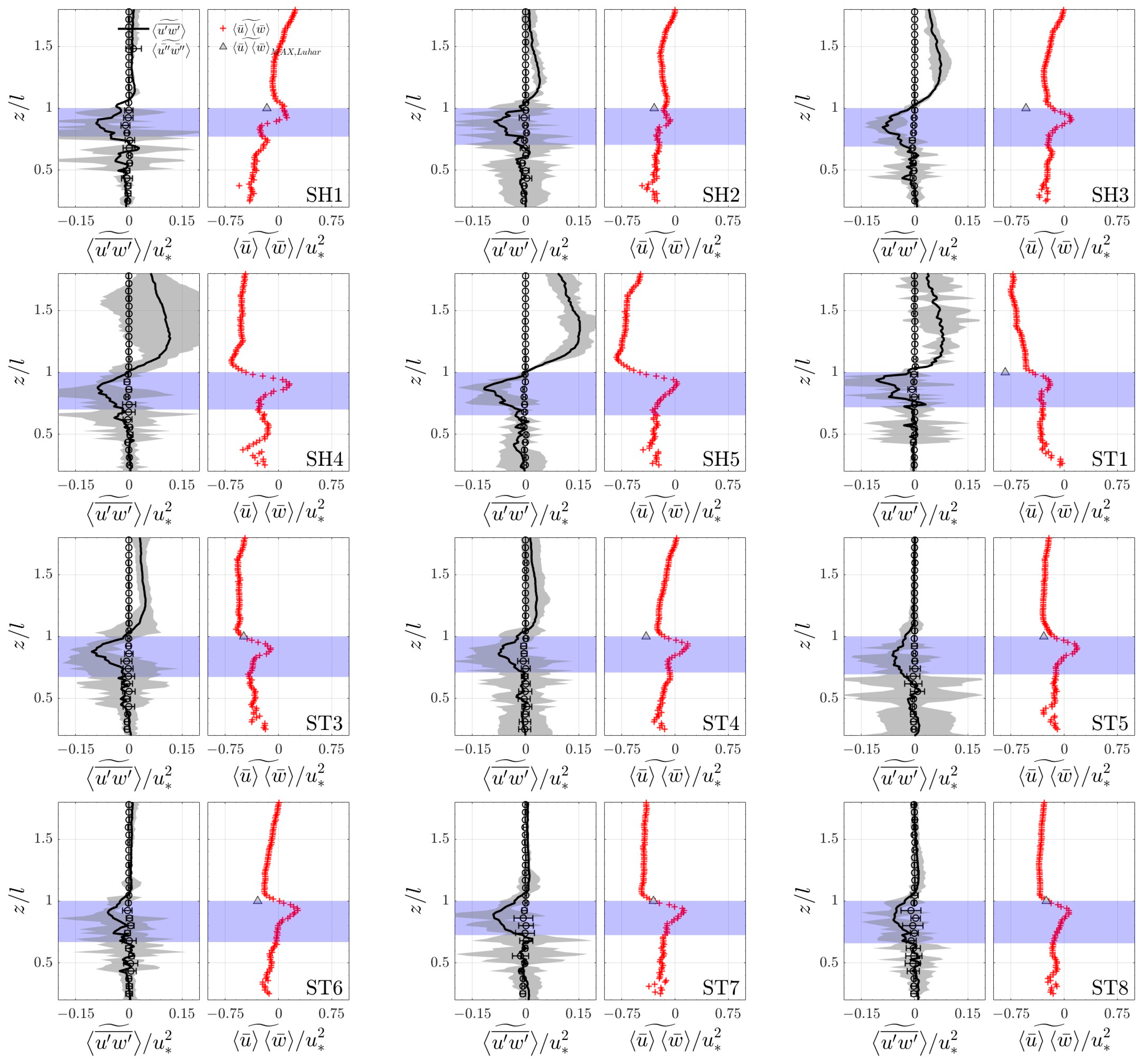
4.1. Wave and Turbulent Reynolds Stress
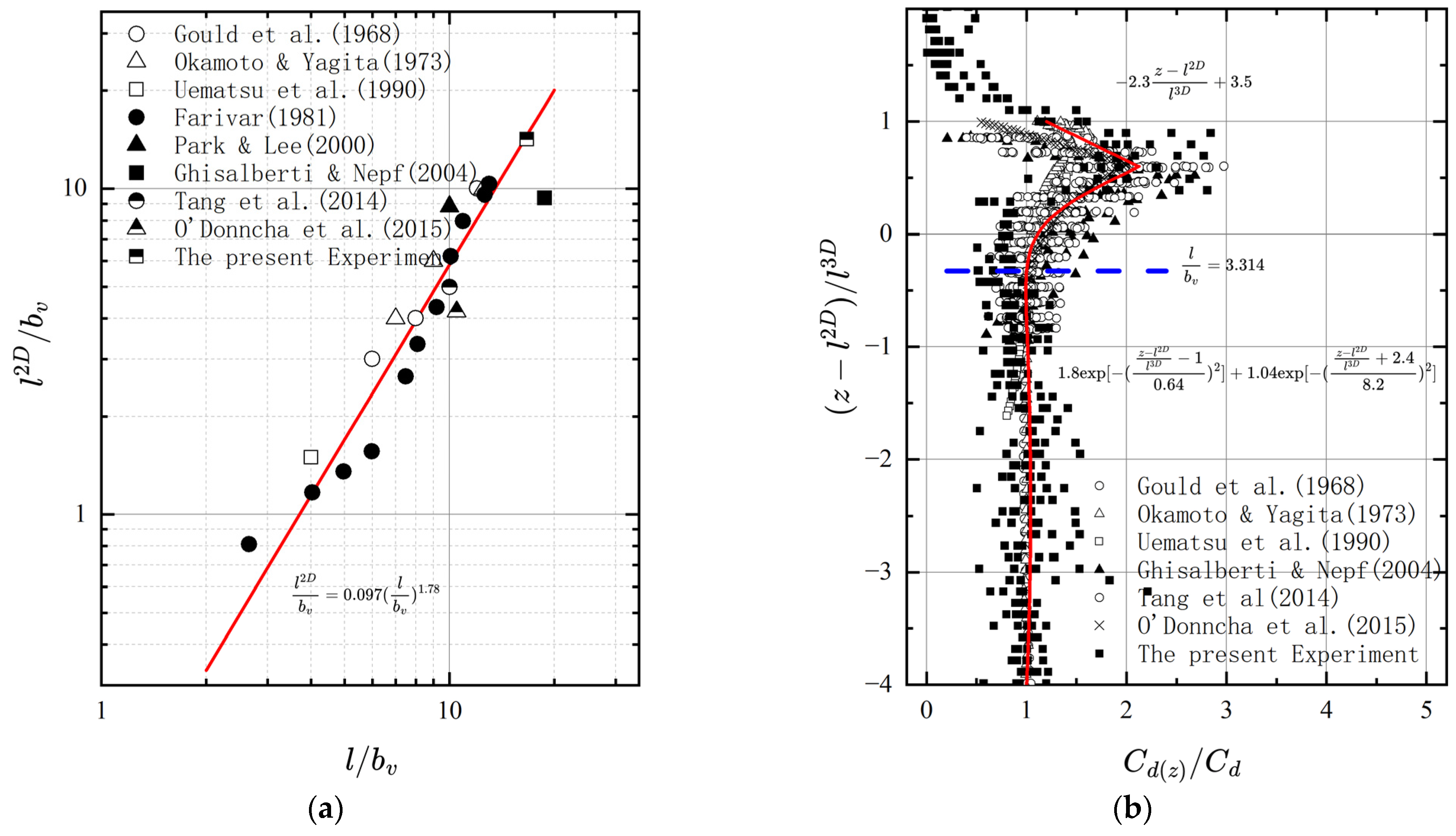
4.2. Drag Coefficient
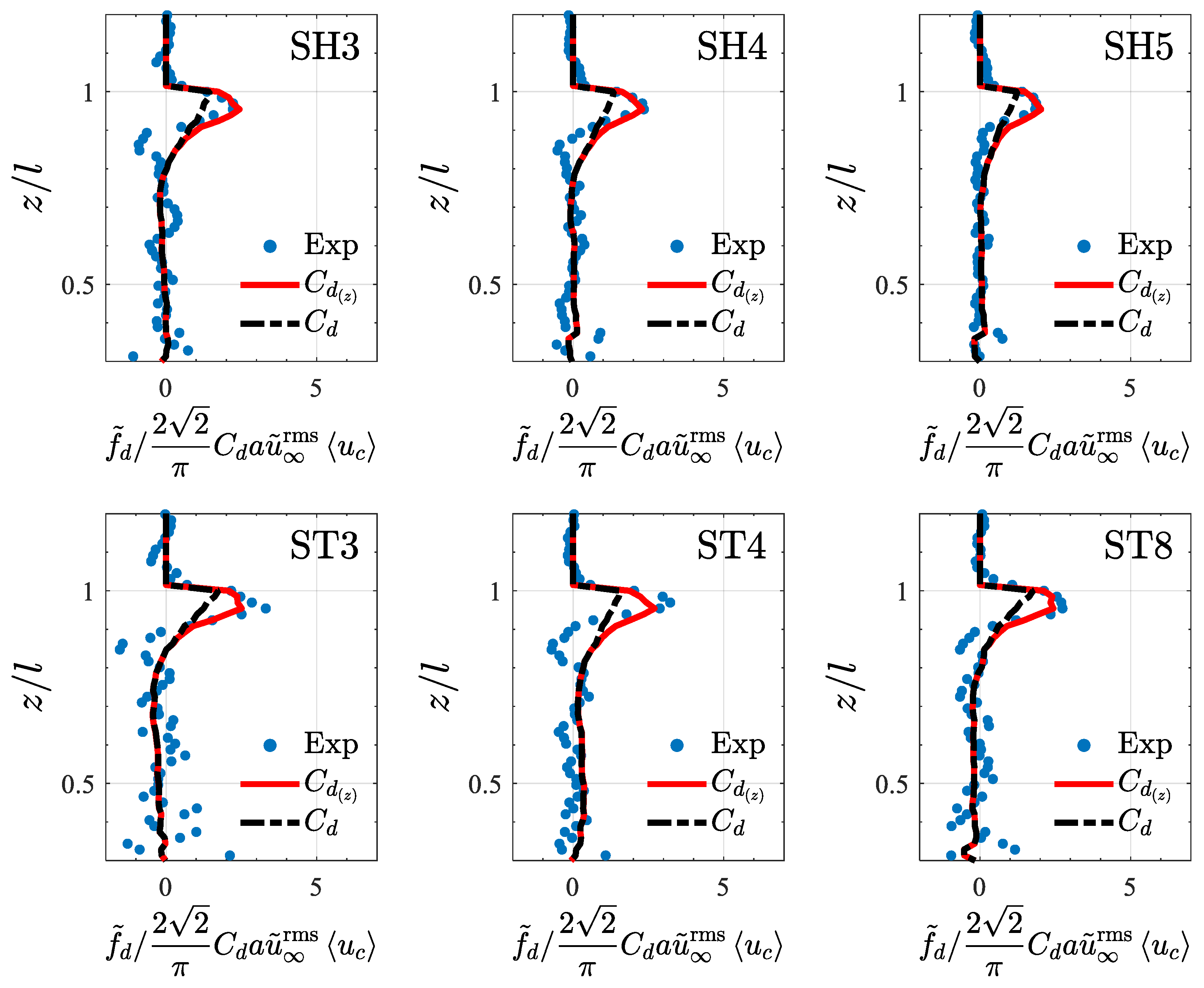
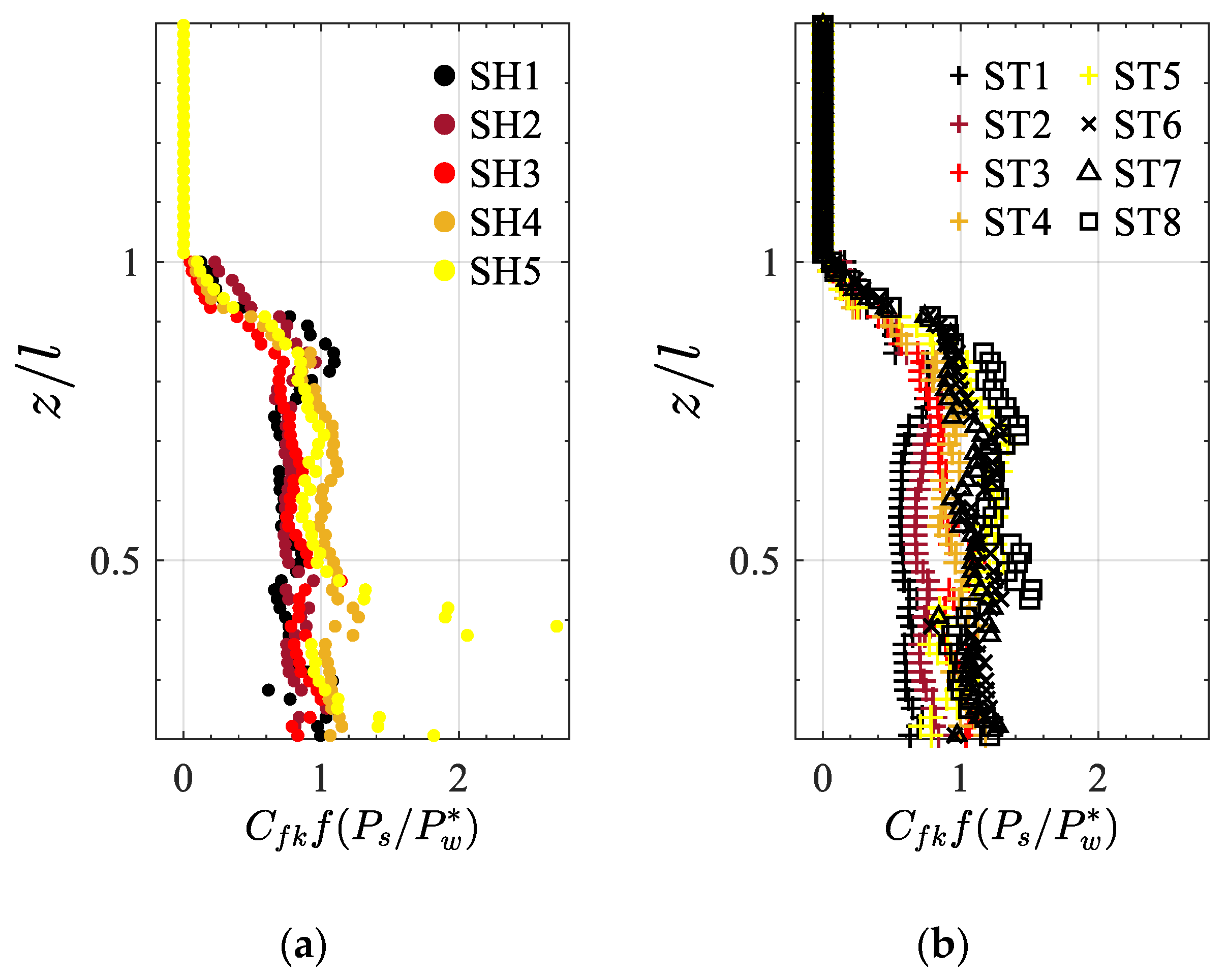
4.3. Turbulence Structure
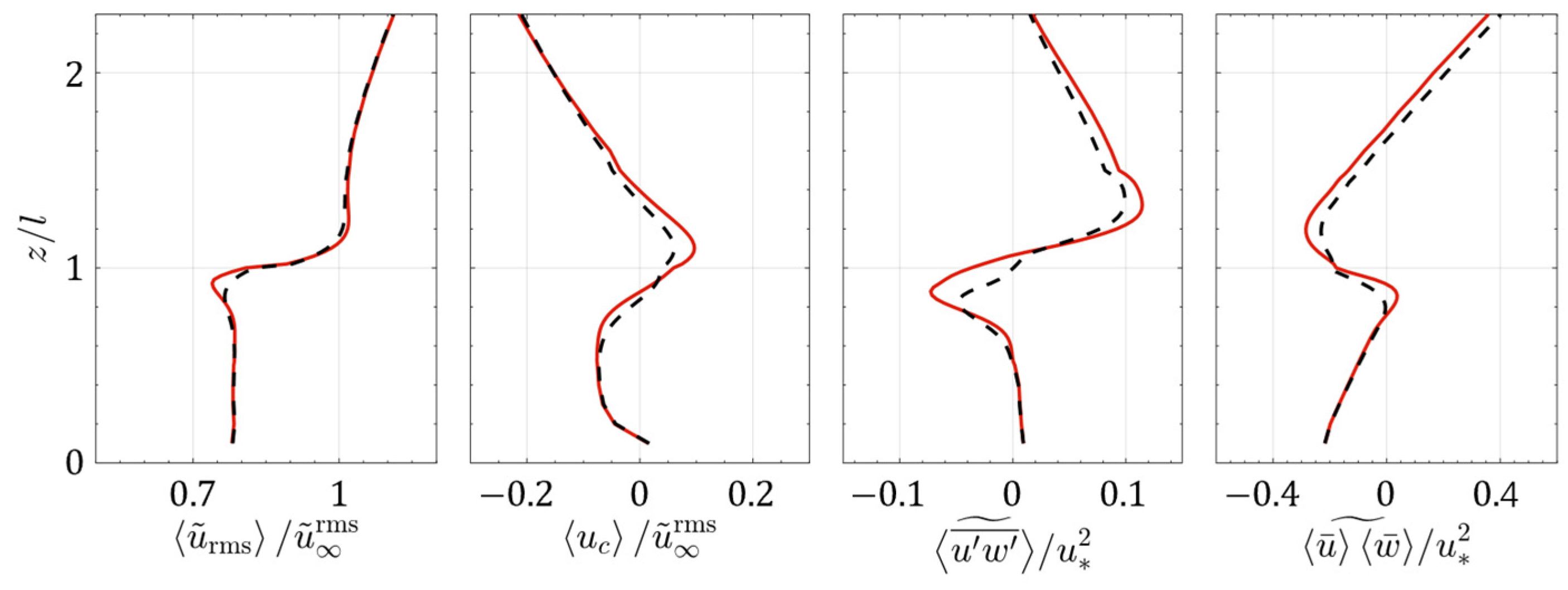
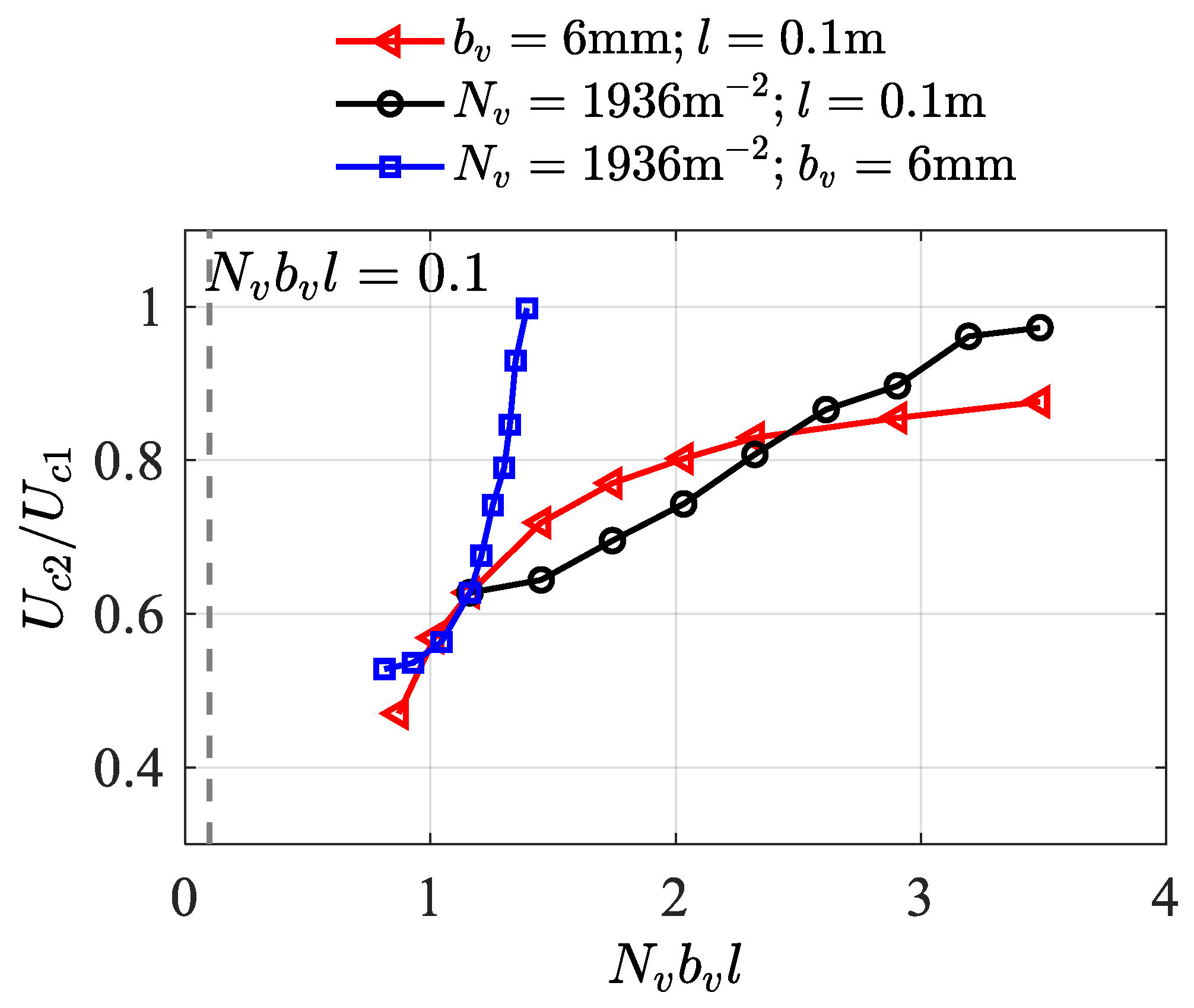
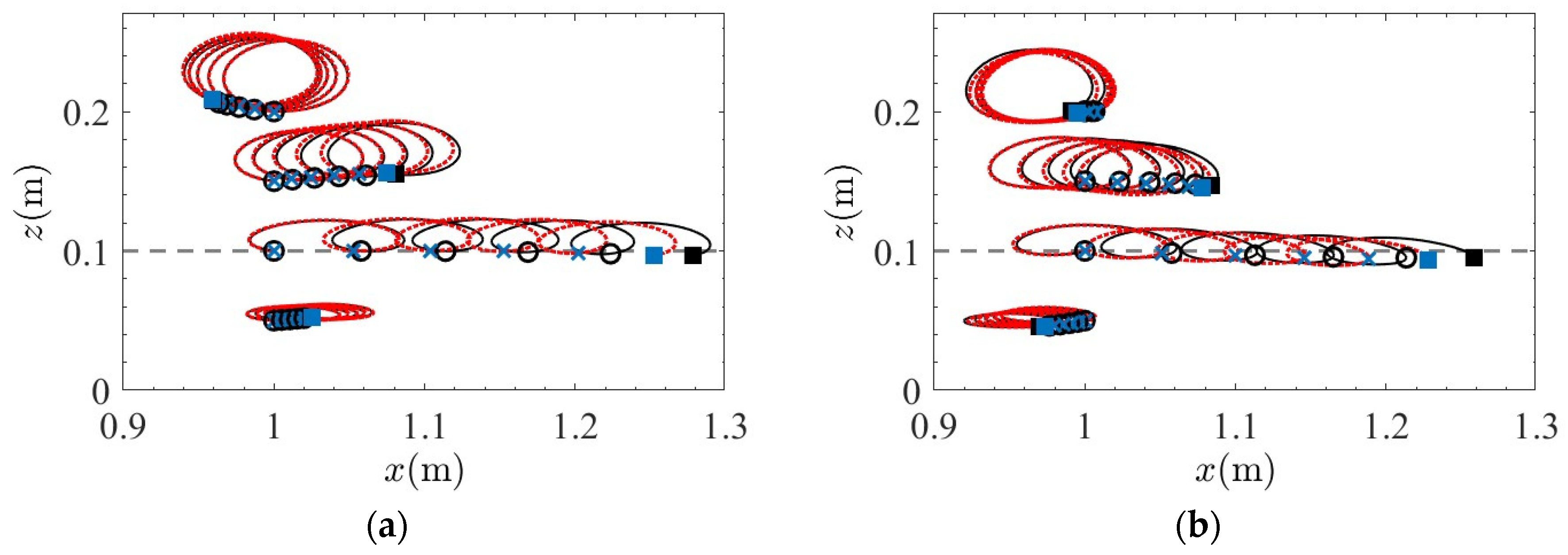
5. Discussions
5.1. Validation with Unidirectional Flows
5.2. Validation with Oscillatory Flows
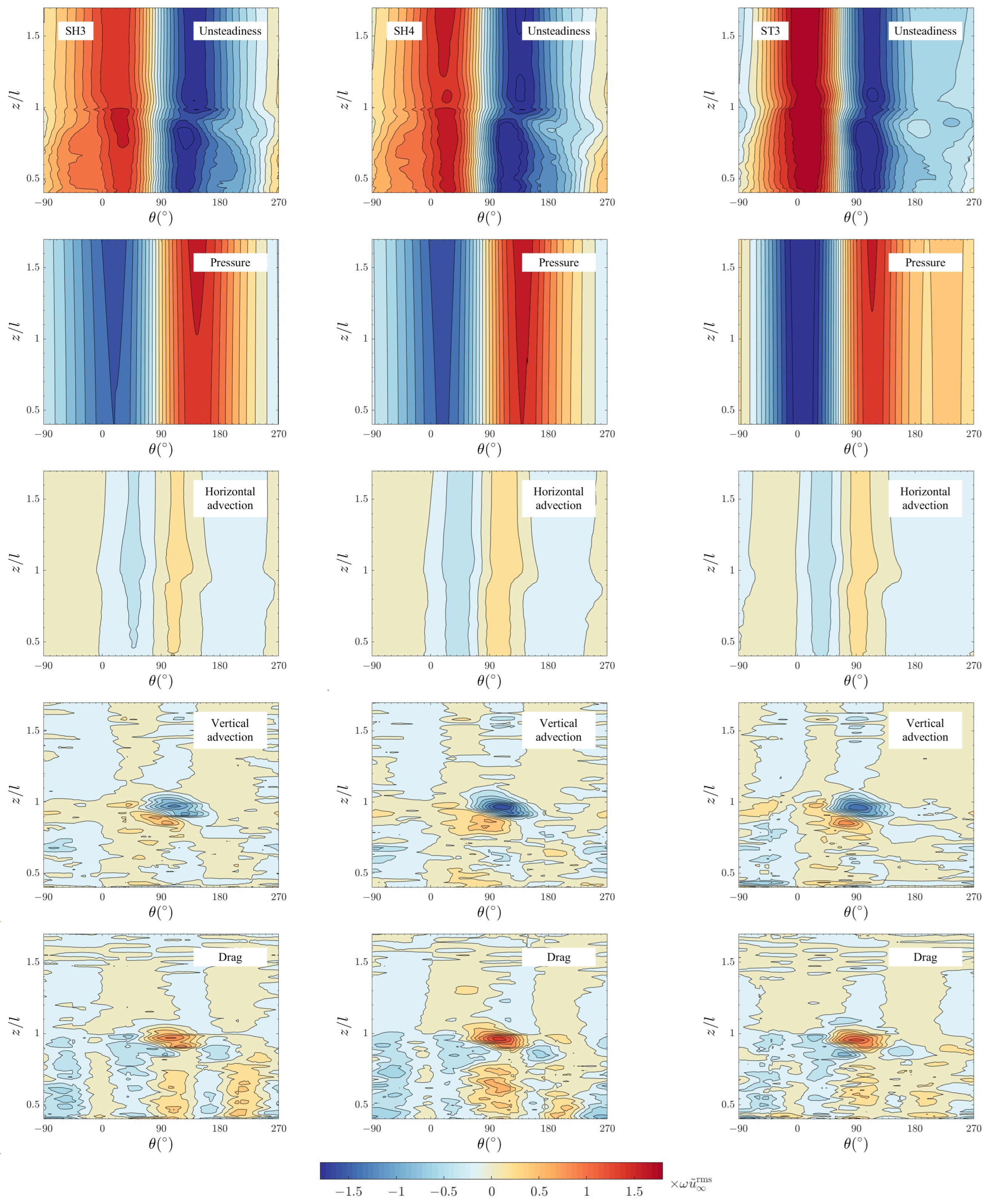
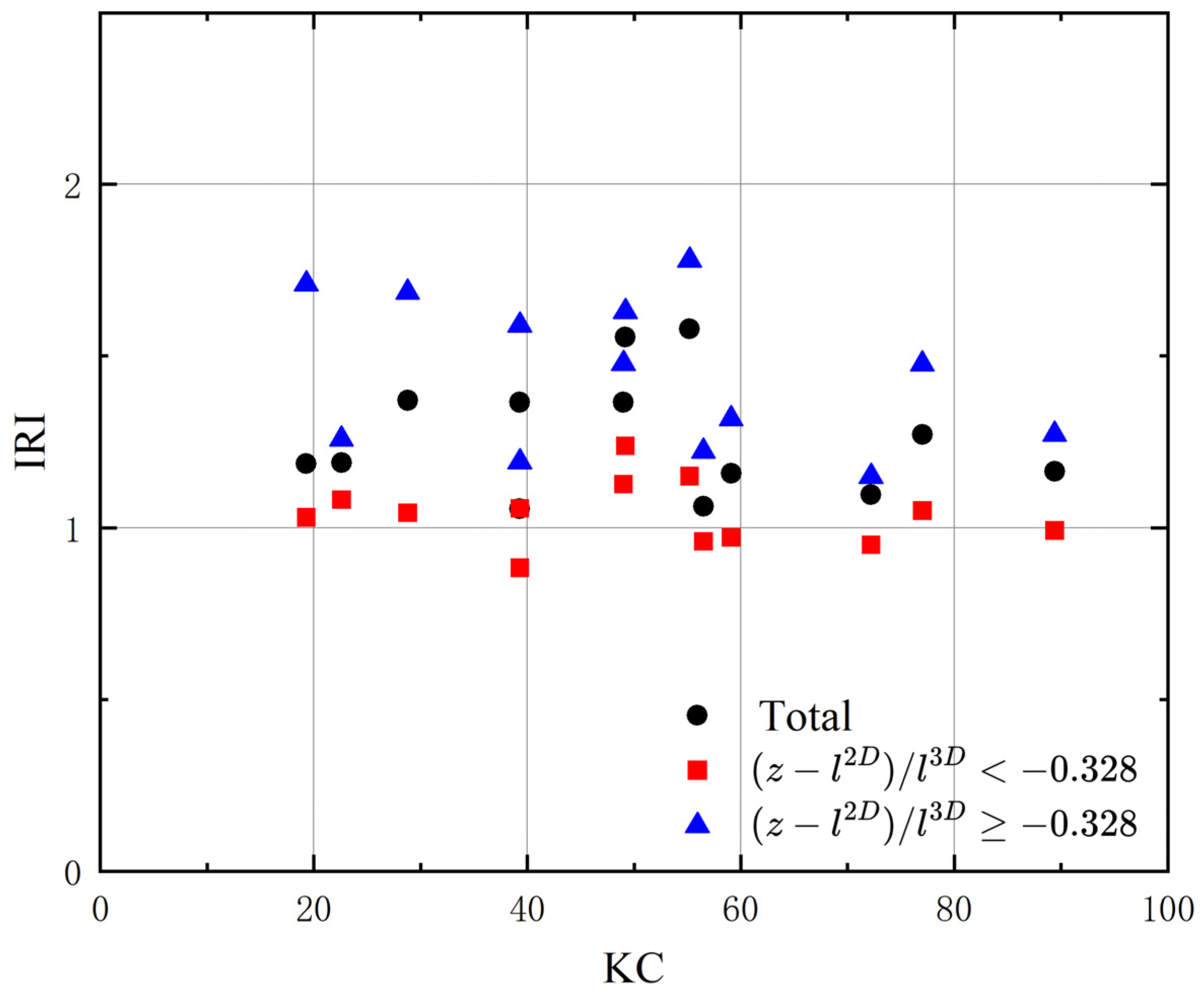
5.3. Tip Effects on Flow Structure
5.4. Tip Effects on Mass Transport
5.5. Tip Effects on SKE and WKE Budgets
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VARANS | Volume-averaged Reynolds-averaged Navier-Stokes |
| TKE | Turbulent kinetic energy |
| SKE | Shear kinetic energy |
| WKE | Wake kinetic energy |
| MKE | Mean kinetic energy |
| VOF | Volume of fluid |
| FOV | Field of view |
| LLSs | Laser light sheets |
| fps | Frames per second |
| RMSE | Root mean square error |
| MSE | Mean square errors |
Appendix A
References
- Jadhav, R.S.; Chen, Q.; Smith, J.M. Spectral Distribution of Wave Energy Dissipation by Salt Marsh Vegetation. Coast. Eng. 2013, 77, 99–107. [Google Scholar] [CrossRef]
- Casas-Ruiz, J.P.; Bodmer, P.; Bona, K.A.; Butman, D.; Couturier, M.; Emilson, E.J.S.; Finlay, K.; Genet, H.; Hayes, D.; Karlsson, J.; et al. Integrating Terrestrial and Aquatic Ecosystems to Constrain Estimates of Land-Atmosphere Carbon Exchange. Nat. Commun. 2023, 14, 1571. [Google Scholar] [CrossRef] [PubMed]
- Mendez, F.J.; Losada, I.J. An Empirical Model to Estimate the Propagation of Random Breaking and Nonbreaking Waves over Vegetation Fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Lowe, R.J.; Koseff, J.R.; Monismith, S.G. Oscillatory Flow through Submerged Canopies: 1. Velocity Structure. J. Geophys. Res. 2005, 110, C10016. [Google Scholar] [CrossRef]
- Losada, I.J.; Maza, M.; Lara, J.L. A New Formulation for Vegetation-Induced Damping under Combined Waves and Currents. Coast. Eng. 2016, 107, 1–13. [Google Scholar] [CrossRef]
- Hu, Z.; Lian, S.; Zitman, T.; Wang, H.; He, Z.; Wei, H.; Ren, L.; Uijttewaal, W.; Suzuki, T. Wave Breaking Induced by Opposing Currents in Submerged Vegetation Canopies. Water Resour. Res. 2022, 58, e2021WR031121. [Google Scholar] [CrossRef]
- El Rahi, J.; Martínez-Estévez, I.; Almeida Reis, R.; Tagliafierro, B.; Domínguez, J.M.; Crespo, A.J.C.; Stratigaki, V.; Suzuki, T.; Troch, P. Exploring Wave–Vegetation Interaction at Stem Scale: Analysis of the Coupled Flow–Structure Interactions Using the SPH-Based DualSPHysics Code and the FEA Module of Chrono. J. Mar. Sci. Eng. 2024, 12, 1120. [Google Scholar] [CrossRef]
- Reef, R.; Sayers, S. Wave Attenuation by Australian Temperate Mangroves. J. Mar. Sci. Eng. 2025, 13, 382. [Google Scholar] [CrossRef]
- Yang, J.Q.; Chung, H.; Nepf, H.M. The Onset of Sediment Transport in Vegetated Channels Predicted by Turbulent Kinetic Energy. Geophys. Res. Lett. 2016, 43, 11261–11268. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Coco, G. Turbulence as the Main Driver of Resuspension in Oscillatory Flow Through Vegetation. J. Geophys. Res. Earth Surf. 2018, 123, 891–904. [Google Scholar] [CrossRef]
- Xing, W.; Cong, X.; Kuang, C.; Wang, D.; An, Z.; Zou, Q. Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation. J. Mar. Sci. Eng. 2024, 12, 2126. [Google Scholar] [CrossRef]
- Mitsova, D.; Cresswell, K.; Bergh, C.; Matos, M.; Wakefield, S.; Freeman, K.; Lima, W.C. A Shoreline Screening Framework for Identifying Nature-Based Stabilization Measures Reducing Storm Damage in the Florida Keys. J. Mar. Sci. Eng. 2025, 13, 543. [Google Scholar] [CrossRef]
- Mass, T.; Genin, A.; Shavit, U.; Grinstein, M.; Tchernov, D. Flow Enhances Photosynthesis in Marine Benthic Autotrophs by Increasing the Efflux of Oxygen from the Organism to the Water. Proc. Natl. Acad. Sci. USA 2010, 107, 2527–2531. [Google Scholar] [CrossRef]
- van Rooijen, A.; Lowe, R.; Rijnsdorp, D.P.; Ghisalberti, M.; Jacobsen, N.G.; McCall, R. Wave-Driven Mean Flow Dynamics in Submerged Canopies. J. Geophys. Res. Ocean 2020, 125, e2019JC015935. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory Investigation of Mean Drag in a Random Array of Rigid, Emergent Cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Nicolle, A.; Eames, I. Numerical Study of Flow through and around a Circular Array of Cylinders. J. Fluid. Mech. 2011, 679, 1–31. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow Structure in Depth-Limited, Vegetated Flow. J. Geophys. Res. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, Turbulence, and Diffusion in Flow through Emergent Vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Lateral Dispersion in Random Cylinder Arrays at High Reynolds Number. J. Fluid. Mech. 2008, 600, 339–371. [Google Scholar] [CrossRef]
- King, A.T.; Tinoco, R.O.; Cowen, E.A. A k–ε Turbulence Model Based on the Scales of Vertical Shear and Stem Wakes Valid for Emergent and Submerged Vegetated Flows. J. Fluid. Mech. 2012, 701, 1–39. [Google Scholar] [CrossRef]
- Ma, G.; Kirby, J.T.; Su, S.-F.; Figlus, J.; Shi, F. Numerical Study of Turbulence and Wave Damping Induced by Vegetation Canopies. Coast. Eng. 2013, 80, 68–78. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A Coupled Model of Submerged Vegetation under Oscillatory Flow Using Navier–Stokes Equations. Coast. Eng. 2013, 80, 16–34. [Google Scholar] [CrossRef]
- Suzuki, T.; Hu, Z.; Kumada, K.; Phan, L.K.; Zijlema, M. Non-Hydrostatic Modeling of Drag, Inertia and Porous Effects in Wave Propagation over Dense Vegetation Fields. Coast. Eng. 2019, 149, 49–64. [Google Scholar] [CrossRef]
- Huang, T.; He, M.; Hong, K.; Lin, Y.; Jiao, P. Effect of Rigid Vegetation Arrangement on the Mixed Layer of Curved Channel Flow. J. Mar. Sci. Eng. 2023, 11, 213. [Google Scholar] [CrossRef]
- Cai, Z.; Xie, J.; Chen, Y.; Yang, Y.; Wang, C.; Wang, J. Rigid Vegetation Affects Slope Flow Velocity. Water 2024, 16, 2240. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. The Limited Growth of Vegetated Shear Layers. Water Resour. Res. 2004, 40, W07502. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. Mixing Layers and Coherent Structures in Vegetated Aquatic Flows. J. Geophys. Res. Ocean 2002, 107, 3-1–3-11. [Google Scholar] [CrossRef]
- Abdolahpour, M.; Ghisalberti, M.; Lavery, P.; McMahon, K. Vertical Mixing in Coastal Canopies. Limnol. Oceanogr. 2017, 62, 26–42. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, Y. Numerical Analysis of Turbulent Open-Channel Flow over a Vegetation Layer Using a k-ε Turbulence Model. J. Hydrosci. Hydraul. Eng. 1994, 11, 57–67. [Google Scholar]
- López, F.; García, M.H. Mean Flow and Turbulence Structure of Open-Channel Flow through Non-Emergent Vegetation. J. Hydraul. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- O’Donncha, F.; Hartnett, M.; Plew, D.R. Parameterizing Suspended Canopy Effects in a Three-Dimensional Hydrodynamic Model. J. Hydraul. Res. 2015, 53, 714–727. [Google Scholar] [CrossRef]
- Xuan, W.; Yang, C.; Wu, X.; Shao, Y.; Bai, Y. A Numerical Model of the Pollutant Transport in Rivers with Multi-Layer Rigid Vegetation. Water 2024, 16, 1397. [Google Scholar] [CrossRef]
- Dunn, C.; Fabian, L.; Marcelo, G. Mean Flow and Turbulence in a Labortory Channel with Simulated Vegetation; University of Illinois: Champaign, IL, USA, 1996. [Google Scholar]
- Tang, H.; Tian, Z.; Yan, J.; Yuan, S. Determining Drag Coefficients and Their Application in Modelling of Turbulent Flow with Submerged Vegetation. Adv. Water Resour. 2014, 69, 134–145. [Google Scholar] [CrossRef]
- Zeller, R.B.; Zarama, F.J.; Weitzman, J.S.; Koseff, J.R. A Simple and Practical Model for Combined Wave–Current Canopy Flows. J. Fluid. Mech. 2015, 767, 842–880. [Google Scholar] [CrossRef]
- Lu, Y.; Luo, Y.; Zeng, J.; Zhang, Z.; Hu, J.; Xu, Y.; Cheng, W. Laboratory Study on Wave Attenuation by Elastic Mangrove Model with Canopy. J. Mar. Sci. Eng. 2024, 12, 1198. [Google Scholar] [CrossRef]
- Fox, T.A.; West, G.S. Fluid-Induced Loading of Cantilevered Circular Cylinders in a Low-Turbulence Uniform Flow. Part 1: Mean Loading with Aspect Ratios in the Range 4 to 30. J. Fluids Struct. 1993, 7, 1–14. [Google Scholar] [CrossRef]
- Tang, X.; Lin, P.; Liu, P.L.-F.; Zhang, X. Numerical and Experimental Studies of Turbulence in Vegetated Open-Channel Flows. Env. Fluid. Mech. 2021, 21, 1137–1163. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, J.; Tong, L.; Guo, Y.; He, R.; Sun, K. Wave Motion and Seabed Response around a Vertical Structure Sheltered by Submerged Breakwaters with Fabry–Pérot Resonance. J. Mar. Sci. Eng. 2022, 10, 1797. [Google Scholar] [CrossRef]
- Larsen, B.E.; Van Der, A.D.A.; Van Der Zanden, J.; Ruessink, G.; Fuhrman, D.R. Stabilized RANS Simulation of Surf Zone Kinematics and Boundary Layer Processes beneath Large-Scale Plunging Waves over a Breaker Bar. Ocean Model. 2020, 155, 101705. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. A Numerical Study of Breaking Waves in the Surf Zone. J. Fluid. Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a Buoyancy-Modified k-ω SST Turbulence Model to Simulate Wave Run-up around a Monopile Subjected to Regular Waves Using OpenFOAM®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Van Maele, K.; Merci, B. Application of Two Buoyancy-Modified k–ε Turbulence Models to Different Types of Buoyant Plumes. Fire Saf. J. 2006, 41, 122–138. [Google Scholar] [CrossRef]
- Rodi, W. Examples of Calculation Methods for Flow and Mixing in Stratified Fluids. J. Geophys. Res. 1987, 92, 5305. [Google Scholar] [CrossRef]
- Inagaki, M. A New Wall-Damping Function for Large Eddy Simulation Employing Kolmogorov Velocity Scale. Int. J. Heat Fluid. Flow. 2011, 32, 26–40. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Wu, Y.; Wang, W.; Li, L. Simulation of Exchange Flow between Open Water and Floating Vegetation Using a Modified RNG K-ε Turbulence Model. Environ. Fluid. Mech. 2017, 17, 355–372. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Coco, G. A Laboratory Study on Sediment Resuspension within Arrays of Rigid Cylinders. Adv. Water Resour. 2016, 92, 1–9. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. Internal Wave-Maker for Navier-Stokes Models. J. Waterw. Port. Coast. Ocean Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Hsieh, S.-C.; Low, Y.M.; Chiew, Y.-M. Flow Characteristics around a Circular Cylinder Subjected to Vortex-Induced Vibration near a Plane Boundary. J. Fluids Struct. 2016, 65, 257–277. [Google Scholar] [CrossRef]
- Lumley, J.L.; Terray, E.A. Kinematics of Turbulence Convected by a Random Wave Field. J. Phys. Oceanogr. 1983, 13, 2000–2007. [Google Scholar] [CrossRef]
- Luhar, M.; Coutu, S.; Infantes, E.; Fox, S.; Nepf, H. Wave-Induced Velocities inside a Model Seagrass Bed. J. Geophys. Res. 2010, 115, C12005. [Google Scholar] [CrossRef]
- Wu, W.-C.; Cox, D.T. Effects of Wave Steepness and Relative Water Depth on Wave Attenuation by Emergent Vegetation. Estuar. Coast. Shelf Sci. 2015, 164, 443–450. [Google Scholar] [CrossRef]
- Keulegan, G.H.; Carpenter, L.H. Forces on Cylinders and Plates in an Oscillating Fluid. J. Res. Natl. Bur. Stan. 1958, 60, 423. [Google Scholar] [CrossRef]
- Stansby, P.K.; Bullock, G.N.; Short, I. Quasi-2-D Forces on a Vertical Cylinder in Waves. J. Waterw. Port. Coast. Ocean Eng. 1983, 109, 128–132. [Google Scholar] [CrossRef]
- An, H.; Cheng, L.; Zhao, M. Two-Dimensional and Three-Dimensional Simulations of Oscillatory Flow around a Circular Cylinder. Ocean Eng. 2015, 109, 270–286. [Google Scholar] [CrossRef]
- Basu, R.I. Aerodynamic Forces on Structures of Circular Cross-Section. Part 2. The Influence of Turbulence and Three-Dimensional Effects. J. Wind. Eng. Ind. Aerodyn. 1986, 24, 33–59. [Google Scholar] [CrossRef]
- Farivar, D.J. Turbulent Uniform Flow around Cylinders of Finite Length. AIAA J. 1981, 19, 275–281. [Google Scholar] [CrossRef]
- Gould, R.W.E.; Raymer, W.G.; Ponsford, P.J. Wind Tunnel Tests on Chimneys of Circular Section at High Reynolds Numbers; Loughborough University of Technology: Loughborough, UK, 1968. [Google Scholar]
- Okamoto, T.; Yagita, M. The Experimental Investigation on the Flow Past a Circular Cylinder of Finite Length Placed Normal to the Plane Surface in a Uniform Stream. Bull. JSME 1973, 16, 805–814. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yamada, M.; Ishii, K. Some Effects of Free-Stream Turbulence on the Flow Past a Cantilevered Circular Cylinder. J. Wind. Eng. Ind. Aerodyn. 1990, 33, 43–52. [Google Scholar] [CrossRef]
- Park, C.-W.; Lee, S.-J. Free End Effects on the near Wake Flow Structure behind a Finite Circular Cylinder. J. Wind. Eng. Ind. Aerodyn. 2000, 88, 231–246. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhou, Y. The Finite-Length Square Cylinder near Wake. J. Fluid. Mech. 2009, 638, 453–490. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in Plant Canopies. Annu. Rev. Fluid. Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Chen, M.; Lou, S.; Liu, S.; Ma, G.; Liu, H.; Zhong, G.; Zhang, H. Velocity and Turbulence Affected by Submerged Rigid Vegetation under Waves, Currents and Combined Wave–Current Flows. Coast. Eng. 2020, 159, 103727. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Cowen, E.A. The Direct and Indirect Measurement of Boundary Stress and Drag on Individual and Complex Arrays of Elements. Exp Fluids 2013, 54, 1509. [Google Scholar] [CrossRef]
- White, B.L. Transport in Random Cylinder Arrays: Canopies; Massachusetts Institute of Technology, MI: Cambridge, MA, USA, 2002. [Google Scholar]
- Longuet-Higgins, M.S. Mass Transport in Water Waves. Phil. Trans. R. Soc. Lond. A 1953, 245, 535–581. [Google Scholar]
- North, E.W.; Hood, R.R.; Chao, S.-Y.; Sanford, L.P. Using a Random Displacement Model to Simulate Turbulent Particle Motion in a Baroclinic Frontal Zone: A New Implementation Scheme and Model Performance Tests. J. Mar. Syst. 2006, 60, 365–380. [Google Scholar] [CrossRef]
- Li, Y.; Karri, N.; Wang, Q. Three-Dimensional Numerical Analysis on Blade Response of a Vertical-Axis Tidal Current Turbine under Operational Conditions. J. Renew. Sustain. Energy 2014, 6, 043123. [Google Scholar] [CrossRef]
- Leng, J.; Wang, Q.; Li, Y. A Geometrically Nonlinear Analysis Method for Offshore Renewable Energy Systems—Examples of Offshore Wind and Wave Devices. Ocean Eng. 2022, 250, 110930. [Google Scholar] [CrossRef]
- Leng, J.; Gao, Z.; Wu, M.C.H.; Guo, T.; Li, Y. A Fluid–Structure Interaction Model for Large Wind Turbines Based on Flexible Multibody Dynamics and Actuator Line Method. J. Fluids Struct. 2023, 118, 103857. [Google Scholar] [CrossRef]

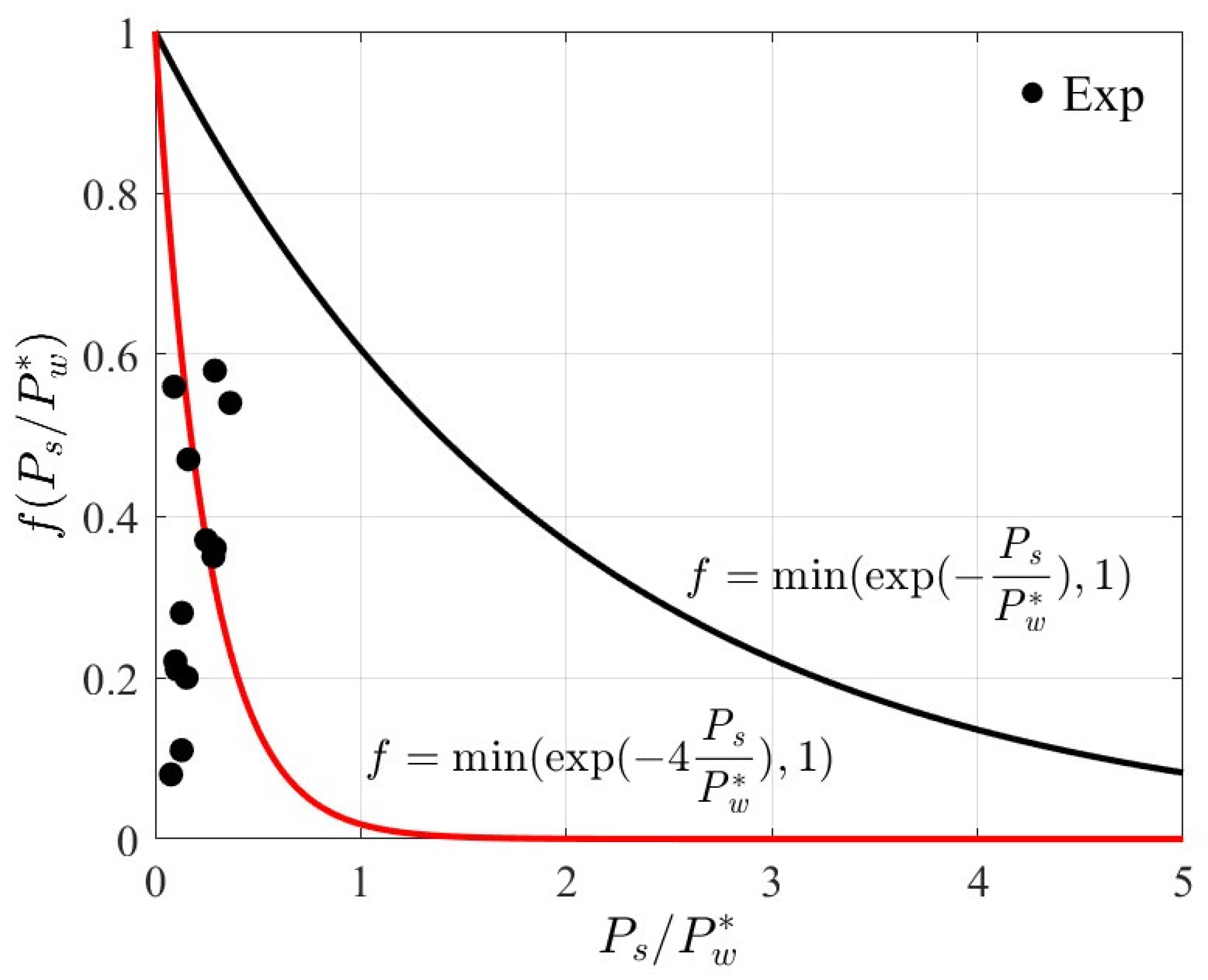
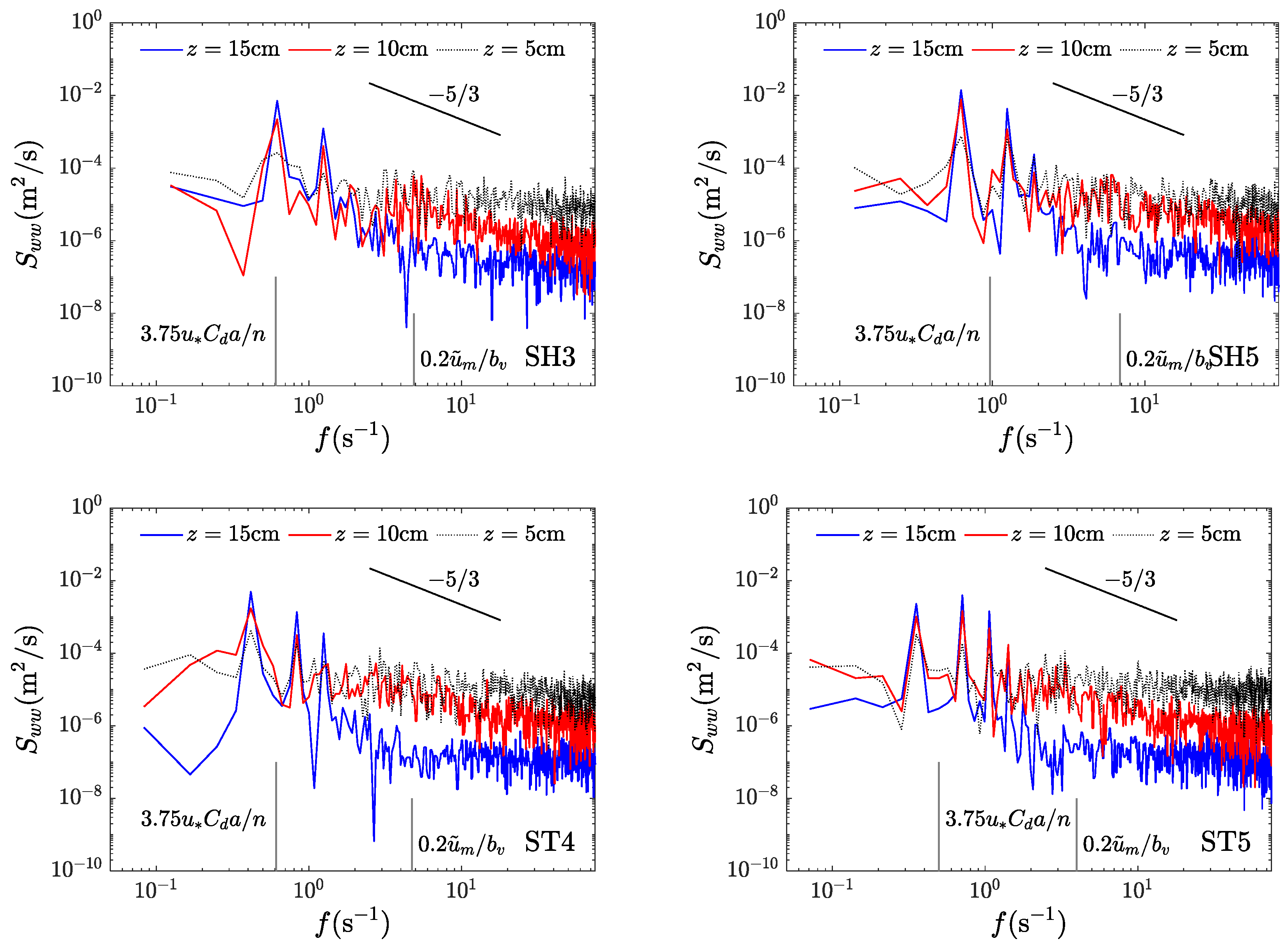
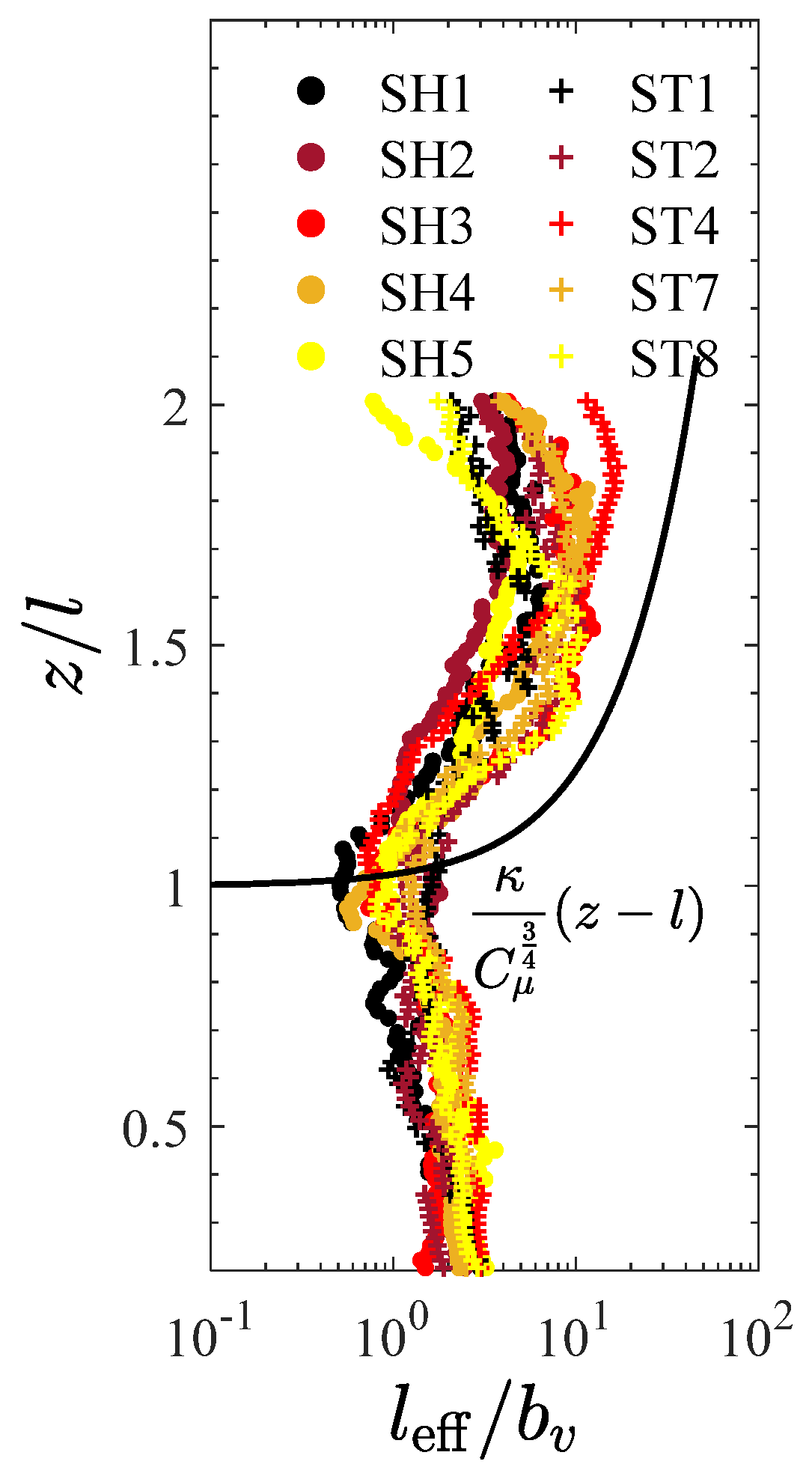


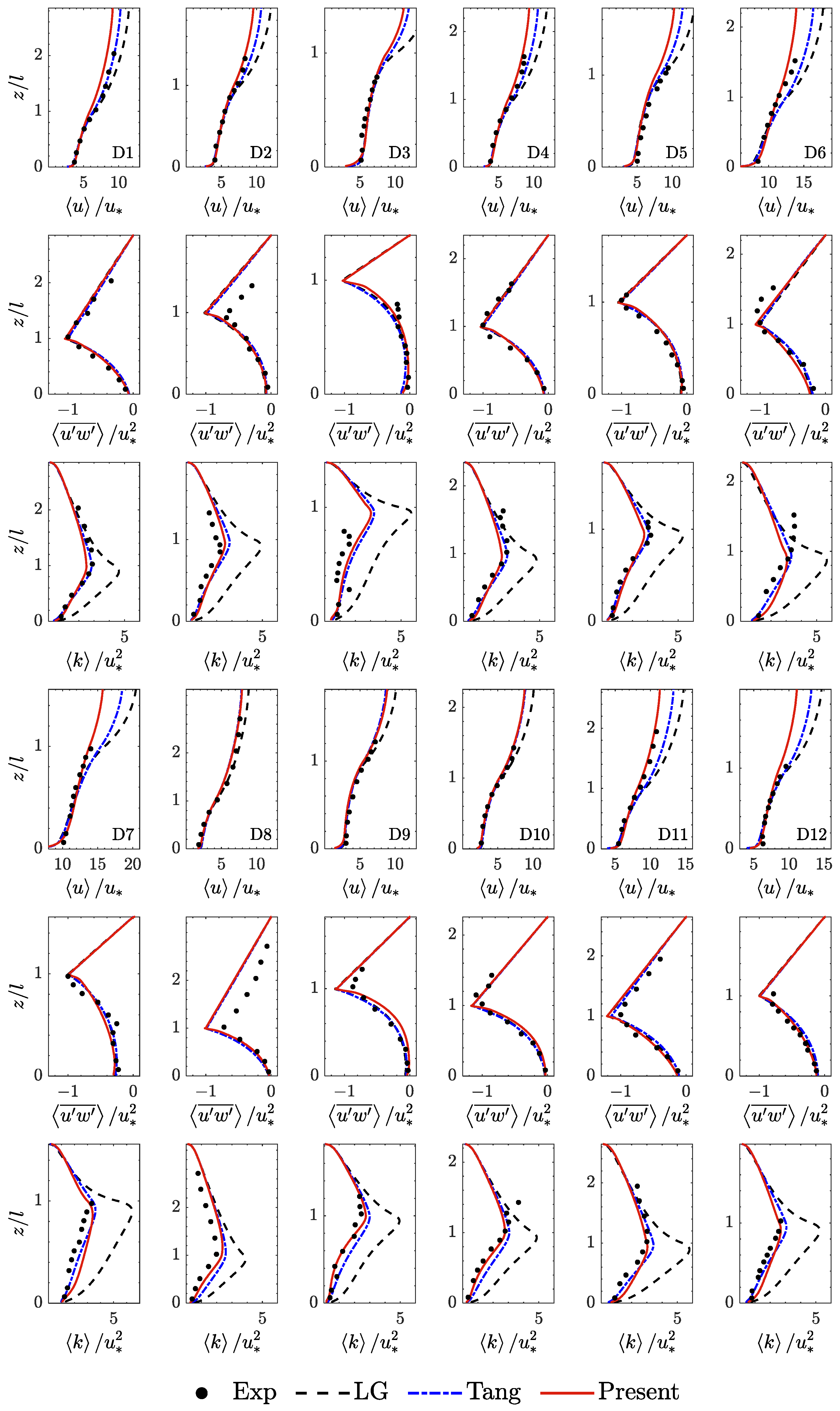

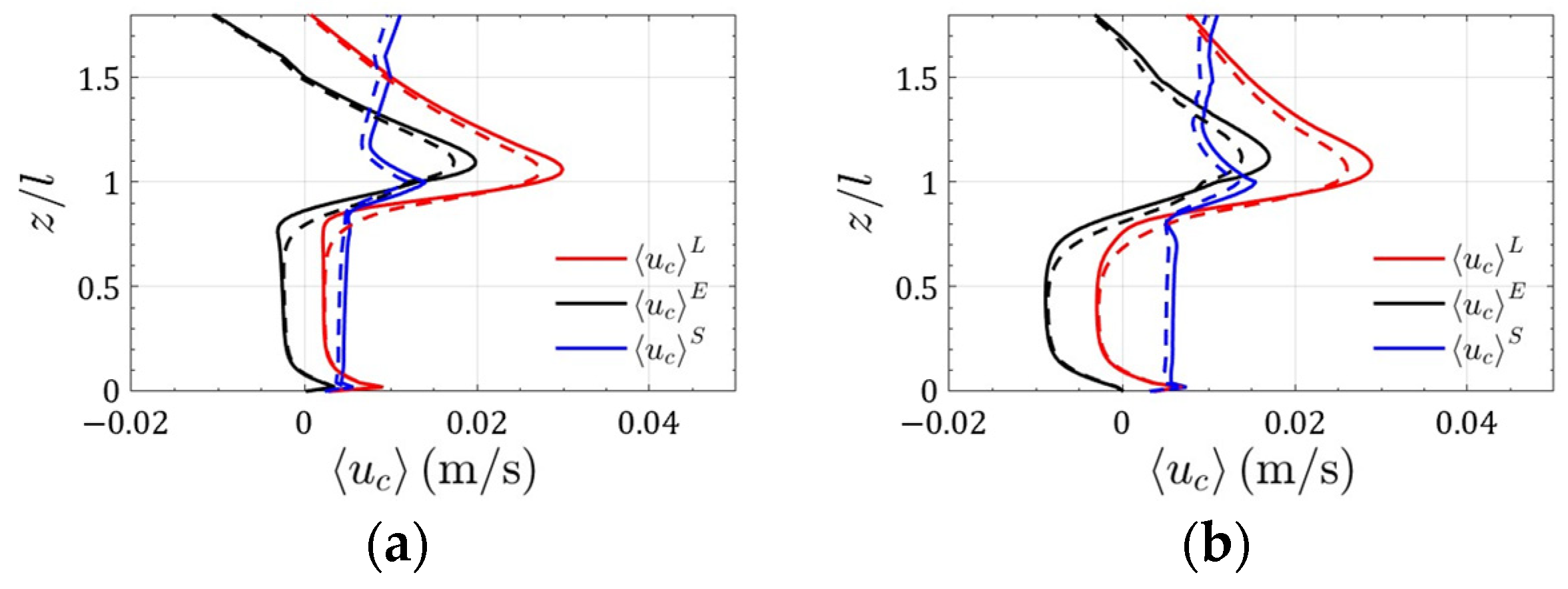


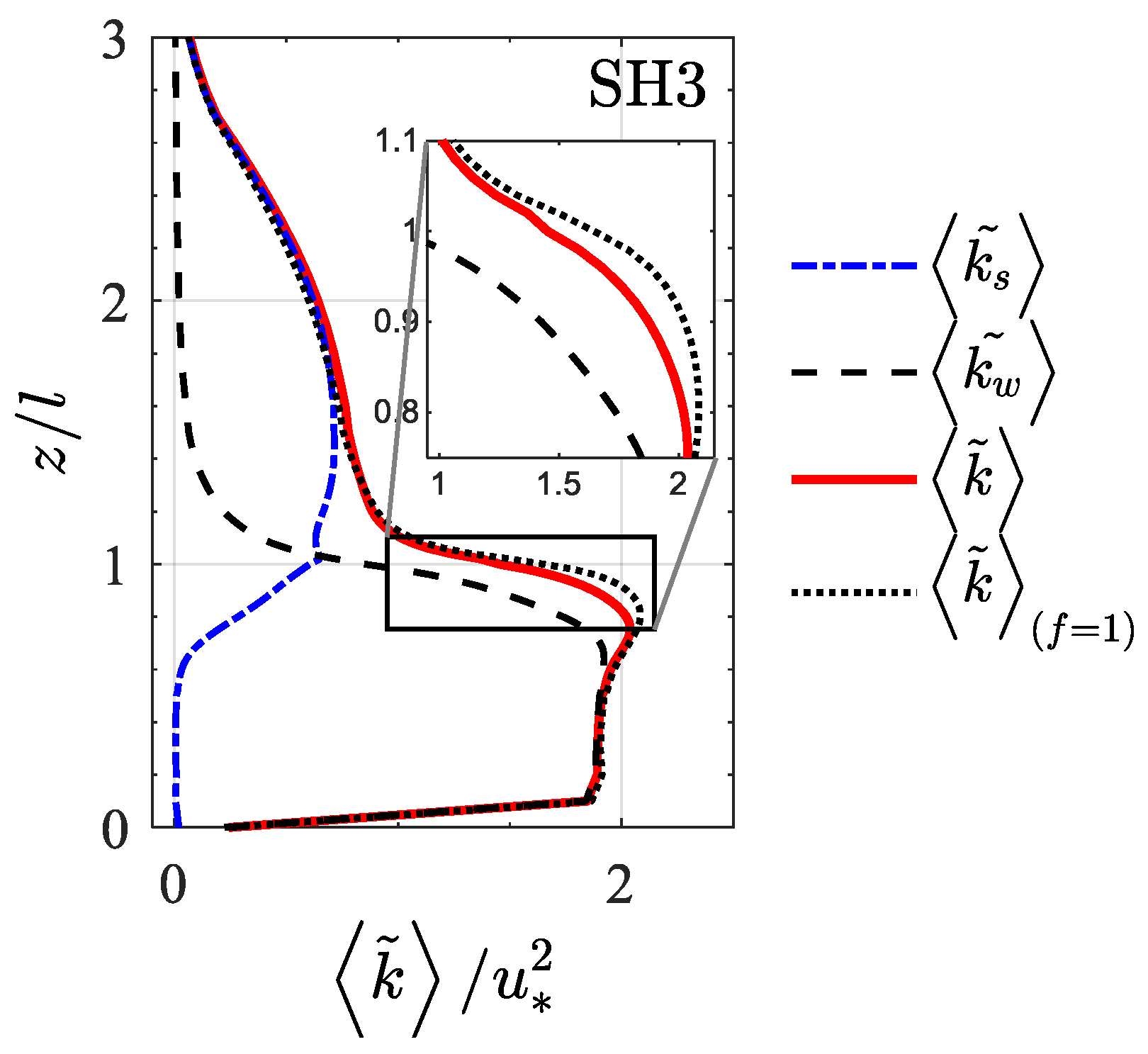
| CASE | H (cm) | T (s) | (cm/s) | (cm/s) | (cm) | ||
|---|---|---|---|---|---|---|---|
| SH1 | 3.8 | 1.6 | 0.28 | 6.3 | 0.82 | 0.18) | 0.65) |
| SH2 | 5.2 | 1.6 | 0.36 | 9.2 | 0.84 | 0.23) | 0.47) |
| SH3 | 7.3 | 1.6 | 0.50 | 11.8 | 0.89 | 0.33) | 0.73) |
| SH4 | 9.4 | 1.6 | 0.69 | 14.3 | 0.91 | 0.26) | 1.04) |
| SH5 | 11.0 | 1.6 | 0.64 | 17.7 | 0.83 | 0.56) | 0.47) |
| ST1 | 6.7 | 1.2 | 1.35 | 10.3 | 0.78 | 0.29) | 0.11) |
| ST2 | 7.4 | 1.6 | 0.44 | 11.7 | 0.89 | 0.59) | 0.56) |
| ST3 | 6.3 | 2.0 | 0.38 | 11.8 | 0.88 | 0.52) | 0.62) |
| ST4 | 6.4 | 2.4 | 0.46 | 10.8 | 0.93 | 0.50) | 0.18) |
| ST5 | 6.4 | 2.8 | 0.45 | 10.4 | 0.86 | 0.79) | 0.26) |
| ST6 | 7.0 | 3.2 | 0.52 | 10.4 | 0.92 | 0.52) | 0.64) |
| ST7 | 7.4 | 3.6 | 0.39 | 11.0 | 0.95 | 0.44) | 0.31) |
| ST8 | 5.5 | 4.0 | 0.55 | 9.1 | 0.90 | 0.53) | 0.75) |
| Source | CASE | (mm) | (m) | (m) | ||
|---|---|---|---|---|---|---|
| King et al. [20] | S1 | 1290 | 3.1 | 0.193 | 0.257 | 0.00168 |
| S2 | 645 | 6.2 | 0.194 | 0.260 | 0.00203 | |
| S3 | 315 | 12.7 | 0.193 | 0.257 | 0.00210 | |
| S4 | 158 | 25.3 | 0.194 | 0.256 | 0.00082 | |
| S5 | 1290 | 3.1 | 0.193 | 0.370 | 0.00015 | |
| S6 | 645 | 6.2 | 0.194 | 0.367 | 0.00075 | |
| S7 | 315 | 12.7 | 0.193 | 0.369 | 0.00012 | |
| S8 | 158 | 25.3 | 0.194 | 0.368 | 0.00066 | |
| Dunn et al. [33] | D1 | 172 | 6.35 | 0.1175 | 0.335 | 0.00360 |
| D2 | 172 | 6.35 | 0.1175 | 0.229 | 0.00360 | |
| D3 | 172 | 6.35 | 0.1175 | 0.164 | 0.00360 | |
| D4 | 172 | 6.35 | 0.1175 | 0.276 | 0.00760 | |
| D5 | 172 | 6.35 | 0.1175 | 0.203 | 0.00760 | |
| D6 | 43 | 6.35 | 0.1175 | 0.267 | 0.00360 | |
| D7 | 43 | 6.35 | 0.1175 | 0.183 | 0.00360 | |
| D8 | 388 | 6.35 | 0.1175 | 0.391 | 0.00360 | |
| D9 | 388 | 6.35 | 0.1175 | 0.214 | 0.00360 | |
| D10 | 388 | 6.35 | 0.1175 | 0.265 | 0.01610 | |
| D11 | 97 | 6.35 | 0.1175 | 0.311 | 0.00360 | |
| D12 | 97 | 6.35 | 0.1175 | 0.233 | 0.01080 |
| CASE | LG Model | Tang Model | The Present Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | 0.10 | 0.10 | 2.25 | 0.10 | 0.04 | 0.19 | 0.03 | 0.06 | 0.25 |
| S2 | 0.01 | 0.07 | 1.14 | 0.13 | 0.09 | 0.39 | 0.01 | 0.03 | 0.27 |
| S3 | 0.01 | 0.08 | 1.50 | 0.19 | 0.14 | 0.52 | 0.11 | 0.04 | 0.23 |
| S4 | 0.05 | 0.13 | 0.71 | 0.45 | 0.09 | 0.58 | 0.03 | 0.16 | 0.19 |
| S5 | 0.03 | 0.18 | 0.85 | 0.03 | 0.13 | 0.20 | 0.05 | 0.13 | 0.26 |
| S6 | 0.24 | 0.15 | 1.16 | 0.36 | 0.12 | 0.38 | 0.02 | 0.15 | 0.17 |
| S7 | 0.03 | 0.39 | 1.07 | 0.48 | 0.42 | 0.63 | 0.17 | 0.12 | 0.13 |
| S8 | 0.13 | 0.39 | 2.70 | 0.49 | 0.56 | 0.98 | 0.13 | 0.22 | 0.23 |
| D1 | 0.06 | 0.06 | 2.68 | 0.01 | 0.06 | 0.06 | 0.10 | 0.05 | 0.21 |
| D2 | 0.19 | 0.95 | 11.24 | 0.04 | 0.74 | 0.84 | 0.02 | 0.83 | 0.21 |
| D3 | 0.10 | 1.81 | 38.05 | 0.14 | 2.55 | 4.52 | 0.14 | 0.96 | 1.46 |
| D4 | 0.22 | 0.05 | 2.81 | 0.04 | 0.07 | 0.18 | 0.04 | 0.05 | 0.28 |
| D5 | 0.07 | 0.02 | 2.46 | 0.09 | 0.02 | 0.02 | 0.25 | 0.04 | 0.14 |
| D6 | 0.51 | 0.18 | 4.70 | 0.23 | 0.16 | 0.55 | 0.06 | 0.13 | 0.86 |
| D7 | 0.40 | 0.07 | 15.57 | 0.33 | 0.06 | 0.47 | 0.07 | 0.10 | 0.19 |
| D8 | 0.03 | 0.97 | 5.77 | 0.03 | 0.91 | 1.22 | 0.02 | 0.95 | 0.48 |
| D9 | 0.04 | 0.08 | 4.11 | 0.05 | 0.07 | 0.29 | 0.06 | 0.12 | 0.08 |
| D10 | 0.03 | 0.03 | 2.22 | 0.01 | 0.02 | 0.29 | 0.02 | 0.05 | 0.18 |
| D11 | 0.55 | 0.13 | 6.00 | 0.20 | 0.10 | 0.24 | 0.02 | 0.12 | 0.20 |
| D12 | 0.09 | 0.11 | 8.71 | 0.07 | 0.12 | 0.23 | 0.11 | 0.08 | 0.08 |
| Average | 0.14 | 0.31 | 5.79 | 0.17 | 0.32 | 0.64 | 0.07 | 0.22 | 0.31 |
| Zone | LG Model | Tang Model | The Present Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Free stream | 0.28 | 0.40 | 1.62 | 0.36 | 0.33 | 0.49 | 0.14 | 0.32 | 0.38 |
| In vegetation | 0.05 | 0.20 | 6.95 | 0.05 | 0.28 | 0.65 | 0.04 | 0.12 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Zhang, J.; Chen, H.; Liu, C.; Zhang, M. Parameterizing the Tip Effects of Submerged Vegetation in a VARANS Solver. J. Mar. Sci. Eng. 2025, 13, 785. https://doi.org/10.3390/jmse13040785
Jiang L, Zhang J, Chen H, Liu C, Zhang M. Parameterizing the Tip Effects of Submerged Vegetation in a VARANS Solver. Journal of Marine Science and Engineering. 2025; 13(4):785. https://doi.org/10.3390/jmse13040785
Chicago/Turabian StyleJiang, Lai, Jisheng Zhang, Hao Chen, Chenglin Liu, and Mingzong Zhang. 2025. "Parameterizing the Tip Effects of Submerged Vegetation in a VARANS Solver" Journal of Marine Science and Engineering 13, no. 4: 785. https://doi.org/10.3390/jmse13040785
APA StyleJiang, L., Zhang, J., Chen, H., Liu, C., & Zhang, M. (2025). Parameterizing the Tip Effects of Submerged Vegetation in a VARANS Solver. Journal of Marine Science and Engineering, 13(4), 785. https://doi.org/10.3390/jmse13040785