Research on Particle Motion Characteristics in a Spiral-Vane-Type Multiphase Pump Based on CFD-DEM
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Calculation Model
2.2. Mesh Division and Independence Verification
2.3. Mathematical Models and Calculation Method Settings
2.3.1. Continuous Phase Control Equations
2.3.2. Discrete Phase Control Equations
2.3.3. CFD-DEM Coupling
2.3.4. Calculation Method Settings
3. Experimental Verification
3.1. Experimental Equipment
3.2. Experimental Results
4. Analysis of Numerical Results
4.1. Time Independence Analysis
4.2. Analysis of Single-Particle Flow in the Pump
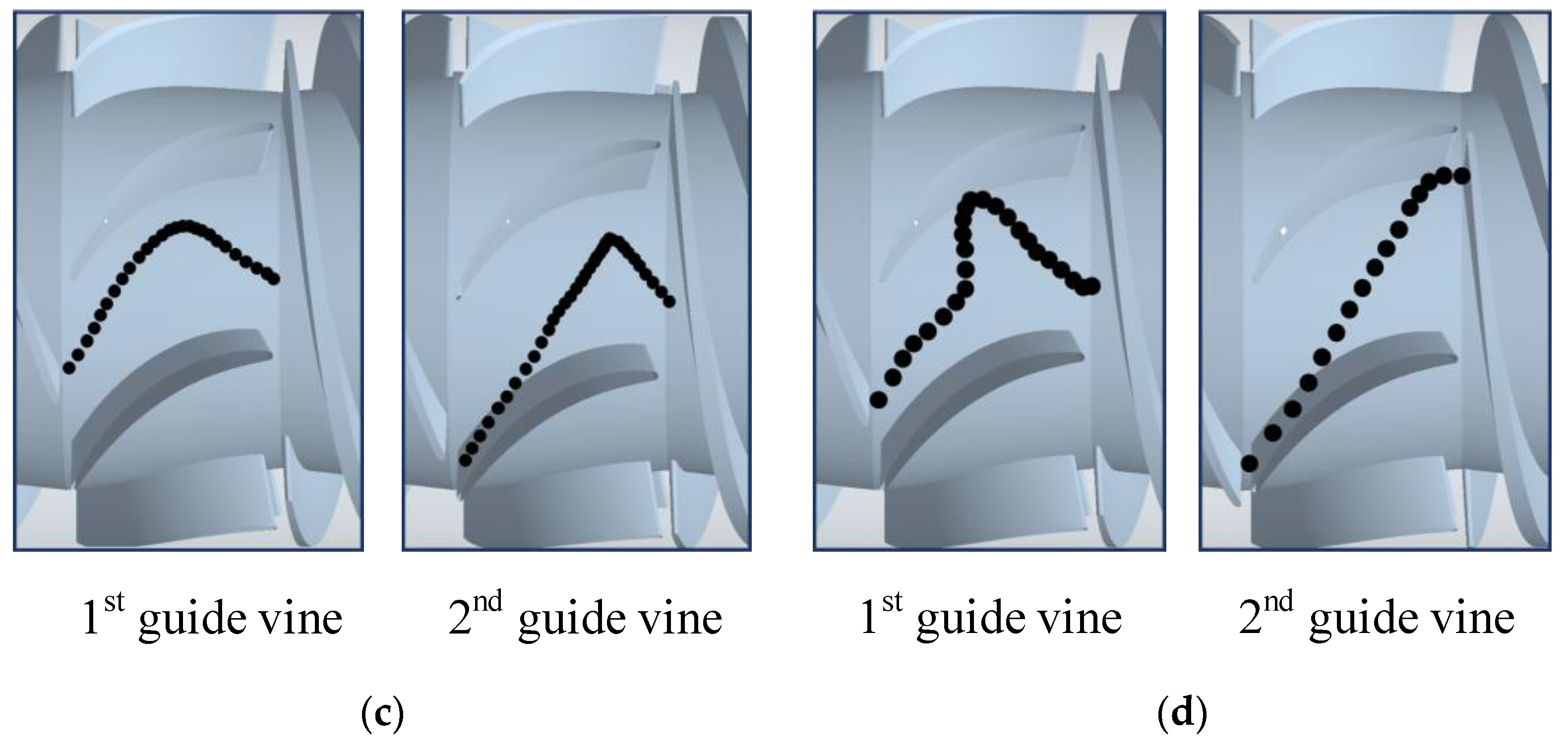
4.2.1. The Particle Trajectories Under Different Diameters in the Guide Vanes
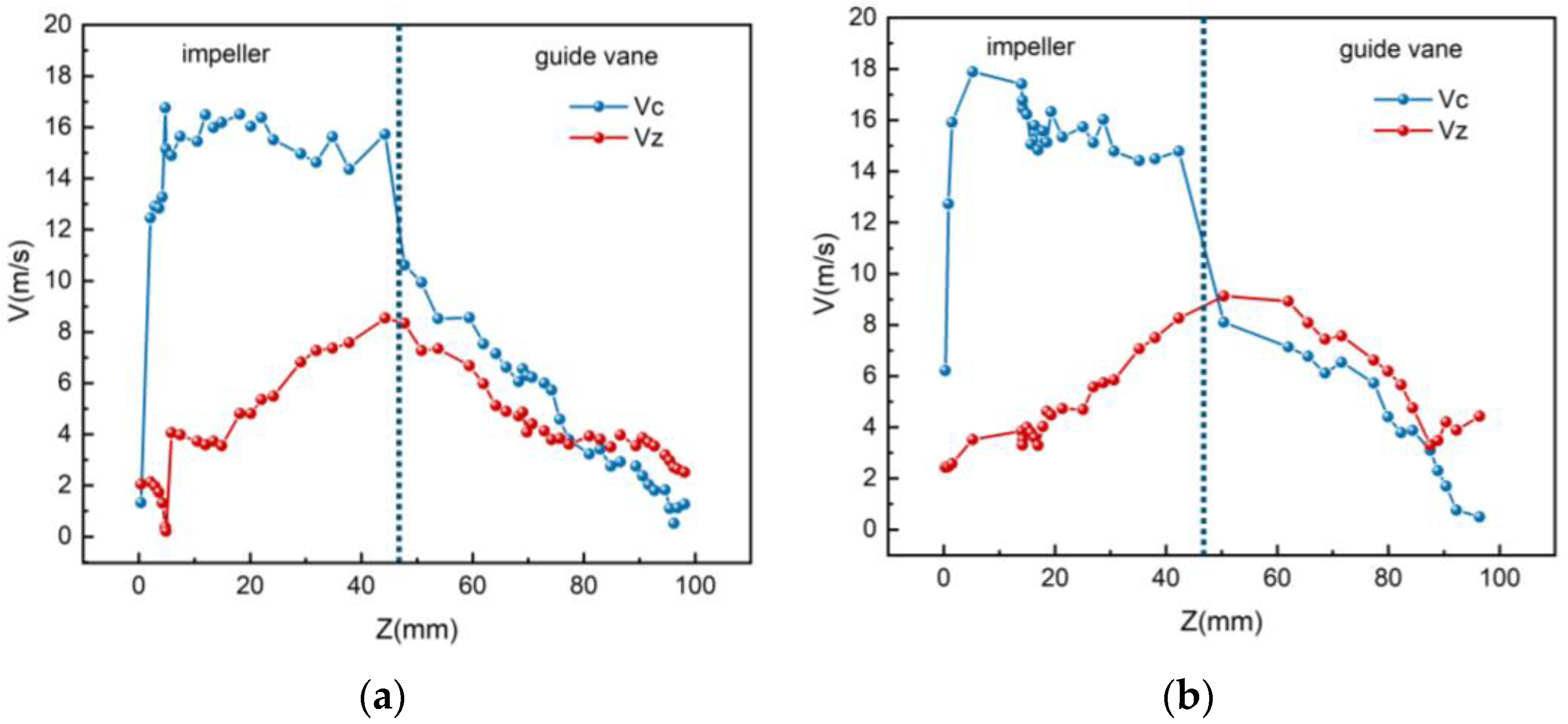
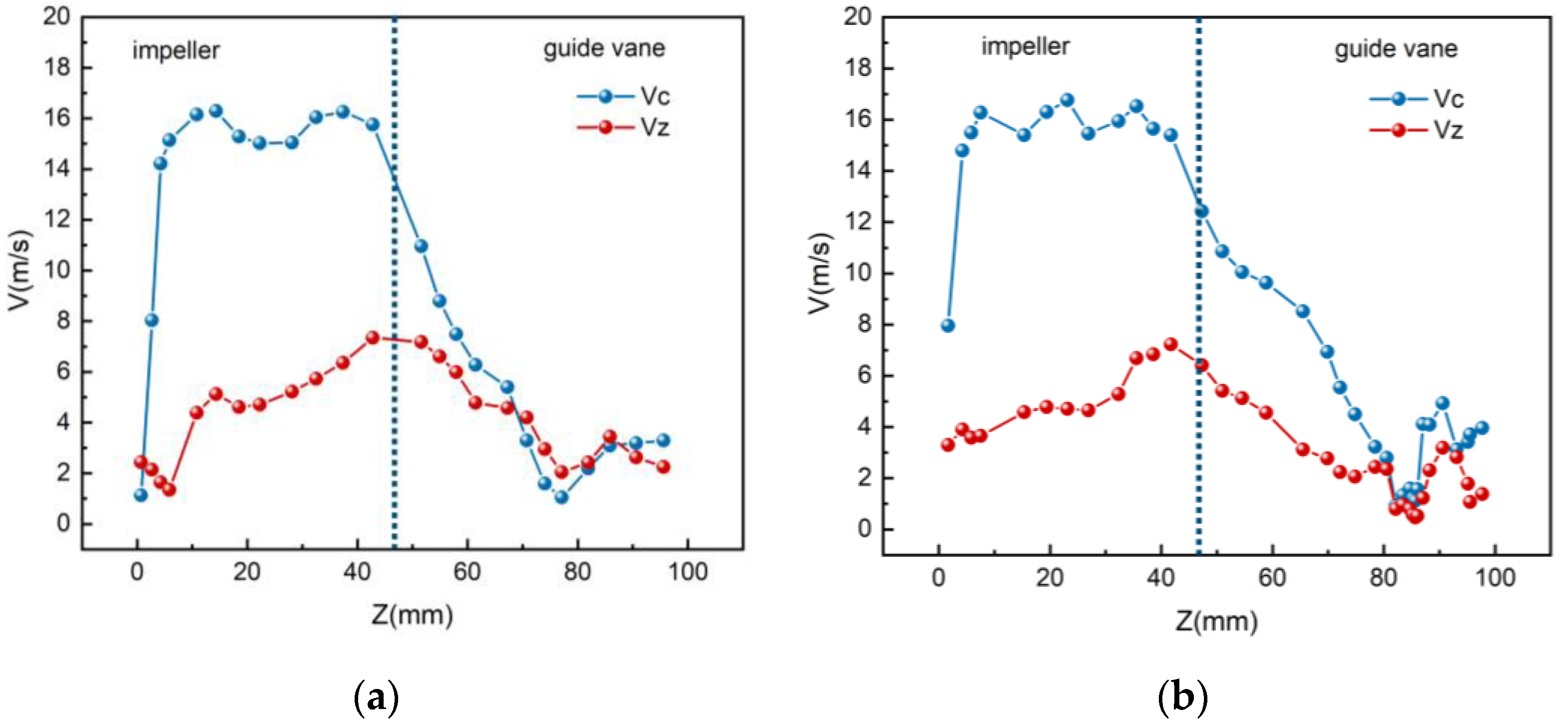
4.2.2. The Velocity Change of the Particles with Different Diameters in the Pressurization Unit
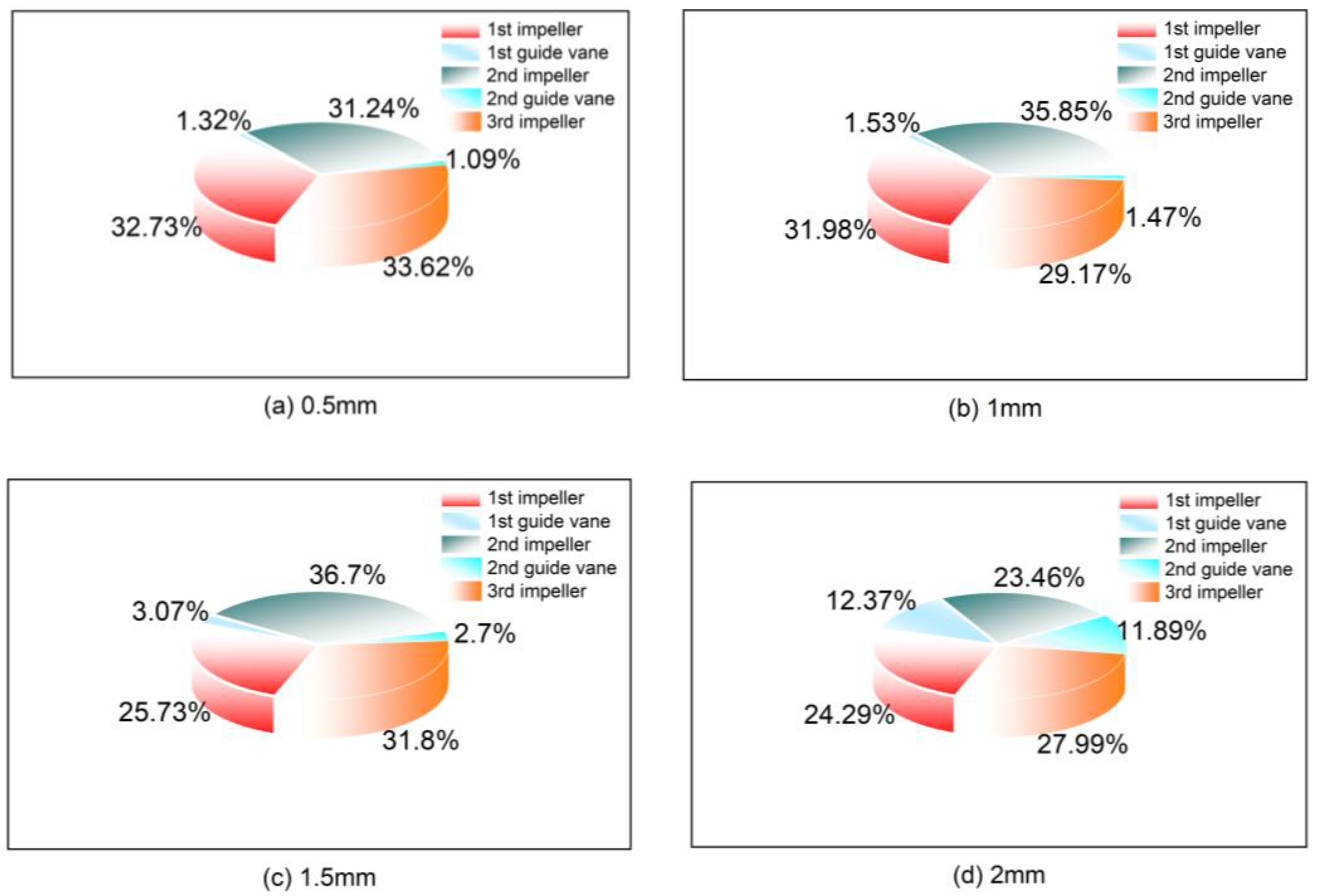
4.3. The Distribution of the Particles in the Pressurization Unit
4.4. Collisions Between Particles and Walls
4.4.1. Collision Distribution of the Particles with Different Diameters in the Pressurization Unit
4.4.2. Particle–Wall Contact Forces at Different Diameters
5. Conclusions
- When the particles enter the guide vanes, the initial spacing between particles is relatively large. Over time, the spacing gradually decreases and becomes uniform, indicating that the particle speed decreases and eventually stabilizes after entering the first stage of the guide vanes. The trajectory angles of the 0.5 mm and 1 mm particles are smaller, while those of 1.5 mm and 2 mm particles are larger and more prone to collision with the wall. This suggests that the coarser particles gain more kinetic energy after passing through the impeller and exhibit worse flow-following behavior.
- The velocity variation patterns of the four different diameter particles in the pressurization unit are similar. After entering the impeller, the particles’ circumferential velocity increases sharply and stabilizes around 15 m/s. Upon leaving the impeller, the circumferential velocity drops sharply, and it gradually decreases after entering the guide vanes. The axial velocity experiences small fluctuations due to dynamic–static interference at the impeller inlet, then increases gradually, reaching its maximum value at the impeller exit, and subsequently decreases after entering the guide vanes.
- The volumetric fraction of the four particle diameters inside the guide vanes is larger than that inside the impeller, with a larger discrepancy in the volumetric fraction within the guide vanes. The volumetric fraction of the particles with a diameter of 1.5 mm or less increases as the particle diameter increases.
- Particles collide more frequently with the impeller wall than with the guide vane wall. As the particle diameter increases, the proportion of collisions with the guide vane wall also increases. For particles of 1.5 mm and smaller, increasing the particle diameter leads to more severe collisions with the impeller wall, but for 2 mm particles, the collision probability decreases due to the reduced number of particles. Inside the guide vanes, as the particle diameter increases, the contact force between the particles and the guide vane wall gradually increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD-DEM | computational fluid dynamics-discrete element method |
| LDV | laser doppler velocimetry |
| PIV | particle image velocimetry |
| DPM | discrete phase model |
| DDPM | dense discrete phase model |
| TFM | two-fluid model |
| Vc | circumferential velocity |
| Vz | axial velocity |
| 1st impeller | first-stage impeller |
| 2nd impeller | second-stage impeller |
| 3rd impeller | third-stage impeller |
| 1st guide vine | first-stage guide vine |
| 2nd guide vine | second-stage guide vine |
References
- Suh, J.-W.; Kim, J.W.; Choi, Y.-S.; Kim, J.-H.; Joo, W.-G.; Lee, K.-Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Pet. Sci. Eng. 2018, 162, 588–601. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, H.-C.; Kim, J.-H.; Choi, Y.-S.; Yoon, J.-Y.; Yoo, I.-S.; Choi, W.-C. Improvement of hydrodynamic performance of a multiphase pump using design of experiment techniques. J. Fluids Eng. 2015, 137, 081301. [Google Scholar] [CrossRef]
- Mehta, M.; Kadambi, J.R.; Sastry, S.; Sankovic, J.; Wernet, M.; Addie, G.; Visintainer, R. Study of particulate flow in the impeller of a slurry pump using PIV. In Proceedings of the Summer Conference, Proceedings of the Heat Transfer, Charlotte, NA, USA, 11–15 July 2004; Volume 46903, pp. 489–499. [Google Scholar]
- Cader, T.; Masbernat, O.; Roco, M.C. LDV measurements in a centrifugal slurry pump: Water and dilute slurry flows. J. Fluids Eng. 1992, 114, 606–615. [Google Scholar] [CrossRef]
- Shi, B.; Wei, J.; Zhang, Y. Phase discrimination and a high accuracy algorithm for PIV image processing of particle–fluid two-phase flow inside high-speed rotating centrifugal slurry pump. Flow Meas. Instrum. 2015, 45, 93–104. [Google Scholar] [CrossRef]
- Shi, B.; Wei, J.; Zhang, Y. A novel experimental facility for measuring internal flow of Solid-liquid two-phase flow in a centrifugal pump by PIV. Int. J. Multiph. Flow 2017, 89, 266–276. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Lin, Z.; He, Z.; Xiang, J.; Su, X. Relationship between wear formation and large-particle motion in a pipe bend. R. Soc. Open Sci. 2019, 6, 181254. [Google Scholar] [CrossRef]
- Wang, K.; Hu, J.; Liu, H.; Zhang, Z.; Zou, L.; Lu, Z. Research on the deposition characteristics of integrated prefabricated pumping station. Symmetry 2020, 12, 760. [Google Scholar] [CrossRef]
- Kadambi, J.R.; Charoenngam, P.; Subramanian, A.; Wernet, M.P.; Sankovic, J.M.; Addie, G.; Courtwright, R. Investigations of particle velocities in a slurry pump using PIV: Part 1, the tongue and adjacent channel flow. J. Energy Resour. Technol. 2004, 126, 271–278. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, J.; Li, G.; Liu, H.; Xiong, W. Numerical simulation of the influence of mixed sand on erosion characteristics of centrifugal pump. Eng. Comput. 2022, 39, 2053–2080. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, L.; Xue, P.; Peng, G.; Zhou, L. Two-way coupling simulation of solid-liquid two-phase flow and wear experiments in a slurry pump. J. Mar. Sci. Eng. 2022, 10, 57. [Google Scholar] [CrossRef]
- Hong, S.; Hu, X. Research on wear characteristics and experiment on internal through-passage components for a new type of deep-sea mining pump. Processes 2021, 10, 58. [Google Scholar] [CrossRef]
- Askaripour, H.; Dehkordi, A.M. Simulation of 3D freely bubbling gas–solid fluidized beds using various drag models: TFM approach. Chem. Eng. Res. Des. 2015, 100, 377–390. [Google Scholar] [CrossRef]
- Shi, W.; Hou, Y.; Zhou, L.; Li, Y.; Xue, S. Numerical simulation and test of performance of deep-well centrifugal pumps with different stages. J. Drain. Irrig. Mach. Eng. 2019, 37, 562–567. [Google Scholar]
- Araoye, A.A.; Badr, H.M.; Ahmed, W.H.; Habib, M.A.; Alsarkhi, A. Erosion of a multistage orifice due to liquid-solid flow. Wear 2017, 390, 270–282. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Deng, L.; Lu, H.; Liu, S.; Hu, Q.; Yang, J.; Kang, Y.; Sun, P. Particle anti-accumulation design at impeller suction of deep-sea mining pump and evaluation by CFD-DEM simulation. Ocean. Eng. 2023, 279, 114598. [Google Scholar] [CrossRef]
- Zhao, R.-J.; Zhao, Y.-L.; Zhang, D.-S.; Li, Y.; Geng, L.-L. Numerical investigation of the characteristics of erosion in a centrifugal pump for transporting dilute particle-laden flows. J. Mar. Sci. Eng. 2021, 9, 961. [Google Scholar] [CrossRef]
- Tang, C.; Yang, Y.-C.; Liu, P.-Z.; Kim, Y.-J. Prediction of abrasive and impact wear due to multi-shaped particles in a centrifugal pump via CFD-DEM coupling method. Energies 2021, 14, 2391. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Li, W.; Zheng, Y.; Li, Y. Research on Two-Phase Flow and Wear of Inlet Pipe Induced by Fluid Prewhirl in a Centrifugal Pump. J. Mar. Sci. Eng. 2024, 12, 950. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, W.; Chen, X.; Cao, G.; Tan, Y.; Xiao, X.; Liu, S.; Yu, Q.; Tong, Z. CFD-DEM simulation research on optimization of spatial attitude of concrete pumping boom based on evaluation of minimum pressure loss. Powder Technol. 2022, 403, 117365. [Google Scholar] [CrossRef]
- Wang, R.; Guan, Y.; Jin, X.; Tang, Z.; Zhu, Z.; Su, X. Impact of Particle Sizes on Flow Characteristics of Slurry Pump for Deep-Sea Mining. Shock. Vib. 2021, 1, 6684944. [Google Scholar] [CrossRef]
- Li, Y.; Liu, D.; Cui, B.; Lin, Z.; Zheng, Y.; Ishnazarov, O. Studying particle transport characteristics in centrifugal pumps under external vibration using CFD-DEM simulation. Ocean. Eng. 2024, 301, 117538. [Google Scholar] [CrossRef]
- Gao, X.; Shi, W.; Shi, Y.; Chang, H.; Zhao, T. DEM-CFD simulation and experiments on the flow characteristics of particles in vortex pumps. Water 2020, 12, 2444. [Google Scholar] [CrossRef]
- Deng, L.; Hu, Q.; Chen, J.; Kang, Y.; Liu, S. Particle distribution and motion in six-stage centrifugal pump by means of slurry experiment and CFD-DEM simulation. J. Mar. Sci. Eng. 2021, 9, 716. [Google Scholar] [CrossRef]
- Su, X.; Tang, Z.; Li, Y.; Zhu, Z.; Mianowicz, K.; Balaz, P. Research of particle motion in a two-stage slurry transport pump for deep-ocean mining by the CFD-DEM method. Energies 2020, 13, 6711. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.; Cao, G.; Tan, Y.; Xiao, X.; Zhou, Y.; Liu, S.; Tong, Z.; Wu, Y. Optimization of fresh concrete pumping pressure loss with CFD-DEM approach. Constr. Build. Mater. 2021, 276, 122204. [Google Scholar] [CrossRef]
- Huang, S.; Su, X.; Qiu, G. Transient numerical simulation for solid-liquid flow in a centrifugal pump by DEM-CFD coupling. Eng. Appl. Comput. Fluid Mech. 2015, 9, 411–418. [Google Scholar] [CrossRef]
- Zhu, Z.; Sun, J.; Lin, Z.; Jin, Y.; Li, Y. Characterization of the ellipsoidal particle motion in a two-stage lifting pump using CFD-DEM method. Comput. Part. Mech. 2024, 1–16. [Google Scholar] [CrossRef]

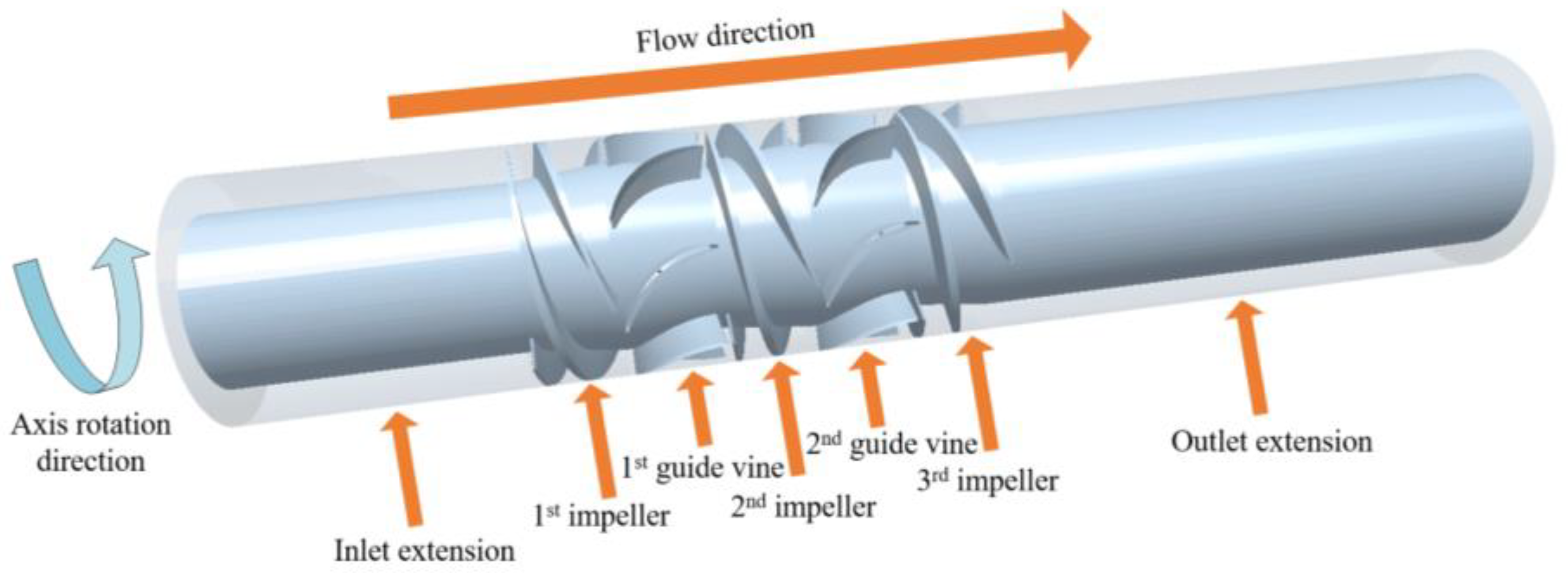


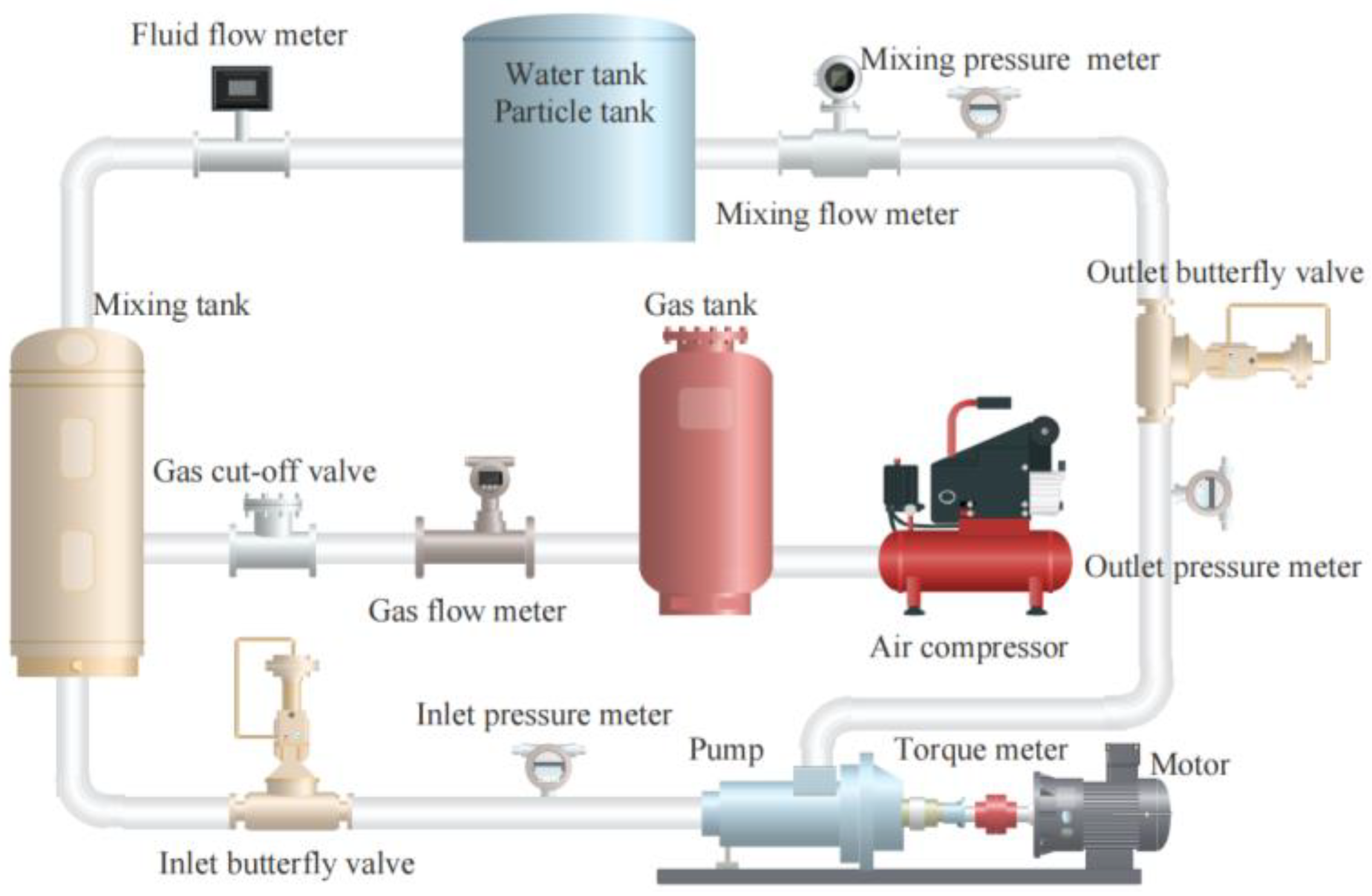


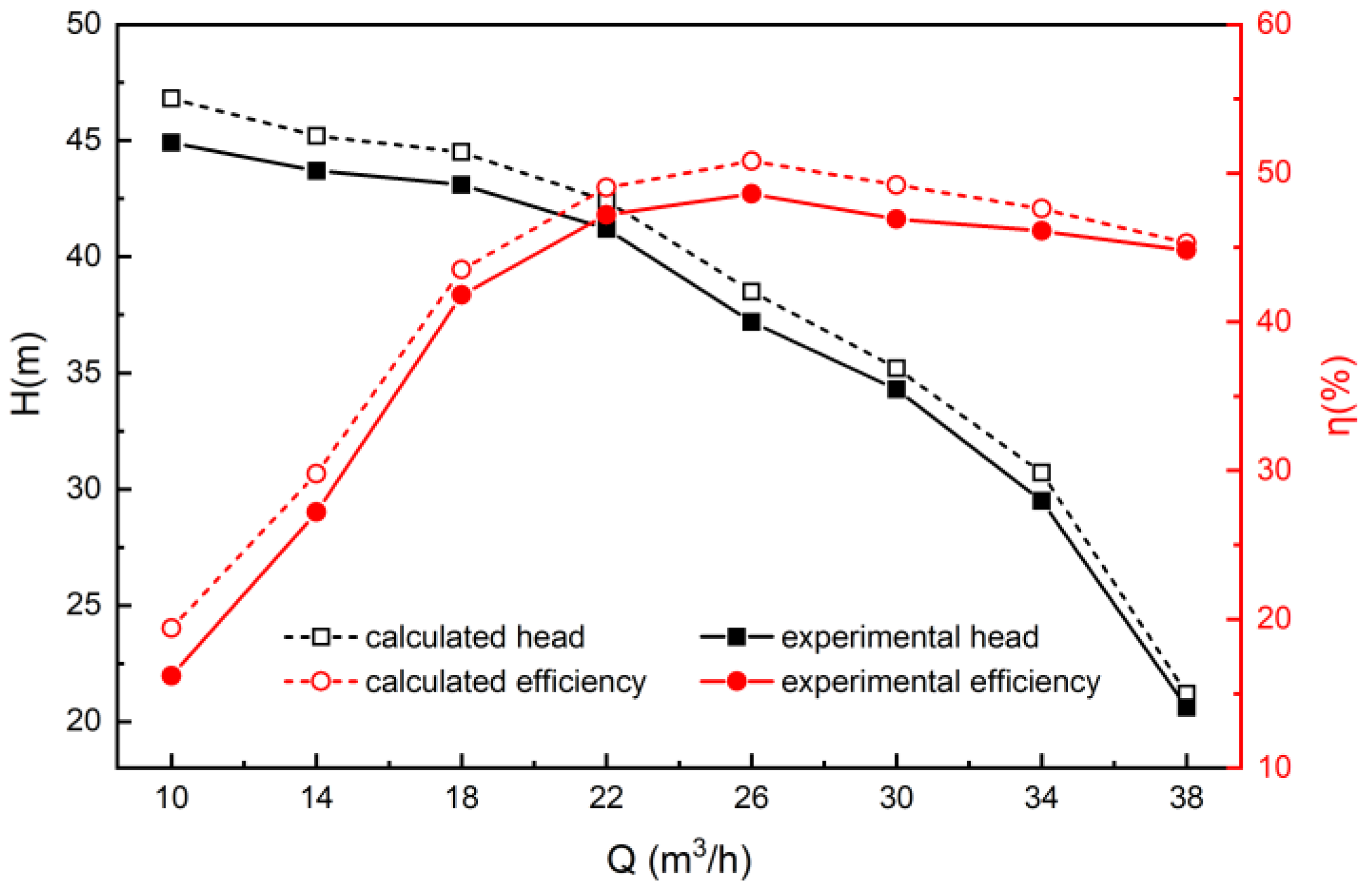

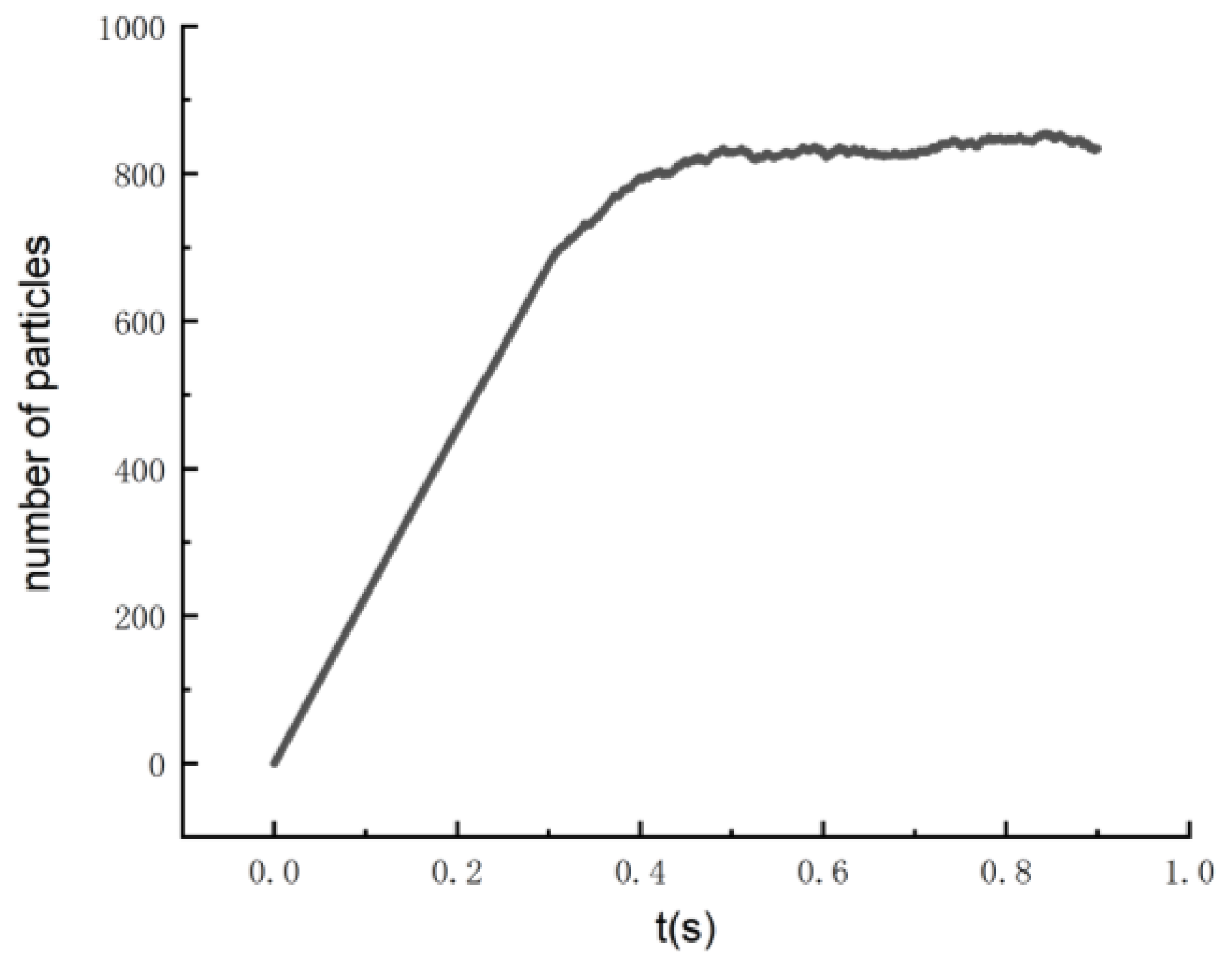





| Design Parameter | Sign | Value | Unit |
|---|---|---|---|
| number of impeller blades | 3 | -- | |
| number of guide vane blades | 7 | -- | |
| the diameter of impeller | 126 | mm | |
| hub ratio | 0.7 | -- | |
| the diameter of impeller inlet hub | 88.4 | mm | |
| the diameter of impeller outlet hub | 98.6 | mm | |
| axial length of impeller | 46.77 | mm | |
| axial length of guide vane | 51.65 | mm | |
| wrap angle of impeller blade | 212 | ||
| wrap angle of guide vane blade | 35 |
| Scheme | Mesh Number | Head (m) | Efficiency (%) |
|---|---|---|---|
| Scheme 1 | 2,984,275 | 33.54 | 47.78 |
| Scheme 2 | 3,872,589 | 34.83 | 48.27 |
| Scheme 3 | 4,389,807 | 36.01 | 49.56 |
| Scheme 4 | 4,789,758 | 36.2 | 49.39 |
| Collision Coefficient | Particle–Particle | Particle–Wall |
|---|---|---|
| Restitution | 0.45 | 0.48 |
| Static friction | 0.28 | 0.16 |
| Rolling friction | 0.01 | 0.01 |
| Test Instrument | Range | Accuracy | Unit |
|---|---|---|---|
| Inlet pressure meter | 0–1.6 | ±0.25% | MPa |
| Outlet pressure meter | 0–1.6 | ±0.25% | MPa |
| Fluid flow meter | 0–50 | ±0.25% | m3/h |
| Torque meter | 0–30 | ±0.25% | Nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Yang, X.; Li, B.; Chai, H.; Qin, H. Research on Particle Motion Characteristics in a Spiral-Vane-Type Multiphase Pump Based on CFD-DEM. J. Mar. Sci. Eng. 2025, 13, 845. https://doi.org/10.3390/jmse13050845
Shi G, Yang X, Li B, Chai H, Qin H. Research on Particle Motion Characteristics in a Spiral-Vane-Type Multiphase Pump Based on CFD-DEM. Journal of Marine Science and Engineering. 2025; 13(5):845. https://doi.org/10.3390/jmse13050845
Chicago/Turabian StyleShi, Guangtai, Xi Yang, Binyan Li, Hongqiang Chai, and Hao Qin. 2025. "Research on Particle Motion Characteristics in a Spiral-Vane-Type Multiphase Pump Based on CFD-DEM" Journal of Marine Science and Engineering 13, no. 5: 845. https://doi.org/10.3390/jmse13050845
APA StyleShi, G., Yang, X., Li, B., Chai, H., & Qin, H. (2025). Research on Particle Motion Characteristics in a Spiral-Vane-Type Multiphase Pump Based on CFD-DEM. Journal of Marine Science and Engineering, 13(5), 845. https://doi.org/10.3390/jmse13050845






