Observations and Predictions of Wave Runup, Extreme Water Levels, and Medium-Term Dune Erosion during Storm Conditions
Abstract
:1. Introduction
2. Geomorphological and Hydrodynamic Setting


3. Methods
3.1. Monitoring of Dune Morphological Changes
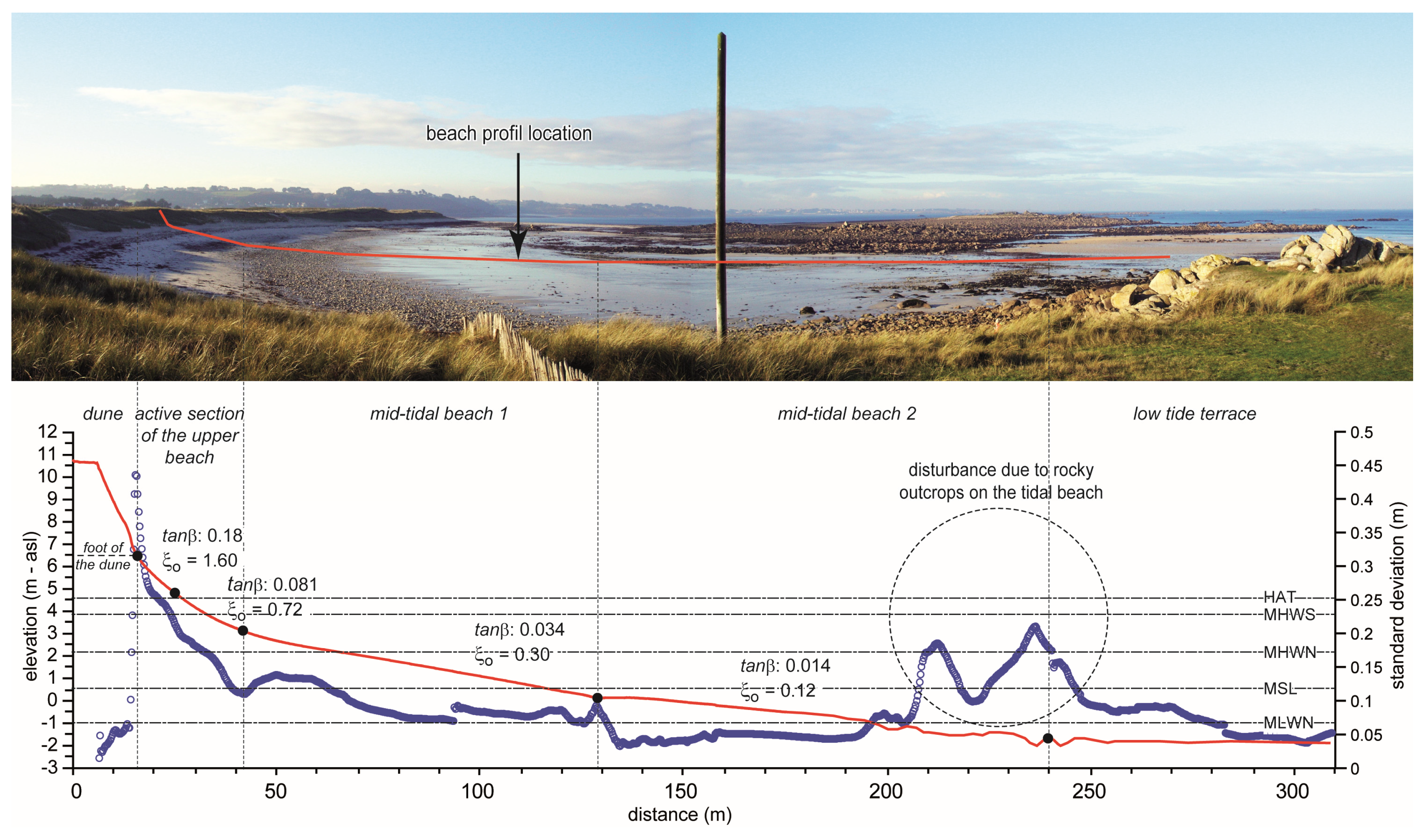
3.2. Survey of Beach Profile and Maximum Swash Elevation (Runup) Rmax

| Date | Hm0 (m) | Tm0,–1 (s) | L0 (m) | Slope (tanβ) | ξ0 | Rmax (m) | HTWL (m) |
|---|---|---|---|---|---|---|---|
| 08 April 2008 | 0.6 | 8.1 | 101 | 0.118 | 1.502 | 0.95 | 4.36 |
| 29 August 2008 | 1.0 | 8.3 | 107 | 0.061 | 0.623 | 0.30 | 3.10 |
| 29 September 2008 | 0.8 | 7.5 | 88 | 0.093 | 1.004 | 0.74 | 3.80 |
| 12 January 2009 | 3.6 | 12.9 | 261 | 0.096 | 0.825 | 3.24 | 4.01 |
| 13 February 2009 | 1.8 | 11.0 | 188 | 0.107 | 1.111 | 1.46 | 4.14 |
| 29 April 2009 | 1.7 | 8.7 | 119 | 0.071 | 0.591 | 0.93 | 3.37 |
| 17 December 2009 | 0.8 | 10.0 | 156 | 0.080 | 1.100 | 0.75 | 3.56 |
| 22 December 2009 | 1.0 | 8.0 | 101 | 0.067 | 0.680 | 0.67 | 3.22 |
| 23 December 2009 | 1.0 | 7.9 | 98 | 0.056 | 0.559 | 0.64 | 2.97 |
| 30 December 2009 | 1.6 | 10.5 | 171 | 0.073 | 0.749 | 1.11 | 3.40 |
| 04 January 2010 | 1.6 | 8.3 | 107 | 0.110 | 0.906 | 1.06 | 4.19 |
| 07 January 2010 | 2.3 | 6.6 | 69 | 0.058 | 0.319 | 0.69 | 3.09 |
| 13 January 2010 | 2.8 | 11.6 | 210 | 0.054 | 0.462 | 1.36 | 3.03 |
| 14 January 2010 | 2.6 | 11.8 | 217 | 0.069 | 0.635 | 1.43 | 3.36 |
| 16 January 2010 | 2.3 | 11.9 | 223 | 0.091 | 0.903 | 1.52 | 3.83 |
| 21 January 2010 | 2.8 | 12.9 | 261 | 0.054 | 0.525 | 1.40 | 3.04 |
| 28 January 2010 | 2.0 | 7.5 | 88 | 0.049 | 0.324 | 0.89 | 2.86 |
| 01 February 2010 | 1.5 | 6.6 | 68 | 0.123 | 0.837 | 1.57 | 4.53 |
| 03 February 2010 | 1.8 | 7.6 | 90 | 0.111 | 0.781 | 1.63 | 4.23 |
| 05 February 2010 | 2.9 | 11.5 | 207 | 0.068 | 0.570 | 1.14 | 3.35 |
| 05 February 2010 | 4.5 | 13.5 | 285 | 0.049 | 0.393 | 1.75 | 2.95 |
| 06 February 2010 | 4.1 | 12.0 | 226 | 0.039 | 0.293 | 1.02 | 2.41 |
| 26 February 2010 | 2.1 | 6.0 | 56 | 0.065 | 0.336 | 1.01 | 3.24 |
| 28 February 2010 | 1.5 | 5.6 | 50 | 0.124 | 0.710 | 1.50 | 4.56 |
| 03 March 2010 | 1.1 | 5.7 | 50 | 0.127 | 0.846 | 1.26 | 4.62 |
| 29 March 2010 | 1.2 | 7.6 | 89 | 0.113 | 0.965 | 1.08 | 4.28 |
| 31 March 2010 | 4.5 | 9.2 | 132 | 0.114 | 0.616 | 3.47 | 4.52 |
| 10 June 2010 | 1.3 | 6.2 | 61 | 0.051 | 0.347 | 0.47 | 2.87 |
| 13 July 2010 | 1.1 | 8.6 | 116 | 0.097 | 0.991 | 0.64 | 3.89 |
| 12 October 2010 | 1.8 | 6.3 | 62 | 0.082 | 0.482 | 0.63 | 3.61 |
| 08 November 2010 | 2.6 | 7.3 | 82 | 0.115 | 0.648 | 1.67 | 4.39 |
| 05 July 2012 | 1.7 | 9.2 | 132 | 0.097 | 0.847 | 1.50 | 3.95 |
| 02 October 2012 | 2.6 | 10.7 | 180 | 0.086 | 0.712 | 1.97 | 3.73 |
| 17 October 2012 | 3.6 | 12.5 | 246 | 0.123 | 1.018 | 3.36 | 4.63 |
| 02 November 2012 | 2.8 | 8.9 | 123 | 0.080 | 0.531 | 1.58 | 3.60 |
| 06 November 2012 | 1.5 | 6.8 | 72 | 0.033 | 0.225 | 0.57 | 2.24 |
| 12 November 2012 | 1.9 | 9.7 | 146 | 0.078 | 0.686 | 1.73 | 3.52 |
| 19 November 2012 | 1.6 | 9.3 | 134 | 0.076 | 0.697 | 1.44 | 3.46 |
| 23 November 2012 | 3.3 | 11.5 | 205 | 0.039 | 0.306 | 1.00 | 2.45 |
| 26 November 2012 | 2.4 | 8.5 | 112 | 0.065 | 0.440 | 1.06 | 3.25 |
| 30 November 2012 | 1.0 | 9.6 | 144 | 0.077 | 0.903 | 0.10 | 3.49 |
| 03 December 2012 | 3.0 | 10.4 | 170 | 0.058 | 0.434 | 1.51 | 3.13 |
| 06 December 2012 | 1.7 | 10.0 | 157 | 0.036 | 0.337 | 1.27 | 2.39 |
| 11 December 2012 | 1.1 | 7.6 | 89 | 0.063 | 0.575 | 0.68 | 3.15 |
| 13 December 2012 | 0.8 | 10.8 | 183 | 0.107 | 1.584 | 1.21 | 4.13 |
| 14 December 2012 | 1.8 | 11.3 | 198 | 0.125 | 1.304 | 2.48 | 4.64 |
| 17 December 2012 | 4.8 | 12.2 | 233 | 0.097 | 0.678 | 3.38 | 4.14 |
| 07 January 2013 | 1.8 | 10.8 | 181 | 0.034 | 0.337 | 0.58 | 2.25 |
| 08 January 2013 | 1.8 | 10.8 | 184 | 0.038 | 0.384 | 0.55 | 2.50 |
| 09 January 2013 | 1.8 | 12.1 | 227 | 0.053 | 0.596 | 0.47 | 2.92 |
| 16 January 2013 | 1.1 | 6.7 | 71 | 0.098 | 0.774 | 1.05 | 3.91 |
| 23 January 2013 | 4.0 | 13.1 | 266 | 0.038 | 0.312 | 1.54 | 2.33 |
| 24 January 2013 | 2.4 | 10.9 | 187 | 0.041 | 0.362 | 1.07 | 2.63 |
| 25 January 2013 | 2.1 | 11.2 | 195 | 0.053 | 0.502 | 0.85 | 2.95 |
| 27 January 2013 | 3.1 | 10.1 | 160 | 0.089 | 0.635 | 2.11 | 3.81 |
| 28 January 2013 | 5.1 | 13.9 | 301 | 0.074 | 0.567 | 3.25 | 3.68 |
| 29 January 2013 | 5.0 | 14.3 | 318 | 0.089 | 0.708 | 3.91 | 3.98 |
| 04 February 2013 | 2.7 | 9.4 | 139 | 0.038 | 0.270 | 1.01 | 2.43 |
| 05 February 2013 | 5.7 | 11.9 | 220 | 0.039 | 0.241 | 1.35 | 2.20 |
| 06 February 2013 | 6.1 | 12.4 | 242 | 0.040 | 0.251 | 1.50 | 2.29 |
| 07 February 2013 | 3.3 | 9.3 | 136 | 0.040 | 0.259 | 1.09 | 2.53 |
| 14 February 2013 | 3.1 | 10.2 | 163 | 0.094 | 0.678 | 1.83 | 3.93 |
| 19 February 2013 | 1.8 | 12.5 | 242 | 0.031 | 0.361 | 0.65 | 1.60 |
| 21 February 2013 | 1.5 | 7.4 | 87 | 0.032 | 0.240 | 0.99 | 1.87 |
| 22 February 2013 | 1.9 | 8.5 | 112 | 0.034 | 0.266 | 0.54 | 2.30 |
| 04 March 2013 | 0.9 | 5.6 | 49 | 0.057 | 0.422 | 0.12 | 2.99 |
| 05 March 2013 | 0.5 | 4.8 | 36 | 0.042 | 0.359 | 0.22 | 2.63 |
| 10 March 2013 | 1.5 | 12.7 | 250 | 0.095 | 1.211 | 1.43 | 3.89 |
| 14 March 2013 | 1.2 | 5.5 | 48 | 0.104 | 0.656 | 0.98 | 4.04 |
| 28 March 2013 | 0.9 | 7.2 | 82 | 0.109 | 1.038 | 0.98 | 4.17 |
| 29 March 2013 | 0.9 | 6.8 | 73 | 0.116 | 1.058 | 0.86 | 4.32 |
| 08 April 2013 | 1.9 | 11.1 | 191 | 0.081 | 0.814 | 1.24 | 3.57 |
| 09 April 2013 | 2.0 | 8.4 | 111 | 0.099 | 0.734 | 1.19 | 3.98 |
| 07 May 2013 | 1.7 | 12.4 | 241 | 0.062 | 0.747 | 0.95 | 3.15 |
| 09 May 2013 | 2.4 | 9.0 | 126 | 0.076 | 0.546 | 1.51 | 3.50 |
| 23 May 2013 | 1.5 | 6.8 | 73 | 0.063 | 0.438 | 0.84 | 3.17 |
| 23 May 2013 | 2.2 | 6.4 | 65 | 0.072 | 0.396 | 1.09 | 3.40 |
| 24 May 2013 | 1.8 | 6.2 | 60 | 0.077 | 0.440 | 1.17 | 3.49 |
| 25 May 2013 | 2.1 | 6.3 | 63 | 0.086 | 0.466 | 1.32 | 3.71 |
| 27 May 2013 | 0.6 | 7.6 | 91 | 0.104 | 1.246 | 1.04 | 4.04 |
| 12 June 2013 | 1.6 | 8.2 | 106 | 0.060 | 0.499 | 1.02 | 3.10 |
| 13 June 2013 | 2.8 | 9.3 | 135 | 0.049 | 0.344 | 0.99 | 2.92 |
| 14 June 2013 | 1.4 | 8.6 | 114 | 0.045 | 0.405 | 1.08 | 2.73 |
| 18 June 2013 | 0.9 | 9.1 | 128 | 0.034 | 0.408 | 0.10 | 2.39 |
| 19 June 2013 | 1.9 | 7.8 | 94 | 0.035 | 0.249 | 0.14 | 2.36 |
| 20 June 2013 | 1.9 | 7.9 | 97 | 0.043 | 0.305 | 0.45 | 2.69 |
| 21 June 2013 | 1.6 | 9.4 | 138 | 0.057 | 0.530 | 0.91 | 3.02 |
| 23 June 2013 | 3.8 | 9.9 | 154 | 0.091 | 0.578 | 1.89 | 3.91 |
| 24 June 2013 | 2.7 | 8.9 | 124 | 0.089 | 0.605 | 1.89 | 3.79 |
| 25 June 2013 | 1.1 | 7.8 | 95 | 0.096 | 0.911 | 0.78 | 3.89 |
3.3. Hydrodynamic Condition Measurements


| Date and High Tide Time | Tide Coefficient | Predicted Tide Level (m) | Observed Tide Level (m) | Surge (m) |
|---|---|---|---|---|
| 17/09/2012—(17:25) | 104 | 4.3 | 4.34 | 0.04 |
| 18/09/2012—(18:15) | 106 | 4.29 | 4.27 | −0.02 |
| 19/09/2012—(06:20) | 103 | 4.13 | 4.07 | −0.06 |
| 16/10/2012—(10:30) | 107 | 4.27 | ||
| 17/10/2012—(05:20) | 109 | 4.36 | 4.73 | 0.37 |
| 18/10/2012—(06:05) | 105 | 4.29 | 4.55 | 0.26 |
| 14/11/2012—(04:15) | 104 | 4.26 | 4.22 | −0.04 |
| 15/11/2012—(05:00) | 107 | 4.40 | 4.35 | −0.05 |
| 16/11/2012—(05:55) | 104 | 4.36 | 4.39 | 0.03 |
| 14/12/2012—(04:50) | 104 | 4.32 | 4.66 | 0.34 |
| 15/12/2012—(05:40) | 104 | 4.38 | 4.58 | 0.20 |
| 12/01/2013—(04:30) | 102 | 4.23 | 4.38 | 0.15 |
| 13/01/2013—(05:20) | 106 | 4.39 | 4.42 | 0.03 |
| 14/01/2013—(06:11) | 104 | 4.37 | 4.31 | −0.04 |
| 11/02/2013—(05:11) | 106 | 4.33 | 4.42 | 0.09 |
| 12/02/2013—05:52) | 106 | 4.35 | 4.32 | −0.03 |
| 12/03/2013—(04:50) | 102 | 4.14 | ||
| 13/03/2013—(05:27) | 103 | 4.16 | 4.26 | 0.1 |
| 28/03/2013—(17:20) | 103 | 4.06 | 4.22 | 0.16 |
| 29/03/2013—(05:40) | 105 | 4.16 | 4.32 | 0.16 |
| 26/04/2013—(16:55) | 103 | 4.12 | 4.05 | −0.07 |
| 27/04/2013—(17:35) | 106 | 4.18 | 4.15 | −0.03 |
| 26/05/2013—(17:20) | 104 | 4.2 | 4.22 | 0.02 |
| 27/05/2013—(18:15) | 104 | 4.16 | 4.31 | 0.15 |
| 24/06/2013—(17:15) | 102 | 4.22 | 4.16 | −0.06 |
| 25/06/2013—(18:00) | 105 | 4.27 | ||
| 26/06/2013—(18:49) | 103 | 4.15 |
4. Results
4.1. Calibration of Battjes (1971) Runup Formula

4.2. Elaboration of a General Empirical Equation


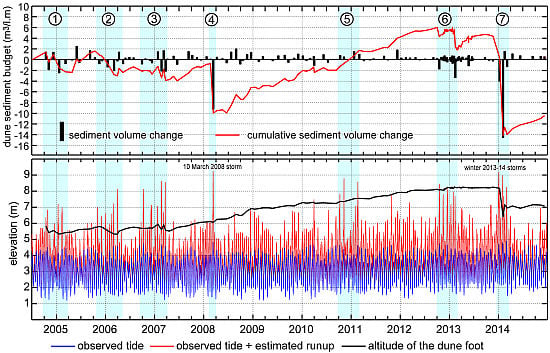
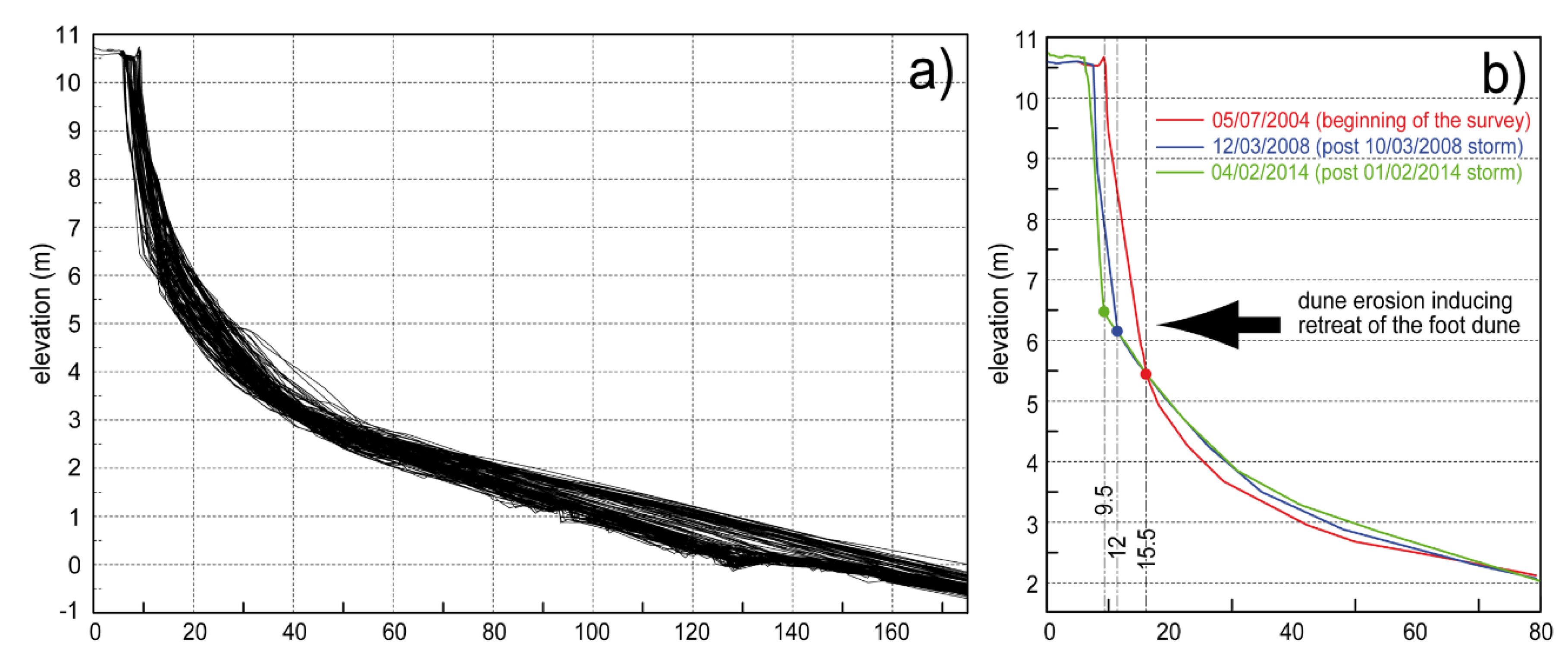
4.3. Long-Term Dune Changes Related to Storm Event Erosion and Recover


5. Discussion

6. Conclusions
- -
- The methodological approach of measuring the maximum swash elevation using wrack deposit and/or the limit of the water mark in the field is relatively easy to implement and requires much less post-treatment compared to classic video measurements. However, this method is extremely time consuming and does not allow for collection of a large dataset, which notably limits the statistical analysis.
- -
- This experiment confirms that the beach slope scaled with ξ0 plays a key role in the parameterization of the runup equation when the morphodynamic context of the beach is shifting from intermediate to reflective according to high–neap or spring–tide water level. In this context, beach slope may be much more important in runup elevation distribution than a wave component such as H0 or L0.
- -
- In comparison to the previous study of Cariolet and Suanez, the use of observed water level changes due to astronomical tide and/or storm surges for the calculation of beach slope gives better results (RMSE decreasing from 0.33 to 0.29 m for Equations (8) and (10), respectively). This is explained by the fact that both the upper and lower bounds defining the beach section on which the slope is calculated are shifting according to the sea level changes. Therefore, the slope values obtained are much more fair and accurate, especially when the beach profile is concave and tidal range is large (≈7 m), as is the case in this study.
- -
- Taking into account the environmental conditions and dimensional swash parameters of the Vougot beach, the Stockdon’s Equations (4)–(6) [21] may also be used with the appropriate beach slope value βƒ.
- -
- Dune retreat, and hence volume of sand eroded, depends on extreme water level (and therefore the frequency and intensity of each runup event) when its height is greater than that the toe of the dune.
- -
- A good relationship seems to be revealed between erosion phases of the dune due to high extreme water levels and NAO+. In contrast, NAO− is associated to phases of dune recovery during cold and non-stormy winters.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| asl | above sea level |
| IGN | Institut Géographique National |
| MHWS | Mean High Water Spring |
| HAT | Highest Astronomical Tide |
| MHWN | Mean High Water Neap |
| NAO | North Atlantic Oscillation |
| NGF | Nivellement Général Français |
| RMSE | Root Mean Square Error |
| SHOM | Service Hydrographique et Océanographique de la Marine |
| WW3 | WAVEWATCH III model |
References
- Battjes, J.A. Run-up distributions of waves breaking on slopes. J. Waterw. Harb. Coast. Eng. Div. ASCE 1971, 97, 91–114. [Google Scholar]
- Edelman, T.I. Dune erosion during storm conditions. In Proceedings of the 11th Conference on Coastal Engineering, London, UK, September 1968; pp. 719–722.
- Van der Meulen, T.; Gourlay, M.R. Beach and dune erosion tests. In Proceedings of the 11th Conference on Coastal Engineering, London, UK, September 1968; pp. 701–707.
- Edelman, T. Dune erosion during storm conditions. In Proceedings of the 13th Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 1305–1311.
- Van de Graaff, J. Dune erosion during a storm surge. Coast. Eng. 1977, 1, 99–134. [Google Scholar] [CrossRef]
- Van de Graaff, J. Probabilistic design of dunes; an example from the Netherlands. Coast. Eng. 1986, 9, 479–500. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Sallenger, A.H.; Holman, R.A.; Howd, P.A. A simple model for the spatially-variable coastal response to hurricanes. Mar. Geol. 2007, 238, 1–20. [Google Scholar] [CrossRef]
- Vellinga, P. Beach and dune erosion during storm surges. Coast. Eng. 1982, 6, 361–387. [Google Scholar] [CrossRef]
- Fisher, J.S.; Overton, M.F. Numerical model for dune erosion due to wave uprush. In Proceedings of the 19th Coastal Engineering Conference, Houston, TX, USA, 3–7 September 1984; pp. 1553–1558.
- Kriebel, D.L.; Dean, R.G. Numerical simulation of time-dependent beach and dune erosion. Coast. Eng. 1985, 9, 221–245. [Google Scholar] [CrossRef]
- Kriebel, D.L. Verification study of a dune erosion model. Shore Beach 1986, 54, 13–21. [Google Scholar]
- Overton, M.; Fisher, J.; Young, M. Laboratory Investigation of Dune Erosion. J. Waterw. Port. Coast. Ocean Eng. 1988, 114, 367–373. [Google Scholar] [CrossRef]
- Carter, R.W.G.; Stone, G.W. Mechanisms associated with the erosion of sand dune cliffs, Magilligan, Northern Ireland. Earth Surf. Process. Landf. 1989, 14, 1–10. [Google Scholar] [CrossRef]
- Pye, K.; Neal, A. Coastal dune erosion at Formby Point, north Merseyside, England: Causes and Mechanisms. Mar. Geol. 1994, 119, 39–56. [Google Scholar] [CrossRef]
- Larson, M.; Erikson, L.; Hanson, H. An analytical model to predict dune erosion due to wave impact. Coast. Eng. 2004, 51, 675–696. [Google Scholar] [CrossRef]
- Erikson, L.H.; Larson, M.; Hanson, H. Laboratory investigation of beach scarp and dune recession due to notching and subsequent failure. Mar. Geol. 2007, 245, 1–19. [Google Scholar] [CrossRef]
- Claudino-Sales, V.; Wang, P.; Horwitz, M.H. Factors controlling the survival of coastal dunes during multiple hurricane impacts in 2004 and 2005: Santa Rosa barrier island, Florida. Geomorphology 2008, 95, 295–315. [Google Scholar] [CrossRef]
- Sallenger, A.H. Storm impact scale for barrier islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Ruggiero, P.; Komar, P.D.; McDougal, W.G.; Marra, J.J.; Beach, R.A. Wave runup, extreme water levels and erosion of properties backing beaches. J. Coast. Res. 2001, 17, 407–419. [Google Scholar]
- Pye, K.; Blott, S.J. Decadal-scale variation in dune erosion and accretion rates: An investigation of the significance of changing storm tide frequency and magnitude on the Sefton coast, UK. Geomorphology 2008, 102, 652–666. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Wassing, F. Model Investigation on Wave Run-Up Carried Out in the Netherland during the Past Twenty Years; Amer. Soc. Civil Engrs: Gainesville, FL, USA, 1957; Volume 6, pp. 700–714. [Google Scholar]
- Hunt, I.A. Design of seawalls and breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. Ocean. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Holman, R.A. Extreme value statistics for wave run-up on a natural beach. Coast. Eng. 1986, 9, 527–544. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stress and mass transport in gravity waves, with application to. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf similarity. In Proceedings of the 14th Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; pp. 466–480.
- Holman, R.A.; Sallenger, A.H. Setup and swash on a natural beach. J. Geophys. Res. Ocean 1985, 90, 945–953. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Kleinhans, M.G.; van den Beukel, P.G.L. Observations of swash under highly dissipative conditions. J. Geophys. Res. 1998, 103, 3111–3118. [Google Scholar] [CrossRef]
- Ruggiero, P.; Holman, R.A.; Beach, R.A. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Mase, H. Random Wave Runup Height on Gentle Slope. J. Waterw. Port Coast. Ocean Eng. 1989, 115, 649–661. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave Runup Distributions on Natural Beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Cariolet, J.-M.; Suanez, S. Runup estimations on a macrotidal sandy beach. Coast. Eng. 2013, 74, 11–18. [Google Scholar] [CrossRef]
- Guilcher, A.; Hallégouët, B. Coastal Dunes in Brittany and Their Management. J. Coast. Res. 1991, 7, 517–533. [Google Scholar]
- Suanez, S.; Cariolet, J.-M.; Fichaut, B. Monitoring of recent morphological changes of the dune of Vougot beach (Brittany, France) using differential GPS. Shore Beach 2010, 78, 37–47. [Google Scholar]
- Suanez, S.; Cariolet, J.-M. L’action des tempêtes sur l’érosion des dunes : Les enseignements de la tempête du 10 mars 2008. Norois 2010, 215, 77–99. [Google Scholar] [CrossRef] [Green Version]
- Suanez, S.; Cariolet, J.-M.; Cancouët, R.; Ardhuin, F.; Delacourt, C. Dune recovery after storm erosion on a high-energy beach: Vougot Beach, Brittany (France). Geomorphology 2012, 139–140, 16–33. [Google Scholar] [CrossRef]
- Blaise, E.; Suanez, S.; Stéphan, P.; Fichaut, B.; David, L.; Cuq, V.; Autret, R.; Houron, J.; Rouan, M.; Floc’h, F.; et al. Bilan des tempêtes de l’hiver 2013–2014 sur la dynamique de recul du trait de côte en Bretagne. Géomorphol. Relief Process. Environ. 2015, in press. [Google Scholar]
- Senechal, N.; Coco, G.; Bryan, K.R.; Holman, R.A. Wave runup during extreme storm conditions. J. Geophys. Res. Ocean 2011, 116. [Google Scholar] [CrossRef]
- Rascle, N.; Ardhuin, F. A global wave parameter database for geophysical applications. Part 2: Model validation with improved source term parameterization. Ocean Model. 2013, 70, 174–188. [Google Scholar] [CrossRef]
- Roland, A.; Ardhuin, F. On the developments of spectral wave models: Numerics and parameterizations for the coastal ocean. Ocean Dyn. 2014, 64, 833–846. [Google Scholar] [CrossRef]
- De Bakker, A.T.M.; Tissier, M.F.S.; Ruessink, B.G. Shoreline dissipation of infragravity waves. Cont. Shelf Res. 2014, 72, 73–82. [Google Scholar] [CrossRef]
- Mayer, R.H.; Kriebel, D.L. Wave runup on composite-slope and concave beaches. In Proceedings of the 24th Coastal Engineering Conference, ASCE, Kobe, Japan, 23–28 October 1994; pp. 2325–2339.
- McCallum, E.; Norris, W.J.T. The storms of January and February 1990. Meteorol. Mag. 1990, 119, 201–210. [Google Scholar]
- Betts, N.L.; Orford, J.D.; White, D.; Graham, C.J. Storminess and surges in the South-Western Approaches of the eastern North Atlantic: The synoptic climatology of recent extreme coastal storms. Mar. Geol. 2004, 210, 227–246. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujan, S.; Splinter, K.D.; Robinet, A.; Sénéchal, N.; Ferreira, S. Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments. Geomorphology 2015, 238, 135–148. [Google Scholar] [CrossRef]
- NOAA’s Climate Prediction Center Home Page. Available online: http://www.cpc.ncep.noaa.gov (accessed on 7 February 2015).
- Masselink, G.; Austin, M.; Scott, T.; Poate, T.; Russell, P. Role of wave forcing, storms and NAO in outer bar dynamics on a high-energy, macro-tidal beach. Geomorphology 2014, 226, 76–93. [Google Scholar] [CrossRef]
- Thomas, T.; Phillips, M.R.; Williams, A.T. Mesoscale evolution of a headland bay: Beach rotation processes. Geomorphology 2010, 123, 129–141. [Google Scholar] [CrossRef]
- Thomas, T.; Phillips, M.R.; Williams, A.T.; Jenkins, R.E. Medium timescale beach rotation; gale climate and offshore island influences. Geomorphology 2011, 135, 97–107. [Google Scholar] [CrossRef]
- O’Connor, M.C.; Cooper, J.A.G.; Jackson, D.W.T. Decadal Behavior of Tidal Inlet-Associated Beach Systems, Northwest Ireland, in Relation to Climate Forcing. J. Sediment. Res. 2011, 81, 38–51. [Google Scholar] [CrossRef]
- Vespremeanu-Stroe, A.; Constantinescu, S.; Tatui, F.; Giosan, L. Multi-decadal Evolution and North Atlantic Oscillation Influences on the Dynamics of the Danube Delta Shoreline. J. Coast. Res. 2007, 2007, 157–162. [Google Scholar]
- Montreuil, A.-L.; Bullard, J.E. A 150-year record of coastline dynamics within a sediment cell: Eastern England. Geomorphology 2012, 179, 168–185. [Google Scholar] [CrossRef] [Green Version]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suanez, S.; Cancouët, R.; Floc'h, F.; Blaise, E.; Ardhuin, F.; Filipot, J.-F.; Cariolet, J.-M.; Delacourt, C. Observations and Predictions of Wave Runup, Extreme Water Levels, and Medium-Term Dune Erosion during Storm Conditions. J. Mar. Sci. Eng. 2015, 3, 674-698. https://doi.org/10.3390/jmse3030674
Suanez S, Cancouët R, Floc'h F, Blaise E, Ardhuin F, Filipot J-F, Cariolet J-M, Delacourt C. Observations and Predictions of Wave Runup, Extreme Water Levels, and Medium-Term Dune Erosion during Storm Conditions. Journal of Marine Science and Engineering. 2015; 3(3):674-698. https://doi.org/10.3390/jmse3030674
Chicago/Turabian StyleSuanez, Serge, Romain Cancouët, France Floc'h, Emmanuel Blaise, Fabrice Ardhuin, Jean-François Filipot, Jean-Marie Cariolet, and Christophe Delacourt. 2015. "Observations and Predictions of Wave Runup, Extreme Water Levels, and Medium-Term Dune Erosion during Storm Conditions" Journal of Marine Science and Engineering 3, no. 3: 674-698. https://doi.org/10.3390/jmse3030674
APA StyleSuanez, S., Cancouët, R., Floc'h, F., Blaise, E., Ardhuin, F., Filipot, J.-F., Cariolet, J.-M., & Delacourt, C. (2015). Observations and Predictions of Wave Runup, Extreme Water Levels, and Medium-Term Dune Erosion during Storm Conditions. Journal of Marine Science and Engineering, 3(3), 674-698. https://doi.org/10.3390/jmse3030674