Geometry of Wave-Formed Orbital Ripples in Coarse Sand
Abstract
:1. Introduction
2. Methods
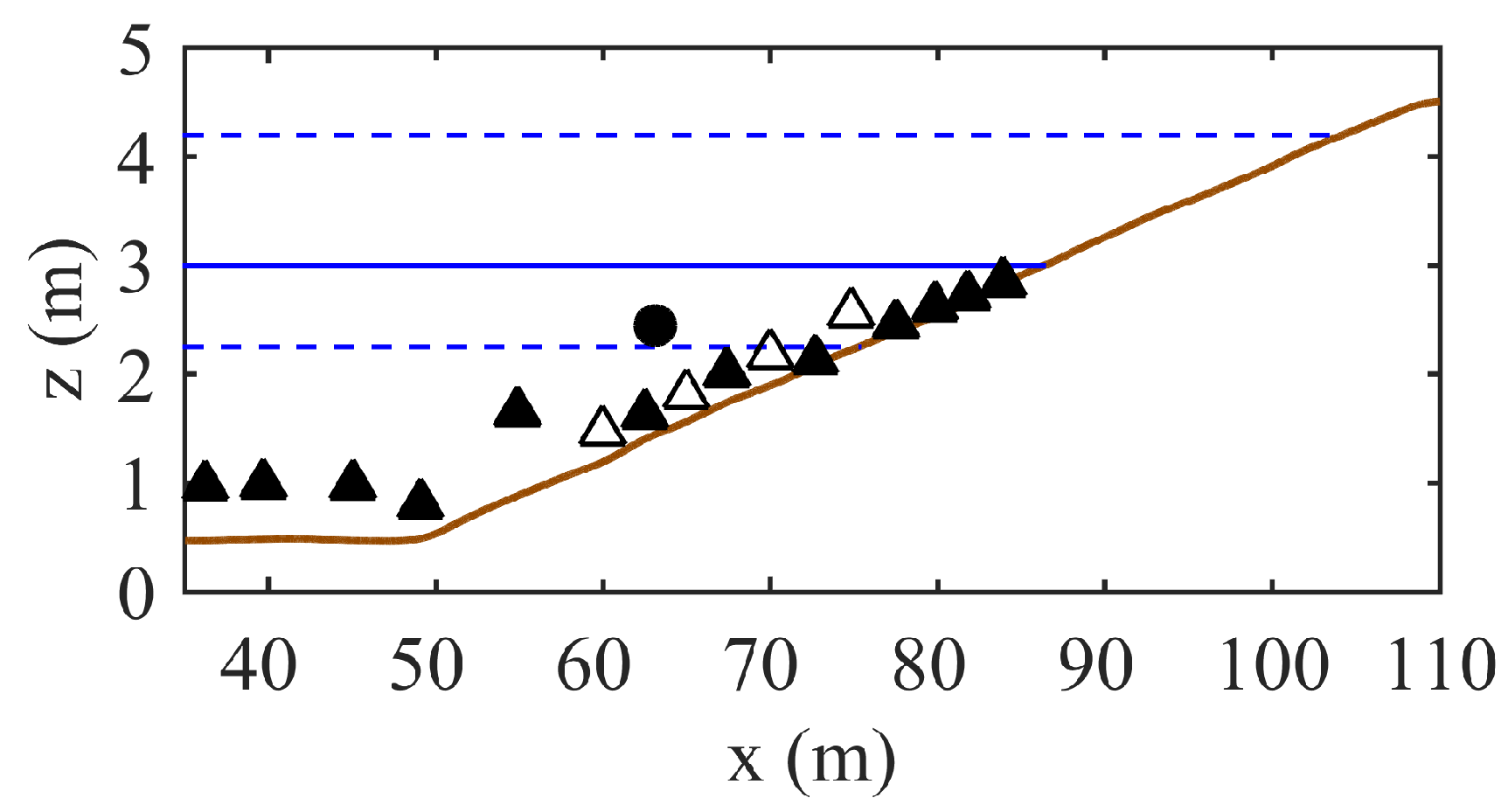
2.1. Bardex II Experiment
| Test | (m) | (s) | (m) | (s) | (m) | (min) | |
|---|---|---|---|---|---|---|---|
| A1 | 0.8 | 8 | 0.92 | 8.0 | 3 | 320 | 13 |
| A2 | 0.8 | 8 | 0.90 | 8.0 | 3 | 200 | 5 |
| A3 | 0.8 | 8 | 0.90 | 7.9 | 3 | 197 | 1 |
| A4 | 0.8 | 8 | 0.90 | 8.0 | 3 | 200 | 5 |
| A6 | 0.6 | 12 | 0.73 | 11.8 | 3 | 335 | 13 |
| A7 | 0.6 | 12 | 0.77 | 12.6 | 3 | 213 | 5 |
| A8 | 0.6 | 12 | 0.79 | 12.6 | 3 | 200 | 5 |
| B1 | 0.8 | 8 | 0.91 | 8.3 | 3 | 165 | 5 |
| B2 | 0.8 | 8 | 0.91 | 7.8 | 2.5 | 255 | 6 |
| C1 | 0.8, 0.6 | 8 | 0.90, 0.57 | 7.3 | 2.25 → 3.65 | 330 | 11 |
| C2 | 0.8, 0.6 | 8 | 0.91, 0.58 | 7.5 | 3.53 → 2.25 | 270 | 9 |
| D1 | 0.8 | 4 | 0.79 | 4.0 | 3.15 → 4.2 | 160 | 8 |
| D2 | 0.8 | 5 | 0.82 | 4.6 | 3.45 → 4.05 | 100 | 5 |
| D3 | 0.8 | 6 | 0.86 | 6.0 | 3.45 → 3.9 | 80 | 4 |
| D4 | 0.8 | 7 | 0.84 | 7.0 | 3.45 → 3.9 | 80 | 4 |
| D5 | 0.8 | 8 | 0.86 | 7.7 | 3.45 → 3.75 | 60 | 3 |
| D6 | 0.8 | 9 | 0.87 | 9.3 | 3.30 → 3.75 | 80 | 4 |
| D7 | 0.8 | 10 | 0.93 | 10.0 | 3.15 → 3.6 | 80 | 4 |
| E1 | 0.8 | 8 | 0.94 | 7.4 | 3.9 | 65 | 5 |
2.2. Measurements: Ripple Data
2.2.1. Profile Data


2.2.2. 3D Sonar Data
2.3. Measurements: Hydrodynamical Data

3. Results
3.1. Cross-section Geometry
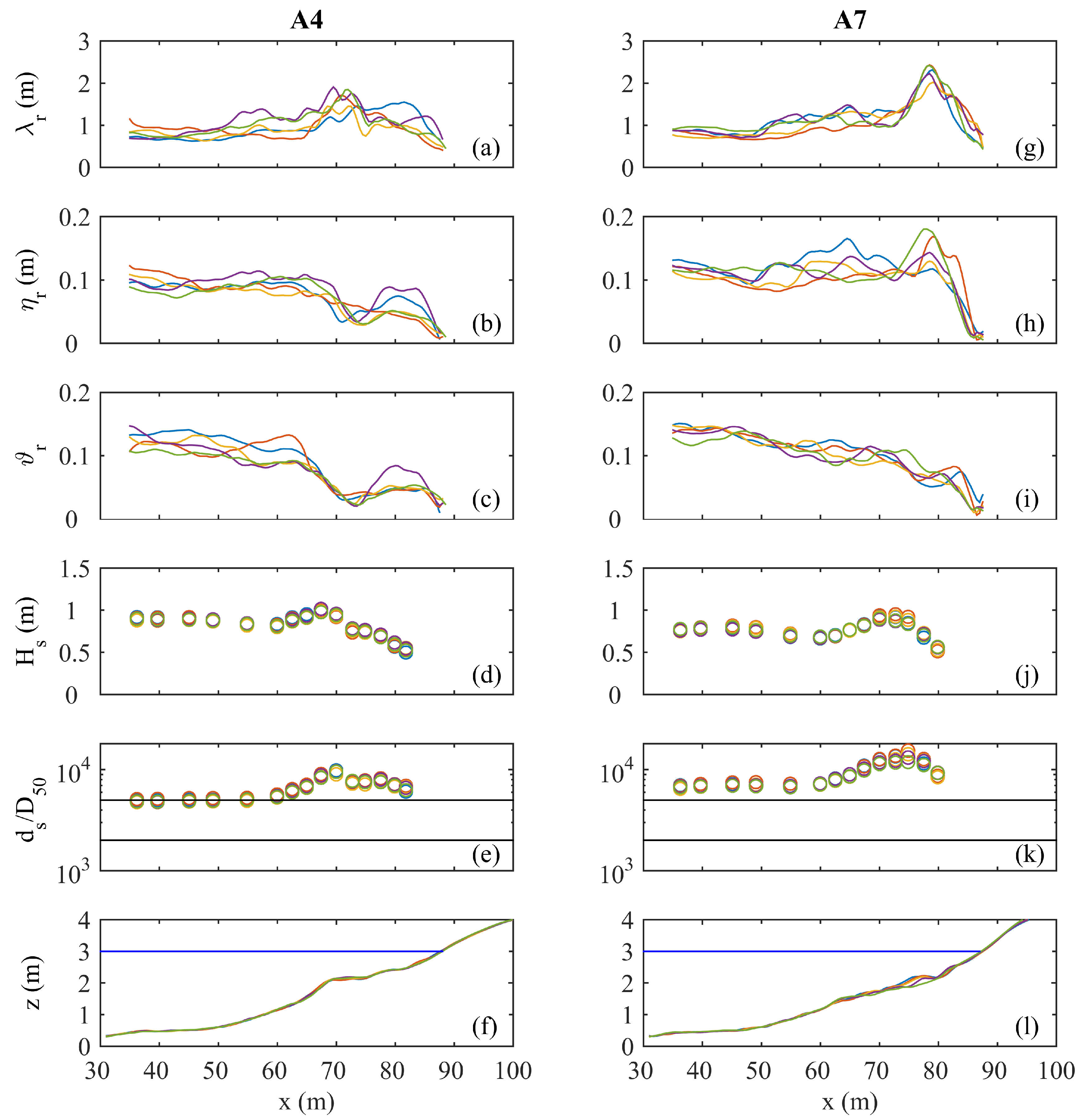


3.2. Planform Geometry



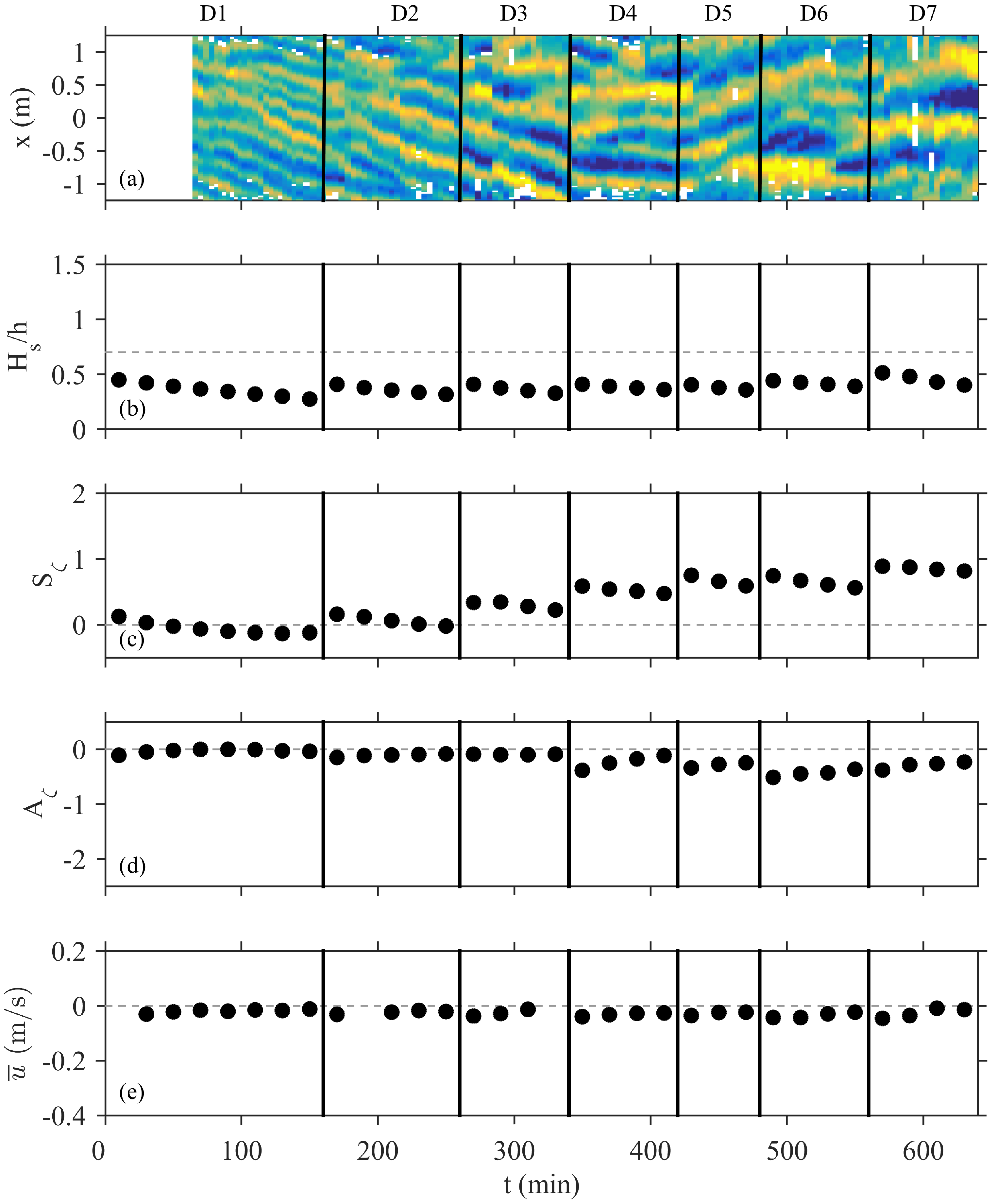
3.3. Ripple Migration
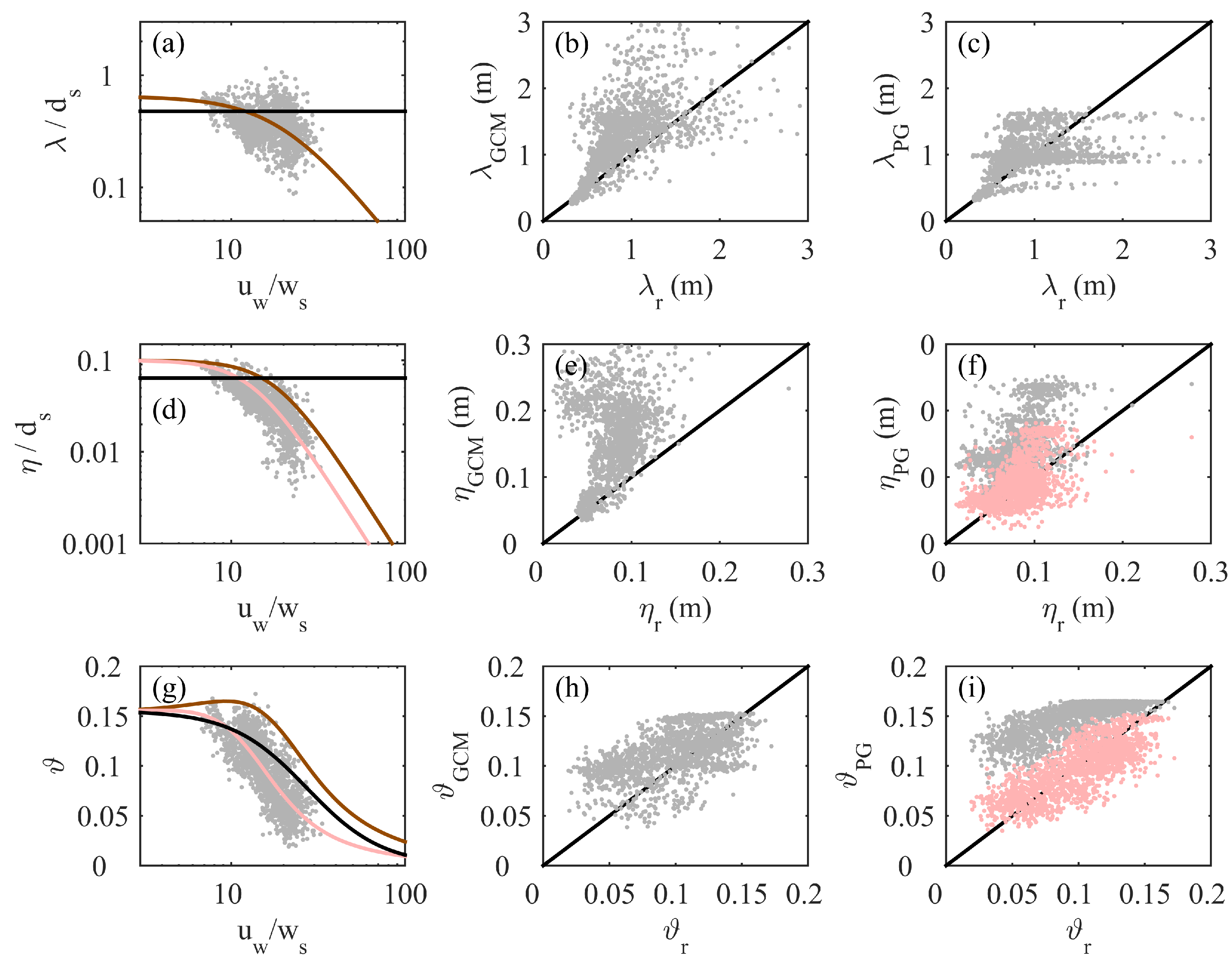
4. Empirical Prediction
| GCM | PG | RBK | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b | 0.11 | 0.34 | 0.10 | 0.02 | 0.23 | 0.32 | 0.00 | 0.02 | 0.01 | ||
| 0.17 | 0.43 | 0.20 | 0.12 | 0.27 | 0.35 | 0.13 | 0.11 | 0.13 | |||
| 0.36 | 0.07 | 0.32 | 0.21 | 0.30 | 0.58 | 0.33 | 0.29 | 0.61 | |||

5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Rijn, L.C.; Walstra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J.P. The predictability of cross-shore bed evolution of sandy beaches at the time scale of storms and seasons using process-based profile models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Walstra, D.J.R.; van Ormondt, M. Unified view of sediment transport by currents and waves. IV: Application of morphodynamic model. J. Hydraul. Eng. 2007, 133, 776–793. [Google Scholar] [CrossRef]
- Ganju, N.K.; Sherwoord, C.R. Effect of roughness formulation on the performance of a coupled wave, hydrodynamic, and sediment transport model. Ocean Model. 2010, 33, 299–313. [Google Scholar] [CrossRef]
- Nelson, T.R.; Voulgaris, G.; Traykovski, P. Predicting wave-induced ripple equilibrium geometry. J. Geophys. Res. 2013, 118, 3202–3220. [Google Scholar] [CrossRef]
- Pedocchi, F.; Garcia, M.H. Ripple morphology under oscillatory flow: 1. Prediction. J. Geophys. Res. 2009, 114, C12014. [Google Scholar] [CrossRef]
- Goldstein, E.B.; Coco, G.; Murray, A.B. Prediction of wave ripple characteristics using genetic programming. Cont. Shelf Res. 2013, 71. [Google Scholar] [CrossRef]
- Masselink, G.; Austin, M.J.; O’Hare, T.J.; Russell, P.E. Geometry and dynamics of wave ripples in the nearshore zone of a coarse sandy beach. J. Geophys. Res. 2007, 112, C10022. [Google Scholar] [CrossRef]
- Cummings, D.I.; Dumas, S.; Dalrymple, R.W. Fine-grained versus coarse-grained wave ripples generated experimentally under large-scale oscillatory flow. J. Sediment. Res. 2009, 79, 83–93. [Google Scholar] [CrossRef]
- Clifton, H.E. Wave-formed sedimentary structures: A conceptual model. In Beach and Nearshore Sedimentation, Special Publication 24; Society for Sedimentary Geology: Tulsa, OK, USA, 1976; pp. 126–148. [Google Scholar]
- Miller, M.C.; Komar, P.D. Oscillation sand ripples generated by laboratory apparatus. J. Sediment. Res. 1980, 50, 173–182. [Google Scholar]
- Wiberg, P.L.; Harris, C.K. Ripple geometry in wave-dominated environments. J. Geophys. Res. 1994, 99, 775–789. [Google Scholar] [CrossRef]
- Van der Werf, J.J.; Doucette, J.S.; O’Donoghue, T.; Ribberink, J.S. Detailed measurements of velocities and suspended sand concentrations over full-scale ripples in regular oscillatory flow. J. Geophys. Res. 2007, 112, F02012. [Google Scholar] [CrossRef]
- Clifton, H.E.; Dingler, J.R. Wave-formed structures and paleoenvironmental reconstruction. Mar. Geol. 1984, 60, 165–198. [Google Scholar] [CrossRef]
- Maier, I.; Hay, A.E. Occurrence and orientation of anorbital ripples in near-shore sands. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Whitehouse, R.J.S.; Marten, K.V. Prediction of time-evolving sand ripples in shelf seas. Cont. Shelf Res. 2012, 38, 47–62. [Google Scholar] [CrossRef]
- Hanes, D.M.; Alymov, V.; Chang, Y.S.; Jette, C. Wave-formed sand ripples at Duck, North Carolina. J. Geophys. Res. 2001, 106, 22575–22592. [Google Scholar] [CrossRef]
- Grasmeijer, B.T.; Kleinhans, M.G. Observed and predicted bed forms and their effect on suspended sand concentrations. Coast. Eng. 2004, 51, 351–371. [Google Scholar] [CrossRef]
- Williams, J.J.; Bell, P.S.; Thorne, P.D. Unifying large and small wave-generated ripples. J. Geophys. Res. 2005, 110, C02008. [Google Scholar] [CrossRef]
- Miles, J.R.; Thorpe, A.; Russell, P.; Masselink, G. Observations of bedforms on a dissipative macrotidal beach. Ocean Dyn. 2014, 64, 225–239. [Google Scholar] [CrossRef]
- Larsen, S.M.; Greenwood, B.; Aagaard, T. Obervations of megaripples in the surf zone. Mar. Geol. 2015, 364. [Google Scholar] [CrossRef]
- Forbes, D.L.; Boyd, R. Gravel ripples on the inner Scotian shelf. J. Sediment. Petrol. 1987, 57, 46–54. [Google Scholar]
- Hunter, R.E.; Dingler, J.R.; Anima, R.J.; Richmond, B.M. Coarse-sediment bands on the inner shelf of Southern Monterey Bay, California. Mar. Geol. 1988, 80, 81–98. [Google Scholar] [CrossRef]
- Leckie, D. Wave-formed, coarse-grained ripples and their relationship to hummocky cross-stratification. J. Sediment. Petrol. 1988, 58, 607–622. [Google Scholar] [CrossRef]
- Traykovski, P.; Hay, A.E.; Irish, J.D.; Lynch, J.F. Geometry, migration, and evolution of wave orbital ripples at LEO-15. J. Geophys. Res. 1999, 104, 1505–1524. [Google Scholar] [CrossRef]
- Doucette, J.S. Bedform migration and sediment dynamics in the nearshore of a low-energy sandy beach in southwestern Australia. J. Coast. Res. 2002, 18, 576–591. [Google Scholar]
- Yoshikawa, S.; Nemoto, K. The role of summer monsoon-typhoons in the formation of nearshore coarse-grained ripples, depression, and sand-ridge systems along the Shimizu coast, Suruga Bay facing the Pacific Ocean, Japan. Mar. Geol. 2014, 353, 84–98. [Google Scholar] [CrossRef]
- Pedocchi, F.; Garcia, M.H. Ripple morphology under oscillatory flow: 2. Experiments. J. Geophys. Res. 2009, 114, C12015. [Google Scholar] [CrossRef]
- O’Donoghue, T.; Doucette, J.S.; Van der Werf, J.J.; Ribberink, J.S. The dimensions of sand ripples in full-scale oscillatory flows. Coast. Eng. 2006, 53, 997–1012. [Google Scholar] [CrossRef]
- Kleinhans, M.G. Large bedforms on the shoreface and upper shelf, Noordwijk, The Netherlands. In SANDPIT: Sand Transport and Morphology of Offshore Sand Mining Pits; van Rijn, L.C., Soulsby, R.L., Hoekstra, P., Davies, A.G., Eds.; Aqua Publications: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Masselink, G.; Ruju, A.; Conley, D.; Turner, I.; Ruessink, G.; Matias, A.; Thompson, C.; Castelle, B.; Puleo, J.; Citerone, V.; et al. Large-scale Barrier Dynamics Experiment II (BARDEX II): Experimental design, instrumentation, test programme, and data set. Coast. Eng. 2015, in press. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Church, M. A simple universal equation for grain settling velocity. J. Sediment. Res. 2004, 74, 933–937. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T.; Puleo, J.A. Analysis of the scale of errors in nearshore bathymetric data. Mar. Geol. 2002, 191, 71–86. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Blenkinsopp, C.; Brinkkemper, J.A.; Castelle, B.; Dubarbier, B.; Grasso, F.; Puleo, J.A.; Lanckriet, T. Sandbar and beachface evolution on a prototype coarse-grained sandy barrier. Coast. Eng. 2016, in press. [Google Scholar]
- Matias, A.; Masselink, G.; Castelle, B.; Blenkinsopp, C.; Kroon, A. Measurements of morphodynamic and hydrodynamic overwash processes in a large-scale wave flume. Coast. Eng. 2015. [Google Scholar] [CrossRef]
- Soulsby, R.L. Dynamics of Marine Sands; Thomas Telford: London, UK, 1997. [Google Scholar]
- De Winter, W.; Wesselman, D.; Grasso, F.; Ruessink, G. Large-scale laboratory observations of beach morphodynamics and turbulence beneath shoaling and breaking waves. J. Coast. Res. 2013, 65, 1515–1520. [Google Scholar]
- Elgar, S. Relationships involving third moments and bispectra of a harmonic process. IEEE Trans. Acoust. Speech Signal Proc. 1987, 35, 1725–1726. [Google Scholar] [CrossRef]
- Nelson, T.R.; Voulgaris, G. Temporal and spatial evolution of wave-induced ripple geometry: Regular versus irregular ripples. J. Geophys. Res. Oceans 2014, 119, 664–688. [Google Scholar] [CrossRef]
- Brinkkemper, J.A.; Lanckriet, T.; Grasso, F.; Puleo, J.A.; Ruessink, B.G. Observations of turbulence within the surf and swash zones of a field-scale sandy laboratory beach. Coast. Eng. 2015, in press. [Google Scholar] [CrossRef]
- Doucette, J.S.; O’Donoghue, T. Response of sand ripples to change in oscillatory flow. Sedimentology 2006, 53, 581–596. [Google Scholar] [CrossRef]
- Arnott, R.W.C.; Southard, J.B. Exploratory flow-duct experiments on combined-flow bed configurations, and some implications for interpreting storm-event stratification. J. Sediment. Petrol. 1990, 60, 211–219. [Google Scholar]
- Southard, J.B.; Lambie, J.M.; Frederico, D.C.; Pile, H.T.; Weidman, C.R. Experiments on bed configurations in fine sands under bidirectional purely oscillatory flow, and the origin of hummocky cross-stratification. J. Sediment. Petrol. 1990, 60, 1–17. [Google Scholar]
- Dumas, S.; Arnott, R.W.C. Origin of hummocky and swaley cross-stratification—The controlling influence of unidirectional current strength and aggradation rate. Geology 2006, 34, 1073–1076. [Google Scholar] [CrossRef]
- Osborne, P.D.; Vincent, C.E. Dynamics of large and small scale bedforms on a macrotidal shoreface under shoaling and breaking waves. Mar. Geol. 1993, 1993, 207–226. [Google Scholar] [CrossRef]
- Perillo, M.M.; Best, J.L.; Yokokawa, M.; Sekiguchi, T.; Takagawa, T.; Garcia, M.H. A unified model for bedform developement and equilibrium under unidirectional, oscillatory and combined-flows. Sedimentology 2014, 61, 2063–2085. [Google Scholar] [CrossRef]
- Dubarbier, B.; Castelle, B.; Marieu, V.; Ruessink, B.G. On the modeling of sandbar formation over a steep beach profile during the large-scale wave flume experiment BARDEX II. In Proceedings of the Coastal Sediments Conference 2015, San Diego, CA, USA, 11–15 May 2015.
- Crawford, A.M.; Hay, A.E. Linear transition ripple migration and wave orbital velocity skewness: Observations. J. Geophys. Res. 2001, 106, 14113–14128. [Google Scholar] [CrossRef]
- Nielsen, P. Dynamics and geometry of wave-generated ripples. J. Geophys. Res. 1981, 86, 6467–6472. [Google Scholar] [CrossRef]
- Nadaoka, K.; Hino, M.; Koyano, Y. Structure of the turbulent flow field under breaking waves in the surf zone. J. Fluid Mech. 1989, 204, 359–387. [Google Scholar] [CrossRef]
- Kimmoun, O.; Branger, H. A particle image velocimetry investigation on laboratory surf-zone breaking waves over a sloping beach. J. Fluid Mech. 2007, 588, 353–397. [Google Scholar] [CrossRef]
- Miller, R.L. Role of vortices in surf zone prediction: Sedimentation and wave forces. In Beach and Nearshore Sedimentation; Davis, R.A., Ethington, R.L., Eds.; SEPM: Tulsa, OK, USA, 1976; pp. 92–114. [Google Scholar]
- Nadaoka, K.; Ueno, S.; Igarashi, T. Sediment suspension due to large scale eddies in the surf zone. In Proceedings of the 21st International Conference on Coastal Engineering, Torremolinos, Spain, 20–25 June 1988; ASCE: Reston, VA, USA, 1988; pp. 1646–1660. [Google Scholar]
- Sato, S.; Homma, K.; Shibayama, T. Laboratory study on sand suspension due to breaking waves. Coast. Eng. Japan 1990, 33, 219–231. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruessink, G.; Brinkkemper, J.A.; Kleinhans, M.G. Geometry of Wave-Formed Orbital Ripples in Coarse Sand. J. Mar. Sci. Eng. 2015, 3, 1568-1594. https://doi.org/10.3390/jmse3041568
Ruessink G, Brinkkemper JA, Kleinhans MG. Geometry of Wave-Formed Orbital Ripples in Coarse Sand. Journal of Marine Science and Engineering. 2015; 3(4):1568-1594. https://doi.org/10.3390/jmse3041568
Chicago/Turabian StyleRuessink, Gerben, Joost A. Brinkkemper, and Maarten G. Kleinhans. 2015. "Geometry of Wave-Formed Orbital Ripples in Coarse Sand" Journal of Marine Science and Engineering 3, no. 4: 1568-1594. https://doi.org/10.3390/jmse3041568
APA StyleRuessink, G., Brinkkemper, J. A., & Kleinhans, M. G. (2015). Geometry of Wave-Formed Orbital Ripples in Coarse Sand. Journal of Marine Science and Engineering, 3(4), 1568-1594. https://doi.org/10.3390/jmse3041568







