Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes
Abstract
:1. Introduction
2. Study Site
3. Materials and Methods
3.1. Three-Dimensional Hydrodynamic Numerical Model: H3D
3.1.1. Theoretical Basis
3.1.2. Grid Geometry
3.1.3. Turbulent Closure
3.1.4. Scalar Transport
3.1.5. Heat Flux at the Air–Water Interface
- Fin: incident short wave radiation. Generally, this is not known from direct observations. Instead, it is estimated from the cloud cover and opacity observations at nearby stations, a theoretical calculation of radiation at the top of the atmosphere based on the geometry of the earth/sun system, and an empirical adjustment based on radiation measurements at Vancouver International Airport for the period 1974–1977. This procedure has worked well for many water bodies, notably Okanagan Lake and the waters of the north coast of British Columbia, in terms of allowing H3D to reproduce the observed temperature distributions in space and time. Values for albedo as a function of solar height are taken from Kondratyev [33].
- Fback: net long wave radiation. This is calculated according to Gill [34], involving the usual fourth power dependence on temperature, a factor of 0.985 to allow for the non-black body behaviour of the ocean, a factor depending on vapor pressure to allow for losses due to back radiation from moisture in the air, and a factor representing backscatter from clouds.
- FL and FS: Latent heat flux (FL) is the heat carried away by the process of evaporation of water. Sensible heat flux (FS) is driven by the air-water temperature difference and is similar to conduction, but assisted by turbulence in the air. Latent and sensible heat fluxes are described by:where qobs and qsat are the observed and saturated specific humidities, Tair and Twater are the air and water temperatures, L is the latent heat of evaporation of water, and Cp is the heat capacity of water, Ua is wind speed, Fl and Fs are latent and sensible factors, which are the scaling factors introduced to account for local factors, and can be adjusted, when needed, to achieve better calibration of the model. Typically, the only adjustment is that sensible factor is doubled when the air temperature is less than the water or ice surface temperature to account for increased turbulence in an unstable air column.
3.2. Model Implementation
3.3. Validation of the Nested Model
3.4. Study Methodology
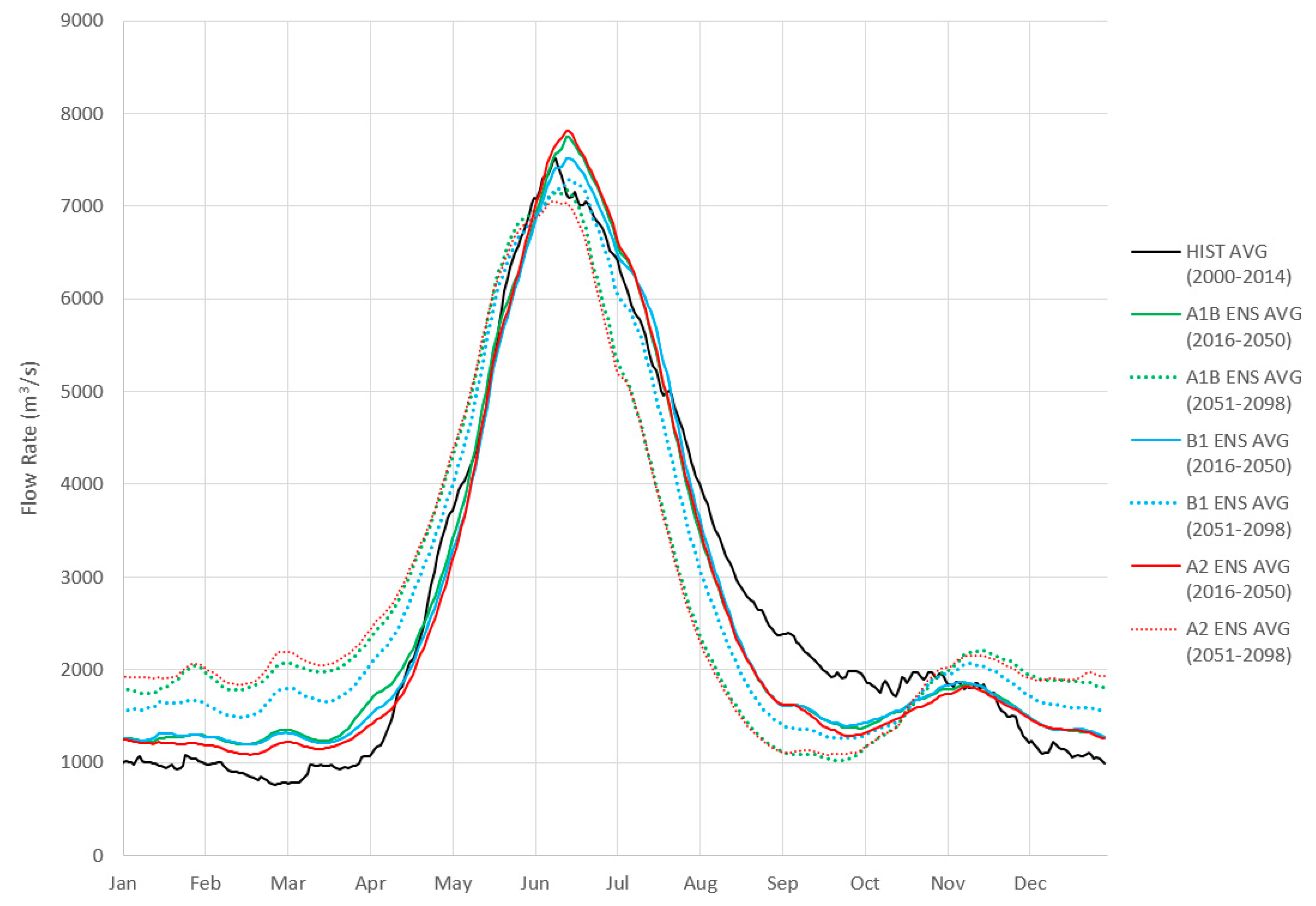
3.4.1. Selecting Climate Scenario and Global Climate Model for Projection of the Fraser River Hydrograph
3.4.2. Selecting Sea Level Rise Scenarios
3.4.3. Selecting River Dredge Depth Scenarios
4. Results
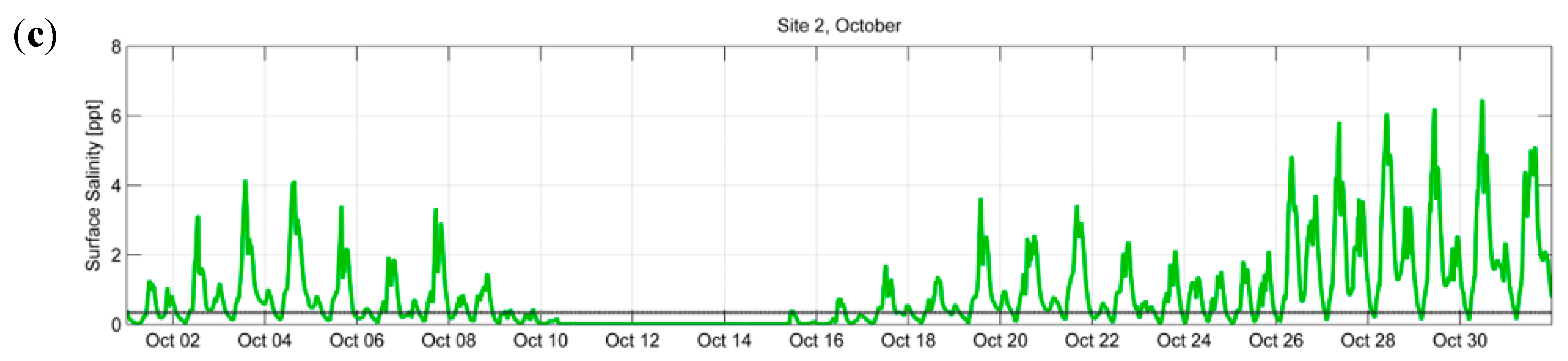
4.1. Difference in Salinity at Different Locations Along the River
4.2. Effects of Sea Level Rise and River Flow
4.2.1. Time Horizon: Present
4.2.2. Time Horizon: Year 2050 and Year 2100
4.3. Effects of Channel Deepening
5. Discussion
5.1. Effect of Sea Level Rise and River Flow
5.2. Effect of Channel Deepening
5.3. Comparison with Past Studies
5.4. Future Studies and Research
6. Conclusions
- Site 1, located 4 km upstream of Site 2, has consistently shown to have a significantly wider window for water availability in all cases and for all criteria compared to Site 2, the present intake location. This indicates that salinity generally decreases in the upstream direction. However, complex hydrodynamic processes would lead to exceptions to the trend.
- The temporal projection of the withdrawal window is that, even in a wet flow year, the sea level rise of 1 m and 2 m will lead to a large reduction (minimum 85% reduction) in and, in some scenarios, complete elimination of water availability.
- This study found that sea level rise and changes in river discharge appear to have a larger impact on the withdrawal availability than does channel deepening. In a low river discharge regime, the impact from sea level change is more significant than it is in the high river discharge regime. On the other hand, the influence of changes in river discharge on withdrawal availability decreases when the sea level is higher than it does when the sea level is lower. It is difficult, however, to draw definitive conclusions regarding which factor (sea level rise or river flow) dominates the salt wedge dynamics from this set of model results because, as presented in Section 3.4.1 and in Figure 10, each of the sea level rise cases incorporates different flow rates associated with the projected normal year, dry year, and wet year as predicted by MIROC for its own time horizon (present, year 2050 and year 2100); simply speaking, these model runs have two varying factors, the flow rate and sea level, and it is not immediately obvious which factor is more important in governing the salinity in the river. However, it is difficult to consider one factor without another, considering that the sea level rise and change in the Fraser River hydrograph are both results of climate change.
- Dredging the channel to accommodate vessels with a 20 m draft will affect the salinity at the intake and will shorten the withdrawal window. The effect of channel deepening becomes more pronounced in the low flow period. However, the degree of impact from dredging on the salt wedge and on withdrawal availability under other different circumstances (i.e., different sea level rise and different dredge depths) have not been investigated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Theoretical Basis of H3D
Appendix B. Notations
References
- Costanza, R.; D’Arge, R.; De Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Stronach, J.A. Observational and Modelling Studies of the Fraser River Plume. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 1978. [Google Scholar]
- Stronach, J.A. The Fraser River plume, Strait of Georgia. Ocean Manag. 1981, 6, 201–221. [Google Scholar] [CrossRef]
- Halverson, M.; Pawlowicz, R. Tide, wind, and river forcing of the surface currents in the Fraser River plume. Atmos. Ocean 2016, 54, 131–152. [Google Scholar] [CrossRef]
- Halverson, M.; Pawlowicz, R. Entrainment and flushing time in the Fraser River estuary and plume from a steady state salt balance analysis. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Halverson, M.; Pawlowicz, R. Estuarine forcing of a river plume by river flow and tides. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Kostaschuk, R.; Atwood, L.A. River discharge and tidal controls on salt-wedge position and implications for channel shoaling: Fraser River, British Columbia. Can. J. Civ. Eng. 2011, 17, 452–459. [Google Scholar] [CrossRef]
- Ward, P.R.B. Seasonal salinity changes in the Fraser River estuary. Can. J. Civ. Eng. 2011, 3, 342–348. [Google Scholar] [CrossRef]
- Yin, K.D.; Harrison, P.J.; Pond, S.; Beamish, R.J. Entrainment of nitrate in the Fraser River estuary and its biological implications. III. Effects of winds. Estuar. Coast. Shelf Sci. 1995, 40, 545–558. [Google Scholar] [CrossRef]
- Neilson-Welch, L.; Smith, L. Saline water intrusion adjacent to the Fraser River, Richmond, British Columbia. Can. Geotech. J. 2011, 38, 67–82. [Google Scholar] [CrossRef]
- Krvavica, N.; Travaš, V.; Ožanić, N. Salt-Wedge Response to Variable River Flow and Sea-Level Rise in the Microtidal Rječina River Estuary, Croatia. J. Coast. Res. 2017, 33, 802–814. [Google Scholar] [CrossRef]
- Funahashi, T.; Kasai, A.; Ueno, M.; Yamashita, Y. Effects of short time variation in the river discharge on the salt wedge intrusion in the Yura Estuary, Japan. J. Water Resour. Prot. 2013, 5, 343–348. [Google Scholar] [CrossRef]
- Shaha, D.C.; Cho, Y.K.; Kim, T.W. Effects of river discharge and tide driven variation on saltwater intrusion in Sumjin River Estuary: An application of finite-volume coastal ocean model. J. Coast. Res. 2013, 29, 460–470. [Google Scholar] [CrossRef]
- Richmond Chamber of Commerce. The Economic Importance of the Lower Fraser River; Richmond Chamber of Commerce: Richmond, BC, Canada, 2014. [Google Scholar]
- Crawford, E.; MacNair, E. Fraser Valley & Metro Vancouver Snapshot Report, B.C. Agriculture Climate Change Adaptation Risk + Opportunity Assessment Series; The British Columbia Agriculture & Food Climate Action Initiative: Victoria, BC, Canada, 2012. [Google Scholar]
- Van der Gulik, T.; Neilsen, D.; Fretwell, R.; Tam, S. Agricultural Water Demand Model—Report for Metro Vancouver; Metro Vancouver: Vancouver, BC, Canada, 2014. [Google Scholar]
- Backhaus, J.O. A semi-implicit scheme for the shallow water equations for applications to shelf sea modelling. Cont. Shelf Res. 1983, 2, 243–254. [Google Scholar] [CrossRef]
- Backhaus, J.O. A three-dimensional model for the simulation of shelf-sea dynamics. Deutsche Hydro. Z. 1985, 38, 165–187. [Google Scholar] [CrossRef]
- Duwe, K.C.; Hewer, R.R.; Backhaus, J.O. Results of a semi-implicit two-step method for the simulation of markedly non-linear flow in coastal seas. Cont. Shelf Res. 1983, 2, 255–274. [Google Scholar] [CrossRef]
- Backhaus, J.O.; Meir-Reimer, E. On seasonal circulation patterns in the North Sea. In North Sea Dynamics; Sundermann, J., Lenz, W., Eds.; Springer: Heidelberg, Germany, 1983; pp. 63–84. ISBN 978-3-642-68840-9. [Google Scholar]
- Kampf, J.; Backhaus, J.O. Ice-ocean interactions during shallow convection under conditions of steady winds: Three-dimensional numerical studies. Deep-Sea Res. Part II 1999, 46, 1335–1355. [Google Scholar] [CrossRef]
- Backhaus, J.O.; Kampf, J. Simulation of sub-mesoscale oceanic convection and ice-ocean interactions in the Greenland Sea. Deep-Sea Res. Part II 1999, 46, 1427–1455. [Google Scholar] [CrossRef]
- Stronach, J.A.; Backhaus, J.O.; Murty, T.S. An update on the numerical simulation of oceanographic processes in the waters between Vancouver Island and the mainland: The G8 model. Oceanogr. Mar. Biol. 1999, 31, 1–86. [Google Scholar]
- Stronach, J.A.; Mulligan, R.P.; Soderholm, H.; Draho, R.; Degen, D. Okanagan lake limnology: Helping to improve water quality and safety. In Innovation; Association of Professional Engineers and Geoscientists of British Columbia: Vancouver, BC, Canada, 2002. [Google Scholar]
- Wang, E.; Stronach, J.A. Summerland water intake feasibility study. In Proceedings of the Canadian Water Resources Association BC Branch Conference, Kelowna, BC, Canada, 23–25 February 2005. [Google Scholar]
- Saucier, F.J.; Roy, F.; Gilbert, D.; Pellerin, P.; Ritchie, H. The formation of water masses and sea ice in the Gulf of St. Lawrence. J. Geophys. Res. 2003, 108, 3269–3289. [Google Scholar] [CrossRef]
- Rego, J.L.; Meselhe, E.; Stronach, J.A.; Habib, E. Numerical modelling of the Mississippi-Atchafalaya rivers’ sediment transport and fate: Considerations for diversion scenarios. J. Coast. Res. 2010, 26, 212–229. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput. Phys. 1977, 17, 173–263. [Google Scholar]
- Smagorinsky, J. General circulation experiment with the primitive equations: I. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulent closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Mellor, G.L.; Durbin, P.A. The structure and dynamics of the ocean surface mixed layer. J. Phys. Oceanogr. 1975, 5, 718–728. [Google Scholar] [CrossRef]
- Zalesak, S.T. Fully multidimensional flux-corrected transport algorithms for fluids. J. Comput. Phys. 1979, 31, 335–362. [Google Scholar] [CrossRef]
- Kondratyev, K.Y. Radiation Processes in the Atmosphere; No. 309; World Meteorological Organization, The University of California: San Diego, CA, USA, 1972. [Google Scholar]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: London, UK, 1982. [Google Scholar]
- Crean, P.B.; Ages, A.B. Oceanographic Records from Twelve Cruises in the Strait of Georgia and Juan de Fuca Strait, 1968; Department of Energy, Mines and Recources, Marine Research Sciences Branch: Ottawa, ON, Canada, 1971. [Google Scholar]
- Water Survey of Canada. Available online: https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/monitoring/survey.html (accessed on 15 February 2016).
- The Intergovernmental Panel on Climate Change. Climate Change 2007: The Fourth Assessment Report; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Werner, A.T. BCSD Downscaled Transient Climate Projections for Eight Select GCMs over British Columbia, Canada; Pacific Climate Impacts Consortium, University of Victoria: Victoria, BC, Canada, 2011. [Google Scholar]
- Schnorbus, M.A.; Bennett, K.E.; Werner, A.T.; Berland, A.J. Hydrologic Impacts of Climate Change in the Peace, Campbell and Columbia Watersheds, British Columbia, Canada; Pacific Climate Impacts Consortium, University of Victoria: Victoria, BC, Canada, 2011. [Google Scholar]
- Pacific Climate Impact Consortium. Available online: https://www.pacificclimate.org (accessed on 1 February 2016).
- Ausenco Sandwell. Sea Dike Guidelines; BC Ministry of Environment: Victoria, BC, Canada, 2011; pp. 4–5. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal circulation model. In Three-Dimensional Coastal Ocean Models; Heaps, N.S., Ed.; American Geophysical Union: Washington, DC, USA, 1987; pp. 1–16. [Google Scholar]

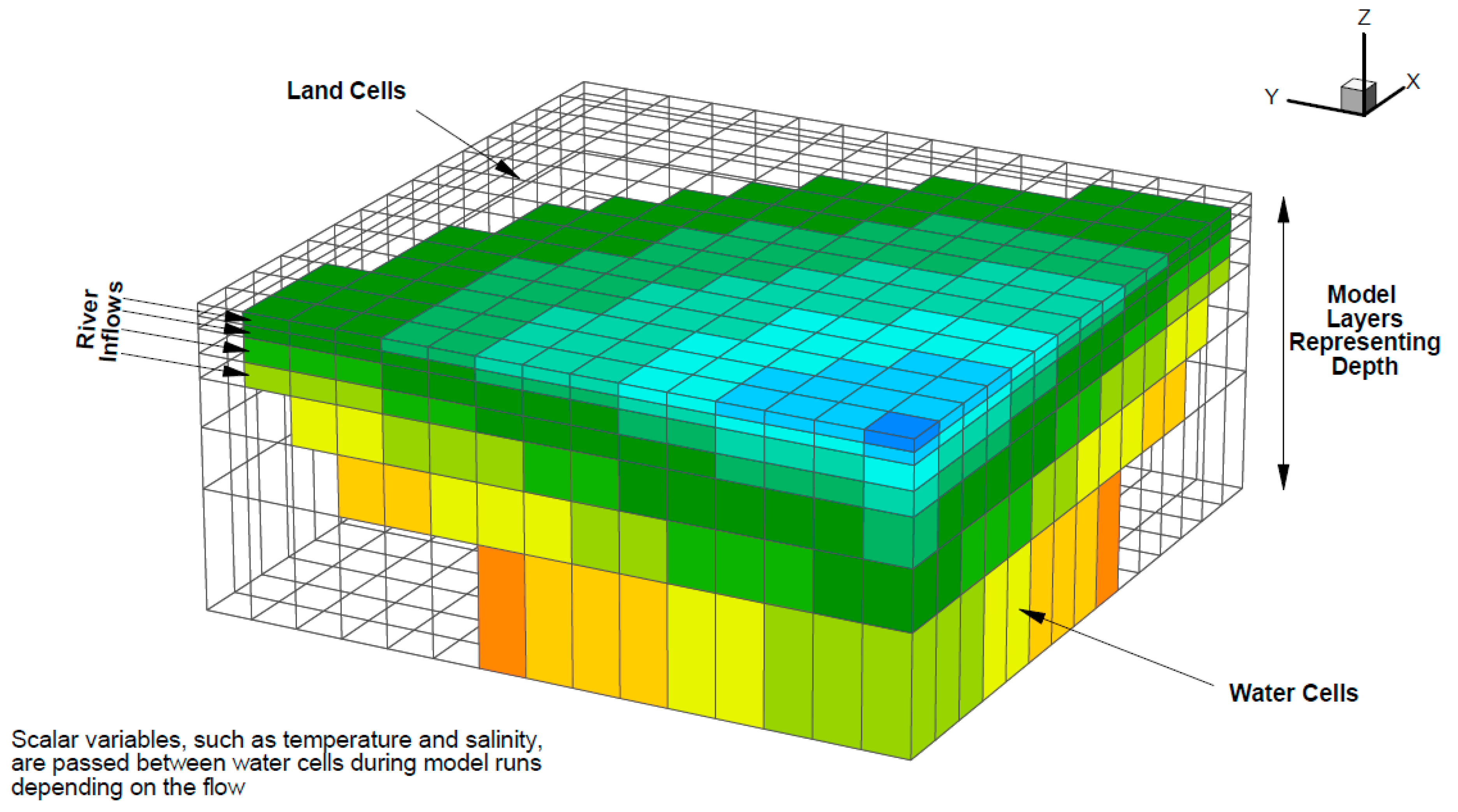


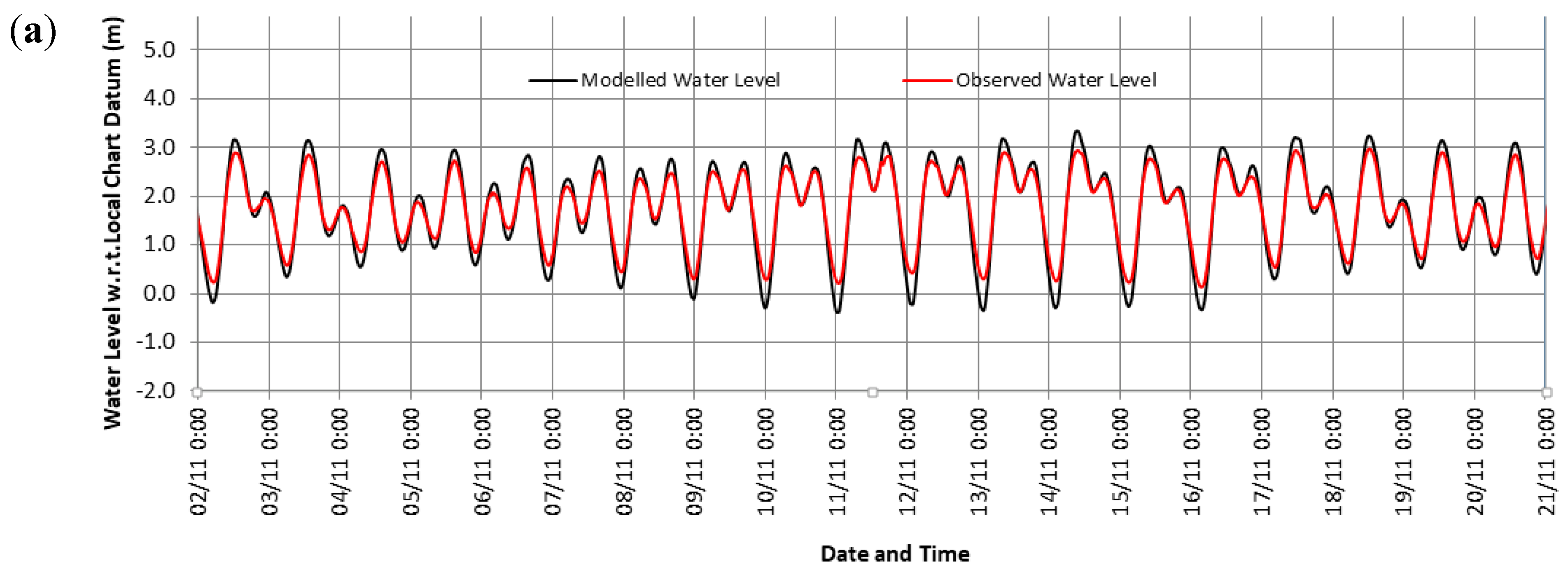
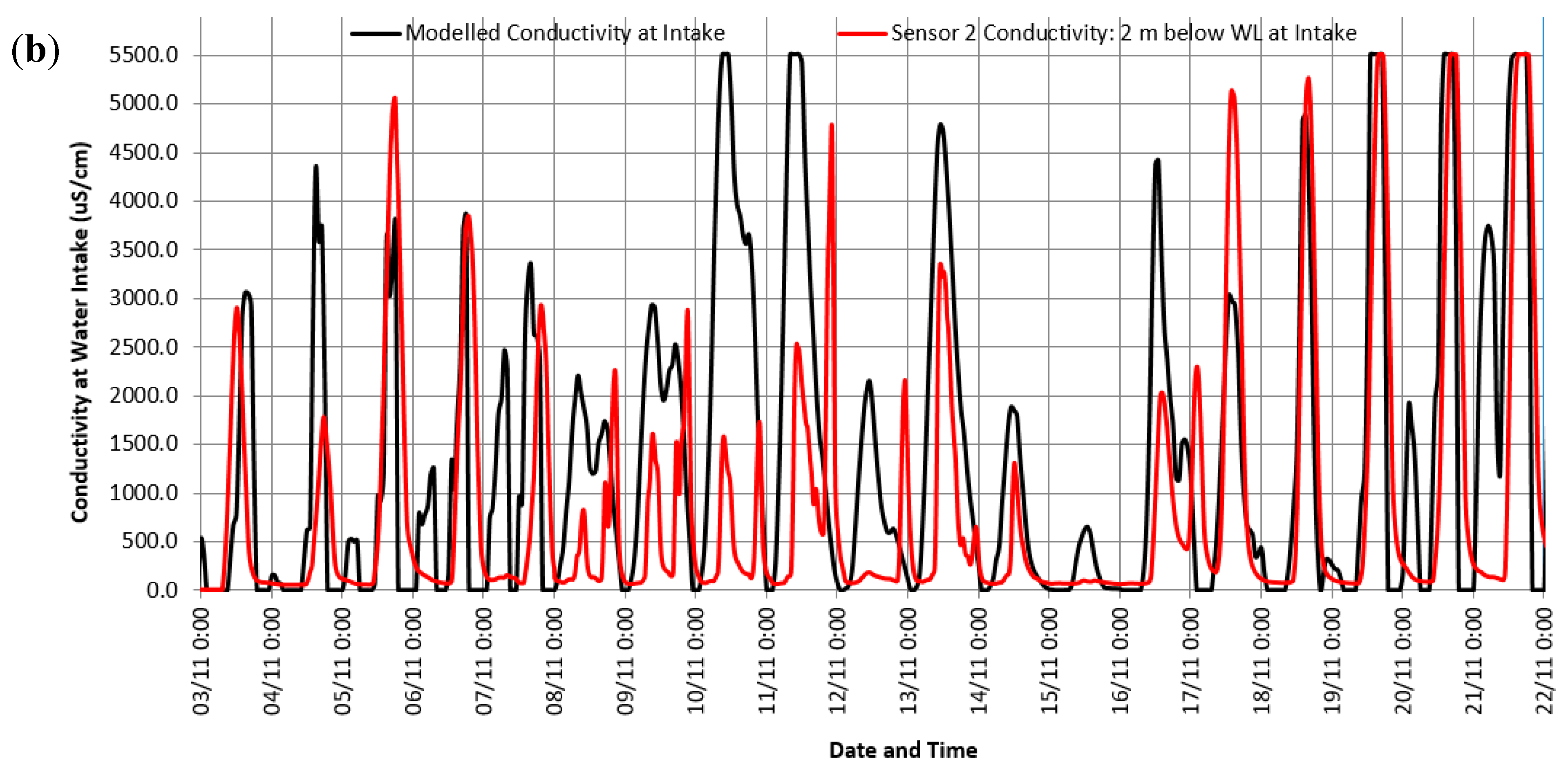
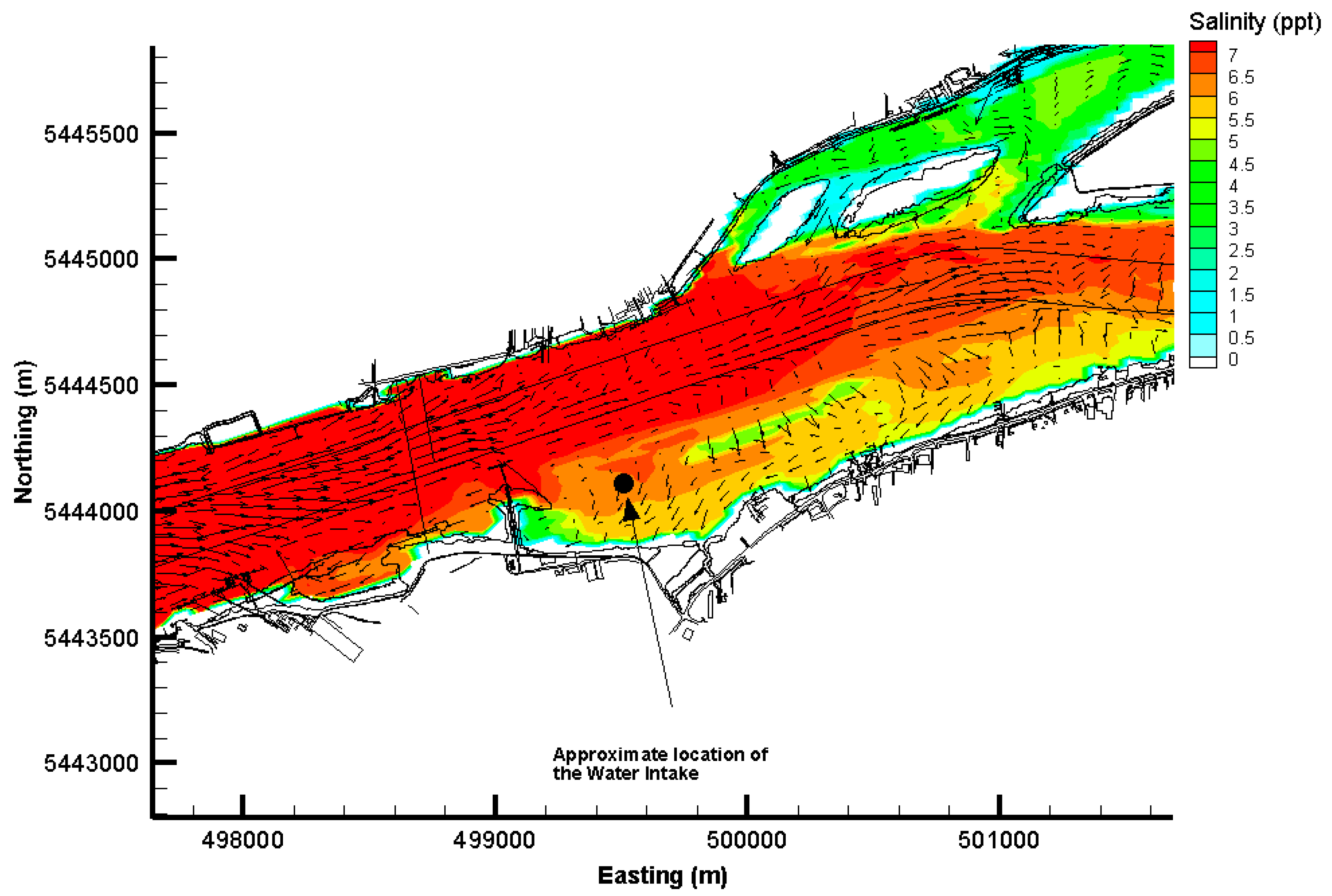












| Seq. # | Model | Initial Conditions | Downstream Boundary Conditions | Upstream Boundary Conditions | Dynamic Model Coupling | Objective |
|---|---|---|---|---|---|---|
| 1a | 1-km SOG | Temperature and salinity profiles | Temperature, salinity and tidal level | Flow conditions provided by the 1-D Fraser River model | 1-D Fraser River model for the 1-km SOG model | To provide boundary conditions to the 50-m Fraser River Model |
| 1b | 1-D Fraser River-for the 1-km SOG | Water level | Water level from the 1-km SOG model | River hydrograph at Hope | 1-km SOG model | To provide upstream boundary conditions to the 1-km SOG model |
| 2a | 50-m Fraser River | Temperature and salinity profiles | Temperature, salinity and tidal level provided by the SOG model | Flow conditions provided by the 1-D Fraser River model | 1-D Fraser River model for the 50-m Fraser River model | To simulate spatial and temporal salinity distributions in the Fraser River |
| 2b | 1-D Fraser River-for the 50-m Fraser River | Water level | Water level from the 1-km SOG model | River hydrograph at Hope | 50-m Fraser River model | To provide upstream boundary conditions to the 50-m Fraser River model |
| Climate Scenario | Description | Characteristics |
|---|---|---|
| A1B | This scenario is of a more integrated world |
|
| A2 | These scenarios are of a more divided world |
|
| B1 | This scenario is of a world more integrated, and more ecologically friendly |
|
| Timeframe | Year of Chosen Hydrographs for Ensemble Analysis | Type of Data |
|---|---|---|
| Present (2014) | 2005–2014 | Observed |
| 2050 | 2045–2055 | Predicted based on MIROC |
| 2100 | 2089–2098 1 | Predicted based on MIROC |
| Site 1 (h) | Site 2 (h) | Site 3 (h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sea Level Rise | Dry | Normal | Wet | Dry | Normal | Wet | Dry | Normal | Wet |
| 0 m | 7.9 | 24.0 | 24.0 | 3.6 | 23.9 | 24.0 | 3.1 | 23.0 | 24.0 |
| 1 m | 0.0 | 3.8 | 23.6 | 0.0 | 0.8 | 21.2 | 0.0 | 0.4 | 18.1 |
| 2 m | 0.0 | 0.1 | 8.3 | 0.0 | 0.0 | 3.9 | 0.0 | 0.0 | 1.7 |
| Site 1 | Site 2 | |||
|---|---|---|---|---|
| Month | 11.5-m Draft (h/Day) | 20.0-m Draft (h/Day) | 11.5-m Draft (h/Day) | 20.0-m Draft (h/Day) |
| August | 24.0 | 19.8 | 23.9 | 15.0 |
| September | 22.0 | 6.1 | 16.9 | 1.1 |
| October | 15.0 | 2.3 | 9.9 | 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsz Yeung Leung, A.; Stronach, J.; Matthieu, J. Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes. J. Mar. Sci. Eng. 2018, 6, 130. https://doi.org/10.3390/jmse6040130
Tsz Yeung Leung A, Stronach J, Matthieu J. Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes. Journal of Marine Science and Engineering. 2018; 6(4):130. https://doi.org/10.3390/jmse6040130
Chicago/Turabian StyleTsz Yeung Leung, Albert, Jim Stronach, and Jordan Matthieu. 2018. "Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes" Journal of Marine Science and Engineering 6, no. 4: 130. https://doi.org/10.3390/jmse6040130
APA StyleTsz Yeung Leung, A., Stronach, J., & Matthieu, J. (2018). Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes. Journal of Marine Science and Engineering, 6(4), 130. https://doi.org/10.3390/jmse6040130




