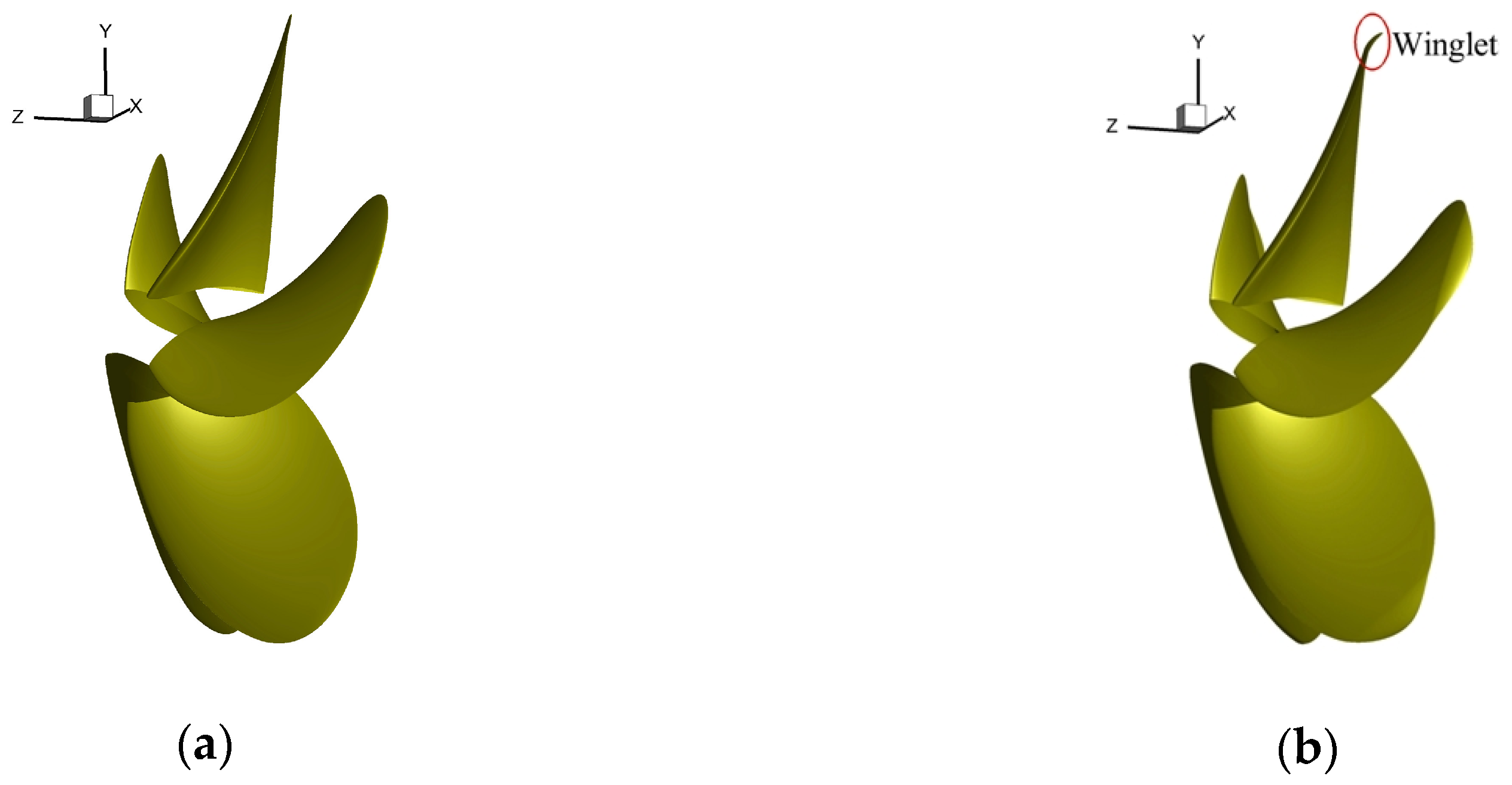Abstract
The generation of tip vortex cavitation (TVC) is a common phenomenon in marine propellers. Therefore, it is important to find a way for the effective suppression of TVC. Based on the enlightenment of bionics, a propeller with winglets was numerically investigated by using a large eddy simulation (LES) model and the commercial software STAR-CCM+. Various variables, such as mesh size, number of prism layers, vapor properties and time step, were analyzed using the benchmark MAU5-80 propeller. The open water characteristics calculated for the benchmark propeller were compared with experimental data. The meshes in the region of the tip vortex wake were refined. The power spectral density (PSD) of the thrust coefficient and axial velocity were investigated. The comparison of TVC between the benchmark propeller and the propeller with winglets was studied with the Q-criterion, helicity and volume fraction of the vapor. The strength of the tip vortex wake is weakened by winglets; therefore, the presence of winglets leads to a reduction in vapor volume, which in turn alleviates TVC.
1. Introduction
The tip vortex cavitation (TVC) of marine propellers has become an increasingly interesting issue for marine engineers, not only because of its first appearance in the cases of cavitation, but also as a major source as a sound pressure level contributor and in cavitation erosion [1,2]. Many researchers have studied the problems associated with the tip vortex in different ways. Felli and Falchi [3,4] addressed the propeller-tip vortex dynamics in interaction with a rudder, and found that the vortex lines organized in two branched structures that developed close to the sides of the rudder. Similarly, Muscari et al. [5] analyzed wall pressure spectra that related to the evolution of a tip vortex. They disclosed the non-obvious behavior of loading on the rudder that could be associated with undesirable, unsteady loads. Zhu [6] numerically studied the characteristic correlation between propeller cavitation flow and cavitation noise. Zhu [6] concluded that the low-spectrum characteristics of the noise signals were very close to the pressure signals in the wake. Baek et al. [7] studied the influence of the advance ratio on tip vortex of a marine propeller. They suggested that the empirical model of radial trajectory and the pitch of tip vortex could reflect the three-dimensional spiral in the wake of a propeller, and the proposed empirical model of tip vortex could help to construct a reliable wake model. Zhu et al. [8] investigated the propeller noise from TVC using the Ffowcs-Williams Hawkings acoustic model, and they summarized that the sound pressure level caused by TVC increased by nearly 7 dB. Asnaghi et al. [9,10] conducted a numerical and experimental analysis of the TVC inception behavior. The inception strongly depends on the initial nuclei sizes. A finer resolution resulted in a stronger tip vortex, and therefore, earlier TVC inception. Viitanen et al. [11] used a delayed detached eddy simulation and computational hydroacoustics simulations to obtain the transient characteristics in the wake of a marine propeller. They pointed out that the TVC was excellently captured with the detached eddy simulation (DES). Yilmaz et al. [12] developed an adaptive mesh refinement approach with absolute pressure as a control parameter in order to more accurately simulate TVC in the wake of a propeller. Posa et al. [13] studied the wake characteristics of a submarine propeller using a large eddy simulation (LES) model; they showed that the coherence structures shed from the inner radii of the blades were stronger than those from the outer radii. Zhang and Jaiman [14] numerically analyzed the wake dynamics of a ducted propeller, and found that the short-wave instability was the main mechanism for the breakdown of the tip vortex. Furthermore, the spectral analysis indicated much broader and more energy-containing frequencies at zero inflow.
In order to suppress the inception of TVC, researchers proposed different methods. Chang et al. [15], for example, investigated the influence of mass (i.e., water and aqueous polymer solution) injections on the inception of TVC when it occurred on an elliptic hydrofoil. Under optimum flux conditions, water injection alone resulted in a reduction of the inception cavitation number by 35%, while the addition of polymer solution reduced it by 45%. Similarly, Lee et al. [16] applied water injection to a marine propeller. They demonstrated that water injection produced a reduction of tangential velocity by 15%. Water injection could effectively delay the inception of TVC, thereby increasing the speed of cavitation inception. Lee et al. [17] experimentally studied the flexible thread attachment at the propeller blade tip. They found that the presence of a flexible thread led to a significant reduction in the field of streamwise velocity. Amini et al. [18] demonstrated, by artificially roughening the hydrofoil tip, that the hysteresis of TVC was entirely suppressed when the laminar separation bubble was avoided. By increasing the angle of attack, the jet-like behavior was enhanced, so the hysteresis was more obvious.
Novel profiles and structures from nature help to improve our limited knowledge of potential options. Biomimetic technology has gradually been applied to the shipbuilding industry. Gao and Zhu [19], for example, investigated a bionic rudder with a sinusoidal leading-edge protuberance. They suggested that the big advantage of such a bionic rudder was mainly manifested in the post-stall regime, and the maximum lift coefficient of this bionic rudder was nearly 9.4% higher than that of conventional rudders at Re = 8 × 105. Zaky et al. [20] discussed the effect of bionic rudders with a fishtail section on maneuverability. The results indicate that the bionic rudder with a fishtail section increases the effective rudder force by approximately 10%, and improves the maneuverability of the Very Large Crude Oil Carrier with a 30% reduction in Energy Efficiency Design Index compared to a conventional rudder. Busch et al. [21] studied the biomimetic surface which helped to stabilize the air layer on the surface of hulls for a long time, and they concluded that the bionic surface provides a reduction of drag by 20% and additional antifouling properties. Based on the winglets of avian wings, Ghassemi et al. [22] numerically studied the influence of the rake angle of the blade tip on the open water characteristics and sound pressure level (SPL) around marine propellers. Higher positive and negative rake angles resulted in slightly less efficiency and significantly lower SPL. Similarly, Gao et al. [23] investigated five winglet-propellers with the Reynolds Average Navier-Stokes (RANS) and volume of fluid (VOF) models. The big advantage of winglets was in the suppression of TVC. Muscari et al. [24] pointed out that the RANS method could well predict open water characteristics, such as thrust coefficients and torque coefficients, with a relatively low number of meshes. However, when the unsteady fluctuation or the instability process was of interest, the RANS model proved to be too dissipative. In contrast, the DES model could track the field of a tip vortex for a long distance and successfully predict the instabilities in the wake, which was in good quantitative and qualitative agreement with experiments. In addition, after comparing the cavitation characteristics between the DES model and the LES model, Yilmaz et al. [12] concluded that the LES model was the preferred model for investigating TVC. In contrast to the RANS equations, the equations that are solved for a LES are obtained by a spatial filtering rather than an averaging process. Therefore, the LES turbulence model is used to numerically study a propeller with winglets herein.
2. Models and Methods
2.1. Geometric Model
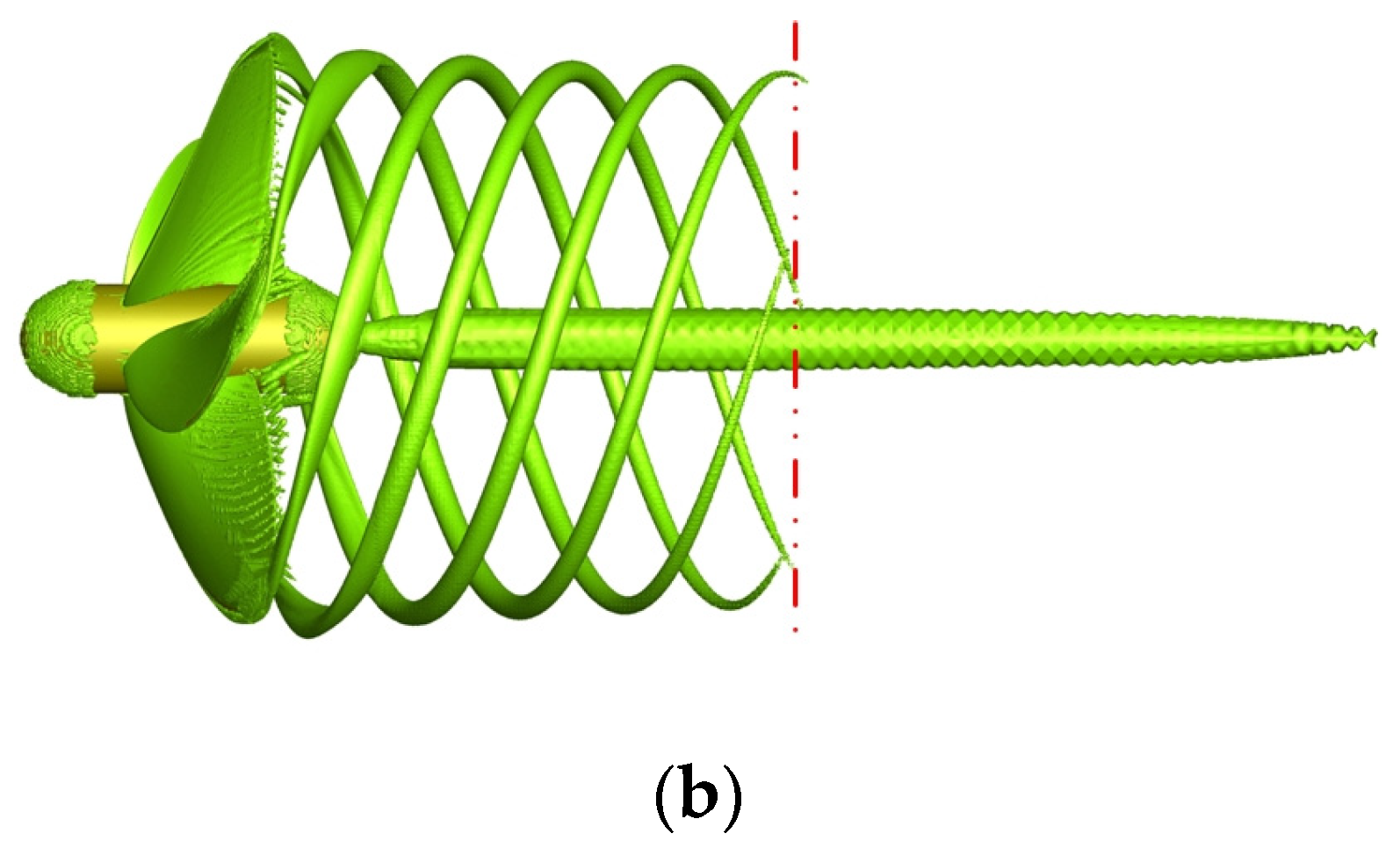
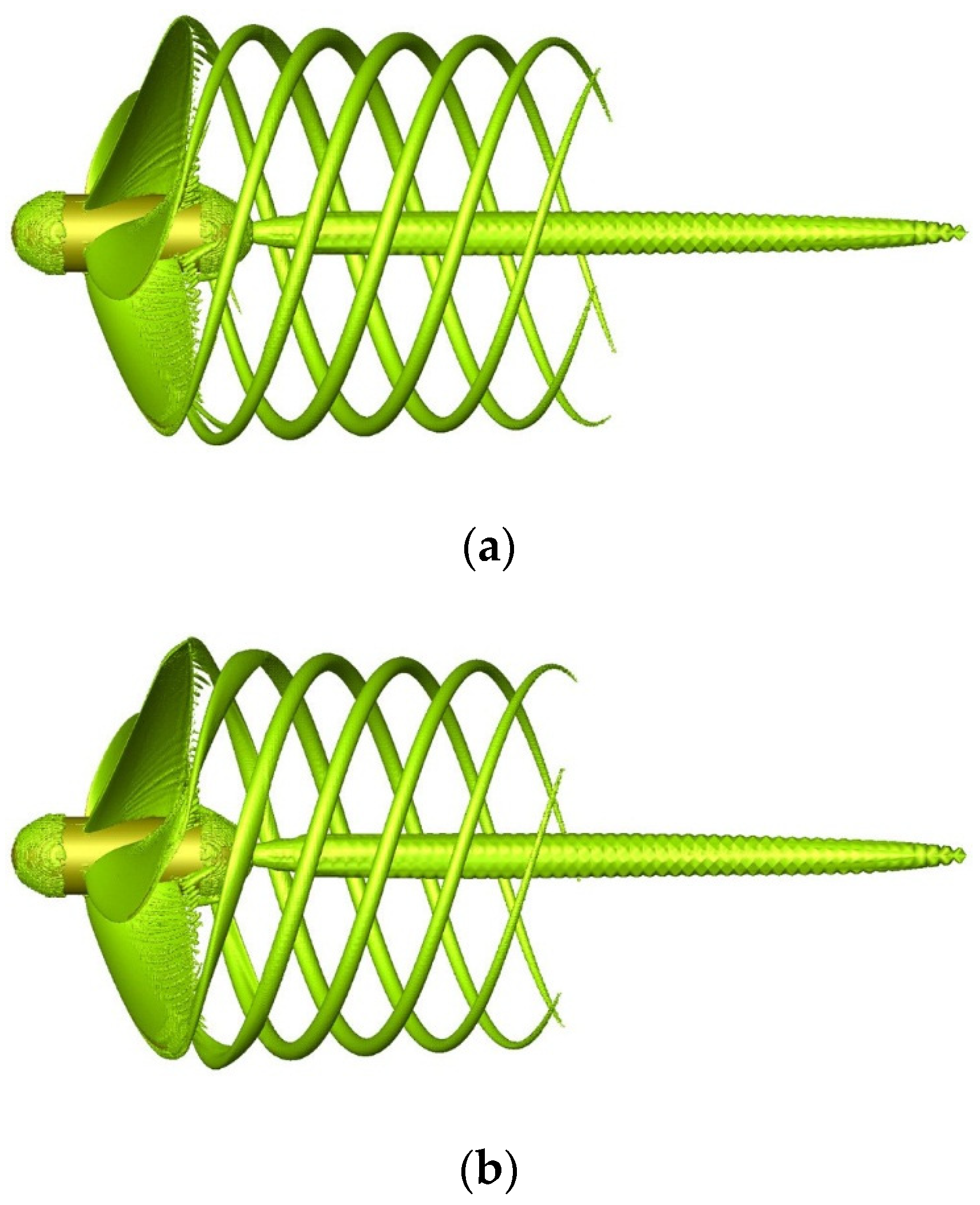
At present, the modified AU-type (MAU) series propeller and Wageningen B-screw series propeller are widely applied for merchant vessels. In this study, the MAU5-80 propeller (Transportation Technical Research Institute of Transportation Ministry, Japan) model was taken as the benchmark model. The main details of the MAU5-80 propeller are listed in Table 1. The hydrodynamic performance of the MAU5-80 propeller was measured in a ship experiment tank by Yazaki et al. [25], and more information on the MAU5-80 propeller, such as geometric parameters and ordinates at various radial positions, can be obtained from Tsuchida et al. [26]. In addition, the winglets of propeller adopted the winglets B (i.e., rake angle at r/R = 1.0 is equal to 12°), while further details of the winglets B propeller can be found in Gao et al. [23]. The geometry of the propeller is shown in Figure 1.

Table 1.
Propeller geometry.

Figure 1.
Propeller geometric model: (a) benchmark propeller and (b) the winglet-propeller, whose blade tips tilt toward the wake of the propeller.
2.2. Mesh Quality
The mesh is an inherent part of a numerical solution. The trimmed mesher, prism layer mesher and surface remesher were selected to control the construction of surface and volume meshes. Three different arrangements of the mesh (i.e., fine, medium and coarse) were set up by increasing the resolution of the mesh in order to analyze the effect of the mesh size on the thrust coefficient, torque coefficient and the volume of the TVC. These three meshes all had fifteen prism layers. The seed diameter and seed density were equal to 1.0 × 10−7 m and 1.0 × 1014 1/m3, respectively. Figure 2 illustrates the generated fine mesh in the whole computational domain and the mesh on the blade surface. In this work, the analysis mainly focused on the tip vortex in the wake of the propeller. Therefore, the mesh in the wake of the blade tip and in the vicinity of the blade tip was refined.

Figure 2.
Mesh characteristics: (a) whole computational domain and (b) blade surface.
Figure 3 depicts the volumetric control refinement for the tip vortex. The shape of the volumetric control is a hollow cylinder. The outer radius of the hollow cylinder is 1.2R, and the inner radius is 0.8R. The same mesh arrangements of the computational domain were also applied for the winglet-propeller. Details of the three different meshes are summarized in Table 2, and the other parameters of the three different meshes are identical. The number of cells of the fine mesh is approximately 11.12 million, 0.26 million of which belong to the stationary domain.
Figure 3.
Volumetric control refinement for the tip vortex.

Table 2.
Mesh details.
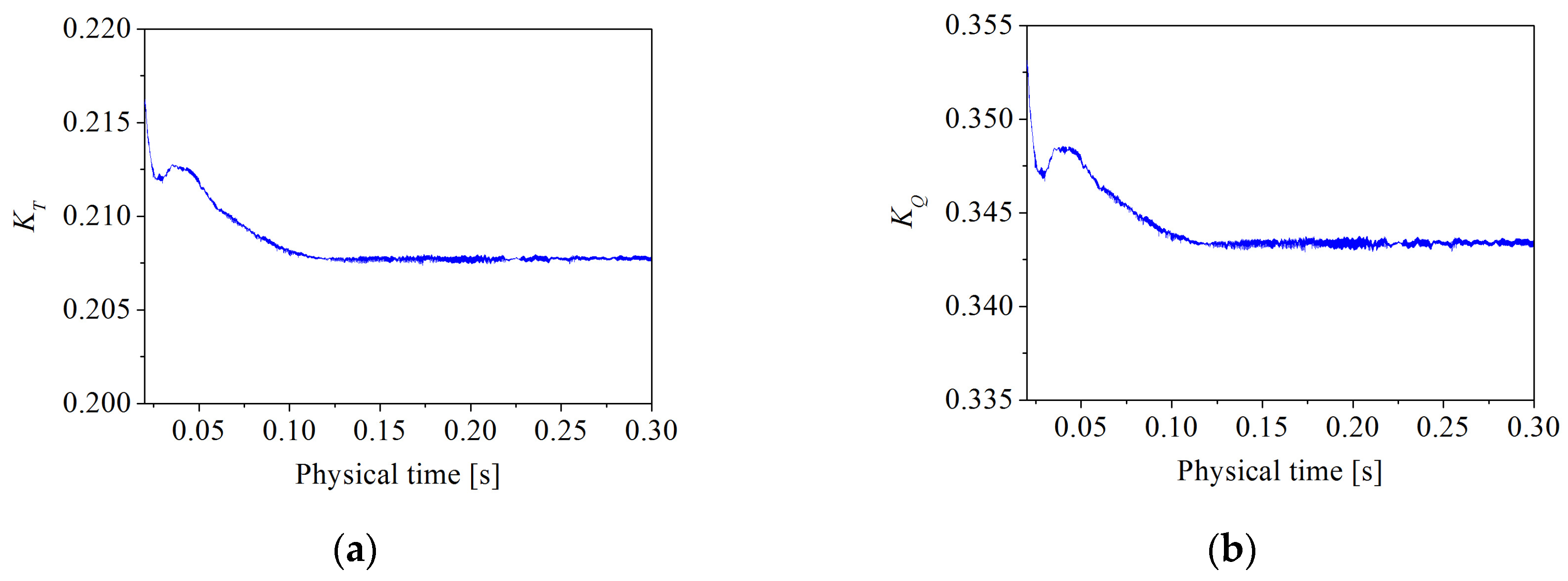
The values of thrust and torque coefficients as a function of physical time at advance coefficient J = 0.7 are reported in Figure 4. Because the thrust and torque of the propeller are unstable at the beginning of the revolution, the physical time on the abscissa started at 0.02 s. The values tend to stabilize with increasing physical time. Therefore, the time-averaged values solved from 0.29 to 0.3 s were taken as the results of thrust KT or torque coefficients KQ; i.e., 1/4 propeller revolutions were used for time-averaging in the following.
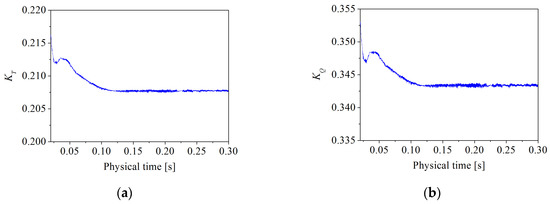
Figure 4.
Thrust and torque coefficients as a function of physical time at advance coefficient J = 0.7: (a) thrust coefficient KT and (b) torque coefficient KQ.
For the three different arrangements of mesh (Table 2), the method of grid convergence index (GCI) is used to estimate the discretization error [27,28]. The mesh convergence ratio and the parameters of discretization error, such as the apparent order of the method , the extrapolated value , the approximated relative error , the extrapolated relative error and the fine mesh convergence index , are defined as follows:
where represents the mesh refinement ratio, and represents the sign function. , and represent the values calculated by the kth mesh. The volume of vapor (Vvap) is expressed in a dimensionless form (i.e., ratio of vapor volume to cube of propeller diameter). The discretization errors in regard to vapor volume, thrust coefficient and torque coefficient at advance coefficient J = 0.7 with three different meshes are listed in Table 3. The mesh convergence ratios RG for vapor volume, thrust coefficient and torque coefficient are all greater than zero and less than one (Table 3); therefore, the grid convergence state is monotonic convergence. The fine mesh convergence indexes for thrust and torque coefficients are both very small, and the fine mesh convergence index for the vapor volume is 0.36%. According to these computed results, an increase of mesh numbers, with respect to the fine mesh, can result in a variation on the vapor volume, and this variation is considered acceptable. Hence, the mesh sizes in the case of the fine mesh were applied to the meshing process of winglet-propeller.

Table 3.
Discretization errors with regard to Vvap/D3, KT and 10KQ.
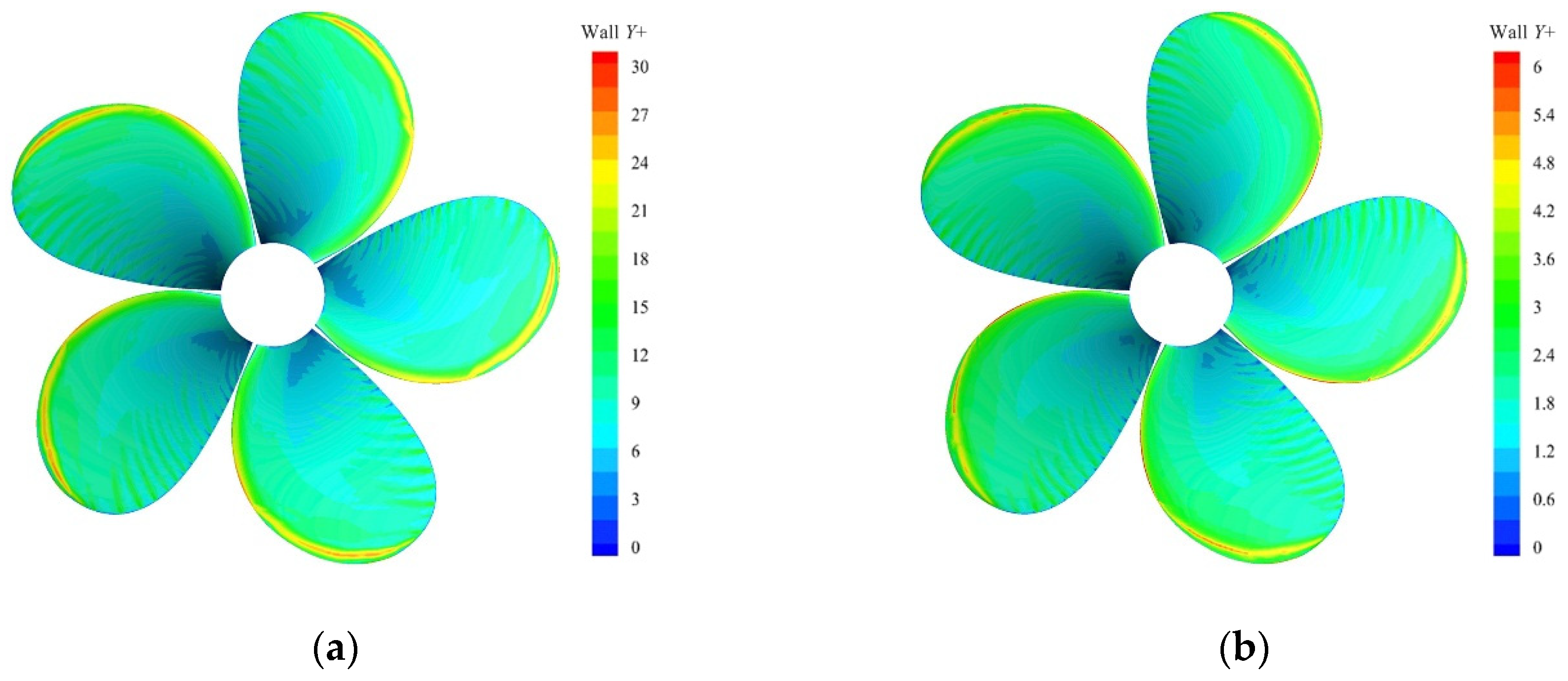
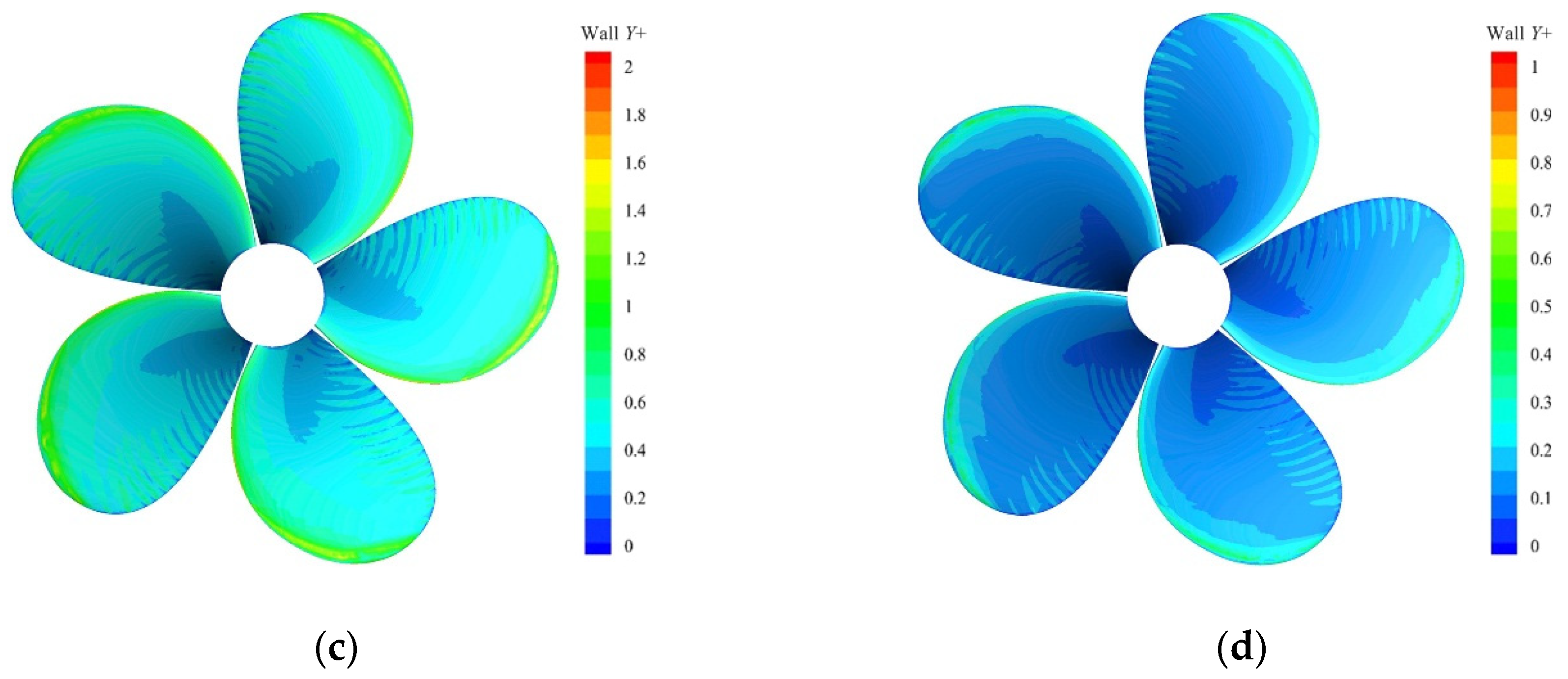
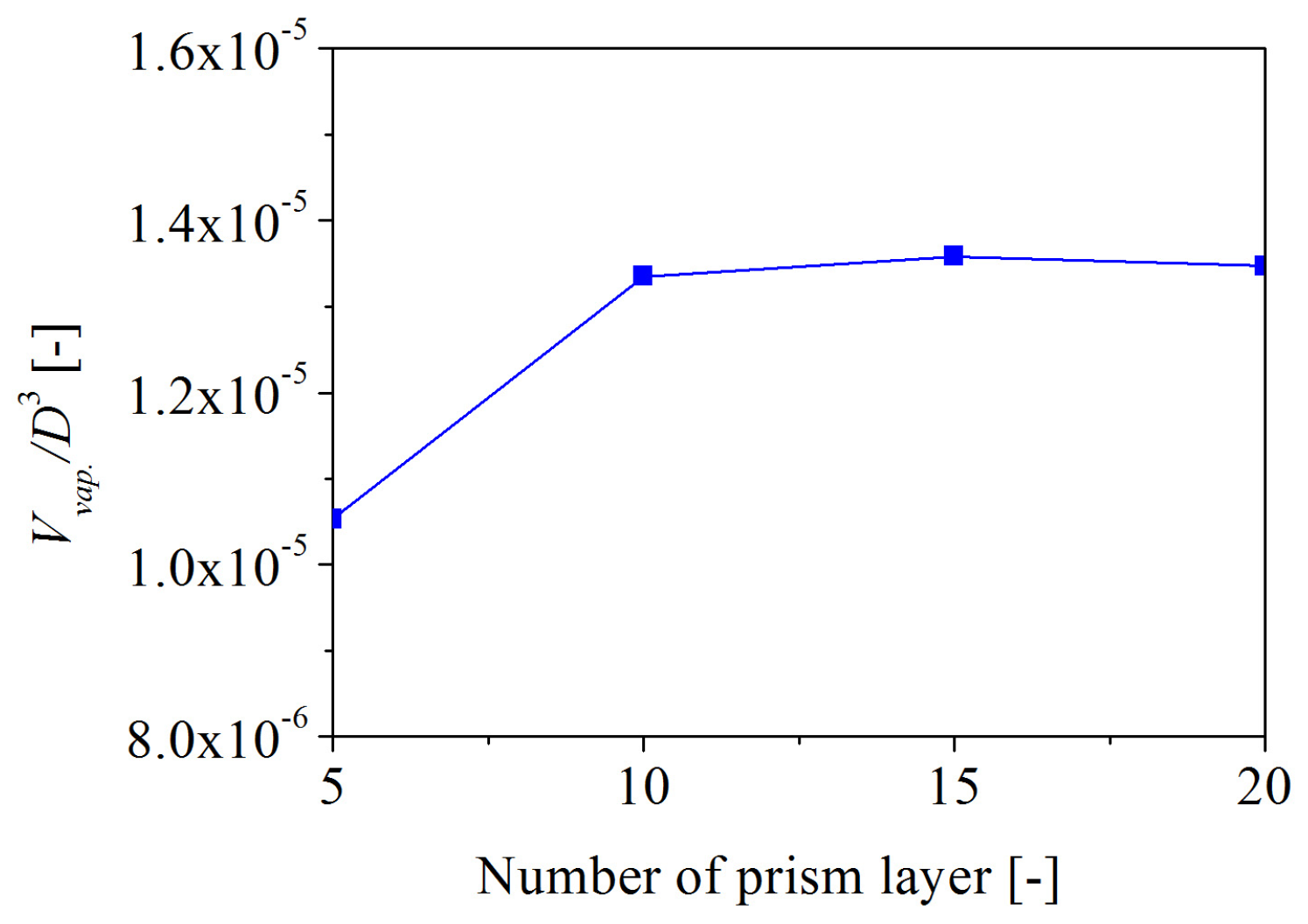
The LES model requires a substantially finer mesh than typically used for RANS simulations. The main shortcoming of the LES model lies in the high-resolution requirements for wall boundary layers, which often results in excessive resolution requirements for the prism layers. Therefore, four different arrangements of prism layers were analyzed by changing the number of prism layers on the blade surface. The thickness of the prism layers of all different arrangements was 0.46 mm [23], and the growth rate of prism layers was 1.3. The study of the prism layers’ estimations was conducted for the case of fine mesh size. The contours of wall Y+ on the blade surface at J = 0.7 with different prism layers are summarized in Figure 5. The main purpose of this paper is to study the tip vortex. With respect to the case of 15 layers, the value of wall Y+ in the vicinity of the leading edge and blade tip is around 1. Figure 6 shows that the increase of the prism layers, in respect to the case of 15 layers, leads to a variation in the volume of vapor lower than 1%. Increasing the number of prism layers may increase the accuracy of the solution, but it requires more cells and time to perform the calculation. Therefore, fifteen prism layers on the blade surface are considered to be a good compromise between the computational time and the accuracy of the solution. For a wall-resolved LES, the mesh spacing scaling (x+ and z+) is an important factor [13,29]. For the fine mesh case with 15 prism layers, the baseline mesh resolution on the propeller blades follows both x+ and z+ below 100, where x is the spanwise direction, and z is the streamwise direction. The finer mesh resolution was applied to the region of the blade tip.
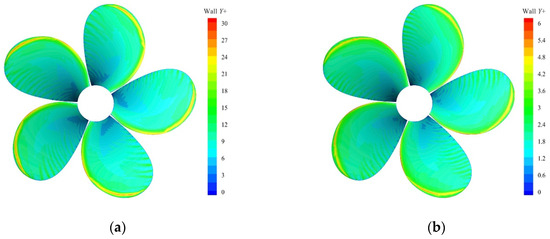
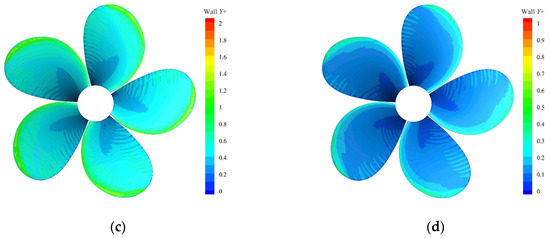
Figure 5.
Contours of wall Y+ on blade surface at J = 0.7: (a) five layers; (b) 10 layers; (c) 15 layers; and (d) 20 layers.
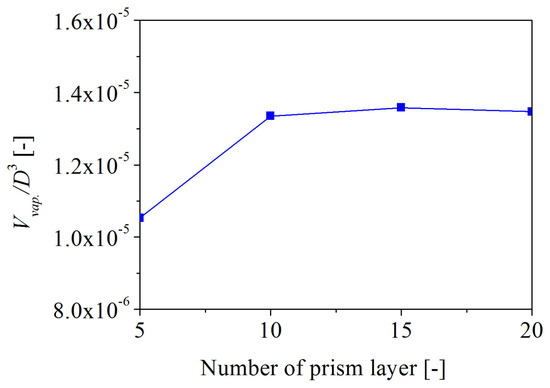
Figure 6.
Effect of prism layer on vapor volume.
2.3. Modeling Physics
The LES is an inherently transient technique in which the large scales of the turbulence are resolved everywhere in the flow domain, and the small-scale motions are modeled. Previously, many researchers have used the LES model to study the tip vortex on marine propellers, such as Lu et al. [30], Bensow [31] and Kumar and Mahesh [32]. Therefore, the LES model was used to investigate a winglet-propeller. The simulations were performed on two identical supercomputers. Each supercomputer consisted of 24 cores with Inter Xeon E5-2695 v3 (2.3 GHz) dual processors and 128 GB RAM.
The Eulerian multiphase flow model and the Schnerr–Sauer cavitation model [33] were selected to implement the phase interaction. This cavitation model, which neglects the effect of bubble growth acceleration, viscous effects and surface tension effects, implements a reduced Rayleigh–Plesset equation. The values of the seed diameter and seed density are very important for the material properties of multiphase flow. Therefore, the analysis of these two parameters is necessary to ensure accurate simulation. The cavitation number σ is defined as
where denotes the reference pressure and represents the vapor pressure of water, corresponding to the saturation pressure. The saturation pressure was selected as 2339 Pa (i.e., saturation temperature at about 20 °C) and the present study was conducted at σ = 2.0.
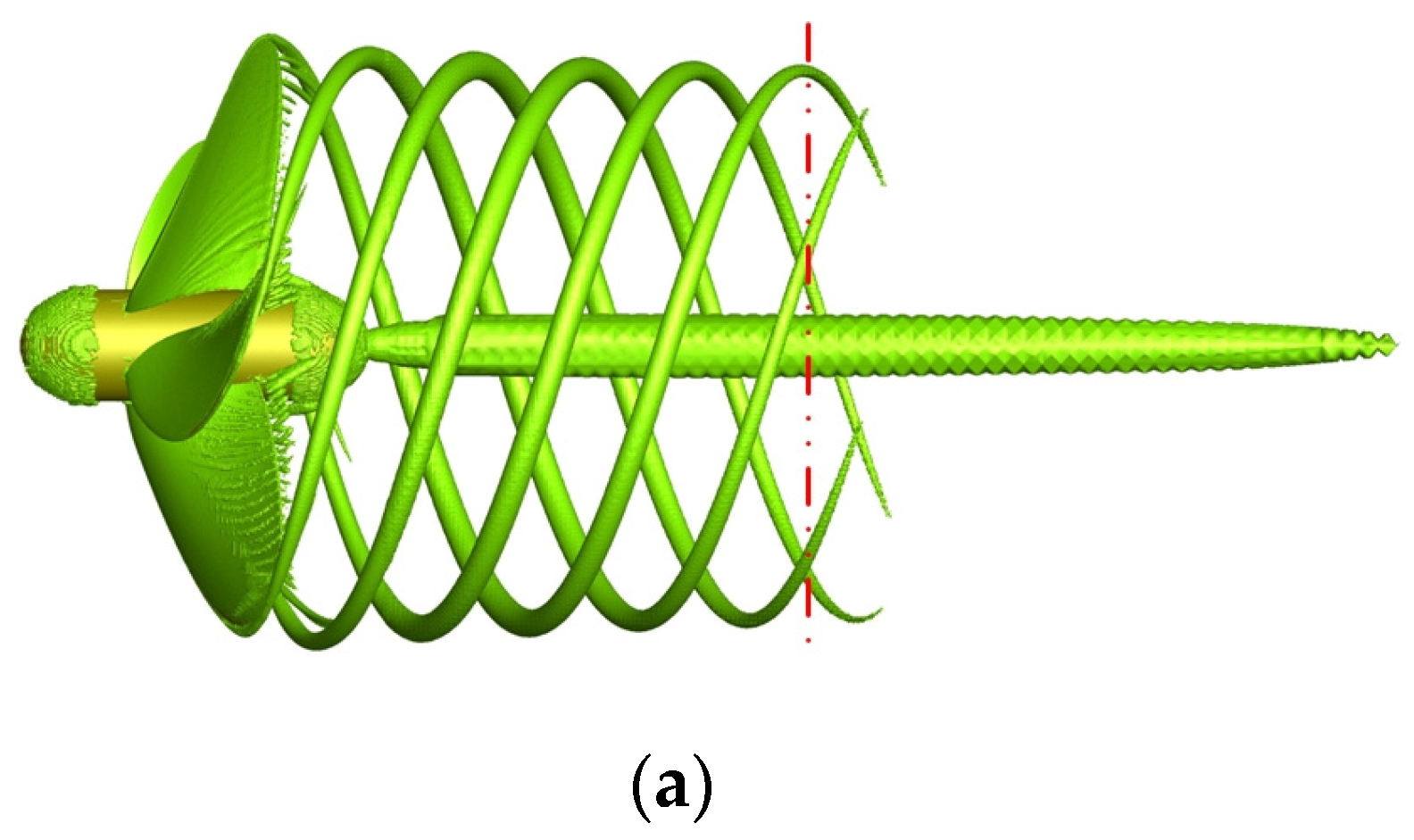
Since an implicit unsteady solver was used for the analytical solution, the solution was related to the physical time. In addition, the adopted results of this paper were considered to be stable. Therefore, the influence of the physical time on the tip vortex wake is discussed. A time step of 1 × 10−4 s was selected to investigate the influence of the physical time. As illustrated in Figure 7, the wake of the tip vortex was well captured in the simulation. When the physical time was 0.2 s (corresponding to five revolutions), the wake of the tip vortex was not yet stable, but it could be considered stable at 0.3 s (7.5 revolutions). Therefore, the following numerical results were all obtained at 0.3 s.
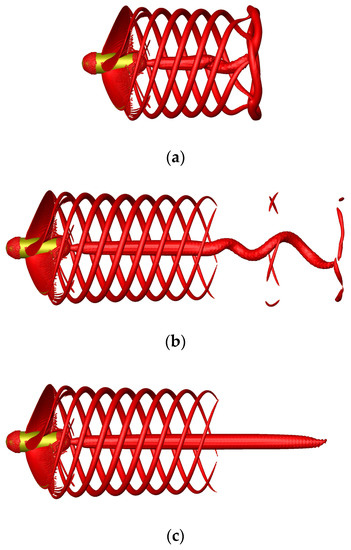
Figure 7.
Effect of the physical time on the tip vortex wake (iso-surface of Q = 8.0 × 103 1/s2): (a) 0.1 s; (b) 0.2 s and (c) 0.3 s.
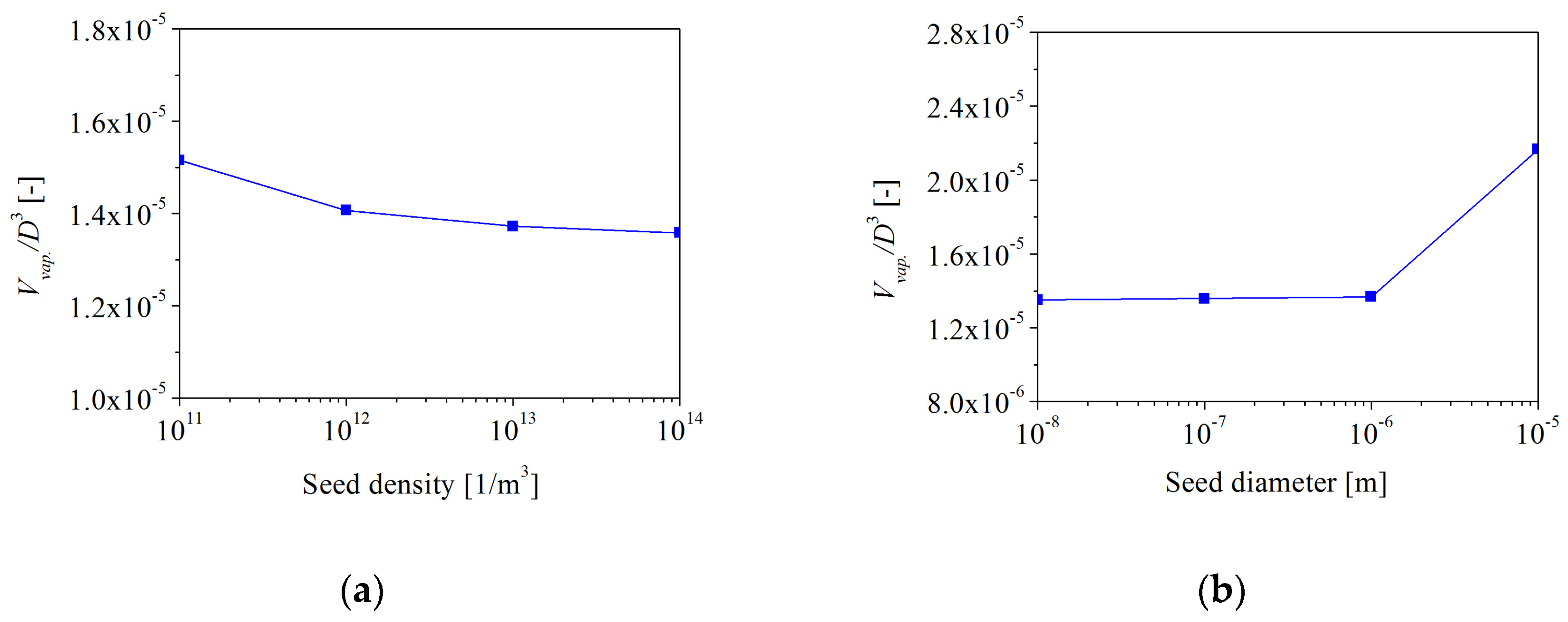
The number of vapor nuclei selected by different scholars has varied [12,34]. Since the vapor properties have little effect on the thrust and torque, the influence of the vapor properties on the vapor volume is relatively large. Hence, this study only considered the impact of the vapor properties on the vapor volume. Figure 8a relies on a constant seed diameter (i.e., 1 × 10−7 m), and Figure 8b relies on a constant seed density (i.e., 1 × 1014 1/m3). The vapor volume gradually decreases with increasing seed density, and the difference in vapor volume between 1 × 1013 and 1 × 1014 1/m3 is only about 1%. In order to minimize the effect of seed density on vapor volume as far as possible, the value of 1 × 1014 1/m3 was selected to investigate TVC. When the seed diameter was equal to 1 × 10−4 m, the simulation was easy to parse. Gaggero et al. [2] and Yilmaz et al. [12] chose a value of 1 × 10−6 m. Therefore, the range of seed diameter from 1 × 10−8 to 1 × 10−5 m was investigated in this paper. When the seed diameter is smaller than 1 × 10−7 m, the variation of the seed diameter has a negligible influence on the vapor volume. Based on the above analysis, the selected values of the seed density and seed diameter for this investigation were 1 × 1014 1/m3 and 1 × 10−7 m, respectively.
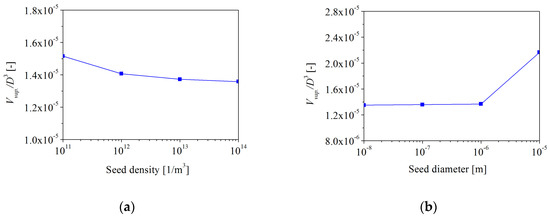
Figure 8.
The effect of vapor properties on vapor volume: (a) seed density and (b) seed diameter.
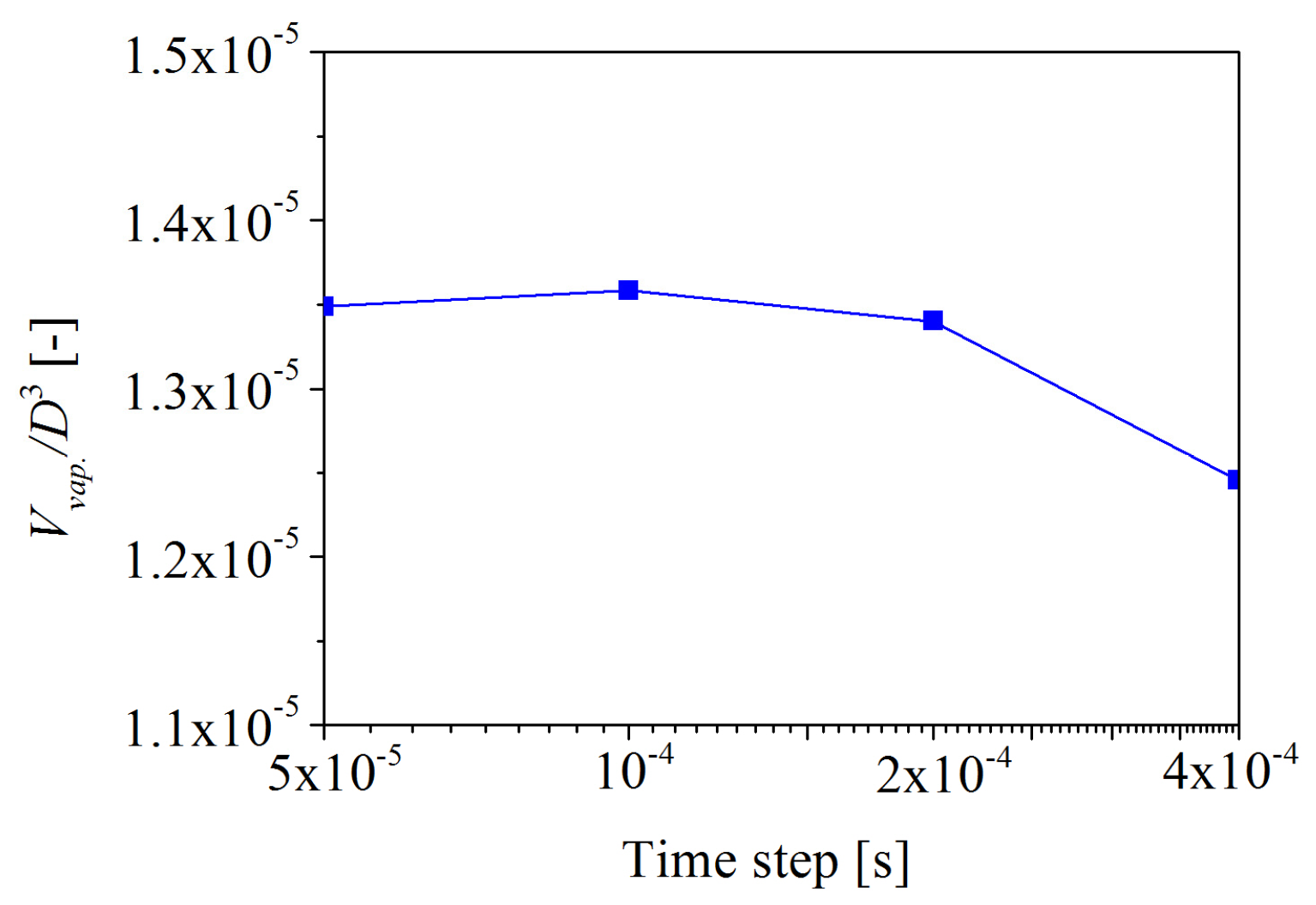
The time step Δt specified by different researchers varies, but the order of magnitude is mostly between 10−5 and 10−4 s [35,36,37]. Since the rotation speed was specified as 25 rps in the present investigation, the time step of 1 × 10−4 s corresponds to a rotation of 0.9° (i.e., the time for one rotation is 0.04 s). Therefore, the value of time step was investigated from Δt = 5 × 10−5 to 4 × 10−4 s, and the corresponding revolution angle per time step is summarized in Table 4. The impact of the time step on the volume of the TVC was implemented at J = 0.7 by using the fine mesh of the conventional propeller, and the calculated results are depicted in Figure 9. The difference in the volume of the TVC between Δt = 5 × 10−5 and 1 × 10−4 s is less than 1%. Hence, the more economical time step of 1 × 10−4 s was preferred for this simulation. The smaller time step may slightly increase the accuracy of the simulation but will lead to a very high computational time. The Courant–Friedrichs–Levy number CFL = VΔt/Δx, where V denotes the magnitude of the velocity and Δx = 0.375D% the length interval. The main purpose of this paper was the study of the blade tip. Thus, the magnitude of the velocity at the blade tip was about 20 m/s at J = 0.7. The CFL number in the case of Δt = 1 × 10−4 s is approximately 2.

Table 4.
Corresponding revolution angle.
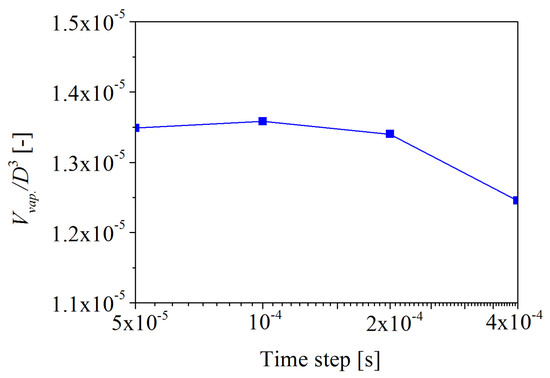
Figure 9.
The effect of time steps on vapor volume at J = 0.7.
The benchmark propeller is the MAU5-80 propeller tested by Yazaki et al. [25]. The thrust and torque coefficients were monitored for the benchmark propeller at advance coefficients J = 0.6 and 0.7, and the Reynolds number at r/R = 0.7 was approximately 1.4 × 106. The relative error of the numerical results is defined by the ratio of the difference between the numerical simulation result (CFD) and the experimental data (Test). As reported in Table 5, the relative error was about 5% in regard to the thrust coefficient and propulsion efficiency. In addition, the relative error of the torque coefficient was less than 1%.

Table 5.
Model verification.
3. Results and Discussion
3.1. Power Spectral Density (PSD)
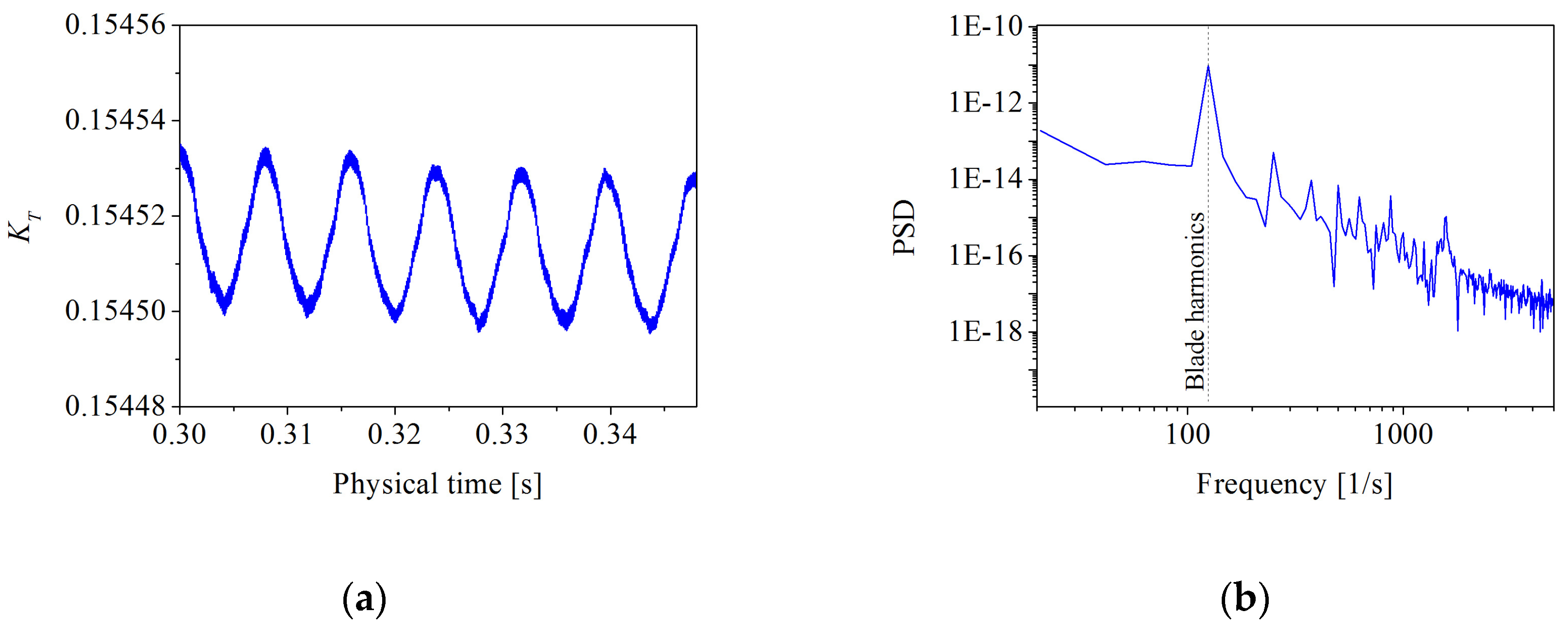
When the LES model is used, the effect of turbulent fluctuations on propeller performance should be analyzed. Many researchers carried out the analysis the PSDs of the different signals [38,39,40]. Therefore, the PSD of the thrust coefficient was investigated in the present paper. The time histories and frequency domain of the thrust coefficient KT are shown in Figure 10a,b respectively. The fluctuation amplitude of the thrust coefficient was about 4 × 10−5, and the amplitude of the PSD of the thrust coefficient was less than 1 × 10−10.
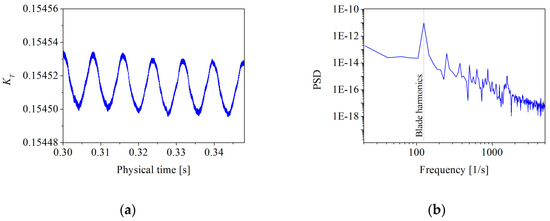
Figure 10.
Thrust coefficient at J = 0.8: (a) time histories and (b) frequency domain.
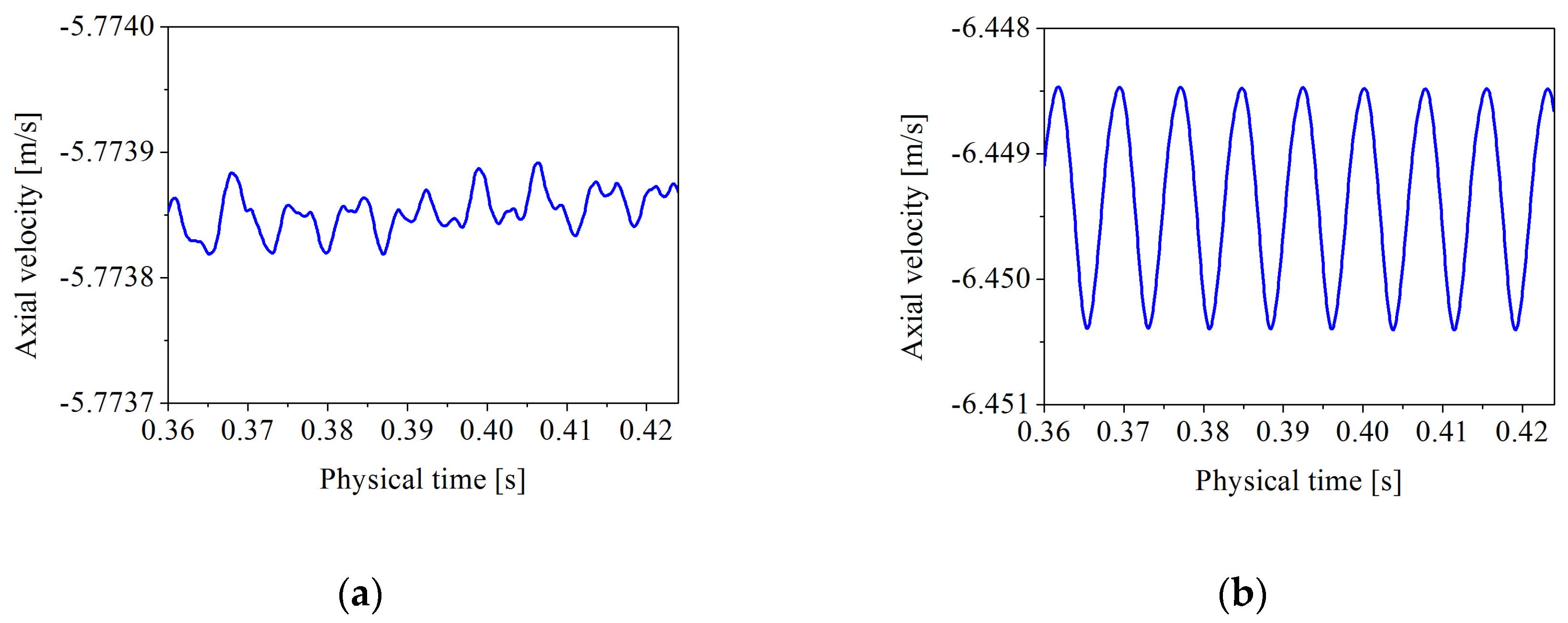
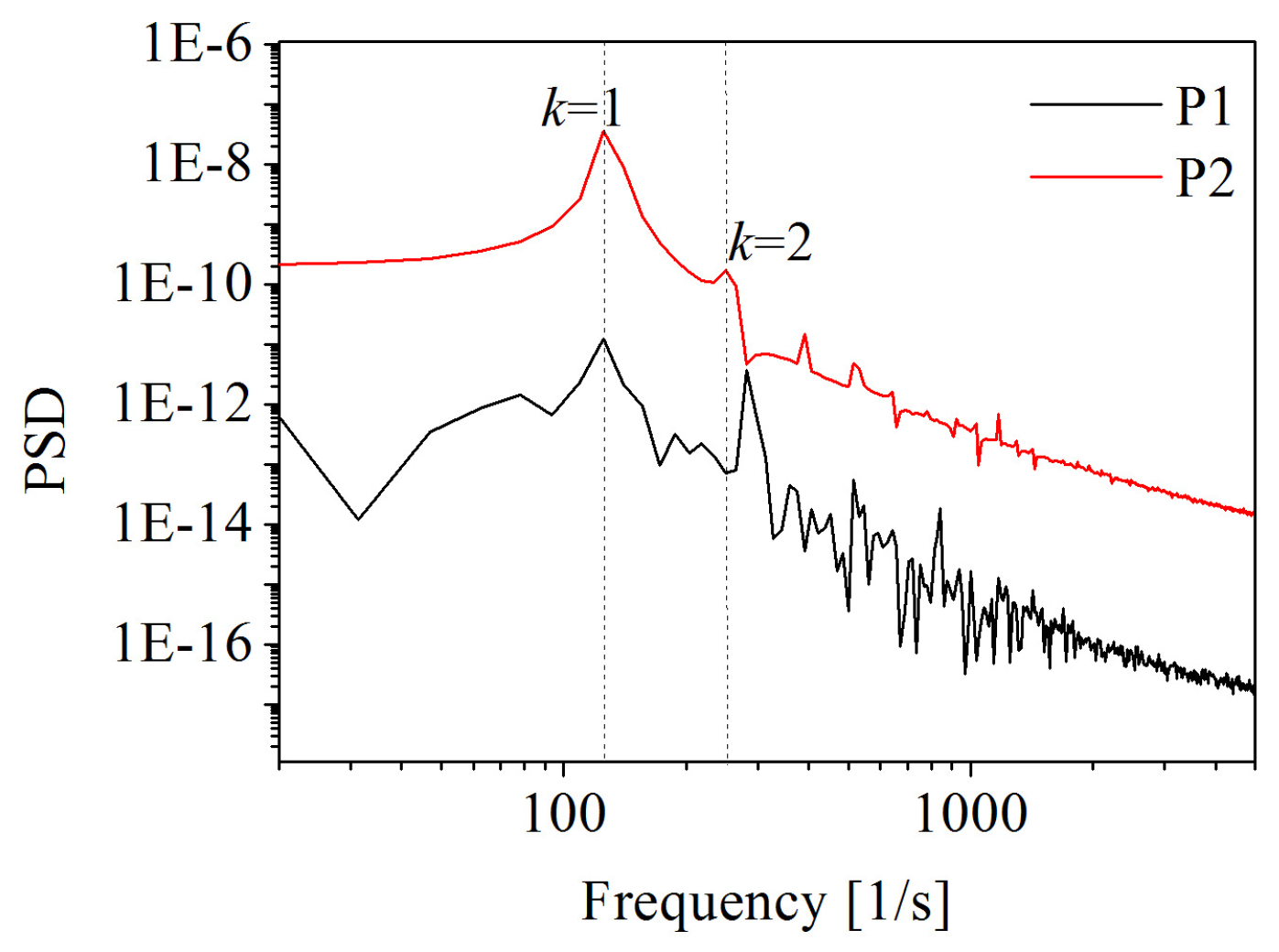
The axial velocity signals in the propeller wake and the PSD of axial velocity were numerically predicted at two locations; i.e., coordinates P1 (0, 0.9R, −0.5R) and P2 (0, 0.5R, −1.0R). As reported in Figure 11, the monitoring points were both stable in fluctuation. The fluctuation amplitude of axial velocity at point P2 was greater than the fluctuation amplitude at point P1. In addition, the PSD of axial velocity at point P2 was higher than that at point P1, as can be seen from Figure 12. The spectrum of point P2 exhibits some sharp peaks at the blade frequency. The blade frequency was k = 1. While, in the wake of near blade tip, due to the instability of the flow and the existence of cavitation, the spectrum of point P1 has only one sharp peak at the blade frequency. The second highest sharp peak is not at the blade frequency of k = 2.
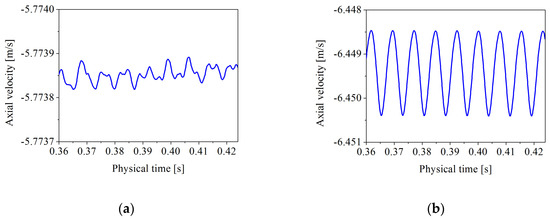
Figure 11.
Axial velocity as a function of physical time at different locations: (a) P1 (0, 0.9R, −0.5R) and (b) P2 (0, 0.5R, −1.0R).
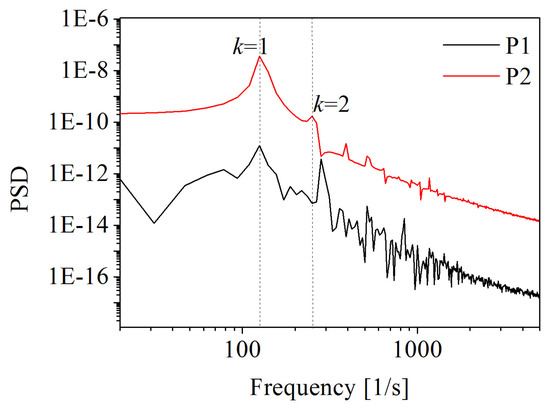
Figure 12.
Power spectral density (PSD) of axial velocity at different locations.
3.2. Tip Vortex Wake
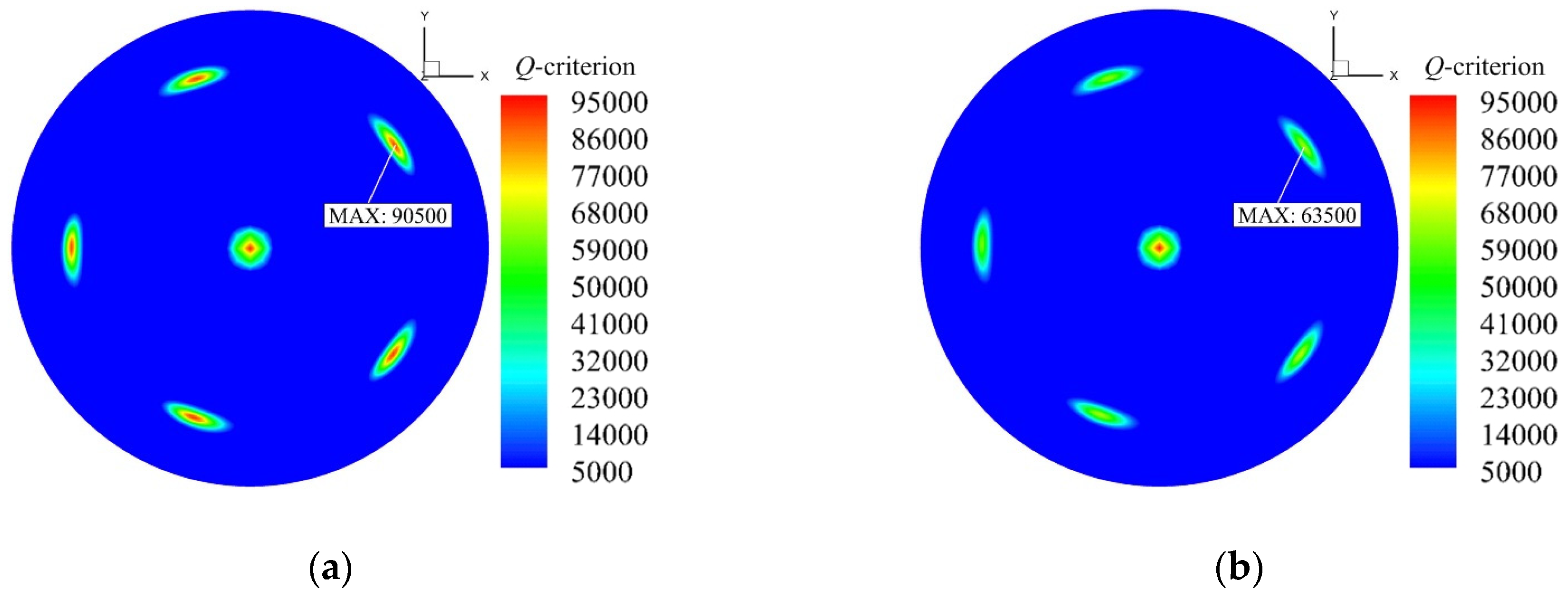
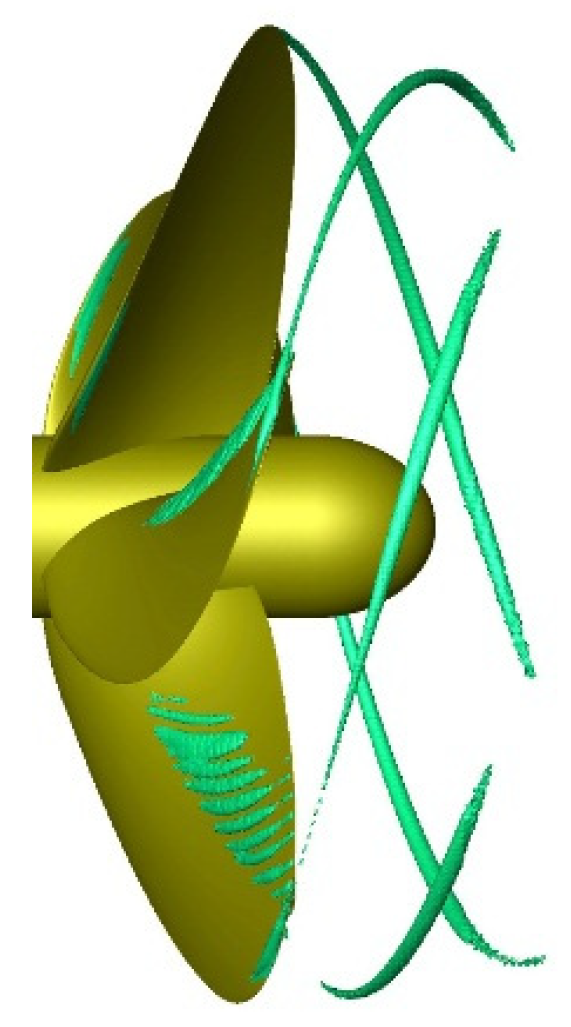
The numerical results of the winglet-propeller were compared to the benchmark propeller in terms of the tip vortex wake. As the iso-surface of the Q-criterion can directly reflect the structure of the tip vortex, Figure 13 presents the comparison of the tip vortices between the benchmark propeller and winglet-propeller at J = 0.7 with iso-surfaces of Q = 2.0 × 104 1/s2. In the propeller axial direction, the length of the tip vortex structure produced by the winglet-propeller was shorter than that produced by the benchmark propeller. Due to flow acceleration in the wake of the propeller, the diameter of the helices in the radial direction was reduced (Figure 13). This is why the inner radius of the hollow cylinder for the mesh refinement around the tip vortex wake started from 0.8R. The winglets have no effect on the propeller hub vortex, which was not considered in this study. Figure 13 only shows the change of the tip vortex in the axial direction. In the radial direction it was difficult to distinguish the difference in the tip vortex strength. Therefore, the contours of the Q-criterion in the radial cross-section Z/R = −1.0 are depicted in Figure 14. The maximum Q-criterion value at the tip vortex core center of the benchmark propeller was 90,500 1/s2, while the maximum Q-criterion value of the winglet-propeller was 63,500 1/s2. It can be inferred that the strength of the blade tip vortex is weakened by the winglets.
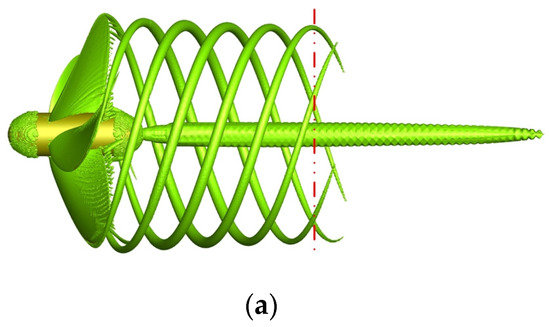
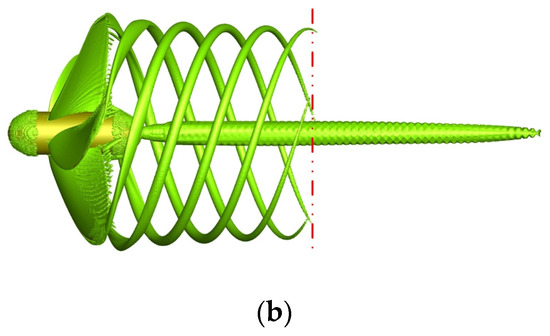
Figure 13.
Iso-surface of Q = 2.0 × 104 1/s2 at J = 0.7: (a) benchmark propeller and (b) winglet-propeller.
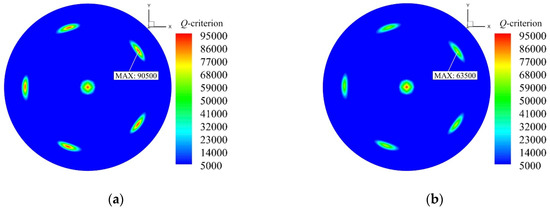
Figure 14.
Contours of the Q-criterion at J = 0.7, Z/R = −1.0: (a) benchmark propeller and (b) winglet-propeller.
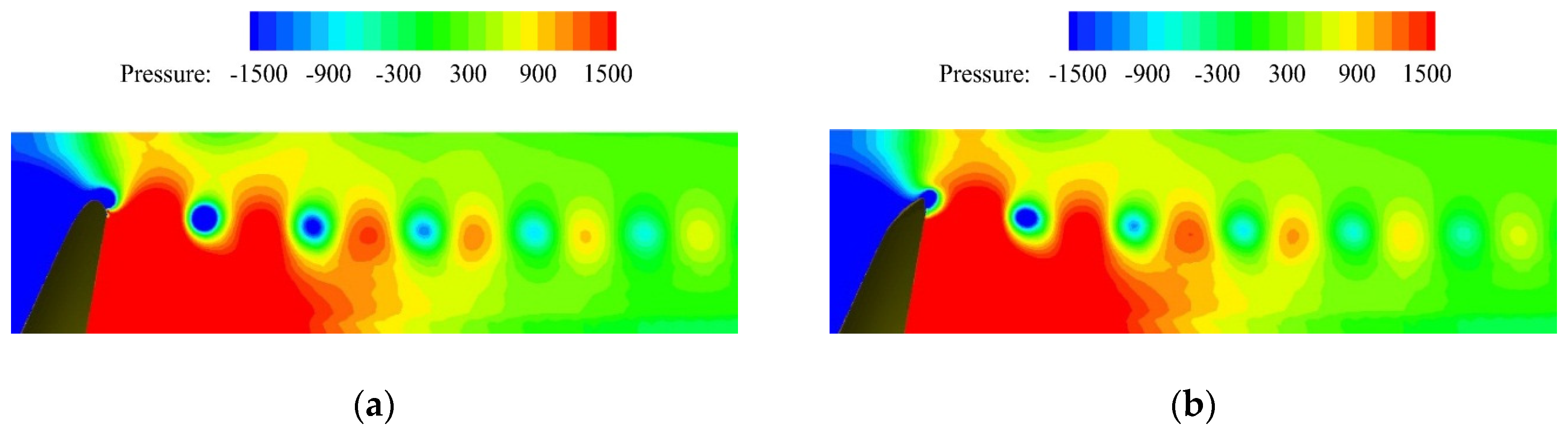
The flow field in the wakes of two propellers was analyzed by means of the contour of pressure on the plane X = 0. In order to clearly display the flow field of the tip vortex, the wake of the propeller is partially intercepted in Figure 15. It is noteworthy that as for each vortex core in the wake of the propeller, the lowest pressure occurred at the center of the vortex core. It can been seen from the second vortex core downstream the propeller that the pressure at the center of the winglet-propeller-tip vortex was higher than that of the benchmark propeller. In other words, owing to the existence of winglets, the pressure of the tip vortex can be improved.
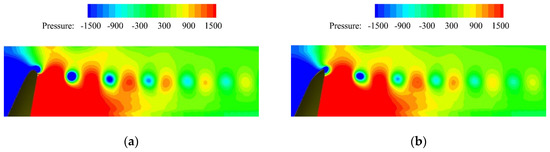
Figure 15.
Contours of pressure in the wake of the propeller at J = 0.7: (a) benchmark propeller and (b) winglet-propeller.
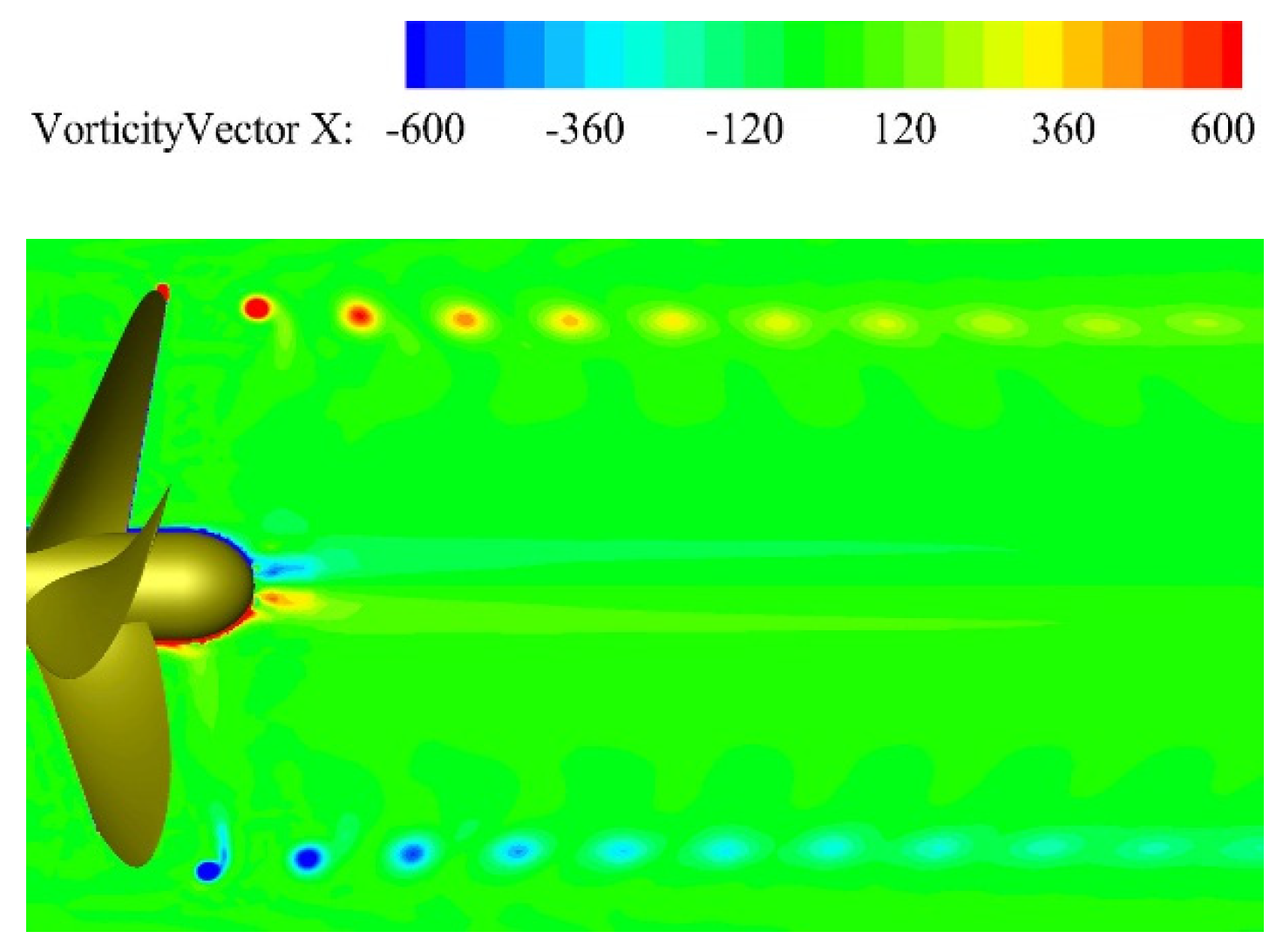
The X-component of the vorticity vector is extracted from the field on the YZ plane, as depicted in Figure 16. The tip vortices and hub vortices are of opposite sign. It can also be seen that the tip vortices are closer to their own axial plane as the wake evolves from the near field to the intermediate field. The LES model can nicely capture the field of tip vortex over a long distance in the wake of the propeller.
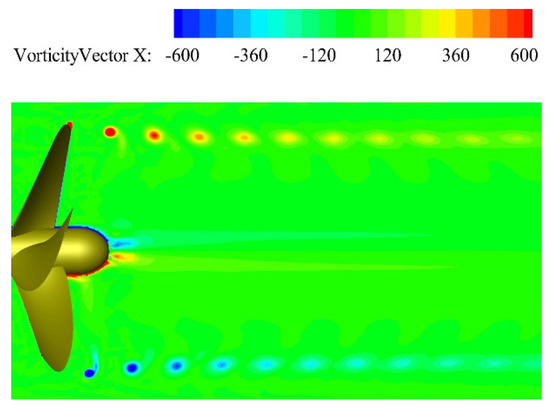
Figure 16.
Vorticity vector X at J = 0.7 (on the YZ plane).
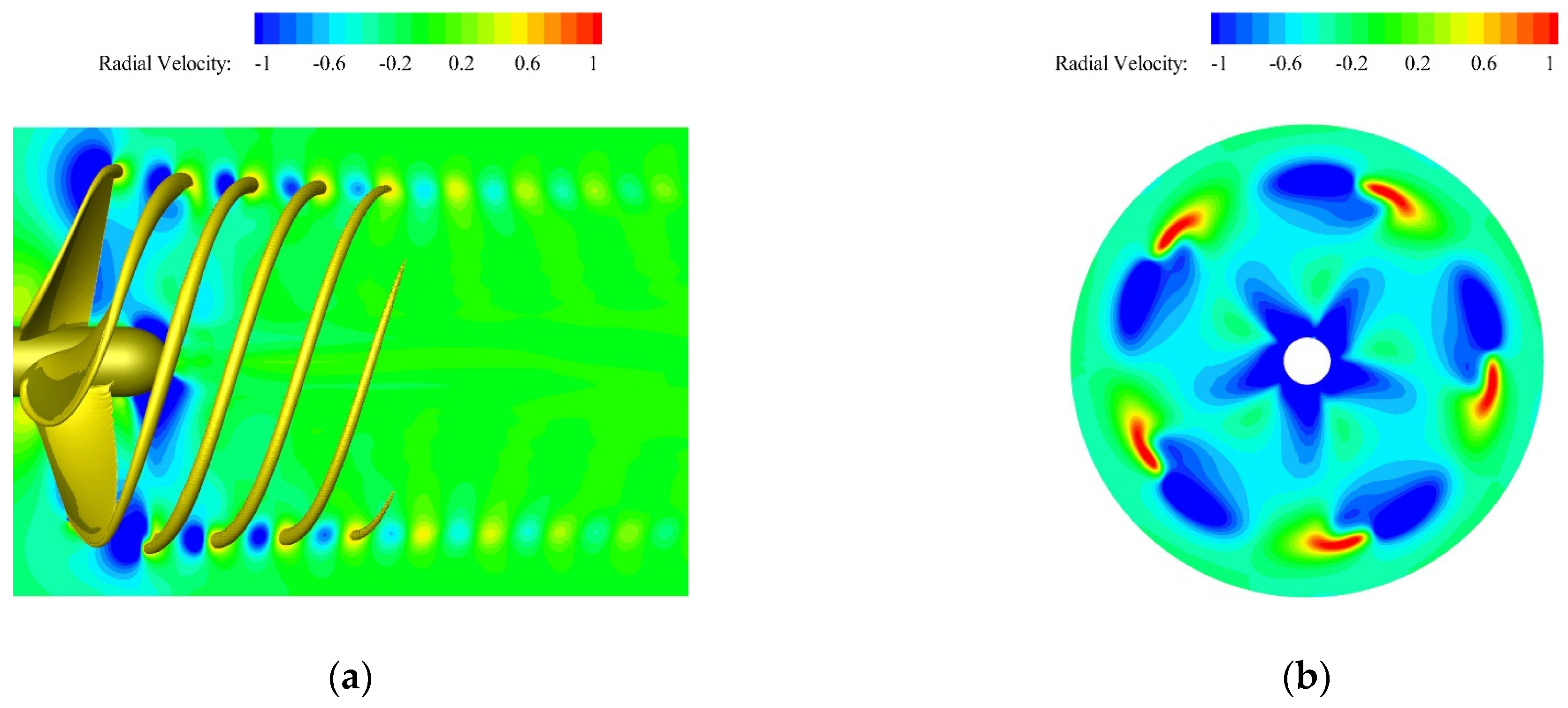
The contours of computed radial velocity fields are shown in Figure 17a–d. It can be seen that the field of radial velocity was properly captured by the present simulations. A large field of negative radial velocity was generated upstream of the blade tip (i.e., above the suction side of the blade tip), and a relatively small field of positive radial velocity was produced in the near propeller’s wake field. Because of the existence of that large field of negative radial velocity, the axial radius of the tip vortex in the near wake was contracted. As the fluid flowed downward in the axial direction, the field of positive radial velocity and the negative radial velocity gradually became the same size, so the tip vortex moved almost parallel to the axial direction. Figure 18 presents the iso-surface of axial velocity VZ = −7 m/s at J = 0.7 (i.e., the advance speed was equal to 4.375 m/s). The value of the axial velocity was negative because the inflow was along the direction of the negative Z-axis. The axial velocity of the flow accelerated as it passed through the propeller [13,32,41]. As can be seen from Figure 18, the axial velocity of the flow in the near blade tip was accelerated more.
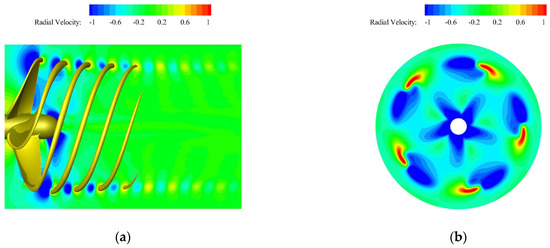
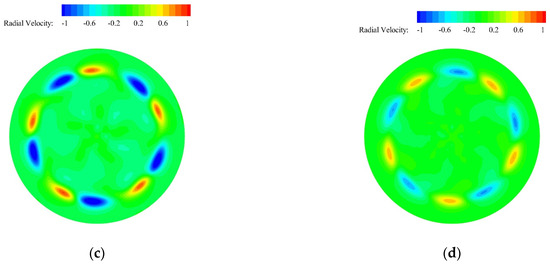
Figure 17.
Radial velocity at J = 0.7: (a) iso-surface of VR = 0.6 m/s and X = 0 plane; (b) Z/R = −0.5 plane; (c) Z/R = −1.0 plane; and (d) Z/R = −1.5 plane.
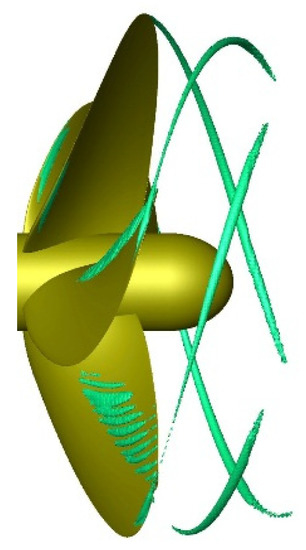
Figure 18.
Iso-surface of VZ = −7 m/s at J = 0.7.
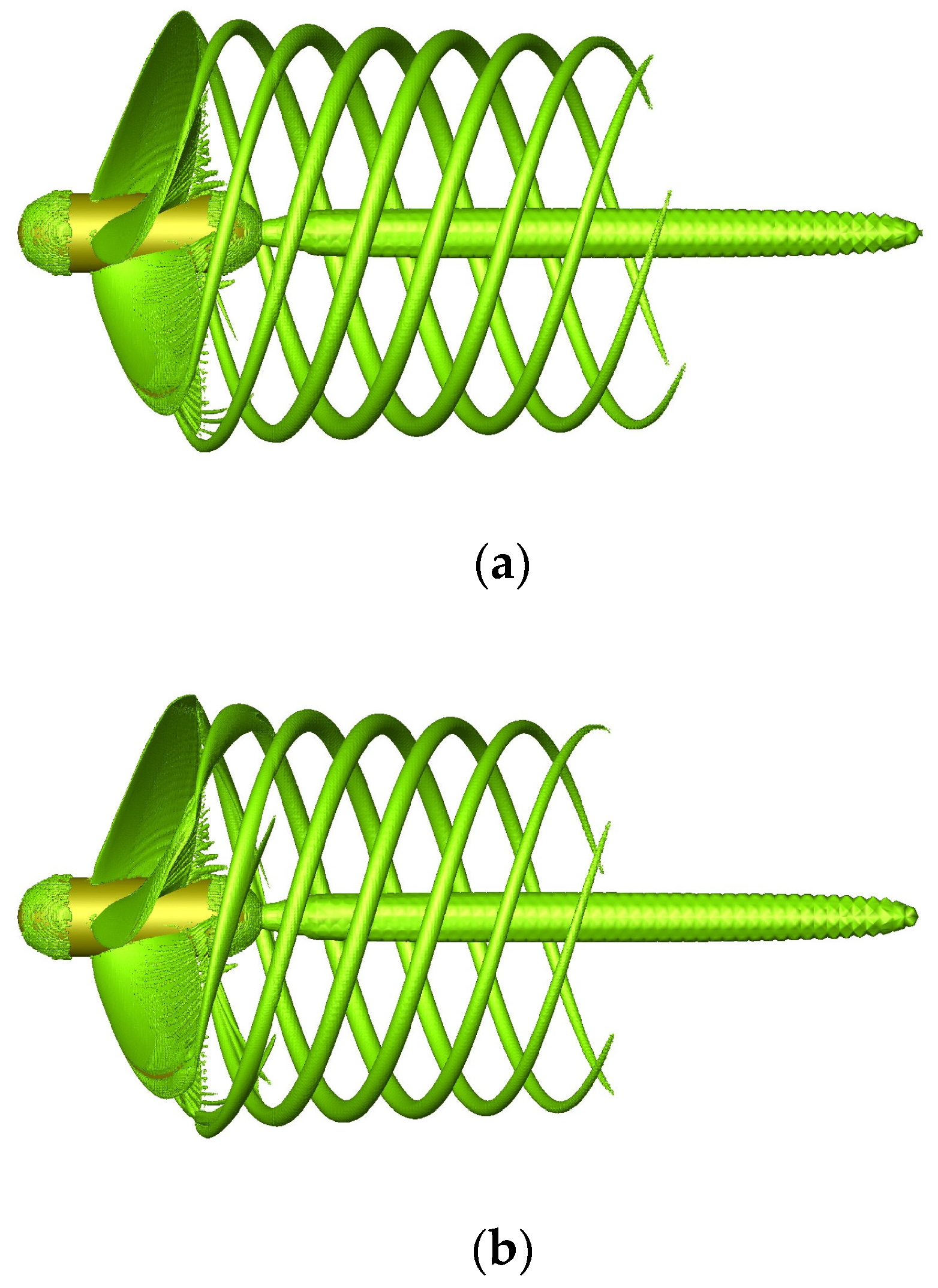
In order to further explore the influence of the winglets on the tip vortex structure at different advance coefficients, Figure 19 illustrates the iso-surface of Q = 2.0 × 104 1/s2 at J = 0.6. Similarly, compared to the benchmark propeller, the winglet-propeller generates a shorter length of the tip vortex structure. In addition, in the case of the same advance coefficient and the same propeller, a lower advance coefficient will result in a larger and longer tip vortex structure.
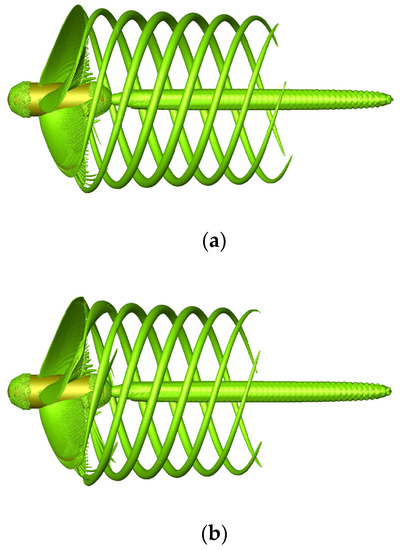
Figure 19.
Iso-surface of Q = 2.0 × 104 1/s2 at J = 0.6: (a) benchmark propeller and (b) winglet-propeller.
The comparison of the tip vortex intensity between the benchmark propeller and the winglet-propeller is inadequate under the constraints of a constant advance coefficient. It is necessary to compare the tip vortex for the same thrust loading coefficient CTh defined as
The thrust loading coefficient of the benchmark propeller was equal to 1.08 at J = 0.7. The advance coefficient of the winglet-propeller was equal to 0.693 by adjusting the advance speed to keep the same thrust loading coefficient as the benchmark propeller. Figure 20 shows that the length of the tip vortex structure produced by the winglet-propeller in the direction of the propeller axis was also shorter than that produced by the benchmark propeller.
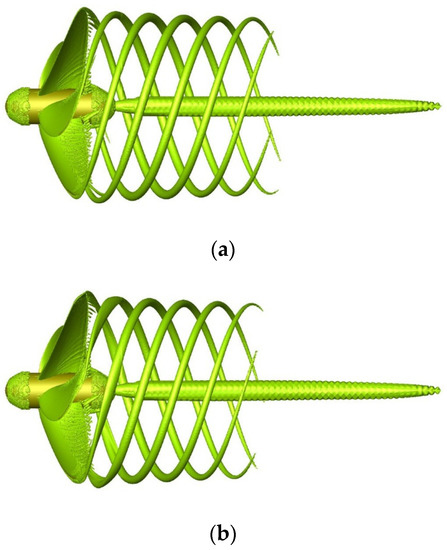
Figure 20.
Iso-surface of Q = 2.0 × 104 1/s2 at CTh = 1.08: (a) benchmark propeller and (b) winglet-propeller.
Another way to directly indicate tip vortex structures is the helicity H expressed as
where V represents the velocity vector and Ω the vorticity vector which is a measure of the rotation of a fluid element as it moves in the flow field. The iso-surface of H = −600 m/s2 at J = 0.7 is depicted in Figure 21. Since the direction of the overall velocity of the flow field moves in the negative direction of the z-axis, the value of H is negative. The cross section of the tip vortex of the benchmark propeller is roughly circular, while that of the winglet-propeller seems comparatively flat. The width of the tip vortex core of the winglet-propeller is wider than that of the benchmark propeller. However, the length of the tip vortex structure of the winglet-propeller in the axial direction is shortened compared to the benchmark propeller. Therefore, it can be inferred that the winglet breaks and disperses the tip vortex, so that the tip vortex wake disappears faster.
H = V·Ω,

Figure 21.
Iso-surface of H = −600 m/s2 at J = 0.7: (a) benchmark propeller and (b) winglet-propeller.
3.3. Cavitation
Finally, the influence of the winglets on the unsteady characteristics of the TVC was analyzed. In fact, the TVC is a highly unstable phenomenon, and numerical dissipation has a great influence on the numerical investigation of the propeller-tip vortex. In order to highlight the difference in the region of vapor between the benchmark propeller and the winglet-propeller, the extent of cavitation at J = 0.7 with 30% vapor volume fraction is shown in Figure 22. It can be clearly seen that cavitation around the benchmark propeller was larger than that around the winglet-propeller. As for the benchmark propeller, the vapor region with 30% vapor volume fraction was along the leading edge of the blade tip. However, for the winglet-propeller, the vapor region with 30% vapor volume fraction was fairly small in the vicinity of r/R = 1.0. Quantitatively speaking, the vapor volume of the winglet-propeller was 34% less than that of the benchmark propeller at J = 0.7, and less than 13% at J = 0.6.

Figure 22.
Iso-surface of 30% vapor volume fraction: (a) benchmark propeller and (b) winglet-propeller.
4. Conclusions
The LES turbulence model was employed to numerically analyze the tip vortex in the wake of marine winglet-propeller. The mesh independence verification and the discretization error estimation were investigated. In addition, the vorticity vector X and the radial velocity fields were studied.
The tip vortex structure of the winglet-propeller was shorter than that of the benchmark propeller under the same operating conditions. The existence of winglets reduced the maximum Q-criterion value by approximately 30% at J = 0.7. The cross section of the tip vortex of the benchmark propeller was roughly circular, while the cross section of the tip vortex of the winglet-propeller seemed comparatively flat relative to the benchmark propeller. The width of the tip vortex core of the winglet-propeller was wider than that of the benchmark propeller. However, the length of the helicity of the winglet-propeller in the direction of the propeller axis was shortened compared to the benchmark propeller. It is concluded that the winglets break and disperse the tip vortex, so that the tip vortex wake disappears faster. The vapor volume of the winglet-propeller was 34% less than that of the benchmark propeller at J = 0.7, and less than 13% at J = 0.6. The tip vortex cavitation of the propeller can be successfully attenuated by winglets.
Author Contributions
Conceptualization, W.Z. and H.G.; investigation, W.Z. and H.G.; methodology, W.Z. and H.G.; software, W.Z. and H.G.; writing—original draft preparation, W.Z.; writing—review and editing, H.G.; supervision, H.G.
Funding
This research was funded by Research Funds of the Maritime Safety Administration of the People’s Republic of China, 2012_27; the Fundamental Research Funds for the Central Universities, 3132019305; and the Innovative Talents Training Project for the PhD Student, CXXM2019BS011.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, J.H.; Seo, J.S. Application of spectral kurtosis to the detection of tip vortex cavitation noise in marine propeller. Mech. Syst. Signal Proc. 2013, 40, 222–236. [Google Scholar] [CrossRef]
- Gaggero, S.; Tani, G.; Viviani, M.; Conti, F. A study on the numerical prediction of propellers cavitating tip vortex. Ocean Eng. 2014, 92, 137–161. [Google Scholar] [CrossRef]
- Felli, M.; Falchi, M. Propeller tip and hub vortex dynamics in the interaction with a rudder. Exp. Fluids 2011, 51, 1385–1402. [Google Scholar] [CrossRef]
- Felli, M.; Falchi, M. Propeller wake evolution mechanisms in oblique flow conditions. J. Fluid Mech. 2018, 845, 520–559. [Google Scholar] [CrossRef]
- Muscari, R.; Dubbioso, G.; Di Mascio, A. Analysis of the flow field around a rudder in the wake of a simplified marine propeller. J. Fluid Mech. 2017, 814, 547–569. [Google Scholar] [CrossRef]
- Zhu, Z. Characteristic correlation between propellers cavitating wake and cavitation noise. Appl. Acoust. 2014, 81, 31–39. [Google Scholar] [CrossRef]
- Baek, D.G.; Yoon, H.S.; Jung, J.H.; Kim, K.S.; Paik, B.G. Effects of the advance ratio on the evolution of a propeller wake. Comput. Fluids 2015, 118, 32–43. [Google Scholar] [CrossRef]
- Zhu, W.; Gao, H.; Song, Y. Numerical investigation of propeller noise from tip vortex cavitation. In Proceedings of the 36th ASME International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Asnaghi, A.; Svennberg, U.; Bensow, R.E. Numerical and experimental analysis of cavitation inception behaviour for high-skewed low-noise propellers. Appl. Ocean Res. 2018, 79, 197–214. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Bensow, R.E. Analysis of tip vortex inception prediction methods. Ocean Eng. 2018, 167, 187–203. [Google Scholar] [CrossRef]
- Viitanen, V.; Hynninen, A.; Sipilä, T.; Siikonen, T. DDES of wetted and cavitating marine propeller for CHA underwater noise assessment. J. Mar. Sci. Eng. 2018, 6, 56. [Google Scholar] [CrossRef]
- Yilmaz, N.; Atlar, M.; Khorasanchi, M. An improved Mesh Adaption and Refinement approach to Cavitation Simulation (MARCS) of propellers. Ocean Eng. 2019, 171, 139–150. [Google Scholar] [CrossRef]
- Posa, A.; Broglia, R.; Felli, M.; Falchi, M.; Balaras, E. Characterization of the wake of a submarine propeller via Large-Eddy simulation. Comput. Fluids 2019, 184, 138–152. [Google Scholar] [CrossRef]
- Zhang, Q.; Jaiman, R.K. Numerical analysis on the wake dynamics of a ducted propeller. Ocean Eng. 2019, 171, 202–224. [Google Scholar] [CrossRef]
- Chang, N.; Ganesh, H.; Yakushiji, R.; Ceccio, S.L. Tip vortex cavitation suppression by active mass injection. J. Fluids Eng. 2011, 133, 111301. [Google Scholar] [CrossRef]
- Lee, C.S.; Ahn, B.K.; Han, J.M.; Kim, J.H. Propeller tip vortex cavitation control and induced noise suppression by water injection. J. Mar. Sci. Technol. 2018, 23, 453–463. [Google Scholar] [CrossRef]
- Lee, S.J.; Shin, J.W.; Arndt, R.E.; Suh, J.C. Attenuation of the tip vortex flow using a flexible thread. Exp. Fluids 2018, 59, 23. [Google Scholar] [CrossRef]
- Amini, A.; Reclari, M.; Sano, T.; Iino, M.; Dreyer, M.; Farhat, M. On the physical mechanism of tip vortex cavitation hysteresis. Exp. Fluids 2019, 60, 118. [Google Scholar] [CrossRef]
- Gao, H.; Zhu, W. Numerical investigation of bionic rudder with leading-edge protuberances. J. Offshore Mech. Arct. Eng. 2020, 142, 011802. [Google Scholar] [CrossRef]
- Zaky, M.; Sano, M.; Yasukawa, H. Improvement of maneuverability in a VLCC by a high lift rudder. Ocean Eng. 2018, 165, 438–449. [Google Scholar] [CrossRef]
- Busch, J.; Barthlott, W.; Brede, M.; Terlau, W.; Mail, M. Bionics and green technology in maritime shipping: An assessment of the effect of Salvinia air-layer hull coatings for drag and fuel reduction. Philos. Trans. R. Soc. A 2018, 377, 20180263. [Google Scholar] [CrossRef]
- Ghassemi, H.; Gorji, M.; Mohammadi, J. Effect of tip rake angle on the hydrodynamic characteristics and sound pressure level around the marine propeller. Ships Offshore Struc. 2018, 13, 759–768. [Google Scholar] [CrossRef]
- Gao, H.; Zhu, W.; Liu, Y.; Yan, Y. Effect of various winglets on the performance of marine propeller. Appl. Ocean Res. 2019, 86, 246–256. [Google Scholar] [CrossRef]
- Muscari, R.; Di Mascio, A.; Verzicco, R. Modeling of vortex dynamics in the wake of a marine propeller. Comput. Fluids 2013, 73, 65–79. [Google Scholar] [CrossRef]
- Yazaki, A.; Takahashi, M.; Minakata, J. Open water test series of modified AU-type five-bladed propeller models of area ratio 0.80. J. Zosen Kiokai 1967, 122, 77–80. [Google Scholar] [CrossRef]
- Tsuchida, K.; Yazaki, A.; Takahashi, M. Open water test series with modern five-bladed propeller models. J. Zosen Kiokai 1957, 102, 110–114. [Google Scholar] [CrossRef][Green Version]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 1–4. [Google Scholar]
- Mizzi, K.; Demirel, Y.K.; Banks, C.; Turan, O.; Kaklis, P.; Atlar, M. Design optimisation of Propeller Boss Cap Fins for enhanced propeller performance. Appl. Ocean Res. 2017, 62, 210–222. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Bensow, R.E. Evaluation of curvature correction methods for tip vortex prediction in SST k−ω turbulence model framework. Int. J. Heat Fluid Flow 2019, 75, 135–152. [Google Scholar] [CrossRef]
- Lu, N.X.; Bensow, R.E.; Bark, G. Large eddy simulation of cavitation development on highly skewed propellers. J. Mar. Sci. Technol. 2014, 19, 197–214. [Google Scholar] [CrossRef]
- Bensow, R.E. Large eddy simulation of a cavitating propeller operating in behind conditions with and without pre-swirl stators. In Proceedings of the 4th International Symposium on Marine Propulsors, Austin, TX, USA, 4 June 2015. [Google Scholar]
- Kumar, P.; Mahesh, K. Large eddy simulation of propeller wake instabilities. J. Fluid Mech. 2017, 814, 361–396. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Li, Z.; Terwisga, T. On the capability of multiphase RANS codes to predict cavitation erosion. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Pereira, F.A.; Di Felice, F.; Salvatore, F. Propeller cavitation in non-uniform flow and correlation with the near pressure field. J. Mar. Sci. Eng. 2016, 4, 70. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, T.; Sciacchitano, A.; Veldhuis, L.L.M.; Eitelberg, G. Experimental investigation of the impact of a propeller on a streamwise impinging vortex. Aerosp. Sci. Technol. 2017, 69, 582–594. [Google Scholar] [CrossRef]
- Usta, O.; Korkut, E. A study for cavitating flow analysis using DES model. Ocean Eng. 2018, 160, 397–411. [Google Scholar] [CrossRef]
- Felli, M.; Roberto, C.; Di Felice, F. Mechanisms of evolution of the propeller wake in the transition and far fields. J. Fluid Mech. 2011, 682, 5–53. [Google Scholar] [CrossRef]
- Gong, J.; Guo, C.Y.; Zhao, D.G.; Wu, T.C.; Song, K.W. A comparative DES study of wake vortex evolution for ducted and non-ducted propellers. Ocean Eng. 2018, 160, 78–93. [Google Scholar] [CrossRef]
- Zhu, Z. Numerical study on characteristic correlation between cavitating flow and skew of ship propellers. Ocean Eng. 2015, 99, 63–71. [Google Scholar] [CrossRef]
- Vysohlid, M.; Mahesh, K. Large eddy simulation of crashback in marine propellers. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).