Hydrodynamic Effects Produced by Submerged Breakwaters in a Coastal Area with a Curvilinear Shoreline
Abstract
:1. Introduction
2. Governing Equations
3. Results
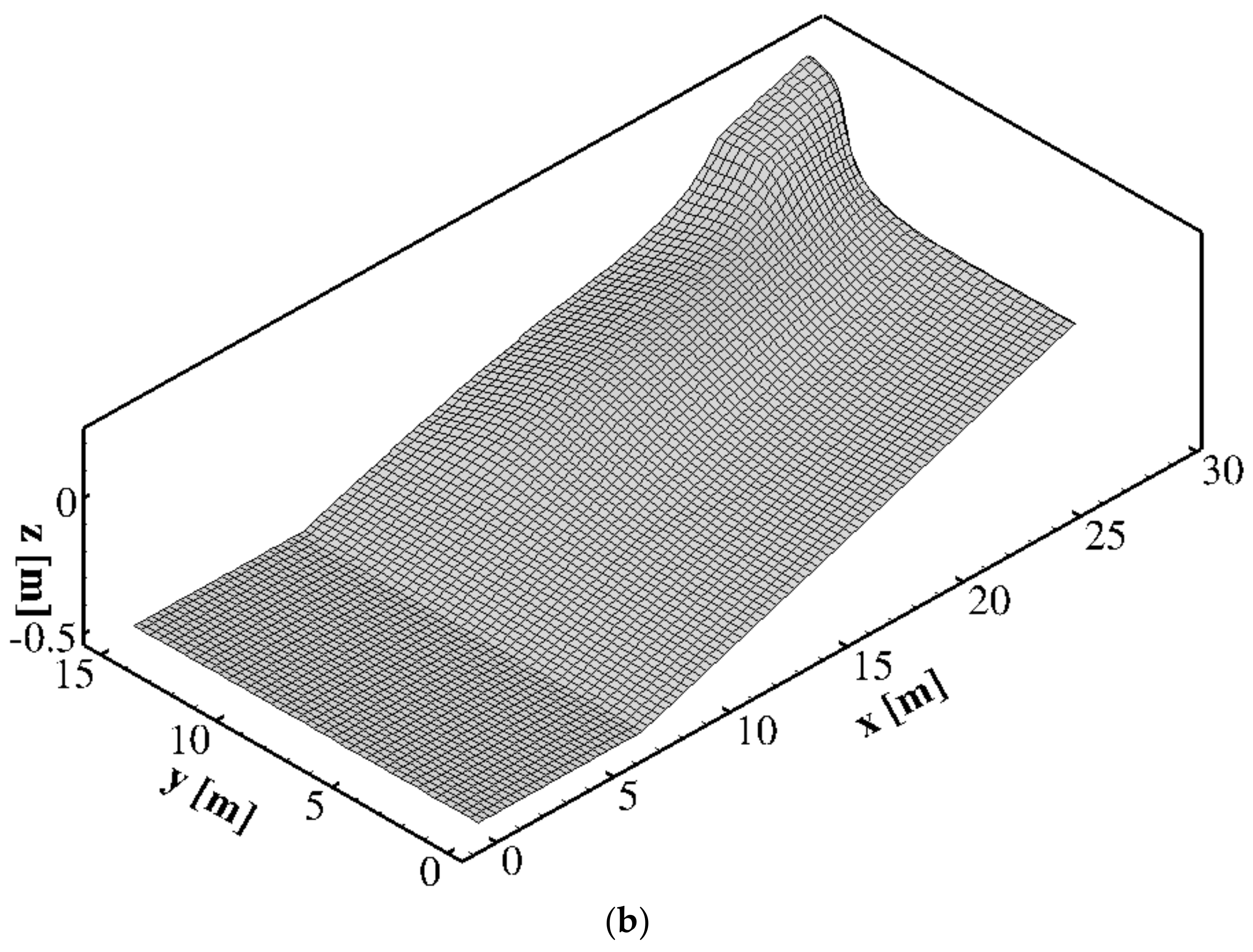
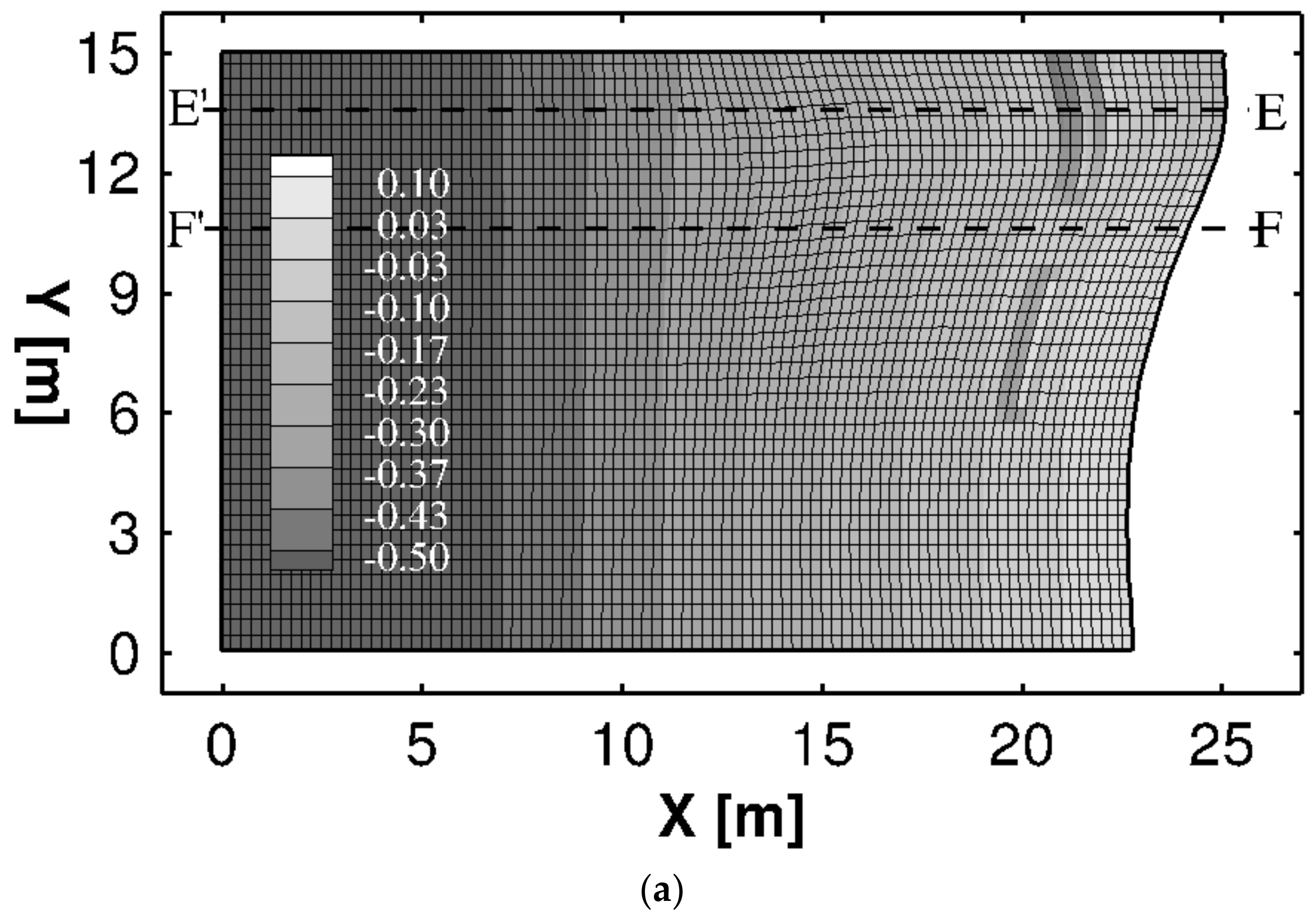
3.1. Wave Induced Currents in a Coastal Area with a Curvilinear Shoreline
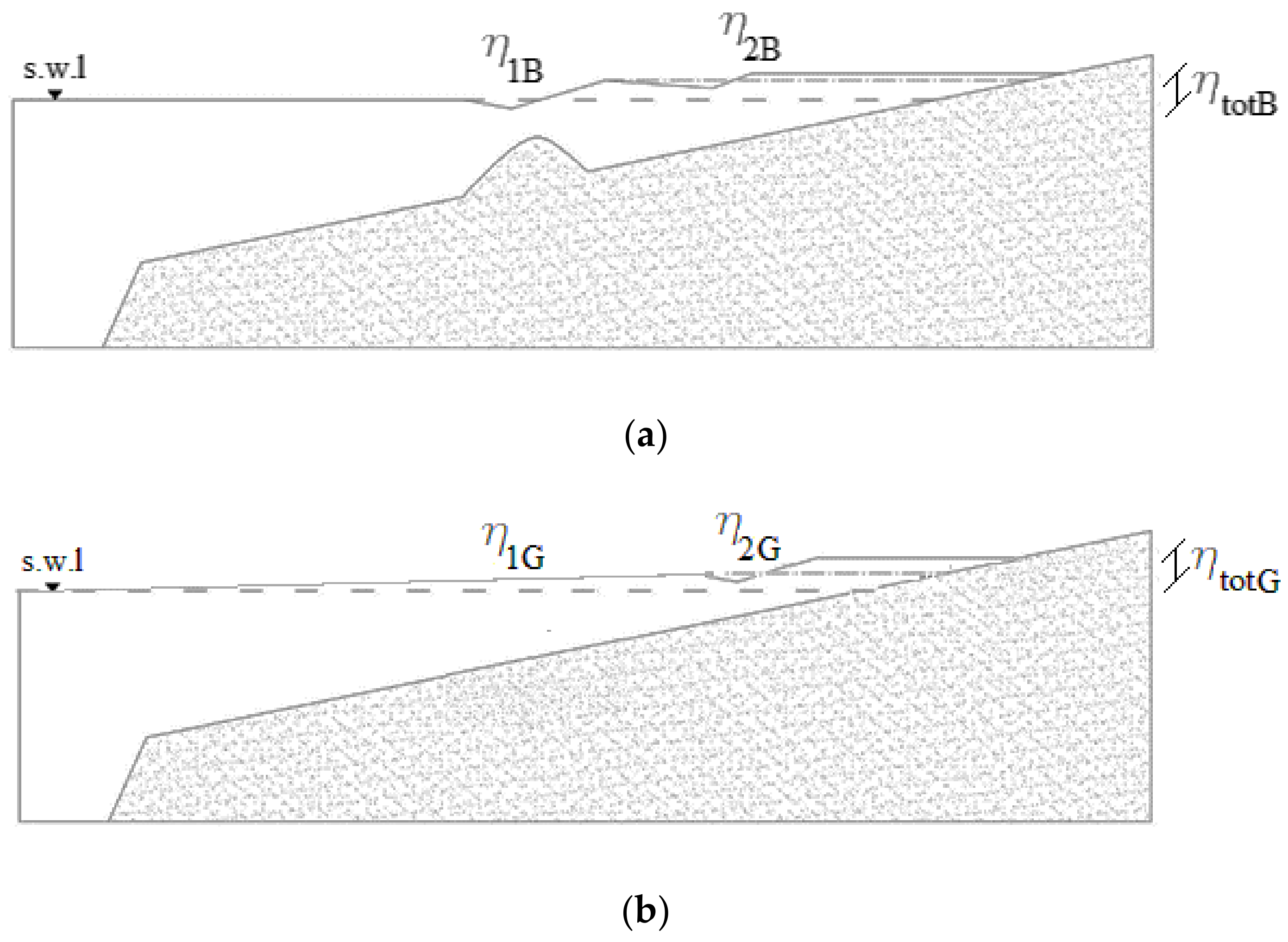
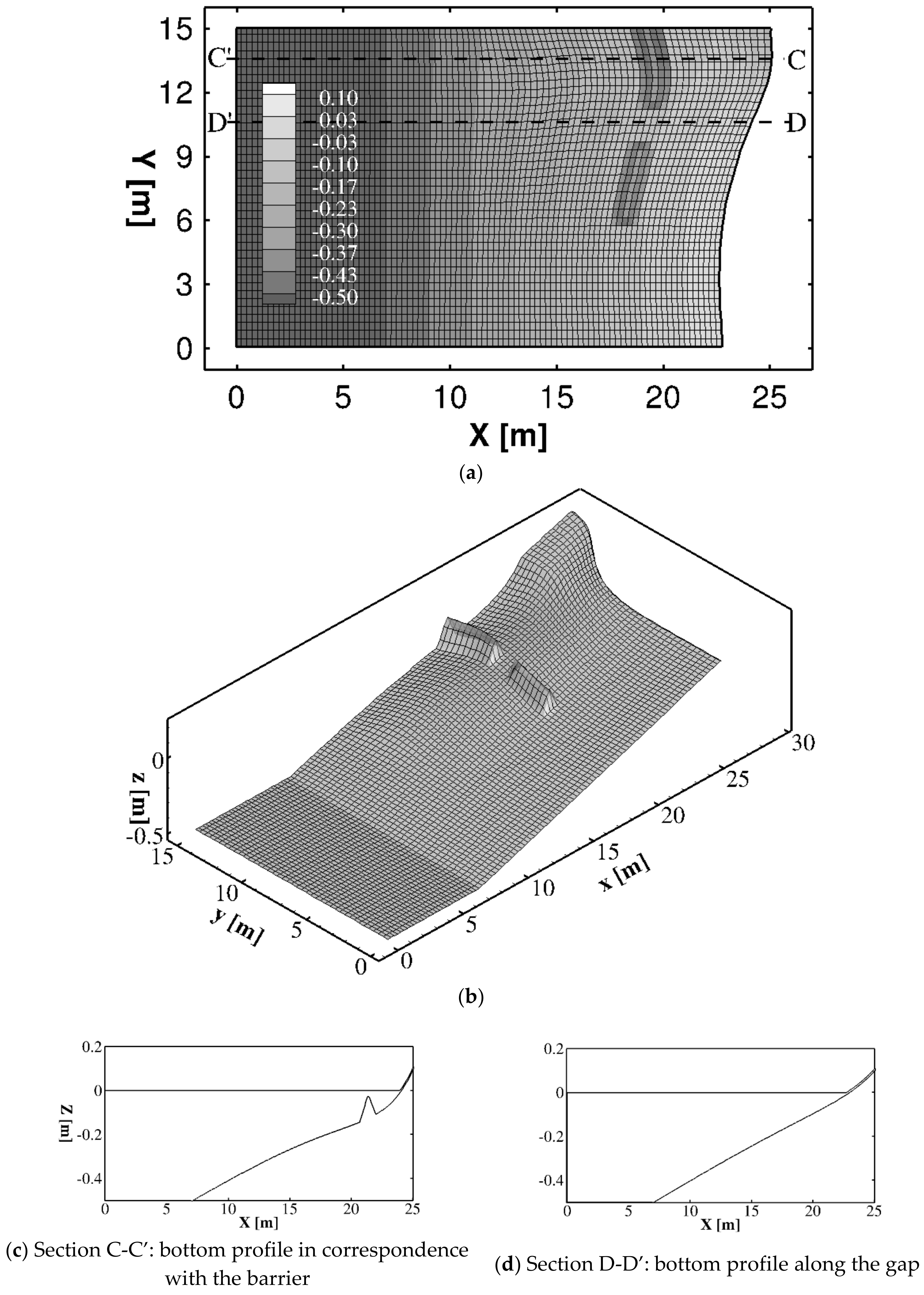
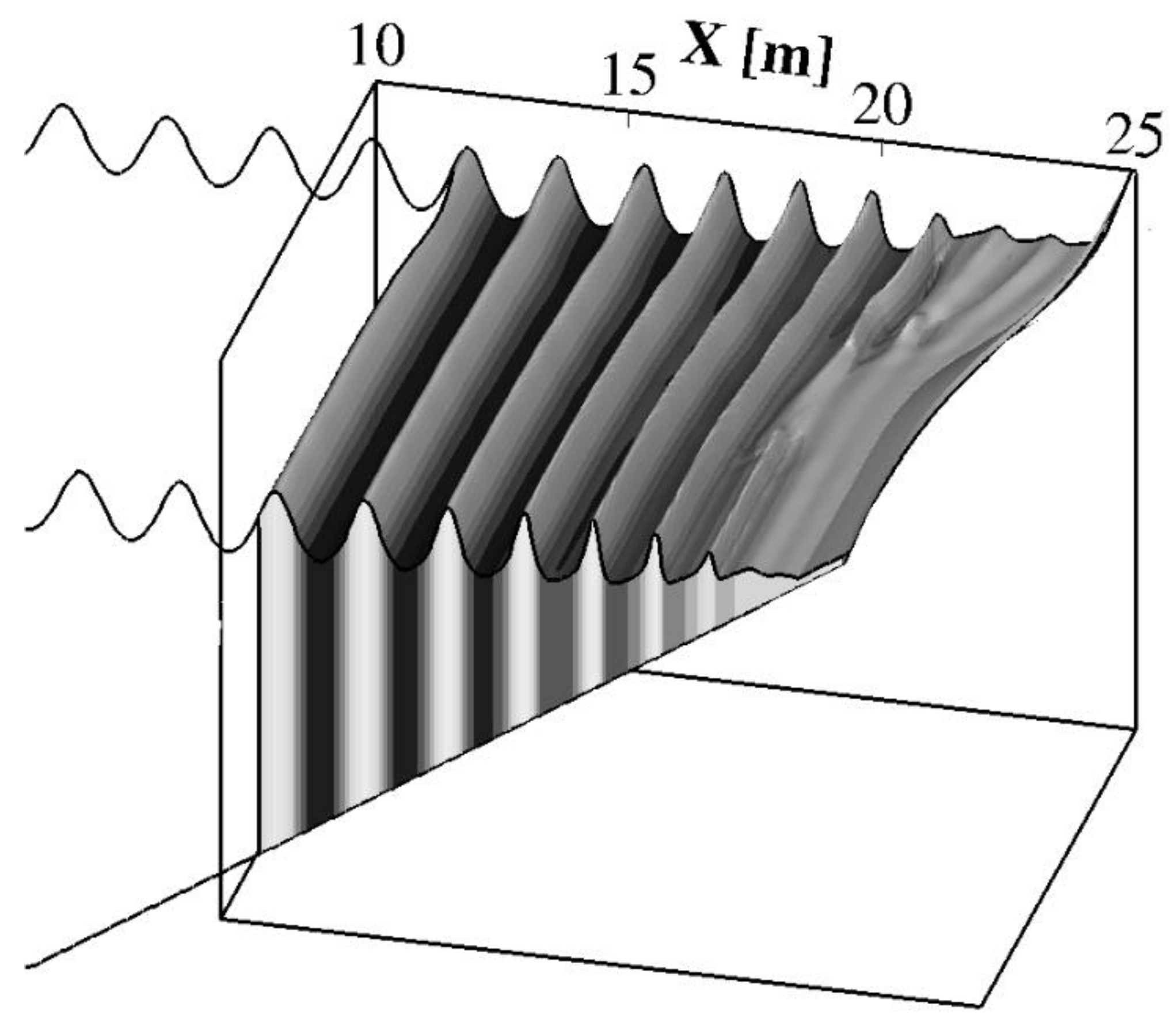
3.2. The Effects of a System of Submerged Breakwaters in a Coastal Area with a Curvilinear Shoreline
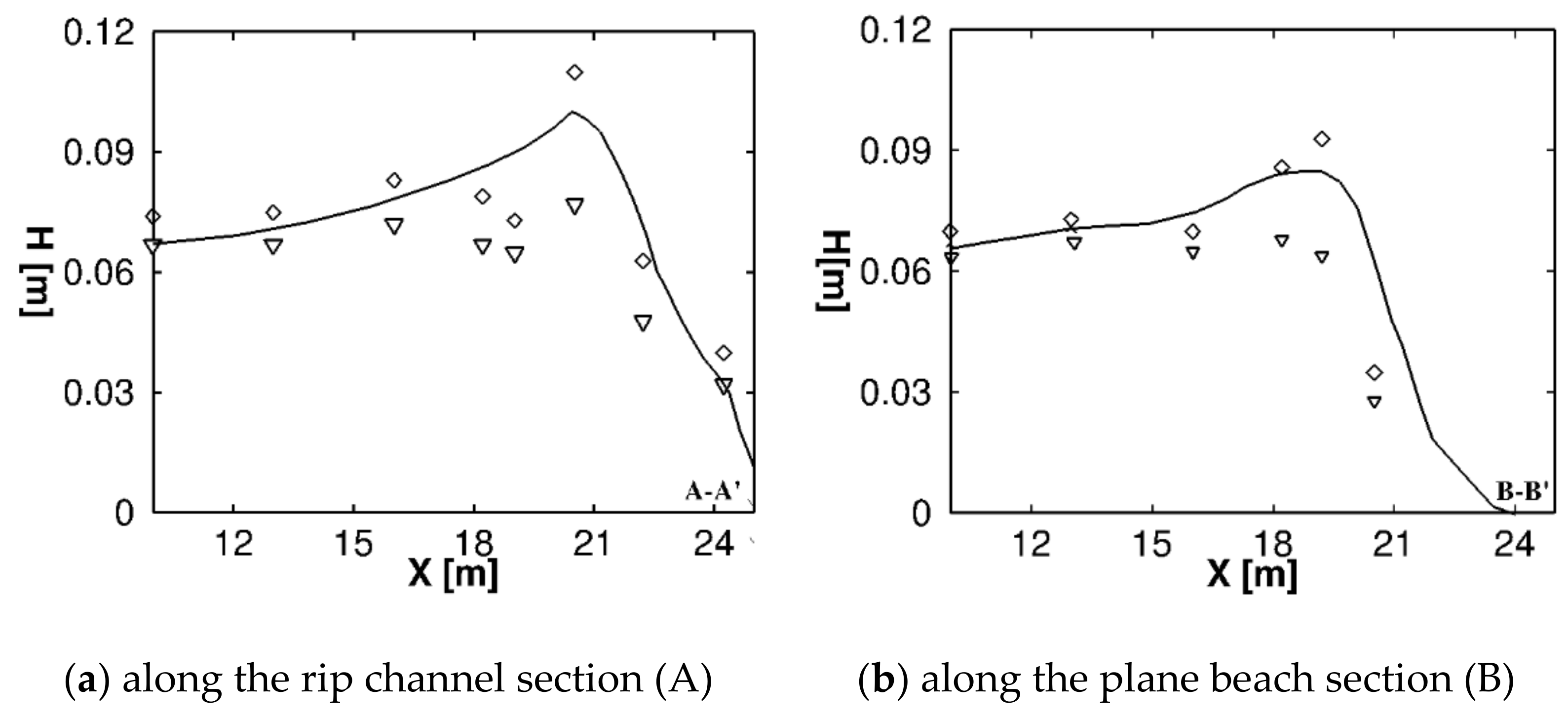
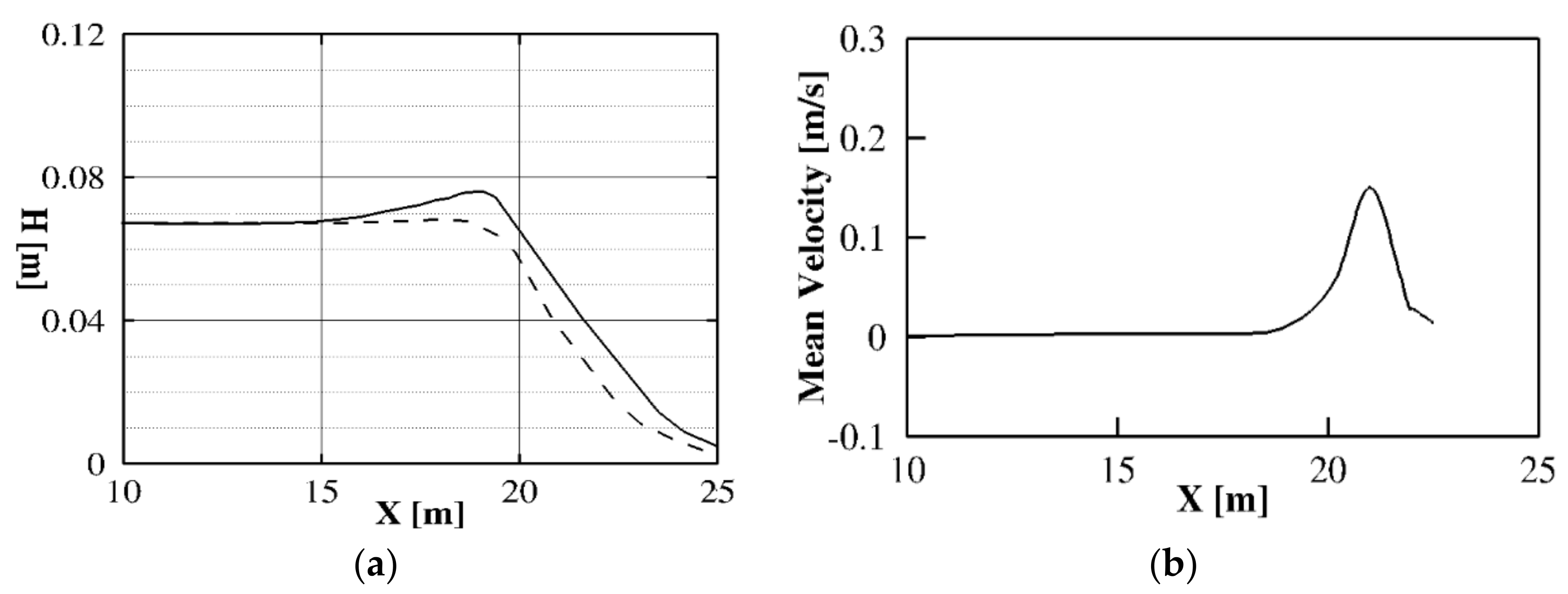
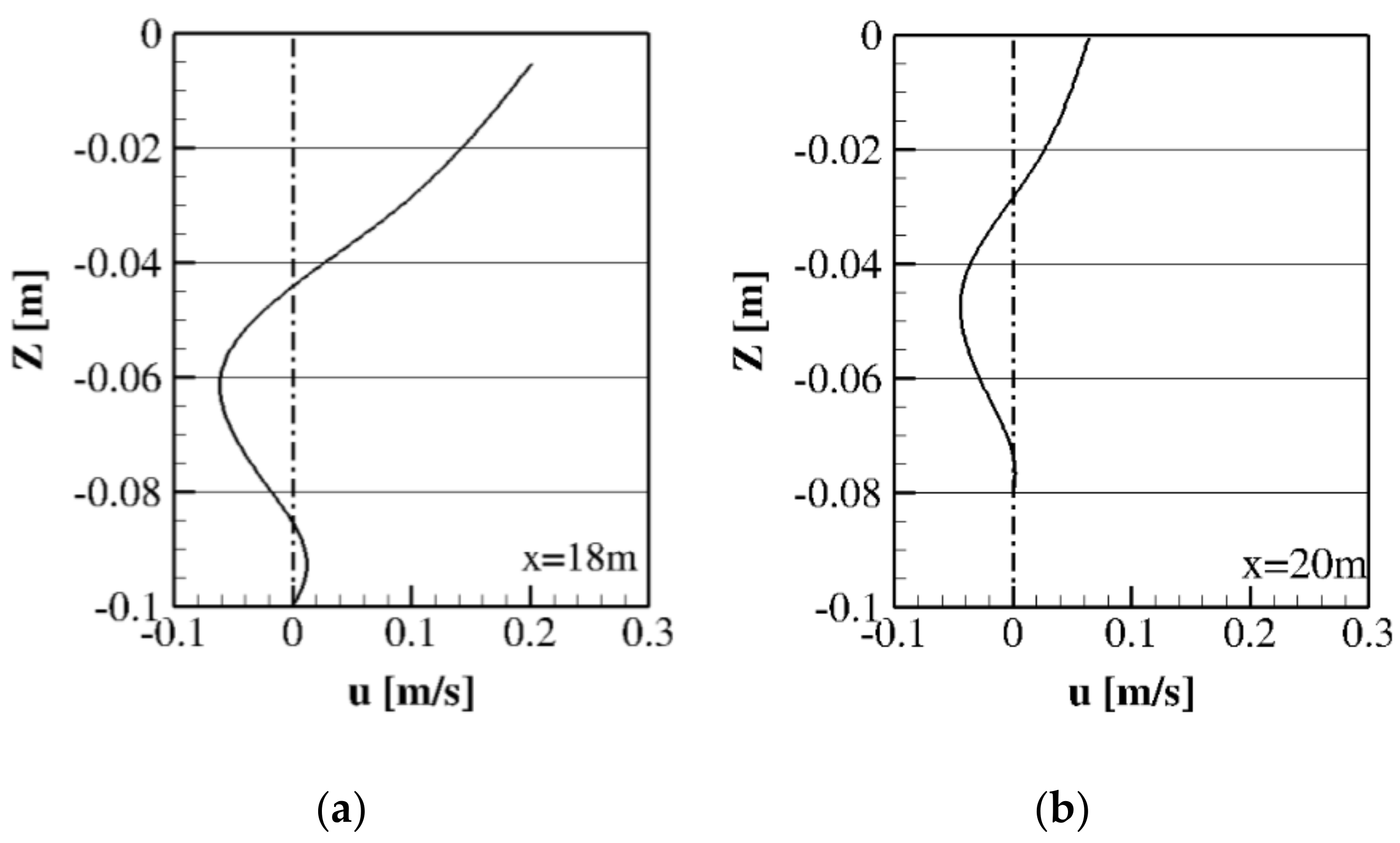
3.3.1. Case 1
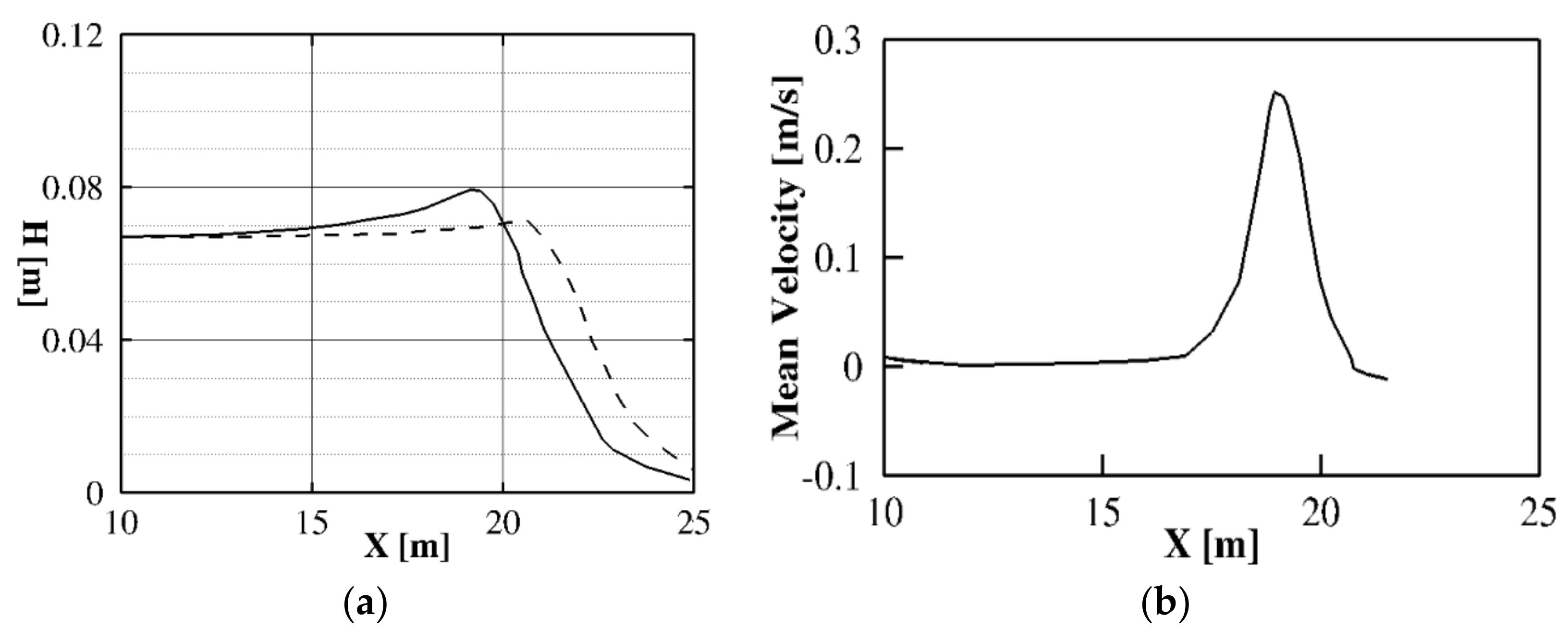
3.3.2. Case 2
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Williams, H.E.; Briganti, R.; Romano, A.; Dodd, N. Experimental analysis of wave overtopping: A new small scale laboratory dataset for the assessment of uncertainty for smooth sloped and vertical coastal structures. J. Mar. Sci. Eng. 2019, 7, 217. [Google Scholar] [CrossRef]
- Van Doorslaer, K.; Romano, A.; De Rouck, J.; Kortenhaus, A. Impacts on a storm wall caused by non-breaking waves overtopping a smooth dike slope. Coast. Eng. 2017, 120, 93–111. [Google Scholar] [CrossRef]
- Romano, A.; Bellotti, G.; Briganti, R.; Franco, L. Uncertainties in the physical modelling of the wave overtopping over a rubble mound breakwater: The role of the seeding number and of the test duration. Coast. Eng. 2015, 103, 15–21. [Google Scholar] [CrossRef]
- Franco, L.; Geeraerts, J.; Briganti, R.; Willems, M.; Bellotti, G.; De Rouck, J. Prototype measurements and small-scale model tests of wave overtopping at shallow rubble-mound breakwaters: The Ostia-Rome yacht harbour case. Coast. Eng. 2009, 56, 154–165. [Google Scholar] [CrossRef]
- Cannata, G.; Lasaponara, F.; Gallerano, F. Non-linear Shallow Water Equations numerical integration on curvilinear boundary-conforming grids. WSEAS Trans. Fluid Mech. 2015, 10, 13–25. [Google Scholar]
- Cannata, G.; Petrelli, C.; Barsi, L.; Fratello, F.; Gallerano, F. A dam-break flood simulation model in curvilinear coordinates. WSEAS Trans. Fluid Mech. 2018, 13, 60–70. [Google Scholar]
- Lorenzoni, C.; Postacchini, M.; Brocchini, M.; Mancinelli, A. Experimental study of the short-term efficiency of different breakwater configurations on beach protection. J. Ocean Eng. Mar. Energy 2016, 2, 195–210. [Google Scholar] [CrossRef] [Green Version]
- Postacchini, M.; Russo, A.; Carniel, S.; Brocchini, M. Assessing the Hydro-Morphodynamic response of a beach protected by detached, impermeable, submerged breakwaters: A numerical approach. J. Coast. Res. 2016, 32, 590–602. [Google Scholar]
- Hsiao, S.C.; Liu, P.L.-F.; Hwung, H.H.; Woo, S.B. Nonlinear water waves over a three-dimensional porous bottom using Boussinesq-type model. Coast. Eng. J. 2005, 47, 231–253. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Choi, B.H.; Talipova, T.; Woo, S.B.; Kim, D.C. Solitary wave transformation on the underwater step: Asymptotictheory and numerical experiments. Appl. Math. Comput. 2010, 217, 1704–1718. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1. highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Chen, Q.; Kirby, J.T.; Dalrymple, R.A.; Shi, F.; Thornton, E.B. Boussinesq modeling of longshore currents. J. Geophys. Res. 2003, 108, 26-1–26-18. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; De Gaudenzi, O.; Scarpone, S. Modeling bed evolution using weakly coupled phase-resolving wave model and wave-averaged sediment transport model. Coast. Eng. J. 2016, 58, 1650011-1–1650011-50. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Tatlock, B.; Briganti, R.; Musumeci, R.E.; Brocchini, M. An assessment of the roller approach for wave breaking in a hybrid finite-volume finite-difference Boussinesq-type model for the surf-zone. Appl. Ocean Res. 2018, 73, 160–178. [Google Scholar] [CrossRef]
- Lin, P.; Li, C.W. A σ-coordinate three-dimensional numerical model for surface wave propagation. Int. J. Numer. Methods Fluids 2002, 38, 1045–1068. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H. A σ-coordinate non-hydrostatic model with embedded Boussinesq-type-like equations for modeling deep-water waves. Int. J. Numer. Methods Fluids 2010, 63, 1448–1470. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Camilli, F.; Gallerano, F. 3D free surface flow simulations based on the integral form of the equations of motion. WSEAS Trans. Fluid Mech. 2017, 12, 166–175. [Google Scholar]
- Gallerano, F.; Cannata, G.; Lasaponara, F.; Petrelli, C. A new three-dimensional finite-volume non-hydrostatic shock-capturing model for free surface flow. J. Hydrodyn. 2017, 29, 552–566. [Google Scholar] [CrossRef]
- Bradford, S.F. Non-hydrostatic model for surf zone simulation. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 163–174. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Cannata, G.; Gallerano, F.; Palleschi, F.; Petrelli, C.; Barsi, L. Three-dimensional numerical simulation of the velocity fields induced by submerged breakwaters. Int. J. Mech. 2019, 13, 1–14. [Google Scholar]
- Cannata, G.; Petrelli, C.; Barsi, L.; Gallerano, F. Numerical integration of the contravariant integral form of the Navier–Stokes equations in time-dependent curvilinear coordinate systems for three-dimensional free surface flows. Contin. Mech. Thermodyn. 2019, 31, 491–519. [Google Scholar] [CrossRef]
- Palleschi, F.; Iele, B.; Gallerano, F. Integral contravariant form of the Navier-Stokes equations. WSEAS Trans. Fluid Mech. 2019, 14, 101–113. [Google Scholar]
- Luo, H.; Bewley, T.R. On the contravariant form of the Navier-Stokes equations in time-dependent curvilinear coordinate systems. J. Comput. Phys. 2004, 199, 355–375. [Google Scholar] [CrossRef]
- Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics; Dover Publications: New York, NY, USA, 1989. [Google Scholar]
- Hamm, L. Directional nearshore wave propagation over a rip channel: An experiment. In Proceedings of the 23rd International Conference of Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 226–239. [Google Scholar]
- Ranasinghe, R.; Turner, I.L. Shoreline response to submerged structures: A review. Coast. Eng. 2006, 53, 65–79. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Larson, M.; Savioli, J. Shoreline response to a single shore-parallel submerged breakwater. Coast. Eng. 2010, 57, 1006–1017. [Google Scholar] [CrossRef]
- Haller, M.C.; Dalrymple, R.A.; Svendsen, I.A. Experimental modeling of a rip current system. In Proceedings of the 1997 3rd International Symposium on Ocean Wave Measurement and Analysis, WAVES, Virginia Beach, VA, USA, 3–7 November 1997; pp. 750–764. [Google Scholar]
- Haller, M.C.; Dalrymple, R.A.; Svendsen, Ib.A. Experimental study of nearshore dynamics on a barred beach with rip channels. J. Geophysical Res. 2002, 107, 14-1–14-21. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallerano, F.; Cannata, G.; Palleschi, F. Hydrodynamic Effects Produced by Submerged Breakwaters in a Coastal Area with a Curvilinear Shoreline. J. Mar. Sci. Eng. 2019, 7, 337. https://doi.org/10.3390/jmse7100337
Gallerano F, Cannata G, Palleschi F. Hydrodynamic Effects Produced by Submerged Breakwaters in a Coastal Area with a Curvilinear Shoreline. Journal of Marine Science and Engineering. 2019; 7(10):337. https://doi.org/10.3390/jmse7100337
Chicago/Turabian StyleGallerano, Francesco, Giovanni Cannata, and Federica Palleschi. 2019. "Hydrodynamic Effects Produced by Submerged Breakwaters in a Coastal Area with a Curvilinear Shoreline" Journal of Marine Science and Engineering 7, no. 10: 337. https://doi.org/10.3390/jmse7100337




