Vibration Performance of a Flow Energy Converter behind Two Side-By-Side Cylinders

Abstract

Flow-induced vibrations of a flexible cantilever plate, placed in various positions behind two side-by-side cylinders, were computationally investigated to determine optimal location for wake-excited energy harvesters. In the present study, the cylinders of equal diameter D were fixed at center-to-center gap ratio of $T/D=1.7$ and immersed in sub-critical flow of Reynold number $R{e}_D=10,000$. A three-dimensional Navier–Stokes flow solver in an Arbitrary Lagrangian–Eulerian (ALE) description was closely coupled to a non-linear finite element structural solver that was used to model the dynamics of a composite piezoelectric plate. The cantilever plate was fixed at several positions between $0.5<x/D<1.5$ and $-0.85<y/D<0.85$ measured from the center gap between cylinders, and their flow-induced oscillations were compiled and analyzed. The results indicate that flexible plates located at the centerline between the cylinder pairs experience the lowest mean amplitude of oscillation. Maximum overall amplitude in oscillation is predicted when flexible plates are located in the intermediate off-center region downstream of both cylinders. Present findings indicate potential to further maximize wake-induced energy harvesting plates by exploiting their favorable positioning in the wake region behind two side-by-side cylinders.

1. Introduction

The flow around single cylinder or group of cylinders is a fundamental fluid dynamics problem that has attracted considerable research due to its wide engineering significance. The flow past a cylinder typically involves boundary layer separation/reattachments, free shear layers, and vortex shedding, which induces cylinder vibrations and noise generation. These flow dynamics become more complicated when there are interferences or interactions with neighboring cylinders. The understanding behind such flow past multiple cylinders provide important insight as they are found in many branches of engineering applications, for example, cooling cores in nuclear reactors, heat exchanger tube bundles, offshore structures, marine risers, and pipelines. Among flow past multiple cylinders, the case involving two cylinders has been investigated both numerically and experimentally under several configurations, in-tandem, side-by-side, or staggered arrangements, and provides some fundamental understanding of flow or wake interactions [1,2].

The flow characteristics past two side-by-side cylinders are strongly influenced by the gap between cylinders and their diameter-based Reynolds number, $R{e}_D$. Denoting T as the transverse center-to-center distance between cylinders and D as the cylinder diameter, the flow behavior around side-by-side cylinders may be classified into three main regimes [3,4]: (i) When $T/D<$ 1.1–1.2, the gap between cylinders is small and the flow behaves similar to passing a single bluff body where vortices are shed alternately from the outer surfaces of the top and bottom cylinders, forming an asymmetric single vortex street. In this single-bluff body regime, the Strouhal number ($St=f\left(2D\right)/U_{\infty }$) is approximately 0.2—similar to a single-bluff body case, but with characteristic length of $2D$ [5]. (ii) When $1.2<T/D<$ 2.0–2.2, this intermediate spacing between cylinders is within a critical range where the flow between the gap is bistable and switches direction (flip-flopping) towards either cylinders at irregular intervals (with periods several orders of magnitude larger than the vortex shedding period). As a result, in this biased flow regime, a narrower and wider wake region forms behind either cylinders, corresponding to higher ($S{t}_n\approx$ 0.2–0.4) and lower ($S{t}_w\approx$ 0.1–0.2) vortex shedding frequencies, respectively [6]. Within this regime, the Reynolds number $Re$ may also influence the transition between single and twin vortex streets [7,8]. In their 3D numerical study, Liu et al. [9] also showed the influence of cylinder inclination (or conversely, flow angle) on formation of these vortex streets. (iii) When $T/D>2.2$, the gap is sufficiently large that both cylinders behaves more as isolated bluff bodies resulting in predominantly symmetric (or anti-phase) parallel wake patterns that are coupled with a single Strouhal number $St$ of approximately 0.21 [6]. Intermittent in-phase wake patterns may also take place in this symmetric flow regime, but would then synchronize back to the more stable anti-phase or symmetric pattern. At much higher gaps ($T/D>4.5$), any interference associated with proximity of cylinders are negligible and each cylinder behaves as independent bluff bodies with uncoupled flow patterns [3].

Previous studies on flow around bluff bodies with adjacent plates may also provide useful context for the present work. The flow past a single cylinder with plates has received much attention in the past decades, especially for passive flow/vortex control (and, subsequently, flow-induced vibration control) of a cylinder (see, for example, [10,11,12,13]), understanding of plate dynamics (for instance, [14,15]), and potential for energy harvesting (see, for example, [16,17]). Less well explored is the flow with plates behind two or multiple cylinders. Furquan et al. [18] computationally investigated vibration response of two flexible splitter plates, each placed behind two side-by-side square cylinders (that are separated by center-to-center distance equal to twice the square edge length L) at $Re=100$ under varying reduced velocities ($U^{*}=U_{\infty }/f_{n}L$, where $f_n$ is plate natural frequency). Their results indicate initial anti-phase plate vibration as the plates are attracted towards each other with the accelerating gap flow, before finally synchronizing into an in-phase plate vibration pattern that also exhibits the “lock-in” phenomenon at certain range of $U^{*}$, as either plate undergoes large vibration amplitudes when its response frequency approaches the plate’s first mode natural frequency. The effect of short splitter plates behind two side-by-side square cylinders (with center-to-center distance equal 3.6 times the square edge length) on their vortex shedding and subsequent sound generation were examined experimentally for $Re$ of 10,000–33,000 by Octavianty and Asai [19]. In this symmetric flow regime and high $Re$, generated vortices past the side-by-side square cylinders were highly synchronized and coherent spanwise, allowing effective sound reduction even with shorter splitter plates—in contrast to a single square cylinder where vortices were more three-dimensional and the effect of splitter plate was limited. Oruc et al. [20] experimented with splitter plates centrally placed between two side-by-side circular cylinders and examined their effect on the flip-flopping gap flow in the biased flow regime. It was found that, at sufficient plate lengths, the asymmetric and bistable wake flow were suppressed, resulting in two symmetric and stable wake patterns.

Demand for clean and sustainable energy that requires minimal human intervention or maintenance (for example, to power wireless sensors in remote areas, electronic devices for structural health monitoring of airborne vehicles or deep ocean structures) have prompted increasing development of various energy harvesting systems. One of a number of prototypes include exploiting wakes behind a single bluff body (for example, [16,17,21,22]) and wake-induced vibration of cylinders (for example, [23]) to induce oscillations of flexible membranes or plates consisting of piezoelectric materials—converting the fluctuating mechanical strains or energy into electrical energy and have been shown to reach outputs up to 30 V [24,25]. Although multiple bluff bodies are ubiquitous in many engineering applications, limited investigation on their potential to excite piezoelectric energy harvesters may be found.

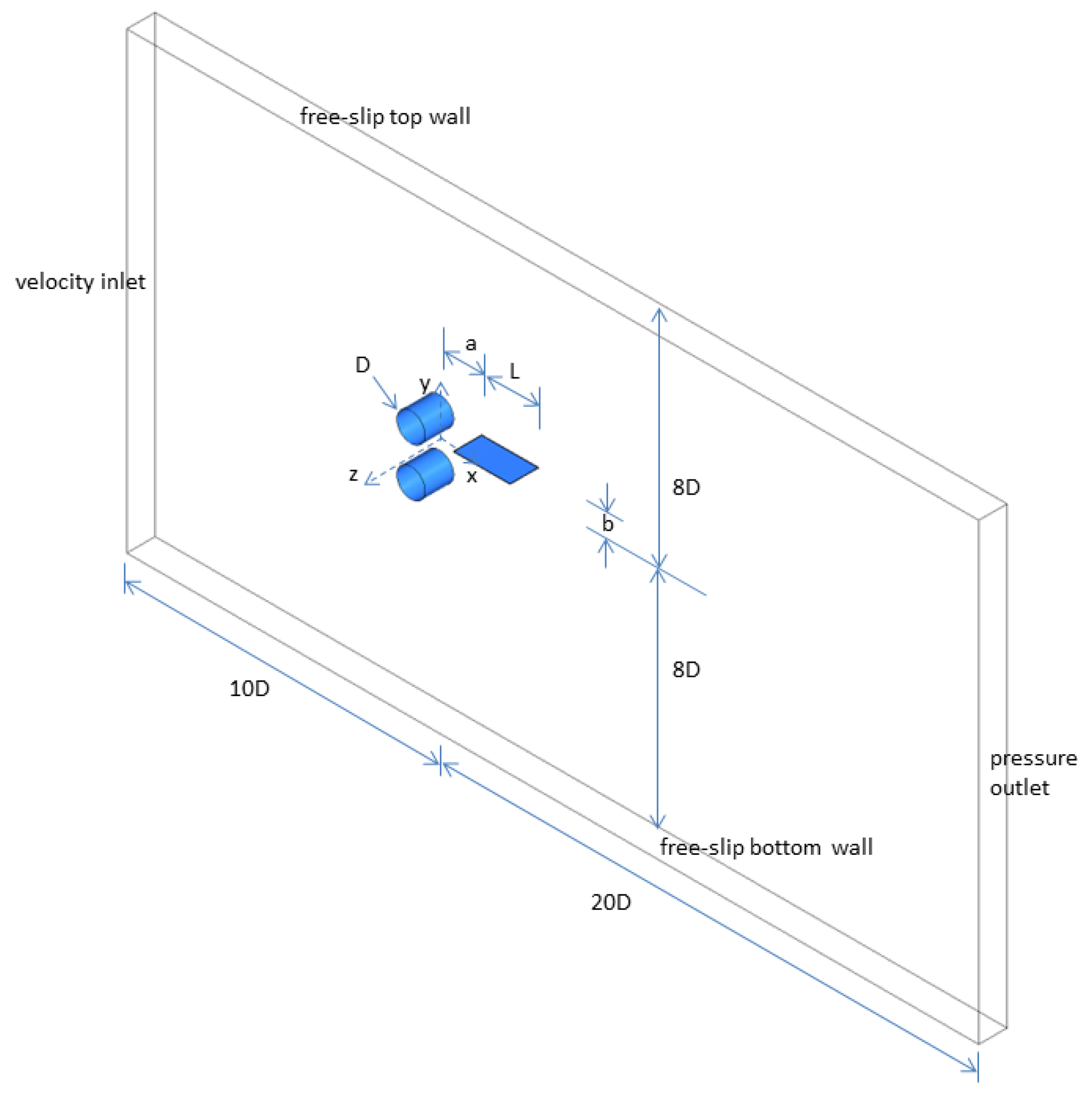
Therefore, in the present study, we aimed to extend the current results in the literature by exploring wake-excited piezoelectric energy harvesters placed behind two side-by-side cylinders and also analyze their vibrations at various placements in the wake region with the view of maximizing energy harvesting performance. To that end, we performed a computational investigation on the unsteady flow past two side-by-side circular cylinders interacting with a thin flexible plate placed at a number of streamwise and crossflow positions behind both cylinders. As the side-by-side cylinders behave as a single bluff body, either in unison or separated when the gap is small or large enough, respectively, we considered a center-to-center cylinder spacing of $T/D=1.7$ (in the bias flow regime) for the present study, to include effects of multiple bluff body flow interaction or interference. In addition, a moderately high sub-critical flow past cylinders of $R{e}_D=$ 10,000 was considered in the present work.

2. Computational Methodology

2.1. Flow Equations

Although vortex shedding behind a circular cylinder may be initiated at $R{e}_D\approx 49$, numerous bluff-body energy harvesting prototypes suggest operations at much higher Reynolds numbers (for example, $R{e}_D$ = 5000–40,000 for harvesting eel of Allen and Smits [21], $R{e}_D$ = 3000–8000 for harvesting concept of Weinstein et al. [26], $R{e}_D=6024$ for proposed miniature energy generator of Nguyen et al. [27], $R{e}_D$ in excess of 10,000 in the investigation by Yu and Liu [16], and $R{e}_D$ ranging 3200–12,000 in the design by Shi et al. [17]). As a result, we considered $R{e}_D=$ 10,000 in the present study, which falls in the sub-critical flow regime of flow past circular cylinders. Within this regime, flow is three-dimensional and boundary layers remain laminar prior to separation, which then become turbulent in the wake region. To better simulate flow separation and turbulence but with more practical computational cost, a recently developed Scale-Resolving or Scale-Adaptive Simulation (SAS) modification on the $k-\omega$ Shear Stress Transport (SST) turbulence model proposed by Menter and Egorov [28] was employed. This involves the incompressible, three-dimensional Unsteady Reynolds-Averaged Navier Stokes (URANS) equation for conservation of momentum and the continuity equations, both of which in this case are described in the Arbitrary Lagrangian–Eulerian (ALE) frame of reference in order to accommodate fluid grid movements or deformation, as the grids follow the motion of the interfacing flexible plate [29,30]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\partial u_i}{\partial t}+(u_j-\widetilde{u_j})\frac{\partial u_i}{\partial x_j}& =-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{1}{\rho }\frac{\partial }{\partial x_j}\left\{(\mu +{\mu }_t)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right\}\hfill \end{array}\end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{\partial (u_i-\widetilde{u_i})}{\partial x_i}& =0\hfill \end{array}$$

(2)

where $u_i$, $\widetilde{u_j}$ and p are the time-averaged fluid velocities, fluid grid velocities, and time-averaged fluid pressure, respectively ($i,j=1,2,3$ represent the 3D Cartesian directions). $\rho$ is the constant fluid density, $\mu$ denotes the fluid dynamic viscosity, and ${\mu }_t$ is the turbulent eddy viscosity. In the $k-\omega$ SST model, ${\mu }_t$ is estimated from the turbulent kinetic (k) energy and specific rate of dissipation ($\omega$) equations. SAS treatment of the $k-\omega$ shear stress transport turbulence model estimates a von Kármán length-scale and introduces a corresponding source term into the $\omega$ equation, allowing the model to switch between RANS and LES-like simulations [28,31]. Thus, more unsteady turbulent structures are able to be resolved as mesh is refined, but at lower computational costs compared to LES or DNS simulations. Fluid grid velocities are solved using a Laplacian diffusion model, which smoothly distributes the grid velocities in the whole fluid domain, from a value matching the plate motion near the fluid–plate interface to zero at the fluid domain boundaries.

2.2. Structural Equations

The flexible plate dynamics is described by the unsteady equation of motion in Equation (3).

$$\begin{array}{cc}\hfill {\rho }_s\ddot{\mathbf{d}}& =\nabla ·{\sigma }_{ij}+\mathbf{f}-c\dot{\mathbf{d}}\hfill \end{array}$$

(3)

where ${\sigma }_{ij}$ is the stress tensor and the first term on the right-hand side accounts for the stiffness of the structure, allowing for non-linear large plate deformation and accounting for the effect of induced in-plane tension on bending deflection. In addition, c represents damping ratio, ${\rho }_s$ denotes density of structure material, $\mathbf{d}$ represents displacement vector of structure, and $\mathbf{f}$ represents a time-dependent external force acting on structure (coming from the interfacing fluid pressure and shear). In the present work, we considered neglecting structural damping.

2.3. Computational Model

Figure 1 shows the computational domain used in the present study, which spans $30D\times 16D\times 1D$ in the streamwise (x), crossflow (y), and spanwise (z) directions, respectively. The inlet and outlet boundaries are, respectively, located $10D$ upstream and $20D$ downstream of the side-by-side cylinders. As the cylinder centers are spaced $T/D=1.7$ apart, we employed a symmetrical height of $8D$ from both top and bottom boundaries to the middle of the gap between cylinders. In addition, a spanwise width of $1D$ was considered in the present domain. Alkishriwi et al. [32] and Shen et al. [33] showed that results with spanwise width of $1D$ agreed well with experiments.

Table 1. Geometrical parameters.

Parameters	Values
cylinder diameter (D)	100 mm
cylinder distance (T)	170 mm	$T/D=1.7$
plate length (L)	200 mm	$L/D=2$
plate thickness (h)	2 mm
plate x-location (a)	$x/D=0.5,1.0,1.5$
plate y-location (b)	$y/D=-0.85,-0.425,$
	$0,0.425,0.85$

summarizes the geometrical parameters employed in the present study for both fluid and structural components.

Boundary conditions prescribed in the computational domain are shown in Figure 1. In addition, both left and right faces of the fluid domain are defined as symmetric conditions and both cylinder surfaces are prescribed as no-slip walls. The fluid faces that interface with the flexible plate are also specified as no-slip walls, implying a dynamic condition that requires matching fluid and plate velocities at these boundaries. For the structural domain, the leading edge of the cantilever flexible plate is fixed, while both left and right side faces of the plate are prescribed as symmetric conditions.

The physical parameters used for both the fluid and structure are compiled in

Table 2. Flow parameters in the present study.

Parameters	Values
inlet velocity ($U_{\infty }$)	1.545 m/s
inlet turbulent intensity (I)	0.2%
outlet pressure	1 atm
Reynolds number ($R{e}_D$)	10,000

and

Table 3. Structural parameters for the plate.

Parameters	Values
material density (${\rho }_s$)	1780 kg/m${}^3$
elastic modulus (E)	286.9 MPa
poisson ratio ($\nu$)	0.346

, respectively. Furthermore, a $T/D=1.7$ in the biased flow regime is used. In doing so, we anticipate effects of interference or interactions between flow past side-by-side cylinders may be observed and analyzed. The flexible energy harvesting plate is made of a silicone rubber plate (elastic modulus $E=13.1$ MPa, poisson ratio $\nu$ = 0.48) with two layers of piezoelectric PVDF sheets (E = 2500 MPa, $\nu$ = 0.34) attached along its top and bottom surfaces. The composite properties of this plate are summarized in Table 3.

Figure 2 illustrates the unstructured grids employed to discretize the fluid computational domain. A three-dimensional meshing scheme is used where finer meshing is prescribed in the vicinity of the two cylinders and flexible plate. In addition, denser grid points representing the boundary layer meshing is employed close to the surfaces of the cylinders and flexible plate, in order to better resolve their boundary layers. The first grid point normal to both cylinders and flexible plate in the boundary layer mesh were defined $0.001D$ away from their surfaces, maintaining maximum $y+<2$ in all simulation cases. As a result, depending on the simulation case, the baseline grid for the fluid domain consisted of 86,847–95,075 nodes (with 253,243–291,778 elements), while the plate was meshed using structured grids having 76 nodes (with 18 solid elements).

A commercial computational fluid dynamics and finite element solver (ANSYS Workbench 2019 R1) was employed to undertake the flow and structural modeling and coupling. The fluid–structural solver coupling was achieved using a partitioned framework, where the loads (from the fluid solver) were transferred to the structural solver (and applied to the plate), and the resulting plate deformation was feedback to the fluid solver to redefine the fluid domain (and corresponding mesh motion). A number of coupling iterations is typically required within each time step until convergence, and a coupling under-relaxation factor of 0.75 was considered for both loads and displacements interchange, to closely couple the fluid–structure iterations. Implicit second-order backward Euler and Hilbert–Hughes–Taylor (HHT) schemes were used for time-integration of the discretized flow and structural equations, respectively. Considering the vortex shedding frequencies of both cylinders and the flip-flopping period of the bistable gap flow that is several orders of magnitude greater than the vortex shedding period, a timestep size of 0.01 s was used, which also showed adequate stability in the numerical iterations. The steady-state solution for a given stationary plate condition was used as the initial condition for all the unsteady fluid–structure simulations, corresponding to all of the plate placement cases. Steady state flow condition was typically reached after non-dimensional time $t{U}_{\infty }/D=75$ (corresponding to at least 15 vortex shedding periods) but were extended to run until $t{U}_{\infty }/D=300$. Fluid–structure computations were then continued for a further $t{U}_{\infty }/D=150$. Taking into account initial transients in the fluid–structure solutions, statistical results are presented by time-averaging quantities beyond overall $t{U}_{\infty }/D=300$.

2.4. Simulation Cases

As vortex strength weakens further downstream of a cylinder, we considered a window in the wake region between $0.5<x/D<1.5$ and $-0.85<y/D<0.85$ to place a flexible plate in the present study. In total, 15 cases were simulated corresponding to locations where leading edge of cantilever plate was fixed, as depicted in Figure 3. These cases are also tabulated in Table 6, highlighting their corresponding streamwise (x) and crossflow (y) coordinate positions.

2.5. Validation

A preliminary numerical simulation on two side-by-side cylinders at $R{e}_D=6000$ and 10,000 was firstly undertaken to verify the present modeling and meshing scheme.

Table 4. Benchmarking with previous results at $R{e}_D=6000$ and 10,000 (* denotes data at $R{e}_D=5000$ and subscripts “1” and “2” denote upper and lower cylinders, respectively).

	$\mathbf{T}/\mathbf{D}$	${\mathit{Re}}_{\mathit{D}}=6000$						${\mathit{Re}}_{\mathit{D}}=10,000$
		${\mathit{C}}_{\mathit{d}\mathbf{1}}$	${\mathit{C}}_{\mathit{d}\mathbf{2}}$	${\mathit{C}}_{\mathit{l}\mathbf{1}}$	${\mathit{C}}_{\mathit{l}\mathbf{2}}$	${\mathit{St}}_{\mathbf{1}}$	${\mathit{St}}_{\mathbf{2}}$	${\mathit{C}}_{\mathit{d}\mathbf{1}}$	${\mathit{C}}_{\mathit{d}\mathbf{2}}$	${\mathit{C}}_{\mathit{l}\mathbf{1}}$	${\mathit{C}}_{\mathit{l}\mathbf{2}}$	${\mathit{St}}_{\mathbf{1}}$	${\mathit{St}}_{\mathbf{2}}$
Present study	1.7	1.38	1.21	0.29	−0.23	0.28	0.19	1.31	1.10	0.29	−0.21	0.27	0.17
num. [34]	1.5	-	-	-	-	-	-	1.32	1.34	-	-	0.20	0.20
	1.75	-	-	-	-	-	-	1.25	1.27	-	-	0.21	0.21
num. [35]	1.5	-	-	-	-	-	-	1.36	1.32	-	-	-	-
num. [36]	2.0	-	-	-	-	-	-	1.37	1.37	0.22	−0.22	-	-
num. [3]	1.7	1.21		−0.24		-	-	-	-	-	-	-	-
exp. [3]	1.7	1.06		−0.23		-	-	-	-	-	-	-	-
exp. [7]	1.5	-	-	-	-	0.38	0.11	-	-	-	-	0.37	0.11
	2.0	-	-	-	-	0.26	0.18	-	-	-	-	0.22	0.22
exp.${}^{*}$ [6]	1.75	-	-	-	-	0.32	0.15	-	-	-	-	-	-
exp. [37]	1.7	1.12	0.84	0.18	−0.26	-	-	1.18	0.89	0.12	−0.14	-	-
exp. [38]	1.5	-	-	-	-	-	-	1.29		-	-	0.20

summarizes comparison of present results against published numerical and experimental data from previous works.

Overall performance of the present model shows reasonable agreement with previous results based on their drag coefficients ($C_d$), lift coefficients ($C_l$), and Strouhal numbers ($St$). Considering differences in $T/D$, $St$ in the present model indicates values within range of previous experiments performed at $T/D=1.5,2.0$ and numerical simulations at $T/D=1.5,1.75$. More importantly, the present model captures two distinct $St$ indicating different vortex shedding periods corresponding to narrower and wider wakes in each cylinder, which is predominant in the biased flow regime. Consequently, this is also reflected in the distinct drag and lift coefficients reported for each cylinder in the present numerical model.

Although $C_d$ and $C_l$ in the present model are consistent with previous numerical studies (for example, $C_d=1.21$ and $C_l=-0.24$ for $R{e}_D=6000$ at $T/D=1.7$ [3] and $C_d$ of 1.25–1.32 for $R{e}_D=$ 10,000 at $T/D$ between 1.5 and 1.75 [34], about which $T/D=1.7$ in the present case falls within), the present numerical model overestimated their values in comparison to the experimental results in [37]. However, this difference in $C_d$ and $C_l$ with experimental results can be seen in all previous numerical studies reported in Table 4. This is potentially due to, firstly, the difference in actual experimental to numerical conditions, and, secondly, the difficulty in capturing flow separation using turbulence modeling in these sub-critical flow regimes, where the boundary layer remains laminar but the wake region is turbulent. Alternatively, comparison with Bearman and Wadcock [38] (albeit for $T/D=1.5$) suggests closer agreement with experimental data.

In addition, while the present numerical model shows biased gap flow pattern expected at this intermediate gap spacing [2,38], previous numerical studies at $R{e}_D=$ 10,000 show symmetric unbiased flow. This may highlight the advantage of the present three-dimensional and Scale-Adaptive Simulation (SAS) turbulence model, which has been shown to better capture the unsteady fluctuations under separated flow conditions than previous URANS turbulence models [31].

Further validation of the present model was performed by undertaking a grid- and time-independence test for flow past two side-by-side cylinders with a stationary plate placed behind the upper cylinder (corresponding to Case a1 in Figure 3). A finer grid model (Model B), where mesh size was effectively reduced by 1.6–2.0—yielding a total of 226,075 nodes in the fluid domain—was constructed. In addition, another simulation using the baseline grid model for Case a1 but using a timestep size an order of magnitude lower (i.e., Model A with $\Delta t=0.001$ s) was undertaken.

Table 5. Comparison of flow parameters with models using finer grids (Model B) and smaller timestep (Model A) for Case a1.

	Models
	Baseline	Model A	Model B
$C_{d1}$	1.002	1.003	1.004
$C_{d2}$	1.353	1.353	1.363
$C_{l1}$	0.123	0.123	0.157
$C_{l2}$	−0.325	−0.335	−0.350
$St$	0.050	0.052	0.055

shows small differences between the baseline model results and their corresponding finer grid model and smaller timestep simulation, respectively, indicating that the present baseline model is sufficiently insensitive to the size of the mesh and timestep.

3. Results and Discussion

Overall, 10–20 internal coupling iterations were necessary for fluid–structure coupling convergence at each time step. Computations for the initial stationary plate could take up to 24 h, while the following fluid–structure computations could run up to 45 h, depending on the case simulated. We begin by presenting the oscillation history of the flexible plate when they are placed at each of the 15 locations highlighted in Figure 3. Plate tip displacements (in the y-direction) over time, when the plate is positioned along various streamwise locations at each $-0.85<y/D<0.85$, are shown in Figure 4a–e. Tip oscillations show lowest amplitudes when flexible plate is placed along the centerline ($y/D=0$) between the two side-by-side cylinders, compared to other $y/D$ locations. Furthermore, their oscillating amplitude appears to be lowest when the plate is closest to the cylinders ($x/D=0.5$) before maximizing at $x/D=1.0$ and decreases as the plate is placed further downstream, as shown in Figure 4c. To better quantify plate vibration behavior behind the cylinders, the mean y-displacements ($\overline{y}$) of the tip was calculated for each case. In addition, as piezoelectric effect is affected by their mechanical strains, which occur irrespective of positive or negative direction in plate deflection, we considered taking their vibration amplitude (A) over time and calculated their root-mean-square ($A_{rms}$) as an indication of the overall level in mechanical strains experienced by the piezoelectric beam (and, hence, energy harvesting potential), for all 15 cases.

Table 6. Mean of plate displacement and root-mean-square of oscillating amplitude against plate location.

Case ID	Location		Results
	$\mathit{x}/\mathit{D}$	$\mathit{y}/\mathit{D}$	$\overline{\mathit{y}}$ (mm)	${\mathit{A}}_{\mathbf{rms}}$ (mm)
a1	0.5	0.85	−0.037	1.514
a2		0.425	−0.309	1.031
a3		0	−0.012	0.283
a4		−0.425	0.343	1.193
a5		−0.85	0.068	1.551
b1	1.0	0.85	0.079	0.960
b2		0.425	0.053	1.417
b3		0	−0.057	1.133
b4		−0.425	−0.157	1.412
b5		−0.85	−0.027	1.129
c1	1.5	0.85	0.124	1.142
c2		0.425	0.251	1.230
c3		0	0.017	0.856
c4		−0.425	−0.248	1.618
c5		−0.85	−0.112	0.999

summarizes these $\overline{y}$ and $A_{rms}$ values for all the cases simulated in the present study. Inspecting the table, a number of observations may be hypothesized in regards to variation in $\overline{y}$ and $A_{rms}$ with respect to plate placement in the wake region:

• The mean y-displacements $\overline{y}$ show opposing deflections between plate positioned above and below the centerline $y/D=0$. At locations immediately behind both cylinders (i.e., $x/D=0.5$), the plate placed above the centerline ($y/D>0$) tended to oscillate about a mean position that is deflected downwards ($\overline{y}<0$), while the plate placed below the centerline ($y/D<0$) tended to oscillate about a mean position that deflects upwards ($\overline{y}$ > 0). However, away from the cylinders (i.e., $x/D=1.0,1.5$), the opposite occurs, where the plate positioned above the centerline appears to oscillate about a mean position that is deflected upwards (i.e., $\overline{y}$ > 0) and the plate positioned below the centerline appears to deflect more downwards (i.e., $\overline{y}$ < 0).
• In the vicinity immediately behind the cylinders (i.e., $x/D=0.5$), putting the flexible plate on the rear center point of either cylinder (i.e., $y/D=0.85,-0.85$) was found to promote highest overall plate oscillations (as indicated by maximum $A_{rms}$). However, further downstream from both cylinders (i.e., $x/D=1.0,1.5$), placing the flexible plate at intermediate region above or below the centerline $y/D=0$ (i.e., at $y/D=0.425$ and $y/D=-0.425$) was shown to generate highest overall amplitudes in plate oscillations along their respective streamwise positions.
• The flexible plate placed along the centerline $y/D=0$ showed the lowest root-mean-square in their oscillation amplitude. Furthermore, root-mean-square in amplitude of plate oscillation with respect to their placement behind two side-by-side cylinders appears to be mirrored about the centerline $y/D=0$ (i.e., $A_{rms}$ at $y/D=0.85$ are closer in values to $A_{rms}$ at $y/D=-0.85$, and $A_{rms}$ at $y/D=0.425$ are closer in values to $A_{rms}$ at $y/D=-0.425$) along a streamwise location. This is further evident from the contour plot showing distribution of $A_{rms}$ behind both cylinders, as depicted in Figure 5.

Figure 5 shows the variation in root-mean-square of the oscillation amplitude ($A_{rms}$) with respect to plate placement behind two side-by-side cylinders. The contours were generated from the results at the 15 locations in Table 6 using a cubic spline interpolation, giving predicted $A_{rms}$ for the flexible plate if they are located along various ($x/D$, $y/D$) locations behind the two cylinders. Thus, Figure 5 indicates potential locations where the flexible plate may be placed to undergo high overall vibration amplitudes. This include rear center points on either cylinders or in the intermediate region off-center from the centerline between the cylinders (for placements further downstream). Overall, maximum mean amplitude of oscillation was recorded when the flexible plate is placed at $x/D=1.5,y/D=-0.425$ (i.e., Case c4), where their mean amplitude is almost twice the mean amplitude on the centerline at similar streamwise (x) position. Figure 6a–c highlights spanwise vorticity contour plot corresponding to cases with maximum mean amplitude for each streamwise locations $x/D=0.5,1.0,1.5$. While biased flow regime (with narrow and wide asymmetric wake patterns behind either cylinder) is expected to take place for side-by-side cylinders in the present $T/D=1.7$, it was found that this wake pattern still persists in the presence of a flexible plate. Comparing at instances when their respective plate amplitude is maximum, the narrow–wide wake pattern is more pronounced for Cases b2 and c2 (see Figure 6b,c), where the plate is placed at $y/D=\pm 0.425$, compared to Case a5 where plate is placed centrally behind a cylinder at $y/D=-0.85$. In contrast, the wake pattern for Case a3 (corresponding to lowest mean amplitude case located along centerline $y/D=0$) in Figure 6d shows minimal difference in wake size between cylinders, highlighting: (i) the potential suppression of biased gap flow when the flexible plate is centrally positioned and close to both cylinders (similar to previous study by Oruc et al. [20] but with plate length not extending upstream in the present study); and (ii) the important role of biased gap flow on plate vibrations behind two side-by-side cylinders. Consequently, the wake-excited energy harvesting plate may be positioned away from the centerline $y/D=0$ to maximize their energy output for this type of bluff body configuration.

4. Conclusions

Wake-excited vibrations of a flexible plate behind two side-by-side cylinders was computationally investigated in their biased flow regime at $R{e}_D=10,000$. Using a Scale-Adaptive SST turbulence flow model and partitioned coupling to a finite element solver, vibration responses of a flexible plate placed at various locations in the wake region were simulated and analyzed. Numerical results indicate that placing the flexible plate along the centerline between both cylinders generated low mean amplitude of oscillations and may potentially suppress biased gap flow if positioned close to both cylinders. It was found that plate vibrations are maximized when placed immediately behind either cylinders or further downstream within some intermediate region off-center from the centerline, where biased asymmetric wake interactions are present. These numerical findings may be exploited to identify favorable placements to maximize wake-excited energy harvesters behind side-by-side circular cylindrical structures. It is remarked that the present study focused on $R{e}_D=1000$, biased flow regime $T/D=1.7$, and wake region within $0.5<x/D<1.5$ and $-0.85<y/D<0.85$. Future simulations at various other $R{e}_D$ and $T/D$ and wider region behind both cylinders are anticipated, to further understand the effects of $R{e}_D$, $T/D$, and other plate positions on their vibration and energy harvesting potential.