Analysis of Hydrodynamic Performance of L-Type Podded Propulsion with Oblique Flow Angle
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
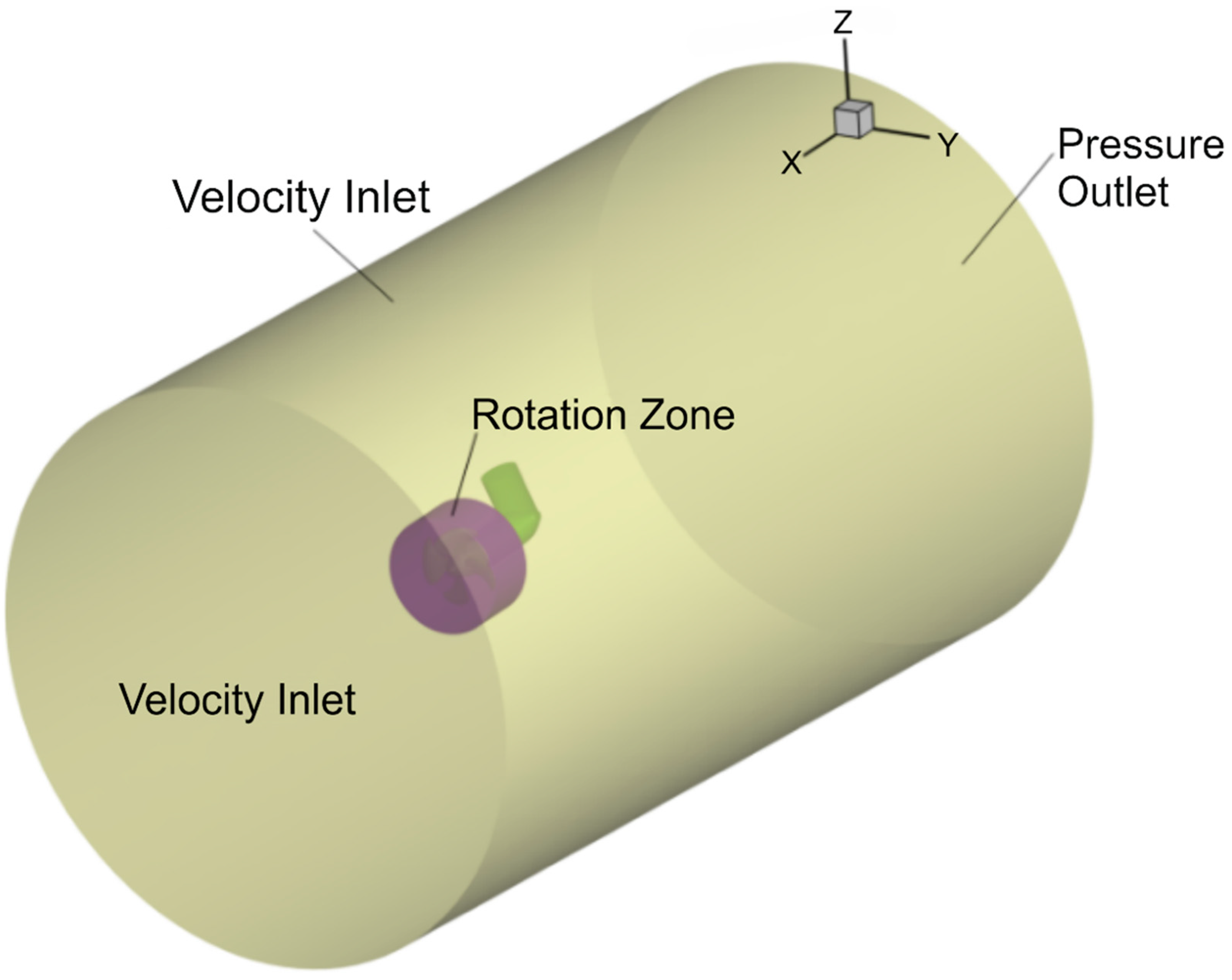
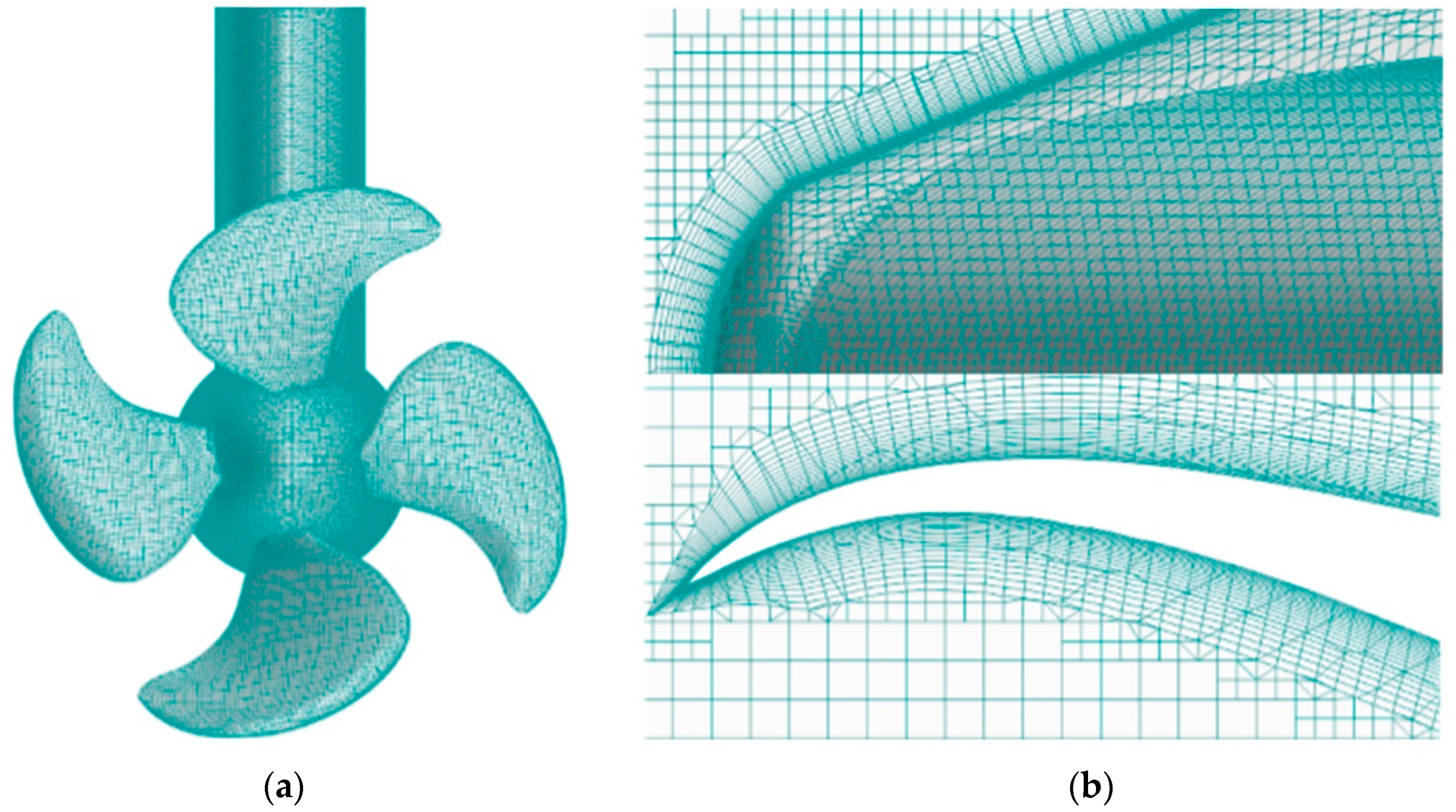
2.2. Geometric Model and Computational Grid
2.3. Parameter Setting and Operating Conditions
2.4. Model Experimental Test
3. Results and Analysis
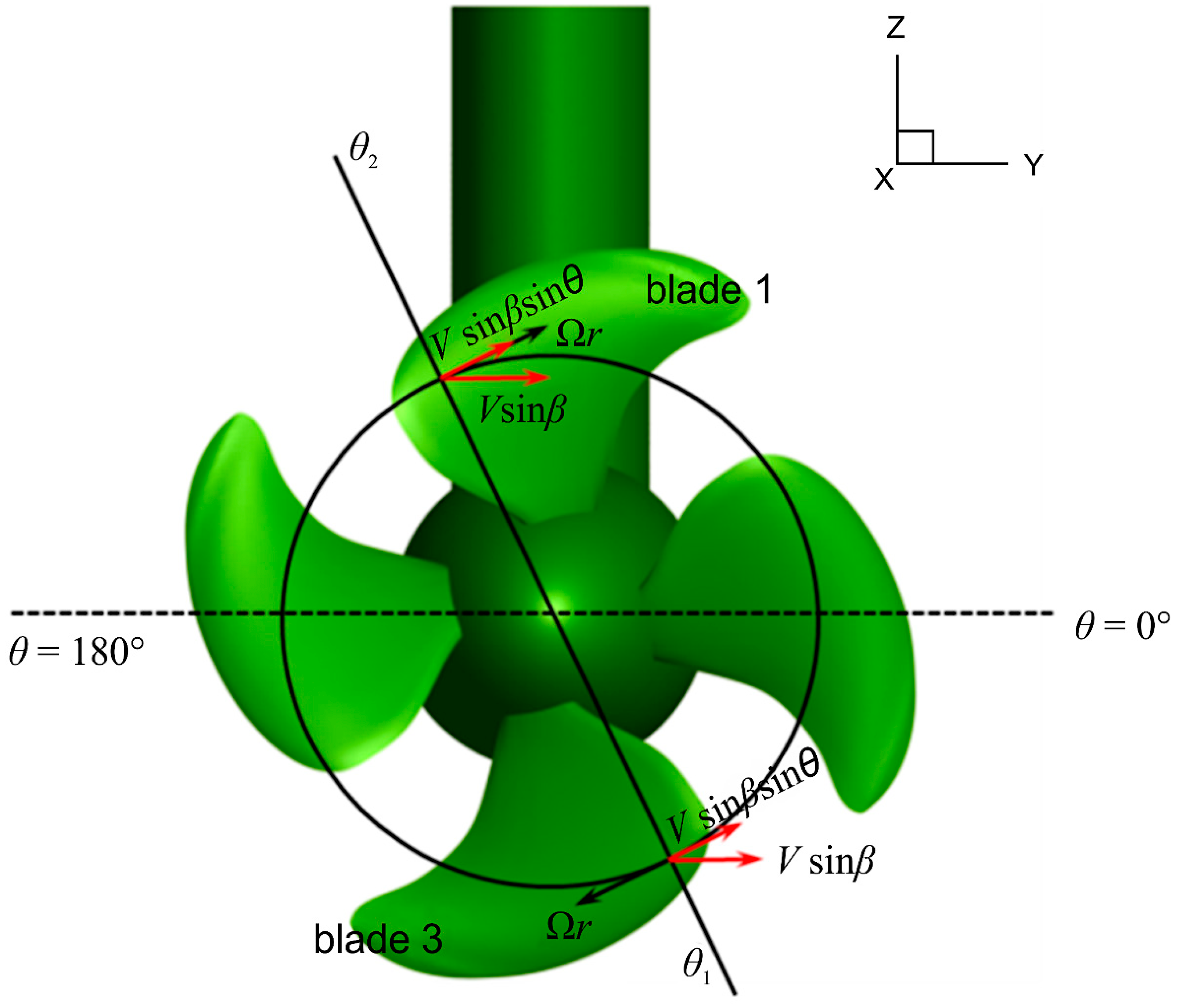
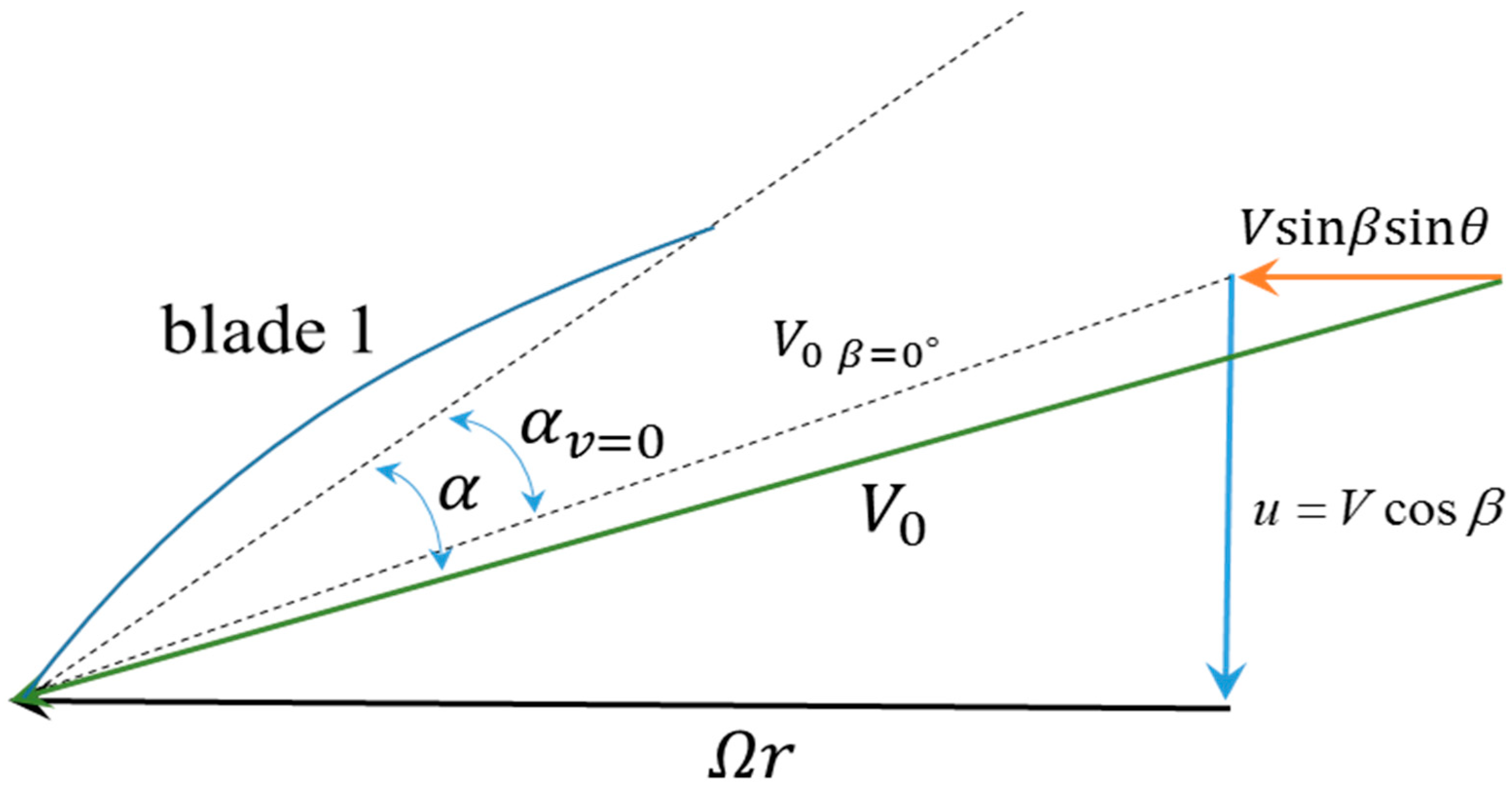
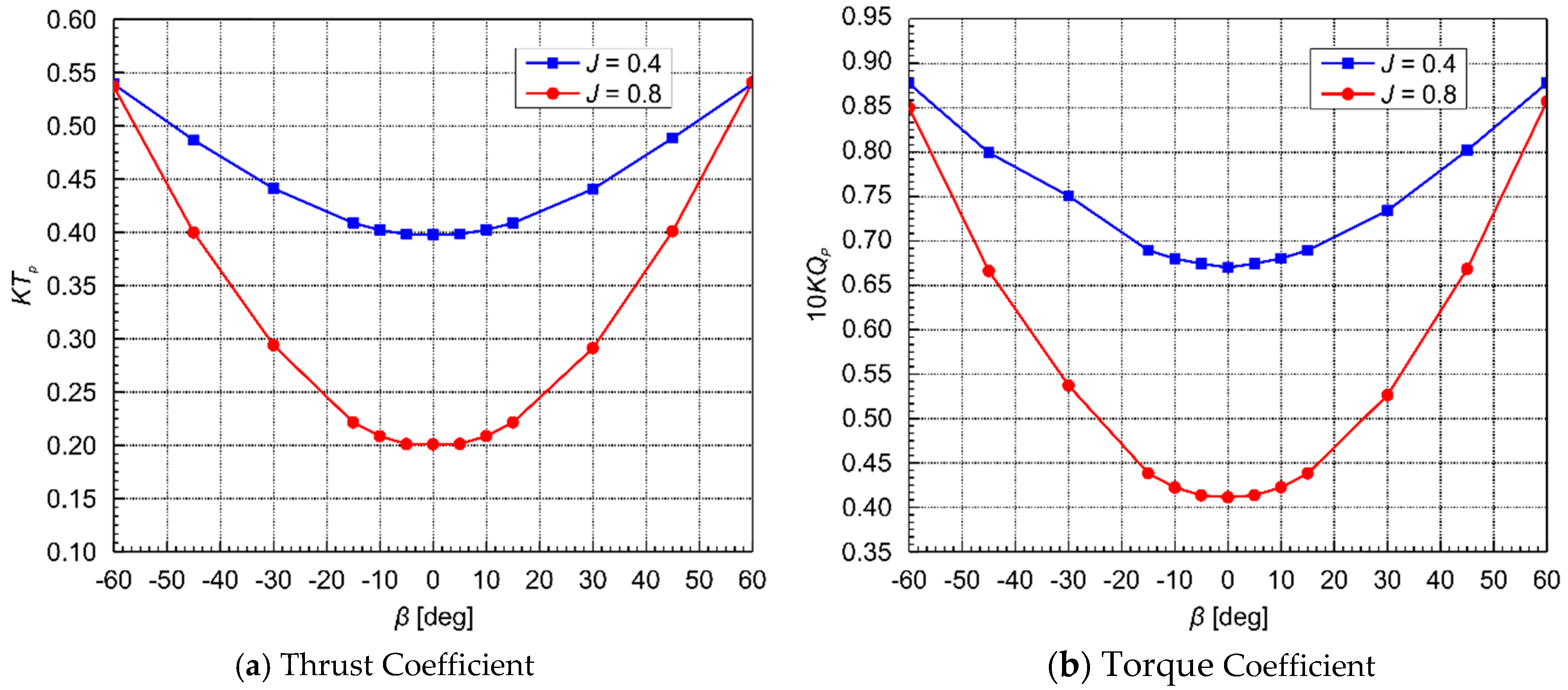
3.1. Calculation Results of Single Blade
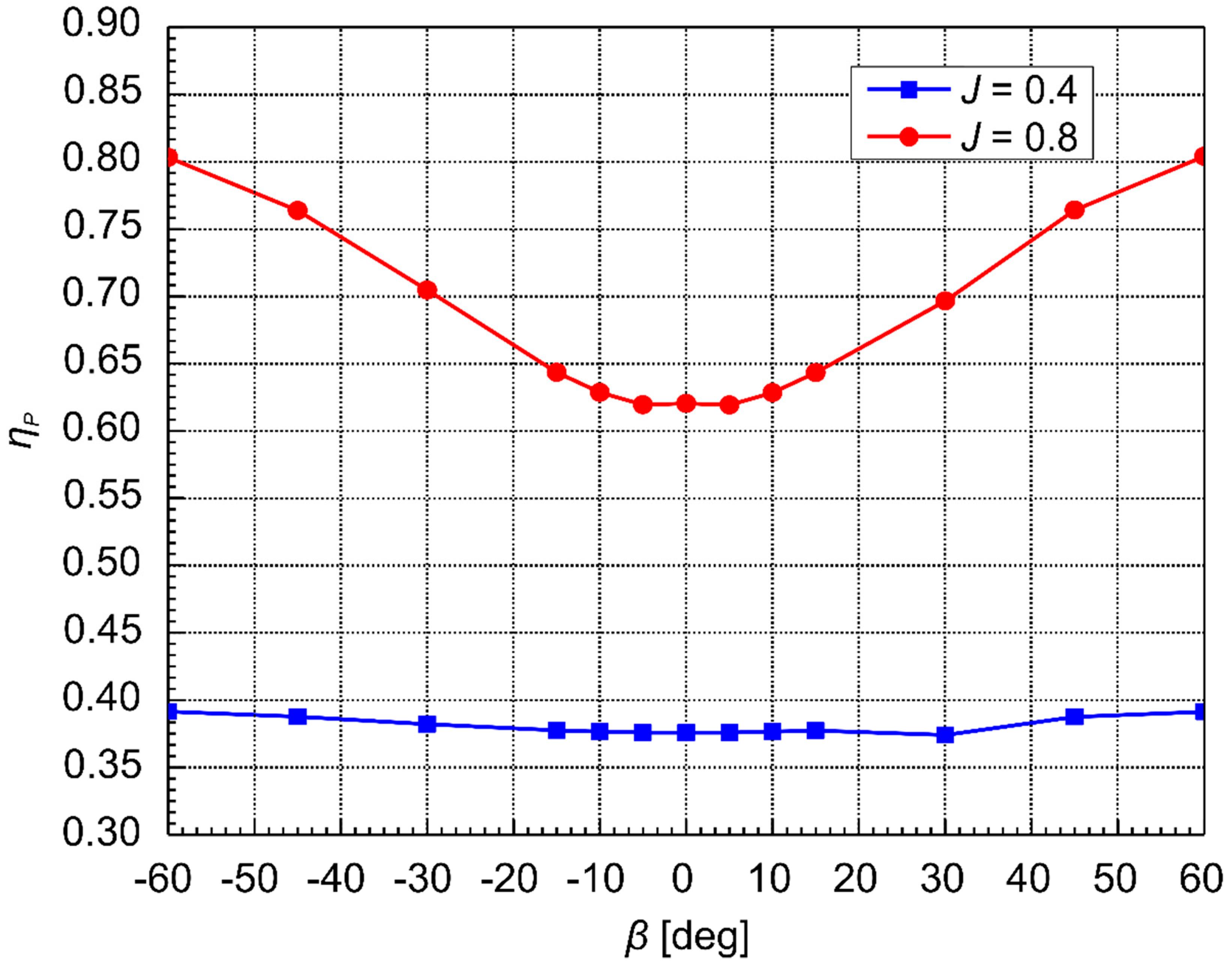
3.2. Experimental Results of Propeller
3.3. Experimental Results of Pod
4. Discussion
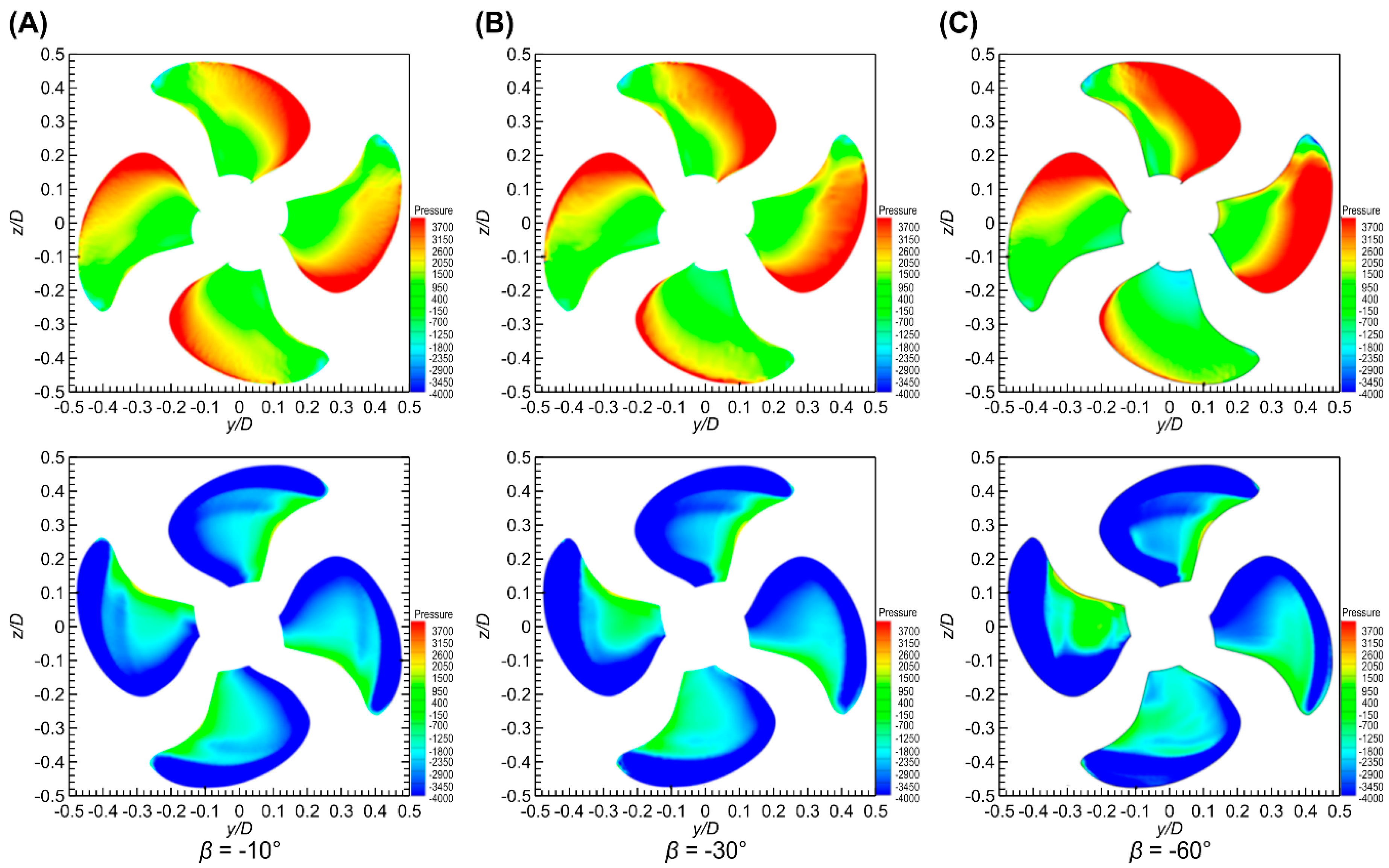
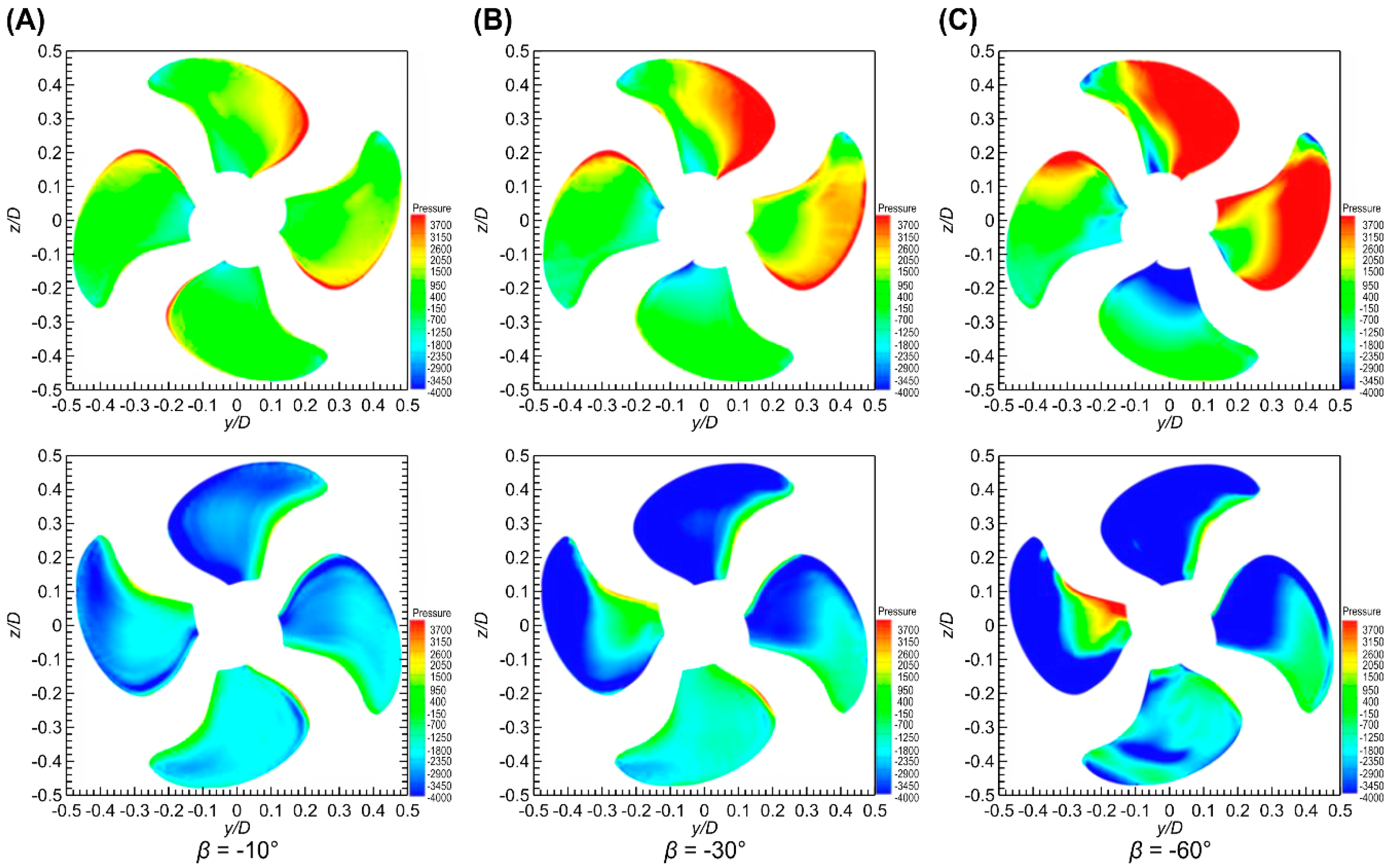
4.1. Calculation Results of Pressure Distribution
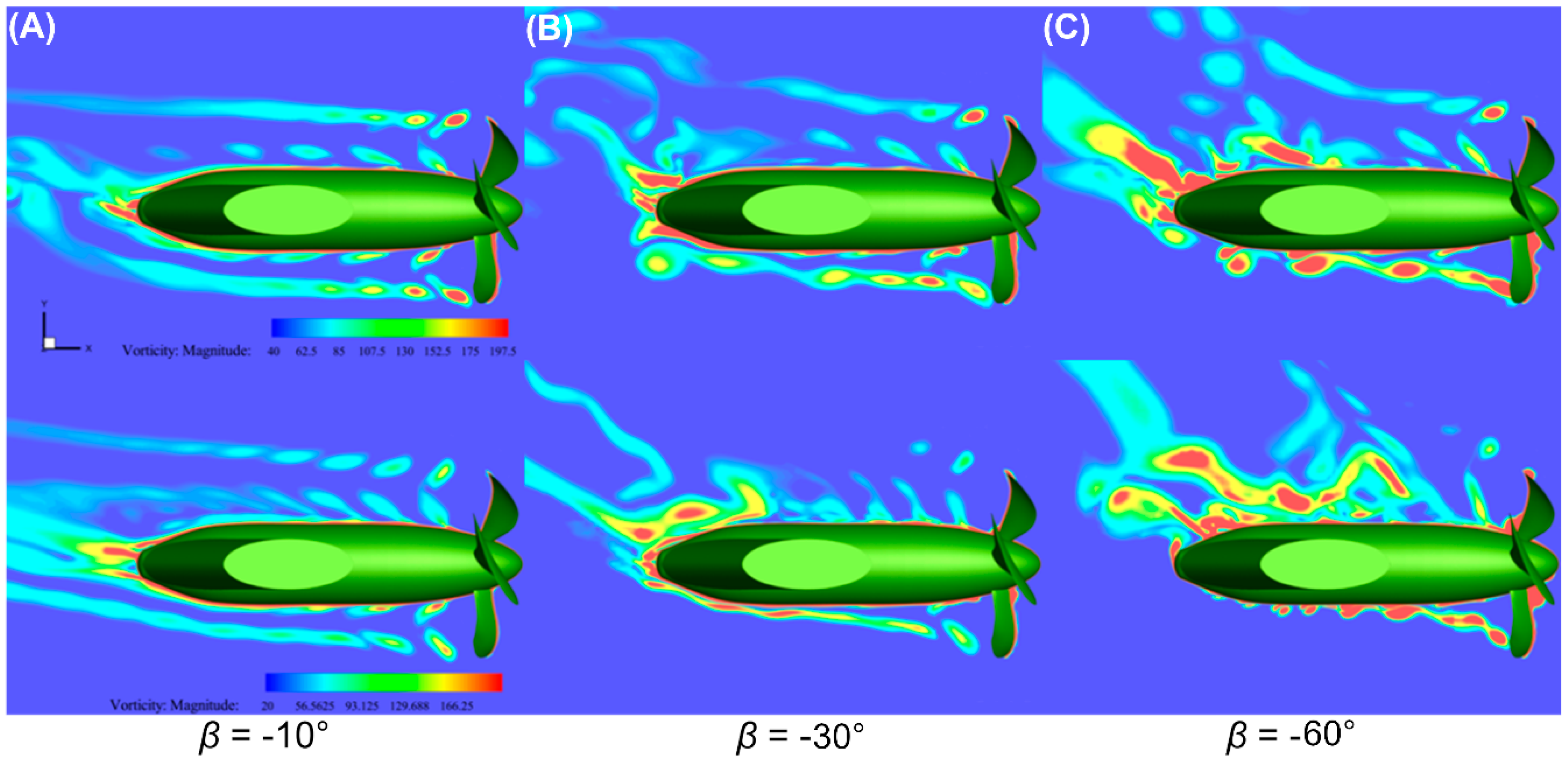
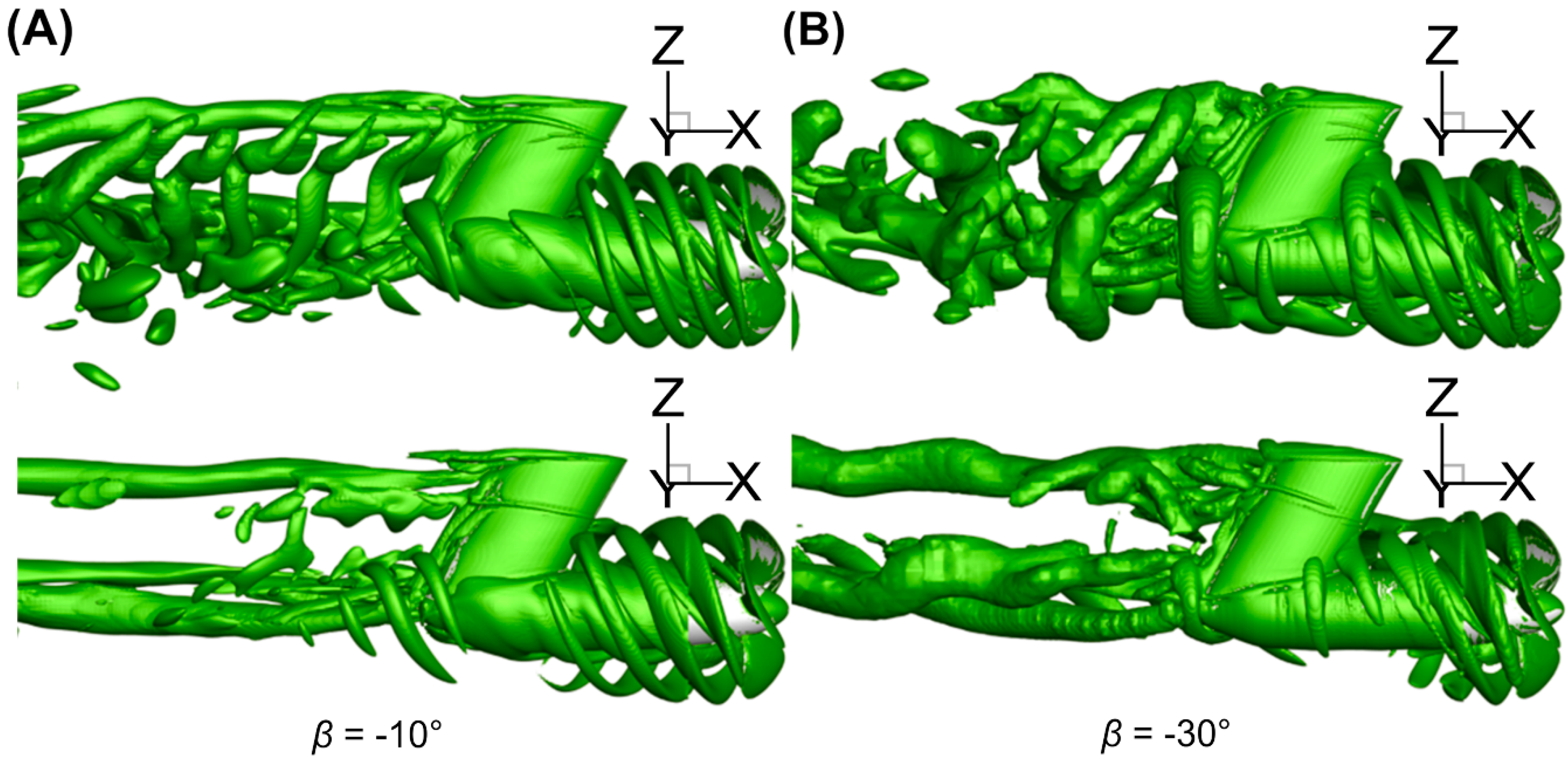
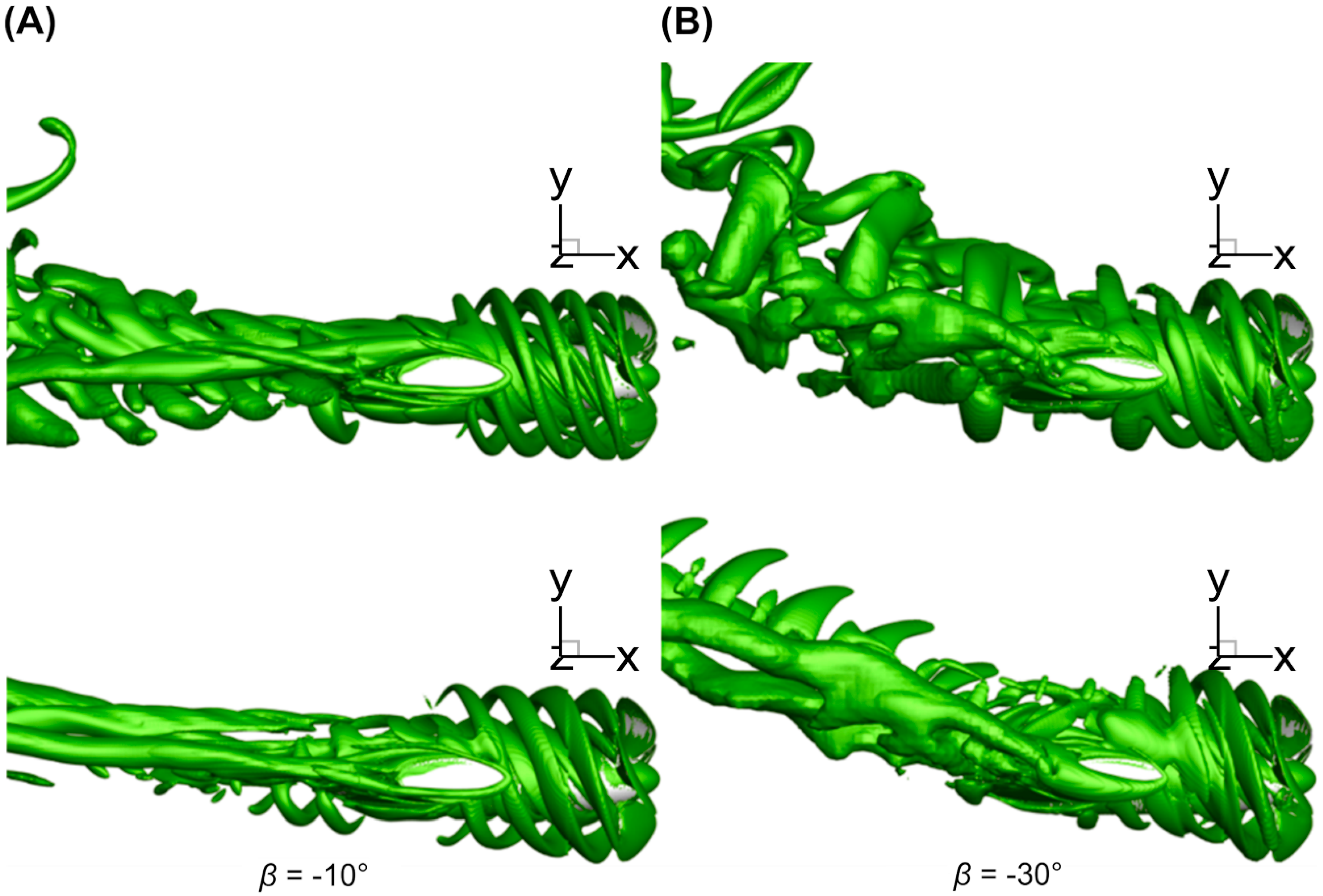
4.2. Calculation Results of Wake Flow Field
5. Conclusions
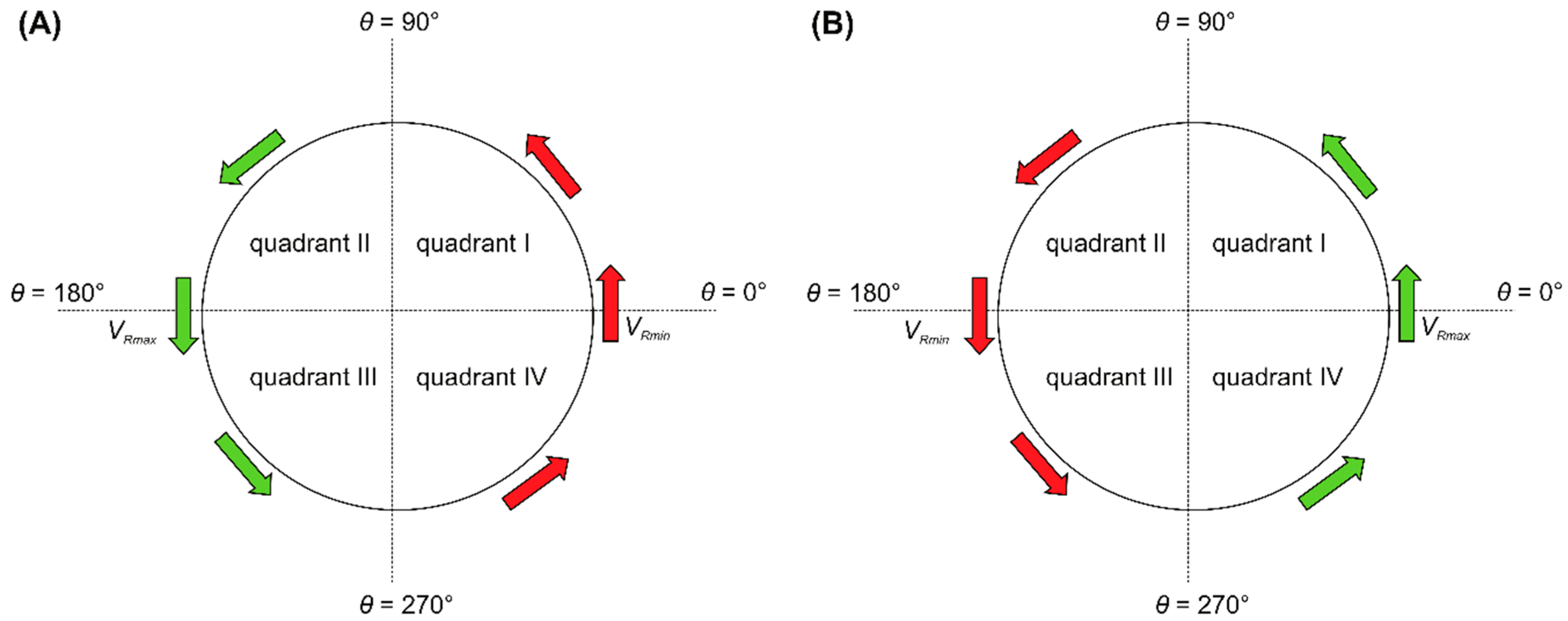
- The change in circumferential velocity when the propeller rotates in an oblique flow leads to a constant change in the attack angle of the blade section. Under negative flow, the blade thrust and torque are the highest at and smallest at .
- The load of the propeller under oblique flow will increase with the oblique flow angle. The increased resistance caused by water flow leads to a decrease in the podded propulsion thrust coefficient with an increase in the oblique flow angle. Under a high advance coefficient, the speed of increase of the pressure effect is higher than that of the viscous effect, and therefore, the propeller efficiency shows an increasing trend with the increase of the oblique flow angle. Under a low advance coefficient, the propeller efficiency curve changes gently.
- The nonuniformity of inflow results in varying degrees of asymmetry in the horizontal and vertical distributions of the propeller blade pressure, and this asymmetry is closely related to the size of the oblique flow angle and circumferential position of blades.
- The velocity field after the blade shows different degrees of asymmetry and nonuniformity due to the lateral velocity component of the incoming flow. When the oblique flow angle was large, relatively strong interference effects between venting vortexes and the cabin after the blades were identified, leading to a disorderly venting vortex system after the blade.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, X.; Sun, Q.; Wei, Y.; Wu, Y.; Wang, H. Experimental investigation on hydrodynamic performance of podded propulsor under static azimuthing conditions. Shipbuild. Chin. 2016, 3, 9–18. (In Chinese) [Google Scholar]
- Zhao, C.; Yang, C.J. CFD simulation of propeller open-water performance considering induced velocity at the inlet of computational domain. Ocean Eng. 2014, 3, 72–77. [Google Scholar]
- Fu, H.P. Numerical study of methods for predicting integral hull and propeller and propeller-induced hull surface pressure fluctuations. J. Harbin Eng. Univ. 2009, 7, 728–734. (In Chinese) [Google Scholar]
- Chicherin, I.A.; Lobatchev, M.P.; Pustoshny, A.V.; Sanchez, C.A. On a propulsion prediction procedure for ships with podded propulsors using RANS-code analysis. In Proceedings of the 1st International Conference on Technological Advances in Podded Propulsion, Newcastle University, Newcastle, UK, 14–16 April 2004; pp. 223–236. [Google Scholar]
- Ohashi, K.; Hino, T. Numerical simulations of flows around a ship with podded propulsor. In Proceedings of the 1st International Conference on Technological Advances in Podded Propulsion, Newcastle University, Newcastle, UK, 14–16 April 2004; pp. 211–221. [Google Scholar]
- Liu, P.; Islam, M.; Veitch, B. Unsteady hydromechanics of a steering podded propeller unit. Ocean Eng. 2009, 36, 1003–1014. [Google Scholar] [CrossRef]
- Amini, H.; Sileo, L.; Steen, S. Numerical calculations of propeller shaft loads on azimuth propulsors in oblique inflow. J. Mar. Sci. Technol. 2012, 17, 403–421. [Google Scholar] [CrossRef]
- Guo, C.Y.; Ma, N.; Yang, C.J. Numerical simulation of a podded propulsor in viscous flow. J. Hydrodyn. Ser. B 2009, 21, 71–76. [Google Scholar] [CrossRef]
- Zhou, K.F.; Yan, T.; Guo, C.Y. CFD study of the hydrodynamic performances of L-type podded propulsor. Ship Eng. 2011, S2, 65–68. [Google Scholar]
- Xiong, Y.; Sheng, L.; Yang, Y. Hydrodynamics performance of podded propulsion at declination angles. J. Shanghai Jiaotong Univ. 2013, 6, 956–961. (In Chinese) [Google Scholar]
- The 23rd International Towing Tank Conference. Recommended Procedures. Propulsion Performance—Podded Propeller Tests and Extrapolation 7.5-02-03-01.3, Revision 00. 2002. Available online: https://ittc.info/media/1832/75-02-03-013.pdf (accessed on 20 February 2019).
- Reichel, M. Manoeuvring forces on azimuthing podded propulsor model. Pol. Marit. Res. 2007, 14, 3–8. [Google Scholar] [CrossRef]
- Islam, M.F.; Akinturk, A.; Veitch, B.; Liu, P. Performance characteristics of static and dynamic azimuthing podded propulsor. In Proceedings of the 1st International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009; pp. 482–492. [Google Scholar]
- Islam, M.F.; Veitch, B.; Liu, P.F. Experimental Research on Marine Podded Propulsors. J. Nav. Archit. Mar. Eng. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Palm, M.; Jurgens, D.; Bendl, D. Boundary layer control of twin skeg hull form with reaction podded propulsion. In Proceedings of the 2nd International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1993; p. 460. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 2012, 32, 1598–1605. [Google Scholar] [CrossRef]
- Baek, D.G.; Yoon, H.S.; Jung, J.H.; Kim, K.S.; Paik, B.G. Effects of the advance ratio on the evolution of a propeller wake. Comput. Fluids 2015, 118, 32–43. [Google Scholar] [CrossRef]
- Meinke, M.; Schneiders, L.; Günther, C.; Schröder, W. A cut-cell method for sharp moving boundaries in Cartesian grids. Comput. Fluids 2013, 85, 135–142. [Google Scholar] [CrossRef]
- Weiss, J.M.; Smith, W.A. Preconditioning applied to variable and constant density flows. AIAA J. 1995, 33, 2050–2057. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows; Center for Turbulence Research Report CTR-S88; Stanford University: Palo Alto, CA, USA, November 1988; pp. 193–208. [Google Scholar]







| Parameter (Units) | Value |
|---|---|
| Long axis distance of cross section of inclined bracket (m) | 0.16 |
| Short axis distance of cross section of inclined bracket (m) | 0.062 |
| Height between upper surface of inclined bracket and y-axis (m) | 0.19 |
| Inclined angle of bracket (°) | 60 |
| Total length of cabin (m) | 0.473 |
| Length of propeller hub (m) | 0.075 |
| Maximum radius of cabin (m) | 0.049 |
| Number of blades of propeller | 4 |
| Propeller diameter (m) | 0.24 |
| Pitch ratio of propeller (0.7R) | 1.284 |
| Domain | Coarse | Medium | Fine |
|---|---|---|---|
| Rotating | 2.21 M | 3.78 M | 6.59 M |
| Background | 0.52 M | 0.81 M | 1.37 M |
| Total | 2.73 M | 4.59 M | 7.96 M |
| Grid Name | Grid size | Error (%) | Error (%) | ||
|---|---|---|---|---|---|
| Experimental Value | 0.2379 | 0.4705 | |||
| Coarse | 2.73 M | 0.2497 | 4.96 | 0.4834 | 2.74 |
| Medium | 4.59 M | 0.2466 | 3.66 | 0.4808 | 2.19 |
| Fine | 7.96 M | 0.2432 | 2.23 | 0.4781 | 1.62 |
| Calculation Number | ① | ② | ③ | ④ | ⑤ | ⑥ |
|---|---|---|---|---|---|---|
| Advance coefficient | 0.4, 0.8 | 0.4, 0.8 | 0.4, 0.8 | 0.4, 0.8 | 0.4, 0.8 | 0.4, 0.8 |
| Incoming flow velocity V (m/s) | 0.96, 1.92 | 0.96, 1.92 | 0.96, 1.92 | 0.96, 1.92 | 0.96, 1.92 | 0.96, 1.92 |
| Oblique flow angle (°) | ±5° | ±10° | ±15° | ±30° | ±45° | ±60° |
| Rotation speed (rps) | 10 | 10 | 10 | 10 | 10 | 10 |
| Experimental Value | Calculated Value | % Error | Experimental Value | Calculated Value | % Error | |
|---|---|---|---|---|---|---|
| 0.5 | 0.3452 | 0.3413 | −1.13 | 0.5617 | 0.5698 | 1.44 |
| 0.6 | 0.2838 | 0.2872 | 1.20 | 0.5174 | 0.5274 | 1.93 |
| 0.7 | 0.2379 | 0.2432 | 2.23 | 0.4705 | 0.4781 | 1.62 |
| 0.8 | 0.2047 | 0.2007 | −1.95 | 0.4113 | 0.4120 | 0.17 |
| 0.9 | 0.1585 | 0.1652 | 4.23 | 0.3512 | 0.3659 | 4.19 |
| 1.0 | 0.1155 | 0.1205 | 4.33 | 0.2762 | 0.2713 | −1.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhao, D.; Guo, C.; Pang, Y. Analysis of Hydrodynamic Performance of L-Type Podded Propulsion with Oblique Flow Angle. J. Mar. Sci. Eng. 2019, 7, 51. https://doi.org/10.3390/jmse7020051
Wang W, Zhao D, Guo C, Pang Y. Analysis of Hydrodynamic Performance of L-Type Podded Propulsion with Oblique Flow Angle. Journal of Marine Science and Engineering. 2019; 7(2):51. https://doi.org/10.3390/jmse7020051
Chicago/Turabian StyleWang, Wei, Dagang Zhao, Chunyu Guo, and Yongjie Pang. 2019. "Analysis of Hydrodynamic Performance of L-Type Podded Propulsion with Oblique Flow Angle" Journal of Marine Science and Engineering 7, no. 2: 51. https://doi.org/10.3390/jmse7020051
APA StyleWang, W., Zhao, D., Guo, C., & Pang, Y. (2019). Analysis of Hydrodynamic Performance of L-Type Podded Propulsion with Oblique Flow Angle. Journal of Marine Science and Engineering, 7(2), 51. https://doi.org/10.3390/jmse7020051





