Laboratory Testing to Research the Micro-Structure and Dynamic Characteristics of Frozen–Thawed Marine Soft Soil
Abstract
:1. Introduction
2. Materials and Methods
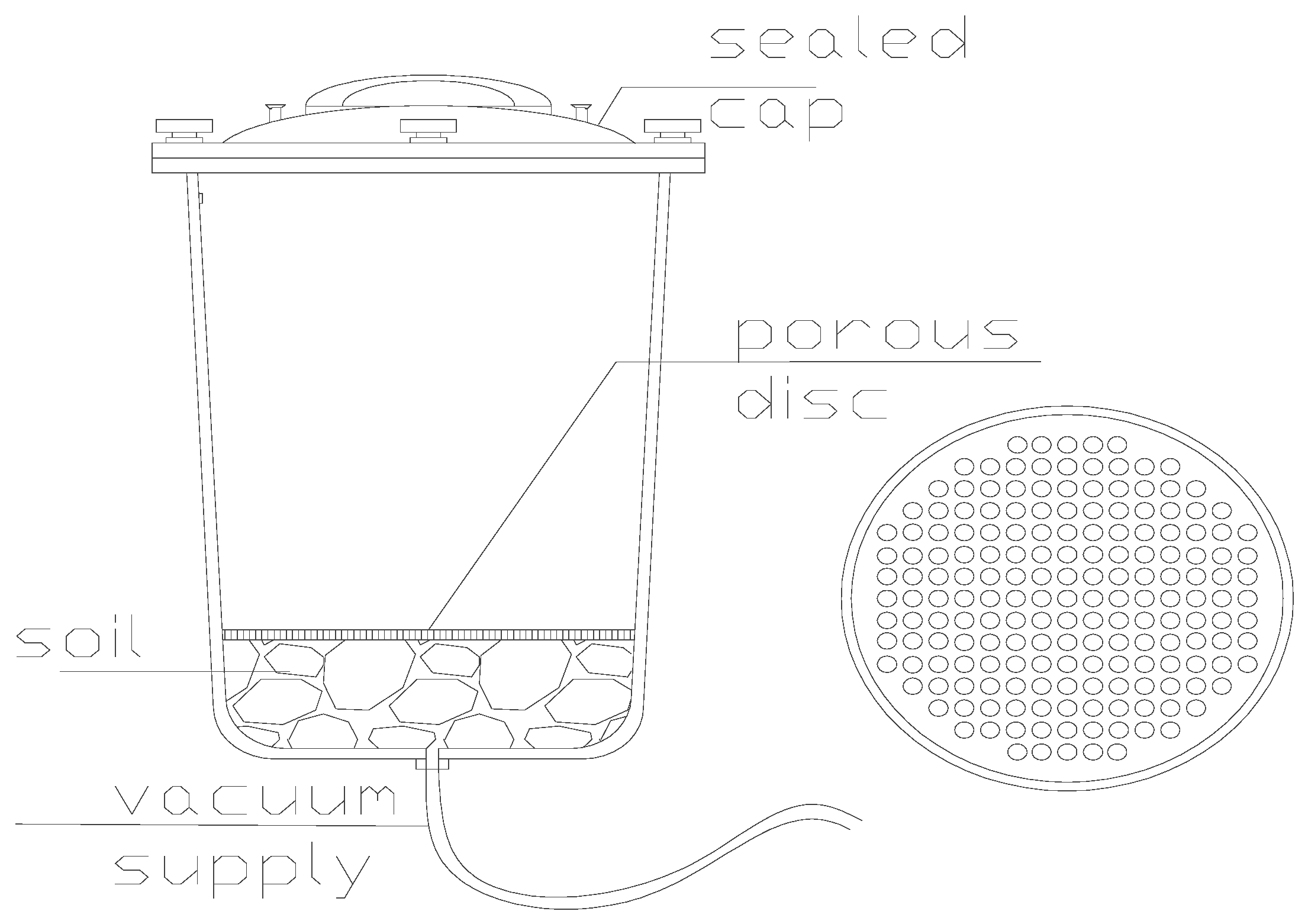
2.1. Remolded Soil Samples
2.2. Cyclic Loading
2.3. Freeze–Thaw Cycles
2.4. Microscopic Observation
2.5. Experimental Plan
3. Qualitative Analysis of the Microstructure
3.1. Microstructure of Soil under a Freeze–Thaw Cycle
3.2. Microstructure of Frozen–Thawed Soil under Cycle Loading
4. Quantitative Analysis of the Microstructure
4.1. Microstructure Analysis of Soil under Freeze–Thaw Cycles
4.1.1. Method and Parameters
- The area corresponds to the area occupied by the outline of the object.
- Equivalent diameter (mean): After connecting two points on the outline of the selected object, this is calculated as the average value of the length of the line passing through the centroid.
- The fractal dimension is calculated by the area–circumference method. The basic principle is as follows:where P is the pore perimeter, A is the pore area, and D is the fractal dimension of the pore.
- Surface void ratio ew: the ratio of pore area to particle area.where Sw is the pore area, and S is the particle area.
4.1.2. Distribution of Pore Diameters after Freeze–Thaw Cycles
4.1.3. Distribution of Pore Area after Freeze-Thaw Cycles
4.1.4. Surface Void Ratio under Freeze–Thaw Cycles
4.1.5. Pore Fractal Dimensions under Freeze–Thaw Cycles
4.2. Under Cyclic Loading
4.3. Accumulative Distribution of the Pore Area
4.4. Changes of Pore Fractal Dimension
5. Results and Discussion
5.1. Relationship of the Void Ratio and Axial Strain
5.2. Relationship of Void Ratio Change and Axial Strain
6. Conclusions
- After freeze–thaw cycles, the flaky structure in the soil sample sharply increased. The increment became more and more significant with the increase of the freeze–thaw cycle number and the decrease of temperature. Because of the freeze–thaw cycle, the number of tiny pores (D < 0.5 μm) decreased, while the number of large pores (D ≥ 1 μm) increased, and so the void ratio also rose. Under a temperature of below zero, the complexity structure of pores became more complex, indicating the average fractal dimension of the pores increased.
- After loading, the number of large pores were reduced, resulting in a decrease in the porosity ratio. The shift of the cumulative distribution curves indicated that the proportion of tiny pores increased and the proportion of large pores decreased, so that the structure became denser.
- At the beginning of cyclic loading, the accumulated energy of the external load exceeded the binding energy of the partial soil particles. Then, the proportion of the external load that the pore water bore was increased due to the displacement of the particles, resulting in a faster accumulation rate of excess pore pressure.
- After cyclic loading, the soil skeleton unit was gradually steadied, and the squeezing effect of the soil was reduced. At this time, the soil structure reached a stable state, shown as a reduction in the accumulation of excess pore pressure and axial strain.
Author Contributions
Funding
Conflicts of Interest
References
- Wu, X.; Jin, S.; Chang, L. Monitoring bare soil freeze–thaw process using GPS-interferometric reflectometry: Simulation and validation. Remote Sens. 2017, 10, 14. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Weihermüller, L.; McCabe, M.F.; Moghadas, D.; Vereecken, H.; Lambot, S. Temporal monitoring of the soil freeze-thaw cycles over a snow-covered surface by using air-launched ground-penetrating radar. Remote Sens. 2015, 7, 12041–12056. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Stockamp, J.; Hajnsek, I.; Ludwig, R. Identification of soil freezing and thawing states using SAR polarimetry at C-band. Remote Sens. 2014, 6, 2008–2023. [Google Scholar] [CrossRef]
- Zhao, Z.; Shen, R.; Feng, W.; Zhang, Y.; Zhang, Y. Soil thermal balance analysis for a ground source heat pump system in a hot-summer and cold-winter region. Energies 2018, 11, 1206. [Google Scholar] [CrossRef]
- Miao, C.; Chen, J.; Zheng, X.; Zhang, Y.; Xu, Y.; Du, Q. Soil water and phreatic evaporation in shallow groundwater during a freeze-thaw period. Water 2017, 9, 396. [Google Scholar] [CrossRef]
- Bing, H.; He, P.; Zhang, Y. Cyclic freeze-thaw as a mechanism for water and salt migration in soil. Environ. Earth Sci. 2015, 74, 675–681. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Chen, Y.; Wang, A.; Maeyer, P.D. The spatiotemporal response of soil moisture to precipitation and temperature changes in an arid region, China. Remote Sens. 2018, 10, 468. [Google Scholar] [CrossRef]
- Zwieback, S.; Paulik, C.; Wagner, W. Frozen soil detection based on advanced scatterometer observations and air temperature data as part of soil moisture retrieval. Remote Sens. 2015, 7, 3206–3231. [Google Scholar] [CrossRef]
- Hua, W.; Wang, C.; Chen, G.; Yang, H.; Zhai, Y. Measurement and simulation of soil water contents in an experimental field in delta plain. Water 2017, 9, 947. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Kong, L.; Xiao, H.; Chen, Q.; Xia, Y.A. Simple fractal-based model for soil-water characteristic curves incorporating effects of initial void ratios. Energies 2018, 11, 1419. [Google Scholar] [CrossRef]
- Feng, H.; Chen, J.; Zheng, X.; Xue, J.; Miao, C.; Du, Q.; Xu, Y. Effect of sand mulches of different particle sizes on soil evaporation during the freeze-thaw period. Water 2018, 10, 536. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, S.; Liu, S.; Qin, L.; Xu, J. Experimental study on coal pore structure deterioration under freeze–thaw cycles. Environ. Earth Sci. 2017, 76, 507. [Google Scholar] [CrossRef]
- Watanabe, K.; Kugisaki, Y. Effect of macropores on soil freezing and thawing with infiltration. Hydrol. Process. 2017, 31, 270–278. [Google Scholar] [CrossRef]
- Leroueil, S.; Tardif, J.; Roy, M.; Rochelle, P.L.; Konrad, J.M. Effects of frost on the mechanical behaviour of Champlain Sea clays. Can. Geotech. J. 1991, 28, 690–697. [Google Scholar] [CrossRef]
- Chamberlain, E.J.; Gow, A.J. Effect of freezing and thawing on the permeability and structure of soils. Eng. Geol. 1979, 13, 73–92. [Google Scholar] [CrossRef]
- Chamberlain, E.J. Effect of freeze-thaw cycles on the permeability and macrostructure of soils. Cold Reg. Res. Eng. Lab. 1990, 90, 145–155. [Google Scholar]
- Viklander, P. Permeability and volumxe changes in till due to cyclic freeze/thaw. Can. Geotech. J. 1998, 35, 471–477. [Google Scholar] [CrossRef]
- Sangrey, D.A.; Henkel, D.J.; Esrig, M.I. The effective stress response of a normally consolidated clay. Soils Found. 1969, 22, 77–91. [Google Scholar]
- Zhao, Y.; Si, B.; He, H.; Xu, J.; Peth, S.; Horn, R. Modeling of coupled water and heat transfer in freezing and thawing soils, Inner Mongolia. Water 2016, 8, 424. [Google Scholar] [CrossRef]
- Zhou, J.; Tang, Y. Artificial ground freezing of fully saturated mucky clay: Thawing problem by centrifuge modeling. Cold Reg. Sci. Technol. 2015, 117, 1–11. [Google Scholar] [CrossRef]
- He, P.P.; Cui, Z.D. Dynamic response of a thawing soil around the tunnel under the vibration load of subway. Environ. Earth Sci. 2015, 73, 2473–2482. [Google Scholar] [CrossRef]
- Sheahan, T.C.; Ladd, C.C.; Germaine, J.T. Rate-dependent undrained shear behavior of saturated clay. J. Geotech. Eng. 1996, 122, 99–108. [Google Scholar] [CrossRef]
- Graham, J.; Au, V.C.S. Effects of freeze-thaw and softening on a natural clay at low stresses. Can. Geotech. J. 2011, 22, 69–78. [Google Scholar] [CrossRef]
- Kazuya, K.; Yamanouchi, T.; Hirao, K. Cyclic strength and deformation of normally consolidated clay. Soils Found. 1982, 22, 77–79. [Google Scholar]
- Larew, H.G.; Leonards, G.A. A strength criterion for repeated loads. Highw. Res. Board Proc. 1962, 41, 529–566. [Google Scholar]
- Zhang, Z.L.; Cui, Z.D. Analysis of microscopic pore structures of the silty clay before and after freezing-thawing under the subway vibration loading. Environ. Earth Sci. 2017, 76, 528. [Google Scholar] [CrossRef]
- Pirastru, M.; Marrosu, R.; Prima, S.D.; Keesstra, S.; Giadrossich, F.; Niedda, M. Lateral saturated hydraulic conductivity of soil horizons evaluated in large-volume soil monoliths. Water 2017, 9, 862. [Google Scholar] [CrossRef]
- Fu, Q.; Hou, R.; Li, T.; Yan, P.; Ma, Z. The critical depth of freeze-thaw soil under different types of snow cover. Water 2017, 9, 370. [Google Scholar]
- Lv, S.; Zeng, Y.; Wen, J.; Zhao, H.; Su, Z. Estimation of penetration depth from soil effective temperature in microwave radiometry. Remote Sens. 2018, 10, 519. [Google Scholar] [CrossRef]
- Xia, H.; Cao, Y.M.; De Roeck, G. Theoretical modeling and characteristic analysis of moving-train induced ground vibrations. J. Sound Vib. 2010, 329, 819–832. [Google Scholar] [CrossRef]
- Jung, A.; Vohland, M.; Thielebruhn, S. Use of a portable camera for proximal soil sensing with hyperspectral image data. Remote Sens. 2015, 7, 11434–11448. [Google Scholar] [CrossRef]
- Kolay, E. Modeling the effect of freezing and thawing for sedimentary rocks. Environ. Earth Sci. 2016, 75, 210. [Google Scholar] [CrossRef]





















| Number | Stress Ratio | Static Deviator Stress | Frequency | Temperature | Freeze–Thaw Cycle Times | Loading Cycle Times |
|---|---|---|---|---|---|---|
| kPa | Hz | °C | ||||
| C-1 | 0.2 | 40 | 1 | - | 0 | 20,000 |
| C-2 | 0.2 | 40 | 1 | −30 | 1 | 20,000 |
| C-3 | 0.2 | 40 | 1 | −20 | 1 | 20,000 |
| C-4 | 0.2 | 40 | 1 | −10 | 1 | 20,000 |
| C-5 | 0.2 | 40 | 1 | −30 | 2 | 20,000 |
| C-6 | 0.2 | 40 | 1 | −20 | 2 | 20,000 |
| C-7 | 0.2 | 40 | 1 | −10 | 2 | 20,000 |
| Sample | Unfrozen | T= −10 °C | T= −20 °C | T= −30 °C | |||
|---|---|---|---|---|---|---|---|
| First Cycle Frozen | Second Cycle Frozen | First Cycle Frozen | Second Cycle Frozen | First Cycle Frozen | Second Cycle Frozen | ||
| Surface void ratio | 0.0364 | 0.0420 | 0.0483 | 0.0501 | 0.0586 | 0.0598 | 0.0697 |
| Area (μm2) | 0.02–0.05 | 0.05–0.1 | 0.1–0.5 | 0.5–1 | 1–3 | >3 | ||
|---|---|---|---|---|---|---|---|---|
| First-cycle frozen Soil | −10 °C | B CL1 | 12.27% | 13.55% | 40.07% | 14.15% | 14.69% | 5.28% |
| A CL2 | 15.08% | 16.90% | 41.63% | 12.97% | 11.64% | 1.77% | ||
| −20 °C | B CL1 | 10.78% | 12.28% | 38.30% | 14.70% | 15.78% | 8.16% | |
| A CL2 | 15.68% | 17.25% | 40.08% | 13.71% | 10.24% | 3.04% | ||
| −30 °C | B CL1 | 10.60% | 11.30% | 37.76% | 15.18% | 17.00% | 8.15% | |
| A CL2 | 17.58% | 20.32% | 39.96% | 12.93% | 5.90% | 3.31% | ||
| Second-cycle frozen Soil | −10 °C | B CL1 | 14.43% | 17.22% | 33.62% | 10.61% | 16.79% | 7.32% |
| A CL2 | 15.65% | 16.20% | 45.34% | 10.71% | 8.23% | 3.86% | ||
| −20 °C | B CL1 | 9.90% | 10.12% | 39.60% | 12.91% | 17.54% | 9.93% | |
| A CL2 | 15.79% | 18.79% | 43.20% | 10.91% | 5.52% | 5.79% | ||
| −30 °C | B CL1 | 10.32% | 10.31% | 34.84% | 13.46% | 18.58% | 12.49% | |
| A CL2 | 10.58% | 12.82% | 41.85% | 12.86% | 13.74% | 8.15% | ||
| First-Cycle Frozen Soil | Second-Cycle Frozen Soil | |||||
|---|---|---|---|---|---|---|
| Temperature | −10 °C | −20 °C | −30 °C | −10 °C | −20 °C | −30 °C |
| B CL1 | 1.4809 | 1.5003 | 1.5301 | 1.5211 | 1.5328 | 1.5531 |
| A CL2 | 1.4103 | 1.4205 | 1.4548 | 1.4528 | 1.476 | 1.4991 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Kong, B.; Wei, X.; Zhang, M.; Xu, B.; Zhao, F. Laboratory Testing to Research the Micro-Structure and Dynamic Characteristics of Frozen–Thawed Marine Soft Soil. J. Mar. Sci. Eng. 2019, 7, 85. https://doi.org/10.3390/jmse7040085
Ding Z, Kong B, Wei X, Zhang M, Xu B, Zhao F. Laboratory Testing to Research the Micro-Structure and Dynamic Characteristics of Frozen–Thawed Marine Soft Soil. Journal of Marine Science and Engineering. 2019; 7(4):85. https://doi.org/10.3390/jmse7040085
Chicago/Turabian StyleDing, Zhi, Bowen Kong, Xinjiang Wei, Mengya Zhang, Baolong Xu, and Fangjie Zhao. 2019. "Laboratory Testing to Research the Micro-Structure and Dynamic Characteristics of Frozen–Thawed Marine Soft Soil" Journal of Marine Science and Engineering 7, no. 4: 85. https://doi.org/10.3390/jmse7040085
APA StyleDing, Z., Kong, B., Wei, X., Zhang, M., Xu, B., & Zhao, F. (2019). Laboratory Testing to Research the Micro-Structure and Dynamic Characteristics of Frozen–Thawed Marine Soft Soil. Journal of Marine Science and Engineering, 7(4), 85. https://doi.org/10.3390/jmse7040085





