An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration
Abstract
:1. Introduction
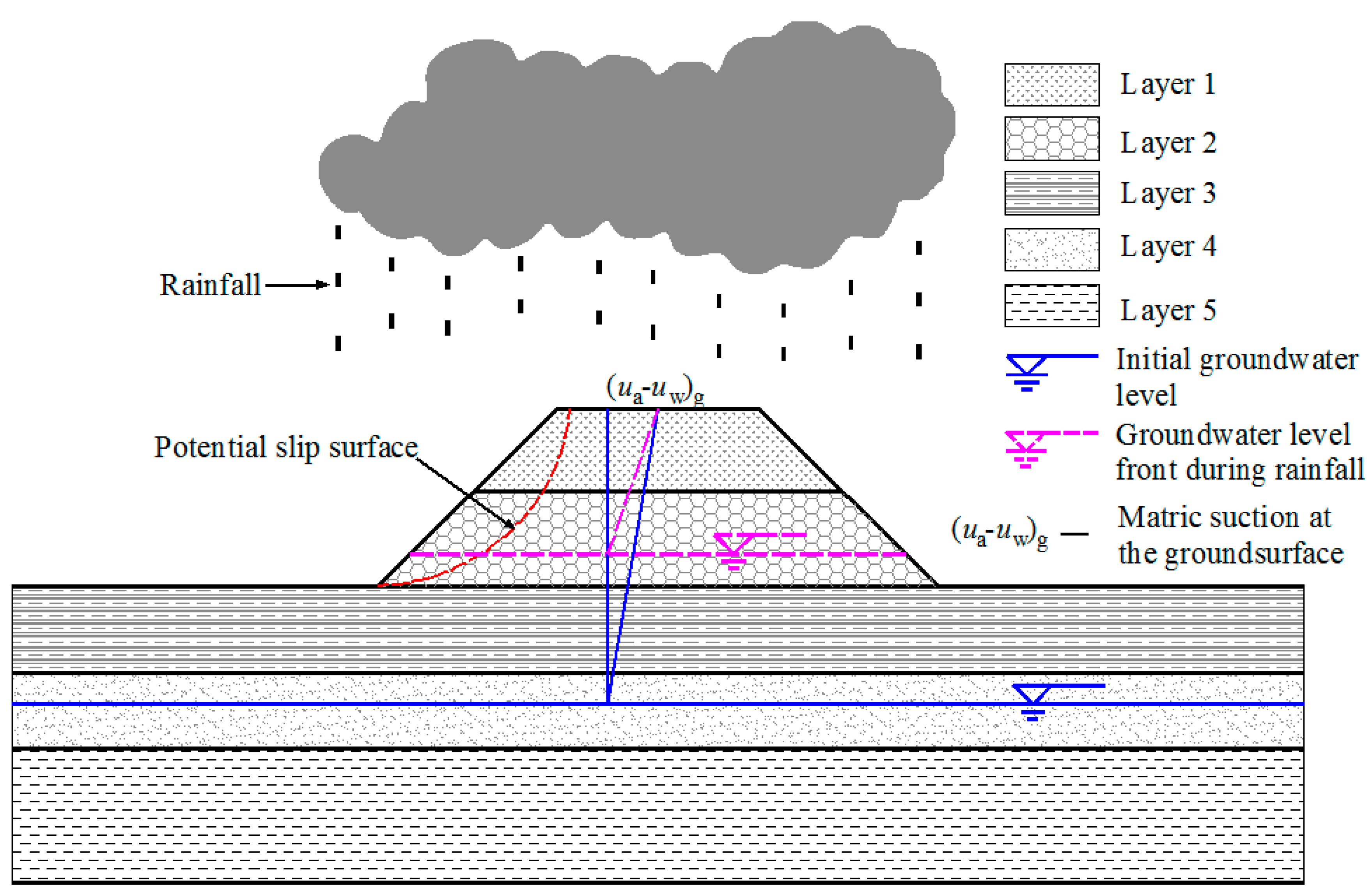
2. A Simple Approach to Simulate Rainfall Infiltration
3. Limit Equilibrium Method of Unsaturated-Multilayered-Soil Slope
3.1. Failure Criterion of Unsaturated-Soil
3.2. Distributions of Matric Suction
3.3. Determination of the Strength Parameters under Different Distributions of Matric Suction
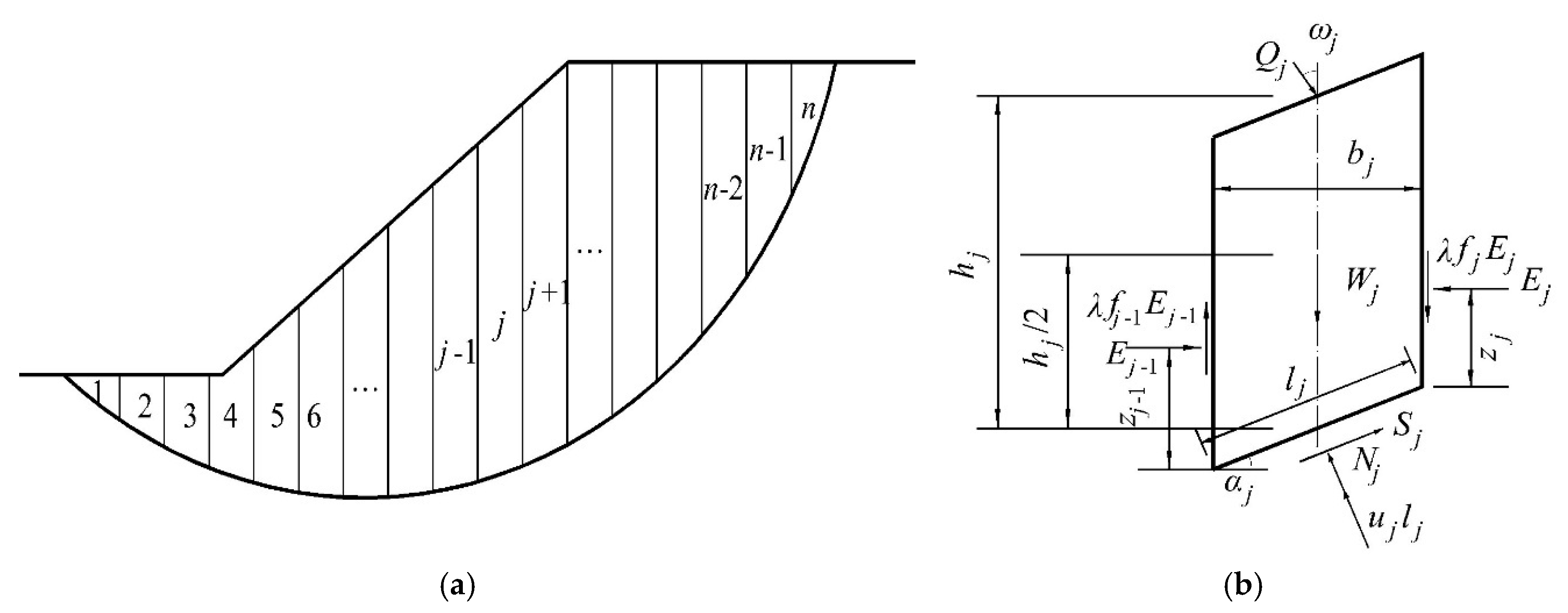
3.4. Modified M-P Method
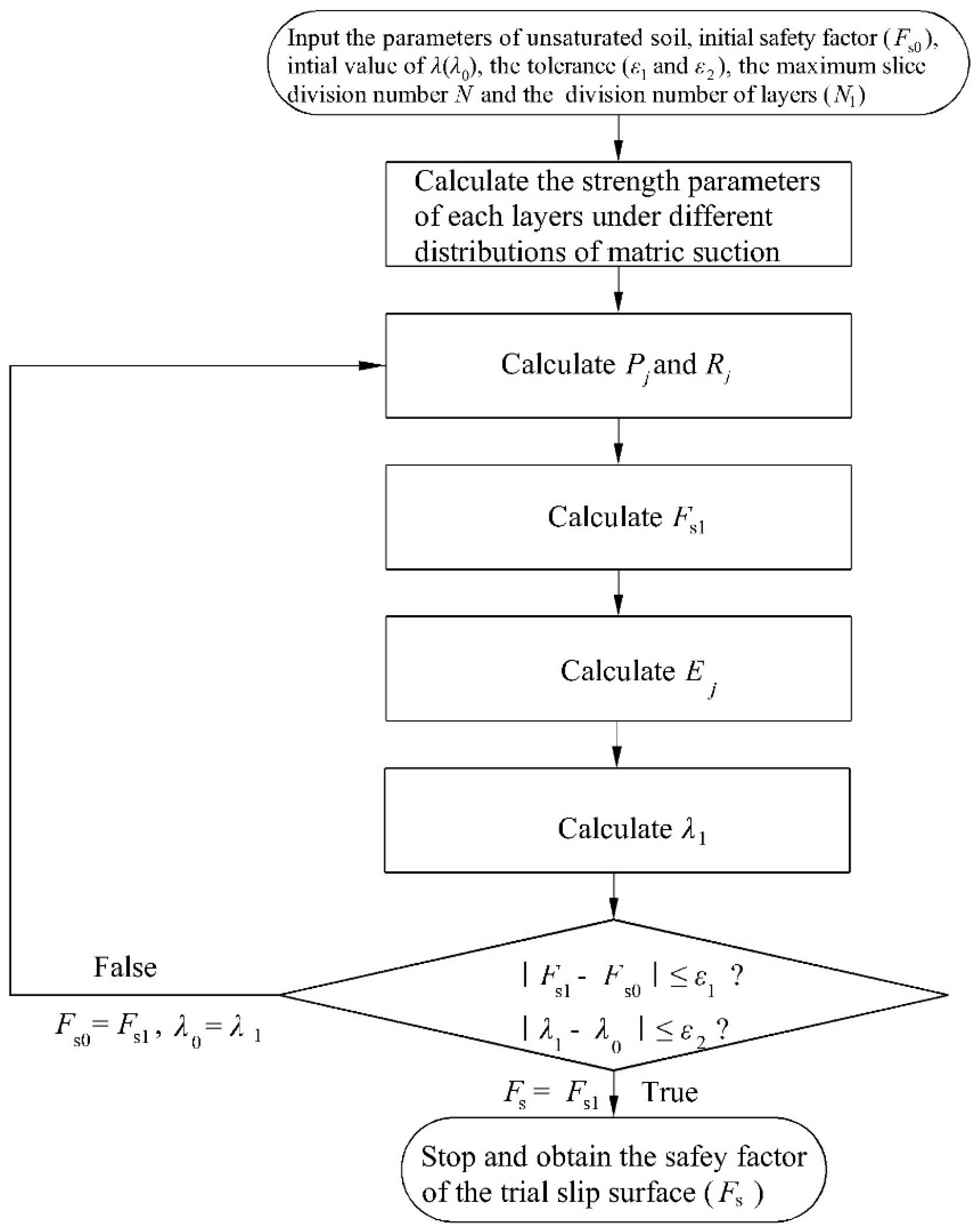
4. A Global Algorithm to Search for the Critical Slip Surface of Unsaturated Coastal-Embankment Slope
5. Application
5.1. Comparison with the Existing Model
5.2. Case Study
5.3. Discussion on the Effect of Distribution of (ua-uw) on Fsmin
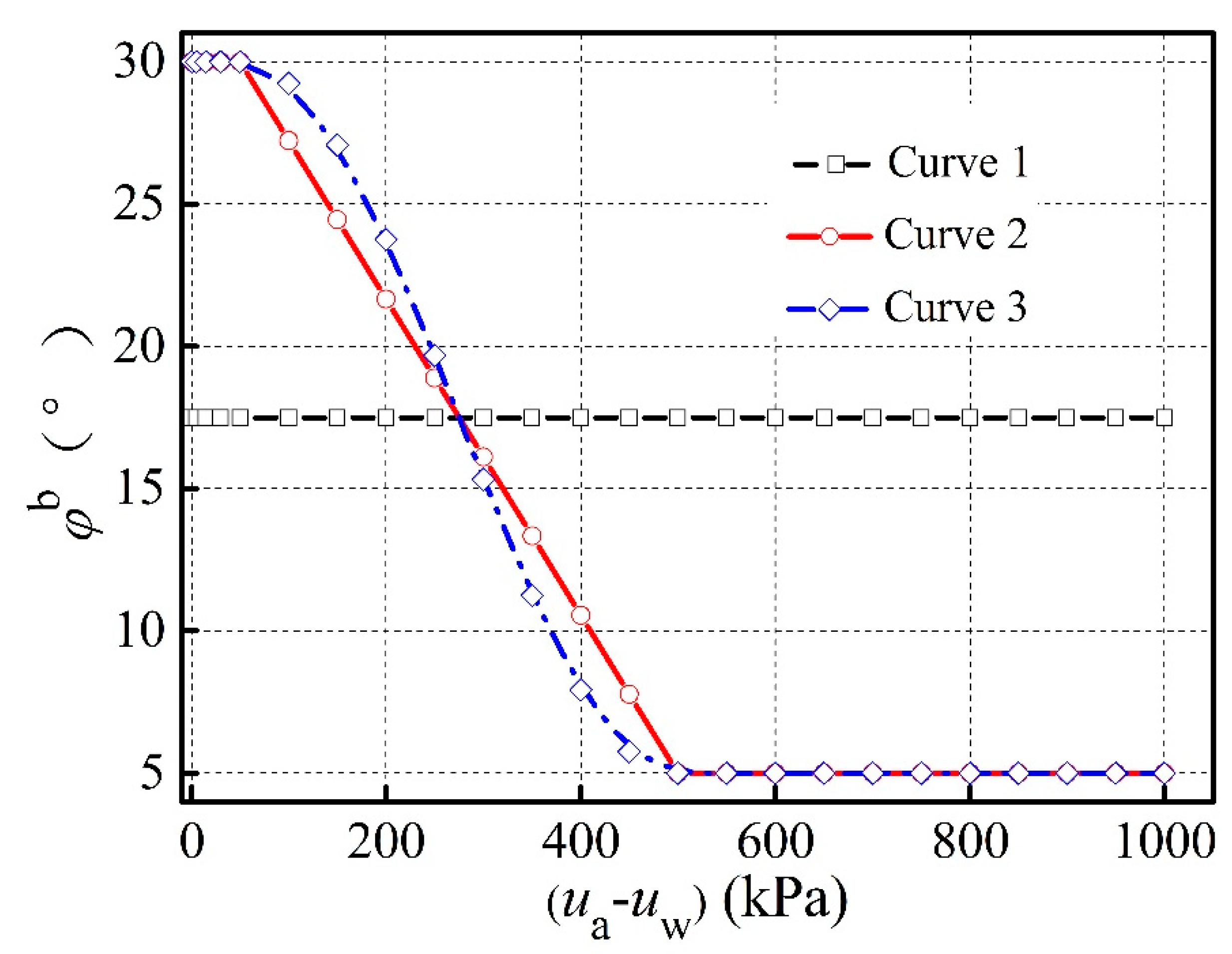
5.4. Discussion on the Relationship between φb and (ua-uw)
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tofany, N.; Ahmad, M.F.; Mamat, M.; Mohd-Lokman, H. The effects of wave activity on overtopping and scouring on a vertical breakwater. Ocean Eng. 2016, 116, 295–311. [Google Scholar] [CrossRef]
- Pourzangbara, A.; Brocchinib, M.; Saberc, A.; Mahjoobid, J.; Mirzaaghasie, M.; Barzegar, M. Prediction of scour depth at breakwaters due to non-breaking wavesusing machine learning approaches. Appl. Ocean Res. 2017, 63, 120–128. [Google Scholar] [CrossRef]
- Li, K.; Guo, Z.; Wang, L.Z.; Jiang, H.Y. Effect of Seepage Flow on Shields Number around a Fixed and Sagging Pipeline. Ocean Eng. 2019, 172, 487–500. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, W.J.; Zhu, C.B.; Yuan, F.; Rui, S.J. Numerical simulations of wave-induced soil erosion in silty sand seabeds. J. Mar. Sci. Eng. 2019, 7, 52. [Google Scholar] [CrossRef]
- Henkel, D.H. The role of waves in causing submarine landslides. Géotechnique 1970, 20, 75–80. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Jeng, D.-S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Meth. Eng. 1994, 18, 785–807. [Google Scholar] [CrossRef]
- Jeng, D.-S. Wave-induced seabed instability in front of a breakwater. Ocean Eng. 1997, 24, 887–917. [Google Scholar] [CrossRef]
- Fukuoka, M. Landslides associated with rainfall. Can. Geotech. J. 1980, 11, 1–29. [Google Scholar]
- Guo, Z.; Jeng, D.-S.; Zhao, H.Y.; Guo, W.; Wang, L.Z. Effect of Seepage Flow on Sediment Incipient Motion around a Free Spanning Pipeline. Coast. Eng. 2019, 143, 50–62. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Liang, Z.D.; Jeng, D.-S.; Zhu, J.F.; Guo, Z.; Chen, W.Y. Numerical investigation of dynamic soil response around a submerged rubble mound breakwater. Ocean Eng. 2018, 156, 406–423. [Google Scholar] [CrossRef]
- Chen, W.Y.; Chen, G.X.; Chen, W.; Liao, C.C.; Gao, H.M. Numerical simulation of the nonlinear wave-induced dynamic response of anisotropic poro-elastoplastic seabed. Mar. Georesour. Geotechnol. 2018. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.-S. Effects of principal stress rotation on wave-induced soil response in a poro-elastoplastic sandy seabed. Acta Geotech. 2019. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.-S. Dynamic characteristics of a sandy seabed under storm wave loading considering the effect of principal stress rotation. Eng. Geol. 2019. [Google Scholar] [CrossRef]
- Lim, T.T.; Rahardjo, H.; Chang, M.F.; Fredlund, D.G. Effect of rainfall on matrix suctions in residual soil slope. Can. Geotech. J. 1996, 33, 618–628. [Google Scholar] [CrossRef]
- Cho, S.E. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Tang, G.P.; Huanga, J.S.; Sheng, D.C.; Sloan, S.W. Stability analysis of unsaturated soil slopes under random rainfall patterns. Eng. Geol. 2018, 245, 322–332. [Google Scholar] [CrossRef]
- Wu, J.H.; Chen, J.H.; Lu, C.W. Investigation of the Hsien-du-shan Landslide Caused by Typhoon Morakot at Kaohsiung, Taiwan. Int. J. Rock Mech. Min. Sci. 2013, 60, 148–159. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. Factors controlling instability of homogeneous soil slopes under rainfall. J. Geotech. Geoenviron. Eng. 2007, 133, 1532–1543. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Regueiro, R.A. Instability of partially saturated soil slopes due to alteration of rainfall pattern. Eng. Geol. 2012, 147–148, 28–36. [Google Scholar] [CrossRef]
- Xu, J.S.; Yang, X.L. Three-dimensional stability analysis of slope in unsaturated soils considering strength nonlinearity under water drawdown. Eng. Geol. 2018, 237, 102–115. [Google Scholar] [CrossRef]
- Chowdhury, R.K.; Beecham, S. Australian rainfall trends and their relation to the southern oscillation index. Hydrol. Process. 2010, 24, 504–514. [Google Scholar] [CrossRef]
- Su, L.-J.; Hu, K.-H.; Zhang, W.-F.; Wang, J.; Lei, Y.; Zhang, C.-L.; Cui, P.; Pasuto, A.; Zheng, Q.-H. Characteristics and triggering mechanism of Xinmo landslide on 24 June 2017 in Sichuan, China. J. Mt. Sci. 2017, 14, 1689–1700. [Google Scholar] [CrossRef]
- Robinson, J.D.; Vahedifard, F.; AghaKouchak, A. Rainfall-triggered slope instabilities under a changing climate: comparative study using historical and projected precipitation extremes. Can. Geotech. J. 2017, 54, 117–127. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Oh, W.T.; Vanapalli, S.K. Influence of rain infiltration on the stability of compacted soil slopes. Comput. Geotech. 2010, 37, 649–657. [Google Scholar] [CrossRef]
- Zhang, C.G.; Chen, X.D.; Fan, W. Overturning stability of a rigid retaining wall for foundation pits in unsaturated soils. Int. J. Geomech. 2016, 16, 06015013. [Google Scholar] [CrossRef]
- Bishop, A.W. The use of the slip circle in the stability analysis of earth slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Morgenstern, N.R. Extensions to the generalized method of slices for stability analysis. Can. Geotech. J. 1983, 20, 104–109. [Google Scholar] [CrossRef]
- Chen, C.F.; Zhu, J.F.; Gong, X.N. Calculation method of earth slope reliability based on response surface method and Morgenstern-Price procedure. Eng. Mech. 2008, 28, 166–172. (In Chinese) [Google Scholar]
- Zhu, J.F.; Chen, C.F. Search for circular and noncircular critical slip surfaces in slope stability analysis by hybrid genetic algorithm. J. Cent. South Univ. 2014, 21, 387–397. [Google Scholar] [CrossRef]
- Nguyen, V.U. Determination of critical slope failure surfaces. J. Geotech. Eng. ASCE 1985, 111, 238–250. [Google Scholar] [CrossRef]
- Yamagami, T.; Ueta, Y. Search for noncircular slip surfaces by the Morgenstern-Price method. In Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, Austria, 16–20 June 1986; pp. 1335–1340. [Google Scholar]
- Greco, V.R. Numerical methods for locating the critical slip surface in slope-stability analysis. In Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, Austria, 11–15 April 1988; pp. 1219–1223. [Google Scholar]
- Boutrup, E.; Lovell, C.W. Search techniques in slope stability analysis. Eng. Geol. 1980, 16, 51–61. [Google Scholar] [CrossRef]
- Greco, V.R. Efficient Monte-Carlo technique for locating critical slip surface. J. Geotech. Eng. ASCE 1996, 122, 517–525. [Google Scholar] [CrossRef]
- Malkawi, A.H.; Hassan, W.F.; Sarma, S.K. An efficient search method for finding the critical circular slip surface using the Monte Carlo technique. Can. Geotech. J. 2001, 38, 1081–1089. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.J.; Dai, F.C.; Wang, M.L. Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Gavin, K.; Xue, J. A simple method to analyze infiltration into unsaturated soil slopes. Comput. Geotech. 2008, 35, 223–230. [Google Scholar] [CrossRef]
- Cho, S.E. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics. Eng. Geol. 2009, 105, 32–43. [Google Scholar] [CrossRef]
- Gan, J.K.M.; Fredlund, D.G.; Rahardjo, H. Determination of the shear strength parameters of an unsaturated soil using the direct shear test. Can. Geotech. J. 1988, 25, 500–510. [Google Scholar] [CrossRef]
- Loukidis, D.; Bandini, P.; Salgado, R. Stability of seismically loaded slopes using limit analysis. Géotechnique 2003, 53, 463–479. [Google Scholar] [CrossRef]
- Wang, J.P.; Yang, Z.J.; Huang, D.R. New pole-searching algorithm with applications to probabilistic circular slope stability assessment. Comput. Geosci. 2013, 51, 83–89. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.Y.; Wang, N.X.; Sun, P.; Yu, S.; Li, S.Y.; Du, X.H. Modeling lateral enlargement in dam breaches using slope stability analysis based on circular slip mode. Eng. Geol. 2016, 209, 70–81. [Google Scholar] [CrossRef]
- Li, D.Q.; Jiang, S.H.; Qi, X.H.; Cao, Z.J. Efficient system reliability analysis of multi-layered soil slopes using multiple stochastic response surfaces. Geotech. Saf. Reliab. 2017, 164–172. [Google Scholar]
- Deng, D.P.; Li, L.; Zhao, L.H. Stability analysis of a layered slope with failure mechanism of a composite slip surface. Int. J. Geomech. 2019, 19, 04019050. [Google Scholar] [CrossRef]
- Zhang, L.L.; Fredlund, D.G.; Fredlund, M.D.; Ward Wilson, G. Modeling the unsaturated soil zone in slope stability analysis. Can. Geotech. J. 2014, 51, 1384–1398. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage. Comput. Geotech. 1998, 22, 1–28. [Google Scholar] [CrossRef]
- Tsaparas, I.; Rahardjo, H.; Toll, D.G.; Leong, E.C. Controlling parameters for rainfall-induced landslides. Comput. Geotech. 2002, 29, 1–27. [Google Scholar] [CrossRef]
- Blatz, J.A.; Ferreira, N.J.; Graham, J. Effects of near-surface environmental conditions on instability of an unsaturated soil slope. Can. Geotech. J. 2004, 41, 1111–1126. [Google Scholar] [CrossRef]
- Cascini, L.; Cuomo, S.; Pastor, M.; Sorbin, G. Modelling of rainfall induced shallow landslides of the flow-type. J. Geotech. Geoenviron. Eng. 2010, 136, 85–98. [Google Scholar] [CrossRef]
- Wang, R.G.; Yan, S.W.; Deng, W.D. Analysis of seepage stability of high-filled embankment slope due to rainfall infiltration. Chin. J. Highw. Transp. 2004, 17, 25–30. (In Chinese) [Google Scholar]
- Xu, H.; Zhu, Y.W.; Cai, Y.Q.; Zhu, F.M. Stability analysis of unsaturated soil slopes under rainfall infiltration. Rock Soil Mech. 2005, 26, 1957–1962. (In Chinese) [Google Scholar]











| Analysis Case | γʹ kN/m3 | cʹ/kPa | φʹ/° | (ua-uw)g/kPa | φb/° |
|---|---|---|---|---|---|
| Case 1 | 18 | 10 | 34 | 200 | 0 |
| Case 2 | 18 | 10 | 34 | 200 | 15 |
| Case 3 | 18 | 10 | 34 | 200 | 34 |
| Layer | γʹ kN/m3 | cʹ/kPa | φʹ/° | (ua-uw)g/kPa | φb/° |
|---|---|---|---|---|---|
| 1 | 20 | 0.5 | 40.0 | 200 | 15 |
| 2 | 20 | 1 | 42.0 | ||
| 3 | 19.5 | 0.0 | 38.0 | ||
| 4 | 17 | 15.0 | 21.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.-f.; Chen, C.-f.; Zhao, H.-y. An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration. J. Mar. Sci. Eng. 2019, 7, 165. https://doi.org/10.3390/jmse7060165
Zhu J-f, Chen C-f, Zhao H-y. An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration. Journal of Marine Science and Engineering. 2019; 7(6):165. https://doi.org/10.3390/jmse7060165
Chicago/Turabian StyleZhu, Jian-feng, Chang-fu Chen, and Hong-yi Zhao. 2019. "An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration" Journal of Marine Science and Engineering 7, no. 6: 165. https://doi.org/10.3390/jmse7060165
APA StyleZhu, J.-f., Chen, C.-f., & Zhao, H.-y. (2019). An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration. Journal of Marine Science and Engineering, 7(6), 165. https://doi.org/10.3390/jmse7060165






