1. Introduction
The sea is the general term for the continuous saltwater body that covers the Earth’s surface. The ocean covers about 70.8% of the earth’s surface, accounting for 97.2% of the earth’s water, and is rich in minerals [
1], marine product resources, and energies [
2]. As scientists deepen their research on the ocean, accurate observations of the marine environment are increasingly important, especially the ocean currents. Satellite-tracked surface drifting buoy (drifters) observe currents, sea surface temperature, atmospheric pressure, winds, and salinity [
3].
Figure 1 shows the main components of the SVP drifter. At present, there are two basic sizes of SVP drifters: the original, relatively large SVP drifter and the new “mini” version (
Figure 2) [
4]. They have a thermistor (metallic thermometer) on their base, and an underwater drogue, or sea anchor, located 15 m below the ocean surface, connected to the buoy by a long, thin tether, as shown in
Figure 2. After years of development, a total of 1417 drifters were deployed in the National Oceanic and Atmospheric Administration’s (NOAA, U.S. Department of Commerce) contribution to the Global Drifter Program (GDP) [
4].
The modern drifter is a relatively lean instrument—44 pounds with 16 foot drogues—costing around
$1700 each [
5]. The GDP drifters are fitted with diode-protected, alkaline D-Cell, 12 V, 56 Ah battery packs. Once deployed, a modern SVP drifter lives an average of 400 days before ceasing transmission. To ensure the drifters’ life time is long enough, the sampling frequency of the drifters cannot be too high, and the drifters are inactive during most of the time at sea, because the battery capacity is limited. SVP drifters are typically sampled at intervals of about 5 min.
Researchers in various countries are trying to overcome the power constraint of floaters. Floaters demand high-density energy sources and lithium is light with high oxidation energy. PolyPlus Battery Company has developed a prototype lithium-seawater battery that is attractive for powering long-duration autonomous oceanographic vehicles (floats and underwater gliders) [
6]. Using thermal energy is also a way to supply power for floaters. Several articles [
7,
8,
9] have studied the feasibility of supplying power to floaters with thermal power. An energy storage system has been demonstrated on an Argo style float and has been implemented in a thermal version of the Slocum glider. The energy harvesting system is based on a phase change material with a freeze–thaw cycle that pressurizes hydraulic oil, which is converted to electrical energy [
10]. Another option is solar energy [
11,
12]. A 65 cm
2 solar array was used to power an Argos beacon in reference [
13]. However, the primary lithium batteries are hazardous to the ocean’s environment, the temperature difference between cooler deep and warmer shallow or surface seawaters in many waters is not big enough to generate electricity, and floating buoys on drifters are too small and spherical, so it is difficult to use solar energy for power generation.
The drifters’ work area is full of waves, so the research team hopes to design a wave power plant for drifters without affecting the way the drifters work, which will increase their service life. If there is enough power, drifters can also make measurements more frequently and the amount of data each drifter can measure will increase, so it can provide more accurate data for the study of ocean circulation. In addition, by rational design, increasing the drag of the underwater system makes drifters less affected by the sea wind force.
Wave energy, with the advantages of high energy density and wide distribution, is an inexhaustible renewable clean energy source, and considered an ideal energy source for the power supply of the drifters. For more than two centuries, inventors have proposed many different devices to utilize wave power for human purposes [
14,
15,
16], and several research papers relating to ocean wave energy conversion have been emerged in an endless stream [
17,
18,
19,
20]. Control strategies for wave energy conversion systems also have been studied in several papers [
21,
22,
23,
24]. António F. de O. Falcão [
25] categorized ocean wave energy converters (WECs) into three main categories: oscillating water column, overtopping device, and point absorber. The oscillating water column (OWC) [
26,
27] is by far the most developed and investigated wave energy device [
28]. Dorrell et al. [
29] described the OWC operation, modeling, and experimental equipment in 2004. The overtopping device works much like a hydroelectric dam, which is another type of ocean WEC. The Wave Dragon, placed in Nissum Bredning, Denmark, was grid-connected in May 2003 as the world’s first offshore WEC [
30]. Reference [
31] presents results on the wave loading acting on a hybrid WEC named Overtopping BReakwater for Energy Conversion (OBREC). A point absorber is an offshore floating device which captures energy from its wave induced motion via hydraulic rams and a high-pressure power take-off (PTO) system [
32]. The Archimedes wave swing (AWS), mainly consisting of a bottom-fixed air-filled cylindrical chamber (the silo) and a movable upper cylinder (the floater), is an offshore fully-submerged WEC. Several articles [
33,
34,
35] have discussed modeling and control of an AWS-based wave energy conversion system. Another type of ocean WEC is produced by Ocean Power Delivery Ltd. (Scotland, UK), named Pelamis [
36], which consists of floaters moving along with respect to each other when waves pass. The point absorber (PA) is a heaving buoy type wave energy converter. The analysis and discussion of PA-based wave energy devices have been discussed in several articles [
37,
38,
39]. However, the current wave energy research is mainly for commercialization, and mostly focuses on the power grid. The WECs are not necessary to be designed and installed in the deep seas. Only a small amount of literature has studied the energy supply of small monitoring buoys [
40]. Since the power needs of drifters are relatively small and most of them work in deep seas, it is difficult to directly apply the existing wave energy technology to drifters.
The surface float of an SVP drifter ranges from 30.5 cm (the smallest mini) to 40 cm in diameter. The WEC, which provides energy supplementation for drifters, first needs to meet three requirements: (1) The WEC needs to be a small power generation device—because drifters are relatively small in size and limited in space, large energy conversion devices are not suitable for this role. In addition, the energy requirement of the drifter device only needs to meet the demand of its detection functions, so there is no need to install a large energy conversion device; (2) The point absorber is better suited for power supplying to the drifter, since the size of drifters is relatively small compared to the wavelength of random waves in the sea, and the size of the point absorber is relatively the smallest in terms of the wavelength of the incident wave [
41,
42]; (3) The WEC does not affect the function of SVP drifters.
Referring to the distribution of the global drifter array and sea state wave characteristics and average global distribution [
43], the distribution of SVP drifters and the sea state at their location can be known. The sea state at most drifters’ locations is greater than 2, so when the wave energy device can generate a certain amount of electricity under a low sea state to meet the needs of the drifter, the wave energy device can solve the problem of the drifter’s battery life.
Considering the working environment and energy demands of drifters, this paper proposes a counter-rotating self-adaptable wave energy converter (WEC) for powering drifters. The wave energy-powered SVP drifter concept is illustrated in
Figure 3 for a counter-rotating self-adaptable PTO module fixed under the drogue. The WEC uses an underwater absorber to convert the reciprocating motion in the vertical direction into the relative rotation of the two blade groups of the absorber, to drive the generator to generate electricity. The buoy is a sphere with a radius of 25 cm. The size of the absorber is shown in the figure. The drogue can ensure the drifter follows the movements of the water and is unaffected by wind and instruments, and reduce slippage between the drifter package and the water [
4], the drifter is mainly used to investigate ocean currents and other parameters like temperature or salinity. Common electrical devices include the radio frequency transmitter, atmospheric pressure sensor, temperature sensor, and salinity sensor. Therefore, the WEC placed at a depth of about 30 m from the ocean surface will hardly affect the measurement results of sensors near the wave surface.
The WEC is a point absorber with the advantages of easy installation on SVP drifters and a simple power generation process. Through this simple and effective integration, it will provide continuous power supply to SVP drifters and will hardly affect the monitoring results. It is expected to be an efficient way for improving the sampling intervals of drifters, on the basis of an easy integration method.
The counter-rotating self-adaptable WEC has been numerically simulated in [
44], where computational fluid dynamics (CFD) technology was used to numerically analyze the simplified model of the WEC. Based on the computer simulation of the interaction between seawater and the WEC, the effects of water velocity and blade inclination on the power and efficiency characteristics of the device have been investigated.
Figure 4 shows the main work and research results and conclusions of [
44]. The absorbed power of the upper absorber increases with the increase in relative water flow velocity. The ideal blade inclination is 20–30° when the velocity through the blades is low (≤1.4 m/s), and 30–40° when the velocity is high (≥2.0 m/s). However, there is obviously a large boundary effect in the bucket in the experiment in [
44]. It is very necessary to verify the principle and characteristics of the WEC in the artificial wave basin. In addition, there are many factors affecting the performance of the counter-rotating self-adaptable WEC. Wave conditions, absorber weight, and other factors will have an impact on the final power generation. The dynamic simulation of the whole system is time-consuming and laborious, and it is difficult to ensure the accuracy of the calculation. Therefore, it is necessary to verify and further study the new WEC in the wave basin.
In this paper, the experimental analysis method was used to analyze the most important factors (wave height and wave period) affecting the power generation efficiency of the WEC. This paper is organized as follows:
Section 2 describes the conversion principle of the WEC,
Section 3 presents the experimental arrangement and different experimental conditions,
Section 4 discusses the power generation performance of the ACWEC,
Section 5 draws the conclusions.
3. Experiment Platform
3.1. Prototype and Method
In order to verify the power generation performance of the WEC, a semi-scale ACWEC was designed and manufactured, as shown in
Figure 8. Referring to the Pierson–Moskowitz spectrum (PM spectrum), when the sea state is 3, the wave height in the real ocean is 0.5–1.25 m. The maximum wave height that can be generated in the wave tank is 0.6 m, so it cannot generate the wave height in full scale in a small tank. In order to enable the wave tank to simulate the corresponding wave height of sea state 3, the geometry of the buoy and the absorber was reduced by 50%. According to the similarity principle of fluid, the wave height generated by the wave tank can be approximated as a proportional reduction of sea state 3 wave height.
The outer caging rings of the UBG and LBG were made of aluminum alloy—eight fan-shaped blades per blade group. Due to its high modulus and strength and its good corrosion resistance, a carbon fiber tube was used for the blade shaft. The rest of the PTO was mainly made of stainless steel 304. A DC generator with built-in accelerator was integrated into the PTO. The maximum output power was 30 W. The mass of the PTO was 6 kg.
The experimental platform in the wave tank was set up as shown in
Figure 10. The platform contained a wave tank, a DAQ card (Data Acquisition Card), a control room, two wave height measuring sensors (Sensor (A) and Sensor (B)), and an upper computer with data acquisition program. In order to verify the design concept of the ACWEC, which was introduced in
Section 2, there was a flexible connection (tether) between the buoy and the PTO.
A servo motor-driven irregular wave-making machine was installed at the head of the tank. A board that pushed water into waves and the mechanical frame of the wave-making machine were installed about 1.5 m from the head of the water tank. There was an energy dissipation net at the back of the wave-making machine to prevent splashing, and another energy dissipation net at the other end of the wave tank to eliminate waves. The wave-making system consisted of hardware equipment and control software. The hardware equipment mainly consisted of a board that pushed water into waves, mechanical frame, lower computer, servo motor and driver, servo controller, position sensor, motion control interface card, wave height measuring sensors, computer, and the acquisition system. The control software mainly included various wave-making control programs, wave spectrum analysis, and wave feature statistical analysis procedures.
The control room could control the wave period, wave height, and waveform of the waves in the wave tank. The experimental platform used a data acquisition card (DAQNavi–USB4716) to collect data. Due to the limitations of the DAQ card measurement range, voltage signals could only be measured in the range of (0 ± 10V).
As shown in
Figure 11, the total length of the wave tank was
, the height of the wave tank was
, and the width of the wave tank was 0.8 m. The floating buoy was a cylinder with a diameter of 0.3 m and a height of 0.35 m, the material of the buoy was foam plastic. In order to make the wave tank have a full waveform with a maximum wave height of 0.3 m, the water depth in the wave tank was set to
. As shown in
Figure 8, the height of the PTO was 0.4 m. Considering the depth of the wave tank was not sufficient to accommodate the ACWEC’s complete device (buoy and PTO), this test designed a water basin in the tank at a distance
from the head of the tank. The length of the water basin was
. The width of the water basin was equal to the width of other locations in the wave tank, which was 0.8 m. The height of the water basin was
. Sensor (A) and Sensor (B), with a measuring range of 0–0.6 m, were used to measure the wave height before and after the ACWEC, respectively. The distance between Sensor (A) and Sensor (B) was 3 m, with the ACWEC located at the midpoint of the two sensors. In the experiment, the ACWEC was laid out as shown in
Figure 11. The buoy was connected to the PTO with a rope. At the bottom of the ACWEC (below the PTO), a cylinder drogue with a mass of M
1 was connected to adjust the weight of the ACWEC.
Since the water depth of the wave tank was only 0.6 m, when the wave height was greater than 0.3 m the wave was broken, so the maximum wave height was 0.3 m in the experiment. On the other hand, it was found in the experiment that when the wave height created by the wave tank was less than 0.15 m, the power generated by the ACWEC was very weak, even equal to zero, so the minimum wave height in this paper was 0.15 m. Therefore, the wave height range in the experiment described in this paper was 0.15–0.3 m.
The typical wave spectrum in the ocean of sea state 3 is 0.14–1.0 Hz. However, in the experiment, when the wave period of the created wave was less than 1.5 s, a complete waveform could not be produced when the wave height was high (greater than 0.25 m). When the wave period of the created wave was greater than 3 s, the output power of the ACWEC was seriously reduced and the power generation efficiency was not improved either. Thus, the wave period range in this experiment was 1.5–3.0 s. By the frequency limitations of the wave tank, the spectrum 0.33–0.66 Hz was selected in the experiments.
In the experiments, the main source of error was measurement error, which consisted of the wave height error of Sensor (A) and Sensor (B) and the voltage error of the DAQ. The measurement error of Sensor (A) and Sensor (B) was ± 5% of the measured value. After the analog input of the DAQ was calibrated, the measurement error of the DAQ was ± 0.1 V. Since the data measured in the experiment was much larger than the error range and only the power generation feasibility of the ACWEC is analyzed in this paper, very accurate measurement values were not required. Therefore, the influence of the error on the power generation performance was not considered in the discussions.
3.2. Power and Efficiency Calculation Method
In a sea state, the average energy density per unit area of gravity waves on the water surface is proportional to the wave height squared, according to linear wave theory: [
46,
47]
where
E is the mean wave energy density per unit of horizontal area (
)—the sum of kinetic and potential energy density per unit of horizontal area. The potential energy density is equal to the kinetic energy [
44,
45], both contributing half to the wave energy density
E, as can be expected from the equipartition theory.
H is the wave height,
ρ is the density of water, and
g is the gravity.
As the waves propagate, their energy is transported. The energy transport velocity is the group velocity. As a result, through a vertical plane of unit width perpendicular to the wave propagation direction, the wave energy flux is equal to:
where
is the group velocity (m/s). Due to the dispersion relation for water waves under the action of gravity, the group velocity depends on the wavelength λ, or equivalently on the wave period T. Furthermore, the dispersion relation is a function of the water depth
h. As a result, the group velocity behaves differently in the limits of deep or shallow water and at intermediate depths.
Waves in the limits of shallow water, with wavelengths λ much larger than the water depth h, travel with the following phase velocity [
48]:
where g is the acceleration by gravity and
the phase speed. Since this shallow water phase speed is independent of the wavelength, shallow water waves do not have frequency dispersion. Therefore, the wave energy flux with a wave height of
H, through a vertical plane of unit width perpendicular to the wave propagation direction, is equal to:
where
is the wave height before the WEC,
is the wave height after the WEC, and
is the input power to the WEC.
The direct current generator includes a conductive disk or cylinder that rotates in a plane that is perpendicular to a uniform static magnetic field. A potential difference is created between the center of the disc and the rim. The polarity of the electricity depends on the direction of rotation and the orientation of the field. The power of the generator is the output power of the WEC:
where U is the voltage at both ends of the external resistance and
R is the value of the external resistance.
This paper studies the overall efficiency (
η) of the PTO. The overall efficiency (
η) is defined as the conversion efficiency from the kinetic energy captured by the buoy to the generated power in the form of electricity:
3.3. The Effect of System Mass on Power and Efficiency
Inertial-based kinetic energy harvesters are modelled as second-order, spring-mass systems. The generic model of kinetic energy harvesters was first developed by Williams and Yates [
49].
Figure 12 shows a generic model of such a generator, which consists of a seismic mass,
m, and a spring with the spring constant of
k.
When the WEC vibrates, the mass moves out of phase with the WEC housing. There is a relative movement between the mass and the housing. This displacement is sinusoidal in amplitude and can drive a suitable transducer to generate electrical energy. c is the damping coefficient, which consists of mechanically induced damping (parasitic damping) coefficient and electrically induced damping coefficient , i.e., c = cm + ce. y(t) is the displacement of the generator housing and z(t) is the relative motion of the mass with respect to the housing. For a sinusoidal excitation, y(t) can be written as , where Y is the amplitude of the vibration and ω is the angular frequency of vibration.
For the analysis, it is assumed that the mass of the vibration source is much greater than the seismic mass in the generator, and the vibration source is unaffected by the movement of the generator. Then, the differential equation of the movement of the mass with respect to the generator housing from the dynamic forces on the mass can be derived as follows:
As mentioned above, damping in kinetic energy harvesters consists of mechanically induced damping (parasitic damping) and electrically induced damping. The overall damping factor of the system,
, is given by
where
is the mechanically induced damping factor and
is the electrically induced damping factor.
is the resonant frequency.
Assume that the input is a sinusoid excitation, i.e.,
. The solution to Equation (10) is given by:
Or
The average power dissipated within the damper—the sum of the power extracted by the transduction mechanism and the power lost in mechanical damping—is given by:
Equations (13) and (15) give the average power dissipated within the damper as follows:
When the generator is at resonance, i.e.,
, the power dissipation reaches maximum. The maximum dissipated power is
The power dissipation is the sum of the maximum electrical energy extracted by the transduction mechanism,
Pe, and mechanical loss,
Pm.
and
are as follows:
Maximum power conversion from the mechanical domain to the electrical domain occurs when
, i.e., damping arising from the electrical domain equals mechanical losses. Therefore, the maximum electrical power that can be extracted by the kinetic energy harvester,
, is given by
It can be seen that not only does the increase in wave height increase the output power of a power generation system, but the increase in mass also improves the output power of the power generation system.
5. Conclusions
This paper proposed an adaptively counter-rotating wave energy converter for powering drifters. In this paper, the power generation performances of the WEC in regular and irregular waves were studied, and the conclusions are drawn as follows:
- (1)
The mechanism of the adaptively counter-rotating converter is feasible. The generated electricity is a direct current, and it can prove that the PTO can adaptively adjust the deflecting direction of the blades under the water impact direction so as to keep the unidirectional rotation of the UBG and LBG. Otherwise, the output current will be AC (Alternating Current). The underwater PTO can avoid damage from wind and waves on the surface of the sea. This WEC can theoretically adaptable to any sea state.
- (2)
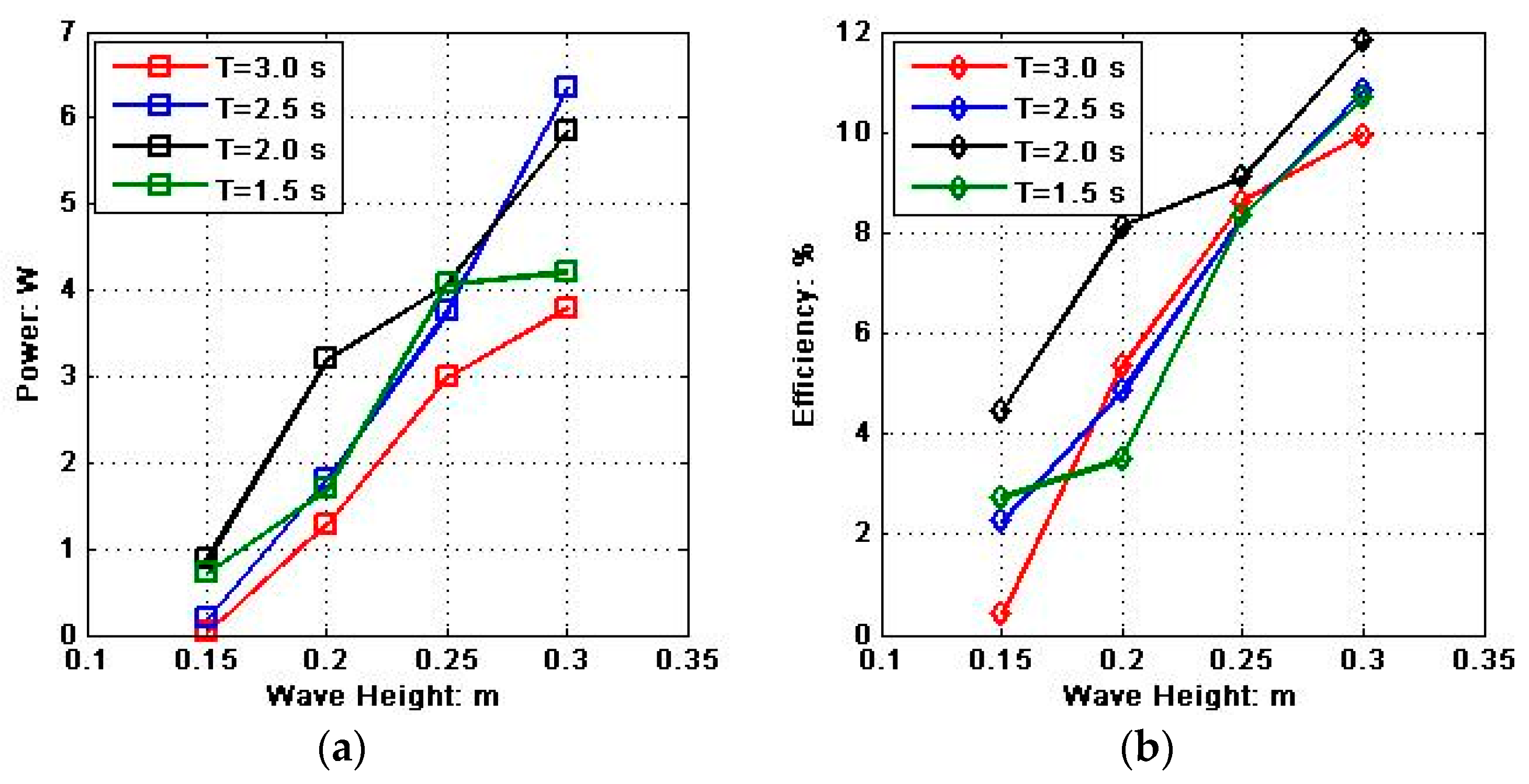
The interaction between the WEC and the water was analysed. The working depth of the PTO is equal to the length of the tether in current SVP drifters, which is 15 m. Due to the limitations of the wave tank, experiments under different conditions at a depth of 0.6 m were carried out. As a result, the maximum output power was 6.36 W and the maximum generation efficiency was 11.87%, with a wave height of 0.3 m. Experiments in deeper wave tanks will reduce the impact of horizontal flow velocity, which can improve power generation efficiency.
- (3)
Experiments under M1 = 14.21 kg and M1 = 20.11 kg were carried out. Increasing the mass of M1 will reduce the natural period of the ACWEC, which can improve the power generation performance of the ACWEC.
- (4)
Experiments in irregular waves were also carried out. As a result, the maximum output power was 3.71 W and the maximum generation efficiency was 10.77% when the significant wave height is 0.3 m.
In conclusion, the parameters of the created waves were selected for analysis, which could effectively optimize the design of ACWECs and guide WECs to achieve optimal working status in different wave statuses and meet different energy requirements.
The GDP drifters are fitted with diode-protected, alkaline D-Cell, 12 V, 56 Ah battery packs to be able to work for around 400 days [
52]. Due to the limitation of buoy volume, the battery capacity is not very large. This is also because the power demands of drifters are not very high. A power system with a maximum output power of 6.36 W is enough to make a drifter work continuously. This is an efficient way to improve the sampling intervals of drifters. The use of clean wave energy can reduce the amount of battery used and reduce the pollution of damaged batteries in seawater.
Although this paper has conducted a series of experiments in regular and irregular waves on the influence factors of the created waves, the research on WECs is still not thorough. Some important influencing factors, such as the blade angles, the number of blades, the distance between the UBG and LBG, and the stability of the output power, still need to be studied further.
Due to the limitation of the size of the wave tank, the waves generated in the wave tank are different from ocean waves. For example, deep water waves cannot be generated in the wave tank, and the water depth of the wave tank limits the position of the absorber such that it can only be placed close to the water surface. The semi-scale WEC experiment in the wave tank makes it difficult to simulate the case of an ACWEC in a real ocean. Experimental conclusions are based on the specific wave conditions in the wave tank. The wave tank experiment can only qualitatively verify the feasibility of the ACWEC and the influence of key parameters on the power generation performance of the ACWEC. In order to obtain more detailed and rigorous experimental results, an experiment of a full-scale ACWEC in the ocean needs to be carried out after completing a larger experimental prototype and obtaining better experimental support.
In addition, the entire marine environment is very complicated, and considering various failure modes of marine engineering structure, such as corrosion, bio-fouling and dynamic sediments, a new prototype of ACWECs with sufficient reliability needs to be designed. Finally, due to the high conductivity of seawater, an effective waterproofing method would increase the service life of the equipment.