Research on a Method for Simulating Multiview Ocean Wave Synchronization Data by Networked SAR Satellites
Abstract
1. Introduction
2. Basic Principle of SAR Imaging Simulation
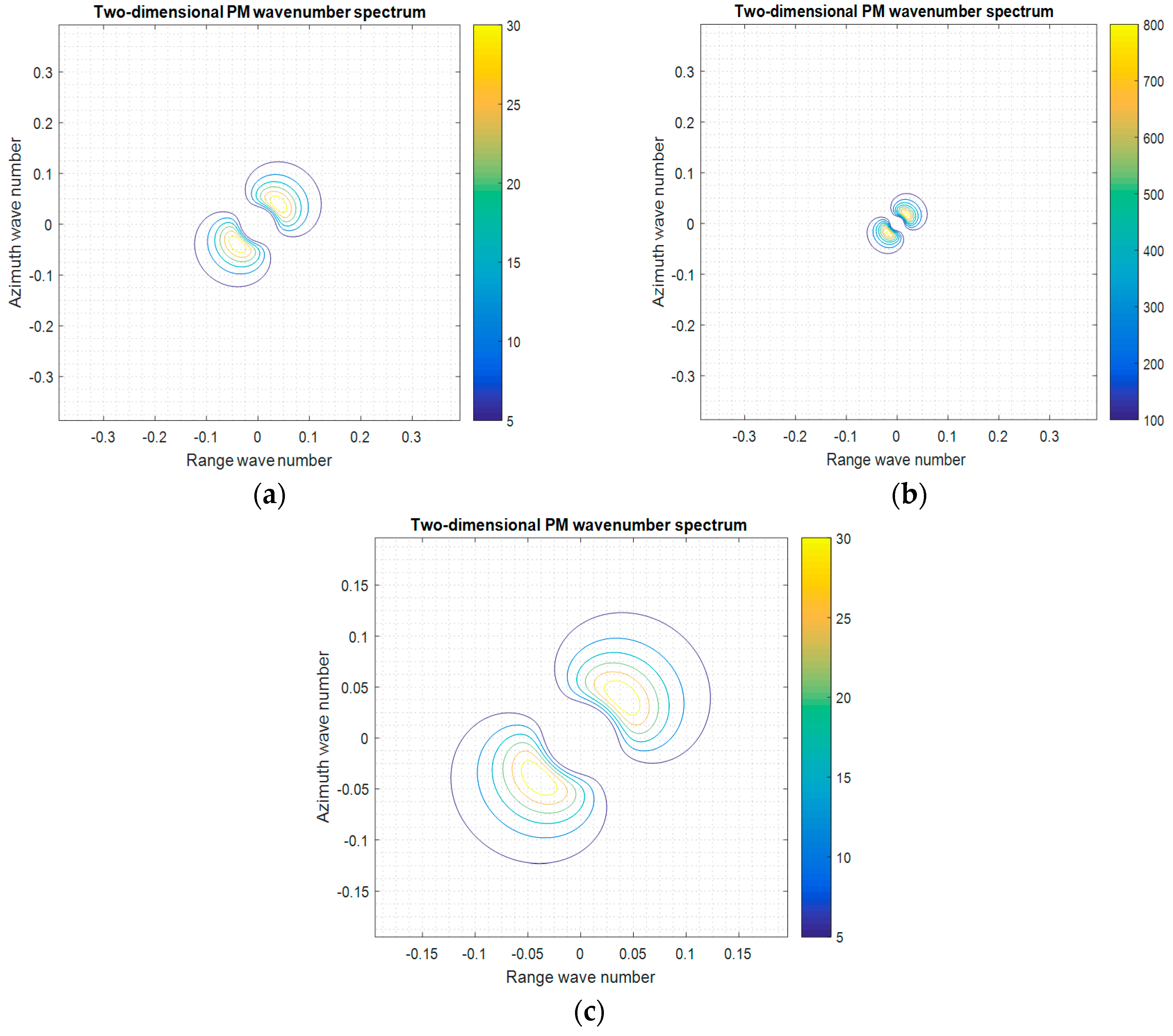
2.1. Wave Spectrum Simulation
2.2. Ocean Surface Simulation
2.3. SAR Echo Signal Simulation
2.3.1. Generation of the Ocean Surface Backscattering Coefficient
2.3.2. Calculation of the Ocean Surface Echo Signals
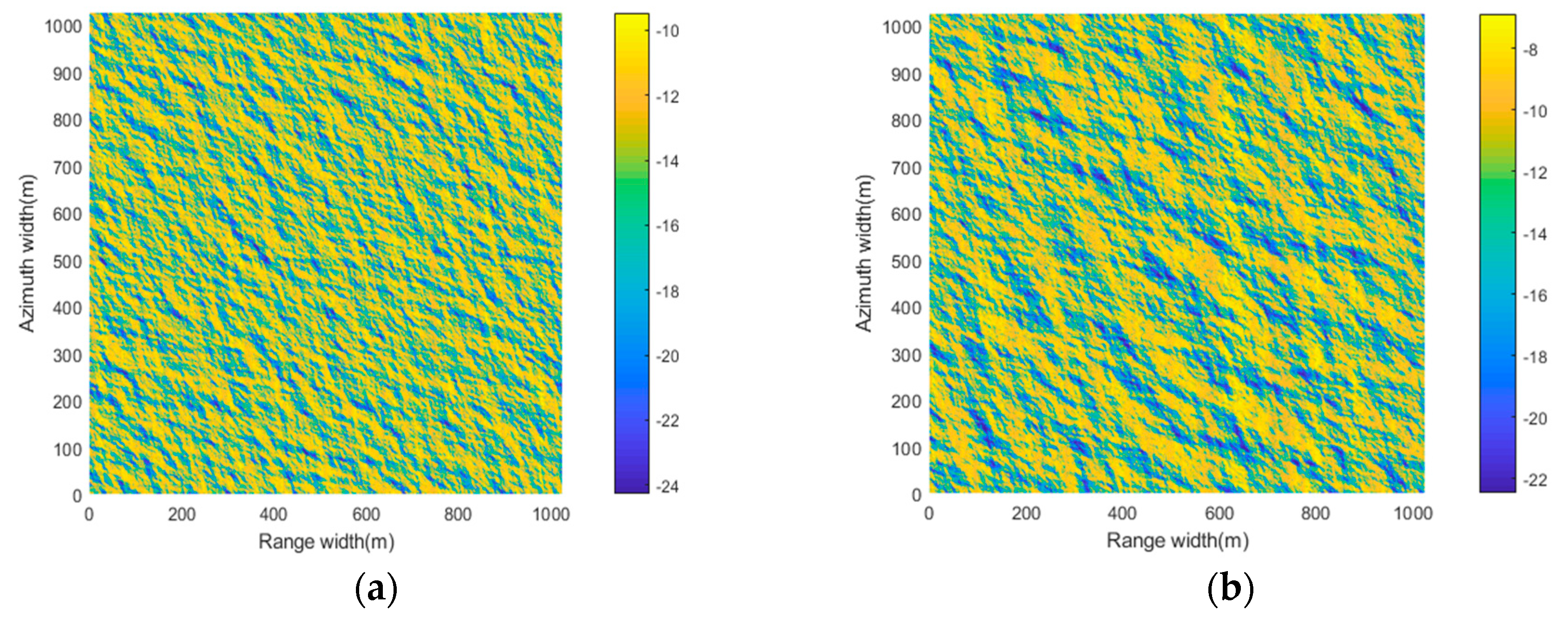
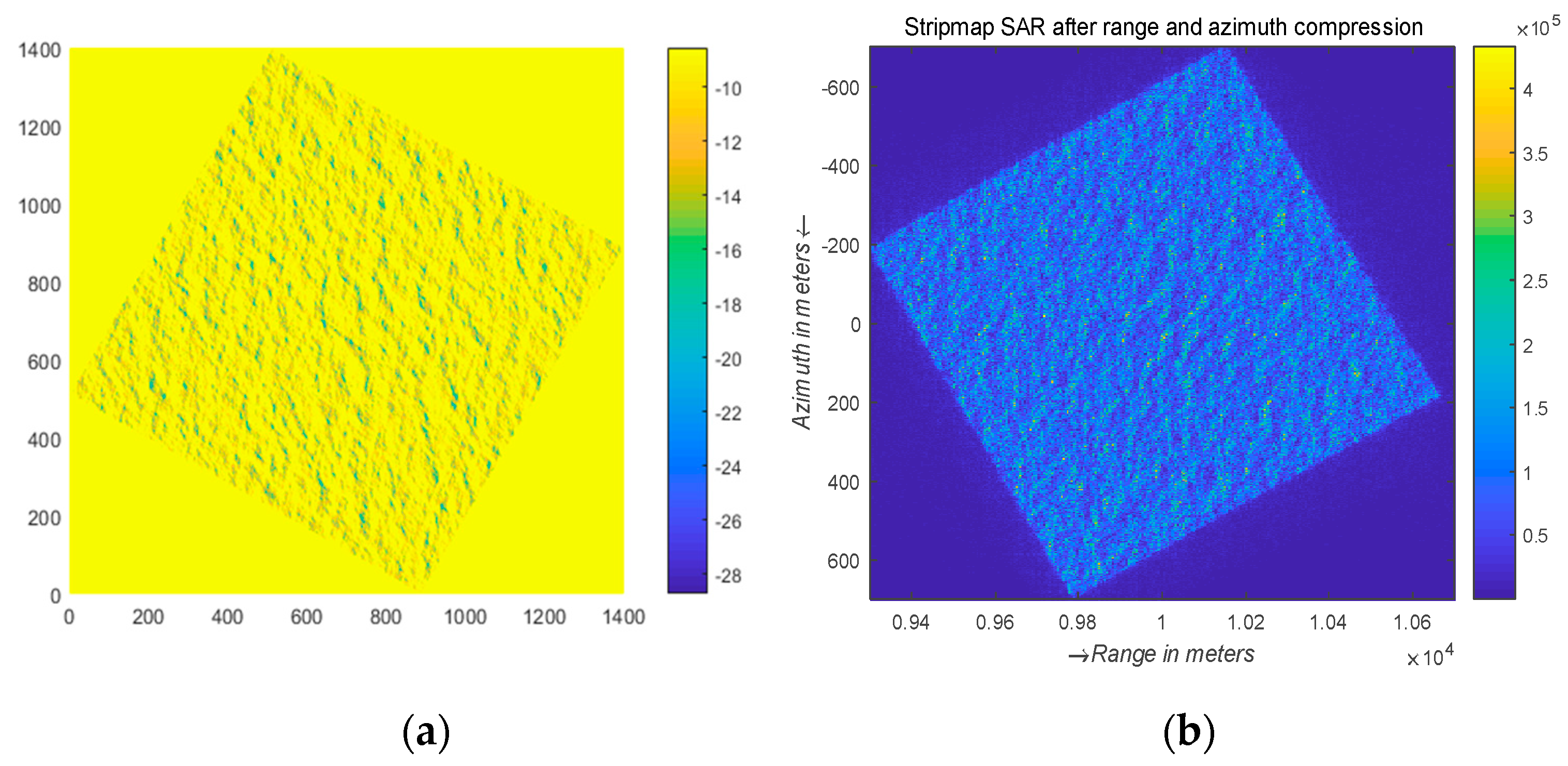
2.4. SAR Imaging of the Ocean Surface
3. Results and Analysis
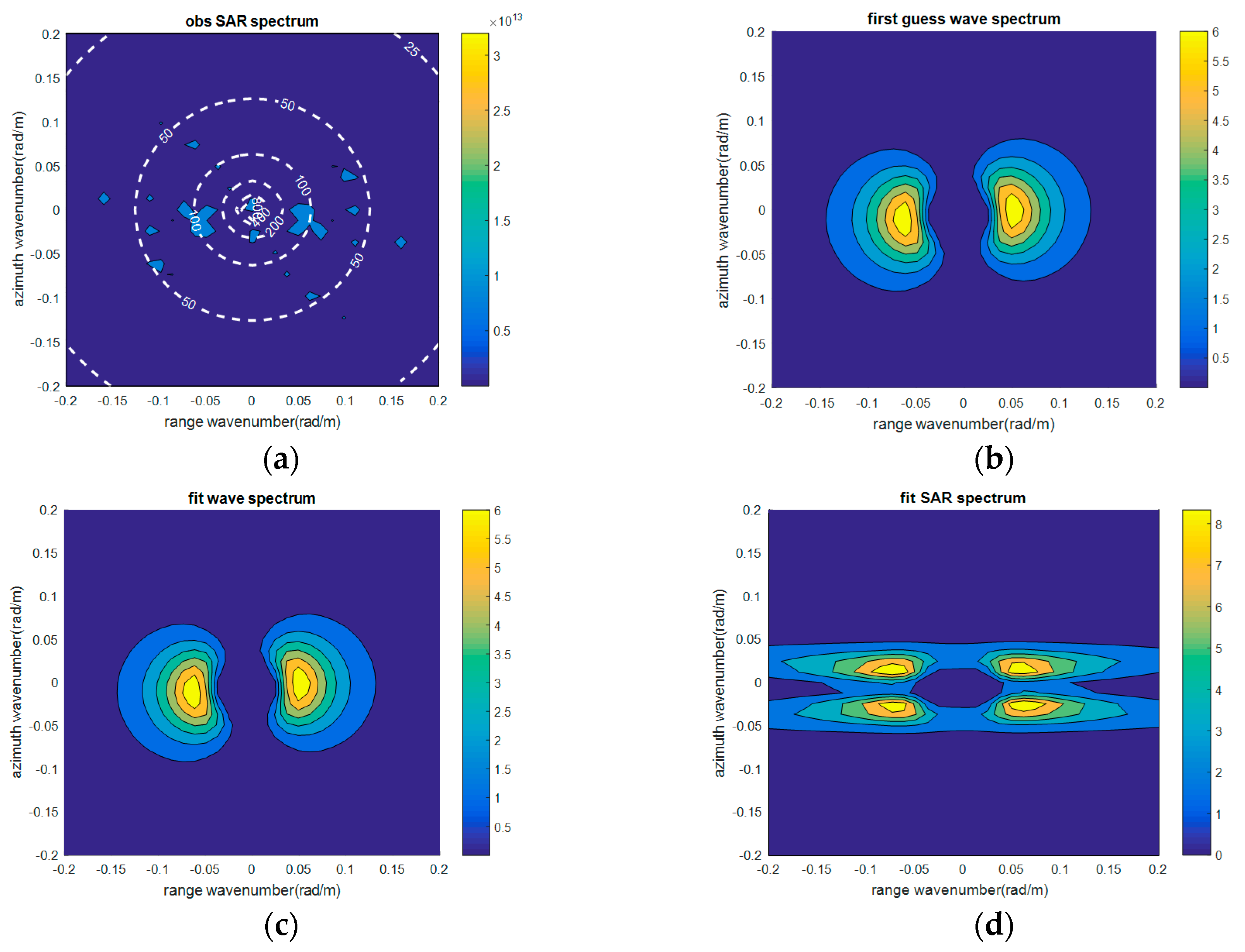
3.1. Analysis of the Single-SAR Imaging Simulation Results
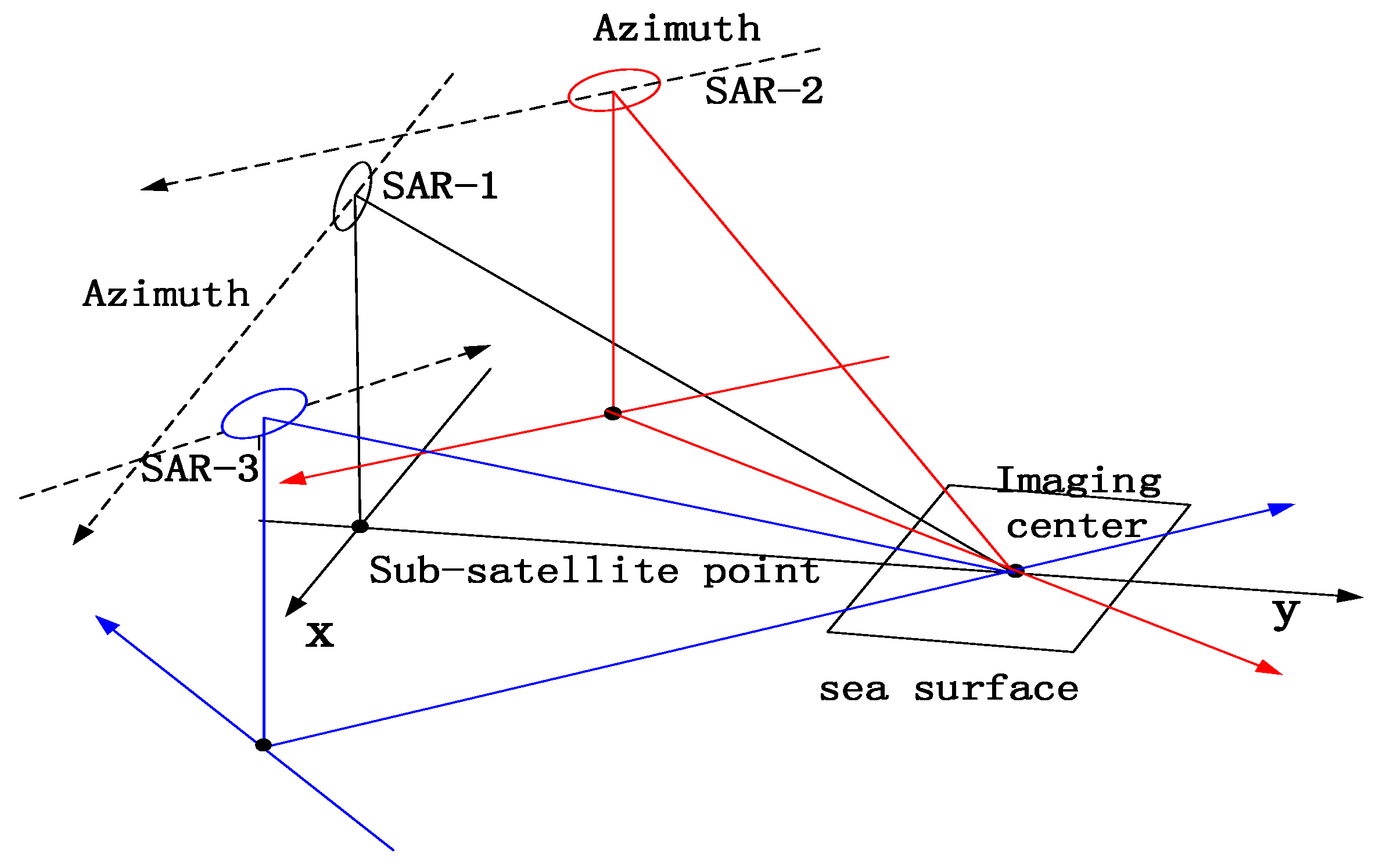
3.2. Simulation of Networked SAR Satellites and Multiview Ocean Wave SAR Synchronization Data
3.3. Accuracy Assessment of the Multiview Ocean Wave SAR Synchronization Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.M.; Lehner, S.; Bruns, T. Ocean Wave Integral Parameter Measurements Using Envisat ASAR Wave Mode Data. IEEE Trans. Geosci. Remote Sens. 2010, 49, 155–174. [Google Scholar] [CrossRef]
- Rani, S.I.; Das Gupta, M.; Sharma, P.; Prasad, V.S. Intercomparison of Oceansat-2 and ASCAT Winds with In Situ Buoy Observations and Short-Term Numerical Forecasts. Atmos. Ocean 2014, 52, 92–102. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.H.; Fore, A.G.; Hayashi, A. Validation of Aquarius sea surface salinity with in situ measurements from Argo floats and moored buoys. J. Geophys. Res. Oceans 2014, 119, 6171–6189. [Google Scholar] [CrossRef]
- Han, W.X.; Yang, J.G.; Wang, J.Z. Calibration and evaluation of satellite radar altimeter wave heights with in situ buoy data. Acta Oceanol. Sin. 2016, 38, 73–89. [Google Scholar]
- Shaeb, K.H.B.; Anand, A.; Joshi, A.K.; Bhandari, S.M. Comparison of Near Coastal Significant Wave Height Measurements from SARAL/AltiKa with Wave Rider Buoys in the Indian Region. Mar. Geod. 2015, 38, 422–436. [Google Scholar] [CrossRef]
- Woo, H.J.; Park, K.A. Long-term trend of satellite-observed significant wave height and impact on ecosystem in the East/Japan Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 143, 1–14. [Google Scholar] [CrossRef]
- Mathew, T.; Chakraborty, A.; Sarkar, A.; Kumar, R. Comparison of oceanic winds measured by space-borne scatterometers and altimeters. Remote Sens. Lett. 2012, 3, 6. [Google Scholar] [CrossRef]
- Kim, D.J.; Moon, W.M.; Moller, D.; Imel, D.A. Measurements of ocean surface waves and currents using L- and C-band along-track interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2821–2832. [Google Scholar]
- Zhang, B.; Perrie, W.; He, Y.J. Validation of RADARSAT-2 fully polarimetric SAR measurements of ocean surface waves. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Lehner, S.; Pleskachevsky, A.; Gebhardt, C.; Rosenthal, W.; Bruns, T.; Hoffmann, P.; Kieser, J. High resolution wind and wave measurements from TerraSAR-X and Tandem-X satellites in comparison to marine forecast. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2519–2522. [Google Scholar]
- Yoshida, T.; Rheem, C.K. SAR Image Simulation in the Time Domain for Moving Ocean Surfaces. Sensors 2013, 13, 4450–4467. [Google Scholar] [CrossRef]
- Lin, B.; Shao, W.; Li, X.; Li, H.; Du, X.; Ji, Q.; Cai, L. Development and validation of an ocean wave retrieval algorithm for VV-polarization Sentinel-1 SAR data. Acta Oceanol. Sin. 2017, 36, 95–101. [Google Scholar] [CrossRef]
- Grieco, G.; Lin, W.; Migliaccio, M.; Nirchio, F.; Portabella, M. Dependency of the Sentinel-1 azimuth wavelength cut-off on significant wave height and wind speed. Int. J. Remote Sens. 2016, 37, 5086–5104. [Google Scholar] [CrossRef]
- Dowd, M.; Vachon, P.W.; Dobson, F.W.; Olsen, R.B. Ocean wave extraction from RADARSAT synthetic aperture radar inter-look image cross-spectra. IEEE Trans. Geosci. Remote Sens. 2002, 39, 21–37. [Google Scholar] [CrossRef]
- Kerbaol, V.; Chapron, B.; El Fouhaily, T.; Garello, R. Fetch and wind dependence of SAR azimuth cutoff and higher order statistics in a mistral wind case. In Proceedings of the 1996 International Geoscience and Remote Sensing Symposium (IGARSS’96), Lincoln, NE, USA, 31 May 1996. [Google Scholar]
- Ren, L.; Yang, J.S.; Zheng, G.; Wang, J. Significant wave height estimation using azimuth cutoff of C-band RADARSAT-2 single-polarization SAR images. Acta Oceanol. Sin. 2015, 34, 93–101. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Chapron, B.; Collard, F. Estimating wave orbital velocity through the azimuth cutoff from space-borne satellites. J. Geophys. Res. Oceans 2015, 120, 7616–7634. [Google Scholar] [CrossRef]
- Liu, B.C.; He, Y.J. SAR Raw Data Simulation for Ocean Scenes Using Inverse Omega-K Algorithm. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6151–6169. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Luo, X.Y.; Nie, Z.P. Simulation of polarization SAR imaging of sea wave using two-Scale model. J. Univ. Electron. Sci. Technol. China 2009, 38, 651–655. [Google Scholar]
- Guo, D.; YU, T.; Fernado, N. Simulation of polarization SAR imaging of ocean surface based on the two-scale model. J. Electron. Meas. Instrum. 2011, 25, 81–88. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D. On ocean SAR raw signal simulation. IEEE Trans. Geosci. Remote Sens. 1998, 36, 84–100. [Google Scholar] [CrossRef]
- Zhu, M.B.; Zou, J.W.; Dong, W. Imaging simulation of dynamic sea surface with missile-borne SAR. Chin. J. Radio Sci. 2012, 3, 592–597. [Google Scholar]
- Fan, W.N.; Zhang, M.; Li, J.X. Highly squinted SAR imaging simulation of ship-ocean scene based on EM scattering mechanism. IET Microw. Antennas Propag. 2018, 12, 1160–1165. [Google Scholar] [CrossRef]
- Xu, X.J.; Li, X.F. Radar Phenomenological Models for Ships on Time-Evolving Sea Surface; National Defense Industry Press: Beijing, China, 2013; pp. 5–6. [Google Scholar]
- Mao, C.; Qiu, Z.M.; Liu, Z.; Lu, F.X. Monte Carlo simulation of three-dimensional random rough sea surface. Ship Sci. Technol. 2013, 35, 25–28. [Google Scholar]
- He, Z.H. Study on Ocean Modeling, Imaging and Along-Track InSAR. Master’s Thesis, National University of Defense Technology, Hunan, China, 2007. [Google Scholar]
- Huang, Y.K. Modeling Simulation and System Design of Synthetic Aperture Radar Echo Simulator. Master’s Thesis, University of Electronic Science and Technology of China, Sichuan, China, 2008. [Google Scholar]
- Klein, L.; Swift, C.T. An improved model for the dielectric constant of sea water at microwave frequencies. IEEE Trans. Antennas Propag. 2003, 25, 104–111. [Google Scholar] [CrossRef]
- Zhang, Y.D. Study on Electromagnetic and Light Scattering Characteristics of Sea Surface. Ph.D. Thesis, Xidian University, Shanxi, China, 2004. [Google Scholar]
- Guo, D. SAR Imaging Simulations Based on the Ocean Scenes and The Electromagnetic Scattering Study. Ph.D. Thesis, University of Electronic Science and Technology of China, Sichuan, China, 2011. [Google Scholar]
- Pi, Y.M.; Yang, J.Y.; Fu, Y.S.; Yang, X.B. Synthetic Aperture Radar Imaging Principle; University of Electronic Science and Technology of China Press: Sichuan, China, 2007; pp. 78–82. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithhms and Implementation; Publishing house of electronics industry: Beijng, China, 2012; pp. 154–166. [Google Scholar]
- Wen, S.C.; Yu, Z.W. Wave Theory and Calculation Principle; Science Press: Beijing, China, 1984; pp. 142–149. [Google Scholar]
- Hersbach, H.; Stoffelen, A.; Haan, S.D. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. J. Geophys. Res. 1991, 96, 10713. [Google Scholar] [CrossRef]









| Parameters | Numerical Value |
|---|---|
| Platform height | 10 km |
| Speed | 200 m/s |
| Observation angle of incidence | 30° |
| Carrier frequency | 3 GHz |
| Pulse duration | 5 μs |
| Chirp frequency modulation bandwidth | 18.75 MHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Y.; Zhang, X.; Dai, Y.; Shi, X. Research on a Method for Simulating Multiview Ocean Wave Synchronization Data by Networked SAR Satellites. J. Mar. Sci. Eng. 2019, 7, 180. https://doi.org/10.3390/jmse7060180
Wan Y, Zhang X, Dai Y, Shi X. Research on a Method for Simulating Multiview Ocean Wave Synchronization Data by Networked SAR Satellites. Journal of Marine Science and Engineering. 2019; 7(6):180. https://doi.org/10.3390/jmse7060180
Chicago/Turabian StyleWan, Yong, Xiaoyu Zhang, Yongshou Dai, and Xiaolei Shi. 2019. "Research on a Method for Simulating Multiview Ocean Wave Synchronization Data by Networked SAR Satellites" Journal of Marine Science and Engineering 7, no. 6: 180. https://doi.org/10.3390/jmse7060180
APA StyleWan, Y., Zhang, X., Dai, Y., & Shi, X. (2019). Research on a Method for Simulating Multiview Ocean Wave Synchronization Data by Networked SAR Satellites. Journal of Marine Science and Engineering, 7(6), 180. https://doi.org/10.3390/jmse7060180






