Effects of Wave Conditions and Particle Size on the Release of Oil from Oil-Contaminated Sediments in a Wave Tank
Abstract
:1. Introduction
2. Materials and Methods
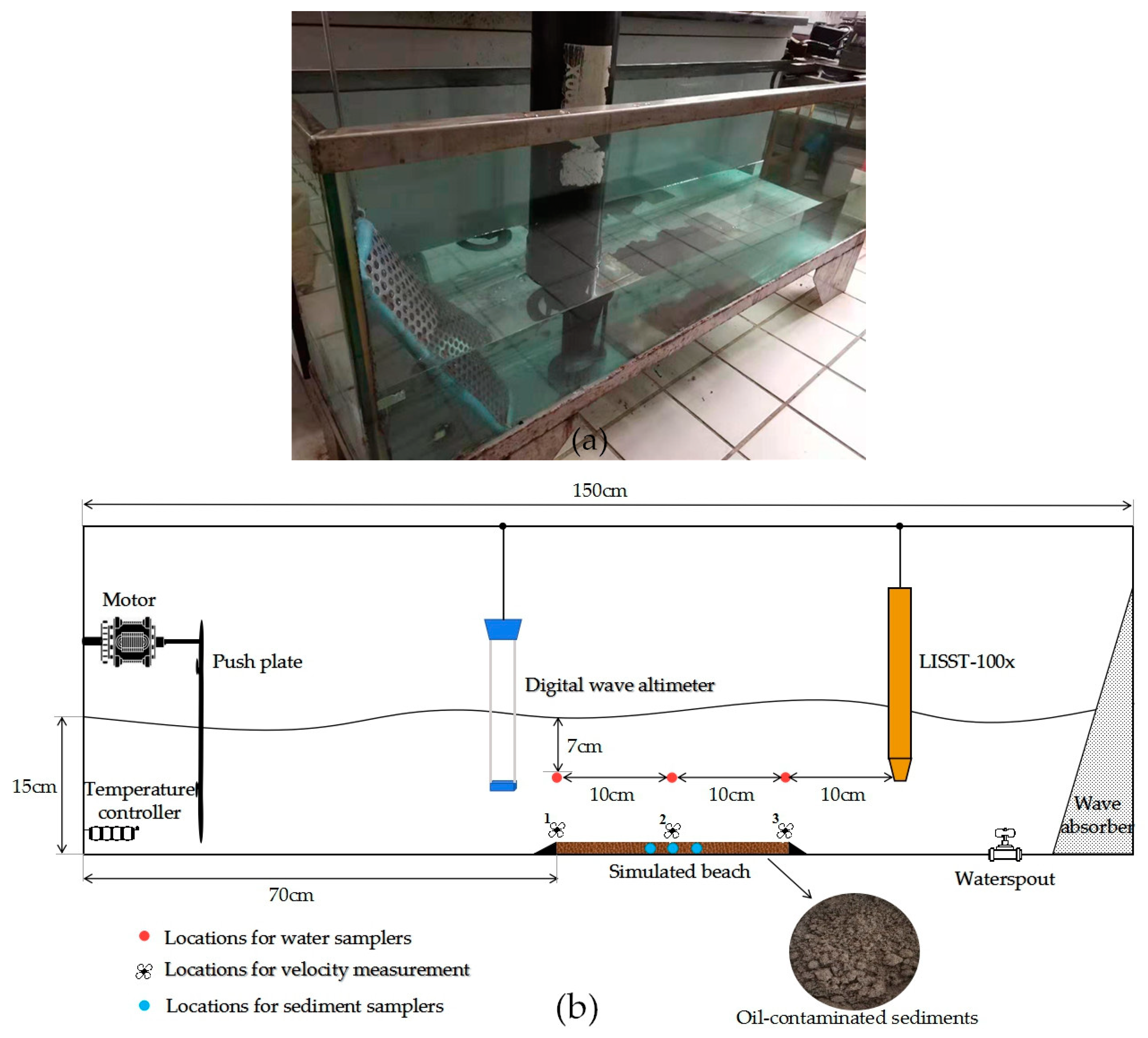
2.1. Wave Tank Facility
2.2. Oil and Sediment Property
2.3. Preparation of the Oil-Contaminated Sediments
2.4. Analytical Methods for Measuring Oil Concentration
3. Results and Discussion
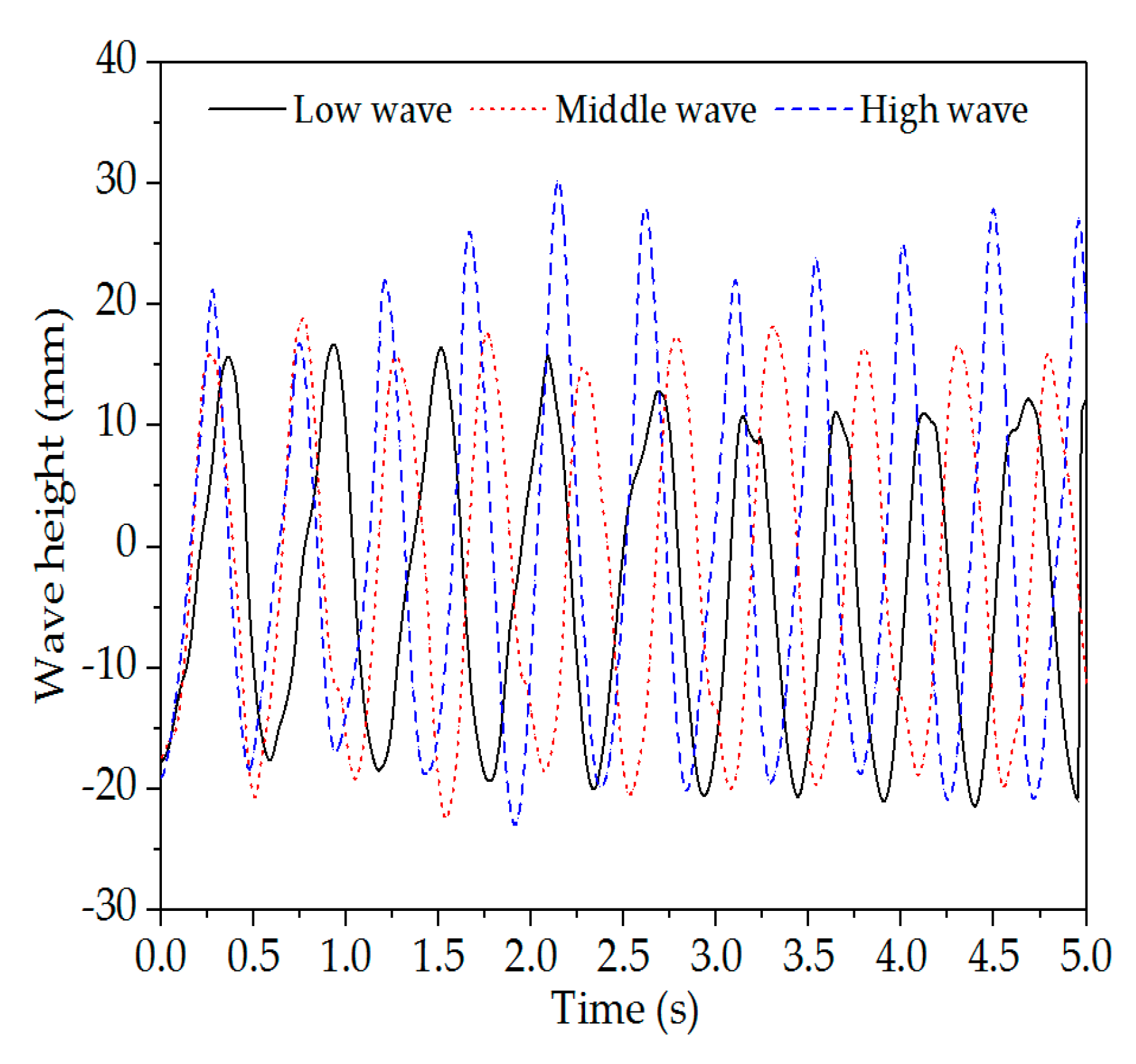
3.1. Characterization of Energy Levels
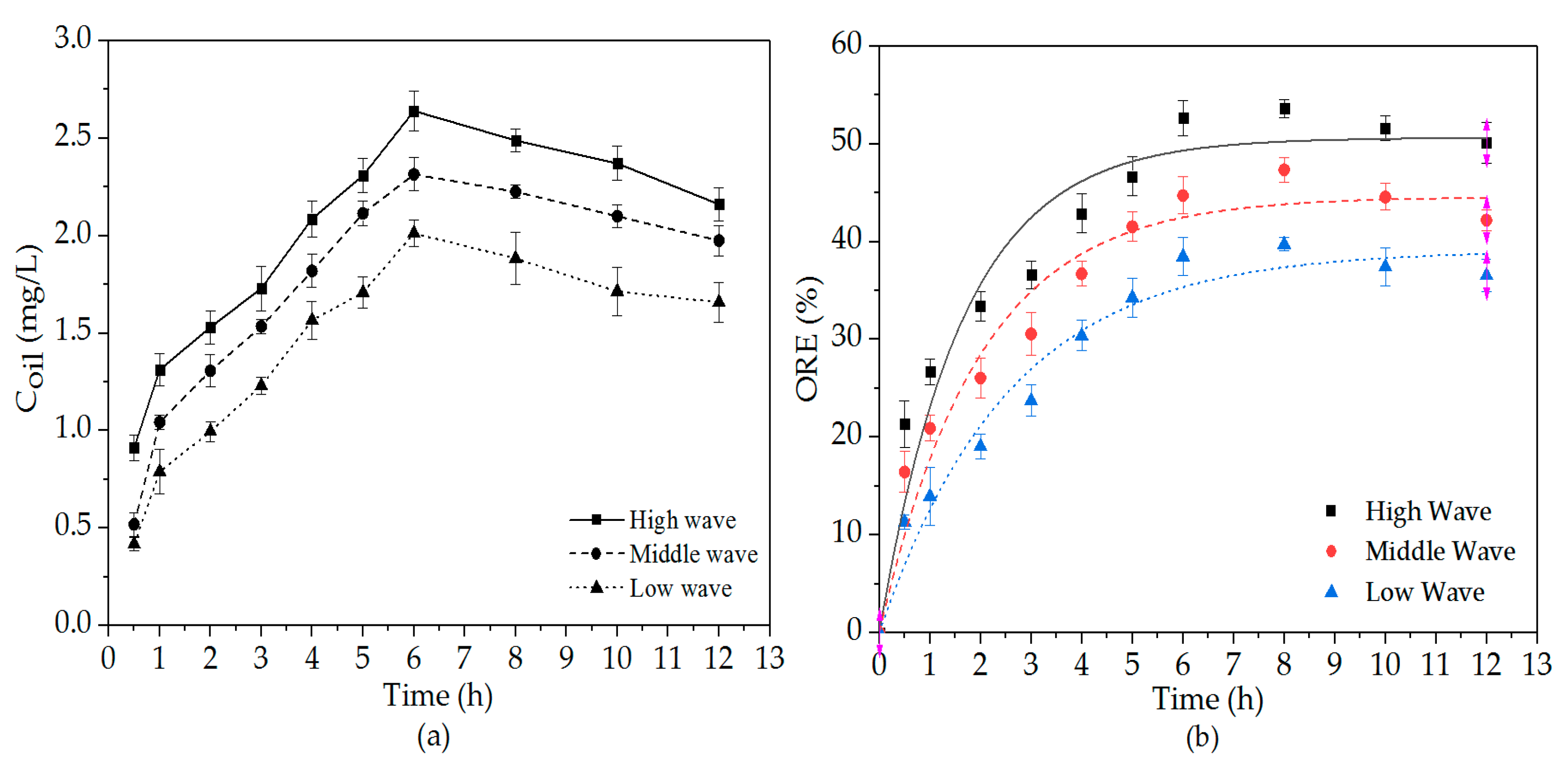
3.2. Effect of Wave Conditions on the Release of Oil from Oil-Contaminated Sediments
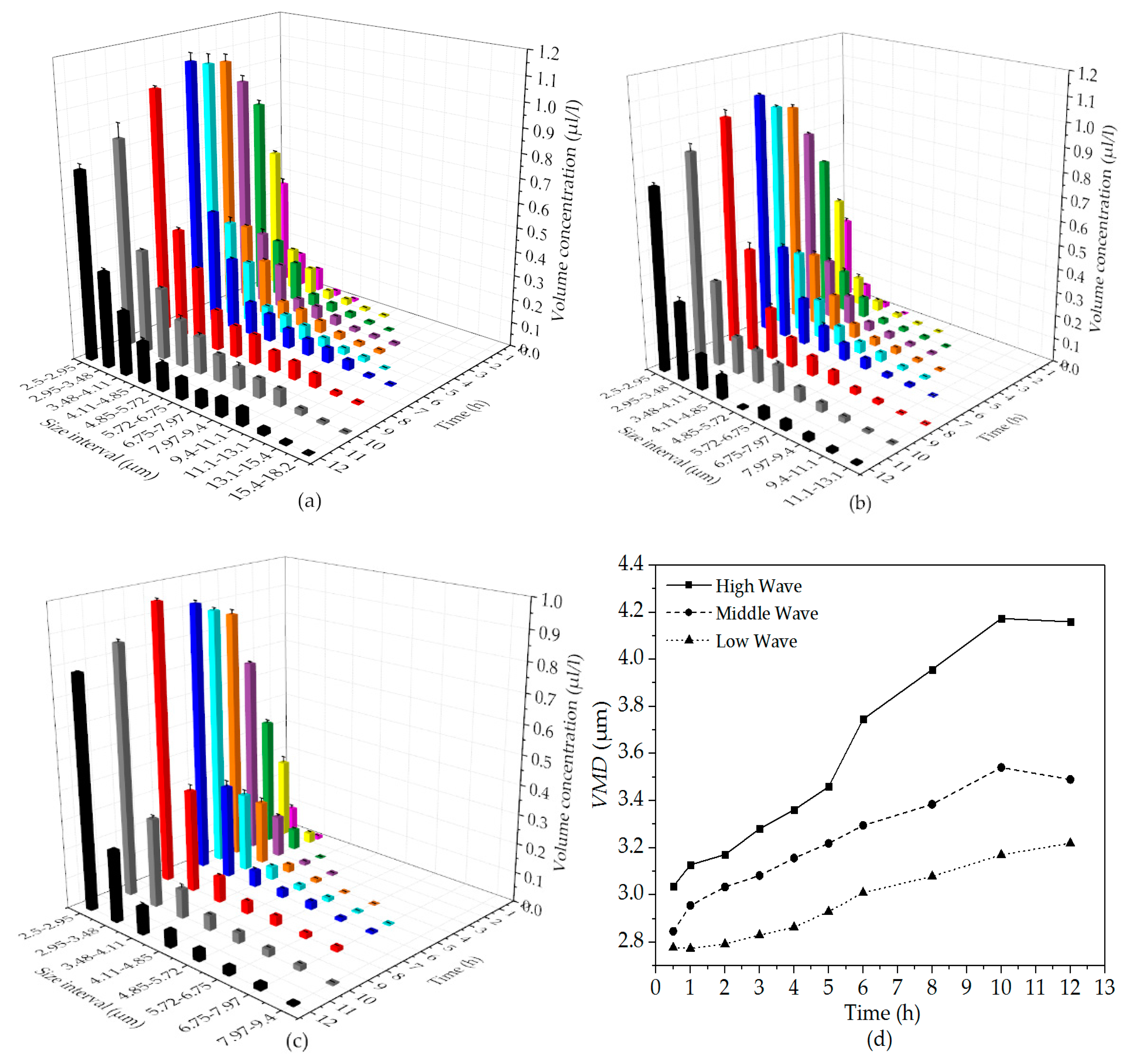
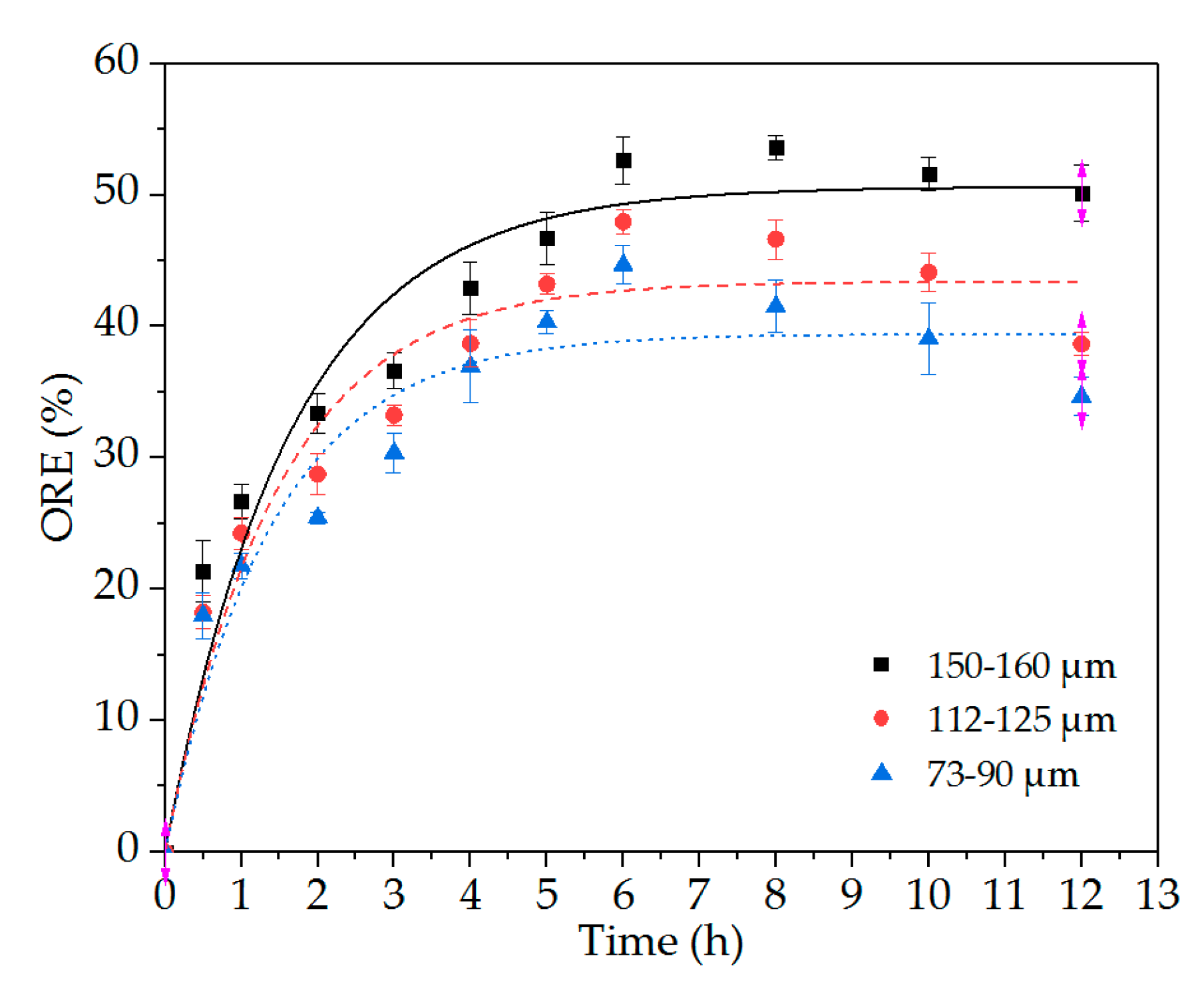
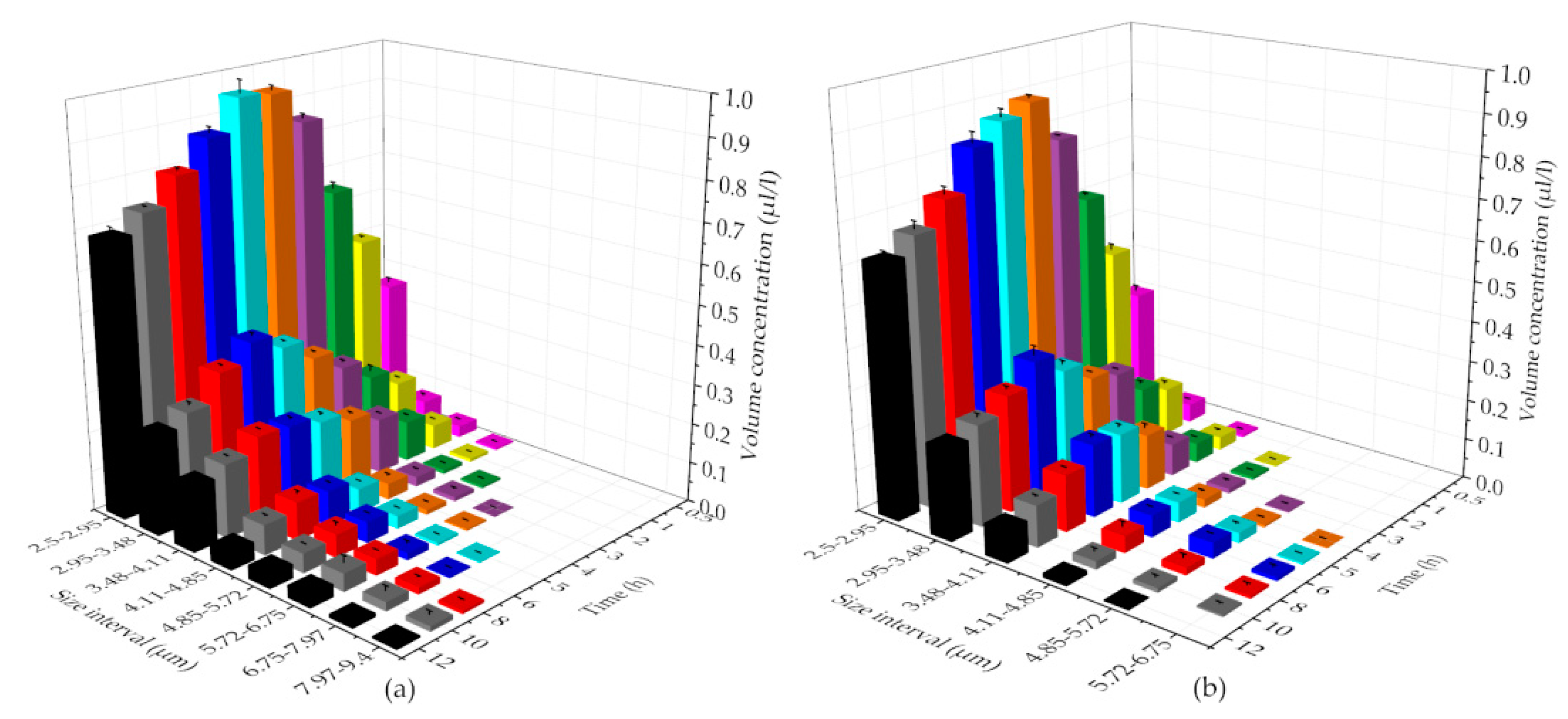
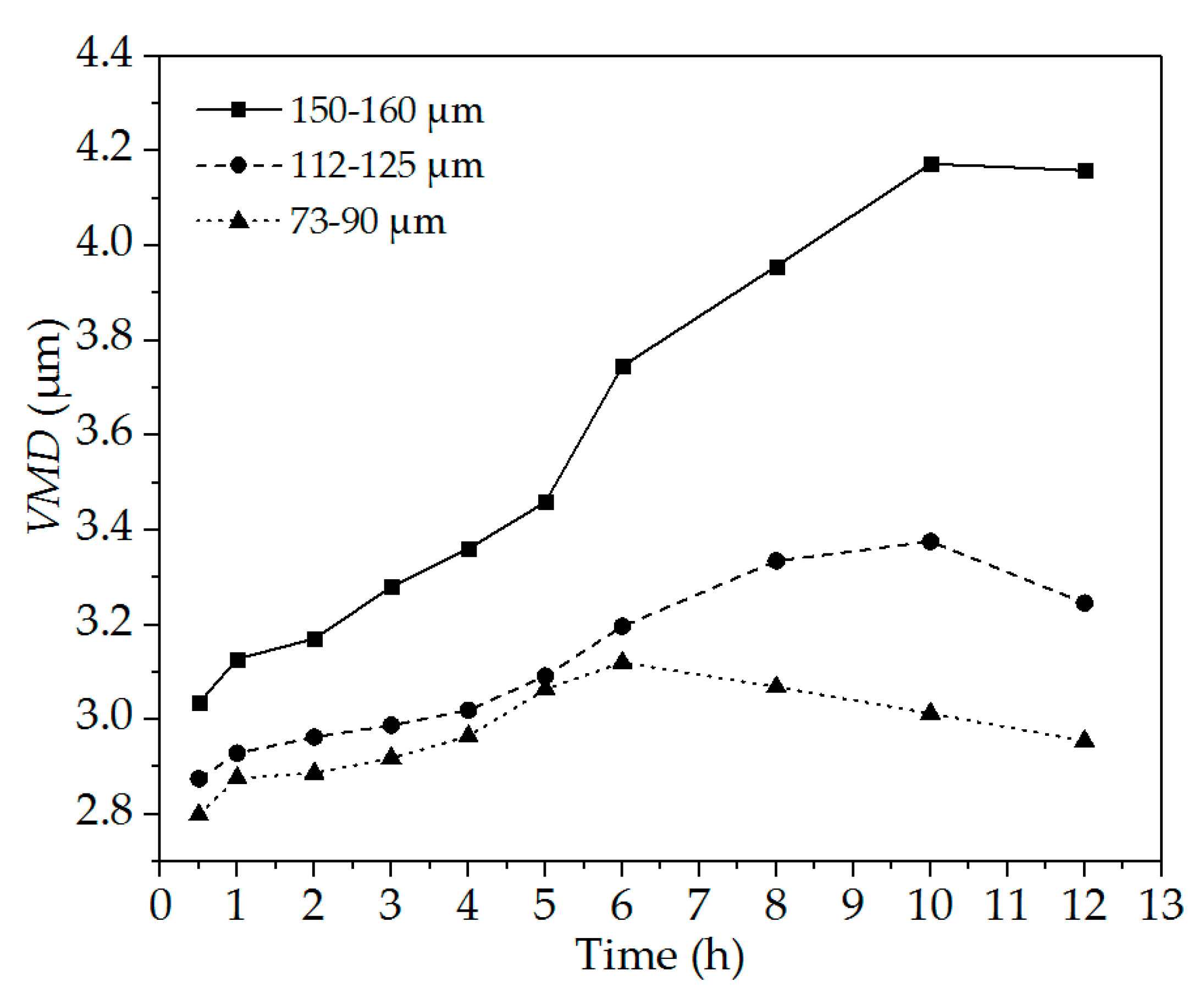
3.3. Effect of Particle Size on the Release of Oil from Oil-Contaminated Sediments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qi, Z.X.; Zhang, C.C.; Han, J.S.; Gao, Y.L.; Xiong, D.Q. A decision model responding to the refuge request from a ship in need of assistance. Mar. Policy 2018, 95, 294–300. [Google Scholar] [CrossRef]
- French McCay, D.; Rowe, J.J.; Whittier, N.; Sankaranarayanan, S.; Schmidt Etkin, D. Estimation of potentialimpacts and natural resource damages of oil. J. Hazard. Mater. 2004, 107, 11–25. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J.; Grubesic, T. The Implications of Oil Exploration off the Gulf Coast of Florida. J. Mar. Sci. Eng. 2018, 6, 1–21. [Google Scholar] [CrossRef]
- King, T.; Robinson, B.; Ryan, S.; Lee, K.; Boufadel, M.; Clyburne, J. Estimating the usefulness of chemical dispersant to treat surface spills of oil sands products. J. Mar. Sci. Eng. 2018, 6, 2–8. [Google Scholar] [CrossRef]
- Owens, E.H.; Sergy, G.A.; Chantal, C.C.; Prince, R.C.; Lee, K. The reduction of stranded oil by in situ, shoreline treatment options. Spill Sci. Technol. Bull. 2003, 8, 257–272. [Google Scholar] [CrossRef]
- Lucas, Z.; Macgregor, C. Characterization and source of oil contamination on the beaches and seabird corpses, Sable Island, Nova Scotia, 1996–2005. Mar. Pollut. Bull. 2006, 52, 778–789. [Google Scholar] [CrossRef]
- Hansel, T.C.; Osofsky, H.J.; Osofsky, J.D.; Speier, A.H. Longer-term mental and behavioral health effects of the deepwater horizon gulf oil spill. J. Mar. Sci. Eng. 2015, 3, 1260–1271. [Google Scholar] [CrossRef]
- Yim, U.H.; Ha, S.Y.; An, J.G.; Won, J.H.; Han, G.M.; Hong, S.H.; Kim, M.; Jung, J.H.; Shim, W.J. Fingerprint and weathering characteristics of stranded oils after the Hebei Spirit oil spill. J. Hazard. Mater. 2011, 197, 60–69. [Google Scholar] [CrossRef]
- Warnock, A.M.; Hagen, S.C.; Passeri, D.L. Marine Tar Residues: A Review. Water Air Soil Pollut. 2015, 226, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Delvigne, G.A.L. Physical appearance of oil in oil-contaminated sediment. Spill Sci. Technol. Bull. 2002, 8, 55–63. [Google Scholar] [CrossRef]
- Jonker, M.T.O.; Sinke, A.J.C.; Brils, J.M.; Koelmans, A.A. Sorption of Polycyclic Aromatic Hydrocarbons to Oil Contaminated Sediment: Unresolved Complex. Environ. Sci. Technol. 2003, 37, 5197–5203. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A.; Liu, Y. Remediation technologies for oil-contaminated sediments. Mar. Pollut. Bull. 2015, 101, 483–490. [Google Scholar] [CrossRef] [PubMed]
- Stout, S.A.; Payne, J.R.; Emsbo-Mattingly, S.D.; Baker, G. Weathering of field-collected floating and stranded Macondo oils during and shortly after the Deepwater Horizon oil spill. Mar. Pollut. Bull. 2016, 105, 7–22. [Google Scholar] [CrossRef] [PubMed]
- Chapman, N. Operational Guidelines on Sunken and Submerged Oil Assessment and Removal Techniques; International Maritime Organization: London, UK, 2013; pp. 3–5. [Google Scholar]
- Van Noort, P.C.M.; Cornelissen, G.; ten Hulscher, T.E.M.; Vrind, B.A.; Rigterink, H.; Belfroid, A. Slow and very slow desorption of organic compounds from sediment: Influence of sorbate planarity. Water Res. 2003, 37, 2317–2322. [Google Scholar] [CrossRef]
- Yu, H.; Huang, G.H.; An, C.J.; Wei, J. Combined effects of DOM extracted from site soil/compost and biosurfactant on the sorption and desorption of PAHs in a soil-water system. J. Hazard. Mater. 2011, 190, 883–890. [Google Scholar] [CrossRef] [PubMed]
- Portet-Koltalo, F.; Ammami, M.T.; Benamar, A.; Wang, H.; Le Derf, F.; Duclairoir-Poc, C. Investigation of the release of PAHs from artificially contaminated sediments using cyclolipopeptidic biosurfactants. J. Hazard. Mater. 2013, 261, 593–601. [Google Scholar] [CrossRef]
- Poot, A.; Jonker, M.T.; Gillissen, F.; Koelmans, A.A. Explaining PAH desorption from sediments using Rock Eval analysis. Environ. Pollut. 2014, 193, 247–253. [Google Scholar] [CrossRef]
- Bandara, U.C.; Yapa, P.D.; Xie, H. Fate and transport of oil in sediment laden marine waters. J. Hydro-Environ. Res. 2011, 5, 0–156. [Google Scholar] [CrossRef]
- Cao, X.Y.; Han, H.; Yang, G.P.; Ding, H.B.; Zhang, H.H. A Study on the release of oil from oil-contaminated sediment through laboratory experiments. Water Air Soil Pollut. 2013, 224, 2–8. [Google Scholar] [CrossRef]
- Yuan, L.L.; Han, L.; Bo, W.; Chen, H.; Gao, W.S.; Chen, B. Simulated oil release from oil-contaminated marine sediment in the Bohai Sea, China. Mar. Pollut. Bull. 2017, 118, 79–84. [Google Scholar] [CrossRef]
- Li, M.; Garrett, C. The relationship between oil droplet size and upper ocean turbulence. Mar. Pollut. Bull. 1998, 36, 961–970. [Google Scholar] [CrossRef]
- Nissanka, I.D.; Yapa, P.D. Calculation of oil droplet size distribution in ocean spills. Mar. Pollut. Bull. 2018, 135, 723–734. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Zhao, L.; Boufadel, M.C.; King, T.; Robinson, B.; Conmy, R.; Lee, K. Impact of mixing time and energy on the dispersion effectiveness and droplets size of oil. Chemosphere 2017, 166, 246–254. [Google Scholar] [CrossRef]
- Marques, M.; Fábio, M.; Gameiro, L.; António, M.; Ferreira, A.D. Numerical simulation of regular waves: Optimization of a numerical wave tank. Ocean Eng. 2018, 170, 89–99. [Google Scholar] [CrossRef]
- Rodolfo, B.; Peter, D.T.; Judith, W. Comparison of measurements and models of bed stress, bedforms and suspended sediments under combined currents and waves. Coast. Eng. 2012, 62, 19–30. [Google Scholar] [Green Version]
- Sara, P.; Marco, P.; Silvia, B. On the wave bottom shear stress in shallow depths: The role of wave period and bed roughness. Water 2018, 10, 1348. [Google Scholar]
- Jia, Y.; Zhang, Y.; Liu, H. Wave-induced sediment resuspension of seabed in the Yellow River Delta. Acta Oceanol. Sin. 2012, 34, 100–110. [Google Scholar]
- Boyson, T.K.; Pashley, R.M. A study of oil droplet coalescence. J. Colloid Interface Sci. 2007, 316, 59–65. [Google Scholar] [CrossRef]
- Nissanka, I.D.; Yapa, P.D. Oil slicks on water surface: Breakup, coalescence, and droplet formation under breaking waves. Mar. Pollut. Bull. 2017, 114, 480–493. [Google Scholar] [CrossRef]
| Wave Condition | E0 (%) | k (%/h) | R2 |
|---|---|---|---|
| High wave | 50.63 | 60.83 | 0.9441 |
| Middle wave | 44.58 | 50.86 | 0.9532 |
| Low wave | 39.11 | 40.00 | 0.9673 |
| Particle Size (μm) | E0 (%) | k (%/h) | R2 |
|---|---|---|---|
| 150–160 | 50.63 | 60.83 | 0.9441 |
| 112–125 | 43.42 | 68.76 | 0.9331 |
| 73–90 | 39.42 | 71.36 | 0.9162 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Qi, Z.; Fu, S.; Yu, X.; Li, W.; Xiong, D. Effects of Wave Conditions and Particle Size on the Release of Oil from Oil-Contaminated Sediments in a Wave Tank. J. Mar. Sci. Eng. 2019, 7, 256. https://doi.org/10.3390/jmse7080256
Yu Y, Qi Z, Fu S, Yu X, Li W, Xiong D. Effects of Wave Conditions and Particle Size on the Release of Oil from Oil-Contaminated Sediments in a Wave Tank. Journal of Marine Science and Engineering. 2019; 7(8):256. https://doi.org/10.3390/jmse7080256
Chicago/Turabian StyleYu, Yue, Zhixin Qi, Sinan Fu, Xinping Yu, Wenxin Li, and Deqi Xiong. 2019. "Effects of Wave Conditions and Particle Size on the Release of Oil from Oil-Contaminated Sediments in a Wave Tank" Journal of Marine Science and Engineering 7, no. 8: 256. https://doi.org/10.3390/jmse7080256
APA StyleYu, Y., Qi, Z., Fu, S., Yu, X., Li, W., & Xiong, D. (2019). Effects of Wave Conditions and Particle Size on the Release of Oil from Oil-Contaminated Sediments in a Wave Tank. Journal of Marine Science and Engineering, 7(8), 256. https://doi.org/10.3390/jmse7080256





