Dynamic Analysis of an Array of Connected Floating Breakwaters
Abstract
1. Introduction
2. Overview of the Floating Breakwater Designs
3. Mathematical Model
3.1. Multi-Body Hydrodynamics
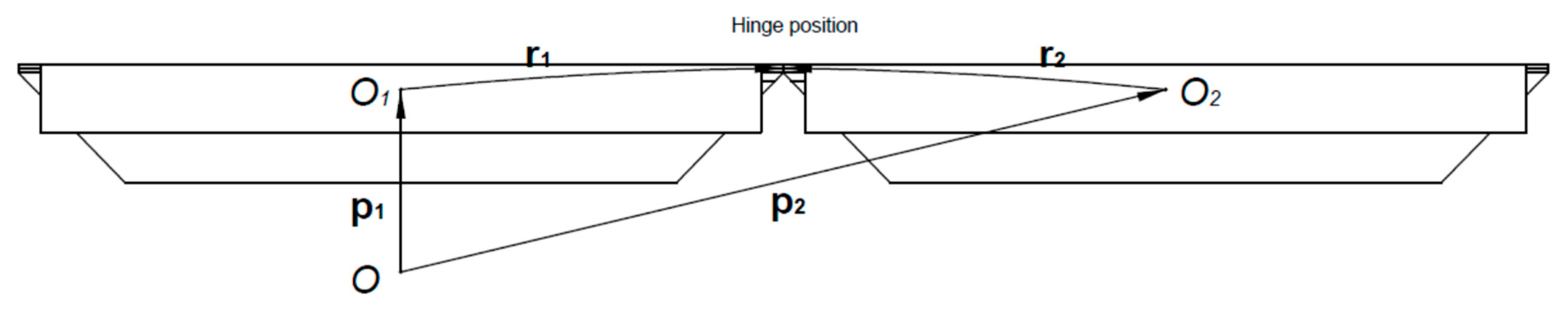
3.2. The Connection Model
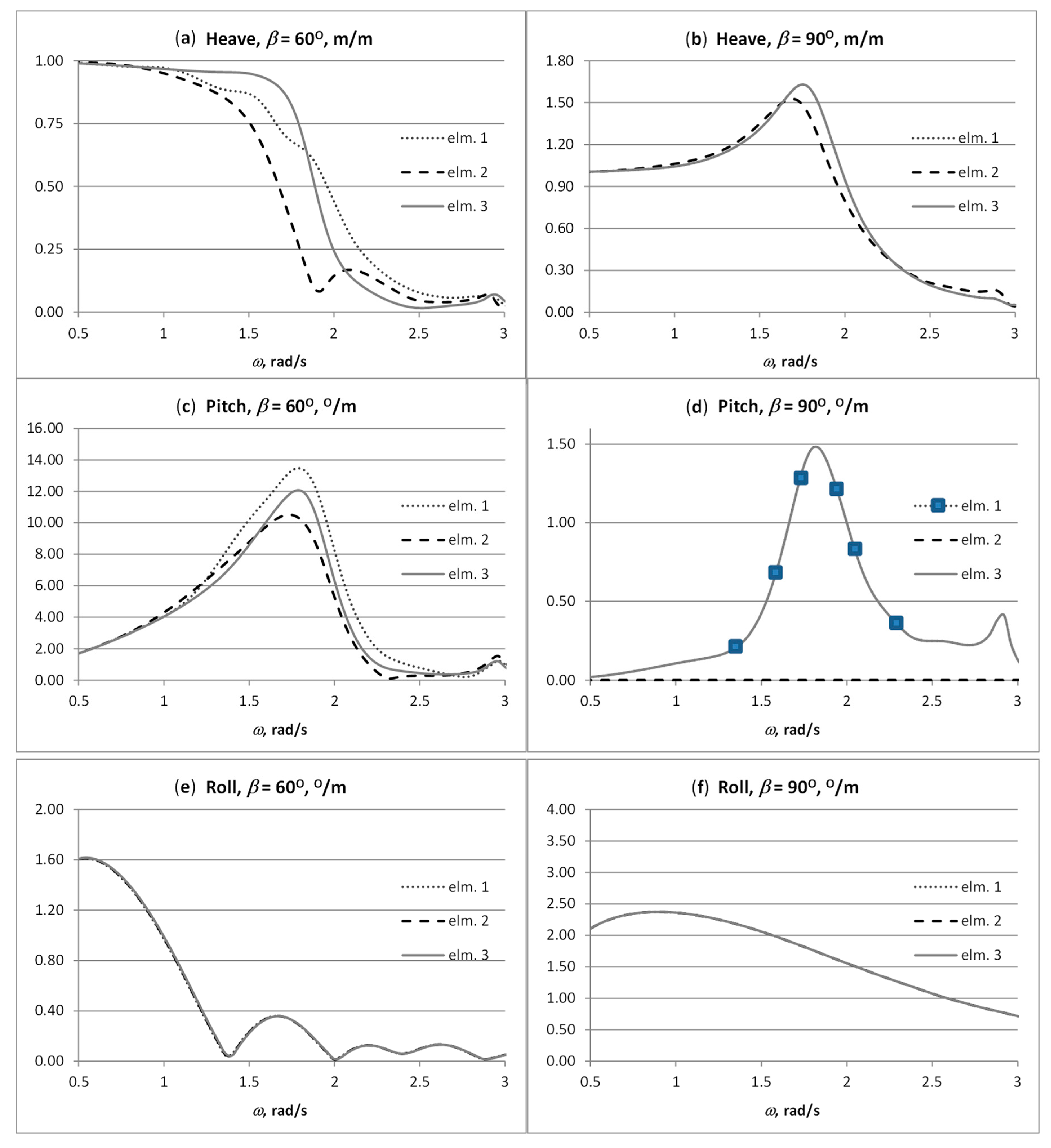
4. Case Studies
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sawaragi, T. Coastal Engineering—Waves, Beaches, Wave-structure Interaction, 1st ed.; Elsevier Science: Armsterdam, The Netherlands, 1995. [Google Scholar]
- Carević, D.; Mostečak, H.; Bujak, D.; Lončar, G. Influence of water-level variations on wave transmission through flushing culverts positioned in a breakwater body. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 04018012. [Google Scholar] [CrossRef]
- Leach, P.A. Hinged Floating Breakwater: Theory and Experiments. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 1983. [Google Scholar]
- Newman, J.N. Wave effects on deformable bodies. Appl. Ocean Res. 1994, 16, 47–59. [Google Scholar] [CrossRef]
- Lee, C.H.; Newman, J.N. An assessment of hydroelasticity for very large hinged vessels. J. Fluids Struct. 2000, 14, 957–970. [Google Scholar] [CrossRef]
- Angelides, D.C.; Diamantoulaki, I. Analysis of performance of hinged floating breakwaters. Eng. Struct. 2010, 32, 2407–2423. [Google Scholar]
- Angelides, D.C.; Diamantoulaki, I. Modeling of cable-moored floating breakwaters connected with hinges. Eng. Struct. 2011, 33, 1536–1552. [Google Scholar]
- Kim, M.S.; Ha, M.K.; Kim, B.W. Relative motions between LNG-FPSO and side-by-side positioned LNG carrier in waves. In Proceedings of the Thirteenth International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003. [Google Scholar]
- Buchner, B.; van Dijk, A.; de Wilde, J. Numerical multiple-body simulations of side-by-side mooring to an FPSO. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001. [Google Scholar]
- Dai, J.; Wang, C.M.; Utsunomiya, T.; Duan, W. Review of recent research and developments on floating breakwaters. Ocean Eng. 2018, 158, 132–151. [Google Scholar] [CrossRef]
- McCartney, B.L. Floating breakwater design. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 304–318. [Google Scholar] [CrossRef]
- Carver, R.D. Floating Breakwater Wave-Attenuation Tests for East Bay Marina, Olympia Harbor, Washington; Technical Report HL-79–13; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1979. [Google Scholar]
- Nece, R.E.; Richey, E.P. Wave Transmission Tests of Floating Breakwater for Oak Harbor. Water Resources Series; Technical Report No. 32; Department of Civil Engineering, University of Washington: Seattle, DC, USA, 1972. [Google Scholar]
- Ikeno, M.; Shimoda, N.; Iwata, K. A new type of breakwater utilizing air compressibility. In Proceedings of the 21st Coastal Engineering Conference, Torremolinos, Spain, 20–25 June 1988; pp. 2326–2339. [Google Scholar]
- Koo, W. Nonlinear time-domain analysis of motion-restrained pneumatic floating breakwater. Ocean Eng. 2009, 36, 723–731. [Google Scholar] [CrossRef]
- Allyn, N.; Watchorn, E.; Jamieson, W.W.; Yang, G. Port of Brownsville floating breakwater. In Proceedings of the Ports Conference, Norfolk, VA, USA, 29 April–2 May 2001; pp. 1–10. [Google Scholar]
- Ji, C.Y.; Chen, X.; Cui, J.; Yuan, Z.M.; Incecik, A. Experimental study of a new type of floating breakwater. Ocean Eng. 2015, 105, 295–303. [Google Scholar] [CrossRef]
- Candle, R.D. Goodyear scrap tire floating breakwater concepts. In Proceedings of the Floating Breakwaters Conference, Kingston, RI, USA, 23–25 April 1974; pp. 193–212. [Google Scholar]
- Kowalski, T. Scrap tire floating breakwaters. In Proceedings of the Floating Breakwater Conference, Kingston, RI, USA, 23–25 April 1974; pp. 233–246. [Google Scholar]
- Harms, V.W.; Westerink, J.J.; Sorensen, R.M.; McTamany, J.E. Wave Transmission and Mooring-Force Characteristics of Pipe-Tire Floating Breakwaters; Technical Paper 82–84; U.S. Army Coastal Engineering Research Center: Fairfax, VA, USA, 1982. [Google Scholar]
- Hegde, A.V.; Kamath, K.; Magadum, A.S. Performance characteristics of horizontal interlaced multilayer moored floating pipe breakwater. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 275–285. [Google Scholar] [CrossRef]
- Shugan, I.V.; Hwung, H.H.; Yang, R.Y.; Hsu, W.Y. Elastic plate as floating wave breaker in a beach zone. Phys. Wave Phenom. 2012, 20, 199–203. [Google Scholar] [CrossRef]
- Koley, S.; Sahoo, T. Oblique wave scattering by horizontal floating flexible porous membrane. Meccanica 2017, 52, 125–138. [Google Scholar] [CrossRef]
- Dong, G.H.; Zheng, Y.N.; Li, Y.C.; Teng, B.; Guan, C.T.; Lin, D.F. Experiments on wave transmission coefficients of floating breakwaters. Ocean Eng. 2008, 35, 931–938. [Google Scholar] [CrossRef]
- Takaki, M.; Fujikubo, M.; Higo, Y.; Hamada, K.; Kobayashi, M.; Nakagawa, H.; Morishita, S.; Ando, K.; Tanigami, A. A new type VLFS using submerged plates: Sub-plate VLFS. Part 1 Basic concept of system. In Proceedings of the 20th International Conference on Ocean, Rio de Janeiro, Brazil, 3–8 June 2001; pp. 3–8. [Google Scholar]
- Jones, D.B. An Assessment of Transportable Breakwaters with Reference to the Container Off-Loading and Transfer System (COTS); Technical Note No. N-1529; Civil Engineering Laboratory, Naval Construction Battalion Center: Gulfport, MS, USA, 1978. [Google Scholar]
- Hales, L.Z. Floating Breakwater: State-of-the-Art Literature Review; Technical Report No. 81-1; U.S. Army Coastal Engineering Research Center: Fairfax, VA, USA, 1981. [Google Scholar]
- Seymour, R.J.; Hanes, D.M. Performance analysis of tethered float breakwater. J. Waterw. Port Coast. Ocean Eng. 1979, 105, 265–280. [Google Scholar]
- Vethamony, P. Wave attenuation characteristics of a tethered float system. Ocean. Eng. 1995, 22, 111–129. [Google Scholar] [CrossRef]
- Ćatipović, I.; Čorić, V.; Veić, D. Calculation of floating crane natural frequencies based on linearized multibody dynamics equations. In Proceedings of the 30th International Conference on Ocean, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Ćatipović, I.; Čorić, V.; Radanović, J. An improved stiffness model for polyester mooring lines. Brodogradnja 2011, 62, 235–248. [Google Scholar]
- Lyu, B.; Wu, W.; Yao, W.; Wang, Y.; Zhang, Y.; Tang, D.; Yue, Q. Multibody dynamical modeling of the FPSO soft yoke mooring system and prototype validation. Appl. Ocean Res. 2019, 84, 179–191. [Google Scholar] [CrossRef]
- Parunov, J.; Čorak, M.; Pensa, M. Wave height statistics for seakeeping assessment of ships in the Adriatic Sea. Ocean Eng. 2011, 38, 1323–1330. [Google Scholar] [CrossRef]
- Bureau Veritas. HydroStar for Experts—User Manual; Bureau Veritas: Paris, France, 2018. [Google Scholar]



| Designation | Quantity | Unit |
|---|---|---|
| Length | 19.5 | m |
| Beam | 5.8 | m |
| Depth | 2.3 | m |
| Draught | 0.75 | m |
| Displacement | 87.4 | t |
| Vertical center of gravity | 0.62 | m |
| Roll radius of gyration | 6.03 | m |
| Pitch/yaw radius of gyration | 2.42 | m |
| Tabain Spectrum | ||||
| Significant Values | ||||
| Heave, m | Pitch, ° | Roll, ° | ||
| Hs = 1.1 m | elm. 1, β = 60° | 0.84 | 9.52 | 0.35 |
| elm. 2, β = 60° | 0.74 | 8.04 | 0.36 | |
| elm. 3, β = 60° | 0.90 | 8.24 | 0.36 | |
| elm. 1, β = 90° | 1.29 | 0.72 | 2.14 | |
| elm. 2, β = 90° | 1.27 | 0.00 | 2.14 | |
| elm. 3, β = 90° | 1.29 | 0.72 | 2.14 | |
| Hs = 1.2 m | elm. 1, β = 60° | 0.95 | 10.05 | 0.44 |
| elm. 2, β = 60° | 0.85 | 8.59 | 0.45 | |
| elm. 3, β = 60° | 1.01 | 8.73 | 0.45 | |
| elm. 1, β = 90° | 1.40 | 0.74 | 2.40 | |
| elm. 2, β = 90° | 1.38 | 0.00 | 2.40 | |
| elm. 3, β = 90° | 1.40 | 0.74 | 2.40 | |
| Hs = 1.3 m | elm. 1, β = 60° | 1.06 | 10.52 | 0.55 |
| elm. 2, β = 60° | 0.96 | 9.09 | 0.56 | |
| elm. 3, β = 60° | 1.11 | 9.18 | 0.56 | |
| elm. 1, β = 90° | 1.51 | 0.76 | 2.66 | |
| elm. 2, β = 90° | 1.50 | 0.00 | 2.66 | |
| elm. 3, β = 90° | 1.51 | 0.76 | 2.66 | |
| JONSWAP Spectrum | ||||
| Significant Values | ||||
| Heave, m | Pitch, ° | Roll, ° | ||
| Hs = 1.1 m | elm. 1, β = 60° | 0.71 | 10.90 | 0.28 |
| Tp = 3.8 s | elm. 2, β = 60° | 0.52 | 8.78 | 0.27 |
| elm. 3, β = 60° | 0.78 | 9.53 | 0.27 | |
| elm. 1, β = 90° | 1.36 | 0.98 | 1.89 | |
| elm. 2, β = 90° | 1.29 | 0.00 | 1.89 | |
| elm. 3, β = 90° | 1.36 | 0.98 | 1.89 | |
| Hs = 1.2 m | elm. 1, β = 60° | 0.83 | 11.62 | 0.31 |
| Tp = 4.0 s | elm. 2, β = 60° | 0.66 | 9.55 | 0.31 |
| elm. 3, β = 60° | 0.92 | 10.10 | 0.31 | |
| elm. 1, β = 90° | 1.47 | 0.95 | 2.16 | |
| elm. 2, β = 90° | 1.43 | 0.00 | 2.16 | |
| elm. 3, β = 90° | 1.47 | 0.95 | 2.16 | |
| Hs = 1.3 m | elm. 1, β = 60° | 0.95 | 12.15 | 0.33 |
| Tp = 4.2 s | elm. 2, β = 60° | 0.80 | 10.13 | 0.33 |
| elm. 3, β = 60° | 1.04 | 10.48 | 0.33 | |
| elm. 1, β = 90° | 1.57 | 0.91 | 2.43 | |
| elm. 2, β = 90° | 1.55 | 0.00 | 2.43 | |
| elm. 3, β = 90° | 1.57 | 0.91 | 2.43 | |
| Tabain Spectrum | |||||
| Wave Direction, ° | Hs, m | Ht, m | Attenuation, % | ||
| 60 | 1.1 | 0.86 | 28.4 | ||
| 60 | 1.2 | 0.98 | 22.4 | ||
| 60 | 1.3 | 1.10 | 18.0 | ||
| 90 | 1.1 | 0.97 | 13.8 | ||
| 90 | 1.2 | 1.08 | 11.3 | ||
| 90 | 1.3 | 1.19 | 9.4 | ||
| JONSWAP Spectrum | |||||
| Wave direction, ° | Hs, m | Tp, s | Ht, m | Attenuation, % | |
| 60 | 1.1 | 3.8 | 0.60 | 45.5 | |
| 60 | 1.2 | 4.0 | 0.77 | 36.2 | |
| 60 | 1.3 | 4.2 | 0.93 | 28.6 | |
| 90 | 1.1 | 3.8 | 0.83 | 24.4 | |
| 90 | 1.2 | 4.0 | 0.98 | 18.0 | |
| 90 | 1.3 | 4.2 | 1.12 | 13.7 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ćatipović, I.; Ćorak, M.; Alujević, N.; Parunov, J. Dynamic Analysis of an Array of Connected Floating Breakwaters. J. Mar. Sci. Eng. 2019, 7, 298. https://doi.org/10.3390/jmse7090298
Ćatipović I, Ćorak M, Alujević N, Parunov J. Dynamic Analysis of an Array of Connected Floating Breakwaters. Journal of Marine Science and Engineering. 2019; 7(9):298. https://doi.org/10.3390/jmse7090298
Chicago/Turabian StyleĆatipović, Ivan, Maro Ćorak, Neven Alujević, and Joško Parunov. 2019. "Dynamic Analysis of an Array of Connected Floating Breakwaters" Journal of Marine Science and Engineering 7, no. 9: 298. https://doi.org/10.3390/jmse7090298
APA StyleĆatipović, I., Ćorak, M., Alujević, N., & Parunov, J. (2019). Dynamic Analysis of an Array of Connected Floating Breakwaters. Journal of Marine Science and Engineering, 7(9), 298. https://doi.org/10.3390/jmse7090298






