The Performance of Low-Pressure Seawater as a CO2 Solvent in Underwater Air-Independent Propulsion Systems
Abstract
:1. Introduction
2. Experimental Setup and Procedure
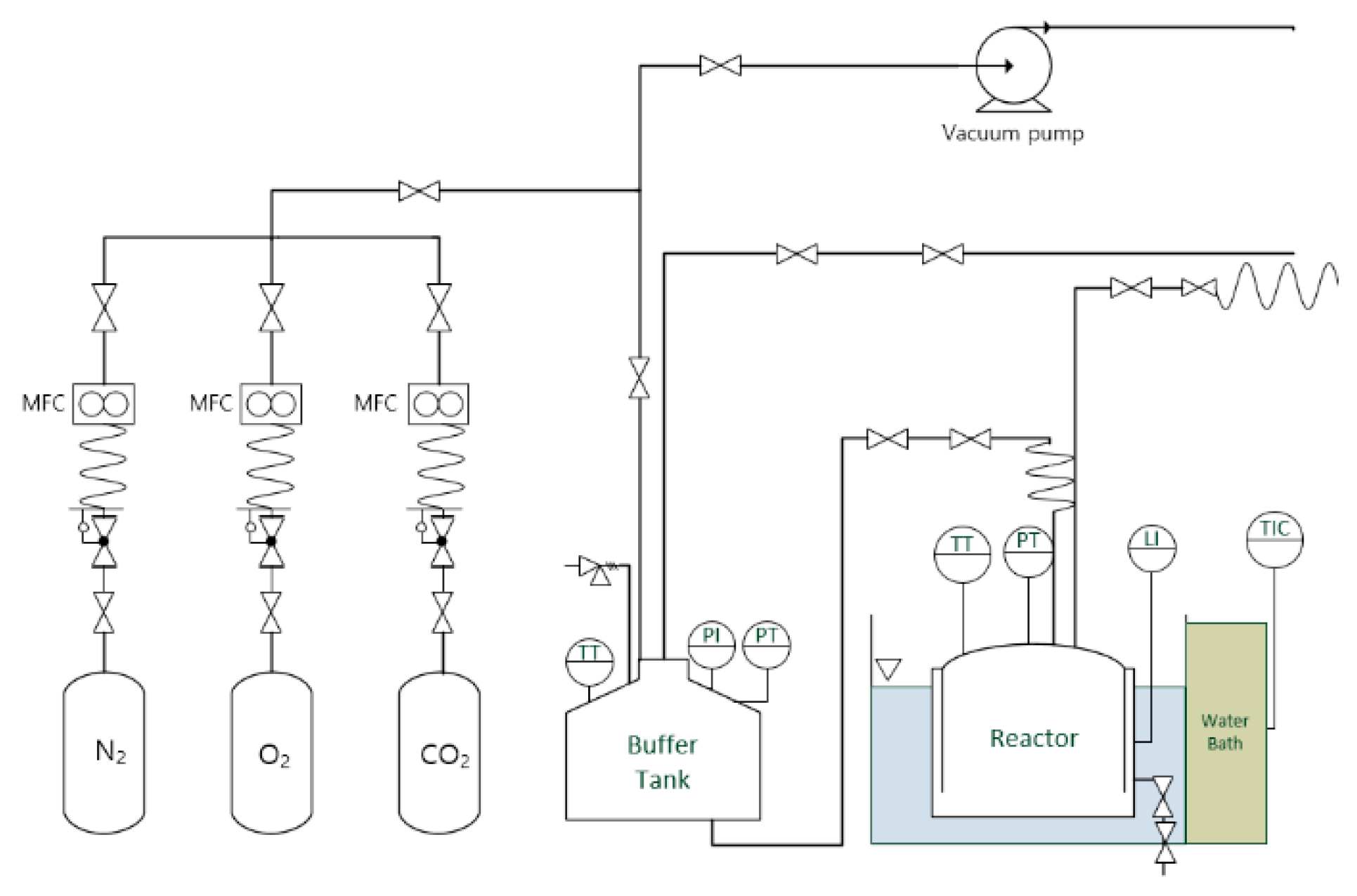
2.1. Experimental Setup
2.2. Experimental Procedure
2.3. Amount of Gas Dissolved as a Function of Pressure and Temperature
3. Modelling Equations
3.1. Governing Equation
3.2. Liquid-Phase Equation
- = molar flux of A, mol·cm−2·s−1;
- = gas-phase mass transfer coefficient, (mol flue gas)·cm−2·s−1·atm−1;
- = liquid-phase mass transfer coefficient, cm·s−1;
- = bulk gas-phase mole fraction of A, mol A/mol flue gas;
- = interfacial gas-phase mole fraction of A, mol Ai/mol flue gas;
- = Total pressure, atm;
- = bulk liquid-phase concentration of A, mol A·cm−3;
- = interfacial liquid-phase concentration of A, mol Ai·cm−3.
- Heat transfer by conduction and radiation can be ignored in the axial direction;
- Henry’s law is applicable to the CO2 solubility in the liquid phase;
- Absorption reactions occur only in liquids;
- Vaporization of liquids does not occur;
- The reactor is adiabatic.
3.3. Sensitivity Analysis
4. Results and Discussion
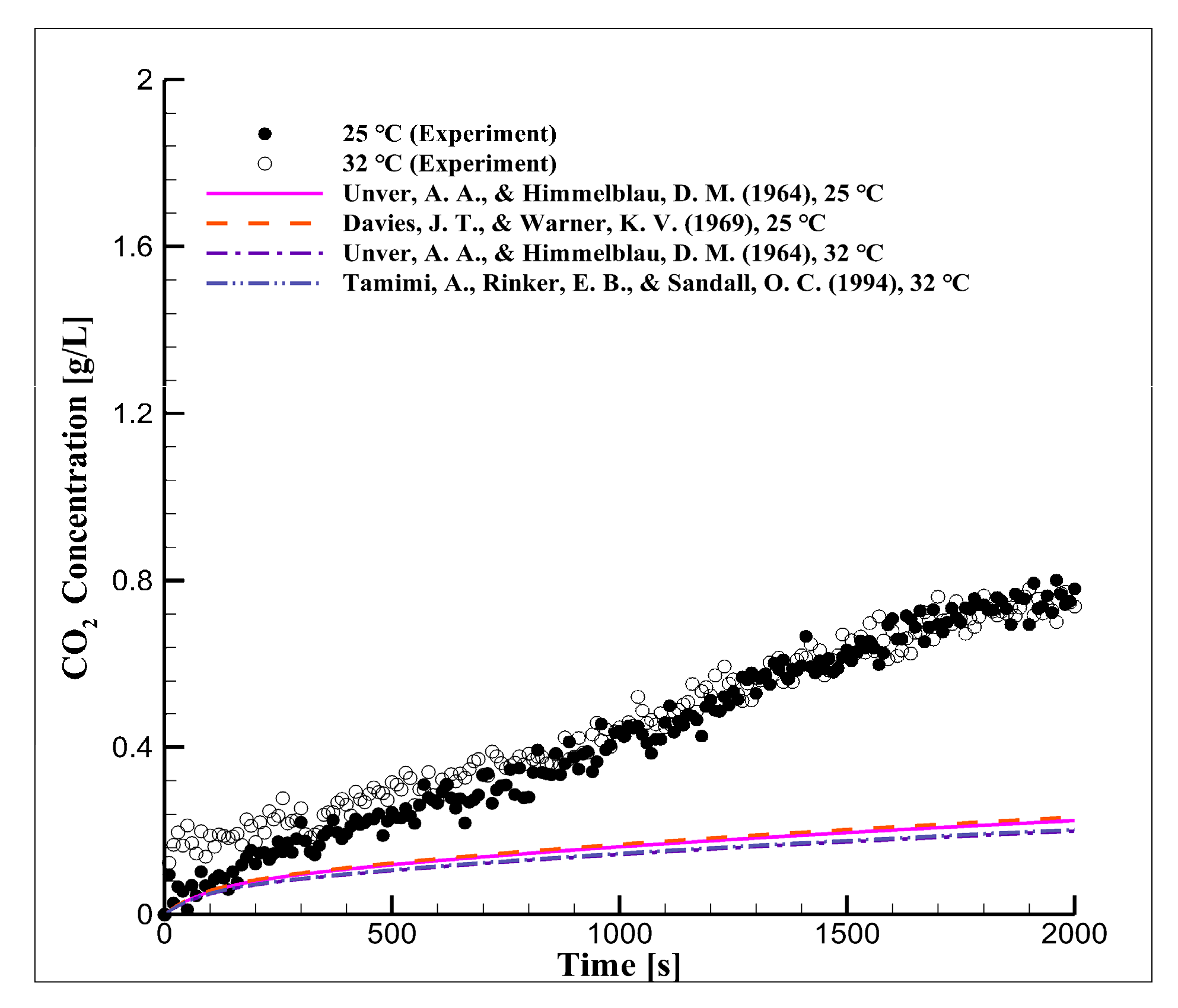
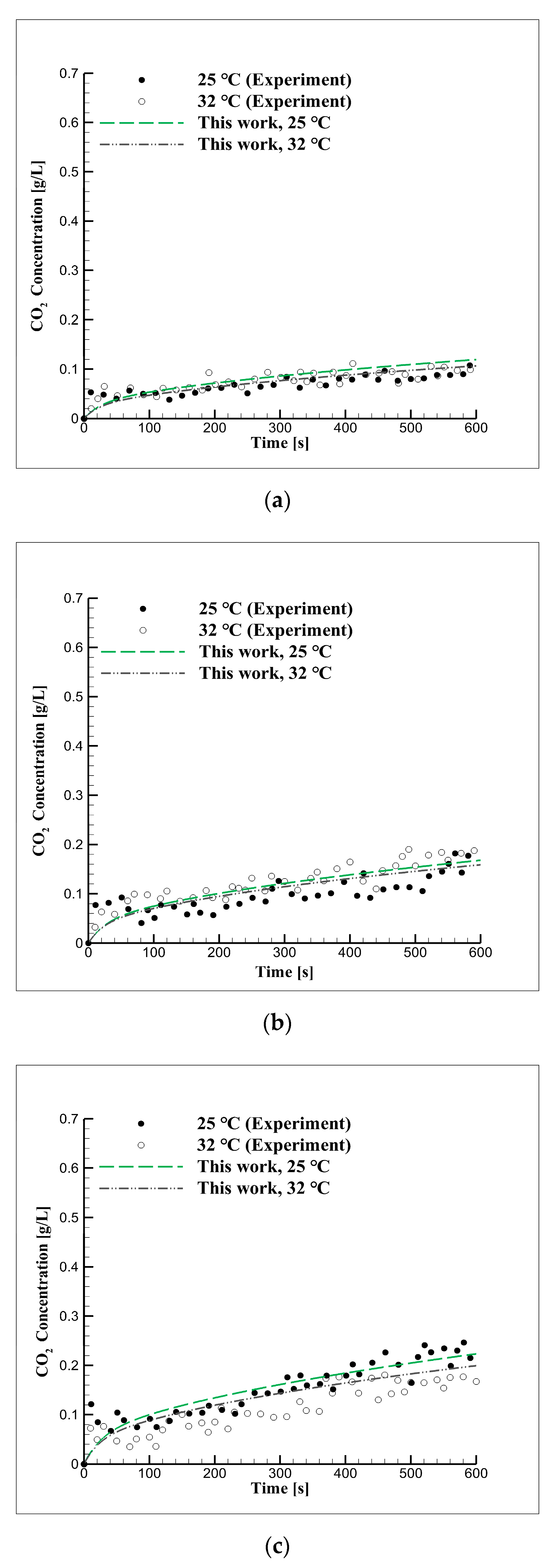
4.1. Long-Term Reaction Characteristics Using Distilled Water
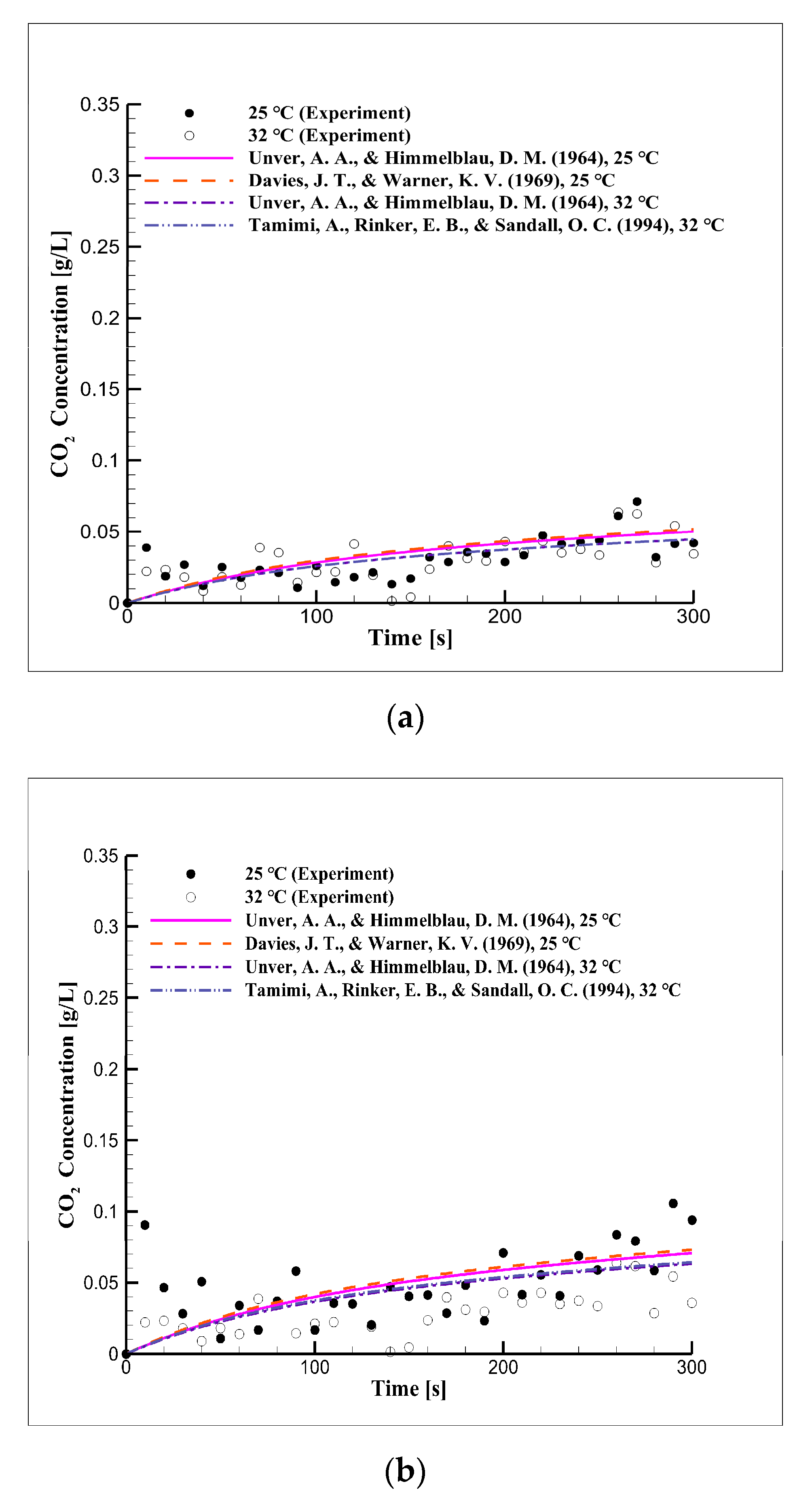
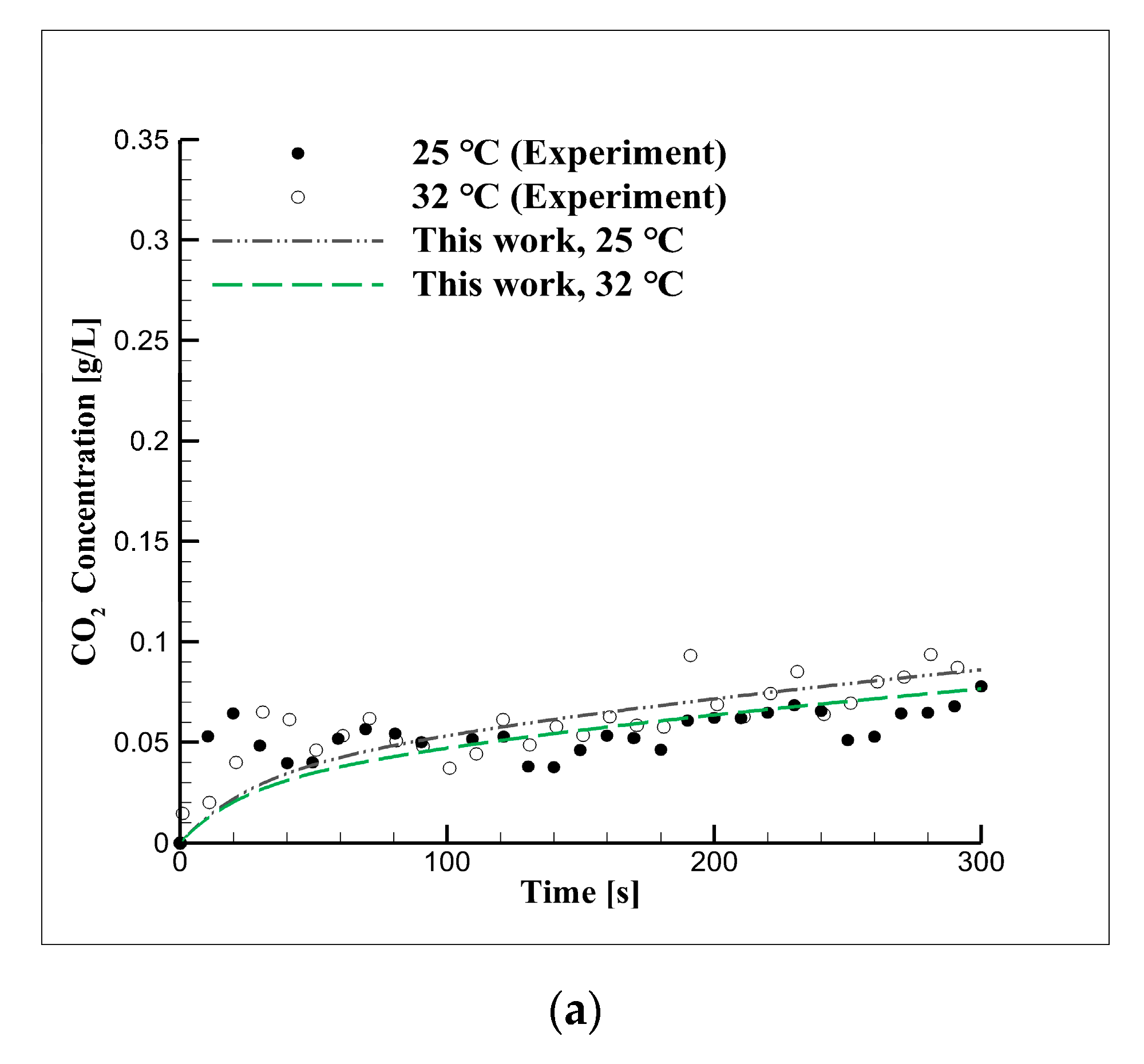
4.2. Short-Term Reaction Characteristics Using Distilled Water
4.3. Experimental Approach Considering Concentration in Distilled Water
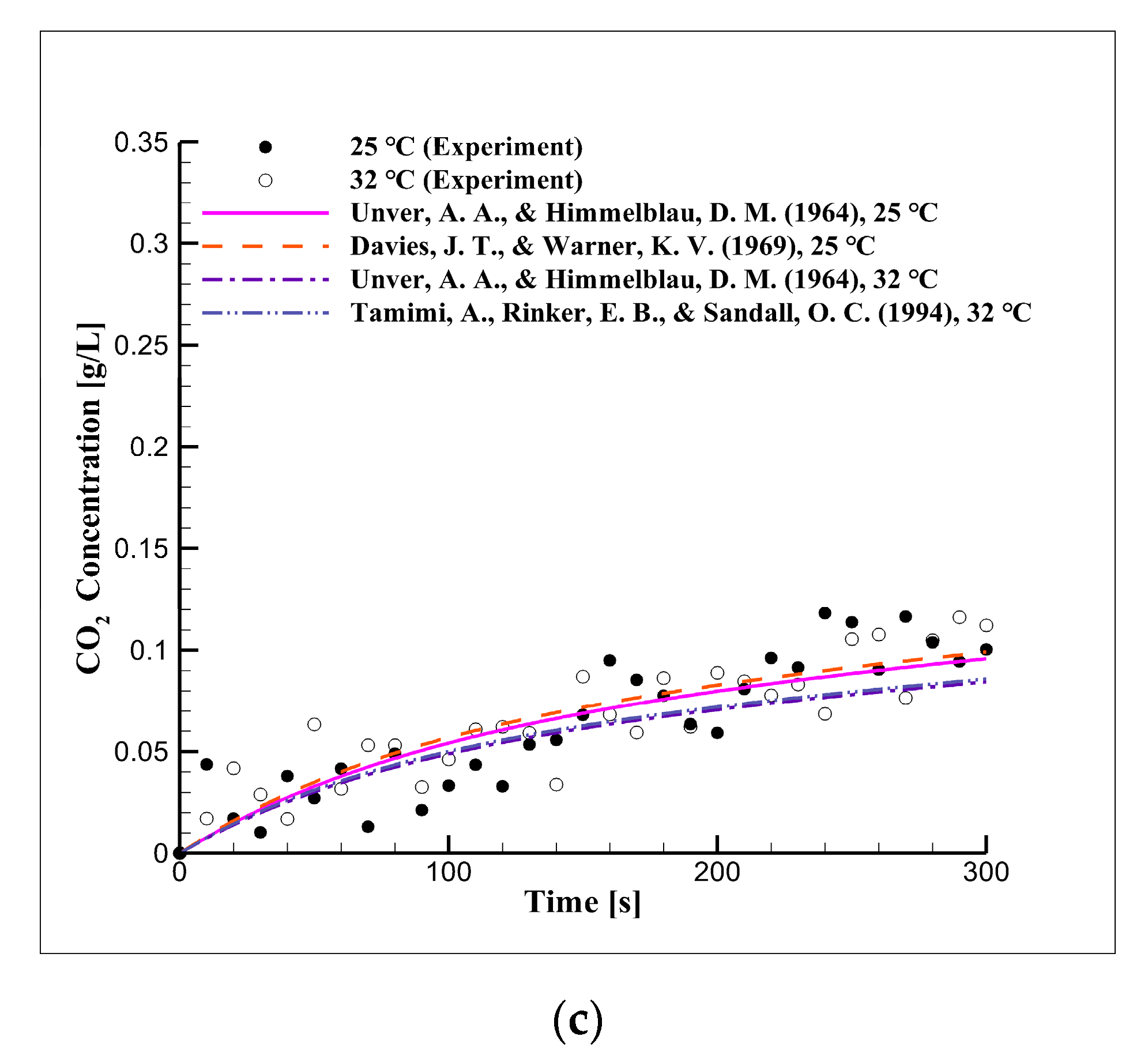
4.4. Mid-Term Reaction Characteristics Using Distilled Water
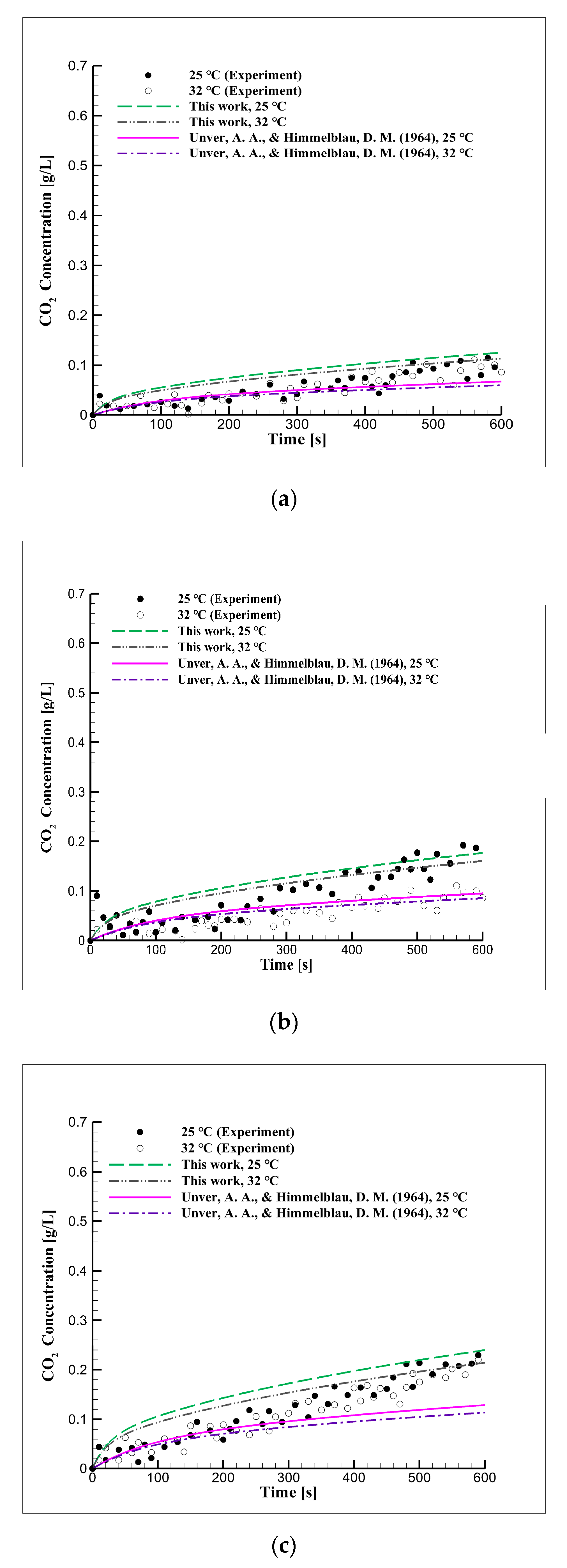
4.5. Experimental Approach Considering Concentration in Seawater
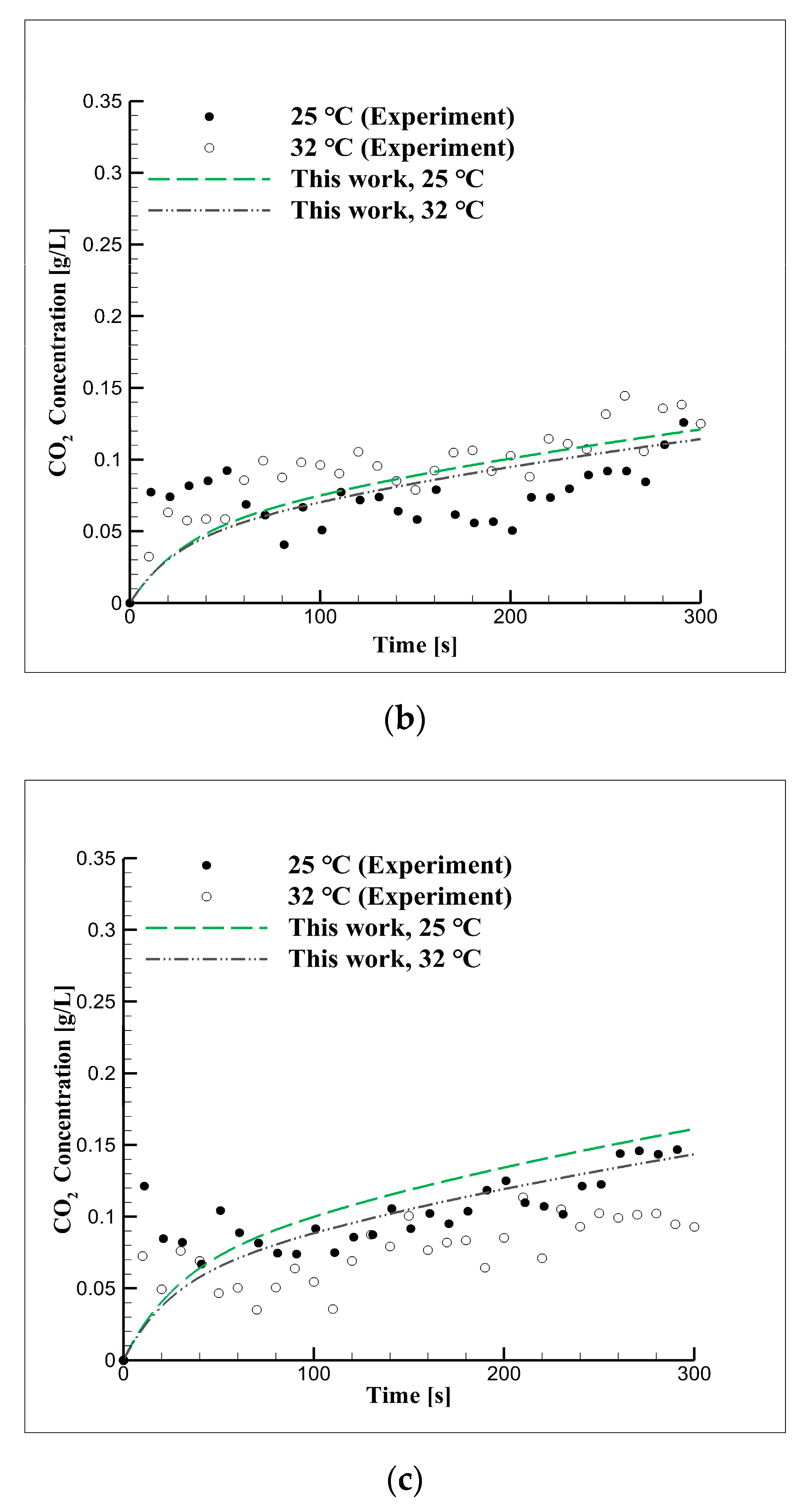
4.6. Short-Term Reaction Characteristics in Seawater
4.7. Mid-Term Reaction Characteristics in Seawater
5. Conclusions
- (1)
- For the treatment of the residual gas generated in the reformer, the concentration of CO2, a residual gas component, was observed at different pressures and temperatures from the perspective of dissolution using seawater and the CO2 diffusion coefficient was derived through numerical analysis using MATLAB;
- (2)
- It was confirmed that the experimental time, temperature, and pressure could be variables in selecting the CO2 diffusion coefficient for each solvent;
- (3)
- The CO2 concentration in seawater was approximately 55% higher when the equilibrium pressure was 5 bar and the reaction temperature was 25 °C than when these parameters were 2 bar and 32 °C;
- (4)
- Under the actual operating conditions of underwater weapon systems, the CO2 diffusion coefficient in distilled water and seawater, according to the dissolution time, was derived by temperature. The CO2 diffusion coefficient in seawater was 6.3 × 10−5 cm2/s at 25 °C and 7.24 × 10−5 cm2/s at 32 °C. The CO2 diffusion coefficient was approximately 13% higher at 32 °C than at 25 °C;
- (5)
- It is possible to accurately estimate the concentration of CO2, a residual gas component of the reformer, under the operating conditions of each vessel using the derived CO2 diffusion coefficient as a function of temperature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Psoma, A.; Sattler, G. Fuel cell systems for submarines: from the first idea to serial production. J. Power Sources 2002, 106, 381–383. [Google Scholar] [CrossRef]
- Brighton, D.R.; Mart, P.L.; Clark, G.A.; Rowan, M.J.M. The use of fuel cells to enhance the underwater performance of conventional diesel electric submarines. J. Power Sources 1994, 51, 375–389. [Google Scholar] [CrossRef]
- Rostami, H.; Zhiani, M.; Zamani, A.R.; Madhkhan, M. Fuel cells application in subsea industries. In Proceedings of the 3rd Fuel Cell Seminar of Iran, Tehran, Iran, 28 October 2009. [Google Scholar]
- Krummrich, S.; Llabrés, J. Methanol reformer–The next milestone for fuel cell powered submarines. Int. J. Hydrog. Energ. 2015, 40, 5482–5486. [Google Scholar] [CrossRef]
- Cavenati, S.; Grande, C.A.; Rodrigues, A.E. Adsorption equilibrium of methane, carbon dioxide, and nitrogen on zeolite 13X at high pressures. J. Chem. Eng. Data 2004, 49, 1095–1101. [Google Scholar] [CrossRef]
- Dash, S.K.; Samanta, A.N.; Bandyopadhyay, S.S. Experimental and theoretical investigation of solubility of carbon dioxide in concentrated aqueous solution of 2-amino-2-methyl-1-propanol and piperazine. J. Chem. Thermodyn. 2012, 51, 120–125. [Google Scholar] [CrossRef]
- Manic, M.S.; Queimada, A.J.; Macedo, E.A.; Najdanovic-Visak, V. High-pressure solubilities of carbon dioxide in ionic liquids based on bis (trifluoromethylsulfonyl) imide and chloride. J. Supercrit. Fluid. 2012, 65, 1–10. [Google Scholar] [CrossRef]
- Hirai, S.; Okazaki, K.; Araki, N.; Yazawa, H.; Ito, H.; Hijikata, K. Transport phenomena of liquid CO2 in pressurized water flow with clathrate-hydrate at the interface. Energ. Conserv. Manag. 1996, 37, 1073–1078. [Google Scholar] [CrossRef]
- Dang, H.; Rochelle, G.T. CO2 absorption rate and solubility in monoethanolamine/piperazine/water. Sep. Sci. Technol. 2003, 38, 337–357. [Google Scholar] [CrossRef]
- Faiz, R.; Al-Marzouqi, M. CO2 removal from natural gas at high pressure using membrane contactors: model validation and membrane parametric studies. J. Membr. Sci. 2010, 365, 232–241. [Google Scholar] [CrossRef]
- Lawal, A.; Wang, M.; Stephenson, P.; Yeung, H. Dynamic modelling of CO2 absorption for post combustion capture in coal-fired power plants. Fuel 2009, 88, 2455–2462. [Google Scholar] [CrossRef] [Green Version]
- Munusamy, K.; Sethia, G.; Patil, D.V.; Rallapalli, P.B.S.; Somani, R.S.; Bajaj, H.C. Sorption of carbon dioxide, methane, nitrogen and carbon monoxide on MIL-101 (Cr): Volumetric measurements and dynamic adsorption studies. Chem. Eng. J. 2012, 195, 359–368. [Google Scholar] [CrossRef]
- Breault, R.W.; Huckaby, E.D. Parametric behavior of a CO2 capture process: CFD simulation of solid-sorbent CO2 absorption in a riser reactor. Appl. Energy 2013, 112, 224–234. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, Y.; Zhang, L.; Chen, Y.; Ju, S. CFD investigation of CO2 capture by methyldiethanolamine and 2-(1-piperazinyl)-ethylamine in membranes: Part B. Effect of membrane properties. J. Nat. Gas Sci. Eng. 2014, 19, 311–316. [Google Scholar] [CrossRef]
- Giammanco, C.H.; Kramer, P.L.; Yamada, S.A.; Nishida, J.; Tamimi, A.; Fayer, M.D. Carbon dioxide in an ionic liquid: Structural and rotational dynamics. J. Chem. Phys. 2016, 144, 104506. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Pham, D.A.; Lim, Y.I. Gas−liquid multiphase computational fluid dynamics (CFD) of amine absorption column with structured-packing for CO2 capture. Comput. Chem. Eng. 2016, 88, 39–49. [Google Scholar] [CrossRef]
- Standard Practice for the Preparation of Substitute Ocean Water (ASTM D1141-98); ASTM International: West Conshohocken, PA, USA, 1998.
- Liu, S.; Kvamme, B. Improved Newton Raphson Method–An Effective Tool in Solving Flow-Mechanic-Chemistry Equations of CO2 Storage in Saline Aquifers. In Proceedings of the American Conference on Applied Mathematics (MATH 08), Harvard, MA, USA, 24–26 March 2008. [Google Scholar]
- Jiang, N.; Deng, Z.; Liu, S.; Tang, C.; Wang, G. Synthesis of metal organic framework (MOF-5) with high selectivity for CO2/N2 separation in flue gas by maximum water concentration approach. Korean J. Chem. Eng. 2016, 33, 2747–2755. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.; Zhao, Y.; Chen, L.; Dong, C.; Sun, B. Experimental investigation of different factors influencing the replacement efficiency of CO2 for methane hydrate. Appl. Energy 2018, 228, 309–316. [Google Scholar] [CrossRef]
- Westerwalbesloh, C.; Grünberger, A.; Stute, B.; Weber, S.; Wiechert, W.; Kohlheyer, D.; von Lieres, E. Modeling and CFD simulation of nutrient distribution in picoliter bioreactors for bacterial growth studies on single-cell level. Lab Chip 2015, 15, 4177–4186. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Yang, H.; Lu, L.; Qi, R. A review of the mathematical models for predicting the heat and mass transfer process in the liquid desiccant dehumidifier. Renew. Sustain. Energy Rev. 2014, 31, 587–599. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Lai, C.; Sun, X. Beyond the standard two-film theory: Computational fluid dynamics simulations for carbon dioxide capture in a wetted wall column. Chem. Eng. Sci. 2018, 184, 103–110. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, J.; Tang, A.; Wang, Q. A study on mass transfer–reaction kinetics of NO absorption by using UV/H2O2/NaOH process. Fuel 2013, 108, 254–260. [Google Scholar] [CrossRef]
- Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. Gas–liquid and liquid–liquid mass transfer in microstructured reactors. Chem. Eng. Sci. 2011, 66, 3876–3897. [Google Scholar] [CrossRef]
- Fu, K.; Chen, G.; Sema, T.; Zhang, X.; Liang, Z.Z.; Idem, R.; Tontiwachwuthikul, P. Experimental study on mass transfer and prediction using artificial neural network for CO2 absorption into aqueous DETA. Chem. Eng. Sci. 2013, 100, 195–202. [Google Scholar] [CrossRef]
- Ma, S.; Chen, G.; Zhu, S.; Han, T.; Yu, W. Mass transfer of ammonia escape and CO2 absorption in CO2 capture using ammonia solution in bubbling reactor. Appl. Eng. 2016, 162, 354–362. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef] [Green Version]
- Harvey, A.H.; Smith, F.L. Avoid common pitfalls when using Henry’s law. Chem. Eng. Prog. 2007, 103, 33–39. [Google Scholar]
- Dalmolin, I. Solubility of carbon dioxide in binary and ternary mixtures with ethanol and water. Fluid Phase Equilibria 2006, 245, 193–200. [Google Scholar] [CrossRef]
- Weiss, R.F. Carbon dioxide in water and seawater: the solubility of a non-ideal gas. Mar. Chem. 1974, 2, 203–215. [Google Scholar] [CrossRef]
- Hirai, S.; Okazaki, K.; Yazawa, H.; Ito, H.; Tabe, Y.; Hijikata, K. Measurement of CO2 diffusion coefficient and application of LIF in pressurized water. Energy 1997, 22, 363–367. [Google Scholar] [CrossRef]
- Frank, M.J.W.; Kuipers, J.A.M.; van Swaaij, W.P. Diffusion coefficients and viscosities of CO2 + H2O, CO2 + CH3OH, NH3 + H2O, and NH3+ CH3OH liquid mixtures. J. Chem. Eng. Data 1996, 41, 297–302. [Google Scholar] [CrossRef] [Green Version]
- Witherspoon, P.A.; Saraf, D.N. Diffusion of methane, ethane, propane, and n-butane in water from 25 to 43. J. Phys. Chem. 1965, 69, 3752–3755. [Google Scholar] [CrossRef]
- Tang, Y.P.; Himmelblau, D.M. Effect of solute concentration on the diffusivity of carbon dioxide in water. Chem. Eng. Sci. 1965, 20, 7–14. [Google Scholar] [CrossRef]
- Shi, Z.; Wen, B.; Hesse, M.A.; Tsotsis, T.T.; Jessen, K. Measurement and modeling of CO2 mass transfer in brine at reservoir conditions. Adv. Water Res. 2018, 113, 100–111. [Google Scholar] [CrossRef]
- Unver, A.A.; Himmelblau, D.M. Diffusion coefficients of CO2, C2H4, C3H6 and C4H8 in water from 6 to 65 C. J. Chem. Eng. Data 1964, 9, 428–431. [Google Scholar] [CrossRef]
- Thomas, W.J.; Adams, M.J. Measurement of the diffusion coefficients of carbon dioxide and nitrous oxide in water and aqueous solutions of glycerol. Trans. Faraday Soc. 1965, 61, 668–673. [Google Scholar] [CrossRef]
- Tamimi, A.; Rinker, E.B.; Sandall, O.C. Diffusion coefficients for hydrogen sulfide, carbon dioxide, and nitrous oxide in water over the temperature range 293-368 K. J. Chem. Eng. Data 1994, 39, 330–332. [Google Scholar] [CrossRef]
- Nijsing, R.A.T.O.; Hendriksz, R.H.; Kramers, H. Absorption of CO2 in jets and falling films of electrolyte solutions, with and without chemical reaction. Chem. Eng. Sci. 1959, 10, 88–104. [Google Scholar] [CrossRef]
- Renner, T.A. Measurement and correlation of diffusion coefficients for CO2 and rich-gas applications. SPE Reserv. Eng. 1988, 3, 517–523. [Google Scholar] [CrossRef]
- Wang, L.-S.; Lang, Z.-X.; Guo, T.-M. Measurement and correlation of the diffusion coefficients of carbon dioxide in liquid hydrocarbons under elevated pressures. Fluid Phase Equilibria 1996, 117, 364–372. [Google Scholar] [CrossRef]
- Yang, C.; Gu, Y. Accelerated mass transfer of CO2 in reservoir brine due to density-driven natural convection at high pressures and elevated temperatures. Ind. Eng. Chem. Res. 2006, 45, 2430–2436. [Google Scholar] [CrossRef]
- Azin, R.; Mahmoudy, M.; Raad, S.M.J.; Osfouri, S. Measurement and modeling of CO2 diffusion coefficient in saline aquifer at reservoir conditions. Cent. Eur. J. Eng. 2013, 3, 585–594. [Google Scholar] [CrossRef]
- Mojtaba, S.; Behzad, R.; Rasoul, N.M.; Mohammad, R. Experimental study of density-driven convection effects on CO2 dissolution rate in formation water for geological storage. J. Nat. Gas Sci. Eng. 2014, 21, 600–607. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, S.; Ren, S.; Zhang, L.; Li, J. The modeling and experimental studies on the diffusion coefficient of CO2 in saline water. J. CO2 Util. 2015, 11, 49–53. [Google Scholar] [CrossRef]
- Zeebe, R.E. On the molecular diffusion coefficients of dissolved CO2, HCO3−, and CO32− and their dependence on isotopic mass. Geochim. Cosmochim. Acta 2001, 75, 2483–2498. [Google Scholar] [CrossRef]
| Gas Composition | Gas Concentration (%) | Absorbents | Temperature (°C) | Pressure (bar) |
|---|---|---|---|---|
| CO2 | More than 99.8 | Distilled water | 25, 32 | 2, 3, 5 |
| Sea water |
| Compound | Concentration (g/L) |
|---|---|
| NaCl | 24.53 |
| MgCl2 | 5.20 |
| Na2SO4 | 4.09 |
| CaCl2 | 1.16 |
| KCl | 0.695 |
| NaHCO3 | 0.201 |
| KBr | 0.101 |
| H3BO3 | 0.027 |
| SrCl2 | 0.025 |
| NaF | 0.003 |
| Scenario | Mesh Size (m) | Reactor P (bar) | Sensitivity (%) |
|---|---|---|---|
| Case 1 | 0.00384 | 4.373 | 24.25 |
| Case 2 | 0.00192 | 4.369 | 15.98 |
| Case 3 | 0.00096 | 4.366 | 6.75 |
| Case 4 | 0.00048 | 4.364 | 4.39 |
| Case 5 | 0.00024 | 4.363 | 1.99 |
| Case 6 | 0.00012 | 4.362 | - |
| Source | Method | Solution | Temperature (°C) | Diffusion Coefficient (10−5 cm2/s) |
|---|---|---|---|---|
| Tang and Himmelblau [35] | Jet | Water | 25 | 1.92 |
| Unver and Himmelblau [37] | Jet | Water | 6.5–65 | 1.145–4.296 |
| Thomas and Adams [38] | Jet | Water | 18.5–75.1 | 1.65–5.40 |
| Tamimi et al. [39] | - | Water | 20–80 | 1.76–8.20 |
| Source | Solution | Pressure (kPa) | Temperature (°C) | Diffusion Coefficient (10−5 cm2/s) |
|---|---|---|---|---|
| Renner [41] | Brine | 2186–5861 | 25 | 9.07–9.86 |
| Wang et al. [42] | Brine | 1524–5178 | 38 | 2.93–4.83 |
| Yang C and Gu [43] | Brine | 2600–7500 | 27–58 | 170.7–269.8 |
| Azin et al. [44] | Brine | 5858–6898 | 40–45 | 3.52–6.16 |
| Mojtaba et al. [45] | Brine | 3450 | 38 | 1.75 |
| Zhang et al. [46] | Brine | 1170 | 25 | 1.5–1.91 |
| Diffusion Coefficient (10−5 cm2/s) | ||||
|---|---|---|---|---|
| Distilled Water | Seawater | |||
| 25 °C | 32 °C | 25 °C | 32 °C | |
| Reference | 1.85–2.0 | 2.08–2.16 | - | - |
| Experiment | 7.06 | 8.56 | 6.3 | 7.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, E.-Y.; Choi, J. The Performance of Low-Pressure Seawater as a CO2 Solvent in Underwater Air-Independent Propulsion Systems. J. Mar. Sci. Eng. 2020, 8, 22. https://doi.org/10.3390/jmse8010022
Park E-Y, Choi J. The Performance of Low-Pressure Seawater as a CO2 Solvent in Underwater Air-Independent Propulsion Systems. Journal of Marine Science and Engineering. 2020; 8(1):22. https://doi.org/10.3390/jmse8010022
Chicago/Turabian StylePark, Eun-Young, and Jungho Choi. 2020. "The Performance of Low-Pressure Seawater as a CO2 Solvent in Underwater Air-Independent Propulsion Systems" Journal of Marine Science and Engineering 8, no. 1: 22. https://doi.org/10.3390/jmse8010022
APA StylePark, E.-Y., & Choi, J. (2020). The Performance of Low-Pressure Seawater as a CO2 Solvent in Underwater Air-Independent Propulsion Systems. Journal of Marine Science and Engineering, 8(1), 22. https://doi.org/10.3390/jmse8010022





