Ultimate Image Singularities in Oblate Spheroidal Coordinates with Applications in Hydrodynamics

Abstract

This study exploits the Touvia Miloh oblate spheroid theorem with a special focus on hydrodynamical applications. The theorem provides explicit relations that express the oblate spheroidal harmonics, given in terms of the fundamental solutions of the Laplace equation. Here, the theorem is employed to transform the underlying Green’s function into the relevant coordinate system and, consequently, to formulate the diffraction potential. The case considered refers to the axisymmetric placement of the spheroid, namely, symmetrical axis perpendicular to the free surface. The mathematical formulations have been implemented numerically providing exceptionally accurate computations, which manifests the consistency and robustness of the relevant formulas.

1. Introduction

The image system of singularities in oblate spheroidal coordinates mirrors an arbitrary exterior potential within a triaxial oblate spheroid. Briefly, it provides a singular (within the spheroid) oblate spheroidal harmonic in terms of the fundamental solution of the Laplace equation to the exterior of the spheroid. The relevant formula, provided that is available, is of paramount importance, since it allows the analytic elaboration of three-dimensional boundary value problems associated with the concerned geometry. In fact, the task undertaken herein is focused on a relevant challenge, namely, the solution of the hydrodynamic diffraction problem by fully immersed oblate spheroids, in a liquid field of infinite depth and under the action of monochromatic incident waves.

Relevant efforts on image singularity systems in orthotropic geometries started in the 40s and 50s with the sphere theorem [1,2,3]. In addition, Hobson [4] provided an expression for spherical harmonics in terms of singularities (sources, doublets, or multipoles) at the center of the sphere. Image singularities of spheroidal shapes were considered by Havelock [5], who developed an integro-differential operator for the ultimate image singularity system of the prolate spheroid, without, however, a proof for the theorem. The proof was accordingly given by Miloh [6], who showed the validity of Havelock’s [5] prolate spheroid theorem. The concerned theorem was accordingly employed in a series of studies by Chatjigeorgiou and Miloh [7,8,9,10,11], who tackled both diffraction/radiation and wave resistance problems by immersed prolate spheroids and in particular the non-axisymmetric case, where the spheroid’s axisymmetric axis is parallel to the undisturbed free surface. Miloh’s [6] study was extended to consider the ultimate image singularity systems by triaxial ellipsoids for both sources and doublets. The relevant formulas, however, were never rigorously employed to realistic boundary value problems involving ellipsoids, with the only exception being the preliminary study of Chatjigeorgiou et al. [12]. A major drawback in that respect is the lack of an explicit formula to expand exponents into series of ellipsoidal harmonics (products of Lamé functions), while the numerical approximation appears to be problematic.

Although ultimate image singularity system theorems indeed exist for spheres, prolate spheroids, and ellipsoids involving the associated harmonics, there was a lack of information regarding the oblate spheroid case. Only recently Chatjigeorgiou [13] reported in his book on analytical hydrodynamics, a relevant theorem including the proof given by Miloh himself. Nevertheless, this theorem was never implemented for a realistic boundary value problem involving solids of oblate spheroidal geometry. This glitch is remediated herein.

Here, we implement for the first time the oblate ultimate image singularity theorem, developed by Miloh himself and reported by Chatjigeorgiou [13], for a spheroid, immersed in a liquid field of infinite depth. Only the axisymmetric case is considered, i.e., the axis of symmetry is perpendicular to the free surface, and, accordingly, the asymmetric case of the theorem (and the proof) is omitted for brevity. The corresponding formula is, then, employed to transform the fundamental Green’s function that governs the hydrodynamic boundary value problem in order to obtain the auxiliary multipoles and construct the diffraction potentials. The unknown expansion coefficients of these functions are obtained by employing the velocity conditions on the surface of the solid. Simple, compact formulas are accordingly obtained for the hydrodynamic exciting loads. Also, comparisons are made with calculations obtained using the respected Boundary Integral Equation code WAMIT [14] and remarkable coincidence is observed.

The derivation of an efficient methodology for the analytic elaboration of relevant hydrodynamic problems is extremely important as it ensures the realization of numerical computations in practically ‘no time’. The same methodology can be further extended and utilized for semi-immersed spheroids or groups of simultaneously operating (and interacting) solids. The importance of the latter capability is paramount as oblate spheroids are very promising as wave energy converters.

2. Oblate Spheroidal Coordinates

Here, we provide the basic notations that will be used throughout this study. Figure 1 shows the geometry of an oblate spheroid. In the case study of the hydrodynamic applications, the vertical $z$-axis of symmetry will be assumed perpendicular to the undisturbed free surface. This case of placement is referred to as the case of symmetry, since it is connected with symmetrical (with respect to $z$) flow around the solid. The transformation between Cartesian and oblate spheroidal coordinates reads (e.g., [15]):

$$x=c\cosh u\sin \theta \cos \psi ,$$

(1)

$$y=c\cosh u \sin \theta \sin \psi ,$$

(2)

$$z=c\sinh u\cos \theta ,$$

(3)

where $0\le u<\infty$, $0\le \theta \le \pi$, $0\le \psi \le 2\pi$ and $c$ is the half-distance between the foci given by $c=\sqrt{a^2-b^2}$, where $a, b$ denote the semi-major and the semi-minor axes of the spheroid, respectively. Using $\xi =\sinh u$ and $\mu =\cos \theta$ one gets:

$$x+iy=c\sqrt{\left(1+{\xi }^2\right)\left(1-{\mu }^2\right)}{e}^{i\psi }, z=c\mu \xi , R=c\sqrt{\left(1+{\xi }^2\right)\left(1-{\mu }^2\right)}$$

(4)

3. Ultimate Image Singularities in Oblate Spheroidal Coordinates

The so-call image singularity system in the associated coordinates provides an external spheroidal harmonic in terms of the fundamental solution of the Laplace equation. Having achieved that, it is feasible to transform the underlying Green’s function, which governs the investigated boundary value problem, into the concerned coordinates. The analysis that follows starts with the theorem that delivers the general expression of an external oblate spheroidal harmonic. Here, we consider only the symmetrical case with respect to $z$.

The theorem that proves the expression sought, for both symmetry and asymmetry, can be found in a recent book of the first author of this paper [13].

Theorem 1.

An even (in $z$) external oblate spheroidal harmonic may be generated by source distribution over the fundamental disk of the spheroid as:

$$Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi =\frac{{\left(-1\right)}^m}{2\pi P_n^m\left(i0\right)} \frac{\left(n+m\right)!}{\left(n-m\right)!}\underset{0}{\overset{2\pi }{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}\frac{P_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+z^2}}d{\mu }^{\prime }d{\psi }^{\prime },$$

(5)

where$P_n^m$and$Q_n^m$are the associate Legendre functions of the first and the second kind, respectively, and$n-m$is even as required by the symmetrical (in$z$) case. Note that the argument of$Q_n^m$is imaginary, while$\left(x,y,z\right)$and$\left(x^{\prime },y^{\prime },z^{\prime }\right)$are respectively the coordinates of the source point$P$and the field point$Q$; the corresponding oblate spheroidal coordinates are$\left(\xi ,\mu ,\psi \right)$and$\left({\xi }^{\prime },{\mu }^{\prime },{\psi }^{\prime }\right)$.

Proof of the Theorem 1.

We, initially, provide, without a proof, the expansion in oblate spheroidal harmonics of the inverse of the distance between the source point $P\left(x,y,z\right)$ and the field point $Q\left(x^{\prime },y^{\prime },z^{\prime }\right)$ that is coined $R_{PQ}$. Clearly, this distance reads:

$$R_{PQ}=\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z-z^{\prime }\right)}^2}$$

(6)

and is transformed into spheroidal coordinates $\left(\xi ,\mu ,\psi \right)$ according to

$$\frac{1}{R_{PQ}}={\displaystyle \sum }_{n=0}^{\infty }{\displaystyle \sum }_{m=0}^n{\epsilon }_m{\left(-1\right)}^m\left(2n+1\right){\left[\frac{\left(n-m\right)! }{\left(n+m\right)!}\right]}^2{P}_n^m\left(i0\right)P_n^m\left({\mu }^{\prime }\right)Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\left(\psi -{\psi }^{\prime }\right)$$

(7)

where ${\epsilon }_0=1$ and ${\epsilon }_m=2, m=1,2,\dots$, while it was assumed that $c=1$, which implies that the geometry of the spheroid is fully determined by the slenderness $a/b$. In Equation (7), $P_{\nu }^{\lambda }\left(\eta \right)=e^{\pm i\lambda \pi /2}{P}_{\nu }^{\lambda }\left(\eta \pm i0\right)$ (Equation (8.3.2) in [16]) and, therefore, $P_n^m\left(i0\right)\ne 0$ (Equation (8.6.1) in [16]) only if $n-m$ is even, which is the case considered herein.

The analysis continues with the expression that generates the external oblate spheroidal harmonic by the source distribution over the fundamental disk $\left(S_0;x^2+y^2\le 1, z=0\right)$. This reads as:

$$Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi =\frac{1}{2\pi }\underset{S_0}{{\displaystyle \int }}\frac{\sigma \left({\rho }^{\prime },{\psi }^{\prime }\right)}{R_{PQ}}d{S}_0, d{S}_0={\rho }^{\prime }d{\rho }^{\prime }d{\psi }^{\prime },$$

(8)

where $\sigma \left({\rho }^{\prime },{\psi }^{\prime }\right)$ denotes the source distribution over $S_0$ given by

$$\sigma \left({\rho }^{\prime },{\psi }^{\prime }\right)={\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{l=0}^k{C}_{kl}{P}_k^l\left(\lambda \right)\frac{\cos l{\psi }^{\prime }}{\lambda }, {\lambda }^2=1-{{\rho }^{\prime }}^2$$

(9)

where $C_{kl}$ are the unknown coefficients to be determined. The sources are distributed uniformly over the ‘unit’ disk $0\le {\rho }^{\prime }\le 1$. Accordingly, Equations (7) and (9) are substituted into Equation (8) to obtain:

$$\begin{array}{c}{Q}_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi \\ =\frac{1}{2\pi }{\displaystyle {\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{l=0}^k}{C}_{kl}{\epsilon }_t{\left(-1\right)}^t\left(2s+1\right){\left[\frac{\left(s-t\right)! }{\left(s+t\right)!}\right]}^2\hfill \\ \times P_s^t\left(i0\right)P_s^t\left(\mu \right)Q_s^t\left(i\xi \right)\underset{0}{\overset{2\pi }{{\displaystyle \int }}}\cos l{\psi }^{\prime }\cos t\left(\psi -{\psi }^{\prime }\right)d{\psi }^{\prime }\hfill \\ \times \underset{0}{\overset{1}{{\displaystyle \int }}}\frac{P_s^t\left({\mu }^{\prime }\right)P_k^l\left(\sqrt{1-{{\rho }^{\prime }}^2}\right){\rho }^{\prime }d{\rho }^{\prime }}{\sqrt{1-{{\rho }^{\prime }}^2}}.\hfill \end{array}$$

(10)

The cosine functions are orthogonal in $\left[0, 2\pi \right]$ and, consequently, Equation (10) is reduced to:

$$\begin{array}{c}{Q}_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi \\ ={\displaystyle {\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{l=0}^k{\displaystyle \sum }_{s=0}^{\infty }}{C}_{kl}{\left(-1\right)}^l\left(2s+1\right){\left[\frac{\left(s-l\right)! }{\left(s+l\right)!}\right]}^2\hfill \\ \times P_s^l\left(i0\right)P_s^l\left(\mu \right)Q_s^l\left(i\xi \right)\cos l\psi \underset{0}{\overset{1}{{\displaystyle \int }}}\frac{P_s^l\left({\mu }^{\prime }\right)P_k^l\left(\sqrt{1-{{\rho }^{\prime }}^2}\right){\rho }^{\prime }d{\rho }^{\prime }}{\sqrt{1-{{\rho }^{\prime }}^2}}.\hfill \end{array}$$

(11)

When ${{\rho }^{\prime }}^2=1-{{\mu }^{\prime }}^2$ we have:

$$\underset{0}{\overset{1}{{\displaystyle \int }}}\frac{P_s^l\left({\mu }^{\prime }\right)P_k^l\left(\sqrt{1-{{\rho }^{\prime }}^2}\right){\rho }^{\prime }d{\rho }^{\prime }}{\sqrt{1-{{\rho }^{\prime }}^2}}=-\underset{0}{\overset{1}{{\displaystyle \int }}}{P}_s^l\left({\mu }^{\prime }\right)P_k^l\left({\mu }^{\prime }\right)d{\mu }^{\prime },$$

(12)

while due to being orthogonal, the right-hand side integral becomes:

$$\underset{0}{\overset{1}{{\displaystyle \int }}}{P}_s^l\left({\mu }^{\prime }\right)P_k^l\left({\mu }^{\prime }\right)d{\mu }^{\prime } =\frac{1}{2k+1} \frac{\left(k+l\right)!}{\left(k-l\right)!} {\delta }_{sk}.$$

(13)

where ${\delta }_{sk}$ is the Kroneker’s delta function. By invoking Equations (12) and (13), Equation (11) is reduced to:

$$Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi =-{\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{l=0}^k{C}_{kl}{\left(-1\right)}^l\frac{\left(k-l\right)! }{\left(k+l\right)!}{P}_k^l\left(i0\right)P_k^l\left(\mu \right)Q_k^l\left(i\xi \right)\cos l\psi ,$$

(14)

which yields an identity if

$$C_{kl}{\left(-1\right)}^{l+1}{P}_k^l\left(i0\right)\frac{\left(k-l\right)!}{\left(k+l\right)!}={\delta }_{kn}{\delta }_{lm}.$$

(15)

Substituting Equation (15) into the source distribution (Equation (9)) and next into the harmonic (Equation (8)), one gets the sought expression (Equation (5)). This completes the proof of the image singularity theorem in oblate spheroidal harmonics.  □

4. Hydrodynamic Diffraction—The Multipoles of Green’s Function

We are concerned with the linear hydrodynamic diffraction problem by an oblate spheroid, with its center placed at a distance $f$ below the undisturbed free surface that bounds from above a liquid field of infinite depth. Within the realm of the linear potential theory, the velocity and pressure fields are governed by the linear velocity potential:

$$\mathsf{\Phi }\left(x,y,z,t\right)=Re\left[\varphi \left(x,y,z\right)e^{-i\omega t}\right] ,$$

(16)

where $\omega$ is the frequency of the incoming waves and $t$ is the time. The spatial component $\varphi \left(x,y,z\right)$ should satisfy the following boundary value problem:

$${\nabla }^2\varphi =0 ,$$

(17)

in the entire fluid domain,

$$K\varphi +\frac{\partial \varphi }{\partial z}=0 ,$$

(18)

on the undisturbed free surface, i.e., at $z=0$, and

$$\frac{\partial \varphi }{\partial n}=0 ,$$

(19)

on the wet surface of the solid, where $n$ denotes the unit normal on that surface pointing to the fluid domain. Equation (17) is the Laplace equation, Equation (18) is the free-surface condition, while Equation (19) is the Neumann condition on the surface of the solid. In addition, $K={\omega }^2/g$, where $g$ is the gravitational acceleration. The free-surface condition assumes that $z$ is pointing in the direction of gravity. In addition to Equations (17)–(19), $\varphi \to 0$ as $z\to \infty$, while the velocity potential should comply with the far-field radiation condition for outgoing waves at infinity.

The diffraction component, ${\varphi }_D$, of the total velocity potential $\varphi$, will be constructed using the underlying Green’s function associated with the particular boundary value problem. The concerned Green’s function reads (see e.g., [7,8,9,10,11]) as:

$$G\left(x,y,z\right)=\frac{1}{\sqrt{x^2+y^2+{\left(z-f\right)}^2}}-\frac{1}{2\pi }\underset{0}{\overset{\infty }{{\displaystyle \int }}}\underset{-\pi }{\overset{\pi }{{\displaystyle \int }}}\frac{K+k}{K-k}{e}^{-k\left(z+f\right)+ik\left(x\cos a+y\sin a\right)}dadk,$$

(20)

and clearly satisfies the Laplace equation and the free-surface condition, while, furthermore, it complies with the far-field condition for infinite water depth.

The multipoles of the Green’s function (auxiliary potentials) $G_n^m\left(x,y,z\right)$ are obtained by employing the image singularity system theorem of Equation (5), directly in Equation (20). In particular, we may write:

$$G_n^m\left(x,y,z\right)=\frac{{\left(-1\right)}^m}{2\pi P_n^m\left(i0\right)} \frac{\left(n+m\right)!}{\left(n-m\right)!}\underset{0}{\overset{2\pi }{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}G\left(x-x^{\prime },y-y^{\prime },z\right)P_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }d{\mu }^{\prime }d{\psi }^{\prime },$$

(21)

with $x^{\prime }+i{y}^{\prime }=c{\left(1-{{\mu }^{\prime }}^2\right)}^{1/2}{e}^{i{\psi }^{\prime }}$. Substituting Equation (20) into Equation (21) and using Equation (5) it follows that:

$$\begin{array}{c}{G}_n^m\left(x,y,z\right)=Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi \\ -\frac{{\left(-1\right)}^m}{{\left(2\pi \right)}^2{P}_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}\underset{0}{\overset{\infty }{{\displaystyle \int }}}\underset{-\pi }{\overset{\pi }{{\displaystyle \int }}}\frac{K+k}{K-k}{e}^{-2kf}{e}^{k{z}^{*}+ik\left(x\cos a+y\sin a\right)}\hfill \\ \hspace{1em}\times \underset{0}{\overset{2\pi }{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}{e}^{-ik\left(x^{\prime }\cos a+y^{\prime }\sin a\right)}{P}_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }d{\mu }^{\prime }d{\psi }^{\prime }dadk,\hfill \end{array}$$

(22)

where $z^{*}$ is the vertical coordinate, fixed on the center of the spheroid, pointing upwards (towards the free surface). The next step is to transform the exponential term(s) into a spheroidal coordinate representation. To this end, we initially use the expansion in prolate spheroidal coordinates shown by Farell [17], which, for the axisymmetric case, i.e., for a symmetrical axis perpendicular to the free surface, reads as:

$$e^{k{z}^{*}+ik\left(x\cos a+y\sin a\right)}={\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{H}_s^t\left(kc\right)\left(\cos t\psi \cos ta+\sin t\psi \sin ta\right)P_s^t\left(\mu \right)P_s^t\left(\zeta \right),$$

(23)

where

$$H_s^t\left(kc\right)=i^{-t}{\epsilon }_t\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right)\sqrt{\frac{\pi }{2kc}}{I}_{s+1/2}\left(kc\right).$$

(24)

For the prolate spheroid case $\zeta =\cosh u$. In Equation (24), $I_{s+1/2}$ denotes the modified Bessel function of the first kind with fractional order $s+1/2$. Equation (23) is transformed into oblate spheroidal coordinates by replacing $\zeta$ by $i\xi$ and $c$ by $-ic$, which yields:

$$e^{k{z}^{*}+ik\left(x\cos a+y\sin a\right)}={\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{S}_s^t\left(kc\right)\left(\cos t\psi \cos ta+\sin t\psi \sin ta\right)P_s^t\left(\mu \right)P_s^t\left(i\xi \right),$$

(25)

where

$$S_s^t\left(kc\right)={\left(-1\right)}^s{i}^{s-t}{\epsilon }_t\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right)\sqrt{\frac{\pi }{2kc}}{J}_{s+1/2}\left(kc\right).$$

(26)

and $J_{s+1/2}$ denotes the Bessel function of the first kind with fractional order $s+1/2$. The exponential term $\exp \left[-ik\left(x^{\prime }\cos a+y^{\prime }\sin a\right)\right]$ that occurs in Equation (22) is calculated precisely on the fundamental disk and assumes ${\xi }^{\prime }=0$. This term is written as:

$$e^{-ik\left(x^{\prime }\cos a+y^{\prime }\sin a\right)}={\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{C}_s^t\left(kc\right)\left(\cos t{\psi }^{\prime }\cos ta+\sin t{\psi }^{\prime }\sin ta\right)P_s^t\left({\mu }^{\prime }\right)P_s^t\left(i0\right),$$

(27)

where

$$C_s^t\left(kc\right)={\left(-1\right)}^{s+t}{i}^{s-t}{\epsilon }_t\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right)\sqrt{\frac{\pi }{2kc}}{J}_{s+1/2}\left(kc\right).$$

(28)

Substituting Equations (25)–(28) into Equation (22) and performing the integrations, we obtain after laborious mathematical manipulations, the following form for the multipoles of the Green’s function:

$$G_n^m\left(i\xi ,\mu ,\psi \right)=Q_n^m\left(i\xi \right)P_n^m\left(\mu \right)\cos m\psi +{\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{E}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos m\psi .$$

(29)

where

$$\begin{array}{cc}\hfill E_{ns}^{mt}=-\frac{1}{4c}& {\left(-1\right)}^{n+s}{i}^{n+s-m-t}\frac{2\pi }{{\epsilon }_m}{\epsilon }_t\frac{\left(n+m\right)! }{\left(n-m\right)! }\frac{\left(s-t\right)! }{\left(s+t\right)! }\left(2s+1\right){\delta }_{tm}\hfill \\ & \hspace{1em}\hspace{1em}\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{K+k}{K-k}{e}^{-2kf}\frac{1}{k}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)dk.\hfill \end{array}$$

(30)

Equation (29) has not yet satisfied the far-field radiation condition. This is achieved by expressing the improper infinite integral in the Cauchy Principal Value sense and taking (Equation (13.17) in [18]):

$$\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{F\left(k\right)}{K-k}dk=PV\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{F\left(k\right)}{K-k}dk-i\pi F\left(K\right),$$

(31)

which transforms the coefficients of Equation (30) into

$$\begin{array}{cc}\hfill E_{ns}^{mt}=-\frac{1}{4c}& {\left(-1\right)}^{n+s}{i}^{n+s-m-t}\frac{2\pi }{{\epsilon }_m}{\epsilon }_t\frac{\left(n+m\right)! }{\left(n-m\right)! } \frac{\left(s-t\right)! }{\left(s+t\right)! }\left(2s+1\right){\delta }_{tm}\hfill \\ & \hspace{1em}\hspace{1em}\times [PV\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{K+k}{K-k}{e}^{-2kf}\frac{1}{k}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)dk\hfill \\ & \hspace{1em}\hspace{1em}-2i\pi e^{-2Kf}{J}_{n+1/2}\left(Kc\right)J_{s+1/2}\left(Kc\right)]\hfill \end{array}$$

(32)

Having obtained the auxiliary potentials $G_n^m$, the diffraction potential is constructed according to:

$${\varphi }_D=-i\frac{gA}{\omega }{e}^{-Kf}{\displaystyle \sum }_{s=0}^{\infty }{\displaystyle \sum }_{t=0}^s{A}_s^t{G}_s^t\left(i\xi ,\mu ,\psi \right),$$

(33)

where $A$ is the linear amplitude of the incoming waves and $A_s^t$ are the unknown expansion coefficients associated with ${\varphi }_D$. The incident wave component,

$${\varphi }_I=-i\frac{gA}{\omega }{e}^{-Kf}{e}^{K{z}^{*}+iK\left(x\cos \beta +y\sin \beta \right)},$$

(34)

is also expanded into oblate spheroidal harmonics using Equation (25). Here, $\beta$ denotes the angle of heading with respect to the horizontal $x$-axis, which can be assumed to be equal to zero due to symmetry (in $z$). The total velocity potential, for the diffraction problem reads $\varphi ={\varphi }_I+{\varphi }_D$ and the Neumann condition (Equation (19)) becomes:

$$\frac{\partial {\varphi }_D}{\partial \xi }=-\frac{\partial {\varphi }_I}{\partial \xi }, \xi ={\xi }_0, -1\le \mu \le 1, 0\le \psi \le 2\pi$$

(35)

where ${\xi }_0={\tanh }^{-1}\left(b/a\right)$. Substituting Equation (25) into Equation (34) and Equation (29) into Equation (33) and, then, the resulting relations into Equation (35), we obtain, after employing the relations of orthogonality for both the trigonometric and the associate Legendre functions, the following linear system in terms of the unknown expansion coefficients $A_s^t$:

$$A_s^t+{\displaystyle \sum }_{n=0}^{\infty }{\displaystyle \sum }_{m=0}^n{A}_n^m{E}_{ns}^{mt}\frac{{\dot{P}}_s^t\left(i{\xi }_0\right)}{{\dot{Q}}_s^t\left(i{\xi }_0\right)} =-B_s^t\frac{{\dot{P}}_s^t\left(i{\xi }_0\right)}{{\dot{Q}}_s^t\left(i{\xi }_0\right)},$$

(36)

where $B_s^t$ is given by

$$B_s^t={\left(-1\right)}^s{i}^{s-t}{\epsilon }_t\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right)\sqrt{\frac{\pi }{2Kc}}{J}_{s+1/2}\left(Kc\right)$$

(37)

while the dots denote differentiation with respect to the argument. The system of Equation (36) can be solved using standard methods of linear algebra and should be truncated up to the degree that ensures the desirable accuracy. Typically, the method converges quite fast using only a small number of modes (eigenfunctions).

5. Hydrodynamic Loading on the Spheroid

The linear hydrodynamic forces exerted on the spheroid are obtained by direct pressure integration on the wetted surface, $S$, namely:

$$F_i=-i\omega \rho \underset{S}{{\displaystyle \int }}\left({\varphi }_I+{\varphi }_D\right)n_{i}dS, i=1, 3, 5$$

(38)

where the indices 1, 3 and 5 denote the surge force, the heave force, and the pitch moment, respectively, for $\beta =0$. All other loading components are zero due to symmetry. In Equation (38), $n_i$ are the unit normals in the concerned direction, which read:

$$n_1=\frac{b\sin \theta \cos \psi }{{\left(a^2{\cos }^2\theta +b^2{\sin }^2\theta \right)}^{1/2}}=\frac{{\xi }_0{\left(1-{\mu }^2\right)}^{1/2}\cos \psi }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}=-\frac{{\xi }_0{P}_1^1\left(\mu \right)\cos \psi }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}$$

(39)

$$n_3=\frac{a\cos \theta }{{\left(a^2{\cos }^2\theta +b^2{\sin }^2\theta \right)}^{1/2}}=\frac{{\left({\xi }_0+1\right)}^{1/2}\mu }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}=\frac{{\left({\xi }_0+1\right)}^{1/2}{P}_1^0\left(\mu \right)}{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}$$

(40)

$$n_5=\frac{c\mu {\left(1-{\mu }^2\right)}^{1/2}\cos \psi }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}=-\frac{1}{3}\frac{c{P}_2^1\left(\mu \right)\cos \psi }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}$$

(41)

The differential area on the spheroid is:

$$dS=a\sin \theta {\left(a^2{\cos }^2\theta +b^2{\sin }^2\theta \right)}^{1/2}d\theta d\psi =c^2{\left({\xi }_0+1\right)}^{1/2}{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}d\mu d\psi$$

(42)

The final relations that provide the forcing terms are:

$$\frac{F_x}{\rho gA{a}^2}=-\frac{8\pi }{3}\frac{b}{a}{e}^{-Kf}\frac{1}{{\xi }_0^2+1}\frac{A_1^1}{{\dot{P}}_1^1\left(i{\xi }_0\right)}$$

(43)

$$\frac{F_z}{\rho gA{a}^2}=\frac{4\pi }{3}{e}^{-Kf}\frac{1}{{\xi }_0^2+1}\frac{A_1^0}{{\dot{P}}_1^0\left(i{\xi }_0\right)}$$

(44)

$$\frac{M_y}{\rho gA{a}^3}=-\frac{24\pi }{5}\frac{c^3}{a^3}{e}^{-Kf}\frac{1}{{\left({\xi }_0^2+1\right)}^{1/2}}\frac{A_2^1}{{\dot{P}}_2^1\left(i{\xi }_0\right)}$$

(45)

Clearly, we have changed the notation for the surge, heave forces, and the pitching moment to $F_x$, $F_z$, and $M_y$, respectively. For the derivation of the compact forms of Equations (43)–(45), we employed in the products of integration (Equation (38)) the linear system expressed through Equation (36) and the following Wronskian determinant (Equation (5.314) in [13]):

$${\dot{Q}}_n^m\left(i\xi \right)P_n^m\left(i\xi \right)-{\dot{P}}_n^m\left(i\xi \right)Q_n^m\left(i\xi \right)=\frac{{\left(-1\right)}^m}{{\xi }_0^2+1} \frac{\left(n+m\right)!}{\left(n-m\right)! }$$

(46)

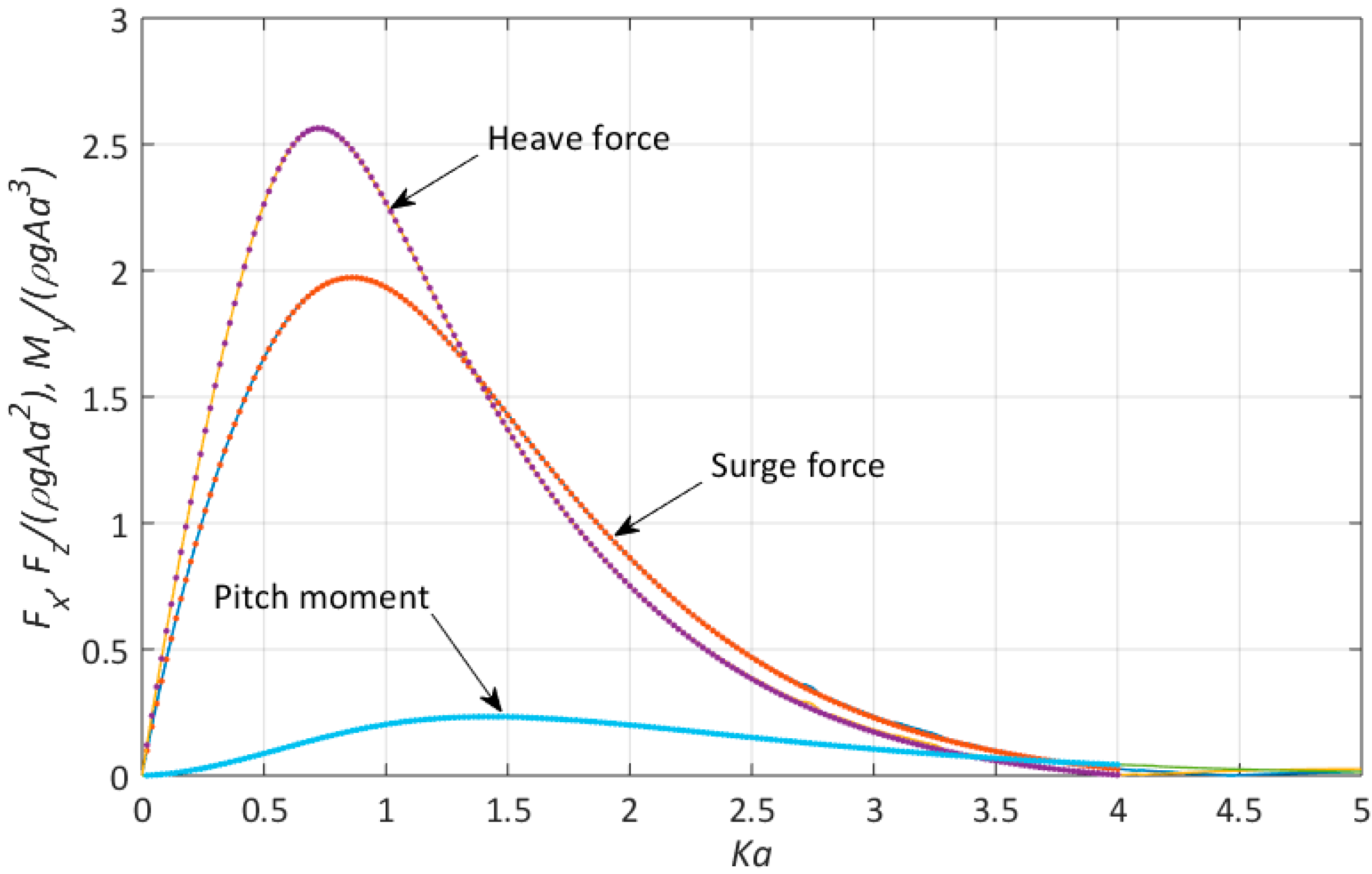
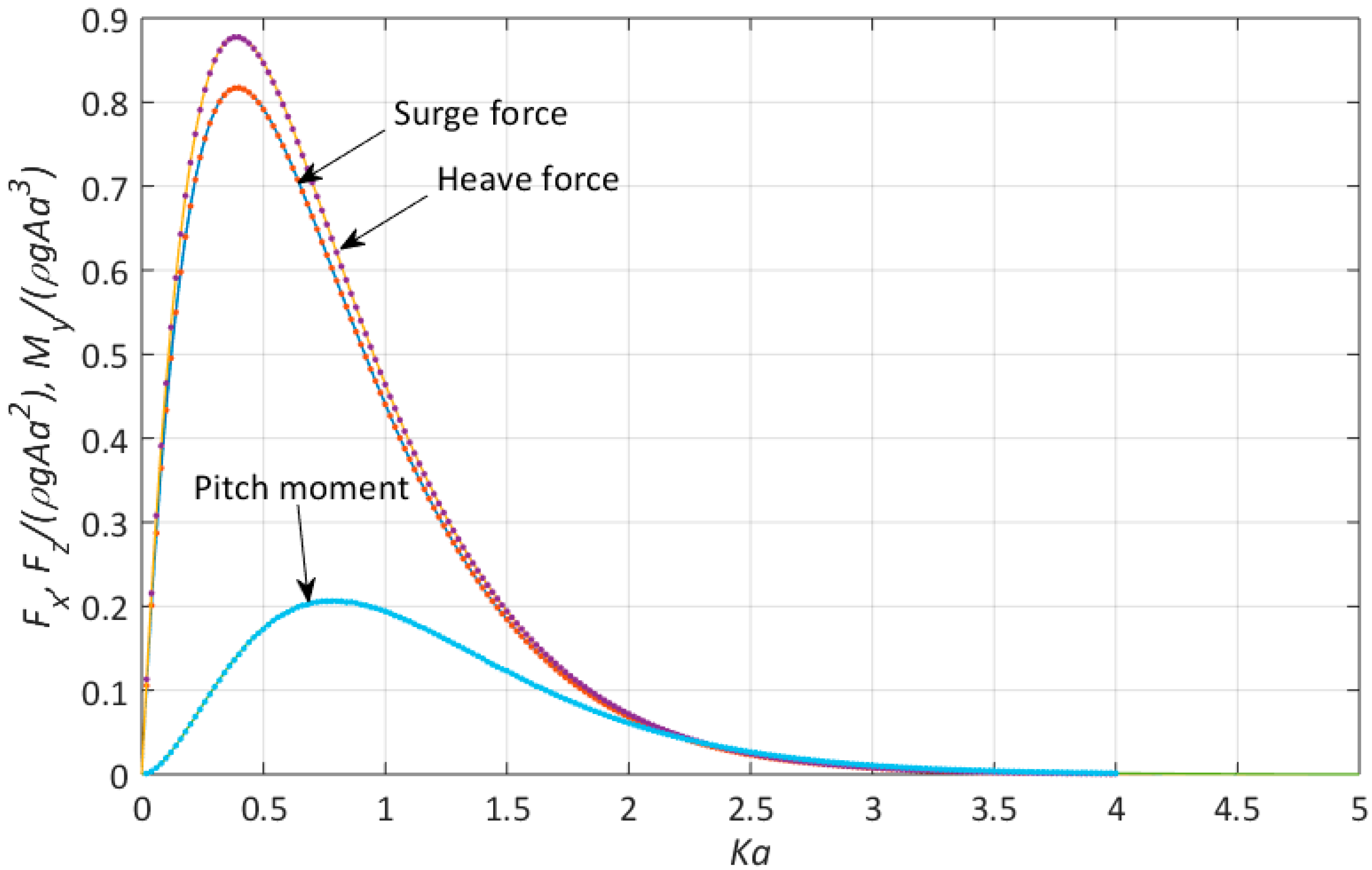
6. Results and Discussion

The methodology outlined above can be effectively employed for the limiting case of the sphere, letting $a/b~1$. Here, the sphere case was approximated letting $a/b=1.001$, while relevant calculations are provided in Figure 2. Two non-dimensional immersions are considered, namely, $f/a=1.5$ and $f/a~1$. The latter case implies a sphere that nearly touches the free surface. The depicted results for the former immersion coincide magnificently with those reported by Linton [19]. Linton’s results have been omitted for better display. The latter limiting case $f/a~1$, demonstrates a peculiar behavior for the exciting forces, which is characterized by local minimizations along the frequency interval considered.

Figure 3 and Figure 4 examine two randomly selected cases of immersed spheroids subjected to regular wave action. The slenderness and immersion are mentioned in the captions. All loading components are considered and comparisons are made with the respected code WAMIT [14]. It is immediately apparent that the comparisons are extremely favorable as the depicted curves are practically indistinguishable. The forcing coefficients increase progressively to a maximum and accordingly, they asymptote to zero for very large wave frequencies. The peak of the pitch moment occurs at slightly larger $Ka$.

The normalized real and imaginary parts of the force components depicted in Figure 3 are listed in

Table 1. Convergence sequence of the computations in terms of the real and imaginary parts of the normalized surge force $F_x/\rho gA{a}^2$ for different mode numbers. Slenderness of the oblate spheroid is $b/a=0.8$ with an immersion of $f/a=1.0$. The normalization is that of Equation (43).

$\mathit{K}\mathit{a}$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{x}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{x}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{x}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{x}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{x}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{x}}\right)$
	$\mathit{n}=5$		$\mathit{n}=8$		$\mathit{n}=11$
0.1	0.45956	0.00048	0.45958	0.00048	0.45958	0.00048
0.2	0.84700	0.00600	0.84700	0.00600	0.84700	0.00600
0.3	1.17229	0.02392	1.17238	0.02392	1.17238	0.02392
0.4	1.43940	0.05986	1.43955	0.05987	1.43955	0.05987
0.5	1.64865	0.11567	1.64874	0.11569	1.64874	0.11569
0.6	1.79919	0.18896	1.79923	0.18897	1.79923	0.18897
0.7	1.89206	0.27403	1.89210	0.27405	1.89210	0.27405
0.8	1.92930	0.36258	1.92939	0.36262	1.92939	0.36262
0.9	1.91660	0.44603	1.91681	0.44616	1.91681	0.44616
1.0	1.86231	0.51724	1.86270	0.51758	1.86271	0.51758
1.5	1.29193	0.60619	1.29221	0.60940	1.29221	0.60942
2.0	0.75105	0.42196	0.74870	0.42538	0.74864	0.42546
2.5	0.41204	0.23062	0.40948	0.23288	0.40938	0.23294
3.0	0.21071	0.10926	0.20807	0.11149	0.20800	0.11152
3.5	0.09238	0.04331	0.08899	0.04503	0.08895	0.04504
4.0	0.02512	0.01056	0.02061	0.01011	0.02059	0.01011
4.5	−0.00129	−0.00043	−0.00738	−0.00123	−0.00741	−0.00330
5.0	−0.01371	−0.00355	−0.02090	−0.00835	−0.02094	−0.00848

,

Table 2. Convergence sequence of the computations in terms of the real and imaginary parts of the normalized heave force $F_z/\rho gA{a}^2$ for different mode numbers. Slenderness of the oblate spheroid is $b/a=0.8$ with an immersion of $f/a=1.0$. The normalization is that of Equation (44).

$\mathit{K}\mathit{a}$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{z}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{z}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{z}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{z}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{F}}_{\mathit{z}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{F}}_{\mathit{z}}\right)$
	$\mathit{n}=5$		$\mathit{n}=8$		$\mathit{n}=11$
0.1	−0.00149	0.57292	−0.00149	0.57298	−0.00149	0.57299
0.2	−0.01956	1.08375	−0.01956	1.08378	−0.01956	1.08378
0.3	−0.08213	1.54201	−0.08218	1.54237	−0.08218	1.54237
0.4	−0.21410	1.93302	−0.21426	1.93364	−0.21426	1.93365
0.5	−0.42058	2.22263	−0.42075	2.22301	−0.42076	2.22301
0.6	−0.67432	2.37560	−0.67443	2.37574	−0.67443	2.37575
0.7	−0.92539	2.38439	−0.92552	2.38450	−0.92552	2.38450
0.8	−1.12140	2.23228	−1.12169	2.27246	−1.12169	2.27246
0.9	−1.23682	2.08709	−1.23752	2.08735	−1.23752	2.08735
1.0	−1.27467	1.87423	−1.27604	1.87446	−1.27604	1.87446
1.5	−0.91534	1.01712	−0.92016	1.01388	−0.92019	1.01386
2.0	−0.49609	0.56508	−0.49885	0.55967	−0.49892	0.55953
2.5	−0.23808	0.31081	−0.23947	0.30711	−0.23950	0.30694
3.0	−0.10085	0.15316	−0.10217	0.15005	−0.10218	0.14996
3.5	−0.03215	0.05613	−0.03254	0.05262	−0.03254	0.05259
4.0	0.00017	−0.00033	0.00268	−0.00453	0.00269	−0.00455
4.5	0.00699	−0.01766	0.01229	−0.02354	0.01236	−0.02355
5.0	0.00756	−0.02503	0.01495	−0.03211	0.01515	−0.03212

and

Table 3. Convergence sequence of the computations in terms of the real and imaginary parts of the normalized pitch moment $M_y/\rho gA{a}^3$ for different mode numbers. Slenderness of the oblate spheroid is $b/a=0.8$ with an immersion of $f/a=1.0$. The normalization in that of Equation (45).

$\mathit{K}\mathit{a}$	$\mathit{R}\mathit{e}\left({\mathit{M}}_{\mathit{y}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{M}}_{\mathit{y}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{M}}_{\mathit{y}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{M}}_{\mathit{y}}\right)$	$\mathit{R}\mathit{e}\left({\mathit{M}}_{\mathit{y}}\right)$	$\mathit{I}\mathit{m}\left({\mathit{M}}_{\mathit{y}}\right)$
	$\mathit{n}=5$		$\mathit{n}=8$		$\mathit{n}=11$
0.1	0.00667	0.00001	0.00668	0.00001	0.00668	0.00001
0.2	0.02038	0.00014	0.02038	0.00014	0.02038	0.00014
0.3	0.03954	0.00081	0.03956	0.00081	0.03956	0.00081
0.4	0.06261	0.00260	0.06266	0.00261	0.06266	0.00261
0.5	0.08798	0.00617	0.08801	0.00618	0.08802	0.00618
0.6	0.11400	0.01197	0.11402	0.01198	0.11402	0.01198
0.7	0.13920	0.02016	0.13921	0.02016	0.13921	0.02016
0.8	0.16201	0.03045	0.16203	0.03045	0.16203	0.03045
0.9	0.18122	0.04217	0.18126	0.04219	0.18126	0.04219
1.0	0.19620	0.05449	0.19631	0.05455	0.19631	0.05455
1.5	0.21157	0.09927	0.21215	0.10005	0.21215	0.10005
2.0	0.17479	0.09820	0.17491	0.09937	0.17491	0.09941
2.5	0.13150	0.07360	0.13107	0.07454	0.13107	0.07458
3.0	0.09359	0.04853	0.09280	0.04973	0.09279	0.04975
3.5	0.06395	0.02998	0.06272	0.03174	0.06271	0.03175
4.0	0.04045	0.01700	0.03870	0.01897	0.03868	0.01900
4.5	0.02394	0.00803	0.02176	0.00963	0.02173	0.00967
5.0	0.01389	0.00359	0.01119	0.00447	0.01116	0.00452

. The tables show the convergence sequence for three different number of modes, $n=5, 8$ and $11$, that define the truncation assumed for the calculations. Clearly, the analytical methodology converges very fast, using only $n=5$ modes, while the use of $n=11$ modes ensures a convergence up to the fourth decimal point for nearly the entire investigated interval of the normalized wave frequencies and for all forcing terms.

7. Conclusions

This study employed the Touvia Miloh theorem on image singularity systems of oblate spheroids with a special focus on hydrodynamical applications. The analysis is conducted in the Laplace domain and accordingly Miloh’s theorem, aside from hydrodynamics, could have substantial applications in relevant fields, such as electromagnetics, electrostatics, optics, acoustics, etc. Here, Miloh’s theorem was applied to solve the hydrodynamic diffraction problem by submerged oblate spheroids having the symmetrical axis perpendicular to the undisturbed free surface (axisymmetric placement). Miloh’s theorem provides rigorous relations for the external spheroidal harmonics, expressed in terms of the fundamental solutions of the Laplace equation. This allows the transformation of the underlying Green’s function in order to be expressed in terms of the governing harmonics and, consequently, to formulate properly the diffraction component of the total velocity potential. The numerical implementation of the mathematical formulations showed, beyond any doubt, the accuracy, reliability, and robustness of the relevant formulas.