Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils
Abstract
:1. Introduction
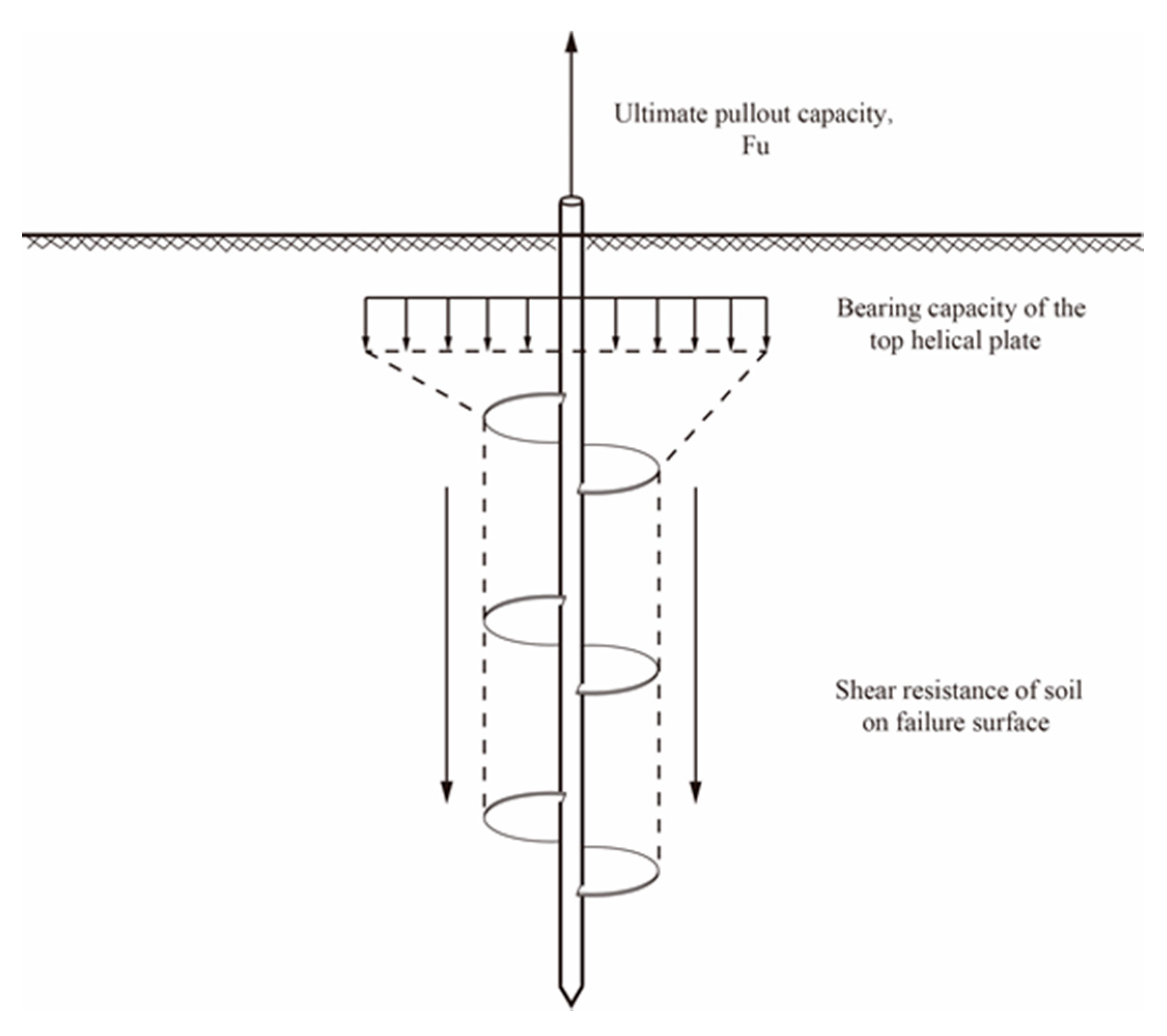
2. The Cylindrical Shear Method
3. Load Test Databases
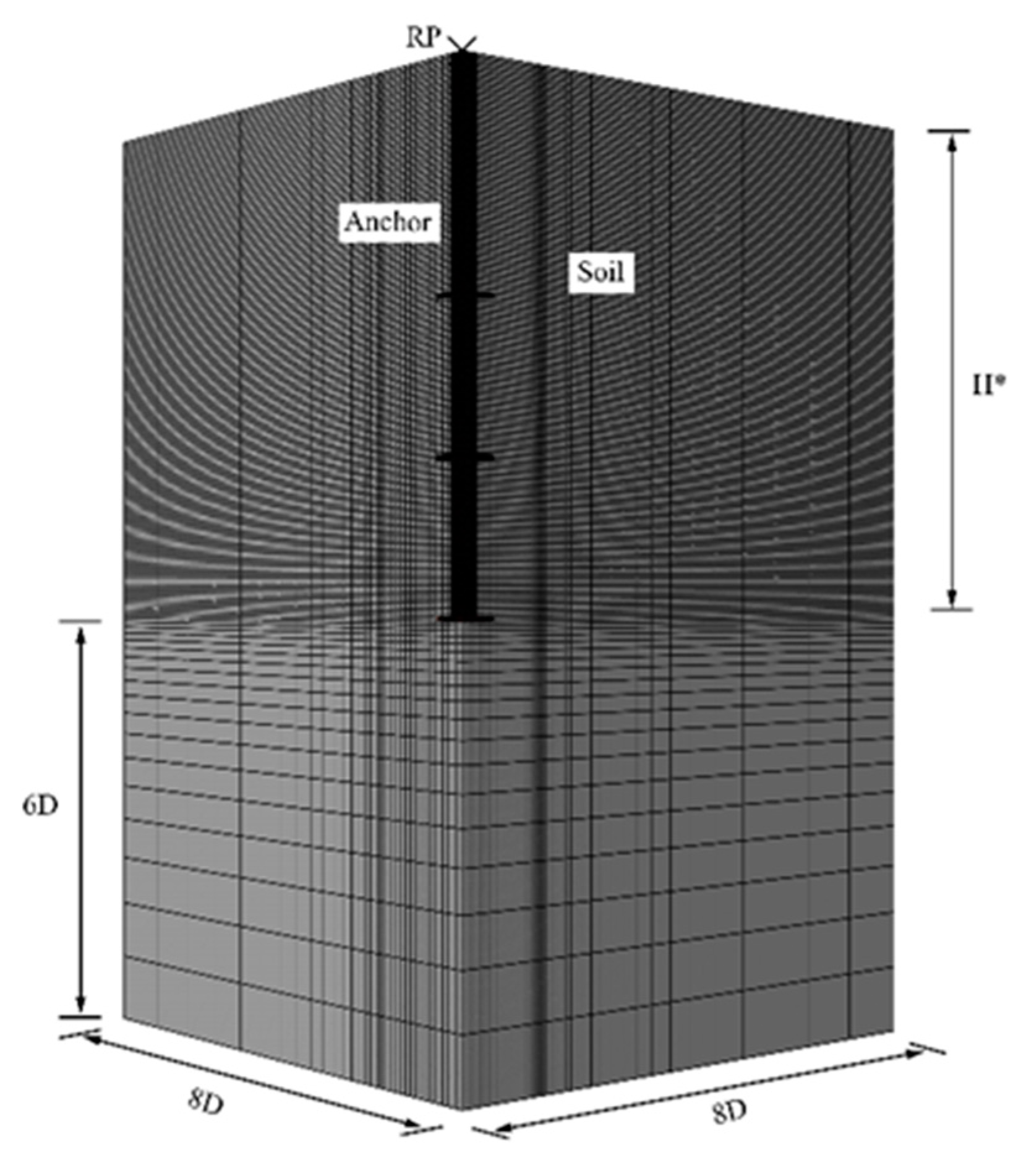
4. The Coupled Eulerian–Lagrangian Analyses
- (1)
- For simplicity, the actual shape of the helical plate was ignored, and the anchor plate was simplified to a regular circular plate with a thickness of 0.03D;
- (2)
- Helical anchors were assumed to be pre-embedded, namely the wished-in-place assumption was adopted.
5. Model Factor for the Pullout Capacity of Helical Anchors
- (1)
- On the basis of CEL analyses, numerical simulations are performed for the load tests in the database
- (2)
- Calculate the model factor Mcel of each CEL analysis, validate its randomness and determine its probability distribution and statistical characteristics
- (3)
- Generate a set of orthogonal experiments to perform regression analysis
- (4)
- Calculate the correction factor η of each orthogonal experiment
- (5)
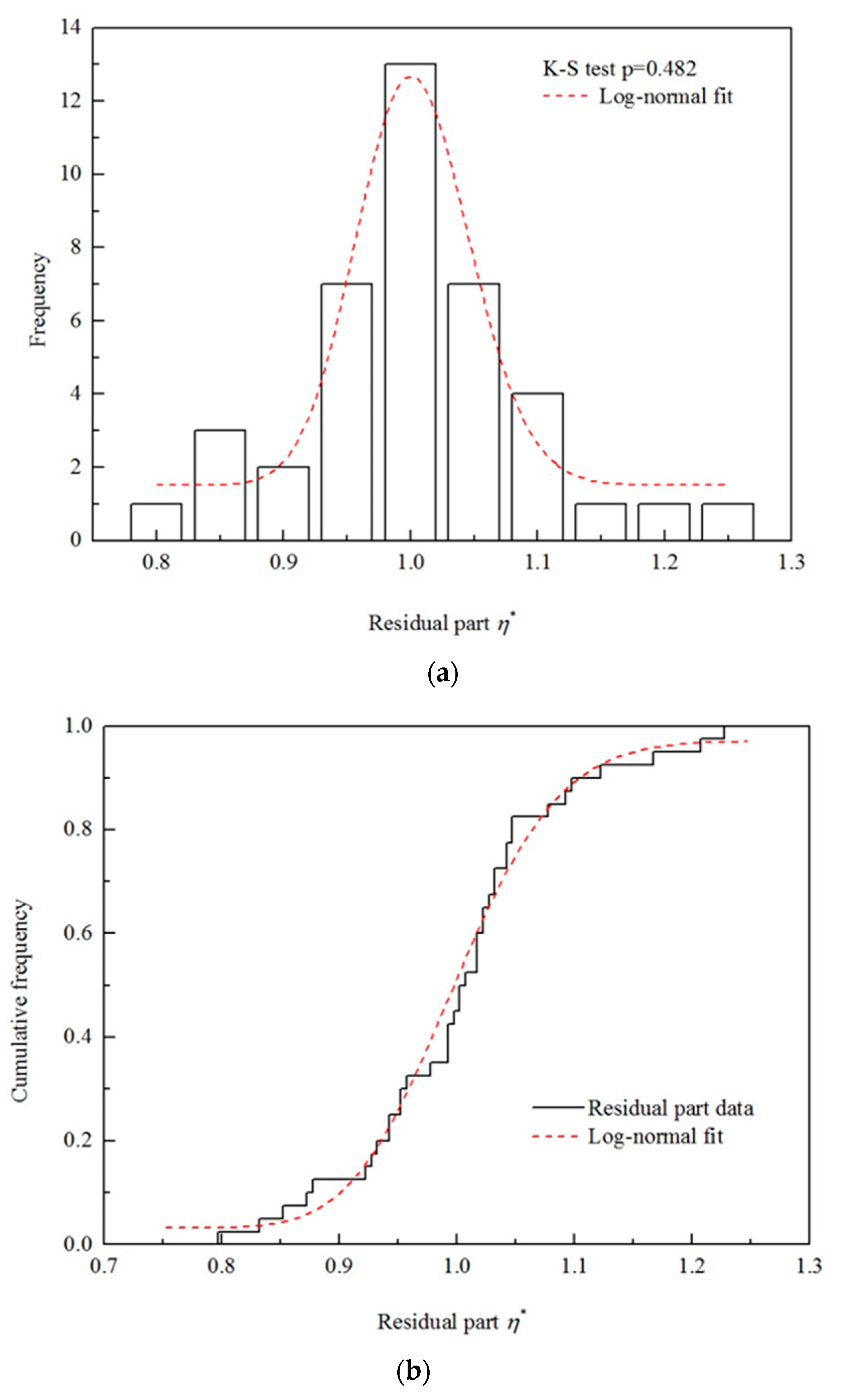
- Determine systemic part f by using regression equations; verify the randomness of residual part η* and characterize its probability distribution
- (6)
- Substitute the regression equation f into the CSM to constitute the modified CSM (MCSM)
- (7)
- Collect another new load tests and verify the accuracy of MCSM
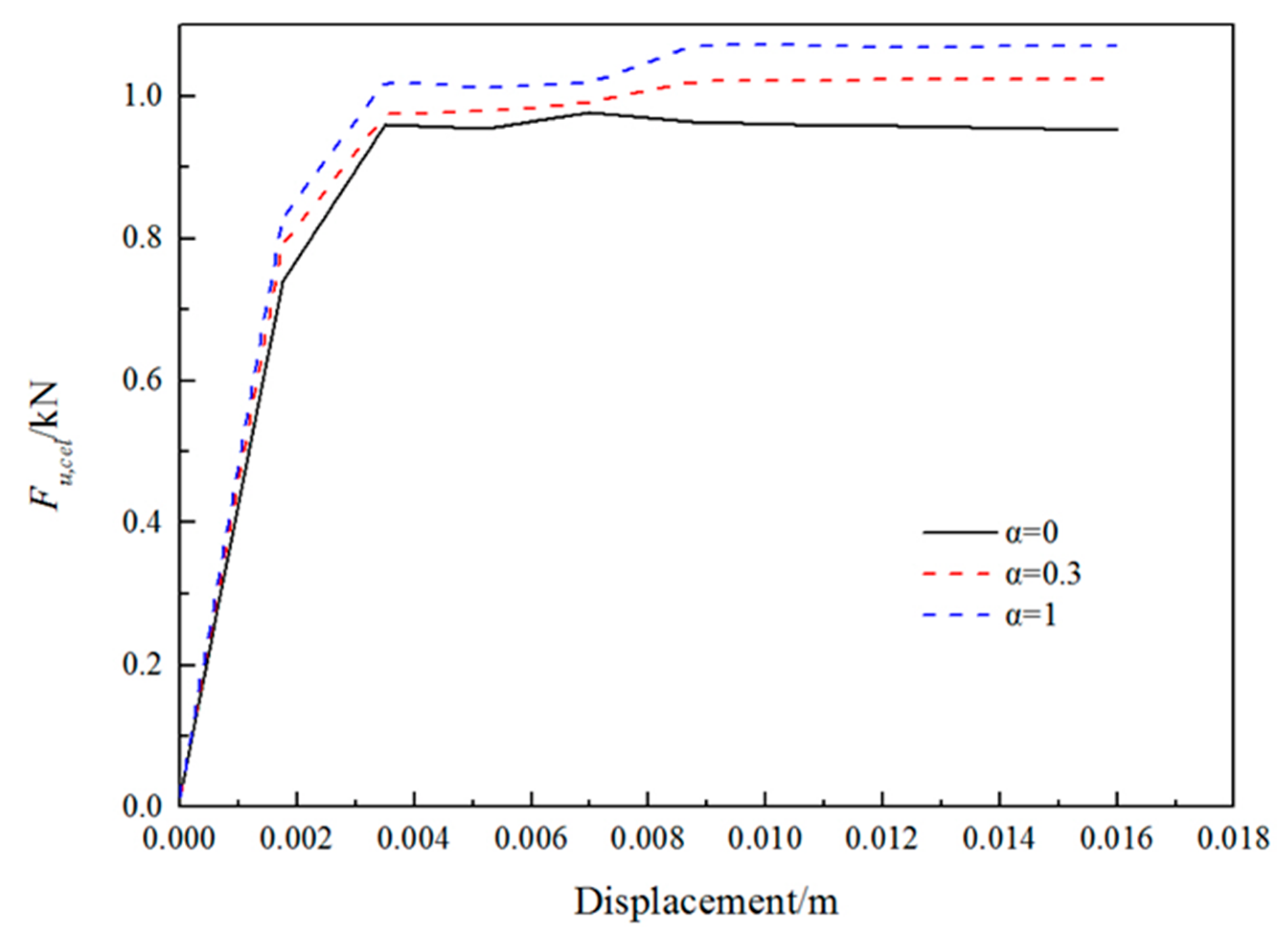
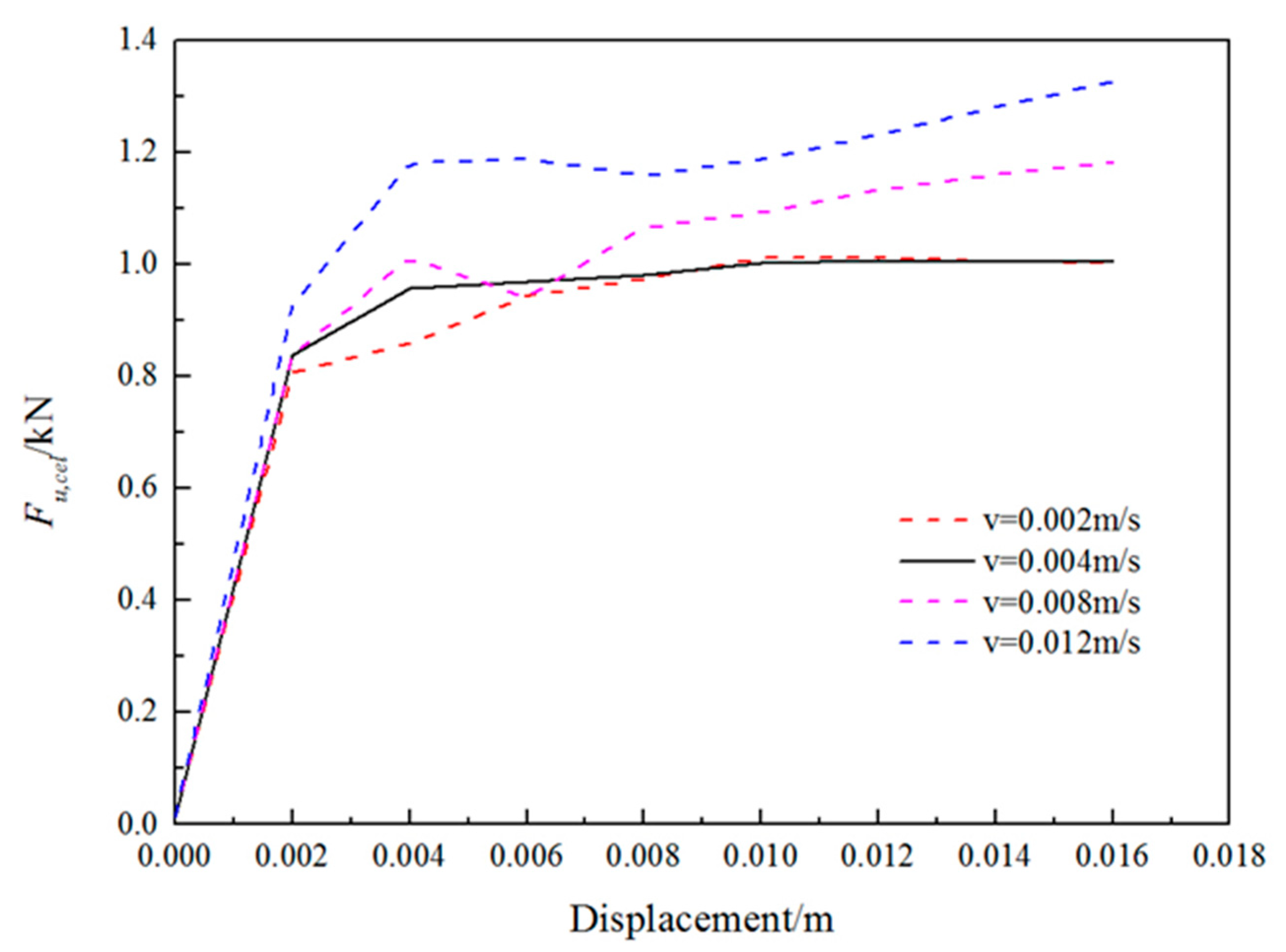
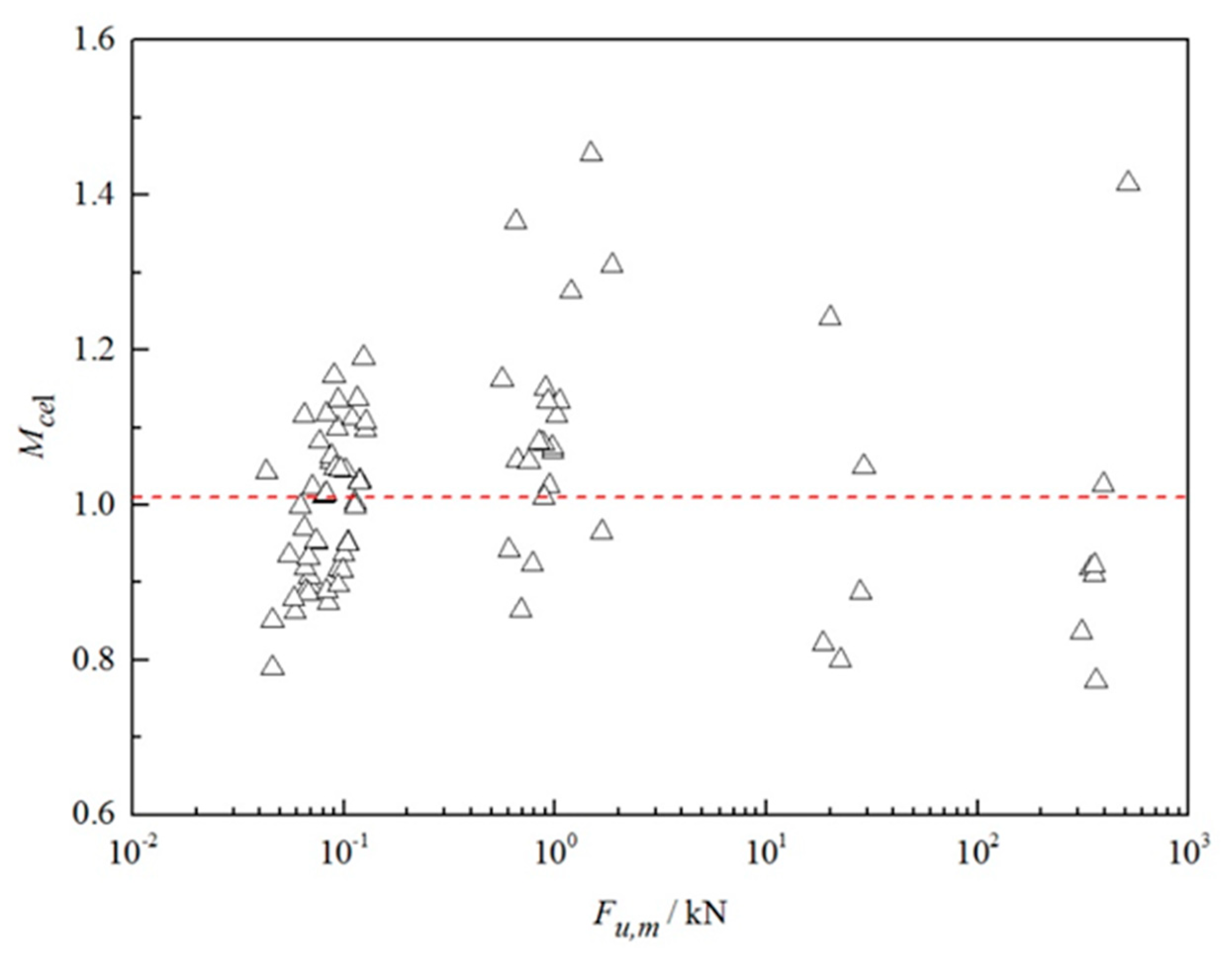
5.1. Comparison of CEL and Load Tests
- (1)
- The cohesive soil is modeled as elastic-perfectly plastic and the strain softening behavior of it is ignored
- (2)
- The actual shape of the helical anchor is simplified in the analysis and the pitch of it is neglected
- (3)
- The anchor-soil interface and contact conditions are assumed to be smooth
- (4)
- The above factors can unavoidably lead to some discrepancy between the estimated pullout capacities of the helical anchors by performing the CEL analysis and the measured pullout capacities, but in general, it is still an effective method to estimate the pullout capacities of helical anchors through the CEL analysis
5.2. Comparison of CSM and CEL
- (1)
- The number of helical plates n = 2, 3, 4, or 5
- (2)
- The dimensionless parameter γH/su = 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0 or 2.2
- (3)
- The embedment ratio H/D = 1, 2, 3, 4, 5, 6, 7, 8, 9 or 10
- (4)
- The ratio of helical plate spacing to diameter S/D = 0.3, 0.6, 0.9, 1.2, 1.5, 1.8, 2.1, 2.4, 2.7, or 3.0
5.3. Correction Factor η
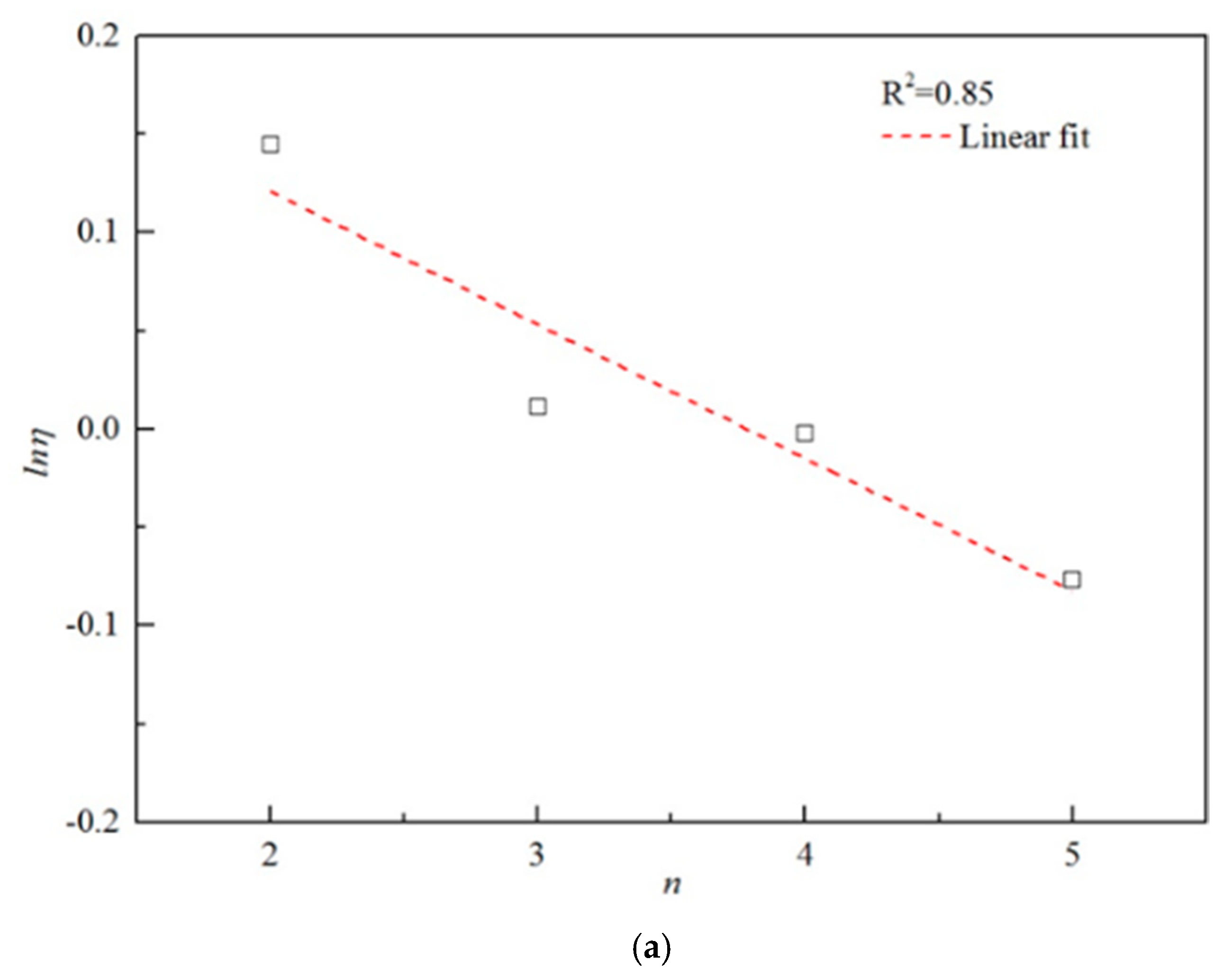
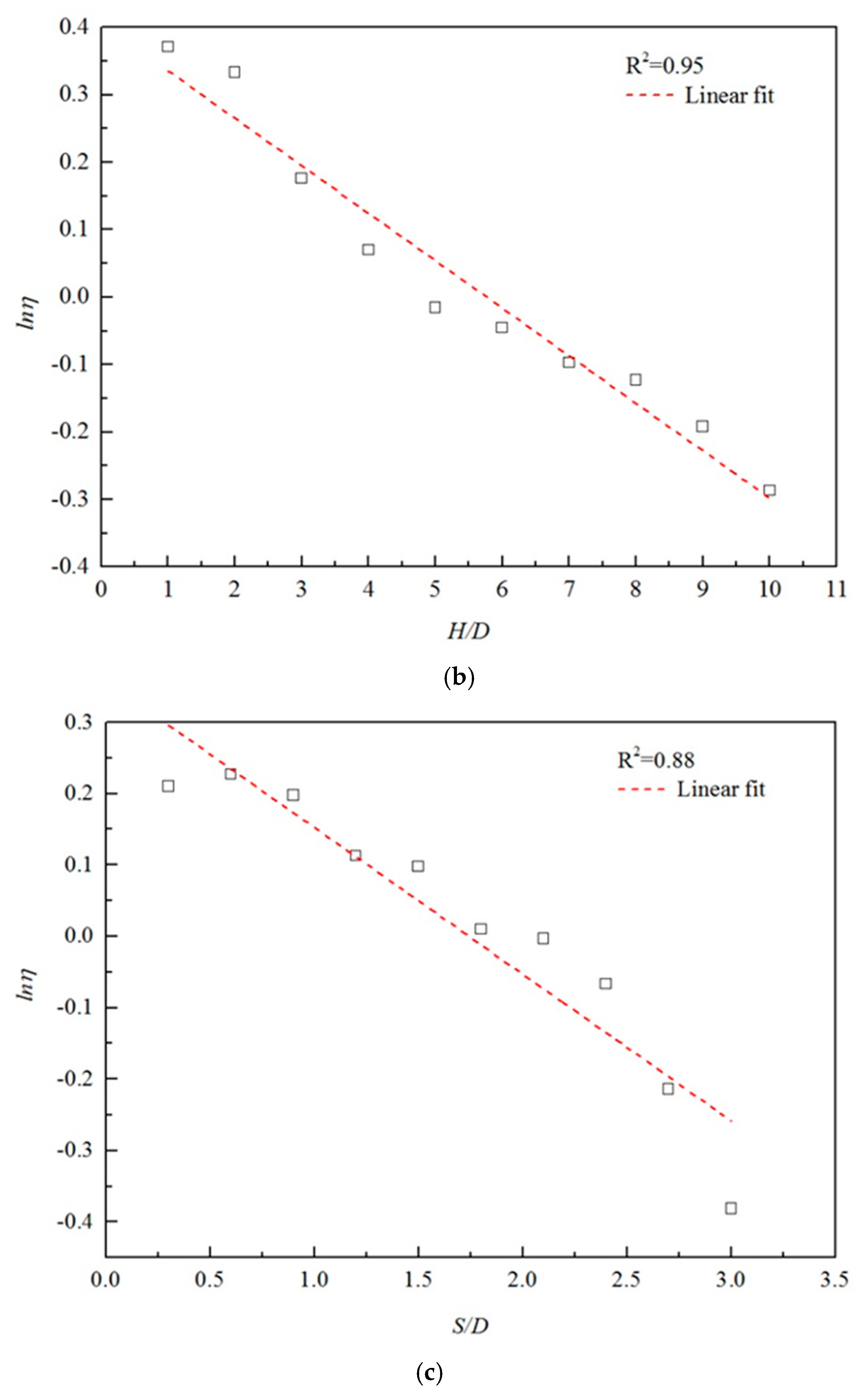
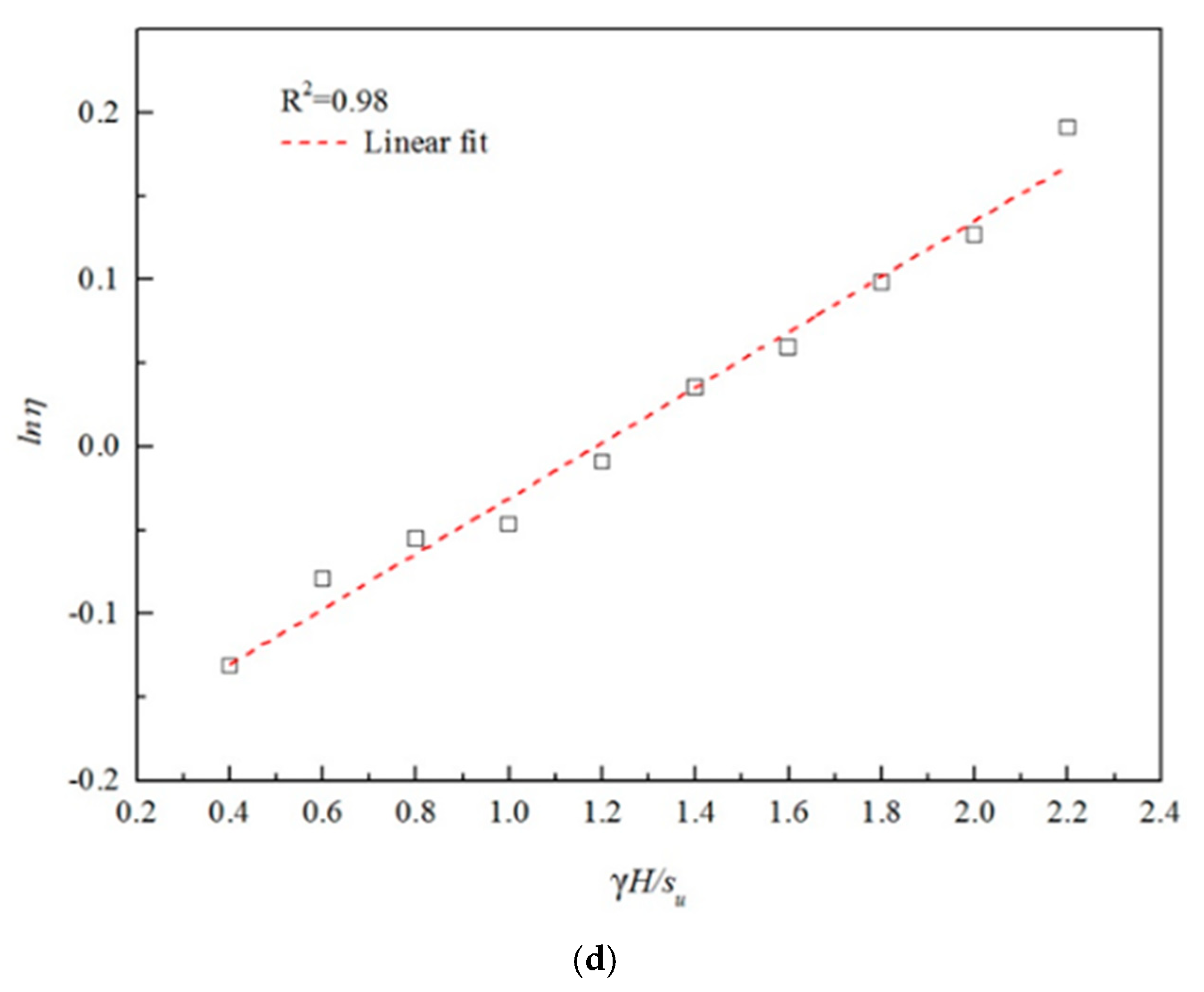
5.4. Regression Analysis
- (1)
- H/D = 1, n = 2, S/D = 0.3, γH/su = 0.4
- (2)
- H/D = 1, n = 3, S/D = 0.9, γH/su = 1.2
- (3)
- H/D = 1, n = 4, S/D = 1.2, γH/su = 1.2
- (4)
- H/D = 1, n = 5, S/D = 1.0, γH/su = 2.0
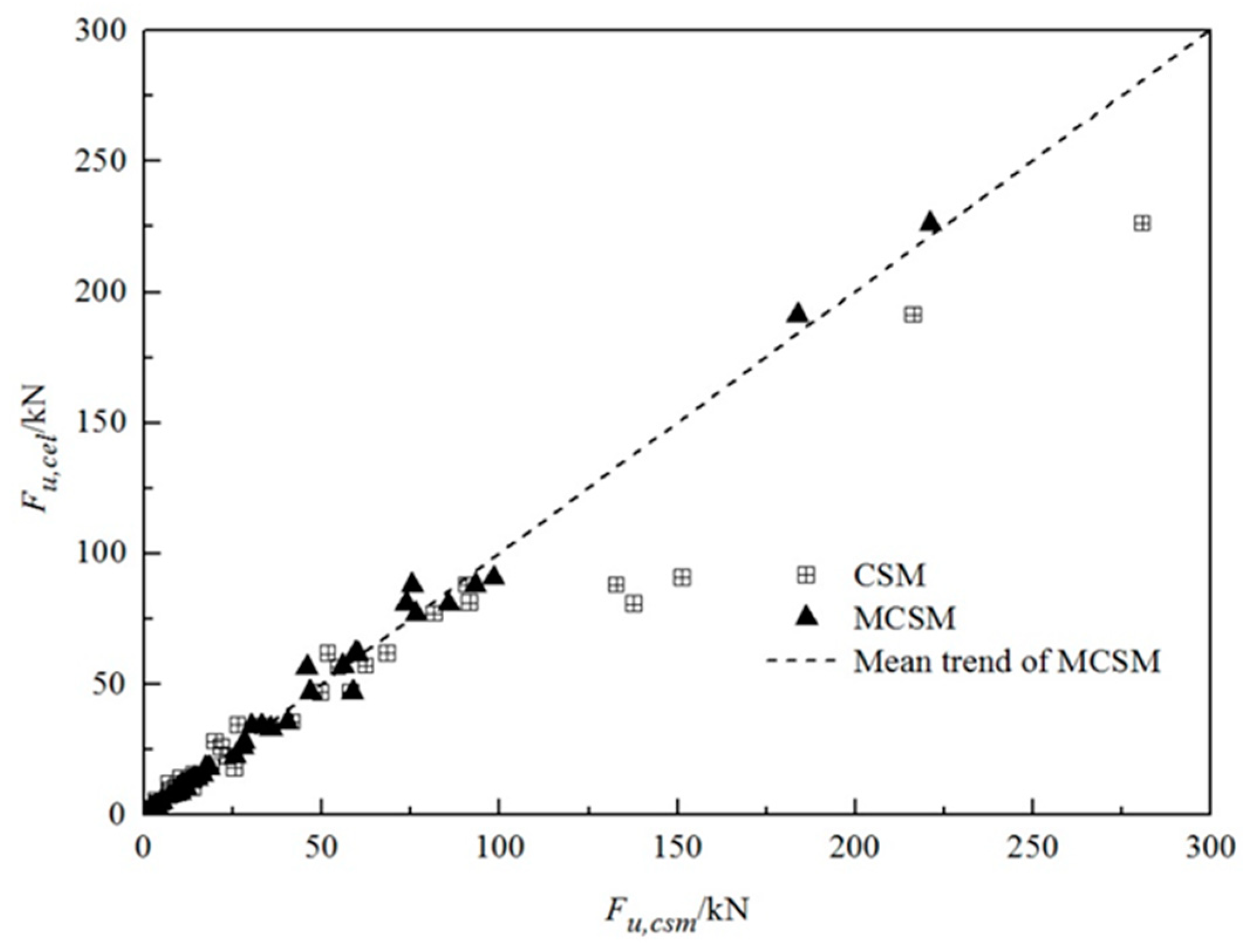
5.5. Comparison of CSM and Load Tests
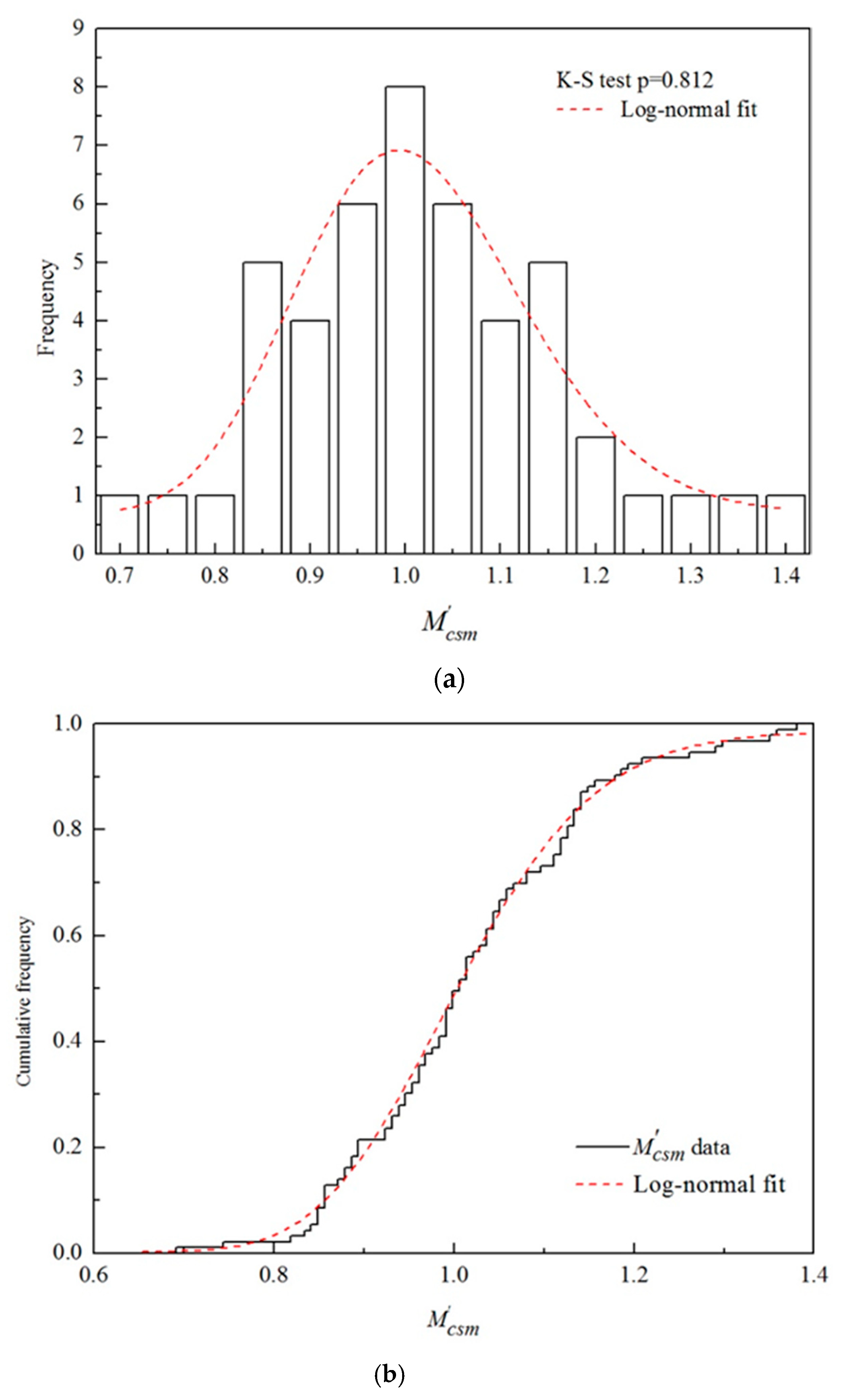
5.5.1. Probability Model for the Modified Model Factor M′csm
5.5.2. Validation of Model Factor M′csm
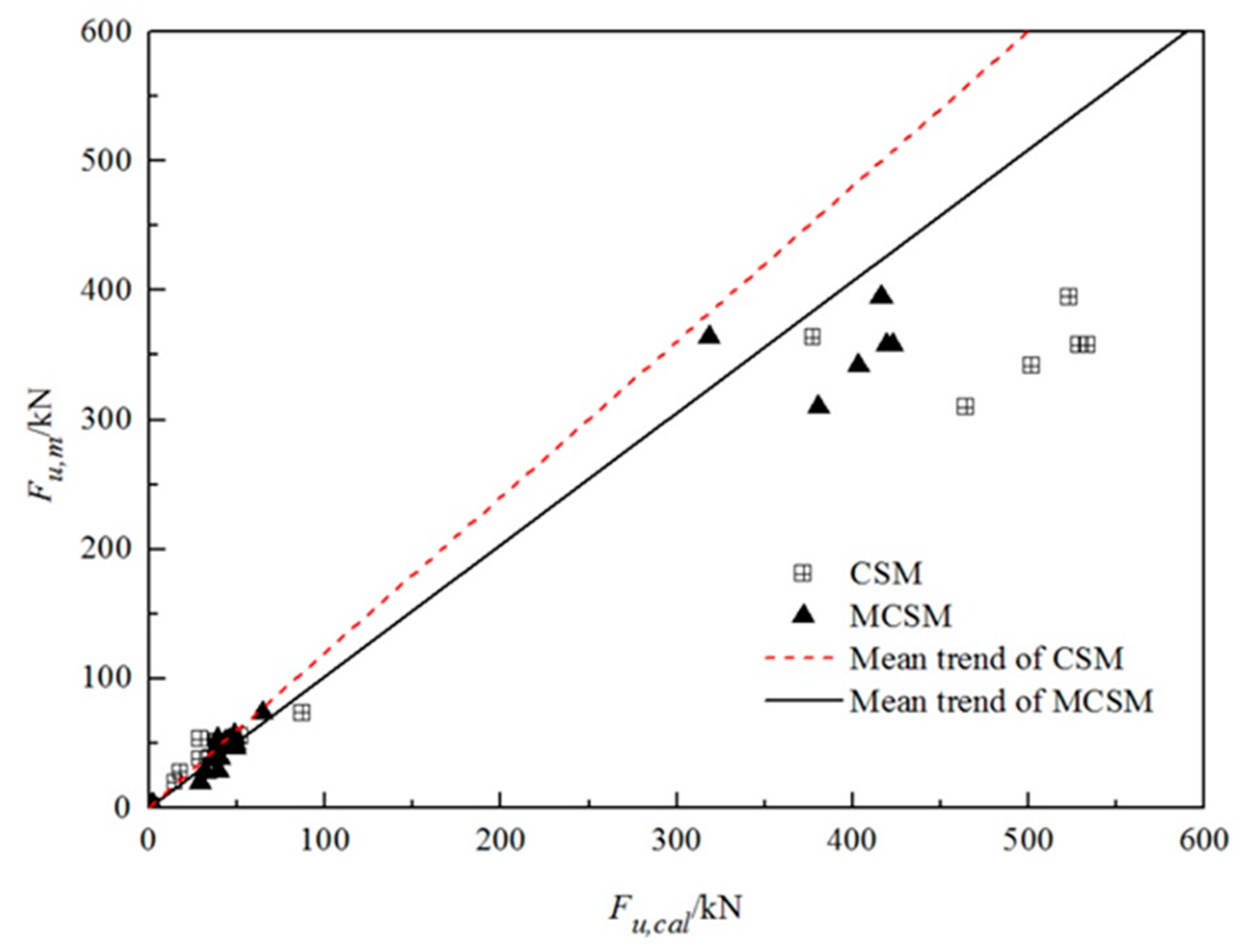
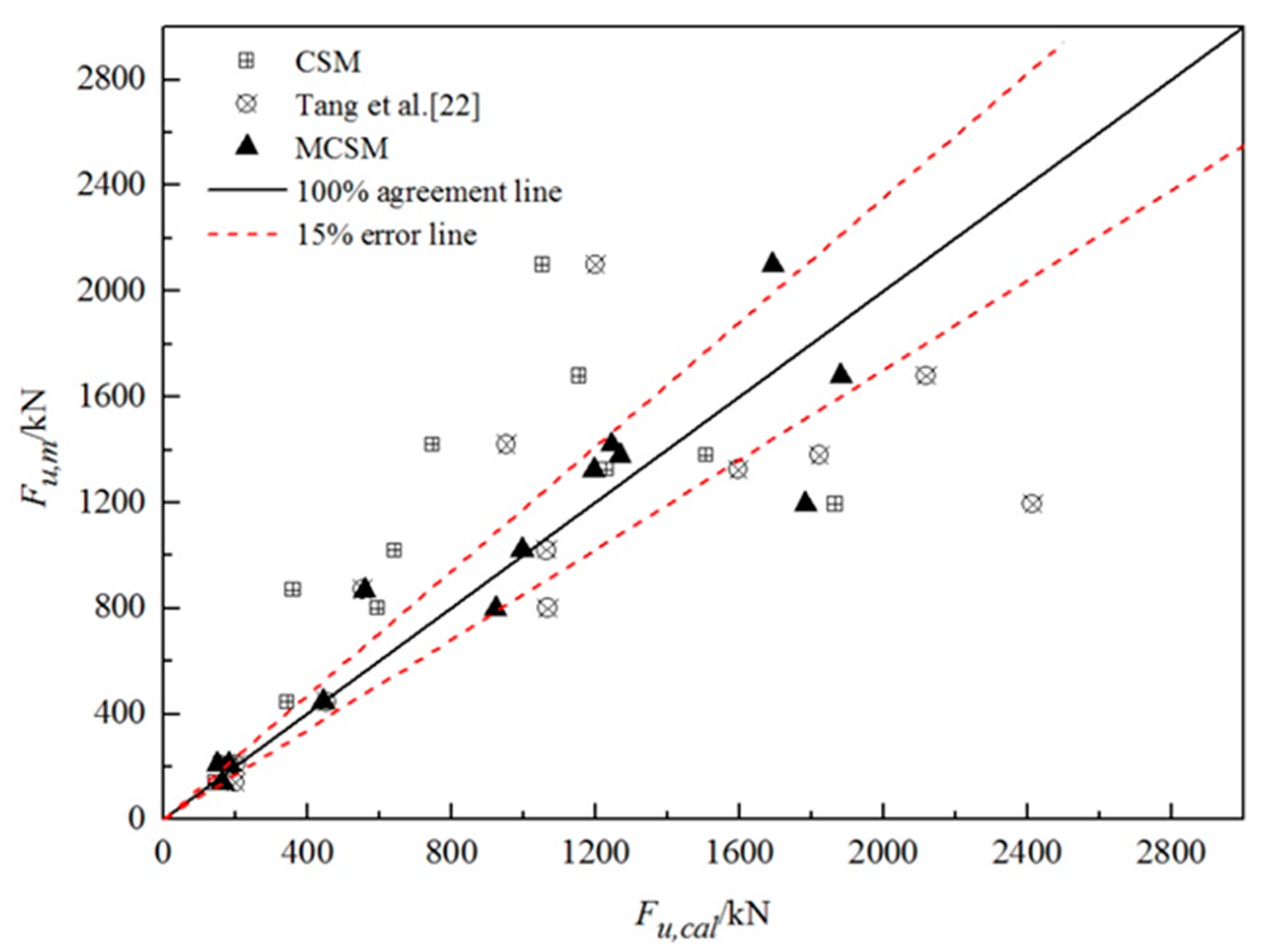
6. Comparison of Prediction Accuracy of MCSM, MCSM in Tang and Phoon [22], and Original CSM
6.1. Load Test Database for Comparing Prediction Accuracy
6.2. Results of Accuracy Comparison
7. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Byrne, B.W.; Houlsby, G.T. Helical piles: An innovative foundation design option for offshore wind turbines. Philos. Trans. R. Soc. A 2015, 373, 20140081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cortes-Garcia, L.D.; Landon, M.E.; Gallant, A.P.; Huguenard, K.D. Assessment of Helical Anchor Capacity in Marine Clays for Aquaculture Applications. In Proceedings of the Geo-Congress 2019, Reston, VA, USA, 24–27 March 2019; pp. 299–307. [Google Scholar]
- Rao, S.N.; Prasad, Y.V.S.N.; Shetty, M.D. The behaviour of model screw piles in cohesive soils. Soils Found. 1991, 31, 35–50. [Google Scholar] [CrossRef] [Green Version]
- Rao, S.N.; Prasad, Y.V.S.N.; Veeresh, C. Behaviour of embedded model screw anchors in soft clays. Geotechnique 1993, 43, 605–614. [Google Scholar] [CrossRef]
- Mooney, J.S.; Adamczak, S.; Clemence, S.P. Uplift capacity of helix anchors in clay and silt. In Proceedings of the Uplift Behavior of Anchor Foundations in Soil, Detroit, MI, USA, 24 October 1985; pp. 48–72. [Google Scholar]
- Stuedlein, A.W.; Holtz, R.D. Bearing Capacity of Spread Footings on Aggregate Pier Reinforced Clay. J. Geotech. Geo Environ. Eng. 2013, 139, 49–58. [Google Scholar] [CrossRef]
- Lutenegger, A.J. Cylindrical Shear or Plate Bearing—Uplift Behavior of Multi-Helix Screw Anchors in Clay. In Proceedings of the International Foundation Congress & Equipment Expo, Orlando, FL, USA, 15–19 March 2009; pp. 456–463. [Google Scholar]
- Hubbell, Inc. Chance® Technical Design Manual-Edition 3. A. B. Chance Div., Hubbel, Inc. 2014. Available online: http://www.ebsgeo.com/ModuleFile/getFile_Chance%20%C2%AE%20Technical%20Design%20Manual%20-%20Edition%203?id=2181 (accessed on 21 September 2020).
- Merifield, R.S. Ultimate uplift capacity of multiplate helical type anchors in clay. J. Geotech. Geo Environ. Eng. 2011, 137, 704–716. [Google Scholar] [CrossRef]
- Wang, D.; Merifield, R.S.; Gaudin, C. Uplift behaviour of helical anchors in clay. Can. Geotech. J. 2013, 50, 575–584. [Google Scholar] [CrossRef]
- Kwon, O.; Lee, J.; Kim, G.; Kim, I.; Lee, J. Investigation of pullout load capacity for helical anchors subjected to inclined loading conditions using coupled Eulerian-Lagrangian analyses. Comput. Geotech. 2019, 111, 66–75. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Dithinde, M.; Phoon, K.K.; Ching, J.; Zhang, L.; Retief, J.V. Statistical characterization of model uncertainty. Reliab. Geotech. Struct. ISO2394 2016, 5, 127–158. [Google Scholar] [CrossRef]
- Yi, J.T.; Huang, L.Y.; Li, D.Q.; Li, Y. A large-deformation random finite-element study: Failure mechanism and bearing capacity of spudcan in a spatially varying clayey seabed. Geotechnique 2019, 70, 392–405. [Google Scholar] [CrossRef]
- Yi, J.T.; Pan, Y.T.; Huang, L.Y.; Xu, S.J.; Liu, Y.; Phoon, K.K. Determination of limiting cavity depths for offshore spudcan foundations in a spatially varying seabed. Mar. Struct. 2020. [Google Scholar] [CrossRef]
- Peng, Y.; Ding, X.; Xiao, Y.; Deng, X.; Deng, W. Detailed amount of particle breakage in nonuniformly graded sands under one-dimensional compression. Can. Geotech. J. 2020, 57, 1239–1246. [Google Scholar] [CrossRef]
- Joint Committee on Structural Safety. Probabilistic Model Code; Joint Committee on Structural Safety, 2006. Available online: https://www.jcss-lc.org (accessed on 21 September 2020).
- Lesny, K.; Akbas, S.O.; Bogusz, W.; Burlon, S.; Vessia, G.; Phoon, K.K.; Tang, C.; Zhang, L. Evaluation and consideration of model uncertainties in reliability based design. In Joint ISSMGE TC 205/TC 304 Working Group on “Discussion of Statistical/Reliability Methods for Eurocodes, 20-64; International Society for Soil Mechanics and Geotechnical Engineering: London, UK, 2017; Available online: http://www.icsmge2017.org/download/19th%20ICSMGE_Workshop_TC205&304.pdf (accessed on 21 September 2020).
- DNV. Recommended Practice: Statistical Representationof Soil Data. DNVGL-RP-C207; Det Norske Veritas (DNV): Oslo, Norway, 2017. [Google Scholar]
- Zhang, D.M.; Phoon, K.K.; Huang, H.W.; Hu, Q.F. Characterization of Model Uncertainty for Cantilever Deflections in Undrained Clay. J. Geotech. Geo Environ. Eng. 2015, 141, 04014088. [Google Scholar] [CrossRef] [Green Version]
- Phoon, K.K.; Tang, C. Model Uncertainty for the Capacity of Strip Footings under Positive Combined Loading. In Geotechnical Safety and Reliability; ASCE: Denver, CO, USA, 4–7 June 2017; pp. 40–60. [Google Scholar] [CrossRef]
- Tang, C.; Phoon, K.K. Model uncertainty of cylindrical shear method for calculating the uplift capacity of helical anchors in clay. Eng. Geol. 2016, 207, 14–23. [Google Scholar] [CrossRef]
- Phoon, K.K.; Tang, C. Characterisation of geotechnical model uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 101–130. [Google Scholar] [CrossRef]
- Kulhawy, F.H. Uplift behavior of shallow soil anchors-an overview. In Uplift Behavior of Anchor Foundation in Soil; ASCE: New York, NY, USA, 1985; pp. 1–25. [Google Scholar]
- Qiu, G.; Henke, S.; Grabe, J. Application of a Coupled Eulerian–Lagrangian approach on geomechanical problems involving large deformations. Comput. Geotech. 2011, 38, 30–39. [Google Scholar] [CrossRef]
- Liu, F.; Yi, J.; Cheng, P.; Yao, K. Numerical simulation of set-up around shaft of XCC pile in clay. Geomech. Eng. 2020, 21, 489–501. [Google Scholar] [CrossRef]
- Merifield, R.S.; Lyamin, A.V.; Sloan, S.W.; Yu, H.S. Three-Dimensional Lower Bound Solutions for Stability of Plate Anchors in Clay. J. Geotech. Geo Environ. Eng. 2003, 129, 243–253. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Hu, Y.; Randolph, M. Three-dimensional large deformation finite-element analysis of plate anchors in uniform clay. J. Geotech. Geo Environ. Eng. 2010, 136, 355–365. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, O.; Kim, I.; Kim, G.; Lee, J. Cyclic pullout behavior of helical anchors for offshore floating structures under inclined loading condition. Appl. Ocean Res. 2019, 92, 101937. [Google Scholar] [CrossRef]
- Osman, A.S.; Bolton, M.D. A new design method for retaining walls in clay. Can. Geotech. J. 2004, 41, 451–466. [Google Scholar] [CrossRef]
- Kung, G.T.; Juang, C.H.; Hsiao, E.C.L.; Hashash, Y.M.A. Simplified Model for Wall Deflection and Ground-Surface Settlement Caused by Braced Excavation in Clays. J. Geotech. Geo Environ. Eng. 2007, 133, 731–747. [Google Scholar] [CrossRef]
- Tan, O.; Zaimoglu, A.S.; Hinislioglu, S.; Altun, S. Taguchi approach for optimization of the bleeding on cement-based grouts. Tunn. Undergr. Space Technol. 2005, 20, 167–173. [Google Scholar] [CrossRef]
- Tappenden, K.M.; Sego, D.C. Predicting the Axial Capacity of Screw Piles Installed in Canadian Soils. In Proceedings of the Canadian Geotechnical Conference, Ottawa, ON, Canada, 21–25 October 2007; pp. 1608–1615. [Google Scholar]
- Sakr, M. Helical Piles for Power Transmission Lines: Case Study in Northern Manitoba Canada; Almita Manufacturing Ltd.: Ponoka, AB, Canada, 2008. [Google Scholar]
- Sakr, M. Installation and Performance Characteristics of High Capacity Helical Piles in Cohesive Soils. DFI J. J. Deep Found. Inst. 2012. [Google Scholar] [CrossRef]
- Harnish, J.; Naggar, M.H.E. Large-diameter helical pile capacity—Torque correlations. Can. Geotech. J. 2017, 54, 968–986. [Google Scholar] [CrossRef] [Green Version]



| References | Serial Number | n | D/(m) | H/D | S/D | su/(kPa) | Fu,m/(kN) |
|---|---|---|---|---|---|---|---|
| Rao et al. [3] | 1 | 3 | 0.075 | 6.13 | 2 | 13.5 | 1.86 |
| 2 | 3 | 0.1 | 1.53 | 1.53 | 7.1 | 0.73 | |
| 3 | 2 | 0.1 | 2.29 | 2.29 | 7.1 | 0.97 | |
| 4 | 2 | 0.075 | 6.13 | 1.67 | 6.2 | 0.65 | |
| 5 | 4 | 0.075 | 6.13 | 1.33 | 6.2 | 0.9 | |
| 6 | 3 | 0.1 | 1.53 | 1.53 | 7.1 | 1.34 | |
| 7 | 2 | 0.15 | 1.53 | 1.53 | 7.1 | 1.67 | |
| 8 | 2 | 0.1 | 2.29 | 2.29 | 7.1 | 0.63 | |
| 9 | 3 | 0.1 | 1.53 | 1.53 | 7.1 | 0.97 | |
| 10 | 3 | 0.15 | 1.02 | 1.02 | 7.1 | 1.72 | |
| 11 | 3 | 0.075 | 6.13 | 2 | 6.2 | 0.83 | |
| 12 | 3 | 0.075 | 6.13 | 0.83 | 13.5 | 1.48 | |
| 13 | 4 | 0.075 | 6.13 | 1.33 | 13.5 | 2.13 | |
| 14 | 2 | 0.075 | 6.13 | 1.67 | 13.5 | 1.19 | |
| 15 | 2 | 0.1 | 2.29 | 2.29 | 7.1 | 0.91 | |
| 16 | 3 | 0.075 | 6.13 | 0.83 | 6.2 | 0.71 | |
| Rao et al. [4] | 17 | 4 | 0.033 | 6 | 1.5 | 4.4 | 0.113 |
| 18 | 3 | 0.033 | 1.5 | 1.5 | 3 | 0.046 | |
| 19 | 5 | 0.033 | 8 | 1.1 | 3 | 0.087 | |
| 20 | 5 | 0.033 | 4 | 1.1 | 3 | 0.074 | |
| 21 | 4 | 0.075 | 5 | 1.3 | 7.7 | 0.973 | |
| 22 | 5 | 0.033 | 10 | 1.1 | 3 | 0.093 | |
| 23 | 3 | 0.075 | 8 | 2 | 7.7 | 1.02 | |
| 24 | 5 | 0.033 | 1 | 1.1 | 4.4 | 0.084 | |
| 25 | 2 | 0.033 | 2.3 | 2.3 | 3 | 0.043 | |
| 26 | 3 | 0.033 | 8 | 2.3 | 3 | 0.083 | |
| 27 | 3 | 0.075 | 1.3 | 1.3 | 7.7 | 0.605 | |
| 28 | 3 | 0.033 | 4 | 2.3 | 3 | 0.071 | |
| 29 | 5 | 0.033 | 6 | 1.1 | 4.4 | 0.113 | |
| 30 | 4 | 0.033 | 10 | 1.5 | 4.4 | 0.127 | |
| 31 | 4 | 0.075 | 1 | 1.3 | 7.7 | 0.691 | |
| 32 | 4 | 0.033 | 2 | 1.5 | 4.4 | 0.094 | |
| 33 | 3 | 0.033 | 10 | 2.3 | 4.4 | 0.124 | |
| 34 | 4 | 0.033 | 3 | 1.5 | 4.4 | 0.1 | |
| 35 | 3 | 0.033 | 1 | 2.3 | 3 | 0.055 | |
| 36 | 3 | 0.033 | 6 | 2.3 | 4.4 | 0.11 | |
| 37 | 3 | 0.033 | 2 | 2.3 | 3 | 0.062 | |
| 38 | 4 | 0.075 | 2 | 1.3 | 7.7 | 0.784 | |
| 39 | 4 | 0.075 | 8 | 1.3 | 7.7 | 1.05 | |
| 40 | 3 | 0.075 | 4 | 2 | 7.7 | 0.884 | |
| 41 | 3 | 0.075 | 3 | 2 | 7.7 | 0.839 | |
| 42 | 5 | 0.033 | 3 | 1.1 | 3 | 0.069 | |
| 43 | 4 | 0.033 | 3 | 1.5 | 3 | 0.069 | |
| 44 | 4 | 0.033 | 8 | 1.5 | 4.4 | 0.119 | |
| 45 | 2 | 0.033 | 2.3 | 2.3 | 4.4 | 0.065 | |
| 46 | 4 | 0.033 | 2 | 1.5 | 3 | 0.066 | |
| 47 | 5 | 0.033 | 2 | 1.1 | 3 | 0.066 | |
| 48 | 5 | 0.033 | 10 | 1.1 | 4.4 | 0.127 | |
| 49 | 4 | 0.033 | 1.1 | 1.1 | 4.4 | 0.068 | |
| 50 | 4 | 0.033 | 1 | 1.5 | 4.4 | 0.083 | |
| 51 | 4 | 0.033 | 6 | 1.5 | 3 | 0.08 | |
| 52 | 4 | 0.033 | 8 | 1.5 | 3 | 0.087 | |
| 53 | 3 | 0.075 | 1 | 2 | 7.7 | 0.662 | |
| 54 | 3 | 0.033 | 10 | 2.3 | 3 | 0.09 | |
| 55 | 5 | 0.033 | 8 | 1.1 | 4.4 | 0.118 | |
| 56 | 3 | 0.033 | 3 | 2.3 | 3 | 0.065 | |
| 57 | 5 | 0.033 | 6 | 1.1 | 3 | 0.081 | |
| 58 | 3 | 0.033 | 8 | 2.3 | 4.4 | 0.116 | |
| 59 | 5 | 0.033 | 1 | 1.1 | 3 | 0.059 | |
| 60 | 3 | 0.033 | 2 | 2.3 | 4.4 | 0.091 | |
| 61 | 3 | 0.033 | 6 | 2.3 | 3 | 0.077 | |
| 62 | 5 | 0.033 | 4 | 1.1 | 4.4 | 0.104 | |
| 63 | 4 | 0.033 | 1 | 1.5 | 3 | 0.058 | |
| 64 | 3 | 0.033 | 1 | 2.3 | 4.4 | 0.082 | |
| 65 | 3 | 0.075 | 2 | 2 | 7.7 | 0.755 | |
| 66 | 4 | 0.075 | 4 | 1.3 | 7.7 | 0.94 | |
| 67 | 3 | 0.033 | 1.5 | 1.5 | 4.4 | 0.068 | |
| 68 | 5 | 0.033 | 3 | 1.1 | 4.4 | 0.099 | |
| 69 | 5 | 0.033 | 2 | 1.1 | 4.4 | 0.094 | |
| 70 | 3 | 0.075 | 5 | 2 | 7.7 | 0.922 | |
| 71 | 4 | 0.075 | 3 | 1.3 | 7.7 | 0.889 | |
| 72 | 4 | 0.033 | 10 | 1.5 | 3 | 0.094 | |
| 73 | 4 | 0.033 | 4 | 1.5 | 4.4 | 0.104 | |
| 74 | 3 | 0.033 | 4 | 2.3 | 4.4 | 0.102 | |
| 75 | 3 | 0.033 | 3 | 2.3 | 4.4 | 0.096 | |
| 76 | 4 | 0.033 | 4 | 1.5 | 3 | 0.074 | |
| 77 | 2 | 0.075 | 2 | 2 | 7.7 | 0.562 | |
| 78 | 4 | 0.033 | 1.1 | 1.1 | 3 | 0.046 |
| References | Serial Number | n | D/(m) | H/D | S/D | su/(kPa) | Fu,m/(kN) |
|---|---|---|---|---|---|---|---|
| Mooney et al. [5] | 79 | 3 | 0.248 | 4 | 0.92 | 48 | 53.2 |
| 80 | 3 | 0.248 | 4 | 0.92 | 48 | 53.2 | |
| 81 | 3 | 0.248 | 8 | 0.92 | 48 | 49.4 | |
| 82 | 3 | 0.248 | 8 | 0.92 | 48 | 51.7 | |
| 83 | 3 | 0.248 | 10 | 0.92 | 48 | 49.5 | |
| 84 | 3 | 0.248 | 10 | 0.92 | 48 | 47.2 | |
| 85 | 3 | 0.248 | 12 | 0.92 | 48 | 49.6 | |
| 86 | 3 | 0.248 | 12 | 0.92 | 48 | 46.9 | |
| Stuedlein [6] | 87 | 5 | 0.345 | 19 | 3 | 93 | 342 |
| 88 | 5 | 0.345 | 19 | 3 | 99 | 358 | |
| 89 | 4 | 0.33 | 19 | 3 | 97 | 364 | |
| 90 | 5 | 0.345 | 19 | 3 | 98 | 358 | |
| 91 | 5 | 0.345 | 19 | 3 | 97 | 395 | |
| 92 | 5 | 0.345 | 19 | 3 | 86 | 310 | |
| 93 | 4 | 0.33 | 19 | 3 | 85 | 516 | |
| Lutenegger [7] | 94 | 3 | 0.2 | 28 | 0.75 | 31 | 20 |
| 95 | 3 | 0.2 | 23 | 3 | 31 | 29 | |
| 96 | 3 | 0.2 | 27 | 1.13 | 31 | 27.9 | |
| 97 | 3 | 0.2 | 26 | 1.5 | 31 | 18.6 | |
| 98 | 3 | 0.2 | 25 | 2.25 | 31 | 22.4 | |
| 99 | 3 | 0.2 | 13 | 0.75 | 61 | 37.9 | |
| 100 | 3 | 0.2 | 12 | 1.13 | 61 | 38.9 | |
| 101 | 3 | 0.2 | 11 | 1.5 | 61 | 51.1 | |
| 102 | 3 | 0.2 | 10 | 2.25 | 61 | 55.7 | |
| 103 | 4 | 0.2 | 8 | 3 | 61 | 73.5 |
| Variables Parameters | H/D | n | S/D | |
|---|---|---|---|---|
| 0.783 | 0.599 | 0.106 | 0.303 | |
| 0.711 | 0.810 | 0.766 | 0.823 | |
| 0.516 | 0.489 | 0.111 | 0.280 |
| Parameters | Range of Values | VIF |
|---|---|---|
| H/su | 0.4–2.2 | 1.01 |
| H/D | 1–10 | 1.11 |
| n | 2–5 | 1.08 |
| S/D | 0.3–3.0 | 1.04 |
| Coefficients | Values |
|---|---|
| 0.823 | |
| −0.068 | |
| −0.172 | |
| −0.056 | |
| 0.161 |
| References | Test Number | n | D/(m) | Embedment Depth/(m) | S/D | su/(kPa) | Fu,m/(kN) |
|---|---|---|---|---|---|---|---|
| Tappenden [33] | T1 | 1 | 0.762 | 5.9 | 145 | 800 | |
| T2 | 2 | 0.356 | 5 | 3 | 75 | 210 | |
| T3 | 2 | 0.762 | 6 | 3 | 145 | 1325 | |
| T4 | 3 | 0.356 | 5 | 1.5 | 75 | 210 | |
| T5 | 3 | 0.356 | 3 | 1.5 | 75 | 140 | |
| Sakr [34] | T6 | 3 | 0.711 | 7.9 | 3 | 24 | 445 |
| Sakr [35] | T7 | 1 | 0.914 | 5.6 | 225 | 1680 | |
| T8 | 2 | 0.762 | 5.9 | 3 | 225 | 1195 | |
| T9 | 2 | 0.813 | 14.3 | 2 | 83 | 1420 | |
| T10 | 2 | 0.813 | 18.5 | 2 | 117.5 | 2100 | |
| Harnish and El Naggar [36] | T11 | 1 | 0.457 | 6.86 | 244 | 870 | |
| T12 | 1 | 0.610 | 6.86 | 244 | 1020 | ||
| T13 | 2 | 0.610 | 6.86 | 3 | 244 | 1380 |
| Test Number | Relative Error of CSM(%) | Tang’s Method Predicted Capacity/(kN) | Relative Error of Tang’s Method(%) | Relative Error of MCSM(%) | |||
|---|---|---|---|---|---|---|---|
| T1 | 800 | 595.13 | −25.61 | 1067.65 | 33.46 | 923.43 | 15.43 |
| T2 | 210 | 158.69 | −24.44 | 185.63 | −11.60 | 150.49 | −28.34 |
| T3 | 1325 | 1229.51 | −7.21 | 1596.12 | 20.46 | 1195.90 | −9.74 |
| T4 | 210 | 158.69 | −24.44 | 201.09 | −4.24 | 181.98 | −13.34 |
| T5 | 140 | 143.58 | 2.55 | 199.71 | 42.65 | 163.79 | 17.00 |
| T6 | 445 | 343.59 | −22.79 | 453.17 | 1.84 | 443.65 | −0.30 |
| T7 | 1680 | 1155.21 | −31.24 | 2118.39 | 26.09 | 1881.95 | 12.02 |
| T8 | 1195 | 1866.40 | 56.18 | 2414.19 | 102.02 | 1783.45 | 49.24 |
| T9 | 1420 | 748.10 | −47.32 | 952.18 | −32.95 | 1245.36 | −12.30 |
| T10 | 2100 | 1052.57 | −49.88 | 1200.09 | −42.85 | 1692.07 | −19.43 |
| T11 | 870 | 360.21 | −58.60 | 553.75 | −36.35 | 559.35 | −35.71 |
| T12 | 1020 | 641.77 | −37.08 | 1063.75 | 4.29 | 996.58 | −2.30 |
| T13 | 1380 | 1507.10 | 9.21 | 1822.32 | 32.05 | 1269.02 | −8.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, P.; Yi, J.T.; Liu, F.; Dong, J.J. Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils. J. Mar. Sci. Eng. 2020, 8, 738. https://doi.org/10.3390/jmse8100738
Cheng P, Yi JT, Liu F, Dong JJ. Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils. Journal of Marine Science and Engineering. 2020; 8(10):738. https://doi.org/10.3390/jmse8100738
Chicago/Turabian StyleCheng, Po, Jiang Tao Yi, Fei Liu, and Jun Jie Dong. 2020. "Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils" Journal of Marine Science and Engineering 8, no. 10: 738. https://doi.org/10.3390/jmse8100738
APA StyleCheng, P., Yi, J. T., Liu, F., & Dong, J. J. (2020). Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils. Journal of Marine Science and Engineering, 8(10), 738. https://doi.org/10.3390/jmse8100738




