Next Article in Journal
Sensitivity and Directivity Analysis of Piezoelectric Ultrasonic Cantilever-Based MEMS Hydrophone for Underwater Applications
Next Article in Special Issue
Storm Tide and Wave Simulations and Assessment
Previous Article in Journal
The Northward Habitat Expansion of the Korean Top Shell Turbo sazae (Gastropoda: Vetigastropoda: Turbinidae) in the Korean Peninsula: Effects of Increasing Water Temperature
Previous Article in Special Issue
On the Sensitivity of Typhoon Wave Simulations to Tidal Elevation and Current
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 8
Issue 10
10.3390/jmse8100783
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands

by
Zhehao Yang
1,
Weizeng Shao
1,2,*,
Yang Ding
3,
Jian Shi
4 and
Qiyan Ji
1
1
Marine Science and Technology College, Zhejiang Ocean University, Zhoushan 316022, China
2
National Satellite Ocean Application Service, Beijing 100081, China
3
Frontier Science Center for Deep Ocean Multispheres and Earth System (FDOMES) and Physical Oceanography Laboratory, Ocean University of China and Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, China
4
College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2020, 8(10), 783; https://doi.org/10.3390/jmse8100783
Submission received: 1 September 2020 / Revised: 1 October 2020 / Accepted: 5 October 2020 / Published: 8 October 2020
(This article belongs to the Special Issue Storm Tide and Wave Simulations and Assessment)
Browse Figures
Versions Notes

Abstract

:
In this study, the numerical wave model Simulating Waves Nearshore (SWAN), which resolves nearshore wave processes, and a hydrodynamic model, the Finite-Volume Community Ocean Model (FVCOM), were coupled to simulate waves and currents during Typhoon Fung-wong (2014) and Typhoon Chan-hom (2015) around the Zhoushan Islands. Both of these models employ the same unique unstructured grid. In particular, the influence of sea-surface currents, e.g., typhoon-induced and tidal currents, as well as the sea-water level, on wave simulation was studied. The composite wind field, which is derived from the parametric Holland model and European Centre for Medium-Range Weather Forecasts (ECMWF) winds (H-E winds), was taken as the forcing field. TPXO.5 tide data, sea-surface temperatures from the HYbrid Coordinate Ocean Model (HYCOM), HYCOM sea-surface salinity, and HYCOM sea-surface current were treated as open-boundary conditions. The comparison of sea-surface-current speed between the FVCOM simulation and the National Centers for Environmental Prediction (NCEP) Climate Forecast System Version 2 (CFSv2) data revealed a root-mean-square error (RMSE) of about 0.1206 m/s, with a correlation (Cor) more than 0.8, while the RMSE of the simulated sea-water level when compared with the HYCOM data was around 0.13 m, with a Cor of about 0.86. The validation indicated that the simulated results in this study were reliable. A sensitive experiment revealed that the sea-water level affected the typhoon-induced wave simulation. Validation against the measurements from the moored buoys showed an RMSE of <0.9 m for the sea-water level, which specifically reflected less overestimation during the high-sea state. Moreover, the significant-wave-height (SWH) difference (SWH without the sea-water level minus SWH with the sea-water level) was as great as −0.5 m around the Zhoushan Islands during the low-sea state. Furthermore, we studied the typhoon-induced waves when Typhoon Fung-wong passed the Zhoushan Islands, revealing that the reduction of SWH could be up to 1 m in the Yangtze Estuary and tidal flats when the maximum waves occurred.

1. Introduction

Sea surface waves play an important role in the air–sea interaction layer. In particular, tropical cyclones induce extreme waves, which are a type of destructive nearshore disaster affecting human activity and offshore oil platform facilities. Given this, wave simulation is a preeminent topic for the oceanography community, especially for coastal waters [1,2] and tropical cyclones [3,4]. Two types of third-generation numerical wave models are popular for wave simulation, i.e., WAVEWATCH-III (WW3) [5], developed by the National Oceanic and Atmospheric Administration/National Centers for Environmental Prediction (NOAA/NCEP), and Simulating Waves Nearshore (SWAN) [6], developed by the Delft University of Technology. Waves are often affected by mesoscale/large-scale circulations, e.g., currents can shift wave energy due to the Doppler effect, and sea-water levels have an impact on wave propagation and dissipation due to depth-limited wave breaking. In these circumstances, the wave–current interaction is highly complex, especially under extreme weather conditions.
It is well known that the SWAN model performs well in the nearshore region, while the WW3 model is widely used for simulating waves in the open sea [7,8]. The advantage of the SWAN model is the application of an unstructured triangular grid employing an analog of the Gauss–Seidel sweeping method, which can portray complex coastal regions and numerous barriers, especially those of islands [9,10]. The discrete implementation of the SWAN model requires special terms, e.g., the nonlinear interactions [11] due to changes in bathymetry, wave-current, and white-cap breaking, which affect the evolution of wind-induced waves. The SWAN model utilized in this study (version 41.20, released in May 2019) has been successfully applied to coastal seas, estuaries [12], reefs, and lakes [13]. Tropical cyclones exhibit complicated physical dynamics at various spatial scales during their movement [14,15,16]. Strong wind-induced waves are generated in deep water, and storm surges on the continental shelf are large, both of which propagate and are transformed in the complex nearshore environment due to rapid changes in bathymetry and bottom friction. Wave dissipation also spreads over long time periods and large spatial scales and smoothly varies on continental shelves, which should be considered, particularly near islands or other breaking zones. Storm surges raise sea-water levels and then interact with waves and currents [17]. These issues clearly influence wave simulations, especially for tropical cyclones [18]. In the typhoon-modeling applications around the Zhoushan Islands for depths ranging from tens of meters to ten kilometers in the East China Sea, the dynamics at various spatial scales necessitate the implementation of unstructured grids, ensuring a variable water depth from kilometers in the deeper East China Seas to hundreds of meters on the continental shelf and tens of meters near the coastal shorelines.
The Finite-Volume Community Ocean Model (FVCOM) [19,20] is a coastal ocean circulation model developed by the University of Massachusetts and the Woods Hole Oceanographic Institution [20]. Its basic features include (1) an unstructured grid, (2) a finite volume, (3) free surfaces, and (4) 3D primitive equations. Similar to the SWAN model, the FVCOM uses the unstructured grid approach, which is advantageous for resolving dynamics in regions with complex irregular geometry, while the finite-element/finite-difference methods provide good numerical representations of the equations for momentum, mass, salt, heat, and tracer conservation. Moreover, the FVCOM makes use of improved computational fluid dynamics in order to better illustrate the convergence of numerical solutions for flow discontinuities and large gradients [21]. A comparison between the FVCOM and the two finite-difference ocean models, i.e., the Princeton Ocean Model (POM) and the Estuarine and Coastal Ocean Model (ECOM), demonstrated that numerical accuracy is significantly improved by depicting the physics of waves, tides, and flow in the coastal oceans [22]. The FVCOM has also been employed to examine the oceanic response to hurricane activity [23,24,25], and experiments have revealed that it accurately illustrates tide- and wind-induced rises in the water level [26].
In our previous research [26,27], the performance of input/dissipation source-term packages in the WAVEWATCH-III model was investigated in typhoons using rectangular meshes. Specifically, it was found that currents can affect typhoon-induced wave simulations at current speeds > 0.5 m/s and have a significant influence at current speeds > 2 m/s [28]. Experiments concerning the influence of the sea-water level on wave simulation based on the FVCOM and SWAN have already been performed [29]. It has been demonstrated that it is critical to include tide and sea-water-level variations in shelf and nearshore wave simulations [30,31]. The sea water level could be significantly affected by strong tide and typhoon-induced wind in complex coastal seas and then modulate the wave properties. Therefore, in this study, the SWAN and FVCOM, with unstructured grids, were coupled in order to simulate the waves in two typhoons passing the Zhoushan Islands in the East China Sea. A sensitive experiment was also performed to analyze the impact of sea-water levels on the wave simulations.
The remainder of this manuscript is organized as follows. The dataset is introduced in Section 2, i.e., the selected typhoons, forcing fields, and open boundary data, as well as the ancillary data used for validation. The model settings for the SWAN and FVCOM simulations are also briefly described. The accuracy of the simulated sea-surface-current speeds, sea-water levels, and ocean waves is confirmed in Section 3, a discussion is presented in Section 4, and the conclusions are summarized in Section 5.

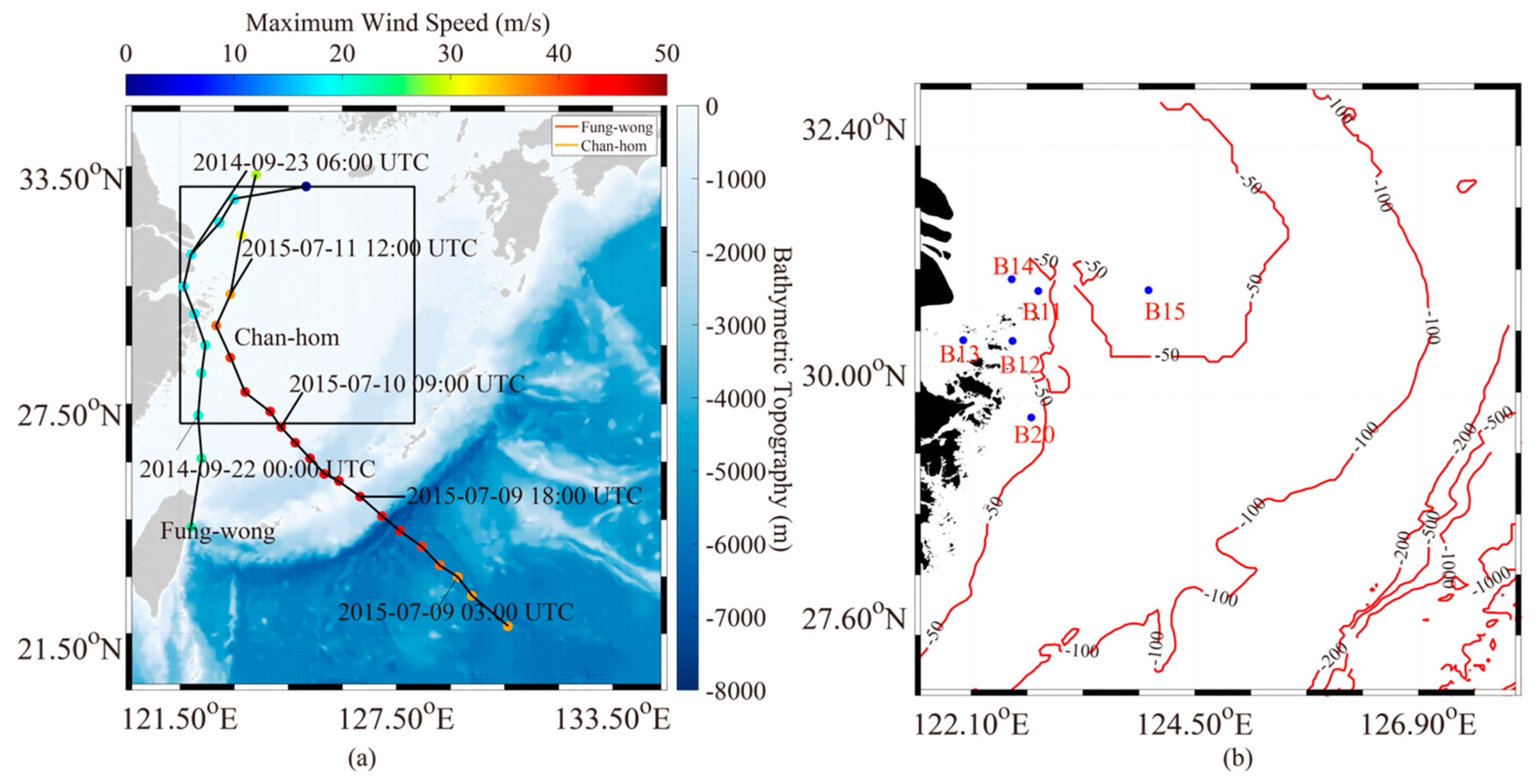
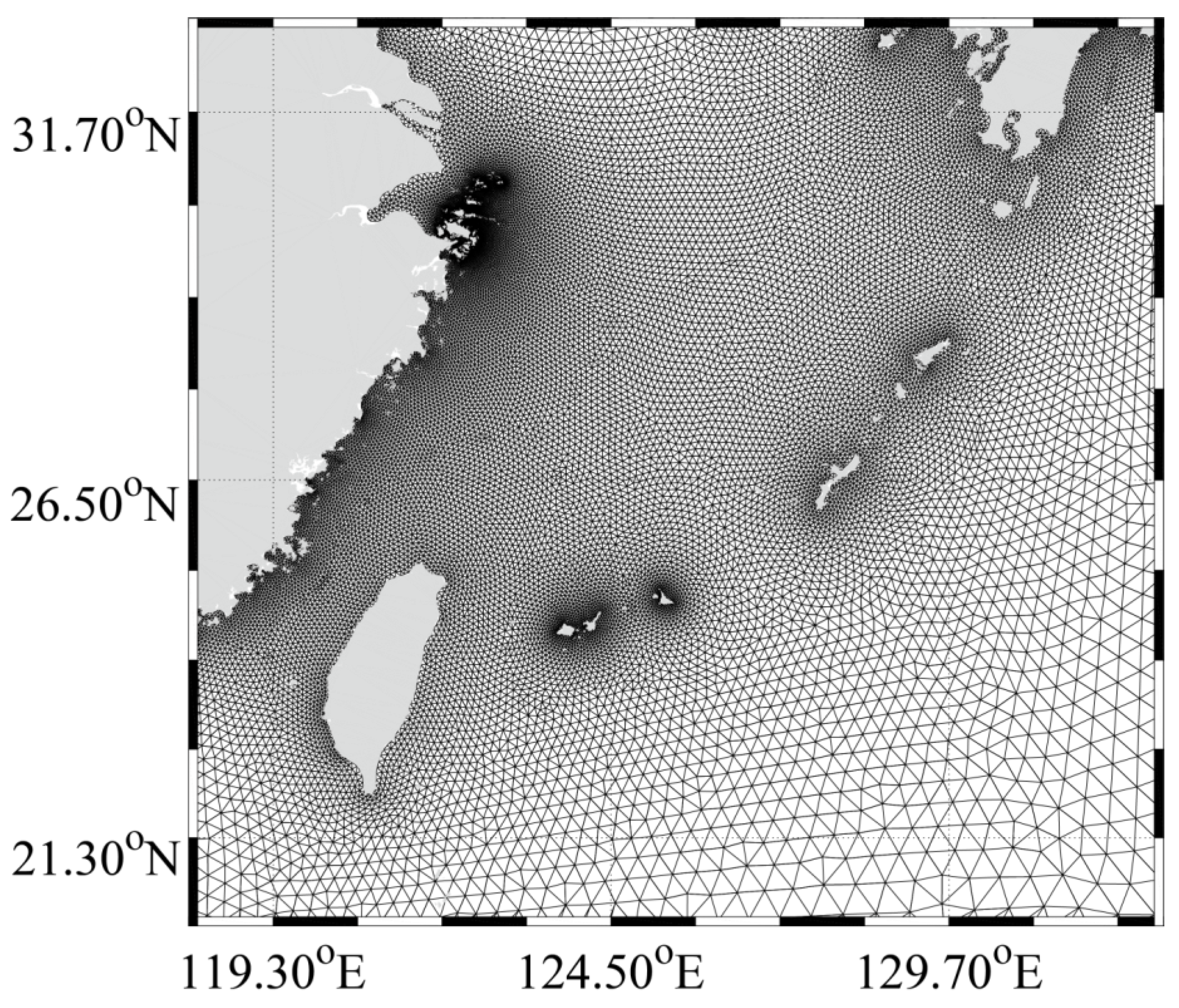
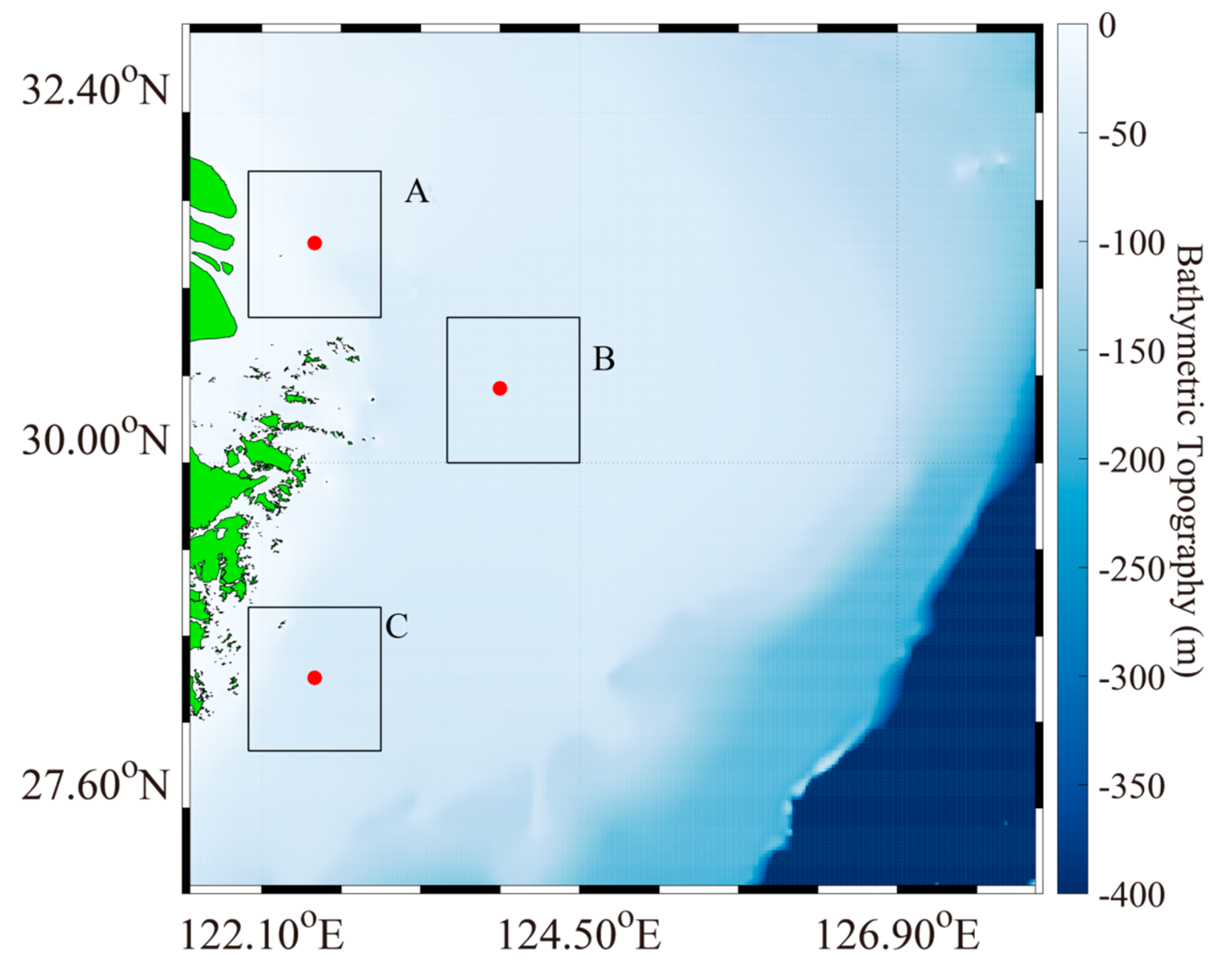
2. Dataset Collection and Methods

Two typhoons, Fung-wong and Chan-hom, which passed over the Zhoushan Islands from 17 to 25 September 2014 and 29 June to 12 July 2015, respectively, were selected. The data for the two cyclones were collected from the Tokyo-Typhoon Center of the Japan Meteorological Agency (JMA). The tracks of the two typhoons overlaid on the water-depth map are presented in Figure 1a, in which the black square encloses the waters around the Zhoushan Islands. It can be seen in Figure 1b that the water depth ranges from kilometers in the East China Seas to tens of meters at the coastal shorelines. In particular, there is a series of islands at the mouth of Hangzhou Bay, indicating that the buoys located between Hangzhou Bay and the island chain provide valuable data, since the strong tidal currents, typhoon-induced currents, and changes in sea-water levels all occur in this area. This confluence of factors provides us with the opportunity to investigate the effects of typhoon-induced current terms and storm water terms on wave simulation for typhoons.
Since 1979, the European Centre for Medium-Range Weather Forecasts (ECMWF) has helpfully provided atmospheric-marine data with a fine spatial resolution up to 0.125° (~12.5 km) at six-hour intervals every day. As for the analysis of global wave distributions, the ECMWF wind data are commonly used in the SWAN [32,33] and WW3 models [34,35,36]. In this study, however, a composite wind field, which was derived from the parametric Holland model and ECMWF winds (H-E winds), was taken as the forcing field for the model simulations. Specifically, the parametric Holland model was trained by fitting the shape parameter to buoy-measured observations (spots Bs in Figure 1b). The details of the H-E winds are discussed in Section 3 of [26], and the validation indicates a root-mean-square error (RMSE) less than 3 m/s for the shape parameter treated as a constant (0.4). Moreover, currents were also included in the wave simulation using the SWAN model [28]. The simulated waves in the East China Sea lasted from 1 September to 1 October 2014 and from 1 July to 1 August 2015. The modeling region was located between 20° and 35°N latitude and 120° and 135°E longitude, in which the bathymetric topography was provided by the General Bathymetric Chart of the Oceans (GEBCO) with a 0.01° (~1 km in the horizontal direction) gridded spatial resolution.
It is well known that storm water inundation is an important factor for assessing marine-hazard risks under extreme weather conditions [37] and also impacts wave simulation for coastal waters through various effects, e.g., wave-induced radiation stress, current–wave energy exchange, and bottom stress. Therefore, the sea-surface current and sea-water level were simulated with the FVCOM for the same region as the SWAN model, in which the H-E wind was the forcing field. The tide data from the TPXO.5 model, as well as the sea-surface temperature, sea-surface salinity, and sea-surface current values derived at 60-minute intervals at a 1/12° (~8 km) grid spatial resolution from the HYbrid Coordinate Ocean Model (HYCOM) were used for the open-boundary condition. The unstructured grids are illustrated in Figure 2 and are uniquely used in the SWAN and FVCOM simulations. It should be noted that the simulated currents lasted from 1 July to 1 October 2014 and from 1 May to 1 August 2015, to ensure the stability of the FVCOM [38]. The basic governing equations of the SWAN and FVCOM simulations are described in Appendix A and Appendix B, respectively. The details concerning the model settings for the FVCOM and SWAN are briefly presented in Table 1 and Table 2, respectively.
In order to validate the simulated current from the FVCOM, sea-surface-current data from the Climate Forecast System Version 2 (CFSv2) from the National Center of Atmospheric Research (NCAR) with a coarse spatial resolution (~50 km) were used [28,40]. As an example, the map of the CFSv2 current vectors at 06:00 UTC on 11 July 2015 during Typhoon Chan-hom is shown in Figure 3. Although the Kuroshio current in the Taiwan Strait is not very apparent in this figure due to the coarse spatial resolution, the strong wind-driven current with a spiral structure can be seen around the Zhoushan Islands. The FVCOM-simulated sea-water levels during the two typhoons were compared with results from the HYCOM data, which were officially released on the HYCOM’s homepage. Figure 4 shows the sea-water-level map from the HYCOM data at 12:00 UTC on 22 September 2014 during Typhoon Fung-wong, exhibiting the storm-surge pattern around the Zhoushan Islands. Moreover, a cyclonic pattern exists, as denoted by the black ellipse in Figure 4, which could be an indicator of offshore upwelling off eastern Guangdong Province, China [41]. In addition, wave measurements from the Jason-2 altimeter mission, which has proven to be good for wave monitoring over global seas [42], were collected during the simulation periods in order to validate the model-simulated waves, i.e., those generated by the WW3 [43] and SWAN [44] models. Figure 5 shows the footprints from the Jason-2 altimeter overlaid on the water-depth map of September 2014, from which the altimeter significant wave height (SWH) data covering the red square were used to validate the simulations by the SWAN model.

3. Results

In order to confirm the FVCOM output, its simulations of currents and sea-water levels were visualized and then compared with the CFSv2 and HYCOM data, respectively. In addition, waves from the SWAN model for the two typhoons were validated against the satellite altimeter observations.

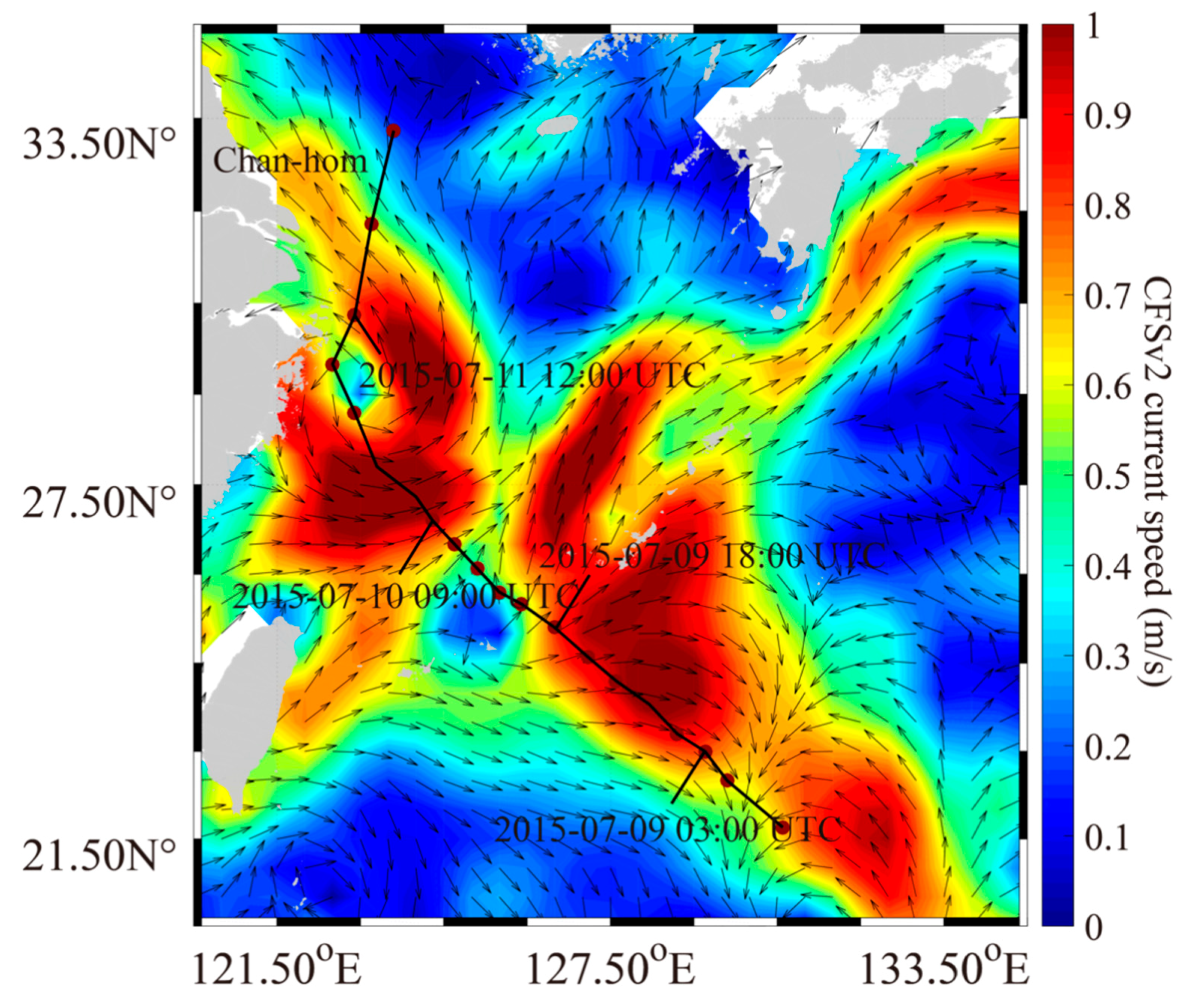
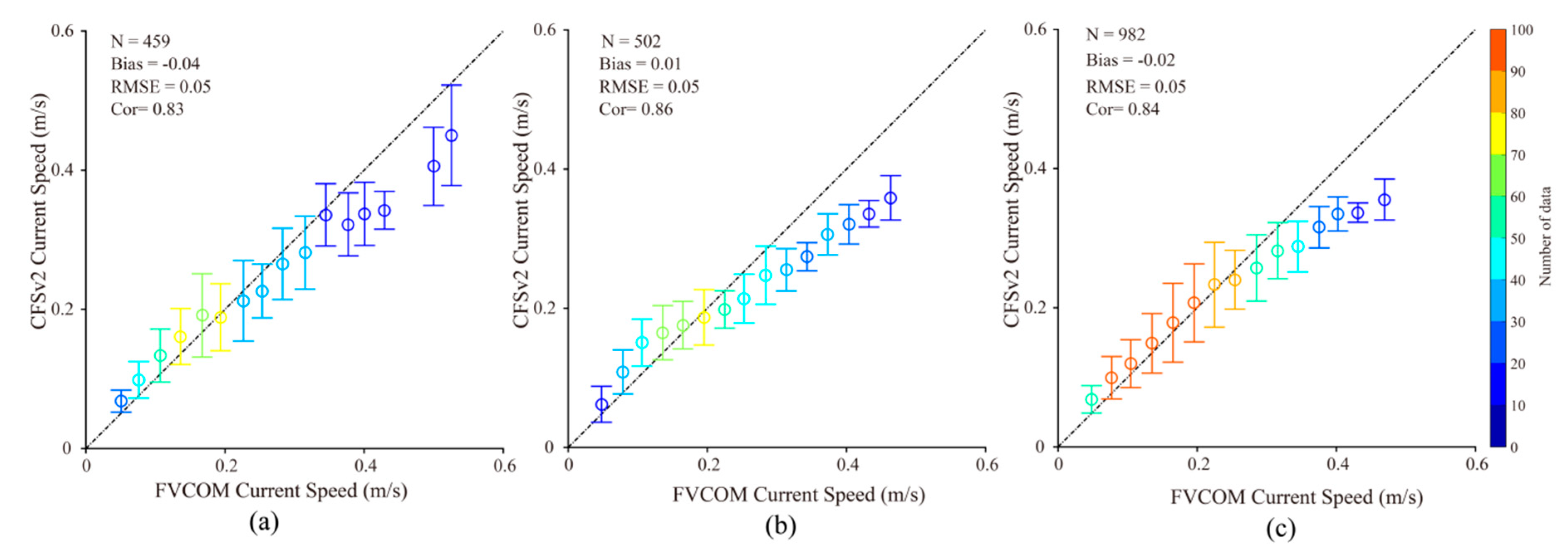
3.1. Simulation of Sea-Surface Current

Figure 6 shows the current maps from the FVCOM simulation for the periods of Typhoon Fung-wong and Typhoon Chan-hom, respectively. These two cases are located in the region around the Zhoushan Islands, corresponding to the red square in Figure 5. Figure 6a was captured at 13:00 UTC on 22 September 2014, and Figure 6b, at 06:00 UTC on 11 July 2015, when the typhoons were close to the Zhoushan Islands [26]. It is observed that the current speed away from the land increased significantly due to strong winds, reaching 1 m/s. In the region far from the Yangtze Estuary in Figure 6a, it can be seen that the current exhibited an approximate spiral pattern, which was induced by the cyclonic winds associated with the typhoon path in Figure 1a. This type of pattern is also clearly observed in Figure 6b, which is south of the Zhoushan Islands. Moreover, the currents (presumably due to the tides [45]) are well simulated around the Zhoushan Islands due to the fine spatial resolution of the triangular grid, although these currents are not apparent in Figure 3. To confirm the accuracy of the currents in the FVCOM model, CFSv2 data were directly employed. We selected three typical regions around the Zhoushan Islands to statistically analyze the current speed, as presented in Figure 7. Note that Region A is located in the Yangtze Estuary and tidal flats where the tidal current is relatively strong. In particular, three representative specific locations were also selected for studying the extreme waves later. Figure 8 shows the comparisons at Regions A to C, revealing that the RMSE of the current speed was around 0.6 m/s, with a correlation (Cor) more than 0.8. It was also found that the simulated current speeds from the FVCOM were generally higher than those from the CFSv2, with values > 0.3 m, probably caused by the typhoons. We believe that this sort of behavior is reasonable since the composite H-E winds were taken as the forcing field, thus indicating that the underestimation of the ECMWF winds was improved [46]. In particular, the maximum current speeds occur in the Yangtze Estuary and tidal flats, indicating that the tidal current is relatively strong in such regions [47].

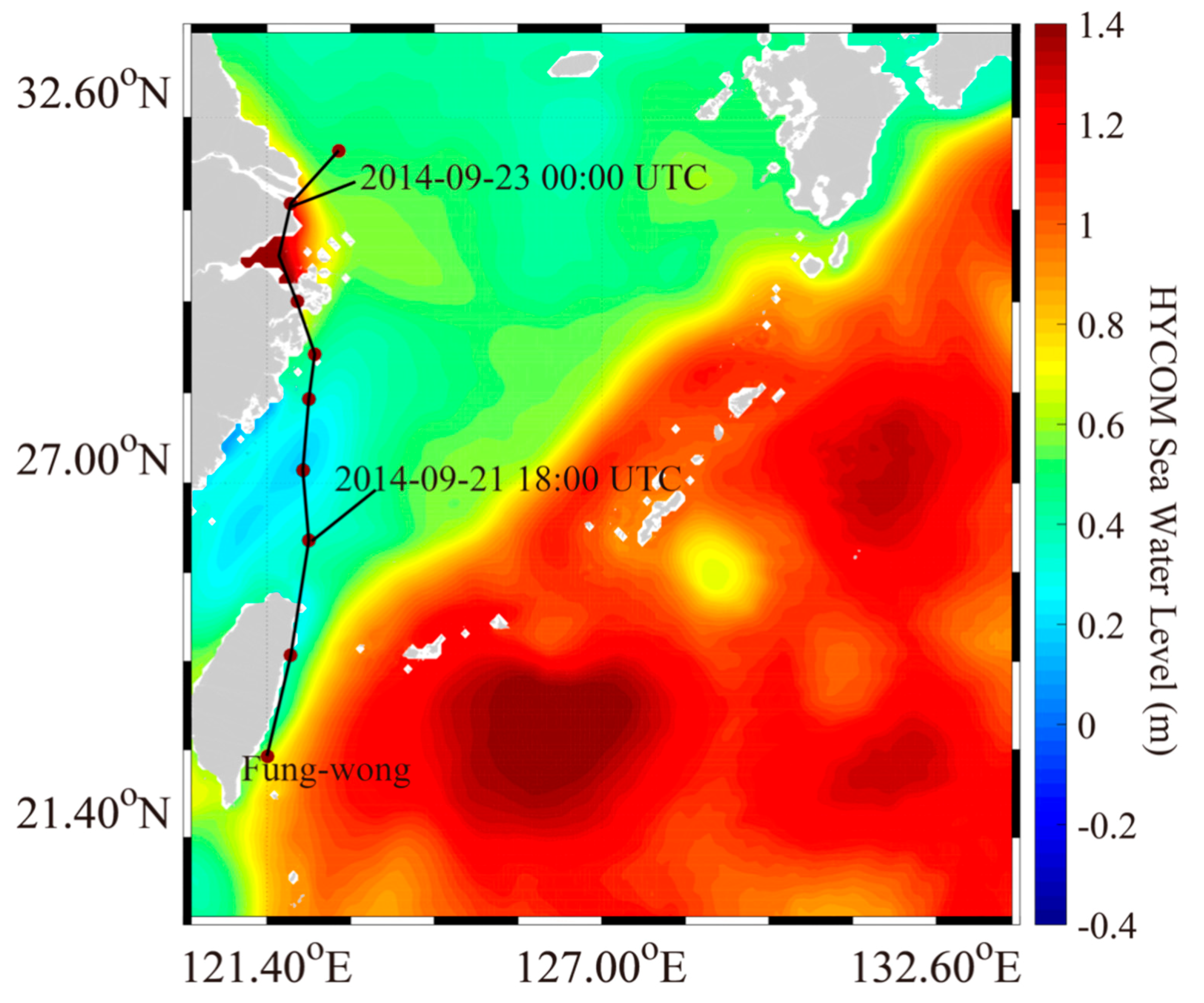
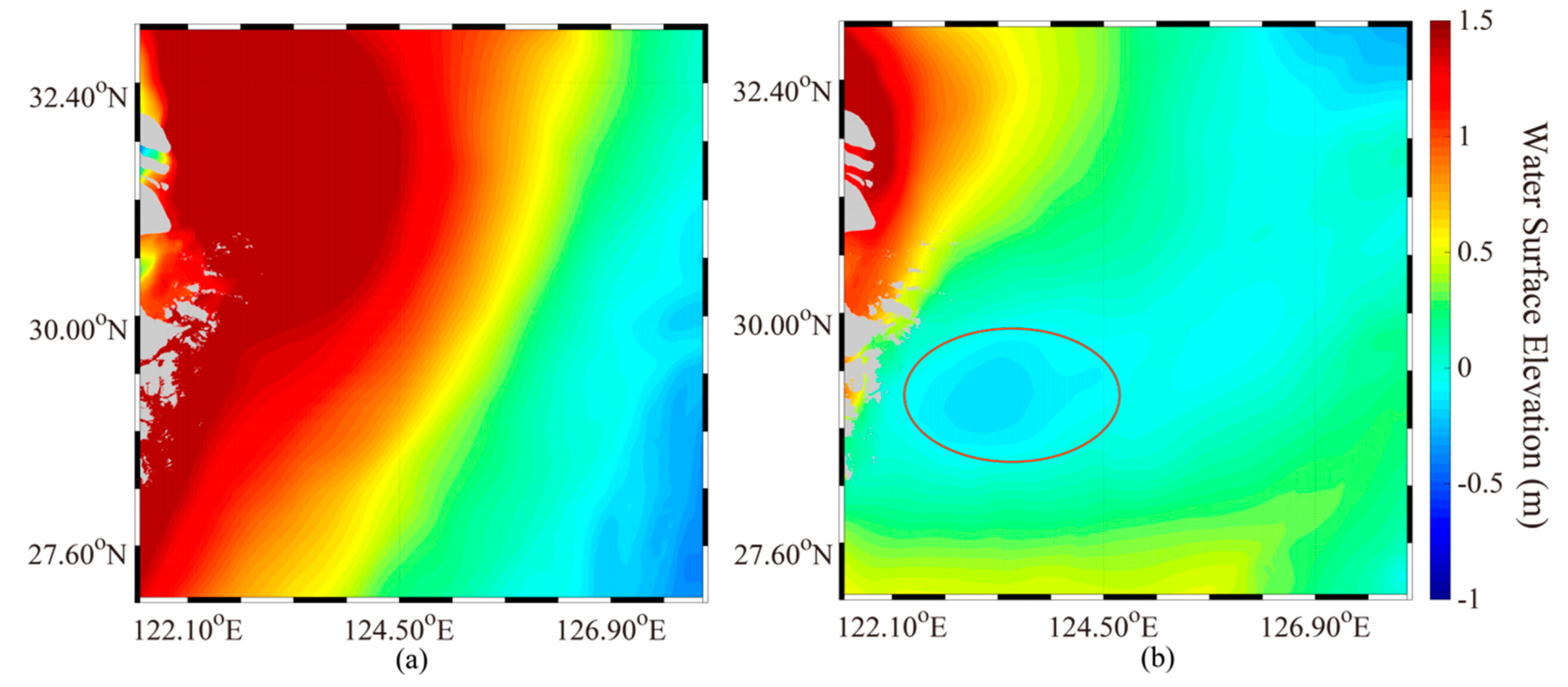
3.2. Simulation of Sea-Water Level

Figure 9 presents the sea-water level maps simulated by the FVCOM at 13:00 UTC on 22 September 2014 (Figure 9a) and 06:00 UTC on 11 July 2014 (Figure 8b). It can be observed that strong winds raise the sea-water level around the Zhoushan Islands, indicating a rise of more than 1 m for the two cases. Interestingly, the sea-water level decreased slightly (~0.2 m) and exhibited a spiral structure, as indicated by the red ellipse in Figure 9b. This pattern is similar to the cyclonic decrease in sea-water level around the Pearl River Estuary shown in Figure 4, and could be the result of either Ekman pumping induced by typhoons or a local mesoscale eddy. This phenomenon is worthy of further study in the future. Unfortunately, independent data, including sea-water levels, are unavailable for public investigators. Therefore, HYCOM sea-water level data were compared with the FVCOM simulations. Figure 10 shows the statistical comparison of the sea-water levels at Regions A to C in Figure 7, revealing an RMSE of around 0.13 m, with a Cor of about 0.86. Thus, the sea-water level simulated by the FVCOM was found to be suitable for conducting the sensitive typhoon-wave-simulation experiment.

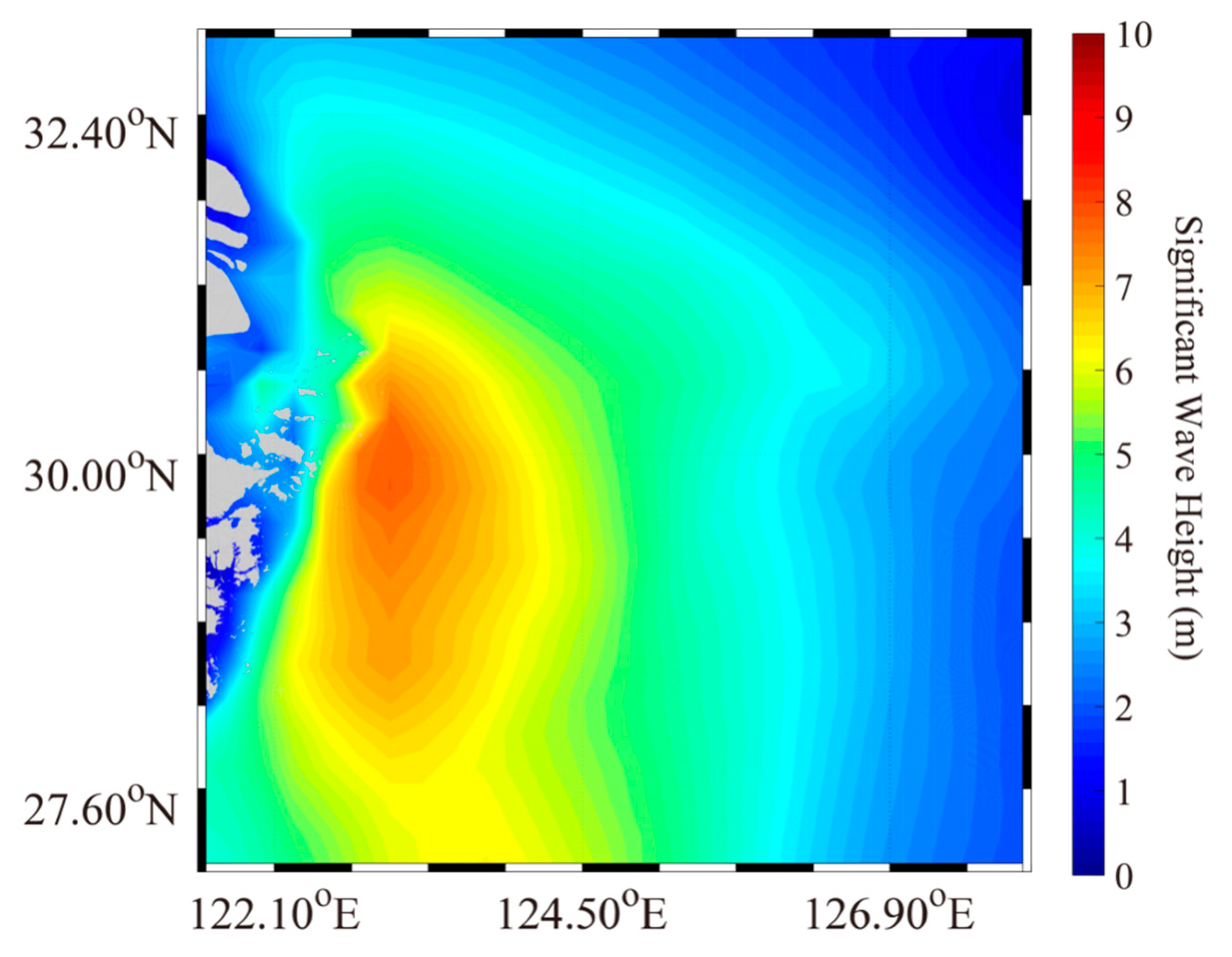
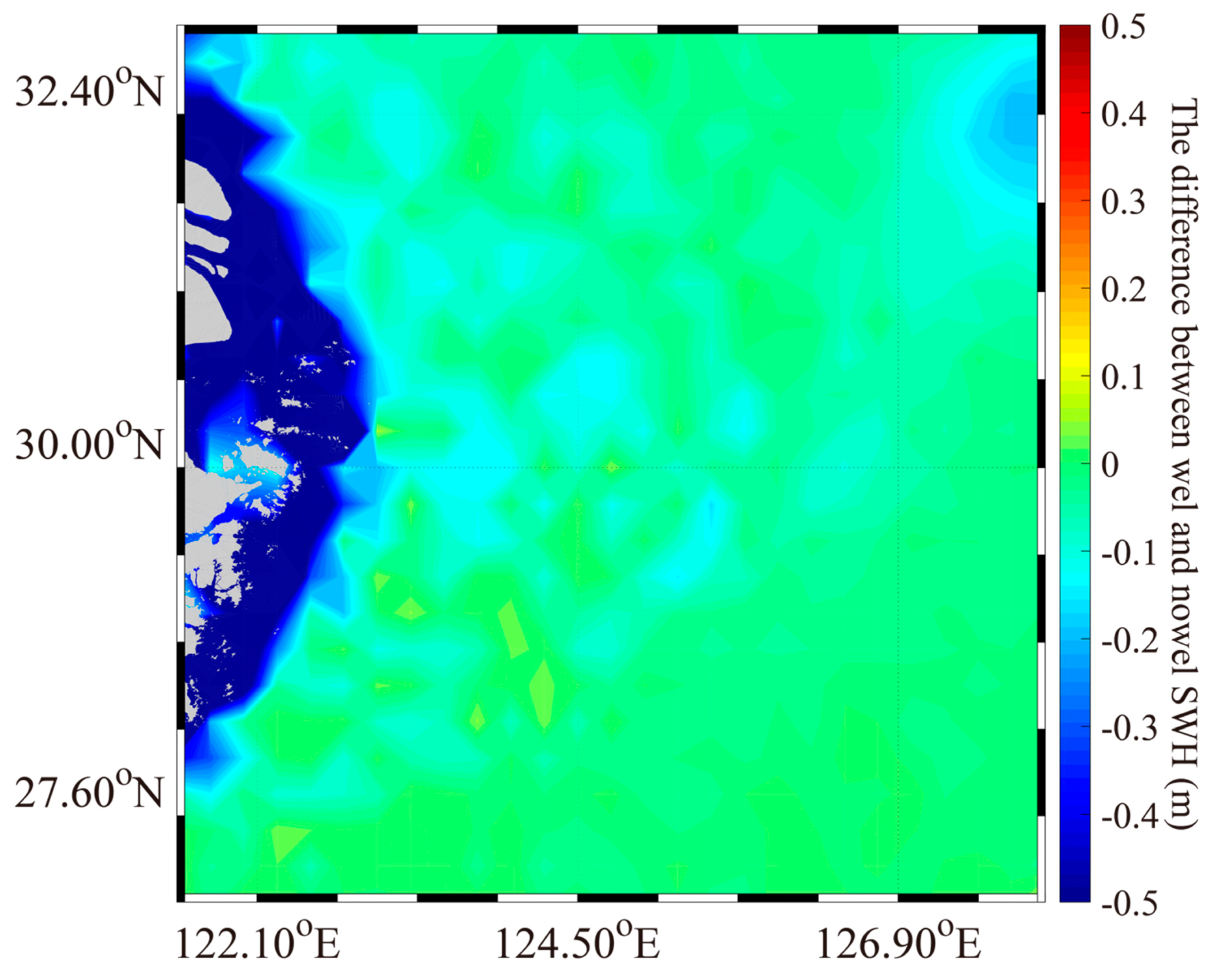
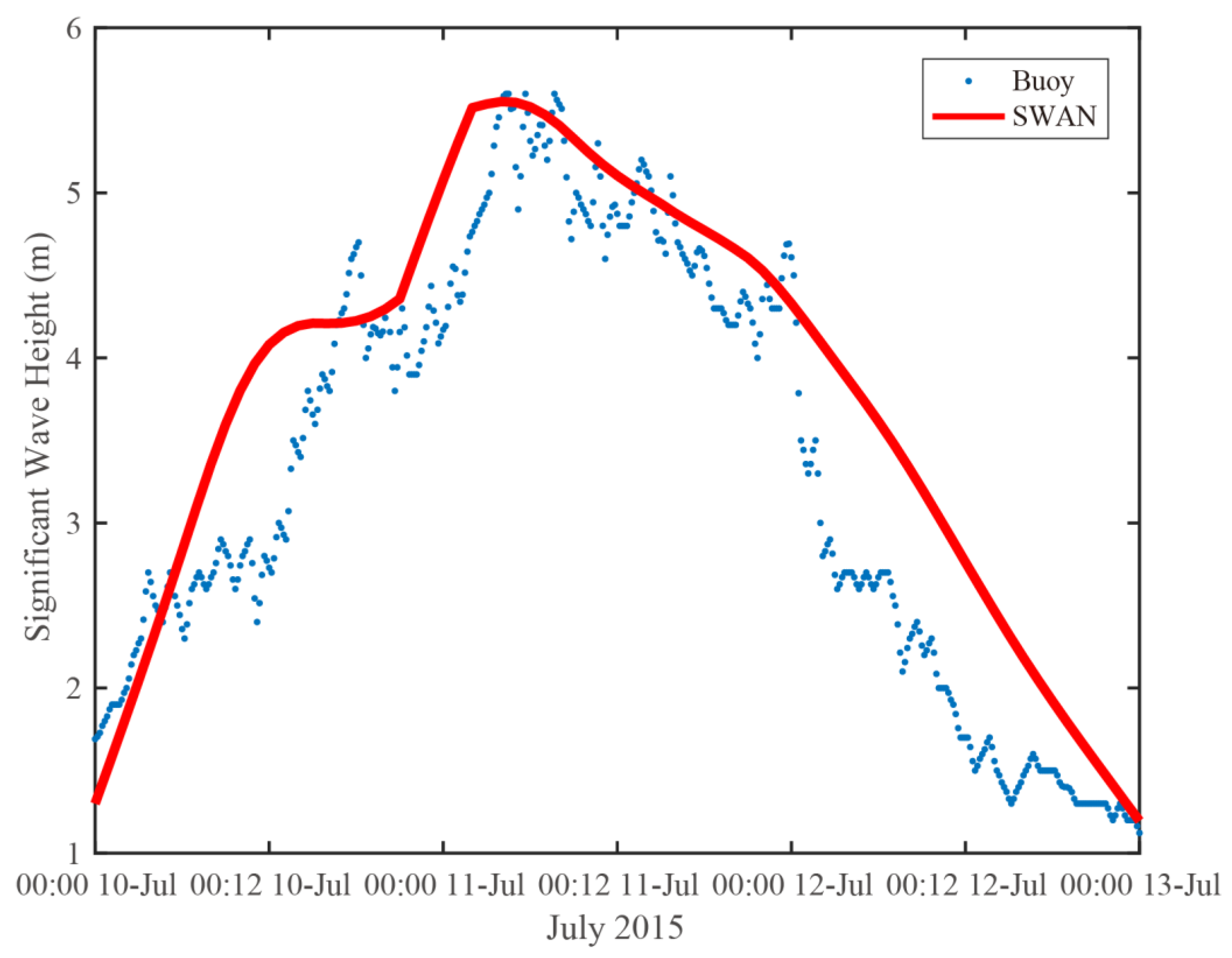
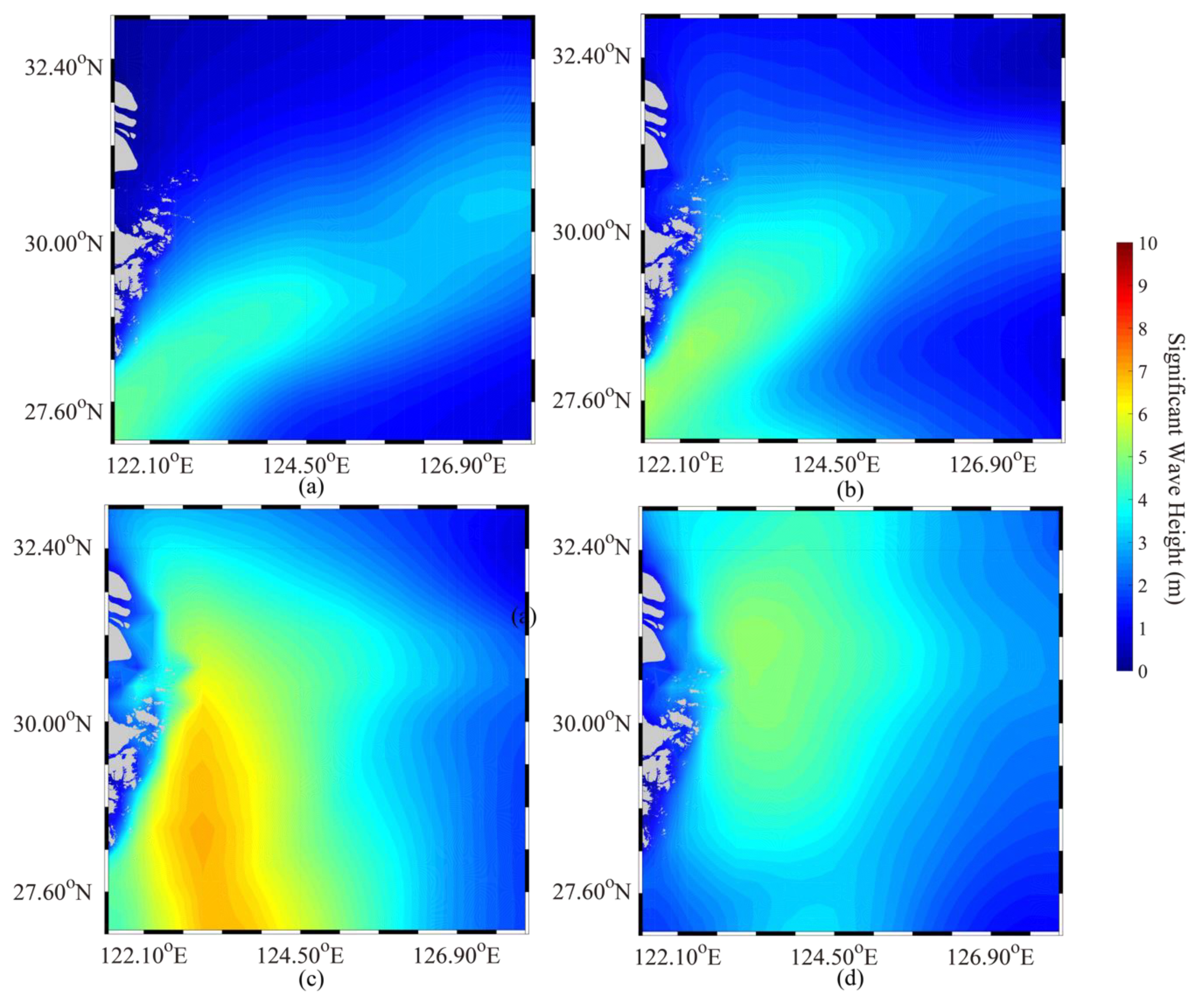
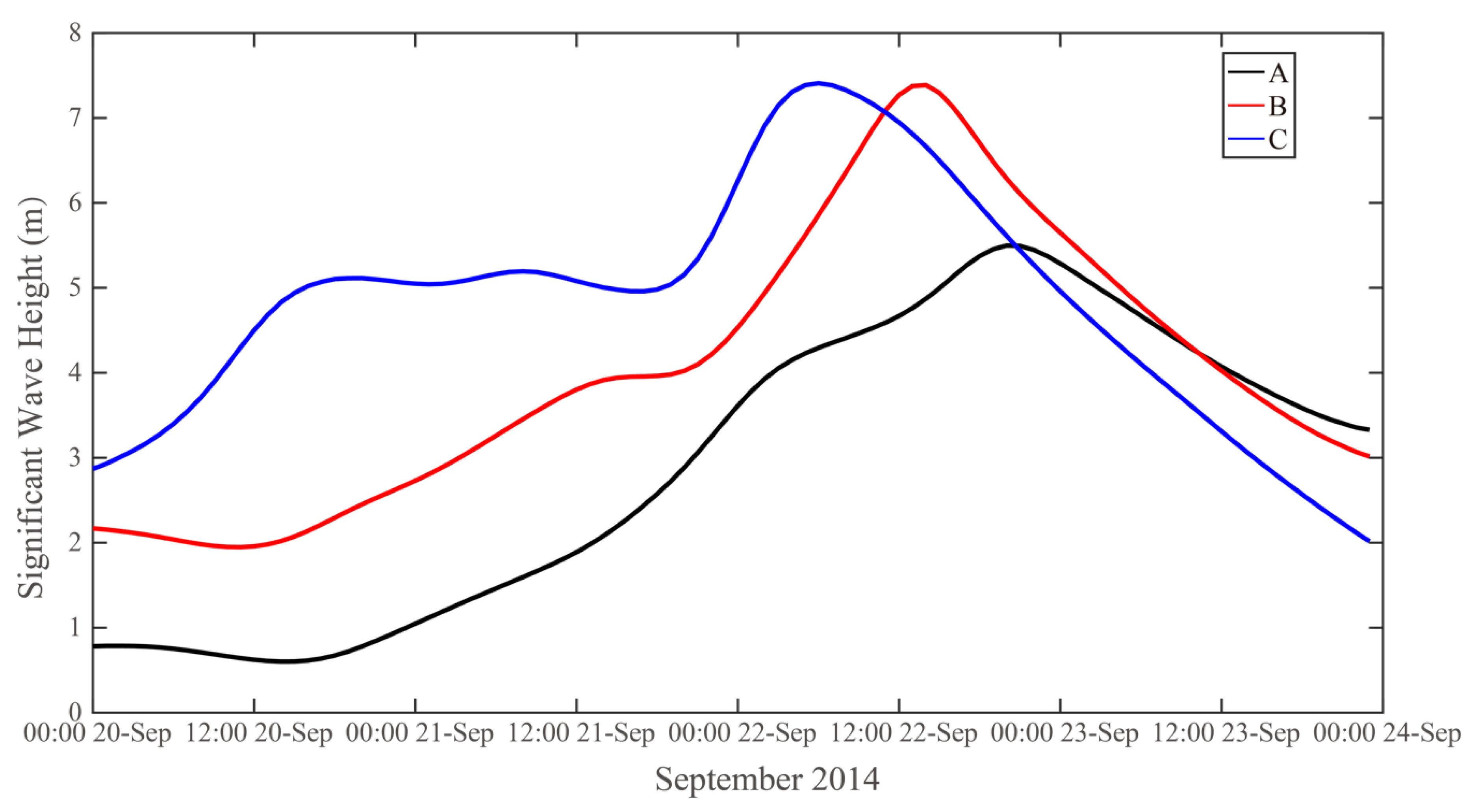
3.3. Simulation of Significant Wave Height

Figure 11 shows the simulated wave maps from the SWAN model considering one condition. It can be seen that the SWH reached 10 m at 14:00 UTC on 22 September 2014 during Typhoon Fung-wong, in which the cyclone center was located over the main island of the Zhoushan Islands. The cyclonic pattern was apparent on the high seas in the East China Sea, although the difference in the coastal regions was significant, e.g., in the Yangtze Estuary and the tidal flats around the Zhoushan Islands. We consistently focused on analyzing the difference between the simulated results from the SWAN model for two conditions, i.e., SWH without the sea-water level minus SWH with the sea-water level. Figure 12 shows that high sea-water level seemed to affect the simulated SWH from the SWAN model; in particular, the difference was up to −0.5 m in the coastal regions due to higher water levels and reduction in breaking/friction. Therefore, we believe that the tidal current and sea-water level play more important roles than the typhoon-induced current in the typhoon-induced wave simulation.
Measurements were collected from the altimeter Jason-2 with spatial coverage around the Zhoushan Islands, as marked by the red rectangle in Figure 5. The time series of the SWH from the SWAN model and buoy ID:B14 during typhoon Fung-wong is shown in Figure 13, and it was found that the SWAN simulations were consist with the measurements from the buoy. We compared the simulated results from the SWAN model with the measurements for more than 15,000 matchups. The statistical analysis is plotted in Figure 14. The RMSE was 0.95 m, and the Cor was 0.84 (Figure 14b)—lower than the 1.21 m RMSE and 0.75 Cor when the sea-water level was not included (Figure 14a). Moreover, overestimation was clearly apparent in the high-sea state (SWH > 6 m) without the sea-water level term, while considering the latter significantly improved the wave simulation’s performance. Moreover, there seems to be an underprediction by the SWAN model in the low-sea state (SWH < 2 m), which is probably caused by low winds in the H-E model. Meanwhile, the simulated waves were also validated against the measurements from the five moored buoys during the periods 21–23 September 2014 and 10–13 July 2015, as listed in Table 3. Note that measurements from ID: B11 were not available during Typhoon Chan-hom. In general, the results were also consistent with the buoy measurements, indicating SWHs with a ~0.8-m RMSE and Cor > 0.8. Collectively, these findings suggest that the sea-water level should be included in the wave simulation using the SWAN model for typhoons and hurricanes, since it modulates waves in both low- and high-sea states.

4. Discussion

We further investigated the characteristics of the typhoon-induced waves when Typhoon Fung-wong passed the Zhoushan Islands. In particular, three points in Regions A to C were selected, which are marked in Figure 7. The average SWH maps simulated by the SWAN model during the period from 20 to 23 September 2014 are shown in Figure 15; the maximum SWH was 6 m, but the high-sea state induced by the typhoon waves seems to have been blocked outside of the Zhoushan Islands when the typhoon track encountered the islands. This kind of behavior is apparent on 22 September 2014. We think that the barrier of islands results in the low-sea state in typhoons.
Figure 16 shows the time series of the simulated SWH from the SWAN model during the period from 20 September to 24 September 2014 corresponding to the three points A–C in Figure 7; the maximum SWH was 7 m on 22 September when the typhoon’s path crossed the islands. It is not surprising that the SWH at Points A and B is smaller than that at Point C, because Point C is located in open sea and the sea-water levels should modify the waves at Points A and B in the Yangtze Estuary and tidal flats. It is also clearly observed that the tendency of the SWH at Points A and B accords with the time series. Especially during the period from 00:00 20 September to 12:00 20 September, the SWH decreases at Points A and B, which is probably caused by the change in sea-water levels, while the SWH decreases at Point C. Interestingly, low SWH is achieved at Point A, e.g., there was a reduction of more than 1m on 23 September, when the maximum SWH occurred.

5. Conclusions

The tidal currents are often strong, and the sea-water levels vary in some areas, e.g., the Yangtze Estuary, Hangzhou Bay, and the Zhoushan Islands. In our previous study [26], typhoon waves were simulated by the WAVEWATCH-III model around the Zhoushan Islands, although these were simulated without considering the influence of currents and sea-water levels during Typhoon Fung-wong (2014) and Typhoon Chan-hom (2015). The effect of typhoon-induced currents and the Kuroshio Current on typhoon-induced wave simulation has been frequently studied, and it has been concluded that SWH is significantly correlated with wind-induced-current speed when the current speed is >0.5 m/s [28]. The main purpose of this study was to investigate the influence of sea-water levels on wave simulation using the SWAN model and the FVCOM in the shallow waters around the Zhoushan Islands. These two numerical ocean models share a unique unstructured grid of the same simulated region. The composited H-E wind was utilized as the forcing field when running the model. The validation of H-E winds against the measurements from moored buoys has been discussed in [26] and could ameliorate the underestimation of ECMWF winds. Specifically, TPXO.5 tide data and HYCOM sea-surface-temperature, sea-surface salinity, and sea-surface-current data were also collected, which were taken as the open-boundary conditions. The comparison of the simulated current speeds from the FVCOM with those from the CFSv2 revealed a 0.12-m RMSE with a 0.73 Cor. Similarly, the HYCOM sea-water level data were used to confirm the accuracy of the simulations from the FVCOM, yielding a 0.2-m RMSE and 0.73 Cor.
Waves were simulated by the SWAN model under two conditions: (1) including the wind and current, and (2) including the wind, current, and sea-water level. The pattern of differences between them (up to −0.5 m) was consistent with the pattern of the simulated wave height from the FVCOM in coastal regions, e.g., in the Yangtze Estuary and tidal flats around the Zhoushan Islands. The validation of the SWH with the sea-water level against Jason-2 altimeter data and moored buoy measurements demonstrated an RMSE < 0.9 m with a Cor > 0.8. In particular, the overestimation in the high-sea state (SWH > 6 m) without the sea-water level term was ameliorated. Therefore, we conclude that the sea-water level should be in included in typhoon-induced wave simulations with the SWAN model.
Three representative specific locations were selected to study the characteristics of extreme waves around the Zhoushan Islands during Typhoon Fung-wong (2014). It was found that the SWHs at Points A and B located in the Yangtze Estuary and tidal flats were generally smaller than the SWH at Point C in open sea due to the barrier of islands. In particular, the reduction of SWH was up to 1 m on 23 September 2014, when the maximum waves occurred. As a matter of fact, mesoscale eddies and upwelling are common in coastal waters. In the near future, we plan to study the coastal oceanic feedbacks of typhoons, e.g., Ekman pumping and sea-surface-temperature cooling.

Author Contributions

Conceptualization, W.S. and Z.Y.; methodology, W.S., Z.Y., and Y.D.; validation, Z.Y., Y.D., and J.S.; formal analysis, W.S. and J.S.; investigation, Z.Y.; resources, Y.D.; writing—original draft preparation, W.S.; writing—review and editing, J.S.; visualization, Z.Y. and Q.J.; funding acquisition, W.S. and Q.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China under contract nos. 2017YFA0604901 and 2016YFC1401605, the National Natural Science Foundation of China under contract nos. 41806005 and 41776183, and the Science and Technology Project of Zhoushan City, China, under contract no. 2019C21008.

Acknowledgments

We appreciate the Simulating WAves Nearshore (SWAN) model developed at the Delft University of Technology. We also thank the Marine Ecosystem Dynamics Modeling Laboratory (MEDML) for providing the Finite-Volume Community Ocean Model (FVCOM) in detail. The European Centre for Medium-Range Weather Forecasts (ECMWF)’s wind data were accessed via http://www.ecmwf.int. The tide data were downloaded from https://www.tpxo.net. The sea-surface temperature, sea-surface-salinity, sea-surface-current, and sea-water-level data from the HYbrid Coordinate Ocean Model (HYCOM) were obtained via https://www.hycom.org. Sea-surface-current data from the National Centers for Environmental Prediction (NCEP) Climate Forecast System Version 2 (CFSv2) were obtained via http://cfs.ncep.noaa.gov. The General Bathymetric Chart of the Oceans (GEBCO) data were downloaded from ftp.edcftp.cr.usgs.gov. The buoy measurements were kindly shared by Dr. Shuiqing Li at the Institute of Oceanology, Chinese Academy of Sciences.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The governing equation of the SWAN model considering ambient current is determined by the evolution of the wave spectrum and expressed as follows:
∂ N ∂ t + Δ · [ ( C g + V ) N ] + ∂ C ω N ∂ ω + ∂ C θ N ∂ θ = S t ω ,  
in which N is the wave-action-density spectrum; t is the time; ω is the wave frequency; θ is the wave-propagation direction; Cω and Cθ are the wave-propagation velocities in terms of the spectral space ω and θ, respectively; Cg is the group-velocity vector; V is the sea-surface-current vector; and Δ is the Hamiltonian divergence operator. St comprises the input and dissipation source terms, stated as
S t = S i n + S b o t + S n l + S t q + S d b ,  
where St includes an atmosphere–wave interaction term of the function for the wind-induced wave growth Sin; Sbot is the friction induced by wave–bottom interaction; Snl is the nonlinear wave–wave interaction term; Stq is the three- (triad) and four-wave components (quadruplets) of the wave–wave interactions; and Sdb is the wave decay due to white capping and depth-induced wave breaking. More detailed descriptions of these terms are provided in the technical manual of the SWAN model.

Appendix B

The governing equations of the FVCOM consist of the following momentum, continuity, temperature, salinity, and density expressions:
∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z − fv = − 1 ρ + ∂ ( p H + p a ) ∂ x − 1 ρ ∂ q ∂ x + ∂ ∂ z ( K m ∂ u ∂ z ) + F u ,
∂ v ∂ t + u ∂ v ∂ x + v ∂ v ∂ y + w ∂ v ∂ z − fu = − 1 ρ + ∂ ( p H + p a ) ∂ y − 1 ρ ∂ q ∂ y + ∂ ∂ z ( K m ∂ v ∂ z ) + F v ,  
∂ w ∂ t + u ∂ w ∂ x + v ∂ w ∂ y + w ∂ w ∂ z = − 1 ρ ∂ q ∂ y + ∂ ∂ z ( K m ∂ w ∂ z ) + F w ,
∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0 ,
∂ T ∂ t + u ∂ T ∂ x + v ∂ T ∂ y + ∂ T ∂ z = ∂ ∂ z ( K h ∂ T ∂ z ) + F T ,
∂ S ∂ t + u ∂ S ∂ x + v ∂ S ∂ y + ∂ S ∂ z = ∂ ∂ z ( K h ∂ S ∂ z ) + F S ,
ρ = ρ ( T , S , P ) ,
where x, y, and z are the east, north, and vertical axes in the Cartesian coordinate system, respectively; u, v, and w are the x, y, and z velocity components, respectively; T is the sea temperature; S is the salinity; ρ is the sea-water density; pa is the air pressure at the sea surface; pH is the hydrostatic pressure; q is the non-hydrostatic pressure; f is the Coriolis parameter; g is the acceleration of gravity; Km is the vertical-eddy-viscosity coefficient; and Kh is the thermal-vertical-eddy-diffusion coefficient. Fu, Fv, and Fw represent the horizontal momentum in the x direction, horizontal momentum in the y direction, and vertical momentum in the z direction, respectively; FT and FS represent the thermal and salt diffusion terms, respectively. The total water-column depth is D = H + ζ, in which H is the bottom depth (relative to z = 0) and ζ is the height of the free surface (relative to z = 0). p = pa + pH + q is the total pressure, in which the hydrostatic pressure pH satisfies
∂ p H ∂ z = − ρ g ⟹ p H = ρ o g ζ + g ∫ z 0 ρ d z ′ .
These terms are described in further detail in the user manual of the FVCOM.

References

  1. Buonaiuto, F.S.; Slattery, M.; Bokuniewicz, H.J. Wave modeling of long island coastal waters. J. Coastal Res. 2011, 27, 470–477. [Google Scholar]
  2. Wang, Z.F.; Zhou, L.B.; Dong, S.; Wu, L.Y.; Li, Z.B.; Mu, L.; Wang, A.F. Wind wave characteristics and engineering environment of the South China Sea. J. Ocean U. China 2014, 13, 893–900. [Google Scholar] [CrossRef]
  3. Liu, Q.X.; Babanin, A.; Fan, Y.; Zieger, S.; Guan, C.L.; Moon, I.J. Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance. Ocean Model. 2017, 18, 73–79. [Google Scholar] [CrossRef]
  4. Wang, N.; Hou, Y.J.; Li, S.Q.; Li, R. Numerical simulation and preliminary analysis of typhoon waves during three typhoons in the Yellow Sea and east China Sea. J. Oceanol. Limn. 2019, 37, 1805–1816. [Google Scholar] [CrossRef]
  5. Zhou, L.M.; Li, Z.B.; Mu, L.; Wang, A.F. Numerical simulation of wave field in the South China Sea using WAVEWATCH III. Chin. J. Oceanol. Limn. 2014, 37, 656–664. [Google Scholar] [CrossRef]
  6. Rogers, W.E.; Hwang, P.A.; Wang, D.W. Investigation of wave growth and decay in the SWAN model: Three regional-scale applications. J. Phys. Oceanogr. 2003, 33, 366–389. [Google Scholar] [CrossRef]
  7. Bi, F.; Song, J.B.; Wu, K.J.; Xu, Y. Evaluation of the simulation capability of the Wavewatch III model for Pacific Ocean wave. Acta Oceanol. Sin. 2015, 34, 43–57. [Google Scholar] [CrossRef]
  8. Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch IIIi in the Mediterranean Sea. Ocean Modell. 2015, 90, 82–94. [Google Scholar] [CrossRef]
  9. Akpınar, A.; Vledder, G.; Kömürcü, M.; Özger, M. Evaluation of the numerical wave model (SWAN) for wave simulation in the Black Sea. Cont. Shelf Res. 2012, 50, 80–99. [Google Scholar]
  10. Rusu, L.; Soares, C.G. Wave energy assessments in the Azores islands. Renew. Energ. 2012, 45, 183–196. [Google Scholar] [CrossRef]
  11. Bottema, M.; Vledder, G.V. Effective fetch and non-linear four-wave interactions during wave growth in slanting fetch conditions. Coast. Eng. 2008, 55, 261–275. [Google Scholar] [CrossRef]
  12. Dragani, W.C.; Garavento, E.; Simionato, C.G.; Nunez, M.N.; Martin, P.; Campos, M.I. Wave simulation in the outer Rio de la Plata estuary: Evaluation of SWAN model. J. Waterw. Port C-ASCE. 2008, 5, 299–305. [Google Scholar] [CrossRef]
  13. Moeini, M.H.; Etemad-Shahidi, A. Wave parameter hindcasting in a lake using the SWAN model. Sci. Iran. 2009, 16, 156–164. [Google Scholar]
  14. Young, I.R.; Vledder, G. A review of the central role of nonlinear interactions in wind-wave evolution. Phil. Trans. Roy. Soc. Lond. 1993, 342, 505–524. [Google Scholar]
  15. Young, I.R. Observations of the spectra of hurricane generated waves. Ocean Eng. 1998, 25, 261–276. [Google Scholar] [CrossRef]
  16. Cui, H.; He, H.L.; Liu, X.H.; Li, Y. 2012. Effect of oceanic current on typhoon-wave modeling in the East China Sea. Chin. Phys. B. 2012, 21, 109201. [Google Scholar] [CrossRef]
  17. Sheng, Y.P.; Alymov, V.; Paramygin, V.A. Simulation of storm surge, wave, currents, and inundation in the outer banks and Chesapeake Bay during Hurricane Isabel in 2003: The importance of waves. J. Geophys. Res. 2010, 115, C04008. [Google Scholar] [CrossRef]
  18. Dietrich, J.C.; Tanaka, S.; Westerink, J.J.; Dawson, C.N.; Luettich, R.A.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the unstructured-mesh, SWAN+ ADCIRC model in computing hurricane waves and surge. J. Sci. Comput. 2012, 52, 468–497. [Google Scholar] [CrossRef]
  19. Chen, C.S.; Liu, H.; Beardsley, R.C. An unstructured, finite-volume, three-dimensional, primitive equation ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Tech. 2003, 20, 159–186. [Google Scholar] [CrossRef]
  20. Pringle, J.M. Sources of variability in Gulf of Maine circulation, and the observations needed to model it. Deep-Sea Res. PT. II. 2006, 53, 2457–2476. [Google Scholar] [CrossRef]
  21. Huang, H.; Chen, C.L.; Cowles, G.W.; Winant, C.D.; Beardsley, R.C.; Hedstrom, K.S. Haidvogel, D.B. FVCOM validation experiments: Comparisons with ROMS for three idealized barotropic test problems. J. Geophys. Res. 2008, 113, C07042. [Google Scholar] [CrossRef] [Green Version]
  22. Chen, C.S.; Huang, H.; Beardsley, R.C.; Liu, H.; Xu, Q.; Cowles, G. A finite-volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models. J. Geophys. Res. 2007, 112, C03018. [Google Scholar] [CrossRef]
  23. Ma, Z.; Han, G.; De Young, B. Oceanic responses to Hurricane Igor over the Grand Banks: A modeling study. J. Geophys. Res. 2015, 120, 1276–1295. [Google Scholar] [CrossRef]
  24. Sun, Y.J.; Perrie, W.; Toulany, B. Simulation of wave-current interactions under hurricane conditions using an unstructured-grid model: Impacts on ocean waves. J. Geophys. Res. 2018, 123, 3739–3760. [Google Scholar] [CrossRef]
  25. Dukhovskoy, D.S.; Morey, S.L. Simulation of the Hurricane Dennis storm surge and considerations for vertical resolution. Nat. Hazards 2011, 58, 511–540. [Google Scholar] [CrossRef]
  26. Sheng, Y.X.; Shao, W.Z.; Li, S.Q.; Zhang, Y.M.; Yang, H.W.; Zuo, J.C. Evaluation of typhoon waves simulated by WaveWatch-III model in shallow waters around Zhoushan Islands. J. Ocean U. China 2019, 18, 365–375. [Google Scholar] [CrossRef]
  27. Shao, W.Z.; Sheng, Y.X.; Li, H.; Shi, J.; Ji, Q.Y.; Tan, W.; Zuo, J.C. Analysis of wave distribution simulated by WAVEWATCH-III model in typhoons passing Beibu Gulf, China. Atmosphere 2018, 9, 265. [Google Scholar] [CrossRef] [Green Version]
  28. Hu, Y.Y.; Shao, W.Z.; Shi, J.; Sun, J.; Ji, Q.Y.; Cai, L.N. Analysis of the typhoon wave distribution simulated in WAVEWATCH-III model in the context of Kuroshio and wind-induced current. J. Oceanol. Limn. 2020. [Google Scholar] [CrossRef]
  29. Moon, I.J. Impact of a coupled ocean wave-tide-circulation system on coastal modeling. Ocean Model. 2005, 8, 203–236. [Google Scholar] [CrossRef]
  30. Masson, D. A case study of wave-current interaction in a strong tidal current. J. Phys. Oceanogr. 1996, 26, 359–372. [Google Scholar] [CrossRef] [Green Version]
  31. Chen, T.Q.; Zhang, Q.H.; Wu, Y.S.; Ji, C.; Yang, J.S.; Liu, G.W. Development of a wave-current model through coupling of FVCOM and SWAN. Ocean Eng. 2018, 164, 443–454. [Google Scholar] [CrossRef]
  32. Lv, X.; Yuan, D.; Ma, X.; Tao, J. Wave characteristics analysis in Bohai Sea based on ECMWF wind field. Ocean Eng. 2014, 91, 159–171. [Google Scholar] [CrossRef]
  33. Kamranzad, B.; Etemad-Shahidi, A.; Chegini, V.; Yeganeh-Bakhtiary, A. Climate change impact on wave energy in the Persian Gulf. Ocean Dynam. 2015, 65, 777–794. [Google Scholar] [CrossRef] [Green Version]
  34. Zheng, K.W.; Sun, J.; Guan, C.L.; Shao, W.Z. Analysis of the global swell and wind-sea energy distribution using WAVEWATCH III. Adv. Meteorol. 2016, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
  35. Zheng, K.W.; Osinowo, A.; Sun, J.; Hu, W. Long term characterization of sea conditions in the East China Sea using significant wave height and wind speed. J. Ocean U. China 2018, 17, 733–743. [Google Scholar] [CrossRef]
  36. Hu, Y.Y.; Shao, W.Z.; Wei, Y.L.; Zuo, J.C. Analysis of typhoon-induced waves along typhoon tracks in the Western North Pacific Ocean, 1998–2017. J. Mar. Sci. Eng. 2020, 8, 521. [Google Scholar] [CrossRef]
  37. Wang, K.; Hou, Y.J.; Li, S.Q.; Li, R. Numerical study of storm surge inundation in the southwestern Hangzhou bay region during Typhoon Chan-Hom in 2015. J. Ocean U. China 2020, 19, 263–271. [Google Scholar] [CrossRef]
  38. Ding, Y.; Yao, Z.G.; Zhou, L.L.; Bao, M.; Zang, Z.C. Numerical modeling of the seasonal circulation in the coastal ocean of the Northern South China Sea. Front. Earth Sci. 2018, 14, 90–109. [Google Scholar] [CrossRef]
  39. Ou, S.H.; Liau, J.M.; Hsu, T.W.; Tzang, S.Y. Simulating typhoon waves by SWAN wave model in coastal waters of Taiwan. Ocean Eng. 2002, 29, 947–971. [Google Scholar] [CrossRef]
  40. Yuan, X.; Wood, E.F.; Luo, L.F.; Pan, M. A first look at Climate Forecast System Version 2 (CFSv2) for hydrological seasonal prediction. Geophys. Res.Lett. 2011, 38, L13402. [Google Scholar] [CrossRef] [Green Version]
  41. Zhuang, W.; Wang, D.X.; Wu, R.S. Coastal upwelling off eastern Fujian\|Guangdong detected by remote sensing. Chin. J. Atmos. Sci. 2005, 29, 438–444. [Google Scholar]
  42. Zhang, H.F.; Wu, Q.; Chen, G. Validation of HY-2A remotely sensed wave heights against buoy data and Jason-2 altimeter measurements. J. Atmos. Ocean. Tech. 2015, 32, 1270–1280. [Google Scholar] [CrossRef]
  43. Chu, P.C.; Qi, Y.; Chen, Y.; Shi, P.; Mao, Q. South China Sea wind-wave characteristics. Part I: Validation of Wavewatch-III using TOPEX/Poseidon data. J. Atmos. Ocean. Tech. 2004, 21, 1718–1733. [Google Scholar] [CrossRef] [Green Version]
  44. Lin, Y.; Dong, S.; Wang, Z.; Guedes Soares, C. Wave energy assessment in the china adjacent seas on the basis of a 20-year SWAN simulation with unstructured grids. Renew. Energ. 2019, 136, 275–295. [Google Scholar] [CrossRef]
  45. Wu, H.; Du, M.; Wang, X.Y.; Meng, J. Study on hydrography and small-scale process over Zhoushan sea area. J. Ocean U. China 2015, 14, 829–834. [Google Scholar] [CrossRef]
  46. Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF reanalysis interim and the NECP climate forecast system reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
  47. Shen, Z.B.; Wu, X.B.; Fei, Y.J.; Xu, X.A.; Chen, X.F. Surface tidal currents in the open sea area to the east of the Zhoushan Islands measured with high frequency surface wave radar. Acta Oceanol. Sin. 2013, 32, 5–10. [Google Scholar] [CrossRef]
Jmse 08 00783 g001 550
Figure 1. (a) Water-depth map of the selected region in the East China Sea, in which the red and blue lines represent the tracks of Typhoons Fung-wong (2014) and Chan-hom (2015), respectively, and the colored dots represent the maximum wind speeds of the typhoons. The area inside the black square is the geographic region around the Zhoushan Islands, China; (b) bathymetric topography of the study area corresponding to the black square in Figure 1a, in which the black dots are the available measurements from moored buoys.
Figure 1. (a) Water-depth map of the selected region in the East China Sea, in which the red and blue lines represent the tracks of Typhoons Fung-wong (2014) and Chan-hom (2015), respectively, and the colored dots represent the maximum wind speeds of the typhoons. The area inside the black square is the geographic region around the Zhoushan Islands, China; (b) bathymetric topography of the study area corresponding to the black square in Figure 1a, in which the black dots are the available measurements from moored buoys.
Jmse 08 00783 g001
Jmse 08 00783 g002 550
Figure 2. Map of the unstructured grids used in the SWAN and FVCOM simulations.
Figure 2. Map of the unstructured grids used in the SWAN and FVCOM simulations.
Jmse 08 00783 g002
Jmse 08 00783 g003 550
Figure 3. Sea-surface-current vector map from the Climate Forecast System Version 2 (CFSv2) model at 06:00 UTC on 11 July 2015, in which the black line is the track of Typhoon Chan-hom.
Figure 3. Sea-surface-current vector map from the Climate Forecast System Version 2 (CFSv2) model at 06:00 UTC on 11 July 2015, in which the black line is the track of Typhoon Chan-hom.
Jmse 08 00783 g003
Jmse 08 00783 g004 550
Figure 4. Sea-water-level map from the HYbrid Coordinate Ocean Model (HYCOM) at 12:00 UTC on 22 September 2014, in which the black line is the track of Typhoon Fung-wong.
Figure 4. Sea-water-level map from the HYbrid Coordinate Ocean Model (HYCOM) at 12:00 UTC on 22 September 2014, in which the black line is the track of Typhoon Fung-wong.
Jmse 08 00783 g004
Jmse 08 00783 g005 550
Figure 5. Footprints from the Jason-2 altimeter overlaid on the water-depth map of September 2014, in which the red square encloses the waters around the Zhoushan Islands.
Figure 5. Footprints from the Jason-2 altimeter overlaid on the water-depth map of September 2014, in which the red square encloses the waters around the Zhoushan Islands.
Jmse 08 00783 g005
Jmse 08 00783 g006 550
Figure 6. Current-speed maps from the FVCOM simulation at (a) 13:00 UTC on 22 September 2014 and (b) 06:00 UTC on 11 July 2015.
Figure 6. Current-speed maps from the FVCOM simulation at (a) 13:00 UTC on 22 September 2014 and (b) 06:00 UTC on 11 July 2015.
Jmse 08 00783 g006
Jmse 08 00783 g007 550
Figure 7. Three typical regions around the Zhoushan Islands used to study the statistical analysis of current speed. Region A is located in the Yangtze Estuary and tidal flats. The three red spots represent the three representative specific locations for studying the extreme waves.
Figure 7. Three typical regions around the Zhoushan Islands used to study the statistical analysis of current speed. Region A is located in the Yangtze Estuary and tidal flats. The three red spots represent the three representative specific locations for studying the extreme waves.
Jmse 08 00783 g007
Jmse 08 00783 g008 550
Figure 8. Comparison between current speeds simulated by the FVCOM and the CFSv2 data for a 0.1-m/s bin between 0 and 0.6 m, in which the error bars represent the standard deviations of each bin for the matchups in (a) Region A, (b) Region B, and (c) Region C.
Figure 8. Comparison between current speeds simulated by the FVCOM and the CFSv2 data for a 0.1-m/s bin between 0 and 0.6 m, in which the error bars represent the standard deviations of each bin for the matchups in (a) Region A, (b) Region B, and (c) Region C.
Jmse 08 00783 g008
Jmse 08 00783 g009 550
Figure 9. Sea-water-level maps from the FVCOM at (a) 13:00 UTC on 22 September 2014 and (b) 06:00 UTC on 11 July 2015.
Figure 9. Sea-water-level maps from the FVCOM at (a) 13:00 UTC on 22 September 2014 and (b) 06:00 UTC on 11 July 2015.
Jmse 08 00783 g009
Jmse 08 00783 g010 550
Figure 10. Comparison between sea-water level simulated by the FVCOM and the HYCOM data for a 0.1-m bin between −0.5 and 1.5 m, in which the error bar represents the standard deviation at each bin for the matchups in (a) Region A; (b) Region B; and (c) Region C.
Figure 10. Comparison between sea-water level simulated by the FVCOM and the HYCOM data for a 0.1-m bin between −0.5 and 1.5 m, in which the error bar represents the standard deviation at each bin for the matchups in (a) Region A; (b) Region B; and (c) Region C.
Jmse 08 00783 g010
Jmse 08 00783 g011 550
Figure 11. Significant-wave-height maps from the SWAN model at 14:00 UTC on 22 September 2014.
Figure 11. Significant-wave-height maps from the SWAN model at 14:00 UTC on 22 September 2014.
Jmse 08 00783 g011
Jmse 08 00783 g012 550
Figure 12. Difference between simulated results from the SWAN model under two conditions (significant wave height (SWH) without sea-water level minus SWH with sea-water level) at 14:00 UTC on 22 September 2014.
Figure 12. Difference between simulated results from the SWAN model under two conditions (significant wave height (SWH) without sea-water level minus SWH with sea-water level) at 14:00 UTC on 22 September 2014.
Jmse 08 00783 g012
Jmse 08 00783 g013 550
Figure 13. Comparison between significant wave heights simulated by the SWAN model and those recorded from the buoy B14 during Typhoon Chan-hom.
Figure 13. Comparison between significant wave heights simulated by the SWAN model and those recorded from the buoy B14 during Typhoon Chan-hom.
Jmse 08 00783 g013
Jmse 08 00783 g014 550
Figure 14. Comparison between significant wave heights simulated by the SWAN model and the measurements from the Jason-2 altimeter for a 0.14-m bin between 0 and 9 m, in which the error bars represent the standard deviation at each bin: (a) without the sea-water level term; (b) with the sea-water level term.
Figure 14. Comparison between significant wave heights simulated by the SWAN model and the measurements from the Jason-2 altimeter for a 0.14-m bin between 0 and 9 m, in which the error bars represent the standard deviation at each bin: (a) without the sea-water level term; (b) with the sea-water level term.
Jmse 08 00783 g014
Jmse 08 00783 g015 550
Figure 15. The average SWH maps simulated by the SWAN model when Typhoon Fung-wong passed the Zhoushan Islands on (a) 20 September 2014, (b) 21 September 2014, (c) 23 September 2014, and (d) 23 September 2014.
Figure 15. The average SWH maps simulated by the SWAN model when Typhoon Fung-wong passed the Zhoushan Islands on (a) 20 September 2014, (b) 21 September 2014, (c) 23 September 2014, and (d) 23 September 2014.
Jmse 08 00783 g015
Jmse 08 00783 g016 550
Figure 16. The time series of the simulated SWH at the selected Points A to C shown in Figure 7 during the period from 20 September to 24 September 2014.
Figure 16. The time series of the simulated SWH at the selected Points A to C shown in Figure 7 during the period from 20 September to 24 September 2014.
Jmse 08 00783 g016
Table
Table 1. Settings for the Finite-Volume Community Ocean Model (FVCOM).
Table 1. Settings for the Finite-Volume Community Ocean Model (FVCOM).
Forcing fieldHolland-European Centre for Medium-Range Weather Forecasts (ECMWF) (H-E) wind with a spatial resolution of 0.125° and time interval of six hours
Open boundaryWater-tide data from TPOX.5;
sea-surface temperature, sea-surface salinity, and sea-surface current values at 60-min intervals at a 1/12° (~8 km) grid spatial resolution from the HYbrid Coordinate Ocean Model (HYCOM)
ResolutionTriangular terrain grid with a 60-min temporal resolution
Table
Table 2. Settings for the Simulating Waves Nearshore (SWAN) model.
Table 2. Settings for the Simulating Waves Nearshore (SWAN) model.
Forcing field H-E wind with a spatial resolution of 0.125° and time interval of six hours; current speed simulated by the FVCOM
Frequency bins Logarithmic, between 0.01 and 1, at intervals of Δf/f = 0. 0.903
Resolution 0.1° grid with a 30-min temporal resolution
Bulk formulaBulk formula in [39] employed for including the white capping induced by the high wind speed
Directional resolution10° grid ranged from 0° to 360°
Propagation schemeWESTHuysen (non-linear saturation-based white-capping combined with wind)
Bottom frictionJONSWAP with a constant friction coefficient
Other settingsWave interactions (QUADrupl); triad wave–wave interactions (TRIad)
Table
Table 3. Comparison between the results from the SWAN model and the moored buoys.
Table 3. Comparison between the results from the SWAN model and the moored buoys.
ID: B11ID: B12ID: B13ID: B14ID: B15ID: B20
RMSE0.840.640.790.840.880.75
Cor0.920.930.840.940.850.94
Bias0.440.190.750.19−0.210.31

Share and Cite

MDPI and ACS Style

Yang, Z.; Shao, W.; Ding, Y.; Shi, J.; Ji, Q. Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands. J. Mar. Sci. Eng. 2020, 8, 783. https://doi.org/10.3390/jmse8100783

AMA Style

Yang Z, Shao W, Ding Y, Shi J, Ji Q. Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands. Journal of Marine Science and Engineering. 2020; 8(10):783. https://doi.org/10.3390/jmse8100783

Chicago/Turabian Style

Yang, Zhehao, Weizeng Shao, Yang Ding, Jian Shi, and Qiyan Ji. 2020. "Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands" Journal of Marine Science and Engineering 8, no. 10: 783. https://doi.org/10.3390/jmse8100783

APA Style

Yang, Z., Shao, W., Ding, Y., Shi, J., & Ji, Q. (2020). Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands. Journal of Marine Science and Engineering, 8(10), 783. https://doi.org/10.3390/jmse8100783

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop