Abstract
Bedform-related roughness affects both water movement and sediment transport, so it is important that it is represented correctly in numerical morphodynamic models. The main objective of the present study is to quantify for the first time the importance of ripple- and megaripple-related roughness for modelled hydrodynamics and sediment transport on the wave- and tide-dominated Ameland ebb-tidal delta in the north of the Netherlands. To do so, a sensitivity analysis was performed, in which several types of bedform-related roughness predictors were evaluated using a Delft3D model. Also, modelled ripple roughness was compared to data of ripple heights observed in a six-week field campaign on the Ameland ebb-tidal delta. The present study improves our understanding of how choices in model set-up influence model results. By comparing the results of the model scenarios, it was found that the ripple and megaripple-related roughness affect the depth-averaged current velocity, mainly over the shallow areas of the delta. The small-scale ripples are also important for the suspended load sediment transport, both indirectly through the affected flow and directly. While the current magnitude changes by 10–20% through changes in bedform roughness, the sediment transport magnitude changes by more than 100%.
1. Introduction
To contribute to answering scientific and practical questions, numerical morphodynamic models are often used to predict the hydrodynamics, sediment transport processes and morphological developments of coastal systems. In such models, many of the processes are parameterised, based on various assumptions. One of the parameterised variables is the bedform-related hydraulic roughness, which has a direct influence on the magnitude of friction between the bed and the flowing water [1]. At a flat seabed, roughness is caused by the individual grains (skin friction), but in many situations bedforms are present, inducing additional drag at the bed (form drag, or bedform-related roughness) [2]. The total effective hydraulic roughness consists of both the grain roughness and the bedform-related roughness. Although it is difficult to measure this roughness directly, it affects the magnitude and vertical structure of both the steady flow and the tidal and wave-driven oscillatory currents, and consequently also the magnitude of the sediment transport [3]. Therefore, it is important that a parameterisation is chosen in morphodynamic models that correctly represents environmental conditions.
There are many ways to describe or parameterise bedform roughness in models, ranging from constants in space and time to predictions of the actual bedforms present. Bedform roughness predictions are often a function of bedform dimensions, either height and length [4] or only bedform height [3], which are predicted based on wave- and/or current velocities and median grain size [3,5]. In the case of a spatio-temporally constant parameters, a Chézy value (e.g., [6,7,8]), Manning’s n value (e.g., [9]) or a constant roughness based on measured ripple heights (e.g., [10,11]) can be used. In numerical models, the hydrodynamic roughness is often used as a calibration parameter to minimize mismatch in observed and predicted water levels, current velocities or even morphological predictions (e.g., [12]). However, in most coastal systems, bedforms occur on various scales, so bedform-related roughness can have various dimensions in both space and time. For example, in tidal inlet systems, dunes (with lengths in the order of 100 m and heights in the order of meters), megaripples (lengths in the order of 10 m and heights in the order of 0.1 m) and small-scale ripples (with lengths in the order of 0.1 m and heights in the order of centimeters) can be found. Especially the small-scale ripples and megaripples respond quickly to the local hydrodynamics [13,14], which implies that ripple and megaripple-related roughness might vary on the time scale of minutes to hours and the spatial scale of meters. To accurately represent this behaviour, roughness predictors were created, so that the parameterised roughness can also vary in space and time (e.g., [3,15]). Most predictors are well-tested on flume data and on field data of wave-dominated coasts [3,16]. For environments with both waves and currents, such as ebb-tidal deltas, less field data are available. Yet, roughness may be different here from wave-only or current-only conditions, especially because wave and current stresses can work in different directions. Therefore, when bedform-related roughness predictors are used, which naturally contain uncertainty, uncertainty is imposed on the current and sediment transport predictions as well. However, the magnitude of this uncertainty is still unknown.
This paper builds on the ripple observations by Brakenhoff et al. [17]. They studied ripple characteristics on the wave-current dominated Ameland ebb-tidal delta in the north of the Netherlands, and also compared those to some common ripple roughness height predictors. While multiple tested models (including Van Rijn [3]) predicted small-scale ripple roughness heights to vary significantly on the timescale of the tides, Brakenhoff et al. [17] found that observed ripple characteristics varied much less in time, and only slightly depended on wave orbital velocity. Even though a large range of hydrodynamic conditions was encountered, the ripple height was nearly always between 0.01 and 0.03 m and ripple length was nearly always between 0.08 and 0.13 m. For the small grain sizes (i.e., = 211 m) at the study site, Brakenhoff et al. [17] hypothesized ripple dimensions to be in response to small-scale three-dimensional turbulence in the water column and not to the ambient flow. Moreover, Brakenhoff et al. [17] found that ripple height was overestimated by the predictor developed by Van Rijn [3], which can be used in various morphodynamic models and is the default parameterisation in the often applied Delft3D model. They suggested that a constant ripple-related roughness might be used in modelling of hydrodynamics and sediment transport, but they did not test the actual effects.
Because only two surveys of megaripples were available per ripple measurement site, Brakenhoff et al. [17] could not study the behaviour of megaripples through time. It was only found that they were present at several parts of the ebb-tidal delta, and co-occurred with the small-scale ripples. Not only are megaripple heights and lengths larger than those of the small-scale ripples, megaripple-related roughness is larger as well [18]. This implies that their effect on the current and sediment transport will be larger as well. Davies and Robins [19] found that for small current velocities (<0.2 m/s) the predictor developed by Van Rijn [3] predicts, however, that the contribution of small-scale ripples to the total roughness exceeds that of the megaripples.
In short, the use of bedform predictors to calculate roughness might affect both predicted hydrodynamics and sediment transport, but this impact has not been quantified yet. The main aim of this paper is to examine and quantify the importance of the ripple and megaripple-related bedform roughness for the calculation of hydrodynamics and sediment transport in the numerical morphodynamic model Delft3D. This model is used, because it is widely used and comparable to other morphodynamic models, such as MIKE21, TELEMAC, and ROMS. Although the way that the roughness predictors are incorporated is slightly different for each model, they can all make use of the Van Rijn [3] roughness predictor. First, it will be explained how roughness, hydrodynamics and sediment transport are computed and interact in Delft3D. Then, several predictors of bedform-related roughness are applied in a high-resolution Delft3D model of the Ameland Inlet. The modelled bedform-related roughness will be compared to the one parameterised from measured ripple characteristics, and the hydrodynamics and sediment transport patterns of the various scenarios are compared. This comparison is done for fair weather and storm conditions separately, because it is anticipated that roughness is different for the associated different wave and current conditions. The Ameland ebb-tidal delta is chosen as study site, because it is a wave- and tide-dominated coastal system. This hypothetically causes a large spatial variability in roughness, which makes it a suitable location to test various roughness parameterisations. On top of that, many measurements, including those of small-scale ripples [17], are available as a basis for a sensitivity analysis. Also, distinct calm weather and storm periods were observed.
2. Materials and Methods
2.1. Interaction of Roughness, Hydrodynamics and Sediment Transport in Delft3D
Delft3D is a numerical morphodynamic model system that incorporates all parts of the morphodynamic feedback loop: hydrodynamics, sediment transport and morphologic change [20]. Both in Delft3D and similar models, roughness elements such as grains, ripples, and megaripples are smaller than the model grid (i.e., sub-grid), so they are not explicitly solved on that scale and hence need to be parameterised. When a single grain size fraction is used, grain-related roughness does not vary in space or time, and is given by , with and the median and 90 percentile of the grain size, respectively. The bedform-related roughness, on the other hand, interacts with the hydrodynamics and affects the sediment transport both directly and indirectly. A schematic overview of all processes in Delft3D that are influenced by the ripple-related roughness is given in Figure 1. There are two ways to impose roughness in Delft3D: either via a direct calculation of each roughness scale (ripples, megaripples and dunes), or via a prescribed roughness value or friction coefficient.
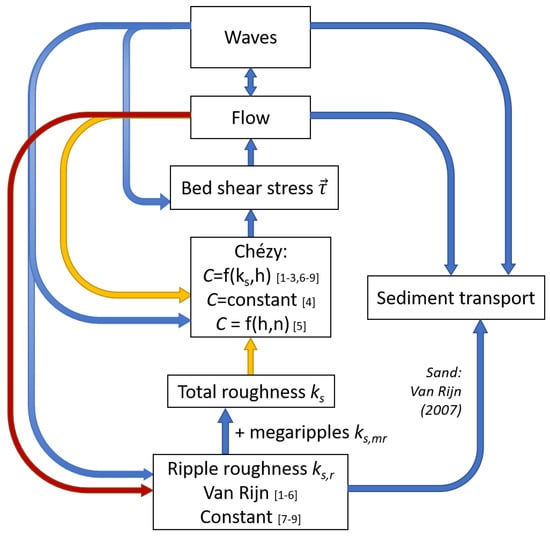
Figure 1.
Schematic overview of interaction and feedbacks related to ripples and megaripples in Delft3D. The numbers refer to the scenarios explained in Section 2.3. Yellow arrow: this effect is removed by choosing a constant Chézy value C (scenarios 4–5, note that sediment transport in this case still depends on ). Red arrow: this effect is removed by choosing a fixed ripple roughness (scenarios 7–9).
In the direct calculation of bedform roughness , the separate parts (ripple-related roughness), (megaripple-related roughness) and (dune-related roughness) are calculated from Van Rijn [3]. The predicted ripple roughness is:
in which is a mobility parameter, with s the ratio of sediment density divided by water density and g the gravitational acceleration. The total combined wave-driven and tide-induced velocity , with the magnitude of the wave-induced orbital motion and the magnitude of the depth-averaged current velocity. is a ripple roughness calibration factor. As given in Equation (1), the ripple-related roughness is related to grain size and wave- and current velocity. Both ripple and megaripple-related roughness are explicitly calculated, so it depends on the flow conditions of the previous time step. Since bedforms do not always immediately react to the hydrodynamics, a relaxation option is included as well, which is calculated implicitly:
with being the relaxation factor: , in which dt is the hydrodynamic time step in minutes and T the relaxation time scale in minutes.
The megaripple-related roughness is given by:
with h the water depth. A relaxation option for megaripples is available in the model as well, but it was not used in the present study. The dune roughness according to Van Rijn [3] is calculated in a similar way, but since dunes are only applicable in rivers [21], the prediction of dunes was turned off in the model and the formulas are not given here.
When all separate roughness scales are computed, the total bedform roughness is calculated as
Using , the Chézy friction coefficient C is calculated as
As stated before, the Chézy value can also be given as input directly. The third possibility is calculating the Chézy value by
with n being Manning’s roughness coefficient. According to Marriott and Jayaratne [22], Manning’s n can be calculated by
In each of the cases with a spatio-temporally constant Chézy value, the bedforms will not affect the flow anymore, but is still calculated and affects the sediment transport (see Equation (8)). In each case, the Chézy coefficient is an input for the bed shear stress calculation, which in turn affects the flow. To solve wave propagation the phase-averaged spectral wave model SWAN was used. SWAN solves the wave action balance equation in order to compute the wave energy spectrum throughout the model grid [23,24]. Delft3D and SWAN are coupled, which means that the effects of waves on hydrodynamics and vice versa are included, so waves can feel and interact with the flow, by which they can affect and . and can only affect the waves indirectly through the affected flow (Figure 1). Although the roughness is not directly coupled to SWAN, it does use a semi-empirical energy decay rate dependent on bed roughness typical for sandy beds and JONSWAP waves of 0.038 [25].
The suspended load is computed by solving the depth-averaged (2DH) advection-diffusion equation [26]. The depth-averaged equilibrium concentration, which is used to calculate the exchange of sediment between the bed and the water column, is solved using the expressions of Van Rijn [27]. This approach includes the computation of the velocity profile including wave-current interaction effects described by Van Rijn [28] and a vertical concentration profile using a 1DV advection-diffusion equation. The expression for vertical sediment mixing contains contributions due to waves and currents, both being affected by the ripple-related roughness. To solve for the vertical sediment concentration profile, the near-bed reference concentration is needed as well, which is calculated by
in which is the critical bed shear stress and is the grain-related bed-shear stress due to both currents and waves, computed using the grain-related roughness . is the non-dimensional grain size and reference height a = 0.5. Below a, the sediment concentration is equal to [29].
The depth-integrated suspended load transport is computed by multiplying the depth-averaged velocity with the depth-averaged sediment concentration c and water depth h:
The instantaneous bedload transport is computed by Van Rijn [27]:
in which and are the density of sediment and water, respectively. For further details on the sediment transport formulae, the reader is referred to Van Rijn [27].
In short, the ripple roughness determines the reference height a and the vertical mixing of suspended sediment and therefore directly affects the suspended load transport. The mega ripple roughness does not directly affect the sediment transport; however, together with the ripple roughness it is a part of the total roughness . This means that both small-scale ripples and megaripples indirectly affect the transport through their effect on bed shear stress, the Chézy friction coefficient an the flow (Figure 1). The grain-related roughness affects the bedload transport and the near-bed reference concentration .
2.2. Model Setup and Boundary Conditions
The study site is the Ameland Inlet, which is located in the north of the Netherlands (in northwestern Europe) and is part of the barrier island chain called the Wadden Islands that borders the coasts of the Netherlands, Germany and Denmark. For the present study, a hydrodynamically validated version of the Delft3D Coastal Genesis II Terschelling-Ameland inlet (CG2TA) model was used, with Delft3D-FLOW version 3.59.01.48550, FLOW2D3D version 6.02.13.7545 and SWAN version 41.10. The model setup, forcing, calibration and validation are described in [25,30] and will be repeated briefly below. The model grid extended from the island of Vlieland to the island of Schiermonnikoog, thus encompassing the Vlie, Ameland and Frisian Inlets. The seaward boundary was located approximately 30 km offshore, while in the basin, the tidal divides south of Vlieland and Schiermonnikoog were taken as boundaries. The grid was obtained from Nederhoff et al. [25], with typical grid cell sizes in the region of interest of 50–150 m (Figure 2), assuring that wave processes were represented in enough detail and also that main bathymetric features were present. At the open boundaries water levels were prescribed, which were derived from a large-scale North Sea model (nesting) that was forced by tides, air pressure and wind. Furthermore, at the open North Sea boundaries time series of significant wave height were prescribed, based on the wave stations given in Figure 2. In the back barrier basin, a zero-gradient Neumann boundary was applied. The model bathymetry was based on the so-called ‘Vaklodingen’, the bathymetry that is measured and processed by Rijkswaterstaat (part of the Dutch Ministry of Infrastructure and Water Management) once every 1–3 years using a singlebeam echosounder [31]. The bathymetry of the Ameland inlet was measured in 2017, and it was combined with data from earlier years (2017–2008) to construct the bathymetry for the entire model grid. At each grid cell, the most recent bathymetric information was used.
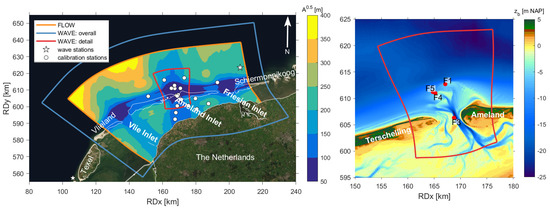
Figure 2.
(Left): extent of the model grids, including grid cell sizes (given by the square root of the grid cell area A) of the FLOW model. (Right): zoom of the model bathymetry at the Ameland Inlet and locations of the measurement frames (F1–F5).
The model ran in depth-averaged (2DH) mode and was forced by water levels, waves, wind and atmospheric pressure. The water levels that were forced on the model boundaries were derived from the Dutch Continental Shelf Model-Zuidelijke Noordzee (DCSMv4ZUNOv6) model, which encompasses the entire southern part of the North Sea and is driven by tides, winds and air pressure [32]. The wave characteristics at the boundaries were derived from wave spectra that were measured at two stations near the western and eastern boundaries (Figure 2), which were interpolated onto the northern boundary. The waves were then propagated through the model domain by the SWAN wave module. SWAN and FLOW communicated every 30 min (two-way coupling).
The model was calibrated on water levels measured throughout 2017 offshore of Terschelling and Ameland and with current speeds, discharges and wave characteristics as measured during a measurement campaign of August–October 2017 (calibration stations are given in Figure 2). In the measurement campaign of 2017, four frames were placed on the ebb-tidal delta (Figure 2) from 29 August until 10 October 2017; their locations were chosen to represent the wide range of hydrodynamic conditions on the delta. Frames 1 and 5 were positioned at the delta lobe, at depths of 8.6 and 8.9 m, respectively, on sediment with = 225 (F1) and 186 m (F5). Frame 3 was placed in the channel, at 15.1 m depth and on sediment with = 216 m. Frame 4 was placed at the ebb-delta shoal, where the average water depth was 6.5 m and the was 186 m. The frames measured water levels, wave heights, periods and directions, current speeds and directions, and bedforms, using pressure sensors, ADVs and Sonars, respectively [31]. More details on the small-scale ripple measurements are given in Section 2.4. Some parts of the delta and the inlet were also measured with a multibeam echosounder before and after the campaign, which showed that on several locations megaripples were present, with heights of 0.1–0.2 m and lengths of 10–20 m. Discharges through the tidal inlet were estimated from ship-mounted ADCP flow measurements, collecting data along inlet cross-sections during 6 tidal cycles. Further information on the field campaign, including the data collection, can be found in van Prooijen et al. [31].
In the reference scenario, the bedform predictor by Van Rijn [3] was used, which directly predicts the ripple and megaripple roughness. According to Van Rijn [3], the small-scale ripple-related roughness is equal to the actual ripple height, so this assumption is used here as well. The model was calibrated to match hydrodynamic observations best using ripple and megaripple-related roughness calibration factors of 0.5 [25] ( and in Equations (1) and (3), respectively), which is why they were set to 0.5 in the present study as well. The relaxation time was set to 0, so the ripples and megaripples respond to the hydrodynamics immediately. Similar to the present study, no morphologic updates were used in calibration and validation of the model.
The calibrated model was validated hydrodynamically using field data of 2008, 2011, November 2017 and January and March 2018, running the model without morphological updates. Measured depth-averaged current speeds derived from the ADCP data of Frames 1, 4 and 5 were reproduced with a root-mean-square error (rmse) of 0.10–0.15 m/s (Table 1). These values are in the same order of magnitude as those of validated models used in previous modelling studies [25,32]. The differences between model predictions and measurements did not depend on the wave- or current conditions, with no variation in rmse between storm and calm conditions. The biases were low (mostly in the order of 0.05 m/s) because the differences in positive and negative values were approximately equal. The rmse values were rather high, especially at Frame 3, where the rmse is 0.34 m/s, but the measured current velocities did not exceed 0.5 m/s. At the other frames, rmse values were lower, but considering that current velocities were up to 1 m/s (Figure 3), they were still rather high. This is due to slight errors in the predictions of the current direction. The timing of the peak ebb and flood velocities was equal in the model predictions and the measurements.

Table 1.
Root-mean-square error [m/s] and bias [m/s] between measured and modelled current velocities (x- (east-) and y- (north-) component and magnitude) at the Frame locations given in Figure 2.
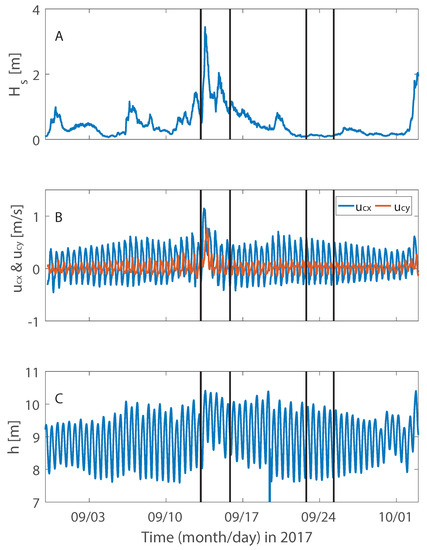
Figure 3.
Hydrodynamics as measured at Frame 5. (A): significant wave height. (B): east () and north () component of the depth-averaged current velocity. (C): water depth. Black lines indicate the representative storm and calm period described throughout this paper.
2.3. Simulations
The CG2TA model was run for the six weeks covering the period of the field campaign of 30 August–8 October 2017. Nine roughness scenarios were run, in order to assess the sensitivity of the model to both ripple and megaripple roughness. The scenarios are described below and are summarized in Table 2. Model output was stored at frame locations every ten minutes, and every 60 min at all other grid points. In all cases, output was given of ripple roughness (same as Equation (1)), depth-averaged current velocity in east and north component, wave height and suspended, bed load and total sediment transport magnitude in east and north component on all grid points. Following Nederhoff et al. [30], a single grain size fraction with = 200 m was used in the model. This is similar to the measured near Ameland of 211 m, which had a standard deviation of only 30 m [33]. No mud fractions were used, as the mud content on the delta was less than 1% by volume [33]. The roughness scenarios are:

Table 2.
Overview of model scenarios.
- 1.
- The Van Rijn (2007) roughness predictor with and = 0.5This is the calibrated model which was referred to in Section 2.2.
- 2.
- The Van Rijn (2007) roughness predictor with = 1 and = 0.5This is the same as scenario 1, but with the predicted ripple roughness twice as high as in scenario 1. This value was also used in Brakenhoff et al. [17] to compare observed and predicted small-scale ripples, although in that study the predictions were based on measured hydrodynamics.
- 3.
- The Van Rijn (2007) roughness predictor with = 0.5 and = 1This is the same as scenario 1, but with the predicted megaripple roughness twice as high as in scenario 1. In this way, the importance of megaripples for currents and sediment transport can be studied.
- 4.
- Fixed Chézy coefficient for hydrodynamicsIn this scenario, a constant Chézy value of 57.2 was adopted. This was calculated manually with Equation (5), using the mean water depth of the model excluding the basin, which was 12.7 m. Measured mega ripples at the Ameland ebb-tidal delta were 0.1 m high and ripples were 0.015 m high, so following Equation (4), the mean (measured) was 0.1011 m. As stated before, in this scenario the Chézy value was used in the prediction of hydrodynamics, but for sediment transport the Van Rijn (2007) roughness with and = 0.5 was still used. In other words, only the coupling between bedforms and the hydrodynamics was removed.
- 5.
- Fixed Manning’s roughnessIn this scenario, using = 0.1011 m, Manning’s n was determined to be 0.0263 m (Equation (7)). This is within the range of 0.014 to 0.028 as was used by Nederhoff et al. [25]. Since Equation (6) depends on water depth h, the Chézy constant in this scenario varied over space and time. Similar to scenario 4, the Van Rijn roughness predictor with and = 0.5 was still used for sediment transport but not for hydrodynamics.
- 6.
- Relaxation 180 minScenario 6 is similar to scenario 1, only the small-scale ripples were given a relaxation time in adapting to the hydrodynamics. This relaxation time T was set to 180 min based on an analysis of the temporal behaviour of the ripples in relation to the hydrodynamics. The measured ripples were very small, so it would be expected that they would respond instantly to the hydrodynamics. However, the measured ripple heights showed small variations only on the time scale of the tide. Therefore, the added relaxation time will probably cause a better resemblance of the measured ripples.
- 7.
- No ripples; constant ripple roughness 0.0002 m (=)For scenarios 7–9, a constant and spatially uniform ripple roughness was defined. As visible in Figure 1, still affected hydrodynamics and sediment transport in these scenarios, the only difference was that the hydrodynamics could not affect anymore. In scenario 7, was set to 0.0002 m. This is equal to the median grain size, to simulate the effect of a sandy bed without small-scale ripples. was still the same as in scenario 1, because it does not directly affect the sediment transport.
- 8.
- Constant ripple roughness 0.015 mIn scenario 8, the ripple roughness was 0.015 m, which is similar to the measured ripple heights [17]. was still the same as in scenario 1.
- 9.
- Constant ripple roughness 0.03 mIn scenario 9, ripple roughness was set to 0.03 m to see the effect of a doubling of the constant roughness, similar to scenario 2. was still the same as in scenario 1.
2.4. Analysis
First, predicted ripple roughness was compared to measurements at the frame locations, to verify that the modelled ripple roughness is realistic in all scenarios. As described in Brakenhoff et al. [17], the bedforms were measured by a 3D Profiling Sonar (Marine Electronics type 2001) on each frame. Ripple heights were calculated with , where is the standard deviation of the detrended bed elevation. Ripple wavelengths were calculated using a wavelet analysis. The ripple dimensions were found to be highly similar at the four frame locations: all ripples were between 0.01 and 0.03 m high, with an average of 0.015 m, and all lengths ranged between 0.08 and 0.20 m, with an average of 0.115 m. Despite a large variation in tidal, wind and wave conditions, the ripple characteristics did not vary notably over time. A more detailed description of the analysis of the ripple characteristics is given in Brakenhoff et al. [17].
After this, the model results of scenarios 2–9 were compared to the default scenario in space and time. All model processes were considered, following the structure of Figure 1 (from roughness and Chézy factors to hydrodynamics and sediment transport). For each of these parameters, the mean absolute relative difference (MARD) on each location in the model was calculated. The MARD is defined as
with = , in which X is a parameter from the scenarios 2 to 9 and X1 belongs to the default scenario. x and y are all grid locations in the model domain and n denotes several output time steps. For vectors such as current velocity and sediment transport, the MARD is calculated for the magnitude. Direction differences are calculated in absolute degrees. The sediment transport is calculated in a time-integrated way, so that n = 1 and values are obtained in kg/m.
Two time periods were considered in this study: (1) a 36-h period of calm weather and (2) a 36-h period of storm conditions (Figure 3). These periods were chosen in such a way that water levels at the beginning and end of each period were the same, which is one of the ways to define a tidal period or multiples thereof [34]. On top of that, various environments were studied, varying from the current-dominated tidal channel to the wave-current dominated ebb-delta shoals. This facilitated in determining the sensitivity of hydrodynamics and sediment transport to ripple-related bedform roughness in various conditions. Because the model was not validated for sediment transport, we focused only on relative changes and absolute transport values are not discussed. The sensitivity in the tidal basins was not considered either, because neither hydrodynamics nor sediment transport were validated here, and the potentially high mud concentrations could result in different processes than considered by the present model.
3. Results
3.1. Bedform Roughness
Ripple roughness predicted in scenarios 1-6 is compared to the heights measured in the field campaign in both space and time (Figure 4). During the storm, ripple measurements at the frames were largely absent, because the sonar could not detect the bed due to the large amount of suspended sediment near the bed. Figure 4 shows that all model scenarios predict that ripples are washed out during the storm: ripple roughness decreases to 2 mm, which is equal to the (Equation (1)). Only in the channel (at Frame 3) ripples were not washed out in either the measurements or the predictions. The measured and modelled ripple roughness at this location were similar, but the model values varied more with time.
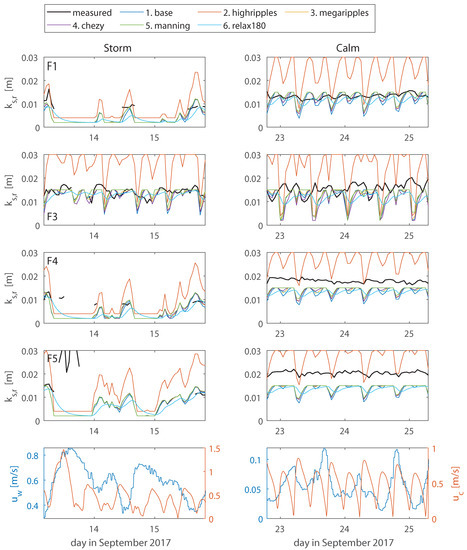
Figure 4.
Top four rows: measured and modelled (scenarios 1–6) ripple roughness through time at all frame locations (F1, F3, F4 and F5) during the storm (left) and the calm (right) period as denoted in Figure 3. Bottom row: near-bed orbital velocity and depth-averaged current velocity at Frame 1 during the storm (left) and the calm (right) period. (As the ripple roughness was constant in scenarios 7–9, they are not plotted in this figure.)
In calm weather, the measured ripple heights were similar at all frames (Figure 4). Still, the variability in time was highest in the main channel (Frame 3). This is the only location where the measured ripple heights showed a clear tidal signal. Modelled ripple roughness values were all highly variable, showing a tidal signal (Figure 4). However, this modelled tidal signal was much stronger than measured and the timing was different. No dependency on the wave-related orbital velocity can be observed in either the modelled or the measured ripple roughness (Figure 4), probably because the current is more dominant in the mobility parameter (Equation (1)). Only the ripples in scenario 6 (180-min relaxation time) look similar to the measured values in terms of semi-diurnal variability.
Overall, all modelled values were in the range of 0.002 to 0.03 m, which is a realistic range for these small-scale ripples. On average, modelled was somewhat lower than in the measurements in all scenarios except the scenario with the high ripples (scenario 2).
Figure 4 also illustrate that modelled ripple roughness was virtually the same in scenarios 1, 3, 4 and 5. This is because in all these scenarios is the same, is affected by the hydrodynamics and no relaxation is included. Especially during calm weather, in scenarios 1–5 varied between two values. Scenario 2 (high ripples) peaked at a different ripple roughness and had a larger range of roughness values, but the range itself was also constant among the frames. The minimum and maximum values in these simulations are caused by the low and high cut-off value for ripple roughness in the Van Rijn predictor (at 20 and 150 times the median grain size, respectively, see Equation (1)). The simulation with the 180-min relaxation time is the only one that did not alternate between two cut-off values. This describes the variability of ripple roughness best, for this situation, as the measured ripple heights were not alternating between two values either, but rather changed more gradually with time. Yet, the difference between measured and modelled ripple roughness, given by the rmse and bias in Table 3, is smallest in the scenario with constant of 0.015 m. The bias and rmse are largest in the scenarios with constant high ripples and without ripples. All other scenarios are similar to the base scenario in terms of rmse and bias.

Table 3.
Root-mean-square error and bias between the modelled and measured ripple roughness (meas-mod), averaged over all frames.
The total roughness for all scenarios at all frames is given in Figure 5. The patterns are similar to those of the small-scale ripples in Figure 4. Again, the ripples and megaripples were washed out in most scenarios for large parts of the storm. Only in the channel (at Frame 3) roughness was not affected by the storm; the patterns at this frame were similar during calm weather and storm conditions. During calm weather, all scenarios at all frames show that the total roughness depends on the tidal signal, with the largest during the peaks of . Similar to the small-scale ripples, no relation with orbital motion or water depth was found.
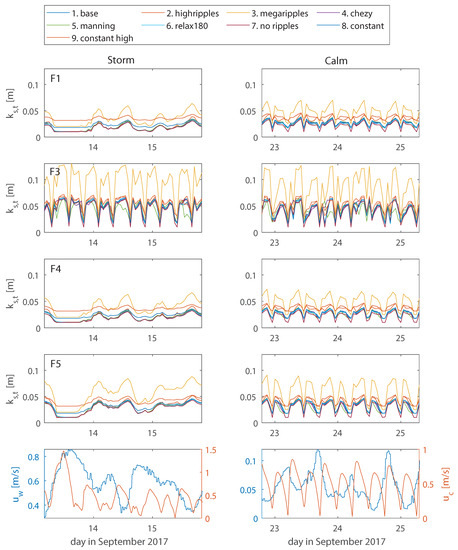
Figure 5.
Top four rows: modelled total bedform roughness through time at all frame locations (F1, F3, F4 and F5) during the storm (left) and the calm (right) period as denoted in Figure 3. Bottom row: modelled near-bed orbital velocity and depth-averaged current velocity magnitude at Frame 1 during the storm (left) and the calm (right) period.
The scenarios were again highly similar, with only two scenarios standing out. First, in the scenario with the doubled megaripple roughness (scenario 3), was twice as high as in all others, at all frames. This suggests that the megaripples are more important to than the small-scale ripples. However, of the scenario with constant high ripples (scenario 9) exceeded even the in the scenario with high megaripples during the storm at Frames 1, 4 and 5. This is caused by the fact that the ripples in scenario 9 were not washed out, because they were fixed at 0.03 m. In all other scenarios, ranged between 0.01 and 0.07 m. Because the small-scale ripples were generally in between 0 and 0.015 m high, a first estimation would be that small-scale ripples constitute up to 20% of the total roughness.
However, many more ripple roughness values and percentages occur throughout the model domain. For example, Figure 6A,B shows that the ripples disappeared during the storm at the margin of the ebb-tidal delta, where Frames 1, 4 and 5 are located. On other locations, for example offshore and on the sandbar that is attached to the Ameland coast, the ripples did not disappear at all. During calm weather, on the other hand, ripple roughness values at the frames were higher than in the deepest part of the channel (west of Frame 3).
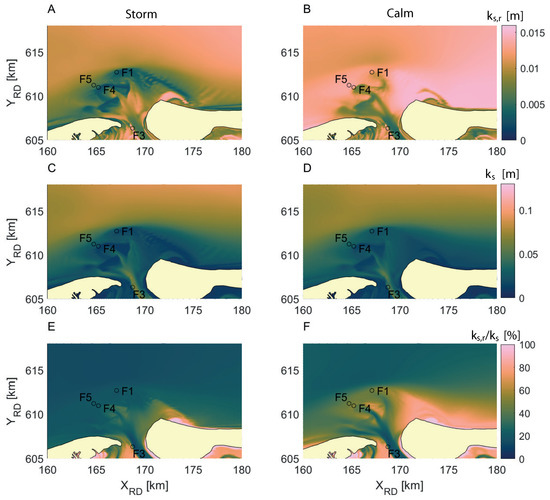
Figure 6.
Modelled ripple roughness (A,B), total roughness (C,D) and ripple roughness as a percentage of total roughness (E,F) averaged over time during the storm (left) and the calm (right) period as denoted in Figure 3 in scenario 1.
Both during calm weather and during the storm, the total bedform-related roughness averaged over time in the default scenario varied from 0.002 m on the shallow shoals to 0.15 m offshore (Figure 6C,D). Because cannot exceed 0.015 m, all values higher than that can be attributed to megaripples. As given in Equations (1) and (3) and Figure 4 and Figure 5 both ripple and megaripple roughness depend on the flow velocity , which explains the different values during storm and calm weather in the default scenario.
The importance of ripples is given by the average over time of ripple roughness as a percentage of total roughness (Figure 6E,F). For both time periods, the lowest importance of ripples (<10%) was found in the deep tidal inlet channels. Offshore, the ripples made up for 20–40% of the total roughness. The importance of ripples increases with decreasing depths and especially during calm weather: on the shoals ripples constituted to 60–90% of the total roughness.
During the storm, the ripples were much less important to the total roughness when averaged over the entire domain excluding the basin; while the spatially average percentage was 40% for the calm period in the base scenario, it was 22% for the storm (Table 4). Because the total modelling period consisted of more calm periods than storms, the percentage of the total period is close to that of the calm period: 35% in the case of the default scenario. The same is found for all other scenarios. Especially the percentages of scenarios 4, 5 and 6 are similar to those of the default scenario. Naturally, the importance of ripples in scenario 7 (with ripple roughness of only 0.0002 m) approaches 0. In scenarios 8 and 9, the ripple roughness was more important than in the default scenario, with 44 and 63% in the calm period and 40 and 59% during the storm. This means that the importance of ripples increased much more during the storm when a constant ripple roughness was used. This is because the ripples are washed away in the base scenario during storm, while they are forced to exist in scenarios 8 and 9.

Table 4.
Ripple-related roughness as a percentage of the total bedform-related roughness, averaged over the model domain excluding the basins, and averaged over time for the calm weather, storm and total modelling period.
Based on these model observations, it can be expected that changes in the small-scale ripple roughness will mainly affect the shoals during calm weather. Changing the megaripple predictor settings will affect the offshore area and the channels, mainly during storms. For example, increased with 80% on the shoals during calm weather when was doubled, while a much smaller change (less than 10%) was found in the same area during the storm.
The Chézy coefficient is a function of and water depth h in all scenarios except 4 and 5. As h varies more than in the model domain (but does not differ between the simulations) and Equation (5) includes a logarithm, differences between the scenarios are dampened out on the shallow ebb-tidal delta. Therefore, differences between modelled Chézy values are relatively small between the different scenarios. The largest differences in Chézy value with respect to the reference scenario are found in scenario 5 (with a constant Manning’s n) on the shallow shoals (up to 30% during both calm weather and the storm).
3.2. Hydrodynamics
Among various hydrodynamic parameters examined, the current magnitude is the most affected by the choice of the roughness parameterisation. Effects on water level and wave height are minimal, because the SWAN wave model does not directly respond to the ripple-related roughness, and are therefore not further discussed. During the storm, the flow was strong across the entire ebb-tidal delta, while it was weaker and more concentrated in the main channel during calm conditions (Figure 7).
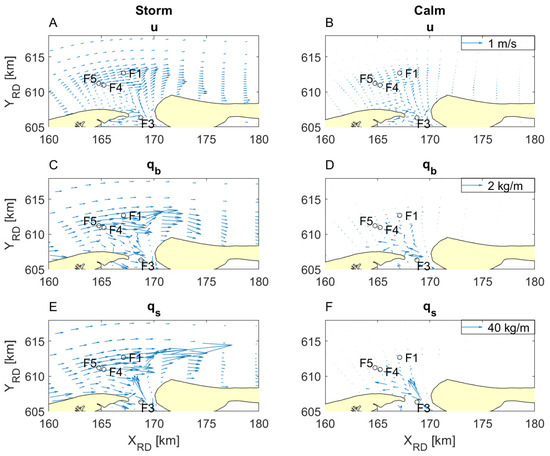
Figure 7.
Time-averaged value of depth-averaged current velocity magnitude (A,B), time-integrated bedload transport (C,D) and time-integrated suspended load transport (E,F) during the storm (A,C,E) and the calm weather period (B,D,F) on a select number of model grid points.
In general, a higher roughness leads to a lower current velocity. When the roughness was changed, the flow direction generally remained the same. Throughout the model domain, direction differences between all scenarios and the base scenario were mostly below 5, with maximum values of 30 on the western shoal in some scenarios. Thus, directions are not affected in such a way that the current is reversed. Only the shape of the tidal ellipse is slightly altered by (temporal) changes in bedform roughness. The largest differences with the base scenario in both current velocity direction and magnitude are found when a constant Chézy or Manning roughness value was prescribed, or when the megaripple roughness was doubled. During calm weather, in these cases relative differences in current velocity exceeded 100%, but this only occurred at locations where the current velocity in the base run was near 0 (Figure 8). On the delta, the current was affected by approximately 50%. During the storm, choosing a constant Manning value resulted in up to 70% relative difference in current velocity on the delta, while the offshore areas were affected by approximately 20% (Figure 9). Choosing a constant Chézy value resulted in 30% relative difference in the entire model domain, with maximum values near the western shoal of 70%. This is similar to the effects of prescribing a doubled megaripple roughness. The use of a constant ripple roughness (scenarios 7–9) mainly affected the current at the shoals. The relative differences with the base scenario were larger for larger ripple roughness, and were 40% at the most. A doubled varying ripple roughness (scenario 2) resulted in a similar pattern, but the changes the current velocity in this case were maximum 10%. Since the effect of doubling the megaripples was much larger, it can be stated that small-scale ripples roughness is not really important for the current. Scenario 6, with a 180-min relaxation time, has even less effect; the maximum relative differences with the base scenario are 5%, but mostly they are below 1%.
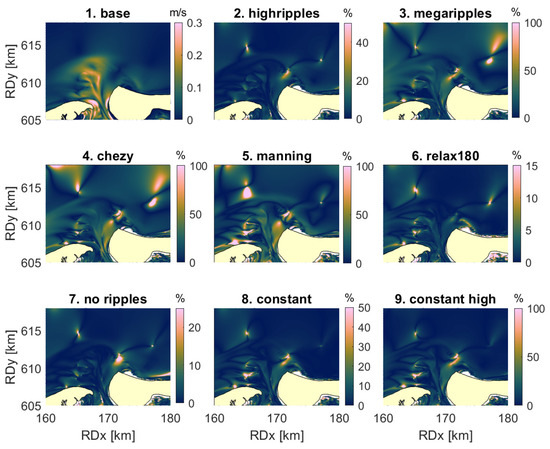
Figure 8.
Mean depth-averaged current velocity (m/s) of the base scenario during calm weather (1), and mean absolute relative difference in of all other scenarios with the base scenario during calm weather (2–9).
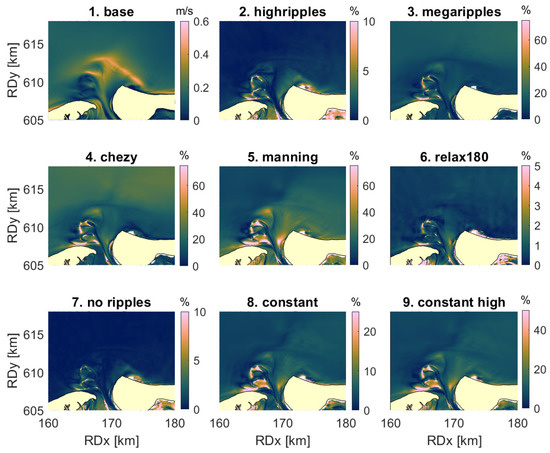
Figure 9.
Mean depth-averaged current velocity (m/s) of the base scenario during the storm (1), and mean absolute relative difference in of all other scenarios with the base scenario during the storm (2–9).
3.3. Sediment Transport
The bed load and suspended load transport are both considered by time-integration over the calm and storm period. The amount of suspended load transport was approximately ten to twenty times larger than the bed load transport, but apart from that the patterns in the base scenario were similar (Figure 7). Most transport takes place during the storm, at the seaward extent of the ebb-tidal delta shoals and at the inlet channel. During calm weather, less transport takes place, and it is mostly confined to the channel.
Similar to the current velocities, transport directions are not significantly affected by the roughness scenario. Direction differences are a little bit larger in sediment transport than in current velocity, with the largest differences occurring on the shallow parts of the delta. In the deeper parts of the model domain, differences with the base scenario are in the order of 10 degrees. Especially for suspended load transport, differences with the base scenario are found of up to 180 degrees, which means that the sediment transport direction is reversed. This happens only in areas in which the directions in the base run also show large variations on small areas. The large differences with the base run are thus caused by the transport patterns that remains the same, but slightly shifts in space.
The patterns in relative difference in time-integrated sediment transport magnitude between the base scenario and the other scenarios are also similar to those of . During calm weather, for both bedload and suspended load transport, the relative differences with the base scenario were generally below 10%. Yet, values of up to 200% were found at the shallow areas, where the time-integrated amount of sediment transport in the base run approached 0 (Figure 10 and Figure 11).

Figure 10.
Time-integrated suspended load transport during calm weather (1), and absolute relative difference in of all other scenarios with the base scenario during calm weather (2–9).
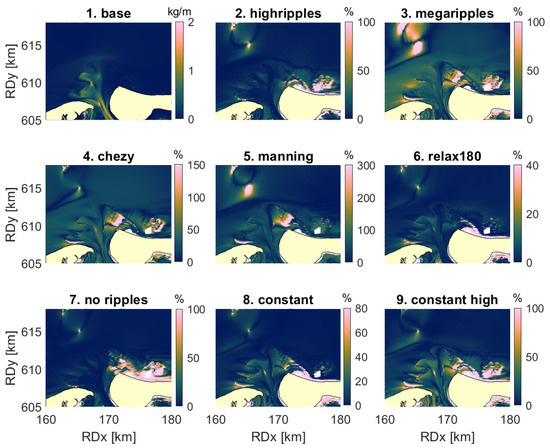
Figure 11.
Time-integrated bedload transport during calm weather (1), and absolute relative difference in of all other scenarios with the base scenario during calm weather (2–9).
During storm, the MARD-patterns of the bedload and the suspended load magnitude are not similar. The time-integrated bedload transport is affected most when a constant Chézy value (scenario 4), Manning coefficient (scenario 5) or a constant high ripple roughness (scenario 9) is prescribed (Figure 12). In these cases, relative differences with the base scenario of more than 100% are found, but they occur only on the locations where the transport magnitude in the base run was very small. In the scenarios with high megaripple roughness (scenario 2), a constant Chézy value (scenario 4), very small ripple roughness (scenario 7) and constant high ripple roughness (scenario 9), the time-integrated bedload transport magnitude is also affected offshore by some 20–30%.
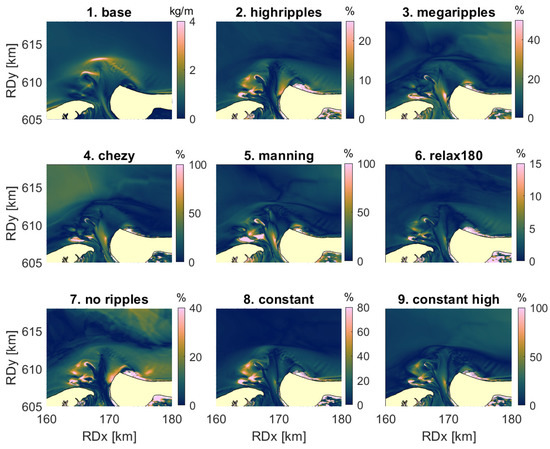
Figure 12.
Time-integrated bedload transport during the storm (1), and absolute relative difference in of all other scenarios with the base scenario during the storm (2–9).
The highest relative differences with the base run are found for suspended load during the storm. Here, relative differences of more than 100% occur in all scenarios (Figure 13). The effects of changing roughness are not confined to the shoals anymore as during calm weather, but are found throughout the model domain. Even when a relaxed ripple roughness (scenario 6) was used, relative differences of up to 70% were found, even though the current was hardly affected. This implies that the change in sediment transport is caused by a change in sediment concentration (see Equation (9)). Apart from the scenarios with the constant Chézy value (scenario 4) or the doubled megaripple roughness (scenario 3), the eastern shoals are most affected. At this location the ripples in the base scenario made up to 60% of the total roughness during the storm (Figure 6). The constant Chézy value was chosen based on an average depth, so offshore and in the deeper parts of the channel, where the water depth is larger than the average, the Chézy value was too high. In all other simulations, the change in transport in the channel is near 0. When the megaripple roughness was doubled, no clear effect was found on the shoals and in the channel, and a larger effect was seen offshore, in the area where megaripples are dominant. As described before, the suspended load does not directly depend on (Figure 1), implying that the change in transport in this scenario was caused by the changes in hydrodynamics. Lastly, it should be noted that low relative differences were found for all scenarios at the northern part of the delta, where the absolute values of the suspended load transport magnitude in the base run were highest.
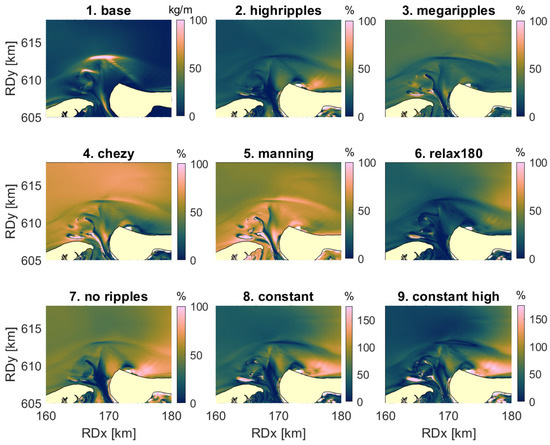
Figure 13.
Time-integrated suspended load transport during the storm (1), and absolute relative difference in of all other scenarios with the base scenario during the storm (2–9).
4. Discussion
The aim of this paper was to assess the effect of the roughness induced by small-scale ripples and megaripples on hydrodynamics and sediment transport in Delft3D. First of all, the modelled ripples were compared to measurements. Measured ripples were found to have relatively stable dimensions. Ripple heights were only weakly related to orbital velocity (which is a function of wave height and water depth), while no relation was found at all between ripple dimensions and current velocity [17]. Brakenhoff et al. [17] therefore suggested to use a constant ripple roughness in modelling. In the present study, the effects of a constant ripple roughness (scenarios 7, 8 and 9) were compared to those of the default Van Rijn roughness predictor (scenarios 2, 3 and 6) and to situations with roughness incorporated into constant Chézy or Manning values (scenarios 4 and 5).
Figure 4 showed that the ripple-related roughness simulated by using a 180-min relaxation time was closest to the measured roughness. Yet, this does not mean that this scenario also gives the best resemblance of the true current and sediment transport. The current in this scenario changes with only 2% with respect to the base scenario. However, no measures of sediment transport are available of the studied location and time period, so it is unclear if the base scenario or the relaxation scenario performs best.
Based on the importance of small-scale ripples and megaripples for the total roughness, it was expected that changes in the small-scale ripple roughness would mainly affect the shoals during calm weather, while megaripples will affect the offshore area and the channels, mainly during storms. This is also confirmed by the model results. During calm weather, both the current and the time-integrated sediment transport are mainly affected on the shallow parts of the delta. During storm, the offshore area is affected as well. In the deep channel in between the islands, the current depends on the chosen roughness scenario, but the transport does not. Since sediment transport q is a function of current velocity u and sediment concentration C, the fact that transport does not change means that higher ripple roughness also causes a higher depth-integrated sediment concentration. It is expected that these different effects of small-scale ripples and megaripple roughness will also be found on other ebb-tidal deltas, since current and depth distributions in space will be similar (i.e., alternating shoals and channels). Yet, differences in grain size distribution might also cause different ripple dimensions and behaviour [17], so one should be careful in extrapolating the results to other deltaic systems.
The transport in the channel is only affected when a constant Chézy value is chosen. This is because this Chézy value is constant throughout the model domain, so it is not dependent on depth. Therefore, in areas deeper than the average depth, the prescribed roughness is higher than when a depth-dependent C is chosen. This is also the case on shallow areas during the storm when constant roughness values are prescribed. Both in the field data and in the model, mobility parameter often exceeds 250 during the storm, which results in the small-scale ripples being washed away. Therefore, when the ripples are forced to be constant in the model, they are too high, resulting in large errors in current velocity and sediment transport. Therefore, contrary to what Brakenhoff et al. [17] suggested, a constant ripple roughness should not be implemented in morphologic studies, especially when shallow (<10 m) areas and/or storm periods are modelled. Davies and Robins [19] drew a similar conclusion when studying bedforms in an estuary with TELEMAC. Even though their study concerned megaripples and dunes predicted by Van Rijn [3], they also found that a spatio-temporally varying resulted in the most accurate prediction of local hydrodynamics. This gives the use of the Van Rijn roughness predictor an advantage over choosing a constant ripple roughness or a constant Chézy value.
The Delft3D model, similar to other numerical morphodynamic models such as MIKE21, TELEMAC and ROMS, is highly complicated and involves numerous feedbacks (see Figure 1). While this resembles reality better, this also makes it difficult to say whether changes in sediment transport are mainly caused directly by changes in roughness or indirectly by changes in hydrodynamics. Figure 1 shows that both causes are possible. In the scenarios with doubled small-scale ripple roughness, relaxed ripple roughness, and a constant very small ripple roughness, the current velocities during the storm in most parts of the domain change with 2% or less. Yet, during storm, the suspended sediment transport in these scenarios changes by 60–70%. This implies that the direct effect of bedform-related roughness is very important: it increases the depth-integrated sediment concentration and therefore also .
In short, the largest effect of roughness is found in the depth-averaged current velocity and the suspended load transport. Changes in transport magnitude appear larger than changes in current magnitude. Yet, it is unknown which of the scenarios shows the most realistic amount of sediment transport, and although the differences with the base scenario are higher, the scenarios with the constant ripple roughness do show similar patterns in MARD-values as the Van Rijn scenario with high ripples. It therefore might be valid to use a spatio-temporally constant roughness value in exploratory studies, when the ’true’ behaviour of the system is unknown, (e.g., determining causes for spatial patterns or morphologic behaviour). Therefore, it is especially important to put effort into choosing a roughness predictor when transport or morphologic calculations are made, e.g., in hindcasting studies. If only hydrodynamic simulations are done, the errors are expected to remain mostly below 10%, and they will be located at the shallow areas. Only if a constant Manning’s n is prescribed, errors can increase further, in our case the differences with the base scenario were up to 40%. On top of that, even with small changes in ripple-related roughness , the sediment transport magnitude still changes. This means that it is important to carefully consider which ripple roughness predictor is used and that coastal models that simulate sediment transport or morphological change should incorporate spatio-temporally varying ripple roughness predictors. Also, a model user should always keep in mind that over time, small changes in the predicted ripple roughness could lead to large changes in the predicted total sediment transport and thus morphology.
The present study is representative of the sediment transport predictor of Van Rijn [3]. This predictor can also be incorporated into other models, such as TELEMAC. It is hypothesised that the results would be similar if a predictor was used that also calculates bedload and suspended load transport separately. Since the present study showed that currents are affected by up to 60% when the roughness scenario is changed, most bedload predictors will be affected by changes in roughness. This is because in all bedload predictors, and even some total load predictors such as the one from Engelund-Hansen [35], the transport depends on the depth-averaged current velocity to a power of 3–5. The calculation of suspended load varies more between various predictors, because it mainly depends on the calculation of the reference height. Therefore, it is advised to perform a similar sensitivity study when a different transport predictor is used.
Further research should also address the long-term morphodynamic feedbacks. Spatial differences in sediment transport can lead to different morphologic development, so the effects of roughness that were found in the present study could be amplified or reduced by these feedbacks. Furthermore, the interaction between the different bedform scales should be addressed. Nikora et al. [36] showed that the migration of larger bedforms (megaripples in our case) could be caused by the movement of small-scale ripples. A time series of measurements of both scales at the same location is, however, not available for our study site.
5. Conclusions
For the first time, the effect of small-scale ripples and megaripples on hydrodynamics and sediment transport was quantified in detail using Delft3D scenarios for a mixed wave-current environment (Ameland ebb-tidal delta). The In Delft3D, small-scale ripples and megaripples together constitute the bedform-related roughness. Although small-scale ripples are lower than megaripples, it was found that small-scale ripple-related roughness can make up to 100% of the total roughness on shallow parts of the ebb-tidal delta. Megaripples are more important in the current-dominated channel and further offshore. The bedforms were found to affect the current velocity and sediment transport on the shallow parts of the ebb-tidal delta. Current velocity magnitudes affected by different bedform roughness scenarios resulted in overall differences of 10–20%, both during calm weather and during storm. In sediment transport, on the other hand, small changes in predicted ripple roughness lead to changes of more than 100%. Transport and flow directions were not significantly affected. During a storm, small-scale ripples are predicted to be washed away, but megaripples remain. This process cannot be simulated if a constant roughness value is prescribed, leading to overestimations in sediment transport. Therefore, it is advised to use a spatio-temporally variable bedform roughness in morphodynamic simulations in Delft3D. Future research should address the long-term morphodynamic feedbacks and the interaction between the different bedform scales.
Author Contributions
Conceptualization, all; methodology, L.B., B.G., J.v.d.W. and R.S.; software, L.B. and R.S.; validation, B.G., J.v.d.W., M.v.d.V. and G.R.; formal analysis, L.B.; investigation, L.B.; resources, B.G., J.v.d.W. and R.S.; data curation, J.v.d.W.; writing–original draft preparation, L.B.; writing–review and editing, all; visualization, L.B.; supervision, M.v.d.V. and G.R.; project administration, L.B.; funding acquisition, M.v.d.V. All authors have read and agreed to the published version of the manuscript.
Funding
This project is part of the research program SEAWAD, a ‘Collaboration Program Water’ with project number 14489, which is financed by the Netherlands Organisation for Scientific Research (NWO) Domain Applied and Engineering Sciences, and co-financed by Rijkswaterstaat (Ministry of Infrastructure and Water Management in The Netherlands). The measurement campaign was co-financed by Rijkswaterstaat as well, in the context of the Coastal Genesis 2.0 project. The PhD project of LB is financed by the SEAWAD project.
Acknowledgments
The scientific colour map batlow [37] is used in this study to prevent visual distortion of the data and exclusion of readers with colour-vision deficiencies [38]. The authors would like to thank Bert Jagers for his help with clarifying the processes incorporated in Delft3D and the creation of a version in which we could simulate constant ripple roughness. Rinse de Swart is thanked for his invaluable help when all was lost. We would like to thank Gerald Herrling, Robert Bialik and 2 anonymous reviewers for their constructive reviews of the initial manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lefebvre, A.; Ernstsen, V.; Winter, C. Influence of compound bedforms on hydraulic roughness in a tidal environment. Ocean. Dyn. 2011, 61, 2201–2210. [Google Scholar] [CrossRef]
- Van Rijn, L. Equivalent roughness of alluvial bed. J. Hydraul. Div. ASCE 1982, 108, 1215–1218. [Google Scholar]
- Van Rijn, L. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef]
- Van Der A, D.A.; Ribberink, J.S.; Van Der Werf, J.J.; O’Donoghue, T.; Buijsrogge, R.H.; Kranenburg, W. Practical sand transport formula for non-breaking waves and currents. Coast. Eng. 2013, 76, 26–42. [Google Scholar] [CrossRef]
- O’Donoghue, T.; Doucette, J.; van der Werf, J.; Ribberink, J. The dimensions of sand ripples in full-scale oscillatory flows. Coast. Eng. 2006, 53, 997–1012. [Google Scholar] [CrossRef]
- Dastgheib, A.; Roelvink, J.; Wang, Z. Long-term process-based morphological modeling of the Marsdiep Tidal Basin. Mar. Geol. 2008, 256, 90–100. [Google Scholar] [CrossRef]
- Lenstra, K.; Pluis, S.; Ridderinkhof, W.; Ruessink, B.; van der Vegt, M. Cyclic channel-shoal dynamics at the Ameland inlet: The impact on waves, tides, and sediment transport. Ocean. Dyn. 2019, 69, 409–425. [Google Scholar] [CrossRef]
- Iglesias, I.; Avilez-Valente, P.; Bio, A.; Bastos, L. Modelling the Main Hydrodynamic Patterns in Shallow Water Estuaries: The Minho Case Study. Water 2019, 11, 1040. [Google Scholar] [CrossRef]
- Herrling, G.; Winter, C. Morphological and sedimentological response of a mixed-energy barrier island tidal inlet to storm and fair-weather conditions. Earth Surf. Dyn. 2014, 2, 363–382. [Google Scholar] [CrossRef]
- Zavala-Garay, J.; Theiss, J.; Moulton, M.; Walsh, C.; van Woesik, R.; Mayorga-Adame, C.; García-Reyes, M.; Mukaka, D.; Whilden, K.; Shaghude, Y.W. On the dynamics of the Zanzibar Channel. JGR Oceans 2015, 120, 6091–6113. [Google Scholar] [CrossRef]
- Ralston, D.; Talke, S.; Geyer, W.; Al-Zubaidi, H.; Sommerfield, C. Bigger Tides, Less Flooding: Effects of Dredging on Barotropic Dynamics in a Highly Modified Estuary. J. Geophys. Res. Ocean. 2019, 124, 196–211. [Google Scholar] [CrossRef]
- Elias, E.P.L.; Hansen, J.E. Understanding processes controlling sediment transports at the mouth of a highly energetic inlet system (San Francisco Bay, CA). Mar. Geol. 2013, 345, 207–220. [Google Scholar] [CrossRef]
- Wengrove, M.E.; Foster, D.L.; Lippmann, T.C.; de Schipper, M.A.; Calantoni, J. Observations of Time-Dependent Bedform Transformation in Combined Wave-Current Flows. J. Geophys. Res. Ocean. 2018, 123, 7581–7598. [Google Scholar] [CrossRef]
- Lefebvre, A.; Ernstsen, V.; Winter, C. Bedform characterization through 2D spectral analysis. J. Coast. Res. 2011, SI64, 781–785. [Google Scholar]
- Ganju, N.; Sherwood, C. Effect of roughness formulation on the performance of a coupled wave, hydrodynamic, and sediment transport model. Ocean. Model. 2010, 33, 299–313. [Google Scholar] [CrossRef]
- Nelson, T.; Voulgaris, G.; Traykovski, P. Predicting wave-induced ripple equilibrium geometry. J. Geophys. Res. Ocean. 2013, 118, 3202–3220. [Google Scholar] [CrossRef]
- Brakenhoff, L.; Kleinhans, M.; Ruessink, B.; van der Vegt, M. Spatio-temporal characteristics of small-scale wave-current ripples on the Ameland ebb-tidal delta. Earth Surf. Process. Landforms 2020. [Google Scholar] [CrossRef]
- Idier, D.; Astruc, D.; Hulscher, S. Influence of bed roughness on dune and megaripple generation. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Davies, A.; Robins, P. Residual flow, bedforms and sediment transport in a tidal channel modelled with variable bed roughness. Geomorphology 2017, 295, 855–872. [Google Scholar] [CrossRef]
- Lesser, G.; Roelvink, J.; van Kester, J.; Stelling, G. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- van Rijn, L.; Walstra, D.; van Ormondt, M. Description of TRANSPOR2004 and Implementation in Delft3D-ONLINE; Techreport Z3748.10; WL | Delft Hydraulics: Delft, The Netherlands, 2004. [Google Scholar]
- Marriott, M.; Jayaratne, R. Hydraulic roughness—Links between Manning’s coefficient, Nikuradse’s equivalent sand roughness and bed grain size. In Proceedings of Advances in Computing and Technology, (AC&T) The School of Computing and Technology 5th Annual Conference; University of East London: London, UK, 2010; pp. 27–32. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104.C4, 7649–7666. [Google Scholar] [CrossRef]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. Ocean. 1999, 104.C4, 7667–7681. [Google Scholar] [CrossRef]
- Nederhoff, C.; Schrijvershof, R.; Tonnon, P.; van der Werf, J. The Coastal Genesis II Terschelling–Ameland Inlet (CGII-TA) Model; Techreport 1220339-008-ZKS-0004; Deltares: Delft, The Netherlands, 2019; Available online: http://publications.deltares.nl/1220339_008.pdf (accessed on 8 November 2020).
- Galappatti, G.; Vreugdenhil, C. A depth-integrated model for suspended sediment transport. J. Hydraul. Res. 1985, 23, 359–377. [Google Scholar] [CrossRef]
- Van Rijn, L. Unified View of Sediment Transport by Currents and Waves. II: Suspended Transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Van Rijn, L. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications Amsterdam: Amsterdam, The Netherlands, 1993; Volume 1006. [Google Scholar]
- Lesser, G. An Approach to Medium-Term Coastal Morphological Modelling. Ph.D. Thesis, IHE Delft Institute for Water Education, Delft, The Netherlands, 2009. [Google Scholar]
- Nederhoff, C.; Schrijvershof, R.; Tonnon, P.; Van Der Werf, J.; Elias, E. Modelling hydrodynamics in the Ameland inlet as a basis for studying sand transport. Coast. Sediments 2019, 1971–1983. [Google Scholar] [CrossRef]
- van Prooijen, B.; Tissier, M.; de Wit, F.; Pearson, S.; Brakenhoff, L.; van Maarseveen, M.; van der Vegt, M.; Mol, J.; Kok, F.; Holzhauer, H.; et al. Measurements of Hydrodynamics, Sediment, Morphology and Benthos on Ameland Ebb-Tidal Delta and Lower Shoreface. Earth Syst. Sci. Data 2020. [Google Scholar] [CrossRef]
- Zijl, F.; Verlaan, M.; Gerritsen, H. Improved water-level forecasting for the Northwest European Shelf and North Sea through direct modelling of tide, surge and non-linear interaction. Ocean. Dyn. 2013, 63, 823–847. [Google Scholar] [CrossRef]
- Pearson, S.; van Prooijen, B.; de Wit, F.; Meijer-Holzhauer, H.; de Looff, A.; Wang, Z. Observations of suspended particle size distribution on an energetic ebb-tidal delta. Coast. Sediments 2019. [CrossRef]
- Duran-Matute, M.; Gerkema, T. Calculating Residual Flows through a Multiple-Inlet System: The Conundrum of the Tidal Period. Ocean Dyn. 2015, 65, 1461–1475. [Google Scholar] [CrossRef]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Technical University of Denmark Ostervoldgade 10; Copenhagen K: Lyngby, Denmark, 1967. [Google Scholar]
- Nikora, V.I.; Sukhodolov, A.N.; Rowinski, P.M. Statistical sand wave dynamics in one-directional water flows. J. Fluid Mech. 1997, 351, 17–39. [Google Scholar] [CrossRef]
- Crameri, F. Scientific Colour Maps. Zenodo 2019. [Google Scholar] [CrossRef]
- Crameri, F. Geodynamic diagnostics, scientific visualisation and StagLab 3.0. Geosci. Model Dev. 2018, 11, 2541–2562. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).