Next Article in Journal
Evaluating the Sensor-Equipped Autonomous Surface Vehicle C-Worker 4 as a Tool for Identifying Coastal Ocean Acidification and Changes in Carbonate Chemistry
Previous Article in Journal
Discussion on Coupling Effect in Structural Load of FOWT for Condensing Wind and Wave Bins for Spectral Fatigue Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 8
Issue 11
10.3390/jmse8110938
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Simulating the Trajectory and Biomass Growth of Free-Floating Macroalgal Cultivation Platforms along the U.S. West Coast

by
Jonathan M. Whiting
1,
Taiping Wang
1,
Zhaoqing Yang
1,*,
Michael H. Huesemann
2,
Phillip J. Wolfram
3,
Thomas F. Mumford
4 and
Dylan Righi
5,6
1
Coastal Sciences Division, Pacific Northwest National Laboratory, Seattle, WA 98109, USA
2
Coastal Sciences Division, Pacific Northwest National Laboratory, Sequim, WA 98382, USA
3
Fluid Dynamics and Solid Mechanics, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
4
Marine Agronomics LLC, Olympia, WA 98502, USA
5
Genwest Systems Inc, Edmonds, WA 98020, USA
6
Office of Response and Restoration, National Oceanic and Atmospheric Administration, Seattle, WA 98115, USA
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2020, 8(11), 938; https://doi.org/10.3390/jmse8110938
Submission received: 5 October 2020 / Revised: 9 November 2020 / Accepted: 11 November 2020 / Published: 18 November 2020
(This article belongs to the Section Marine Biology)
Browse Figures
Versions Notes

Abstract

:
Trajectory tracking and macroalgal growth models were coupled to support a novel macroalgae-harvesting concept known as the Nautical Off-shore Macroalgal Autonomous Device (NOMAD). The NOMAD consists of 5 km long carbon-fiber longlines that are seeded and free float southward along the U.S. West Coast for approximately 3 months before harvesting off the California coast, taking advantage of favorable environmental conditions. The trajectory and macroalgal growth models were applied to answer planning questions pertinent to the techno-economic analysis such as identifying the preferred release location, approximate pathway, timing until harvest, and estimated growth. Trajectories were determined with the General NOAA Operational Modeling Environment (GNOME) model, using 11 years of current and wind data, determining probabilities by running nearly 40,000 Monte Carlo simulations varying the start time and location. An accompanying macroalgal growth model was used to estimate the growth of macroalgae based on the trajectory tracks and environmental forcing products, including light, temperature and nutrients. Model results show that NOMAD lines transit south in the months of April to September due to seasonal currents, taking approximately 3 months to reach Southern California. During transit, NOMAD lines are dispersed but typically avoid beaching or passing through marine sanctuaries. NOMAD lines can yield up to 30 kg wet weight per meter of cultivation line.

1. Introduction

Marine macroalgae, also referred to as seaweed, can be harvested from natural growth or from fixed farms located near natural sources of nutrients such as rivers and coastal upwelling. Harvested macroalgae can be used for human consumption, as animal feed, and as feedstock for fuels and chemicals. While the macroalgal industry has been growing rapidly around the world, products have mostly been marketed for human consumption due to economic constraints. Improving the scale, efficiency, and production cost can make other end uses more viable, such as the production of biofuels to contribute to U.S. and global energy demands [1].
Macroalgal cultivation has been conventionally achieved through anchored farms in coastal waters in which macroalgae grow on supporting structures such as long cultivation lines. Traditional stationary farming systems usually occupy a substantial coastal area and requires substantial investment in farm infrastructure. In comparison, the proposed free-floating farming concept in this study mimics natural macroalgae such as Sargassum rafts which grow and drift freely in the open ocean. Therefore, it not only avoids “permanently” occupying coastal space but also saves high anchoring cost to reduce losses of farm structures and macroalgae as a result of high current and wave forces during storms. The only free-floating macroalgae-harvesting applications known to the authors are those taking place with Sargassum rafts in the northern Caribbean Basin and the Atlantic Ocean [2].
To develop a free-floating macroalgal cultivation system requires a good understanding of its potential pathways in the coastal ocean. Tracking floating objects in the ocean is a challenging task that historically has been undertaken for tracking marine debris such as plastics [3] and oil spills [4,5]. Researchers have used global drifter networks [6], satellite measurements [7], models [8], and even accidental spills [9] to map out global currents and their seasonality. The oil industry has perhaps performed the most predictive modeling, anticipating risks at locations where an oil spill may occur by combining forcing parameters such as hydrodynamics, winds, waves, and diffusion. There are many trajectory models available, including General NOAA Operational Modeling Environment (GNOME) [10], Surface Currents from Diagnostic (SCUD) [11], multivariate ocean variational estimation (MOVE) [12], and Blowout and Spill Occurrence Model (BLOSOM) [13]. Several papers have also explored the ability of these models in recreating hindcasted trajectories of floating debris and oil spills while altering model input parameters such as windage [14,15].
Another important component to help achieve large-scale, economically viable macroalgal production is the capability to predict potential macroalgal biomass yield along the floating pathways. A macroalgal growth model that incorporates environmental conditions such as light, temperature, and nutrient information into biomass growth prediction can serve this purpose [16,17,18,19,20,21,22,23]. When coupled with the trajectory model and targeted at maximum biomass yield, it can be used to identify optimal time and location for macroalgal release and harvest. In this study, a macroalgal growth model was coupled with a trajectory prediction model to estimate macroalgal biomass yield along the farm trajectories. This framework was then used to help identify the optimal time and location for releasing seeding lines and harvesting the biomass over the course of the growing period for a novel macroalgal cultivation system proposed for the U.S. West Coast.

2. Methods

2.1. NOMAD Project

The U.S. Department of Energy’s Advanced Research Projects Agency—Energy (ARPA-E) launched the Macroalgae Research Inspiring Novel Energy Resources (MARINER) program with the goal of developing technologies to greatly reduce the capital and operational expenses related to macroalgae production and enable significant increases in farm size and potential areas of deployment [24]. The Pacific Northwest National Laboratory proposed a concept called the Nautical Off-shore Macroalgal Autonomous Device (NOMAD). The envisioned NOMAD consists of free-floating sensor-equipped recycled carbon-fiber (rCF) longlines (5 km long, 1.5 cm diameter) seeded with two species of kelp that are to be released non-stop for ~100 days each spring from a seeding vessel off the coast of Washington State, and collected, after approximately 3 months of southbound journey (ca. 1500 km) along nutrient-rich ocean currents, by a harvesting boat off the coast of Southern California. By continuously releasing seeded NOMADs, the proposed scalable macroalgae cultivation system is equivalent to a ca. 2300 ha kelp farm. Since the NOMADs can be deployed simultaneously and in parallel at many locations off the coast of Washington State, the entire NOMAD seeding–drifting–harvesting system is in principle scalable by orders of magnitude, with the potential to exceed a 100,000 ha kelp farm, thereby meeting the objectives of the ARPA-E MARINER program for large-scale generation of macroalgae biomass for biofuels and bioproducts.
The use of free-floating lines avoids anchoring costs and failures of earlier offshore growth trials [25]. High-strength, extremely durable, rCF is proposed to minimize capital costs, longline degradation and failure, and risks to marine life. The envisioned longline is seeded with a binary culture of Nereocystis luetkeana (bull kelp) and Saccharina latissima (sugar kelp), and submerged 5 m below the water surface, with buoyancy being provided by equally spaced buoys. The larger floating N. luetkeana serve as canopy species, while the smaller, non-floating S. latissima are the understory species, resulting in improved light utilization efficiency, ecological resilience, and thus biomass yields. Hydrodynamic load modeling showed low risk that the tensions at the holdfast of the kelp breaks during extreme weather conditions, with the modeling assuming a biomass yield of 39 kg wet yield per m of line at the time of harvest [26]. Any kelp to break from the NOMAD system would reduce the biomass yield but would cause no environmental impact. NOMAD lines are strong enough and the bending radius large enough that self-entanglement or entanglement with marine mammals is unlikely. A complete techno-economic analysis of the offshore NOMAD macroalgae cultivation system including a downstream biorefinery was carried out in an accompanying study [27].
The U.S. West Coast (Figure 1) was chosen as the study site to release the NOMAD systems because the California Current provides a consistent southward current and has well-known coastal upwelling [28], which can provide nutrient-rich, cold coastal water habitats that are critical to sustain kelp growth.
Compared to other U.S. coastal regions, the West Coast also experiences fewer extreme weather events such as tropical and extratropical cyclones (Figure 2). Therefore, from the operational risk perspective, the U.S. West Coast appears to be more suitable for large-scale macroalgal cultivation practices. Other locations around the world may also be suitable locations for the NOMAD system, but it would require site-specific analyses to determine spatial and temporal timing and resulting macroalgal growth.

2.2. Trajectory Model

GNOME is a Lagrangian trajectory model developed by the NOAA, Office of Response and Restoration, Emergency Response Division, released in 1999 as the replacement for the On-Scene Spill Model that had been used since 1979 [33]. The NOAA uses the model as an operational tool to respond to oil spills around the U.S. by predicting where oil will travel in the crucial hours after a spill in order to guide emergency response, iteratively correcting the trajectories with overhead helicopter flights to provide the best projections. GNOME functions by combining “movers” such as water currents, winds, and diffusion, to move particles that are experiencing weathering and beaching.
GNOME was selected as the trajectory model for this analysis because it has been proven over decades as the go-to model for spill response in the U.S. and has been applied to a variety of applications including debris tracking [34]. A scripting interface called PyGNOME provides open-source Python scripts to facilitate the batching of many simulations, and in this case, the integration into the growth model. NOMAD lines were modeled as points with no inertial effect.
All model forcing was collected for the years 2000–2010 with a spatial extent between 30° and 50° latitude and −115° and −140° longitude to cover the study site along the U.S. West Coast. The current forcing uses a Navy Coupled Ocean Data Assimilation data assimilation technique to combine model results from the HYbrid Coordinate Ocean Model (HYCOM) with satellite observations, in situ measurements, and other data sources [35]. This HYCOM GLBu0.08 dataset provides three-hourly currents with 1/12° horizontal resolution and 32 vertical layers. The currents layer at 2 m depth was used instead of the surface currents because NOMAD systems are large and extend into the water column as the macroalgae grows. Wind forcing uses the National Centers for Environmental Prediction Climate Forecast System Reanalysis (CFSR) dataset with hourly wind speeds at a 1/2° resolution [36]. GNOME applies a windage coefficient that determines a percent of the wind that directly transfers into the object due to some part of the object being above the surface, and a persistent 3% coefficient was chosen based on studies using GNOME to track tsunami debris [14,34]. Turbulent diffusion was added in GNOME as stochastic random walk with a constant coefficient of 5000 cm2/s, which is considerably less than a typical oil spill because of the large size of the NOMAD system compared to oil particles.

2.3. Macroalgal Growth Model

A macroalgal growth model was adopted in this study based on kinetics formulations that have been widely used for modeling algal growth and loss processes in many previous studies [16,17,18,19,20,21,22,23,37,38]. Reviewing macroalgal growth models in the literature shows that the level of complexity of these models varies greatly among different studies. For instance, kinetic models for sugar kelp [20] and Sargassum [23] differ substantially in the complexity and details of representing the growth process, e.g., the effect of internal nutrient reserve on algal growth was explicitly modeled in the former study but not in the latter. For this study, we think it is necessary to include those key processes controlling macroalgal growth and loss as well as their interactions with environmental variables but should not make the model overly complicated by introducing too many parameter and formulation sets of high uncertainty. Following the similar approach developed by [23] for simulating floating Sargassum mats in the Atlantic Ocean, the feedback process of macroalgal uptake of nutrients to the ambient nutrient field was ignored, although the growth rate is treated as a function of ambient nutrient concentrations. This is a reasonable assumption considering the low spatial density of floating NOMAD lines. In addition, strong wave mixing surrounding the farm structures allow for rapid nutrient replenishment and uptake [39].
Figure 3 shows the conceptual diagram of the macroalgal growth model framework. Upon receiving the trajectory information from the GNOME model, the growth model was used to predict macroalgal growth in both time and space along the farm trajectories. Specifically, the growth model read in the GNOME trajectory information and conducted 3D interpolation in time and space to find the corresponding environmental forcing information from a series of pre-generated environmental forcing datasets. These datasets include representative nutrient fields (e.g., nitrate) produced by the Los Alamos National Laboratory’s Model for Prediction Across Scales Ocean with biogeochemistry (MPAS-O BGC) model within the Energy Exascale Earth System Model (E3SM) [40,41,42], as well as solar radiation and temperature field from the same CFSR and HYCOM reanalysis products used to drive GNOME simulations. The environmental forcing datasets used in this study have been validated with field observations to various extent as possible.
The governing equation for macroalgae biomass growth has the following generic form based on literature [19,20,23,37]:
dC dt = ( μ − r − m ) C
where C is macroalgal biomass density for individual NOMAD lines (g carbon per m of growth line), which is converted to wet weight per m of line using carbon to dry weight ratio = 0.28 and dry weight to wet weight ratio = 0.15; t is time (day, or d); µ is the growth rate (per d); r is respiration or the basal metabolism rate as a function of water temperature (0.01 per d for the base rate under the reference temperature); and m is the sum of the two additional loss terms, grazing and senescence/mortality (0.01 per d).
The growth rate µ is defined as the product of the maximum specific growth rate (µm, 0.2 per d) and major environmental limiting functions, including light, temperature, and nutrients. The maximum specific growth rate is the most important parameter affecting macroalgal biomass yield and the value of 0.2 per d was taken from the literature [20]. For light limiting function, light attenuation by both the water column and macroalgal biomass (i.e., self-shading) is modeled. The effect of photoinhibition (i.e., reduced photosynthesis due to excess light) is not considered in the current model as literature review suggests that the presence or absence of photoinhibition is highly variable as a result of various factors, such as differences in genotype, nutrient and temperature conditions, and the acclimation of algae to light [43,44]. Laboratory/field experiments should be carried out for targeted macroalgal species to derive accurate light limiting functions. The temperature limiting function for the growth rate is based on the same equation in [18] with an optimal temperature range of 3–15 °C and a tolerance temperature range of 0–20 °C. In marine environment, nitrogen is regarded as the most important limiting factor for macroalgal growth [45]. Thus, the nutrient limiting function can be simplified to only consider nitrogen limitation effect. In addition, to account for the luxury uptake and storage capability of nitrogen by macroalgae [46,47,48], the Droop equation similar to that in [17,19] was used for nutrient limitation with a half saturation rate of 4.0 μmol nitrogen per L [20].

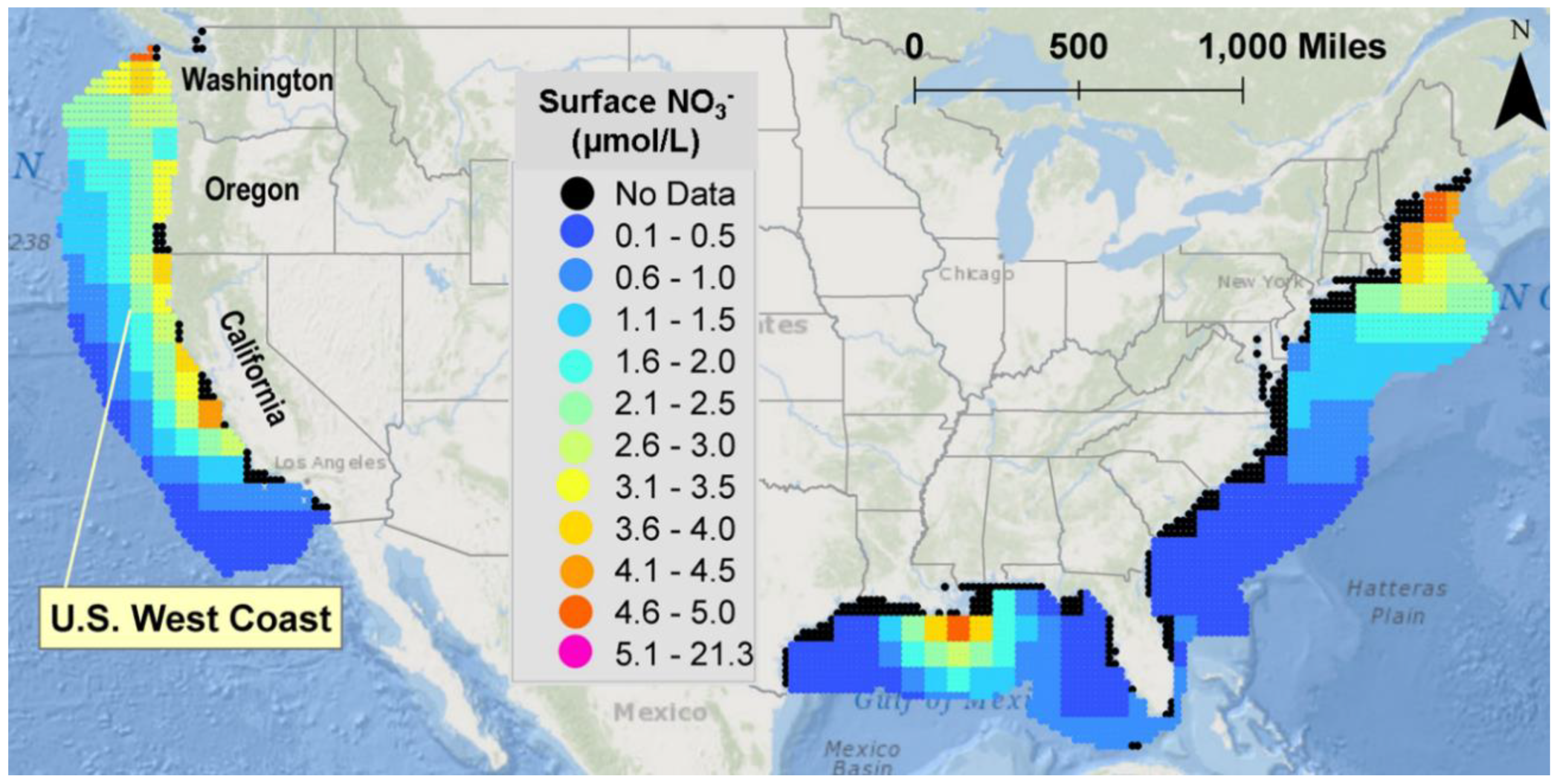
2.4. Simulation Design

An ensemble of nearly 40,000 GNOME simulations was determined to assess different start locations and start times being considered by the NOMAD team. A Monte Carlo approach was taken, randomizing the setup for each simulation and then looking at results using a post-analysis tool called the Trajectory Analysis Planner (TAP) [49]. The TAP analyzes statistics from large ensembles of GNOME simulations, allowing multiple analysis modes that define probabilities across user-defined receptor grid cells, which for this project were determined to be 0.2° by 0.2° squares.
Each simulation lasted for 150 days with a 15–minute model time step. Each simulation released one NOMAD system per hour for the first week, resulting in 168 systems released for each simulation. This was not the planned deployment rate but was representative for the purpose of the analysis. After a series of sensitivity models runs, in total there were 30 different start locations considered and four starting time windows, each with 330 simulations for a total of 39,600 simulations. The full ensemble took 25 physical days to run on four cores.
An even sampling of 28 start locations were identified near the northern extent of the U.S EEZ, assuming that the NOMAD systems would drift south down the coast without passing into marine sanctuaries or beaching and that the macroalgae experiences desired temperatures and nutrients for growth. Locations were selected within the U.S. EEZ and outside of marine sanctuaries, with two locations identified much farther south to explore beaching potential with a farther south release (Figure 4).
It was postulated that the first four months of the year (January–April) would be optimal for biomass production rates due to preferred temperatures and nutrient availability. To provide variability for the Monte Carlo simulation, a random start time was chosen within the time window of each month.
Finally, recognizing that the ocean experiences natural variability across multi-year scales, 11 years of data for the years 2000–2010 were used across the ensemble, with each simulation randomly selecting a year in which to run. Rather than averaging data from the years, this approach allowed real events such as storms to be reflected in the simulations with realistic probabilities representing the 11 years of data. The sampled years showed an average monthly Southern Oscillation Index of 0.25, skewing slightly towards La Niña which generally produces fewer storms along the U.S. West Coast

3. Results and Discussion

Results from this modeling analysis were used to inform a techno-economic analysis (TEA) assessing the economic feasibility of a full-scale commercial operation [27]. Key information needed for the TEA included the preferred release (start) location, the projected pathway (end location), the approximate timing before recapture (end time), and the resulting biomass yield. Seasonality was considered for all these analyses.

3.1. Release Location Analysis

The release location analysis was performed to narrow the 30 potential start locations down to the best candidates, which was defined as those that consistently drifted down the coast without beaching or passing through marine sanctuaries. A NOMAD line was assumed to successfully transit southward without beaching if it passed Cape Mendocino off the coast of Northern California, after which beaching events become unlikely because of the currents. The start locations were assessed with the release starting at different months of the year: January through April.
The TAP tool provided a method for comparing start locations based on the probability for it to pass through a selected receptor cell. A cell was selected approximately 70 miles off the coast of Cape Mendocino, selected as a preferred checkpoint during the path southward. The probability shown for each start location and month indicates the percent of 330 simulations that had at least one of 168 NOMAD lines pass through the selected receptor cell (Figure 5). A NOMAD line moving past the selected receptor cell, but to the east or west, will not show in the percentages; this is meant to provide a high-level assessment of the start locations, but further analysis would be expected.
To aid in the interpretation of start locations, northward velocities were averaged across the 11 years of HYCOM data by month to provide an analysis of seasonality. The results (Figure 6). show that in the early months of January to March the mean current moves to the north, while a shift takes place so the mean current moves to the south during April to June. This explains why the January start showed around 10% of simulations passing through the selected receptor cell, but the April start showed nearly 80% of simulations passing through the receptor cell for some start locations. The full window of southward velocities is between April and September.
The start locations closest to the EEZ showed the highest probability of transiting south without beaching (Figure 5). This is less preferable from an economic perspective because the deployment vessel will have to travel farther before beginning releases, costing fuel and time. The deployments beginning farther south also showed a high likelihood of moving south with a March start, but this option provides less float time for the macroalgae to grow and did not show significantly better probabilities. Balancing these cost considerations against the likelihood that NOMAD lines will travel south suggest that a release approximately 100 nm offshore along the northern boundary of the EEZ is the preferred start location, where approximately 70% of simulations passed through the selected receptor cell with an April start. Starting at a later month may provide better transit to the south, but this should be balanced against available nutrients and temperatures.

3.2. Pathway Analysis

Continuing with one of the outermost release locations, the next major factor in the economic analysis was assessing the expected pathway for NOMAD lines. This reaffirms that NOMAD lines will transit south, while also giving an idea of beaching probability and spread. Monthly seasonality was assessed once again, with releases starting in the months of January through April.
The ensemble of GNOME simulations was assessed with the TAP tool, providing the percent of 330 simulations that had at least one of 168 NOMAD lines pass through a given cell (Figure 7). The resulting plots indicate the expected spread of the trajectories and the best estimated location for harvesting.
Releasing NOMAD lines in January and February is not feasible because the probability of simulations that will transit south is a low 10–30%. Late March is when releases become feasible from a free-floating trajectory perspective, as the probability of simulations transiting south reaches approximately 80%. The greatest potential for beaching appears to be along the Washington and Oregon coasts, with Cape Blanco in Southern Oregon showing the highest probability of beaching.
The plan is to collect and harvest NOMAD lines off the coast of Southern California, and an important economic factor was fuel costs based on the distance between the pickup location and the nearest port and the expected natural spread of NOMAD lines at the planned point of collection. The midpoint for the natural drift was approximately 220 nm from the coast at the 35th parallel north, but this distance could be reduced by collecting NOMAD lines farther north. During the April start, cells with more than 50% of the simulations span 160 nm along the 35th parallel north, presenting a significant challenge for efficiently collecting NOMAD lines. The range of analysis from the 130th to 115th parallels west was not wide enough to capture the spread of outlier trajectories. This wide distribution is because small changes near the start of the deployment can have drastic changes on the end trajectory due to cumulative changes over long periods of time in a complex system of currents. The conclusion of this analysis was that NOMAD lines needed some form of mitigation to correct the issue of spread, assessing the feasibility of an active steering mechanism, GPS tracking with course correction from vessels, and creating longer NOMAD lines to reduce the spread.

3.3. Timing Analysis

While the previous analysis looked at expected pathways, it did not factor in the amount of time it would take to reach the harvesting location. The length of float time factors into the growth analysis and creates a different type of spread across time. This analysis continued with the same outermost release location and factored in monthly seasonality. The TAP provides an analysis mode that creates contours representing the earliest time that a single NOMAD line across all simulations reaches a given cell (Figure 8).
During the March and April starts, the earliest NOMAD lines can be expected to reach Southern California around 70 days after release. This determines a minimum threshold for how much growth time is available before harvest.

3.4. Growth Analysis

Compared to conventional, stationary macroalgal farms, the NOMAD system has several advantages in promoting macroalgal growth. First, the floating system will receive abundant light because of its shallower deployment depth and excellent water clarity in the outer coastal ocean. Second, in addition to a much lower spatial density for NOMAD lines, strong surface wave mixing will enhance nutrient uptake and replenishment from ambient waters. Considering light and nutrient availability is among the most important limiting factors for algal growth, these advantages may potentially help NOMADs reach higher biomass yield than conventional farms. Further, earlier research indicated that floating macroalgae tend to experience less grazing pressure compared to anchored farms [50]. Additionally, the offshore environment with abundant wave exposure may effectively reduce the macroalgae biofouling caused by various marine organisms [51]. Hence, to grow macroalgae on floating NOMAD platforms in offshore waters may have another added benefit to achieve a higher biomass yield.
Figure 9 shows the biomass density distribution for a total of 48 NOMAD lines that were continuously released at hourly intervals within a 48-hour seedling window in early June of 2009. The release location is located near the northern boundary of the U.S. EEZ off the Washington coast. The initial biomass density was specified as 1 kg wet weight per meter (kg ww/m) length of the NOMAD line. The GNOME model was first used to dynamically track the trajectory in time and space for each of the 48 NOMAD lines at hourly intervals. The trajectory information was then passed to the macroalgal growth model as a major input to drive macroalgal growth simulations. The predicted macroalgal biomass distributions along the NOMAD trajectories were subsequently used to assess macroalgal growth in time and space for individual NOMAD lines.
The results suggest all NOMAD lines started to drift southward under the influence of ocean currents and surface wind, which is consistent with the earlier analysis of HYCOM current field (Figure 6). During the approximate 3 month journey, nearly all NOMAD lines reached the southern boundary of U.S. EEZs except for one line, which hit the coast near northern Oregon coast in late June before it could drift farther south. The results indicate that a small portion of NOMAD lines can reach a maximum biomass density of 30 kg ww/m line. The biomass density is highly variable in time and space, depending on the trajectory and associated ambient environmental conditions such as water temperature and nutrient concentration. In general, for NOMAD lines that have trajectories closer to coast, they tend to have a higher biomass density because of lower water temperature and higher nutrient concentrations in the coastal zone. These trajectories also have lower economic cost due to easier access from shore for harvesting.
The biomass distributions (Figure 9) show an overall decreasing trend toward the end of the trajectories, which should be mainly caused by the warming water temperature as NOMAD lines continue drifting southward in the late summer (Figure 10).
Figure 11 shows the time history of macroalgal biomass density, internal N:C ratio, ambient nitrate concentration, and the temperature limiting factor for growth for an example NOMAD line over the 3 month growth period. The biomass (Figure 11a) starts to decrease in mid-August as a result of increasing temperature limitation (Figure 11d) despite that both the internal N content (Figure 11b) and ambient nitrate concentration (Figure 11c) is still capable to sustain continuous growth. In fact, the biomass growth has started to slow down in the beginning of August due to increasing temperature limitation when water temperature continues to rise (Figure 11a,d). The results also indicate that due to low ambient nitrate concentrations following NOMAD release in early June, the macroalgae primarily relies on internal nitrogen stock to sustain growth at a low growth rate but grows more rapidly in July with increased nitrate availability (Figure 11a–c).
The warming seawater temperature in the late summer (Figure 10) will negatively impact macroalgae growth and survival especially in El Niño years [52] unless NOMAD lines can stay sufficiently close to the coast. This also means that in order to achieve the optimal biomass yield, NOMAD lines should be harvested at their peak biomass rather than at the end of growth period when the biomass density already starts to decrease as a result of warming seawater temperature. Alternatively, to release NOMAD lines in the earlier months of the year can help avoid warm summer temperature conditions and potentially allow for a longer growing season that will more closely follow its natural seasonality (i.e., the winter–spring growing season) and thus increase the biological viability of the NOMAD system. However, because of the seasonal pattern of currents at this location (Figure 6), releasing NOMADs in winter to earlier spring time will cause them to mostly travel northward into international waters. Therefore, by considering all these factors, it was concluded that early April should be a preferable timeframe for NOMAD release.
Figure 12 shows the macroalgal biomass and internal nitrogen content distributions along the ensemble mean trajectories of NOMAD lines released from the 30 initial locations in early April.
Figure 13 shows the corresponding biomass distributions for all the 30 NOMAD lines. The results suggest that the maximum biomass yield can reach more than 35 kg ww/m line following a 3–4 month growing period while the mean and median values are approximately 25 kg ww/m line. These values are higher than some conventional farms [53,54] but are well within the range reported in literature, e.g., Table 1 in Broch et al. 2019 [55]. The results clearly show that the final biomass yield near the end of the growth period is considerably smaller than the maximum biomass. Thus, earlier harvest should be conducted to achieve maximum biomass yield.
Another benefit for releasing NOMAD lines earlier in a year allows the macroalgae to take advantage of relatively high nutrient availability in the springtime so that they can uptake and store more nutrients for their later growth. For instance, near the end of the trajectories, the increase in biomass density is largely sustained by internal nitrogen stock, as indicated by the opposite trend in biomass density and internal N:C ratio (Figure 12). This is also one of the unique strengths for macroalgae to thrive in low-nutrient marine environments and is also a key feature of the NOMAD system, especially if outfitted with navigational capabilities; spatiotemporal variations in nutrients can seasonally be harvested to increase biomass yield.
Lastly, the trajectories for both April and June releases show that NOMAD lines tend to drift away from the coast as they continue moving southward while the coast starts to turn eastward in California (Figure 9 and Figure 12). As discussed earlier, this not only affects macroalgal growth due to warming seawater temperature and decreasing nutrient availability but also increases the harvest cost. The present trajectory modeling suggests that most of NOMAD lines tend to remain in the sea without beaching; however, it is uncertain if onshore wind waves will eventually push NOMAD lines onto the beaches during the ~3 month journey. Hence, active intervening to adjust the farm trajectories on an as-needed basis maybe needed to ensure NOMAD lines stay in the nearshore waters along the coast. This will increase the operational cost but may also help the farms to achieve higher biomass yield by taking advantage of cold and nutrient-rich nearshore waters.

4. Conclusions

Modeling was conducted in support of the NOMAD project, which proposes to release free-floating carbon-fiber longlines seeded with two species of marcoalgae to transit from the coast of Washington State, meant to transit southbound for approximately 3 months on natural currents to be harvested off the coast of Southern California. A Monte Carlo ensemble of nearly 40,000 trajectory simulations was completed using the GNOME model and 11 years of historic current and wind data. A statistical analysis was used to inform the preferred release location and timing, the expected travel pathway and identification of harvest location, and the timing for harvest. A macroalgal growth model was used to estimate growth based on average trajectory tracks and environmental forcing products such as light, temperature, and nutrients. This is the first time that a trajectory model and growth model have been coupled, enabling future applications to other non-stationary macroalgae farms or naturally-occurring algae rafts such as Sargassum.
Results of the analysis show a seasonal shift in the north-south currents along the U.S. West Coast that allows a southbound transit window between late March and late September. The preferred release location was around 100 nm offshore along the northern boundary of the EEZ for the U.S. West Coast. Most NOMAD lines transit southward during the seasonal window, though the dispersion is significant towards Southern California, where cells that are transited by more than 50% of scenarios spans 160 nm east-west. The average distance from shore to harvest NOMAD lines off Southern California is 220 nm, implying that there may be cost savings by harvesting further north despite time for algal growth. The earliest time of arrival off Southern California is 70 days after release. During the approximate 3 month transit, some NOMAD lines reach an average biomass density of 25 kg ww/m line, particularly those that remain closer to the coast around Southern California. Warm temperatures eventually reduce the biomass yield, showing a window in time and space where harvest should occur. Model results indicate that the NOMAD design has potential as a scalable commercial operation but needs refinement to manage the timing and spatial distribution of NOMAD lines during transit, potentially exploring self-guidance mechanisms or transit corrections for outliers. Concerns about interference with major shipping lanes and methods to alert nearby ships to the presence of NOMAD lines should also be further explored.
The accuracy of trajectories in GNOME depends largely on the accuracy and resolution of the movers. Wave-induced Stokes drift was not included in this study, but the influence can be on the same order of magnitude as currents [56] and including waves that propagate from the west to the shore may cause NOMAD lines to remain closer to the coast and benefit from shorter transit distances for harvesting, cooler temperatures for growth, and less dispersion. GNOME does not include inertial effects due to mass nor the complex bending motions within the NOMAD system, but this influence is expected to be small compared to inherent uncertainty caused by relatively coarse resolution of forcing data compared to the length of each NOMAD line. Currents had a 1/12° horizontal resolution (~9 km) and wind had a 1/2° horizontal resolution (~56 km), compared to 5 km length of lines. A two-way coupling between the trajectory model and growth model would be required to accurately represent inertia, because the mass of the lines is expected increase as the macroalgae grows. A review of macroalgal growth model literature has revealed some major limitations in biomass prediction. In addition to the accuracy with the forcing products, the high uncertainty with the kinetics equations and parameter values has a major impact on model results. The equations and parameter values should be calibrated against measurements especially for targeted macroalgal species.
Timing is important for macroalgal growth. In order to improve the biological viability of large-scale macroalgal cultivation, it is important to account for the natural seasonality of targeted macroalgal species that typically thrive from late winter to early spring. However, the selected releasing time of early April in this study was largely determined by the trajectory analysis rather than the natural physiology of macroalgae. Hence, additional studies regarding ways in which mariculture practices can be adapted to better accommodate the growing season of viable NOMAD trajectories are warranted, e.g., to examine alternative NOMAD pathways by releasing them from California coast in winter and harvest them in Washington coast in spring or to explore alternate release locations.
Ultimately, to have confidence in the trajectory and growth model projections, a full-size demonstration of a single line would be necessary to calibrate results, tracking location by GPS, measuring nutrients, temperature, and light, and recording growth rates. Model results presented in this study should be viewed as qualitative references to guide the macroalgal biomass yield and the spatial and temporal variabilities as a function of NOMAD releasing location and time. Yet the model can still be used as a diagnostic tool to help understand the effects of different environmental variables, such as nutrient availability and seawater temperature as an approach to design future validation field studies. In summary, the coupling of a macroalgal growth model and trajectory model provides valuable decision support information for NOMAD design. This study’s results illustrate that use of free-floating macroalgae mariculture has great potential and should be further explored, especially as a technique to mitigate seasonality in nutrient availability.

Author Contributions

Conceptualization, J.M.W., T.W., Z.Y., and M.H.H.; formal analysis, J.M.W. and T.W.; writing—original draft preparation, J.M.W., T.W., Z.Y., and M.H.H.; writing—review and editing, J.M.W., T.W., Z.Y., M.H.H., P.J.W.; T.F.M.; and D.R.; visualization, J.M.W. and T.W.; supervision, Z.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Advanced Research Projects Agency—-Energy (ARPA-E) Macroalgae Research Inspiring Novel Energy Resources (MARINER) program, award numbers 17/CJ000/09/01 and 17/CJ000/09/02.

Acknowledgments

We would like to thank Andrea Copping, Scott Edmundson, and Song Gao (PNNL); Jason Quinn and Jonah Greene (Colorado State University); Jascha Gulden (Reliance Laboratories); and Geoff Wood (Composite Recycling Technology Center) from the NOMAD team for conceptualizing the NOMAD approach and for providing useful input for the analysis conducted in this manuscript. We would also like to thank Chris Barker and Amy MacFadyen at the NOAA Emergency Response Division who collaborated with code development for PyGNOME and TAP. Lisa Wickliffe from the NOAA’s Marine Spatial Planning Team is acknowledged for providing GIS datasets used for this study. MPAS-O BGC E3SM simulations were conducted by Los Alamos’ Mathew Maltrud.

Conflicts of Interest

The authors declare no conflict of interests.

References

  1. Oilage Guide to Fuels from Macroalgae; Report by Oilage: Chennai, India, 2010.
  2. Sherman, M.T.; Blaylock, R.; Lucas, K.; Capron, M.E.; Stewart, J.R.; DiMarco, S.F.; Thyng, K.; Hetland, R.; Kim, M.H.; Sullivan, C.; et al. SeaweedPaddock: Initial Modeling and Design for a Sargassum Ranch. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
  3. van Sebille, E.; Aliani, S.; Law, K.L.; Maximenko, N.; Alsina, J.; Bagaev, A.; Bergmann, M.; Chapron, B.; Chubarenko, I.; Cózar, A.; et al. The physical oceanography of the transport offloating marine debris. Environ. Res. Lett. 2020, 15, 023003. [Google Scholar] [CrossRef] [Green Version]
  4. Galt, J.A.; Watabayashi, G.Y.; Payton, D.L.; Petersen, J.C. Trajectory Analysis for the Exxon Valdez: Hindcast Study. Int. Oil Spill Conf. Proc. March 1991, 1991, 629–634. [Google Scholar] [CrossRef]
  5. Liu, Y.; Weisberg, R.; Hu, C.; Zheng, L. Tracking the Deepwater Horizon Oil Spill: A Modeling Perspective. EOS 2011, 92, 45–56. [Google Scholar] [CrossRef]
  6. Lumpkin, R. Global characteristics of coherent vortices from surface drifter trajectories. J. Geophys. Res. Oceans 2016, 121, 1306–1321. [Google Scholar] [CrossRef] [Green Version]
  7. Mulet, S.; Rio, M.; Mignot, A.; Guinehut, S.; Morrow, R. A new estimate of the global 3D geostrophic ocean circulation based on satellite data and in-situ measurements. Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 70–81. [Google Scholar] [CrossRef]
  8. van Sebille, E.; Griffies, S.M.; Abernathey, R.; Adams, T.; Berloff, P.; Biastoch, A.; Blanke, B.; Chassignet, E.; Cheng, Y.; Cotter, C.; et al. Lagrangian ocean analysis: Fundamentals and practices. Ocean Model. 2018, 121, 49–75. [Google Scholar] [CrossRef]
  9. Ebbesmeyer, C.; Ingraham, J., Jr. Pacific toy spill fuels ocean current pathways research. EOS 1994, 75, 425–430. [Google Scholar] [CrossRef]
  10. Beegle-Krause, J. General NOAA Oil Modeling Environment (GNOME): A New Spill Trajectory Model. Int. Oil Spill Conf. Proc. March 2001, 2001, 865–871. [Google Scholar] [CrossRef]
  11. Maximenko, N.; Hafner, J. SCUD: Surface Currents from Diagnostic Model; Technical Note No. 5; International Pacific Research Center (IPRC): Honolulu, HI, USA, 2010; p. 19. [Google Scholar]
  12. Usui, N.; Ishizaki, S.; Fujii, Y.; Tsujino, H.; Yasuda, T.; Kamachi, M. Meteorological Research Institute multivariate ocean variational estimation (MOVE) system: Some early results. Adv. Space Res. 2006, 37, 806–822. [Google Scholar] [CrossRef]
  13. Sim, L.; Graham, J.; Rose, K.; Duran, R.; Nelson, J.; Umhoefer, J.; Vielma, J. Developing a Comprehensive Deepwater Blowout and Spill Model; Technical Report for NETL-TRS-9-2015 EPAct Technical Report Series; U.S. Department of Energy, National Energy Technology Laboratory: Albany, OR, USA, 2015.
  14. Maximenko, N.; Hafner, J.; Kamachi, M.; MacFadyen, A. Numerical simulations of debris drift from the Great Japan Tsunami of 2011 and their verification with observational report. Mar. Pollut. Bull. 2018, 132, 5–25. [Google Scholar] [CrossRef]
  15. Duran, R.; Romeo, L.; Whiting, J.; Vielma, J.; Rose, K.; Bunn, A.; Bauer, J. Simulation of the 2003 Foss Barge—Point Wells Oil Spill: A Comparison between BLOSOM and GNOME Oil Spill Models. J. Mar. Sci. Eng. 2018, 6, 104. [Google Scholar] [CrossRef] [Green Version]
  16. Jackson, G.A. Modeling the Growth and Harvest Yield of the Giant-Kelp Macrocystis Pyrifera. Mar. Biol. 1987, 95, 611–624. [Google Scholar] [CrossRef]
  17. Solidoro, C.; Pecenik, G.; Pastres, R.; Franco, D.; Dejak, C. Modelling macroalgae (Ulva rigida) in the Venice lagoon: Model structure identification and first parameters estimation. Ecol. Model. 1997, 94, 191–206. [Google Scholar] [CrossRef]
  18. Trancoso, A.R.; Saraiva, S.; Fernandes, L.; Pina, P.; Leitão, P.; Neves, R. Modelling macroalgae using 3D hydrodynamic-ecological model in a shallow, temperate estuary. Ecol. Model. 2005, 187, 232–246. [Google Scholar] [CrossRef]
  19. Wang, T. Numerical Modeling of Eutrophication Dynamics in the Shallow Coastal Ecosystem: A Case Study in the Maryland and Virginia Coastal Bays. Ph.D. Thesis, The College of William & Mary, Gloucester Point, VA, USA, 2009. [Google Scholar] [CrossRef]
  20. Broch, O.J.; Slagstad, D. Modelling seasonal growth and composition of the kelp Saccharina latissima. J. Appl. Phycol. 2012, 24, 759–776. [Google Scholar] [CrossRef]
  21. Broch, O.J.; Ellingsen, I.H.; Forbord, S.; Wang, X.; Volent, Z.; Alver, M.O.; Handa, A.; Andresen, K.; Slagstad, D.; Reitan, K.I.; et al. Modelling the cultivation and bioremediation potential of the kelp Saccharina latissima in close proximity to an exposed salmon farm in Norway. Aquac. Environ. Interact. 2013, 4, 187–206. [Google Scholar] [CrossRef] [Green Version]
  22. Hadley, S.; Wild-Allen, K.; Johnson, C.; Macleod, C. Modeling macroalgae growth and nutrient dynamics for integrated multi-trophic aquaculture. J. Appl. Phycol. 2014, 27, 901–916. [Google Scholar] [CrossRef]
  23. Brooks, M.T.; Coles, V.J.; Hood, R.R.; Gower, J.F.R. Factors controlling the seasonal distribution of pelagic Sargassum. Mar. Ecol. Prog. Ser. 2018, 599, 1–18. [Google Scholar] [CrossRef] [Green Version]
  24. Macroalgae Research Inspiring Novel Energy Resources (MARINER). Available online: https://arpa-e.energy.gov/?q=arpa-e-programs/mariner (accessed on 9 September 2020).
  25. Roesijadi, G.; Copping, A.E.; Huesemann, M.H.; Forster, J.; Benemann, J.R. Technoeconomic Feasibility Analysis of Offshore Seaweed Farming for Bioenergy and Biobased Products; Independent Research and Development Report PNWD-3931; Battelle Pacific Northwest Division: St Richland, WA, USA, 2008; p. 115. [Google Scholar]
  26. Chen, M.; Yim, S.C.; Cox, D.; Huesemann, M.; Yang, Z.; Wang, T.; Mumford, T.; Wood, G. Hydrodynamic Load Modeling for Offshore Free-Floating Macroalgal Aquaculture under Extreme Environmental Conditions. In Proceedings of the Offshore Mechanics and Arctic Engineering Conference, Glasgow, Scotland, 9–14 June 2019. [Google Scholar] [CrossRef]
  27. Greene, J.M.; Gulden, J.; Wood, G.; Huesemann, M.; Quinn, J.C. Techno-Economic and Life Cycle Assessment of a Novel Offshore Macroalgae Biorefinery. Algal Res. 2020, 51, 102032. [Google Scholar] [CrossRef]
  28. Hickey, B.M.; Banas, N.S. Oceanography of the U.S. Pacific Northwest Coastal Ocean and estuaries with application to coastal ecology. Estuaries 2003, 26, 1010–1031. [Google Scholar] [CrossRef]
  29. Sayre, R.G.; Wright, D.J.; Breyer, S.P.; Butler, K.A.; Van Graafeiland, K.; Costello, M.J.; Harris, P.T.; Goodin, K.L.; Guinotte, J.M.; Basher, Z.; et al. A three-dimensional mapping of the ocean based on environmental data. Oceanography 2017, 30, 90–103. [Google Scholar] [CrossRef]
  30. Garcia, H.E.; Locarnini, R.A.; Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Zweng, M.M.; Reagan, J.R.; Johnson, D.R. World Ocean Atlas 2013, Volume 4: Dissolved Inorganic Nutrients (phosphate, nitrate, silicate). In NOAA Atlas NESDIS 76; Levitus, S., Mishonov, A., Eds.; U.S. Government Publishing Office: Washington, DC, USA, 2014; p. 25. [Google Scholar]
  31. Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
  32. Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis Project. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
  33. Beegle-Krause, C.J. GNOME: NOAA’s Next-Generation Spill Trajectory Model. In MTS/IEEE Conference Committee, Proceedings of Oceans ‘99 MTS/IEEE, Escondido, CA, USA, 13–16 September 1999; IEEE: New York, NY, USA, 1999; Volume 3, pp. 1262–1266. [Google Scholar] [CrossRef]
  34. NOAA Marine Debris Program. Severe Marine Debris Event Report: Japan Tsunami Marine Debris; Overview and Update to Congress; NOAA Marine Debris Program: Silver Spring, MD, USA, 2013; p. 46.
  35. Cummings, J.A.; Smedstad, O.M. Variational Data Assimilation for the Global Ocean. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S., Xu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, pp. 303–343. [Google Scholar] [CrossRef]
  36. Saha, S.; Moorthi, S.; Pan, H.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. NCEP Climate Forecast System Reanalysis (CFSR) Selected Hourly Time-Series Products, January 1979 to December 2010; Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, 2010. Available online: https://rda.ucar.edu/ (accessed on 7 November 2020). [CrossRef]
  37. Bowie, G.L.; Mills, W.B.; Porcella, D.B.; Campbell, C.L.; Pagenkopt, J.R.; Rupp, G.L.; Johnson, K.M.; Chan, P.W.H.; Gherini, S.A. Rates, Constants and Kinetics Formulations in Surface Water Quality Modeling, 2nd ed.; EPA 600/3-85/040; US Environmental Protection Agency: Athens, GA, USA, 1985.
  38. Cerco, C.F.; Noel, M.R. The 2002 Chesapeake Bay Eutrophication Model. Report No. EPA 903-R-04-004; Springer: New York, NY, USA, 2004. [Google Scholar]
  39. Neushul, M.; Benson, J.; Harger, B.W.W.; Charters, A.C. Macroalgae Farming in Sea: Water Motion and Nutrient Uptake. J. Appl. Phycol. 1992, 4, 255–265. [Google Scholar] [CrossRef]
  40. Ringler, T.; Petersen, M.; Higdon, R.L.; Jacobsen, D.; Jones, P.W.; Maltrud, M. A multi-resolution approach to global ocean modeling. Ocean Model. 2013, 69, 211–232. [Google Scholar] [CrossRef]
  41. Wang, S.; Bailey, D.; Lindsay, K.; Moore, J.K.; Holland, M. Impact of sea ice on the marine iron cycle and phytoplankton productivity. Biogeosciences 2014, 11, 4713–4731. [Google Scholar] [CrossRef] [Green Version]
  42. Petersen, M.R.; Asay-Davis, X.S.; Berres, A.S.; Chen, Q.; Feige, N.; Hoffman, M.J.; Jacobsen, D.W.; Jones, P.W.; Maltrud, M.E.; Price, S.F.; et al. An evaluation of the ocean and sea ice climate of E3SM using MPAS and interannual CORE-II forcing. J. Adv. Model Earth Syst. 2019, 11, 1438–1458. [Google Scholar] [CrossRef]
  43. Gevaert, F.; Creach, A.; Davoult, D.; Holl, A.-C.; Seuront, L.; Lemoine, Y. Photo-inhibition and seasonal photosynthetic performance of the seaweed Laminaria saccharina during a simulated tidal cycle: Chlorophyll fluorescence measurements and pigment analysis. Plant, Cell Environ. 2002, 25, 859–872. [Google Scholar] [CrossRef] [Green Version]
  44. Brush, M.J.; Nixon, S.W. Biomass layering and metabolism in mats of the macroalga Ulva lactuca L. Estuaries 2003, 26, 916–926. [Google Scholar] [CrossRef]
  45. Roleda, M.Y.; Hurd, C.L. Seaweed nutrient physiology: Application of concepts to aquaculture and bioremediation. Phycologia 2019, 58, 552–562. [Google Scholar] [CrossRef] [Green Version]
  46. Ahn, O.; Petrell, R.J.; Harrison, P.J. Ammonium and nitrate uptake by Laminaria saccharina and Nereocystis luetkeana originating from a salmon sea cage farm. J. Appl. Phycol. 1998, 10, 333–340. [Google Scholar] [CrossRef]
  47. Rosenberg, G.; Probyn, T.A.; Mann, K.H. Nutrient uptake and growth kinetics in brown seaweeds: Response to continuous and single additions of ammonium. J. Exp. Mar. Biol. Ecol. 1984, 80, 125–146. [Google Scholar] [CrossRef]
  48. Droop, M.R. An approach to quantitative nutrition of phytoplankton. J. Protozool. 1977, 24, 528–532. [Google Scholar] [CrossRef]
  49. Trajectory Analysis Planner (TAP). Available online: https://response.restoration.noaa.gov/oil-and-chemical-spills/oil-spills/response-tools/trajectory-analysis-planner.html (accessed on 9 September 2020).
  50. Rothäusler, E.; Gutow, L.; Thiel, M. Floating Seaweeds and Their Communities. In Seaweed Biology: Ecological Studies (Analysis and Synthesis) Vol 219; Wiencke, C., Bischof, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
  51. Visch, W.; Nylund, G.M.; Pavia, H. Growth and biofouling in kelp aquaculture (Saccharina latissima): The effect of location and wave exposure. J. Appl. Phycol. 2020, 32, 3199–3209. [Google Scholar] [CrossRef]
  52. Edwards, M.S. Comparing the impacts of four ENSO events on giant kelp (Macrocystis pyrifera) in the northeast Pacific Ocean. Algae 2019, 34, 141–151. [Google Scholar] [CrossRef]
  53. Kim, J.K.; Kraemer, G.P.; Yarish, C. Use of sugar kelp aquaculture in Long Island Sound and the Bronx River Estuary for nutrient extraction. Mar. Ecol. Prog. Ser. 2015, 531, 155–166. [Google Scholar] [CrossRef]
  54. Peteiro, C.; Freire, Ó. Biomass yield and morphological features of the seaweed Saccharina latissima cultivated at two different sites in a coastal bay in the Atlantic coast of Spain. J. Appl. Phycol. 2013, 25, 205–213. [Google Scholar] [CrossRef]
  55. Broch, O.J.; Alver, M.O.; Bekkby, T.; Gundersen, H.; Forbord, S.; Handå, A.; Skjermo, J.; Hancke, K. The kelp cultivation potential in coastal and offshore regions of Norway. Front. Mar. Sci. 2019, 5, 529. [Google Scholar] [CrossRef]
  56. Röhrs, J.; Christensen, K.; Hole, L.; Broström, G.; Drivdal, M.; Sundby, S. Observation-based evaluation of surface wave effects on currents and trajectory forecasts. Ocean Dyn. 2012, 62, 1519–1533. [Google Scholar] [CrossRef]
Jmse 08 00938 g001 550
Figure 1. Surface (0–5 m) nitrate field (μmol/L) in selected U.S. exclusive economic zones (EEZ) showing relatively higher nitrate availability in nearshore waters of the U.S. West Coast. The data are derived from the ESRI Ecological Marine Unit dataset [29], which was assembled from non-supervised statistical clustering of over 52 million points from the U.S. National Oceanic and Atmospheric Administration (NOAA) World Ocean Atlas 2013 database [30].
Figure 1. Surface (0–5 m) nitrate field (μmol/L) in selected U.S. exclusive economic zones (EEZ) showing relatively higher nitrate availability in nearshore waters of the U.S. West Coast. The data are derived from the ESRI Ecological Marine Unit dataset [29], which was assembled from non-supervised statistical clustering of over 52 million points from the U.S. National Oceanic and Atmospheric Administration (NOAA) World Ocean Atlas 2013 database [30].
Jmse 08 00938 g001
Jmse 08 00938 g002 550
Figure 2. (a) The tropical cyclone (TC) track density (i.e., number of storms passing through each 0.5 deg × 0.5 deg grid cell) derived from historical tropical cyclone tracks and (b) extratropical cyclone (ETC) tracks in North America. Data for tropical cyclones were obtained from the International Best Track Archive for Climate Stewardship (IBTrACS v3, [31]). For extratropical cyclones, the data were based on the reanalysis product for extratropical cyclone activity in the Northern Hemisphere for the 1871–2010 winter seasons [32].
Figure 2. (a) The tropical cyclone (TC) track density (i.e., number of storms passing through each 0.5 deg × 0.5 deg grid cell) derived from historical tropical cyclone tracks and (b) extratropical cyclone (ETC) tracks in North America. Data for tropical cyclones were obtained from the International Best Track Archive for Climate Stewardship (IBTrACS v3, [31]). For extratropical cyclones, the data were based on the reanalysis product for extratropical cyclone activity in the Northern Hemisphere for the 1871–2010 winter seasons [32].
Jmse 08 00938 g002
Jmse 08 00938 g003 550
Figure 3. A conceptual diagram of the macroalgal growth model framework. The top panel depicts the major forcing processes affecting NOMAD transport and growth in the coastal ocean. The bottom panel illustrates the forcing field that is included the growth model to drive model simulations.
Figure 3. A conceptual diagram of the macroalgal growth model framework. The top panel depicts the major forcing processes affecting NOMAD transport and growth in the coastal ocean. The bottom panel illustrates the forcing field that is included the growth model to drive model simulations.
Jmse 08 00938 g003
Jmse 08 00938 g004 550
Figure 4. The 30 start locations off the U.S. West Coast represented by white dots, the U.S. EEZ extends 200 nm offshore and is represented by the red line, and a marine sanctuary represented by the hashed green area.
Figure 4. The 30 start locations off the U.S. West Coast represented by white dots, the U.S. EEZ extends 200 nm offshore and is represented by the red line, and a marine sanctuary represented by the hashed green area.
Jmse 08 00938 g004
Jmse 08 00938 g005 550
Figure 5. TAP analysis showing the probability of simulations passing through the selected receptor cell from 30 start locations.
Figure 5. TAP analysis showing the probability of simulations passing through the selected receptor cell from 30 start locations.
Jmse 08 00938 g005
Jmse 08 00938 g006 550
Figure 6. Monthly average northward velocities along the U.S. West Coast for the years 2000–2010. Warm colors represent northward flow and cool colors represent southward flow.
Figure 6. Monthly average northward velocities along the U.S. West Coast for the years 2000–2010. Warm colors represent northward flow and cool colors represent southward flow.
Jmse 08 00938 g006
Jmse 08 00938 g007 550
Figure 7. TAP analysis showing the probability of simulations passing through all cells after 135 days of simulation, providing a visual of the most likely trajectories.
Figure 7. TAP analysis showing the probability of simulations passing through all cells after 135 days of simulation, providing a visual of the most likely trajectories.
Jmse 08 00938 g007
Jmse 08 00938 g008 550
Figure 8. TAP analysis showing the earliest time in days for a NOMAD line to reach each cell in 90% of the simulations.
Figure 8. TAP analysis showing the earliest time in days for a NOMAD line to reach each cell in 90% of the simulations.
Jmse 08 00938 g008
Jmse 08 00938 g009 550
Figure 9. Macroalgal biomass distribution along the farm trajectories for a total of 48 NOMAD lines released in the early summer of 2009.
Figure 9. Macroalgal biomass distribution along the farm trajectories for a total of 48 NOMAD lines released in the early summer of 2009.
Jmse 08 00938 g009
Jmse 08 00938 g010 550
Figure 10. Instantaneous seawater temperature distribution at the beginning of each month (a–f) from April to September (e.g., 1 April 2019, 00:00:00 GMT; 1 May 2019, 00:00:00 GMT) showing colder surface water in the nearshore upwelling region. The plots were based on HYCOM [35] 1/12 degree global reanalysis product at 2 m depth.
Figure 10. Instantaneous seawater temperature distribution at the beginning of each month (a–f) from April to September (e.g., 1 April 2019, 00:00:00 GMT; 1 May 2019, 00:00:00 GMT) showing colder surface water in the nearshore upwelling region. The plots were based on HYCOM [35] 1/12 degree global reanalysis product at 2 m depth.
Jmse 08 00938 g010
Jmse 08 00938 g011 550
Figure 11. Time series plot of (a) macroalgal biomass density (kg ww/m); (b) the corresponding internal N:C mass ratio; (c) water column nitrate concentration; and (d) seawater temperature limiting function for macroalgal growth. The results here are based on model results for one example NOMAD line.
Figure 11. Time series plot of (a) macroalgal biomass density (kg ww/m); (b) the corresponding internal N:C mass ratio; (c) water column nitrate concentration; and (d) seawater temperature limiting function for macroalgal growth. The results here are based on model results for one example NOMAD line.
Jmse 08 00938 g011
Jmse 08 00938 g012 550
Figure 12. (a) macroalgal biomass (kg ww/m) distributions along the ensemble mean trajectories of NOMAD lines released in April and (b) the corresponding internal N:C mass ratios.
Figure 12. (a) macroalgal biomass (kg ww/m) distributions along the ensemble mean trajectories of NOMAD lines released in April and (b) the corresponding internal N:C mass ratios.
Jmse 08 00938 g012
Jmse 08 00938 g013 550
Figure 13. Box plot of macroalgal biomass (kg ww/m) distributions for all 30 NOMAD lines released in April. The arithmetic mean in the box plot is represented by the black dot. The two groups indicated by the x axis are the maximum and final biomass density distributions during the entire growth period.
Figure 13. Box plot of macroalgal biomass (kg ww/m) distributions for all 30 NOMAD lines released in April. The arithmetic mean in the box plot is represented by the black dot. The two groups indicated by the x axis are the maximum and final biomass density distributions during the entire growth period.
Jmse 08 00938 g013
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Whiting, J.M.; Wang, T.; Yang, Z.; Huesemann, M.H.; Wolfram, P.J.; Mumford, T.F.; Righi, D. Simulating the Trajectory and Biomass Growth of Free-Floating Macroalgal Cultivation Platforms along the U.S. West Coast. J. Mar. Sci. Eng. 2020, 8, 938. https://doi.org/10.3390/jmse8110938

AMA Style

Whiting JM, Wang T, Yang Z, Huesemann MH, Wolfram PJ, Mumford TF, Righi D. Simulating the Trajectory and Biomass Growth of Free-Floating Macroalgal Cultivation Platforms along the U.S. West Coast. Journal of Marine Science and Engineering. 2020; 8(11):938. https://doi.org/10.3390/jmse8110938

Chicago/Turabian Style

Whiting, Jonathan M., Taiping Wang, Zhaoqing Yang, Michael H. Huesemann, Phillip J. Wolfram, Thomas F. Mumford, and Dylan Righi. 2020. "Simulating the Trajectory and Biomass Growth of Free-Floating Macroalgal Cultivation Platforms along the U.S. West Coast" Journal of Marine Science and Engineering 8, no. 11: 938. https://doi.org/10.3390/jmse8110938

APA Style

Whiting, J. M., Wang, T., Yang, Z., Huesemann, M. H., Wolfram, P. J., Mumford, T. F., & Righi, D. (2020). Simulating the Trajectory and Biomass Growth of Free-Floating Macroalgal Cultivation Platforms along the U.S. West Coast. Journal of Marine Science and Engineering, 8(11), 938. https://doi.org/10.3390/jmse8110938

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop