Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Data
2.2. Selected Models
2.2.1. Random Forest Regression
2.2.2. Support Vector Regression
3. Results
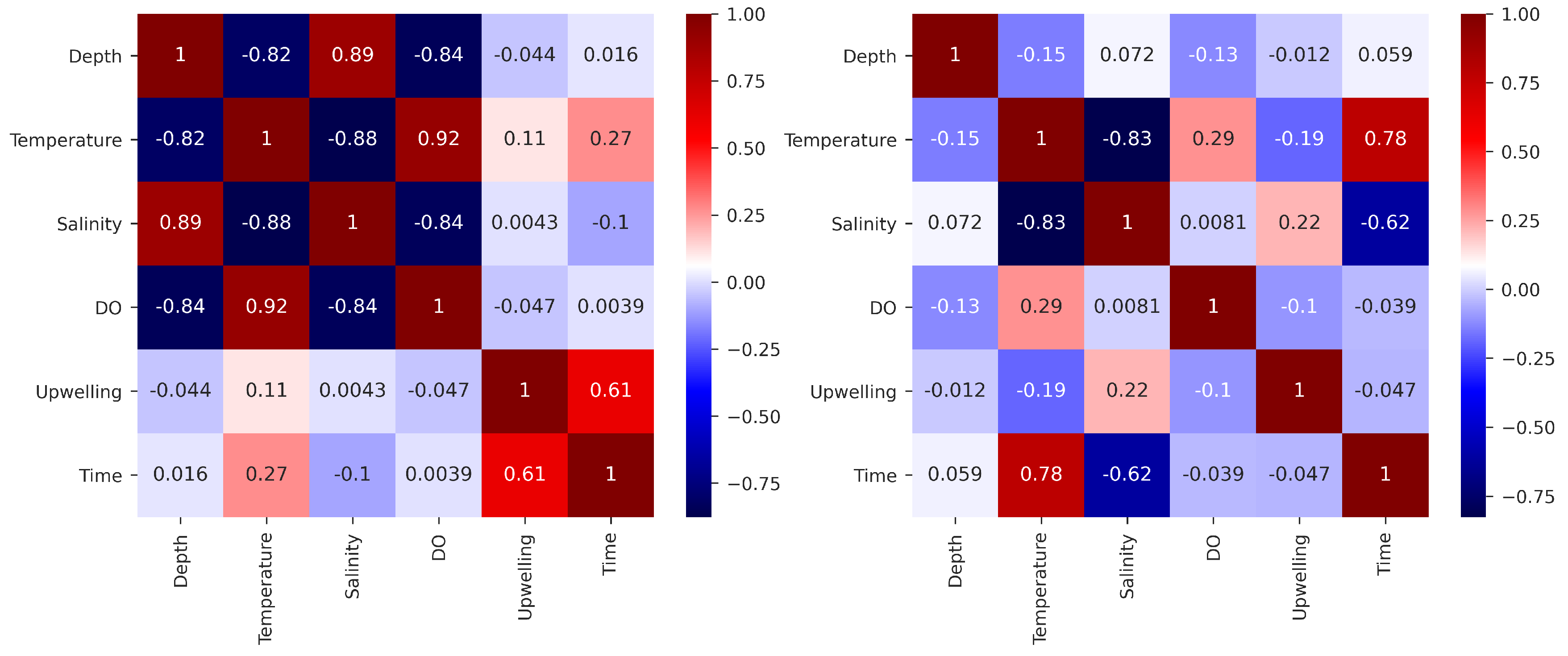
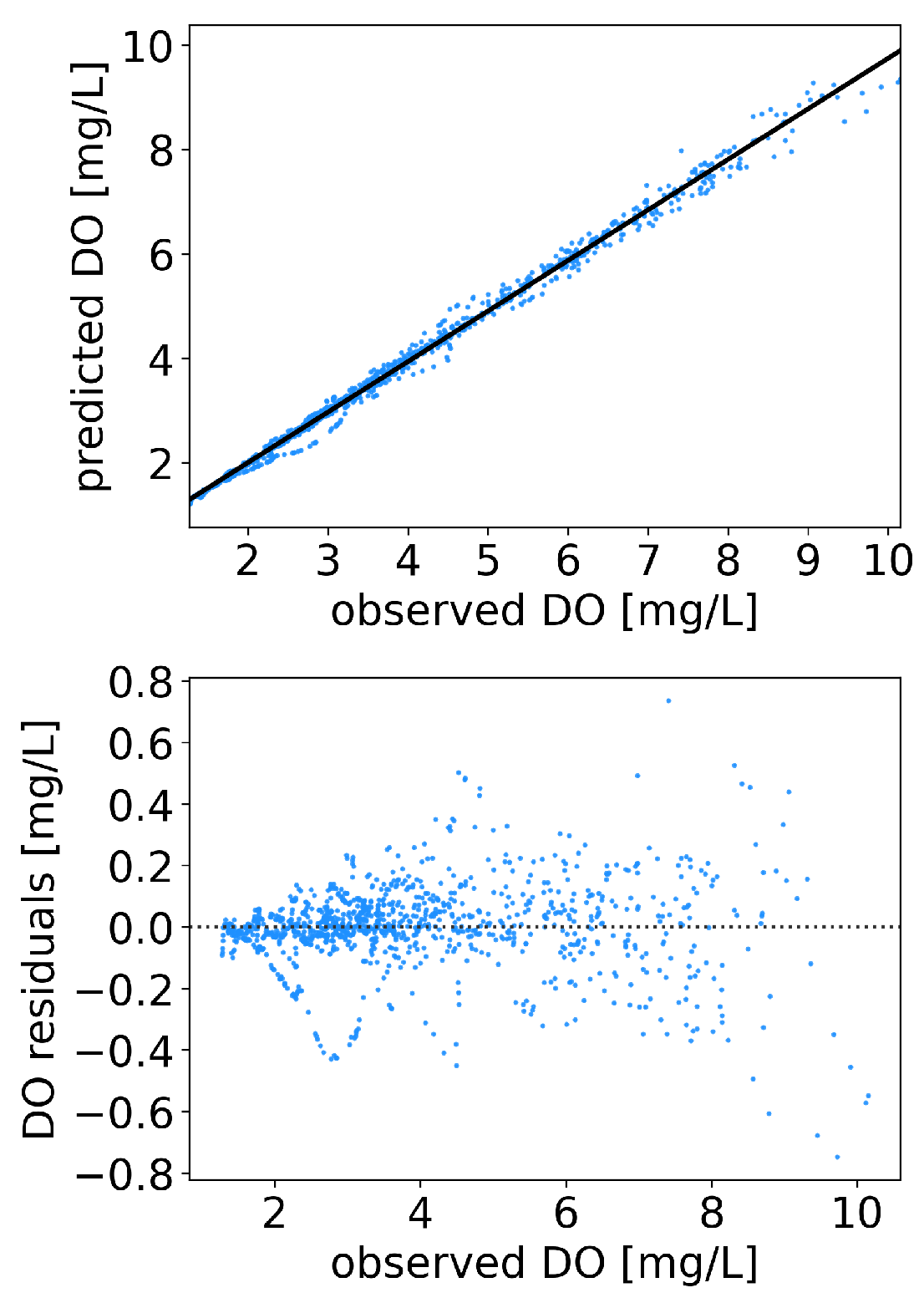
3.1. Offshore DO Predictions
3.2. Nearshore DO Predictions
3.2.1. Nearshore Station-Based Predictions
3.2.2. Combined Nearshore Model Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vaquer-Sunyer, R.; Duarte, C.M. Thresholds of hypoxia for marine biodiversity. Proc. Natl. Acad. Sci. USA 2008, 105, 15452–15457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grantham, B.A.; Chan, F.; Nielsen, K.J.; Fox, D.S.; Barth, J.A.; Huyer, A.; Lubchenco, J.; Menge, B.A. Upwelling-driven nearshore hypoxia signals ecosystem and oceanographic changes in the northeast Pacific. Nature 2004, 429, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Chan, F.; Barth, J.A.; Lubchenco, J.; Kirincich, A.; Weeks, H.; Peterson, W.T.; Menge, B.A. Emergence of anoxia in the California current large marine ecosystem. Science 2008, 319, 920. [Google Scholar] [CrossRef] [PubMed]
- Ekau, W.; Auel, H.; Portner, H.O.; Gilbert, D. Impacts of hypoxia on the structure and processes in pelagic communities (zooplankton, macro-invertebrates and fish). Biogeosciences 2010, 7, 1669–1699. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, E.B.; Coco, G.; Plant, N.G. A review of machine learning applications to coastal sediment transport and morphodynamics. Earth-Sci. Rev. 2019, 194, 97–108. [Google Scholar] [CrossRef] [Green Version]
- Krasnopolsky, V.M. Neural network emulations for complex multidimensional geophysical mappings: Applications of neural network techniques to atmospheric and oceanic satellite retrievals and numerical modeling. Rev. Geophys. 2007, 45, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Keiner, L.E.; Yan, X.H. A neural network model for estimating sea surface chlorophyll and sediments from thematic mapper imagery. Remote Sens. Environ. 1998, 66, 153–165. [Google Scholar] [CrossRef]
- Schiller, H.; Doerffer, R. Improved determination of coastal water constituent concentrations from MERIS data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1585–1591. [Google Scholar] [CrossRef]
- Gross, L.; Thiria, S.; Frouin, R.; Mitchell, B.G. Artificial neural networks for modeling the transfer function between marine reflectance and phytoplankton pigment concentration. J. Geophys. Res. Ocean. 2000, 105, 3483–3495. [Google Scholar] [CrossRef]
- Jamet, C.; Thiria, S.; Moulin, C.; Crepon, M. Use of a neurovariational inversion for retrieving oceanic and atmospheric constituents from ocean colar imagery: A feasibility study. J. Atmos. Ocean. Technol. 2005, 22, 460–475. [Google Scholar] [CrossRef]
- Brajard, J.; Jamet, C.; Moulin, C.; Thiria, S. Use of a neuro-variational inversion for retrieving oceanic and atmospheric constituents from satellite ocean colour sensor: Application to absorbing aerosols. Neural Netw. 2006, 19, 178–185. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.T.; Tissot, P.; Michaud, P. Water level observations and short-term predictions including meteorological events for entrance of Galveston Bay, Texas. J. Waterw. Port, Coast. Ocean. Eng. 2002, 128, 21–29. [Google Scholar] [CrossRef]
- Han, G.; Shi, Y. Development of an Atlantic Canadian Coastal Water Level Neural Network model. J. Atmos. Ocean. Technol. 2008, 25, 2117–2132. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Chevallier, F. Some neural network applications in environmental sciences. Part II: Advancing computational efficiency of environmental numerical models. Neural Netw. 2003, 16, 335–348. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Chalikov, D.V.; Tolman, H.L. A neural network technique to improve computational efficiency of numerical oceanic models. Ocean Model. 2002, 4, 363–383. [Google Scholar] [CrossRef]
- Tolman, H.L.; Krasnopolsky, V.M.; Chalikov, D.V. Neural network approximations for nonlinear interactions in wind wave spectra: Direct mapping for wind seas in deep water. Ocean Model. 2005, 8, 253–278. [Google Scholar] [CrossRef]
- Hsieh, W. Machine Learning in the Enviromental Sciences; Cambridge University Press: Cambridge, UK, 2009; p. 349. [Google Scholar]
- Fourrier, M.; Coppola, L.; Claustre, H.; D’Ortenzio, F.; Sauzède, R.; Gattuso, J.P. A Regional Neural Network Approach to Estimate Water-Column Nutrient Concentrations and Carbonate System Variables in the Mediterranean Sea: CANYON-MED. Front. Mar. Sci. 2020, 7, 620. [Google Scholar] [CrossRef]
- Béjaoui, B.; Ottaviani, E.; Barelli, E.; Ziadi, B.; Dhib, A.; Lavoie, M.; Gianluca, C.; Turki, S.; Solidoro, C.; Aleya, L. Machine learning predictions of trophic status indicators and plankton dynamic in coastal lagoons. Ecol. Indic. 2018, 95, 765–774. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Cecilia, J.M.; Pérez-Sánchez, J. Using machine-learning algorithms for eutrophication modeling: Case study of mar menor lagoon (spain). Int. J. Environ. Res. Public Health 2020, 17, 1189. [Google Scholar] [CrossRef] [Green Version]
- Virtanen, E.A.; Norkko, A.; Nyström Sandman, A.; Viitasalo, M. Identifying areas prone to coastal hypoxia - The role of topography. Biogeosciences 2019, 16, 3183–3195. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Shang, X.; Dahlgren, R.A.; Zhang, M. Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of Wen-Rui Tang River, China. Environ. Sci. Pollut. Res. 2017, 24, 16062–16076. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.J.; Barbero, L.; Pierrot, D. A machine learning approach to estimate surface ocean pCO2 from satellite measurements. Remote Sens. Environ. 2019, 228, 203–226. [Google Scholar] [CrossRef]
- Weber, T.; Wiseman, N.A.; Kock, A. Global ocean methane emissions dominated by shallow coastal waters. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Shen, J.; Du, J. A Machine-Learning-Based Model for Water Quality in Coastal Waters, Taking Dissolved Oxygen and Hypoxia in Chesapeake Bay as an Example. Water Resour. Res. 2020, 56, e2020WR027227. [Google Scholar] [CrossRef]
- Booth, J.A.T.; McPhee-Shaw, E.E.; Chua, P.; Kingsley, E.; Denny, M.; Phillips, R.; Bograd, S.J.; Zeidberg, L.D.; Gilly, W.F. Natural intrusions of hypoxic, low pH water into nearshore marine environments on the California coast. Cont. Shelf Res. 2012, 45, 108–115. [Google Scholar] [CrossRef]
- Ryan, J.P.; Gower, J.F.; King, S.A.; Bissett, W.P.; Fischer, A.M.; Kudela, R.M.; Kolber, Z.; Mazzillo, F.; Rienecker, E.V.; Chavez, F.P. A coastal ocean extreme bloom incubator. Geophys. Res. Lett. 2008, 35, 4–8. [Google Scholar] [CrossRef]
- Walter, R.K.; Stastna, M.; Woodson, C.B.; Monismith, S.G. Observations of nonlinear internal waves at a persistent coastal upwelling front. Cont. Shelf Res. 2016, 117, 100–117. [Google Scholar] [CrossRef] [Green Version]
- Walter, R.K.; Reid, E.C.; Davis, K.A.; Armenta, K.J.; Merhoff, K.; Nidzieko, N.J. Local diurnal wind-driven variability and upwelling in a small coastal embayment. J. Geophys. Res. Ocean. 2017, 122, 955–972. [Google Scholar] [CrossRef]
- Walter, R.K.; Armenta, K.J.; Shearer, B.; Robbins, I.; Steinbeck, J. Coastal upwelling seasonality and variability of temperature and chlorophyll in a small coastal embayment. Cont. Shelf Res. 2018, 154, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Walter, R.K.; Phelan, P.J. Internal bore seasonality and tidal pumping of subthermocline waters at the head of the Monterey submarine canyon. Cont. Shelf Res. 2016, 116, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Barth, A.; Walter, R.K.; Robbins, I.; Pasulka, A. Seasonal and interannual variability of phytoplankton abundance and community composition on the Central Coast of California. Mar. Ecol. Prog. Ser. 2020, 637, 29–43. [Google Scholar] [CrossRef]
- Largier, J.L. Upwelling Bays: How Coastal Upwelling Controls Circulation, Habitat, and Productivity in Bays. Annu. Rev. Mar. Sci. 2020, 12, 415–447. [Google Scholar] [CrossRef] [PubMed]
- Walter, R.K.; Woodson, C.B.; Leary, P.R.; Monismith, S.G. Connecting wind-driven upwelling and offshore stratification to nearshore internal bores and oxygen variability. J. Geophys. Res. Ocean. 2014, 119, 3517–3534. [Google Scholar] [CrossRef] [Green Version]
- NDBC buoy 46011. 2020. Available online: https://www.ndbc.noaa.gov/station_page.php?station=46011 (accessed on 1 September 2020).
- Large, W.G.; Pond, S. Open Ocean Momentum Flux Measurements in Moderate to Strong Winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef] [Green Version]
- Cavazos, T.; Comrie, A.C.; Liverman, D.M. Intraseasonal variability associated with wet monsoons in southeast Arizona. J. Clim. 2002, 15, 2477–2490. [Google Scholar] [CrossRef]
- Ahmad, H. Machine learning applications in oceanography. Aquat. Res. 2016, 2, 161–169. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm Margin for Optimal Classifiers. In Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Hands-On Machine Learning with R. Random For. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Muller, A.C.; Muller, D.L. Forecasting future estuarine hypoxia using a wavelet based neural network model. Ocean Model. 2015, 96, 314–323. [Google Scholar] [CrossRef]
- Ross, A.C.; Stock, C.A. An assessment of the predictability of column minimum dissolved oxygen concentrations in Chesapeake Bay using a machine learning model. Estuarine Coast. Shelf Sci. 2019, 221, 53–65. [Google Scholar] [CrossRef]







| RFR | Offshore | Nearshore |
|---|---|---|
| n_estimators (trees) | 400 | 400 |
| criterion | mse | mse |
| max_features | log2 | log2 |
| SVR | Offshore | Nearshore |
|---|---|---|
| Kernel | RBF | RBF |
| C | 1000 | 100 |
| 0.20 | 0.20 | |
| 0.0031 | 0.019 |
| RFR | SVR | |
|---|---|---|
| R2 | 0.997 | 0.986 |
| mae [mg/L] | 0.044 | 0.089 |
| mse [mg2/L2] | 0.007 | 0.045 |
| Train: | Self | OS | MB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Predict: | OS | SB | NB | MB | SB | NB | MB | SB | NB |
| R2 | 0.997 | 0.993 | 0.995 | 0.990 | 0.426 | 0.567 | 0.554 | 0.701 | 0.438 |
| mae [mg/L] | 0.027 | 0.071 | 0.040 | 0.080 | 0.857 | 0.493 | 0.676 | 0.600 | 0.632 |
| mse [mg2/L2] | 0.002 | 0.015 | 0.005 | 0.020 | 1.351 | 0.509 | 0.913 | 0.704 | 0.661 |
| RFR | SVR | |
|---|---|---|
| R2 | 0.987 | 0.946 |
| mae [mg/L] | 0.076 | 0.182 |
| mse [mg2/L2] | 0.022 | 0.091 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valera, M.; Walter, R.K.; Bailey, B.A.; Castillo, J.E. Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment. J. Mar. Sci. Eng. 2020, 8, 1007. https://doi.org/10.3390/jmse8121007
Valera M, Walter RK, Bailey BA, Castillo JE. Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment. Journal of Marine Science and Engineering. 2020; 8(12):1007. https://doi.org/10.3390/jmse8121007
Chicago/Turabian StyleValera, Manuel, Ryan K. Walter, Barbara A. Bailey, and Jose E. Castillo. 2020. "Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment" Journal of Marine Science and Engineering 8, no. 12: 1007. https://doi.org/10.3390/jmse8121007
APA StyleValera, M., Walter, R. K., Bailey, B. A., & Castillo, J. E. (2020). Machine Learning Based Predictions of Dissolved Oxygen in a Small Coastal Embayment. Journal of Marine Science and Engineering, 8(12), 1007. https://doi.org/10.3390/jmse8121007






